Introduction

Coal mining inevitably causes deformation and failure of the roof and floor strata of the coal seam. Mining–induced fractures serve as the primary channels for the migration of groundwater, gas, slurry, and other substances. Dynamic coal and rock disasters, such as impact ground pressure, water inrush, sandburst, air leakage in fractured roof strata, coal and gas outbursts, CO2 geological storage, and ecological degradation in vulnerable areas, are closely related to mining–induced fractures. With the shift of the coal mining industry to deeper and western regions, the severity of coal and rock dynamic disasters has intensified. Especially in the weakly cemented soft rock stratum, the strength is low and the deformation is large1. Taking roof water hazards as an example, significant water hazards have been observed in Jurassic coal seams in regions such as the Yuanyanghu, Majiawan, Jijia Well, and Wangwa mining areas in Ningxia, the Yushenfu and Huanglongbinchang mining areas in Shaanxi, the Shanghai Temple mining area in Inner Mongolia, and the Dannanhu mining area in Xinjiang, where some mines face production difficulties or even closure. The “14th Five–Year National Safety Production Plan” calls for the implementation of proactive and precise management of major disasters such as impact ground pressure, coal and gas outbursts, and water hazards. Understanding the deformation and failure patterns of mining strata is fundamental for the proactive prevention and control of coal and rock dynamic disasters, particularly mine water hazards2.

Currently, the majority of criteria for mining–induced strata failure are based on elastoplastic strength criteria, which require experimental measurement of strain or displacement, followed by stress calculation using constitutive relations. These criteria assumed that hard strata are difficult to fail due to their higher strength, while softer strata are more prone to failure due to their lower strength. However, this contradicts findings in the “Regulations on the Retention of Coal Pillars in Buildings, Water Bodies, Railways, and Major Shafts” that hard overlying strata with more developed fractures are more prone to failure. Furthermore, the caving of overburden in mining areas results in exceeding critical stress limits (far greater than the critical stress value), which directly impacts the effectiveness of the strength criteria. We counted the theoretical calculation and measured values of the water–conducting fractures zone in 26 western coal mines. By comparison, it was found that the measured values are generally larger, with deviation rates reaching as high as 373%, and more than half of the mines exhibit a fracture–to–mining ratio greater than 20, resulting in excessive development of water–conducting fractures (Fig. 1). Additionally, traditional empirical formulas suggested that mining height is a significant factor in strata failure. However, elastoplastic mechanics cannot explain this, as even large mining heights form spaces that are relatively limited compared to the thickness of the coal seam’s overburden, and the deformation caused by mining is inherently limited3. It is only when the strata deform to a certain extent that failure occurs4. Thus, the question arises: Can deformation data be directly used to establish criteria for mining–induced strata failure in coal seams?

Fig. 1
figure 1

Comparison of theoretical and measured values of water–conducting fractures and statistics of fracture–to–mining ratios.

Full size image

Rocks (masses) have a certain deformation capacity. In the field of coal seam overburden failure, the classic “cantilever beam hypothesis” posits that the bending deformation of the beam allows the “cantilever” structure to bear load5. In recent years, scholars have developed equations for the bending and subsidence deflection of mining–induced overburden6, the mechanical, hydraulic and crack propagation properties of red sandstone samples under the bending–splitting deformation were investigated by laboratorial7, and proposed a method for identifying mining–induced overburden “vertical three–zone” theory based on bending deformation8, which still relies on strength failure criteria. Some scholars have also revised the strength criterion9. However, strength failure criteria have significant limitations. The coordinated deformation of rock masses is a fundamental assumption in elastic mechanics, whereas deep rock masses often exhibit non–coordinated deformation, with shape deformation playing a primary role in rock failure compared to volumetric deformation. Empirical formulas are used to calculate the peak stress corresponding to the maximum principal strain, and combined with displacement or strain data measured on–site, the stability of the rock mass can be evaluated10,11. However, the presence of stress levels complicates the calculations. Liu Baochan was among the first to apply random medium theory to study surface movement patterns in coal mines and proposed a deformation failure criterion independent of stress levels, directly using deformation data to assess the stability of the rock and soil mass12, and further applied basic surface movement parameters to the study of internal movement patterns of rock masses13. Some scholars have also proposed to analyze the maximum subsidence of rock vertical fracture and rotary instability to judge the failure of rock strata14. Since the deformation caused by mining can be predicted, using deformation data to invert for overburden failure is also feasible. By analyzing horizontal tensile deformation, mechanical properties15, lateral strain16, and subsidence17, the development and failure of mining–induced fractures in the roof and floor strata of coal seams can be assessed. It can be seen that most existing mining–induced overburden failure criteria are still based on elastoplastic strength criteria, and existing deformation–based failure criteria have not entirely freed themselves from the constraints of mechanics.

In response to the above issues, this study studies the critical value of rock failure angular displacement from the perspective of deformation. Based on the theory of elastic-plastic mechanics and fracture mechanics, this paper provides a theoretical basis for judging the deformation and failure of coal seam roof and floor strata by using the critical value of angular displacement. Through indoor test and field test, the influencing factors of lithologic deformation performance and the feasibility of using angular displacement to judge the field of rock failure are analyzed. Combined with the prevention and control of water disaster in coal mine roof and floor, the significance of rock deformation performance to analyze the failure of roof and floor strata and the law of groundwater seepage is expounded. The findings of this study have important practical significance for judging the failure of mining strata, analyzing the movement law of mining groundwater, and calculating the depth of water–conducting fracture zone and floor failure zone.

Methodology

Theoretical analysis

The theoretical analysis primarily employs elastoplastic mechanics and fracture mechanics theories to provide a theoretical basis for using critical angle displacement to assess strata deformation and failure.

In coal mining, the roof and floor strata of the coal seam are generally modeled as fixed rock plates. The concept of angle displacement (θ) proposed in this study refers to the change in the angle of the strata after they undergo bending deformation as a result of mining. Therefore, the concept of angle displacement in this study is analogous to the shear strain concept in elastoplastic mechanics. According to previous research, the failure of the roof and floor strata caused by mining is primarily shear failure. From the perspective of elastoplastic mechanics, the critical value of shear strain in the strata can be used as a criterion for determining whether the strata have failed.

During the mining process, the roof and floor strata of the working face undergo bending deformation due to mining–induced stresses, which further evolve into fracture propagation leading to strata failure. According to fracture mechanics’ Crack Opening Displacement (COD) theory, when the displacement at the tip of a fracture (δ) exceeds or equals its critical value (δ0), the fracture propagates18. Therefore, from the perspective of fracture mechanics, the angle displacement of the strata can be used to assess fracture propagation and failure.

Laboratory experiment

The indoor test mainly studies the influencing factors of rock deformation performance, and obtains the critical value of rock angular displacement under various conditions, which provides data support for analyzing the development sequence of rock deformation fracture and its influence on groundwater seepage law.

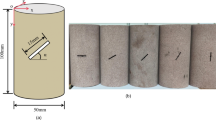
A three–point bending test was conducted using a controlled variable method to measure the critical angle displacement for deformation and failure of rock samples under different lithology, thickness, and cross–sectional area conditions. Three–point bending test is a test method used to evaluate the bending resistance of materials. By applying a vertical load in the center of the sample, the sample produces bending deformation, and the bending deformation of the sample is measured to evaluate its bending resistance, which provides a scientific basis for material selection and application. The underground natural rock core taken from the surface exploration borehole constructed in June 2024 in Majiliang Coal Mine, Zuoyun County, Datong City, Shanxi Province was selected as the research object. The core after drilling was cylindrical, so it needed to be cut into various cuboid specimens of different sizes required for the test in the processing workshop, and the specimens were numbered.

First, lithology was considered the single controlled variable, while keeping other conditions constant, to study the influence of lithology on the critical angle displacement at the moment of rock failure and to determine the critical angle displacement for different lithologies. In this set of experiments, 20 specimens with identical dimensions (120 mm × 40 mm × 30 mm) were used, including 10 sandstone specimens and 10 limestone specimens, all subjected to displacement loading via a servo machine.

Second, thickness was varied as the single controlled variable, with other conditions unchanged, to study the impact of thickness changes on the critical angle displacement at the moment of rock failure under the same lithology. In this set of experiments, the sandstone specimens were divided into two groups: the first group had dimensions of 120 mm × 40 mm × 30 mm, and the second group had dimensions of 120 mm × 40 mm × 50 mm. Only the specimen thickness (30 mm and 50 mm) was changed. The limestone specimens were grouped similarly to the sandstone specimens.

Finally, cross–sectional area was varied as the single controlled variable. The length–to–width ratio was changed while keeping other conditions constant, in order to study the effect of changes in the cross–sectional area (length–to–width ratio) on the critical angle displacement for rock failure under the same lithology. In this set of experiments, the sandstone specimens were divided into two groups: the first group had dimensions of 120 mm × 40 mm × 50 mm, and the second group had dimensions of 150 mm × 50 mm × 50 mm. Only the cross–sectional area (120 mm × 40 mm and 150 mm × 50 mm) was altered. The grouping for the limestone specimens was similar to that for the sandstone specimens19.

The equipment required for the laboratory experiments included a servo machine, three–point bending apparatus, and angle displacement sensors. The experimental principle and equipment are shown in Fig. 2. L1 is the span of the circular bar, L is the length of the specimen, b is the width of the specimen, and h is the thickness of the specimen.

Fig. 2
figure 2

Experimental setup and principle for laboratory testing.

Full size image

Angle Displacement Sensor: The angle displacement sensor used in this study has an accuracy of 0.001 °, providing precise measurements of the critical angle displacement for rock failure in this experiment. It outputs data through a 485–to–USB signal, which connects directly to a computer. The data is then processed using the test control software, allowing the experimenter to conveniently record and analyze the data.

Three–Point Bending Test Apparatus: The apparatus used in this experiment is a self–designed variable span device, enclosed with transparent organic plastic on all sides, providing a clear view of the specimen failure process.

Electro–Hydraulic Servo Testing Machine: The servo system consists of a computer, a pressure machine, and a control box.

Before testing the rock specimens, the angle displacement sensor and servo machine must be calibrated. The servo hydraulic machine controls displacement loading during the experiment, with a displacement rate set to 0.005 mm / s to minimize experimental error. The experimental process is as follows:

  1. (1)

    Instrument Calibration and Warm–up:

  2. (2)

    Preparation of Specimens: The surfaces of the specimens are polished to meet the flatness requirements and reduce experimental error.

  3. (3)

    Fixing the Specimen: The angle displacement sensor is attached to one side of the specimen, ensuring it remains stationary. The sensor is then connected to the computer, and after calibration, the sensor is checked to ensure it properly receives and stores data. The relative zero point for the angle displacement sensor is set, and the servo machine’s data is reset before the experiment begins to ensure real–time and accurate data collection, minimizing errors.

  4. (4)

    Loading and Data Recording: The WES–D1000 computer–controlled electro–hydraulic servo machine applies pressure while monitoring the loading process until the specimen fails.

  5. (5)

    Conclusion of the Experiment: The test data is saved and exported, processed, and used to plot various curves. The specimen is replaced, and the loading process is repeated.

Field test

The field test mainly verifies the feasibility of the application of rock stratum deformation performance based on angular displacement in the field of mine water disaster prevention and control through the application of angular displacement sensor in the test of floor failure zone.

The field test was conducted at the 61,601 working face of a mine in Ordos, Inner Mongolia. The coal seam floor elevation ranged from + 846.6 m to + 858.1 m, located 24 m below the ordovician limestone aquifer water level, with the head pressure of Ordovician limestone being 0.24 MPa. The floor was 44.5 m from the top of the ordovician limestone aquifer, with mudstone and sandstone as the primary strata between the coal seam and the ordovician limestone aquifer. The direct bottom was gray–black mudstone, argillaceous structure, soft, weathered and fragile, with an average thickness of 7.4 m ; the basic bottom was gray–white thick layered sandy mudstone, coarse–grained sandy structure, pore–type argillaceous cementation, with an average thickness of 11.22 m. The main focus of this test was to measure the depth of the mining–induced damage zone in the floor to prevent water inrush from the ordovician limestone aquifer.

The test method involved drilling a hole at a specific angle toward the floor of the working face. A borehole inclinometer containing angle displacement sensors was inserted into the hole, with sensors installed at fixed intervals. This setup allows the measurement of angular displacement at various depths, enabling analysis of the deformation and failure characteristics of the floor strata. The angular displacement monitoring equipment was the HZI–J101S series multi–point angular displacement monitoring system produced by Anhui Huizhou Geological Safety Research Institute Co., Ltd.

The measurement line was arranged in the transport drift of the working face, with a borehole positioned 170 m from the mining cut–off line. To ensure the measurement within the mining face, the borehole was inclined at 49 ° towards the face, with a dip angle of -42 °. The borehole was 60 m deep, with 40 m controlled depth and an 89 mm diameter. A 5 m casing was installed at the borehole opening. A total of 10 sets of angle displacement sensors were placed in the hole, with one sensor every 6 m from top to bottom. The borehole and sensor layout and field working diagram are shown in Fig. 3.

Fig. 3
figure 3

Borehole and sensor layout and field working diagram.

Full size image

The installation work was completed 220 m ahead of the stop–production line. After installation, a background value observation was conducted. Monitoring started 250 m before the stop–production line (leaving a 20 m pre–reserved distance) and continued to the stop–production line. Daily observations were made along the measurement line, forming a dataset that ultimately reflected the dynamic changes of strata angle displacement over time.

Results

Analysis of mining–induced strata deformation

The deformation and failure of the roof and floor strata in coal seams are caused by underground mining activities. From the perspective of spatial compensation, coal mining can be seen as the extraction of a limited thin layer from a massive three–dimensional geological body. The surrounding strata must inevitably compensate for the excavated space or tend to do so. This is most clearly observed in the downward movement of the roof of the working face, causing bending, fracturing, and collapse, while the floor of the working face tends to move upward and deform (commonly referred to as “floor heave”)20. Since the movement and deformation of the strata are aimed at compensating for the space being mined, the strata’s movement occurs progressively from the coal seam toward the periphery3. Taking the movement of the coal seam roof as an example, if the deformation of a certain layer of the roof is SL, and the deformation of the layer above it is SU, according to the theory of layered elastic mechanics21, SU≤SL. The roof of the working face exhibits vertical displacement downward, and angle displacement. Therefore, the angle displacement of the upper layer is smaller than that of the lower layer, i.e., θU ≤ θL. When the angle displacement is less than the deformation limit of the strata, the strata do not break. However, when the angle displacement exceeds the deformation limit, the strata fail.

The following analysis is conducted from the perspectives of elastoplastic mechanics and fracture mechanics:

Elastoplastic mechanics analysis

According to the constitutive relations in elastoplastic mechanics, shear strain (\({\gamma _{xy}}\)) and shear stress (\({\tau _{xy}}\)) are related as follows:

$${\gamma _{xy}}=\frac{1}{G}{\tau _{xy}}$$
(1)

where G is the rigidity modulus, determined by the elastic modulus E and Poisson’s ratio µ, with the relationship:

$$G=\frac{E}{{2\left( {1+\mu } \right)}}$$
(2)

Based on elastoplastic theory, when shear stress (\({\tau _{xy}}\)) reaches the shear strength (\({\tau _0}\)), the strata fail, and the critical shear strain is:

$${\lambda _0}=\frac{1}{G}{\tau _0}=\frac{{2\left( {1+\mu } \right)}}{E}$$
(3)

Since shear strain and angle displacement are conceptually consistent, the critical angle displacement (θ0) for strata failure is:

$${\theta _0}=\frac{{2\left( {1+\mu } \right)}}{E}$$
(4)

The parameters in this equation can be obtained through rock mechanics testing, allowing for convenient calculation of the critical angle displacement of the strata. When the angle displacement exceeds this critical value, strata failure occurs.

Fracture mechanics analysis

According to fracture mechanics theory, assuming there is a micro–crack in the roof or floor strata, after mining, the strata will move toward the mined–out space (as shown in Fig. 4). The angle displacement is θ, and the crack opens. Assuming the crack tip moves from the red dashed line to the blue solid line, the crack angle is α, and the crack growth segment is \({r_y}\). The crack opening displacement can be expressed as:

$$\delta ={r_y}\sin \frac{\alpha }{2}$$
(5)
Fig. 4
figure 4

Relationship diagram between angular displacement and fracture angle of coal seam roof and floor strata.

Full size image

According to elastic mechanics and fracture geometry, in the above formula \(\frac{\alpha }{2}=\mu \theta\), and the formula (5) can be further deformed into the following formula :

$$\theta =\frac{{\arcsin \frac{\delta }{{{r_y}}}}}{\mu }$$
(6)

When the crack tip opening displacement is greater than or equal to its critical value, the crack expands, and the angular displacement (\(\theta\)) is also in a critical state, that is :

$${\theta _0}=\frac{{\arcsin \frac{{{\delta _0}}}{{{r_y}}}}}{\mu }$$
(7)

When the angle displacement of the roof and floor strata in the working face exceeds the critical value, the strata will develop fractures, forming a mining–induced damage zone.

From the above analysis, it can be seen that it is feasible to study the deformation performance of rock strata by angular displacement and then determine the deformation and failure of rock strata.

Experimental results on strata deformation behavior

Experimental results for different lithology specimens

In this set of experiments, a total of 20 specimens with identical dimensions (120 mm × 40 mm × 30 mm) were tested, including 10 sandstone specimens and 10 limestone specimens. A servo machine was used to apply displacement loading to the specimens. By synchronizing the data obtained from the angle displacement sensors with that from the servo machine’s control system, it was found that, at the moment of failure, the servo machine exhibited a clear unloading state. The corresponding angle displacement value at this point is considered the critical angle displacement for rock failure. The load and angle displacement values corresponding to rock failure are shown in Table 1.

Table 1 Statistical table of angular displacement test results of different lithology specimens.
Full size table

Experimental results for specimens with different thicknesses

In this set of experiments, the sandstone specimens were divided into two groups: the first group had dimensions of 120 mm × 40 mm × 30 mm, and the second group had dimensions of 120 mm × 40 mm × 50 mm, with only the thickness of the specimens being varied (30 mm and 50 mm). The limestone specimens were grouped in the same manner as the sandstone specimens. The experimental results are shown in Table 2.

From the table, it can be observed that for the 50 mm thick sandstone specimens, the critical angle displacement ranged from 0.0410 ° to 0.0590 °, with an average value of 0.0516 °; for the 30 mm thick sandstone specimens, the critical angle displacement ranged from 0.0380 ° to 0.0750 °, with an average value of 0.0552 °. For the 50 mm thick limestone specimens, the critical angle displacement ranged from 0.0690 ° to 0.0840 °, with an average value of 0.0774 °; for the 30 mm thick limestone specimens, the critical angle displacement ranged from 0.0460 ° to 0.1050 °, with an average value of 0.0818 °.

Table 2 Statistical table of angular displacement test results of specimens with different thickness.
Full size table

Experimental results for specimens with different cross–sectional areas

In this set of experiments, the sandstone specimens were divided into two groups: the first group had dimensions of 120 mm × 40 mm × 50 mm, and the second group had dimensions of 150 mm × 50 mm × 50 mm, with only the cross–sectional area of the specimens being varied (120 mm × 40 mm and 150 mm × 50 mm). The limestone specimens were grouped in the same manner as the sandstone specimens. The experimental results are shown in Table 3.

Table 3 Statistical table of angular displacement test results of specimens with different cross–sectional areas.
Full size table

From the analysis of the above test results, it can be seen that the rock strata with different lithology, thickness and cross-sectional area have different deformation properties, which is also the basis of the difference in deformation and failure of roof and floor rock strata, and then determines the development sequence of cracks and the law of groundwater seepage. The above test results also provide a basis for field testing.

Field monitoring results of strata deformation

The field monitoring data were selected for analysis based on the results from the 3# and 5# angle displacement sensors, corresponding to the bottom plate mining–induced damage depth between 12 m and 20 m below the floor. The monitoring data are shown in Fig. 5. At the 12 m to 20 m depth, the lithology is sandstone. From the previous experimental results, the critical angle displacement for sandstone is between 0.0552 °. According to the mining face recovery records, by the 30th day of monitoring, the working face had advanced to the borehole ___location. Both the 3# and 4# angle displacement sensors exceeded 0.0552 °. However, the 5# angle displacement sensor had not exceeded 0.0552 °, and by the 33rd day of monitoring, the working face completed recovery. On the 46th day of monitoring, the 5# angle displacement sensor data still had not exceeded 0.0552 °. This indicates that the sandstone layer between the 4# and 5# sensors had failed, with the vertical depth of the 4# angle displacement sensor being 16 m. Therefore, the depth of damage to the bottom plate was 16 m. The field test results and laboratory test results can confirm each other.

Fig. 5
figure 5

Statistical diagram of field test results of rock stratum angular displacement.

Full size image

Discussion

Analysis of factors affecting strata deformation behavior

According to the above theoretical analysis, laboratory test and field test, it is feasible to judge the deformation and failure of rock strata by the critical value of motion angular displacement, but there are obvious differences in the deformation performance of each rock stratum, which is also affected by many factors.

In general, limestone has greater strength than sandstone, and the results of the indoor ultimate load tests are more reliable. The average ultimate load for sandstone is 5307.886 N, while for limestone, it is 7434.053 N. As shown in Fig. 6, lithology has a significant effect on the critical angle displacement of the strata. The critical angle displacement for sandstone ranges from 0.0380 ° to 0.0750 °, with an average value of 0.0552 °, while for limestone, it ranges from 0.0460 ° to 0.1050 °, with an average value of 0.0818 °. Overall, the critical angle displacement and its fluctuation range for sandstone are smaller than for limestone, and there is a positive correlation between the critical angle displacement and the strength of the strata.

Furthermore, by selecting the limit load corresponding to the critical value of the minimum angular displacement of sandstone and limestone to calculate the angular displacement of rock strata under unit load, it was found that the angle displacement for sandstone under unit load is 5.45 × 10− 6 ° / N, while for limestone, it is 4.41 × 10− 6 ° / N. This analysis shows that stronger limestone can withstand higher loads, resulting in a larger critical angle displacement, making it more resistant to failure. In contrast, sandstone, with lower strength, exhibits larger angle displacements under the same unit load, leading to greater deformation.

Fig. 6
figure 6

Comparison of critical angle displacement values for strata with different lithologies.

Full size image

Based on the three–point bending test results for specimens with different thicknesses, the critical value of angular displacement of 50 mm thick sandstone specimens ranged from 0.0410 ° to 0.0590 ° with an average of 0.0516 °, the critical value of angular displacement of 30 mm thick sandstone specimens ranged from 0.0380 ° to 0.0750 ° with an average of 0.0552 °, the critical value of angular displacement of 50 mm thick limestone specimens ranged from 0.0690 ° to 0.0840 ° with an average of 0.0774 °, and the critical value of angular displacement of 30 mm thick limestone specimens ranged from 0.0460 ° to 0.1050 ° with an average of 0.0818 °.

It can be seen that the natural defects within the rock specimens result in a significant difference between the maximum and minimum values of the critical angle displacement, as shown in Fig. 7. Additionally, as the specimen thickness increases, the range between the maximum and minimum critical values narrows. For example, the critical angle displacement range for the 30 mm thick sandstone specimens was 0.0380 ° to 0.0750 °, while for the 50 mm thick specimens, it ranged from 0.0410 ° to 0.0590 °. This indicates that the thinner the strata, the larger the possible deformation.

Fig. 7
figure 7

Comparison of critical angle displacement values for strata with different thicknesses.

Full size image

Based on the three–point bending test results for specimens with different cross–sectional areas, the critical angle displacement range for the 150 mm × 50 mm sandstone specimens was 0.0420 ° to 0.0570 °, with an average value of 0.0483 °. For the 120 mm × 40 mm sandstone specimens, the critical angle displacement range was 0.0410 ° to 0.0590 °, with an average value of 0.0516 °. The critical angle displacement range for the 150 mm × 50 mm limestone specimens was 0.0620 ° to 0.0840 °, with an average value of 0.0720 °, while for the 120 mm × 40 mm limestone specimens, the critical angle displacement range was 0.0690 ° to 0.0840 °, with an average value of 0.0774 °, as shown in Fig. 8.

From this, it can be seen that as the cross–sectional area of the strata increases, the critical angle displacement decreases. This suggests that the larger the thickness and width of the strata, the smaller the ability of the strata to deform.

Fig. 8
figure 8

Comparison of critical angle displacement values for strata with different cross–sectional areas.

Full size image

Significance of strata deformation behavior for mine water hazard prevention and control

As analyzed earlier, the critical angle displacement values differ for strata with different lithologies, which allows for the use of the ultimate values under unit stress as criteria for assessing strata deformation and failure. In the field of mine water hazard prevention, fractures caused by strata deformation and failure serve as the primary channels for groundwater seepage. From a spatial perspective, these can be classified as mining–induced water–conducting fractures in the roof (roof collapse zone and fracture zone, where strata bend without forming fractures, termed the bending zone) and mining–induced water–conducting fractures in the floor (floor failure zone). Studying the deformation behavior of strata provides crucial evidence for the prevention and control of roof and floor water hazards in coal mines22. The specific application scenarios are mainly reflected in the control of fracture development sequence and groundwater seepage law, as well as the judgment of the development degree of mining-induced fractures.

Strata deformation behavior controls fracture development timing and seepage patterns

The depositional environment of deep rock masses dictates their lamination and interlayer compositional differences, leading to variations in their deformation behavior. That is, the deformation under unit stress differs, and the angle displacement θi and critical angle displacement θ0 are not the same for different strata. This causes differences in the timing and dynamic characteristics of horizontal and vertical fractures formed during strata deformation and failure. The timing of mining–induced fractures determines the anisotropic nature of groundwater seepage, leading to “anisotropic seepage” behavior. The fracture development sequence determined by the deformation performance of rock strata is the basis of groundwater seepage. The mining rock strata generally produce bending deformation to produce horizontal cracks between layers. With the increase of the deformation degree of rock strata, vertical cracks are produced. However, due to the difference of deformation ability of each rock strata, the time of vertical cracks in each rock strata is different. The rock strata with poor deformation ability first produce vertical cracks, while the rock strata with strong deformation ability ( or even not ) produce vertical cracks. At the same time, with the movement of broken rock strata, the closure of cracks will occur.

Taking roof water hazards as an example, the mining causes the movement and destruction of the roof rock layer, and the groundwater flows along the fracture23, including the vertical downward or horizontal seepage from the aquifer and vertical upward “backflow” into the aquifer. This results in various forms of water hazards, such as sequential water inflow, delayed water outbursts, and backflow, as shown in Fig. 9.

When θU<θL, if θU<θ0U, θL<θ0L, the strata do not fracture, and a separation layer forms without water accumulation; if θU>θ0U, θL>θ0L, fractures form in both the upper and lower layers, and no water accumulates in the separation layer, with roof water flowing out as mining progresses; if θU>θ0U, θL<θ0L, fractures form in the upper layer, and water accumulate in the separation layer. If the lower layer fractures, a disaster occurs; if the lower layer does not fracture, the upper layer continues to sink, and the water in the separation layer backflows into the aquifer.

When θU>θL, if θU<θ0U, θU<θ0L, the strata do not fracture and no separation layer is formed, so no water is released; if θU<θ0U, θL>θ0L, fractures form in the lower layer, but no water is released; if θU>θ0U, θL>θ0L, fractures occur in both the upper and lower layers, and roof water flows out as mining progresses.

In summary, if vertical fractures develop in both the upper and lower layers, roof water will enter the working face. If only vertical fractures are developed in the upper layer and horizontal interlayer fractures form, groundwater typically remains in the interlayer fractures and is unlikely to cause disaster. In some cases, the interlayer fractures may close, leading to “backflow” into the aquifer.

Fig. 9
figure 9

Relationship between rock deformation performance and anisotropic seepage.

Full size image

Determining the degree of fracture development based on strata deformation behavior

In traditional mechanics, the critical stress value is generally used as a criterion for rock mass failure. However, after mining activities, the working face is in an overstressed state, making the stress criterion unsuitable. The space created by coal seam excavation is limited compared to the entire geological body. Therefore, using the deformation critical value to assess whether the strata in the overstressed, confined space fail is more accurate. Additionally, the deformation amount caused by mining can be determined based on the geometry of the excavated space, making it more convenient to use deformation critical values to judge strata failure3.

Taking the mining–induced damage zone of the coal seam floor as an example, during the mining process, under the action of stress release and high water pressure of the floor, one end of the bent strata is supported by the coal wall, while part of it is supported by the fallen rock from the roof of the mined–out area, as shown in Fig. 10. Let the mining height be m, the height of the fallen rock be h, the distance from the maximum deformation point to the coal wall be L0, and the distance from the mined–out area to the crack initiation point be L1. Then, the total distance from the maximum deformation point to the crack initiation point is L=L0 + L1, and the maximum deformation is S. Let the angle displacement at this point be θ, and based on the geometric relationship, θ≈S / L, From the spatial relationship of the mined–out area, it is known that S=m-(λ-1)h, where λ is the rock swelling coefficient. Based on the collapse angle relationship, L1×h1tan α, where h1 is the depth of the calculation point, and α is the collapse angle of the strata. Therefore,

$$\theta \approx \frac{{m - \left( {\lambda - 1} \right)h}}{{{L_0}+{h_1}\tan \alpha }}$$
(8)

When the angle displacement θ exceeds or equals the critical value θ0, the strata will fracture. Thus, the depth of the floor damage zone, h1, can be determined by the following equation:

$${h_1}=\frac{{m - \left( {\lambda - 1} \right)h - {L_0}{\theta _0}}}{{{\theta _0}\tan \alpha }}$$
(9)
Fig. 10
figure 10

Working face floor rock angular displacement diagram.

Full size image

Because the upper rock layer has an inhibitory effect on the angular displacement development of the lower rock layer, especially the key layer of the floor will have a significant inhibitory effect on the angular displacement development of the lower rock layer. When the upper rock stratum is destroyed, the effect of inhibiting the movement of the lower rock stratum will be obviously weakened, the upward movement of the lower rock stratum will be accelerated under the action of high water pressure of the floor, and the degree of deformation and failure will also increase, that is, the floor failure zone will increase. When the depth of the failure zone reaches the aquifer, the water inrush accident occurs in the working face24. Especially when the angular displacement value of the key stratum of the floor is greater than the critical angular displacement value of the key stratum, the depth of the floor failure zone will increase rapidly, and the water–resisting layer of the floor of the whole working face will be destroyed, and the floor water will enter the working face along the horizontal and vertical fracture network25. According to the theory, the field measurement was carried out in the previous article, and the specific depth of the floor failure zone was obtained through the angular displacement, which provided a key basis for the prevention and control of the floor water disaster.

Conclusion

  1. (1)

    The critical value of rock angular displacement was closely related to lithology. The critical value of angular displacement of rock strata with high strength was larger, the critical value of angular displacement of sandstone was 0.0552 ° on average, and that of limestone was 0.0818 °. The angular displacement of rock strata with small strength under unit load was larger, resulting in greater deformation. The angular displacement of sandstone under unit load was 5.45 × 10− 6 ° / N, and that of limestone was 4.41 × 10− 6 ° / N.

  2. (2)

    The critical values of angular displacement of rock strata with large thickness and cross–sectional area were small. The critical values of angular displacement of sandstone and limestone with thickness of 50 mm were 0.0516 ° and 0.0774 °, respectively, which were less than the critical values of angular displacement of 30 mm with thickness of 0.0552 ° and 0.0818 °. The critical values of angular displacement of sandstone and limestone with a cross–sectional area of 150 mm × 50 mm were 0.0483 ° and 0.0720 °, respectively, which are less than the critical values of angular displacement of 120 mm × 40 mm of 0.0516 ° and 0.0774 °.

  3. (3)

    The angle displacement θi and critical angle displacement θ0 under unit stress differ for different rocks, leading to differences in the timing and dynamic characteristics of horizontal and vertical fractures generated during strata deformation and failure. The timing of mining–induced fractures determines the anisotropy of groundwater seepage, leading to “anisotropic seepage” behavior. This manifests as different water hazard forms such as sequential water inflow, delayed water outbursts, and backflow.

  4. (4)

    The degree of fracture development can be determined by the deformation performance of rock strata, and the development range of mining failure zone can be calculated. The critical value of angular displacement of different rock strata was different. The limit value under the action of unit stress was used as the criterion for judging the deformation and failure of rock strata. The failure depth of the floor of the working face was 16 m directly obtained by the angular displacement data, which was more convenient than the traditional mechanical criterion.