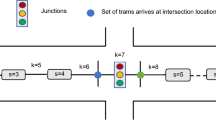
Abstract
Energy-efficient operation is an effective approach for diminishing the operational expenses and carbon emissions of the tram system. Tram operation strategies and signal priority play a vital role in energy-efficient train timetable optimization. However, the impact of trams on road traffic efficiency has limited consideration in traditional optimization methods. This paper develops a bi-objective mixed-integer linear programming (MILP) model incorporating multi-signal priority strategies (e.g., active signal priority strategy, no-signal priority strategy) and road traffic flow to obtain an energy-saving operation scheme. First, the signal priority strategy that trams should adopt based on the intersection traffic flow is determined to improve road traffic efficiency. Second, the speed profiles and stop plans of trams at the intersections are considered to reduce energy consumption and improve passenger comfort. The bi-objective MILP model can be solved by a commercial solver like CPLEX. A variety of comparative experiments using Lijiang Tram Line 1 in China are able to verify the effectiveness of the model. Compared with the timetable obtained by the active signal priority strategy (initial timetable), the proposed model could achieve the total energy consumption reduced by 5.01%, passenger comfort improved by 8.23%, and the number of vehicles delayed reduced by 27.21%.
Similar content being viewed by others
Introduction
The tram system is prevalent for daily commuting in large and medium-sized cities due to its safety, comfort, efficiency, energy-saving, and punctuality. However, unlike the subway system, tram systems typically operate with semi-independent road rights1. Therefore, the efficiency of the tram operations (e.g., travel time, energy consumption) is influenced by the signal lights and the signal priority strategies at intersections. For instance, the tram must stop at intersections when the signal light is red, increasing the travel time and energy consumption. Moreover, different signal priority strategies will influence traffic efficiency and energy consumption in the road network2. For example, the active signal priority strategy (ASPS) could provide a right-of-way for trams to ensure the tram operation efficiency, but this will decrease the efficiency of road traffic at intersections. Therefore, the decision-making of signal priority strategies and signal lights is essential for tram energy-saving operations and traffic efficiency.
The signal priority strategies should be considered to reduce the conflicts between tram operations and road traffic. Common signal priority strategies comprise active signal priority strategy (ASPS) and no-signal priority strategy (NSPS)2. The former guarantees the continuous of trams through intersections, maintains a high operation efficiency, as well as avoids unnecessary energy consumption (e.g., tram start-stops). So, this strategy is often used on trams in large and medium-sized cities. However, the ASPS substantially impacts road traffic flow, and trams with ASPS can amplify social negative utility, especially at intersections with large traffic volumes3,4. Conversely, the NSPS may require trams to stop at red lights, negatively affecting energy-efficient operations and the comfort of the tram system. However, it can reduce the impact of trams on road traffic. Hence, optimizing signal priority strategies is crucial for achieving energy-efficient tram operations and maintaining the effectiveness of road traffic.
To effectively balance the demand between road traffic efficiency and energy-saving tram operation, this study proposes a multi-signal priority strategy (MSPS). The most appropriate strategy for the tram is determined by the real-time road traffic at the intersection. The tram is granted priority access at intersections with small road traffic flow by utilizing an ASPS to reduce the energy consumption caused by the tram start-stops. Then, the energy-saving operation of the tram system is achieved. Also, trams follow the NSPS at intersections with large road traffic flow, adhering to signal light rules to enhance road traffic efficiency. Moreover, we construct the tram speed trajectory optimization constraints to consider passenger comfort and avoid frequent stopping sites when the tram adopts NSPS. Our approach is to ensure that trams can consistently pass through intersections when the signal light is green by optimizing the speed trajectory of the tram at intervals, then reducing the energy consumption associated with tram start-stops and enhancing passenger comfort.
The structure is outlined as follows. Chapter 2 is a literature review, and Chap. 3 delves into analyzing different signal priority strategies and their impact on tram operations at intersections. In Chap. 4, a MILP model for trams is proposed based on multi-signal priority strategies, and the weighted-sum method is employed to solve the bi-objective model. Chapter 5 conducts computational experiments to showcase the effectiveness of the model. Chapter 6 serves as the concluding section of this paper, offering a concise summary of the key findings.
Literature review
The problem of train energy-saving operations has been widely studied in recent years. The studies have focused on optimizing train operations to achieve energy efficiency5,6,7,8 by various means, including optimizing interval running times9,10,11, optimizing single-train operating strategies12,13, and coordinating multi-train operations14,15. A common feature among these studies is their emphasis on optimizing the train speed profile, which is considered a key method for achieving energy-saving operations in rail transit systems16. Anh et al.17 effectively reduced energy consumption during train operation by determining the optimal running speed profiles for trains. Sicre et al.18 provided a model that optimizes the energy consumption of single manually driven trains between stations. They assigned redundant time to the running time of each interval to minimize overall energy consumption. Udriste et al.19 obtained the optimal train operation trajectory and realized energy-saving operation by constructing the train dynamics equation and solving the bi-control problem. To further realize the energy-saving operation between multiple trains, Shang et al.20 proposed an energy-efficient inner-outer model by considering the travel time, speed, and coordinating the various train operations to obtain train energy-saving operations. Su et al.21 proposed a comprehensive operational approach based on driving strategies between trains. Optimizing the speed profiles improved the trains’ running efficiency and energy utilization.
These studies have been relatively mature in high-speed railway and metro systems, but the related research in tram systems needs to be improved. Based on the MAXBAND model, Jeong et al.22 proposed the TRAMBAND model to optimize signal timing and tram dwell time to enable trams to pass through intersections without stopping, thereby improving operational efficiency. In contrast, Zhou et al.23 introduced an arterial signal coordination optimization model for trams based on the Asymmetrical Multi-BAND method. This model incorporates three constraints: dwell time, active signal priority, and minimum bandwidth value. The BAM-TRAMBAND model was proposed based on this foundation to reduce tram travel time and enhance the operational efficiency of other vehicles. Unlike optimizing signal timing, Zhang et al.24 proposed a timetable optimization method for trams based on an active signal priority strategy. By optimizing both running and dwell times to minimize total travel time, dwell time increments, and the negative impacts of the signal priority strategy. Ji et al.25 presented a multi-period tram timetable optimization method that simultaneously adjusts tram spatiotemporal trajectories and traffic signal timings. This method effectively reduces tram travel time and the number of stops at intersections. However, none of these studies consider energy-saving in their models. Some energy-saving optimization models of the tram system have been improved by combining the speed profile optimization method in the metro system. Yan et al.26 constructed an energy-saving model based on the tram operation stage. They optimized speed profiles while focusing on the energy consumption distribution with the stage of the traction and braking. Similarly, based on this research, Xiao et al.27 explored an energy-efficient approach for trams incorporating the disjunctive time constraint of traffic lights. The tram’s speed profile was adjusted to achieve energy savings by introducing constraints on the traffic signal timing for multiple feasible green time windows. Xu et al.28 additionally examined the signal priority mode to build an energy-saving model. This model effectively addressed the optimization of speed profiles and operational energy consumption at specific time intervals while considering signal constraints, resulting in further implementation of energy-saving operations.
Due to the swift expansion of rail transit, the single-objective function of energy-saving operation research has yet to satisfy the demand for train operations. Researchers considered the comfort and safety constraints based on speed profile optimization to improve train service satisfaction. Xing et al.29 considered the tram operation safety and comfort constraints to develop an optimization model for tram energy consumption. Experiments were conducted based on the Guangzhou Haizhu tram in China, and the model showcased its effectiveness in significantly reducing tram energy consumption during operations. Caramia et al.30 considered train dynamics and comfort to establish a speed profile optimization method. Su et al.31 introduced a model to find the optimal train-driving strategies. The objectives were to minimize energy consumption during train operations while considering factors such as travel time, safety, and passenger comfort. Hasanzadeh et al.32 optimized the train timetable considering the line slope and train speed limit, as well as considering the constraints of train travel time and passenger comfort, finally achieving the energy-saving operation. Huang et al.33 considered the energy-saving operation and passenger demand and then constructed a bi-objective model while improving the service quality level. According to the line conditions, Zhang et al.34 and Zheng et al.35 characterized the process of train operation as a bi-objective optimization model. They optimized the stop plan and the running time to obtain an energy-efficient operation scheme while meeting passenger travel demand. These methods achieved the goal of energy-saving train operation, but the studies are based on the ASPS. During the study, they ignored the characteristics of trams sharing road rights at intersections with road traffic. These studies default to the fact that trams in the section (between station and station) do not have parking or running with low-speed limits, which is contrary to reality.
In fact, the decision-making of signal priority strategies not only affects the road traffic efficiency but also affects the tram travel time, energy consumption, and comfort. Some researchers have considered tram operation optimization more deeply to make the research results applicable to the tram system. Luan et al.36 argued that train driving strategies are closely related to train timetables, and collaborative optimization can better achieve train energy-saving operations. Generally, the decrease in total travel time is associated with increased tram speed and higher energy consumption within a fixed time interval37,38. The ASPS or NSPS is adopted by trams also play a crucial role in energy consumption and overall traffic flow. Trams are different from subways: semi-independent road rights and sharing road rights with road traffic at intersections are their most prominent features. The tram is restricted by the signal lights when passing through the intersection. So, the influence of the signal priority strategies on the driving strategy of the tram should also be considered in the research of energy-saving optimization. Some scholars have considered the tram rights-of-way and signal priority strategy in the field of tram timetable optimization. Zhou et al.39 and Zhang et al.40 introduced tailored tram timetable optimization models to NSPS and ASPS perspectives. These models were intricately designed to address tram timetable optimization across different signal priority control regulations. Its goal was to achieve energy-saving operations while decreasing tram travel time and improving tram operation service quality. Shang et al.41 developed a comprehensive internal and external double-layer optimization model that integrated advanced information technologies such as deep reinforcement learning, cloud computing, and edge computing. This model addressed both single-train and multi-train energy-saving timetable design, leading to a notable reduction in train operation energy consumption.
Previous studies have focused on achieving energy-saving operations by optimizing the train operation process, especially considering the optimization of interval running time and speed profile. While demonstrating the efficiency of optimizing speed profiles in reducing tram energy consumption, these studies offer valuable insights for this paper and serve as pertinent references. Although these models demonstrate excellent performance in tram system, they often overlook the interaction between trams and road traffic, particularly the impact of signal priority strategies at intersections on tram operation efficiency (e.g., train energy consumption, train travel time, and passenger comfort). Thus, a comprehensive model needs to be improved to obtain the optimal energy-saving effects of the tram system and improve the road traffic efficiency at intersections. This paper integrates line conditions and intersections, employing a speed profile optimization model to solve the speed profile under different speed limit conditions and stop plans to obtain a speed profile set. Subsequently, combining the signal circle and speed profile set, a tram energy-saving operation optimization model under multi-signal priority strategies (MSPS) is proposed to realize the energy-saving tram operation.
We propose a novel MILP bi-objective model for the problem of energy-efficient timetable optimization. Unlike previous energy-saving timetable optimization research, the characteristics of the tram system with shared road rights at intersections are considered to reduce the impact on road traffic and ensure the operational efficiency of trams. Thus, the proposed model has the following three advantages.
-
(1)
The MSPS is proposed to improve road traffic efficiency. Existing research primarily focuses on the ASPS and ignores its impact on road traffic flow. The model considers the count of delayed vehicles at intersections to minimize the effect of tram operations on road traffic.
-
(2)
The model could optimize the train’s arrival and departure time at both stations and intersections while minimizing the total travel time to ensure the tram’s operating efficiency. Moreover, the tram interval running time is variable; it is determined by the train speed trajectories according to the signal cycle and the stop plan, with the objective of ensuring passenger comfort and reducing energy consumption.
-
(3)
Our extensive experimentation illustrates the tradeoffs between total travel time, energy consumption, passenger comfort, and road traffic delays. The results demonstrate a significant reduction in energy consumption (5.01%) and delayed vehicles (27.21%), coupled with an improvement in passenger comfort (8.23%).
Problem statement
The process of tram operation is affected by signal priority strategies and signal lights, while these effects can be presented on the speed profile. Figure 1 describes the operation scenario of a tram passing through two intersections between two stations. We consider two signal priority strategies: the blue and red lines represent the tram operation scenarios under the multi-signal priority strategies (MSPS) and the active signal priority strategy (ASPS), respectively. The ASPS can ensure that trams pass through intersections on priority. Accordingly, when the tram selects ASPS\(\:\:({\beta\:}_{c,i}=0)\), the green phase is able to remain open for trams. Trams can pass through each intersection without stopping, reducing the dwell time and the energy consumption of tram start-stops, providing passengers with a smoother and more comfortable ride experience. However, it also results in disruptions to road traffic, leading to increased delayed vehicles. When the NSPS is adopted\(\:\:({\beta\:}_{c,i}=1)\), whether the tram passes through the intersection is restricted by the signal lights. If the signal light is red at intersection 1, the tram must stop and wait for other vehicles to pass before continuing its journey. The tram can start to leave the intersection until the light turns green. The process of tram braking to stop and accelerating to start will consume more energy, and this process increases the tram dwell time, as well as increasing the travel time. Meantime, the process of acceleration change will also have a negative impact on comfort. Thus, whether trams should stop at the intersections affects not only their travel time but also their energy consumption and comfort42. As shown in Fig. 2, by monitoring the real-time traffic flow at each intersection, we found that the demand varies across intersections (e.g., Intersection 1 has a large traffic flow, while Intersection 2 has a low flow). If an ASPS is applied at all intersections during this period, the green phase time at Intersection 1 would be occupied, leading to delays for most road traffic, thereby increasing negative utility. On the other hand, if NSPS is used at all intersections, it would be challenging to ensure the operational efficiency of the trams. The previous analysis shows that different signal priority strategies have different impacts on the indexes of the tram system (e.g., energy consumption, travel time, or comfort). In particular, these strategies will also affect road traffic efficiency at intersections, potentially amplifying or mitigating social negative effects. The decision of signal priority strategy is the crux of balancing the trams’ energy-saving operation and the road traffic efficiency. Therefore, we emphasize the importance of comprehensively considering tram energy consumption, travel time, and road traffic efficiency at intersections. Then, a solution for trams to adopt MSPS is proposed, which signal priority strategy will be adopted as determined by traffic flow at the intersection. As indicated by the blue curve in Fig. 1, at Intersection 1 with a large road traffic flow, the tram takes the NSPS \(\:({\beta\:}_{c,i}=1)\) and is required to stop for the red light. At Intersection 2 with a low road traffic flow, the tram can adopt ASPS\(\:\:({\beta\:}_{c,i}=0)\), allowing it to pass directly through the intersection without stopping to optimize tram operation efficiency further.
The frequency of the tram stops directly influences the energy consumption and travel time for the tram system. However, trams will inevitably stop at intersections when the NSPS is adopted. Therefore, reducing the number of tram stops at intersections is immensely important for energy-efficient timetable optimization. The interval speed profiles of the trams are optimized by combining the signal cycle to address this issue. This approach ensures that trams can typically pass through intersections always in the green lights when the NSPS is in effect. The process is achieved by selecting the speed profile in the set of tram speed profiles. We derive the input parameters (the set of speed profiles) through a speed profile optimization model42,43. This model is developed based on train operational dynamics equations, incorporating key geographical and infrastructural parameters such as interval length, gradient, curve radius, and tunnel length. It enables the generation of train speed profiles (interval running time and energy consumption) under diverse scenarios, including varying speed limits, station-stopping strategies, and line conditions.
Figure 3 illustrates two scenarios where trams stop at intersections (solid lines) and pass directly (dotted lines) under speed limit 1 and speed limit 2. When the tram reaches Intersection 1 with a large road traffic flow, it will stop under the NSPS if the signal light is red, as depicted by the blue solid line. However, by selecting the appropriate speed profile in the set, the tram can run slowly in the interval (Station 1 to Intersection 1) and pass through Intersection 1 after the red light turns green, as depicted by the blue dotted line in Fig. 3, and the operation process is shown in Fig. 4. We could prevent the tram stops at intersections by using this method, aligning with the goals of enhancing passenger comfort and reducing energy consumption.
Mathematical model
Model assumptions, inputs, decision variables, outputs
Model assumptions
The following assumptions are made when the energy-efficient tram timetable optimization model under MSPS is constructed:
-
(1)
The regenerative braking energy of the trams is not considered in this model.
-
(2)
The stop plan and dwell time of trams in each station are fixed and the real-time road traffic flow is known.
-
(3)
The signal timing of each intersection is fixed and given. When the ASPS is adopted, the green phase is able to remain open for the tram, and the tram can proceed through the intersection directly.
-
(4)
The tram travels through the intersection with a speed limit of 20 km/h.
Symbol and description
Table 1 defines the subscripts, sets, input parameters, and decision variables for the model formulation.
Objective function and constraints
Objective function
The objective function comprises two terms, one aiming to minimize the total energy consumption of all trams.
The other one is to reduce the travel time of all trams to ensure tram operation efficiency.
The constraints of this model.
-
(1)
Tram interval operation constraints.
Formula 3 calculates the train’s interval running time (\(\:{t}_{c,i,j}\)). \(\:{t}_{c,i,j}={t}_{c,i,j,p}^{\text{r}\text{u}\text{n}}\) if the tram \(\:c\) selects the speed profile \(\:p\).
$$\:{t}_{c,i,j}=\sum\:_{p\in\:P}{t}_{c,i,j,p}^{\text{r}\text{u}\text{n}}\cdot\:{\phi\:}_{c,i,j,p},\:\forall\:c\in\:C;i\in\:I\backslash\:\left\{m\right\};j\in\:I$$(3) -
(2)
The tram dwell time constraints.
Formula 4 ensures the minimum and maximum dwell times at station \(\:i\).
$$\:{{t}_{c,i}^{\text{m}\text{i}\text{n}}\le\:t}_{c,i}\le\:{t}_{c,i}^{\text{m}\text{a}\text{x}},\:\forall\:c\in\:C;i\in\:\stackrel{-}{I}$$(4)Formulas 5–7 represent the dwell time of tram \(\:c\) at intersection \(\:i\) (\(\:{t}_{c,i}^{\text{w}\text{a}\text{i}\text{t}}\)). \(\:{t}_{c,i}^{\text{w}\text{a}\text{i}\text{t}}\) is determined by the binary variables \(\:{\beta\:}_{c,i}\) and \(\:{\alpha\:}_{c,i}\). The binary variable \(\:{\beta\:}_{c,i}\) can be employed to decide whether tram \(\:c\) chooses the NSPS. When \(\:{\beta\:}_{c,i}=0\), tram \(\:c\) does not need to stop, \(\:{t}_{c,i}^{\text{w}\text{a}\text{i}\text{t}}\) = 0. When \(\:{\beta\:}_{c,i}=1\), tram \(\:c\) may stop at node \(\:i\), then the dwell time is determined by the signal light. When tram \(\:c\) encounters a red signal light at intersection \(\:i\) \(\:\left({\alpha\:}_{c,i}=1\right)\), the\(\:\:{t}_{c,i}^{\text{w}\text{a}\text{i}\text{t}}\) equals the waiting time for the red signal light to turn green (i.e., \(\:{t}_{c,i}^{\text{r}\text{t}}\)). Conversely, if tram \(\:c\) encounters a green signal light at node \(\:i\) \(\:\left({\alpha\:}_{c,i}=0\right)\), it can proceed without stopping, i.e., \(\:{t}_{c,i}^{\text{w}\text{a}\text{i}\text{t}}=0\). \(\:M\) is a sufficiently large positive number.
$$\:{t}_{c,i}^{\text{r}\text{t}}+\left({\beta\:}_{c,i}+{\alpha\:}_{c,i}-2\right)\cdot\:M\le\:{t}_{c,i}^{\text{w}\text{a}\text{i}\text{t}},\:\forall\:c\in\:C;i\in\:{I}^{{\prime\:}};{\alpha\:}_{c,i}\in\:\left\{\text{0,1}\right\};{\beta\:}_{c,i}\in\:\left\{\text{0,1}\right\}$$(5)$$\:{t}_{c,i}^{\text{w}\text{a}\text{i}\text{t}}\le\:{t}_{c,i}^{\text{r}\text{t}}+(2-{\alpha\:}_{c,i}-{\beta\:}_{c,i})\cdot\:M,\:\forall\:c\in\:C;i\in\:{I}^{{\prime\:}};{\alpha\:}_{c,i}\in\:\left\{\text{0,1}\right\};{\beta\:}_{c,i}\in\:\left\{\text{0,1}\right\}$$(6)$$\:-{\alpha\:}_{c,i}\cdot\:M\le\:{t}_{c,i}^{\text{w}\text{a}\text{i}\text{t}}\le\:{\alpha\:}_{c,i}\cdot\:M,\:\forall\:c\in\:C;i\in\:{I}^{{\prime\:}};{\alpha\:}_{c,i}\in\:\left\{\text{0,1}\right\};{\beta\:}_{c,i}\in\:\left\{\text{0,1}\right\}$$(7) -
(3)
Mapping between tram stop planning and speed profile selection constraints.
If tram \(\:c\) stops at node \(\:i\), i.e., \(\:{\alpha\:}_{c,i}=1\), then the start velocity of the speed profile of tram \(\:c\) on interval \(\:(i,j)\:\) is 0. Similarly, if tram \(\:c\) stops at node \(\:j\), i.e., \(\:{\alpha\:}_{c,j}=1\), then the end velocity of the speed profile of tram \(\:c\) on interval \(\:(i,j)\:\)is also 0, as shown in formulas 8–10. \(\:M\) is a sufficiently large positive number.
$$\:{v}_{c,i,j,p}^{\text{s}\text{t}\text{a}\text{r}\text{t}}\cdot\:{\phi\:}_{c,i,j,p}\ge\:1-{\alpha\:}_{c,i},\:\forall\:c\in\:C;i,j\in\:I$$(8)$$\:\left(1-{\alpha\:}_{c,i}\right)\cdot\:M+{v}_{c,i,j,p}^{\text{s}\text{t}\text{a}\text{r}\text{t}}\cdot\:{\phi\:}_{c,i,j,p}\le\:0,\:\forall\:c\in\:C;i,j\in\:I$$(9)$$\:\left(1-{\alpha\:}_{c,i}\right)\cdot\:M+{v}_{c,i,j,p}^{\text{e}\text{n}\text{d}}\cdot\:{\phi\:}_{c,i,j,p}\le\:0,\forall\:c\in\:C;i,j\in\:I$$(10) -
(4)
Tram arrival and departure time constraints.
\(\:{t}_{c,i}^{\text{d}\text{e}\text{p}}\) is determined by the arrival time \(\:{t}_{c,i}^{\text{a}\text{r}\text{r}}\), the dwell time of station \(\:{t}_{c,i}\), and the dwell time of intersection \(\:{t}_{c,i}^{\text{w}\text{a}\text{i}\text{t}}\), which is expressed by formulas 11 and 12. Similarly, \(\:{t}_{c,i}^{\text{a}\text{r}\text{r}}\) is determined by the departure time of the previous station and the interval running time, as expressed by formula 13–14.
$$\:{t}_{c,1}^{\text{d}\text{e}\text{p}}={F}_{c}+{t}_{c,1}\:,\:\forall\:c\in\:C$$(11)$$\:{t}_{c,i}^{\text{d}\text{e}\text{p}}={t}_{c,i}^{\text{a}\text{r}\text{r}}+{t}_{c,i}+{t}_{c,i}^{\text{w}\text{a}\text{i}\text{t}},\:\forall\:c\in\:C;i\in\:I\backslash\:\left\{1\right\}$$(12)$$\:{t}_{c,1}^{\text{a}\text{r}\text{r}}={F}_{c\:},\:\forall\:c\in\:C$$(13)$$\:{t}_{c,i}^{\text{a}\text{r}\text{r}}={t}_{c,i-1}^{\text{d}\text{e}\text{p}}+{t}_{c,i-1,i},\forall\:c\in\:C;i\in\:I\backslash\:\left\{1\right\}$$(14) -
(5)
Tram speed selection constraints.
Formula 15 ensures that tram \(\:c\) only selects one speed profile on interval \(\:(i,j)\).
$$\:\sum\:_{p\in\:P}{\phi\:}_{c,i,j,p}=1\:,\:\forall\:c\in\:C;i,j\in\:I$$(15) -
(6)
Tram signal priority strategy selection constraints.
If the road traffic flow exceeds \(\:\sigma\:\) (\(\:\sigma\:\) is the threshold used to determine the signal priority strategy) at intersection \(\:i\), then the tram adopted NSPS, i.e., \(\:{\beta\:}_{c,i}=1\). Otherwise, the ASPS is adopted (\(\:{\beta\:}_{c,i}=0\)). The constraints for this decision are expressed in formulas 16–17. \(\:\delta\:\) is a sufficiently small positive number.
$$\:{\omega\:}_{i}-\sigma\:+\delta\:\le\:M\cdot\:{\beta\:}_{c,i},\:\forall\:c\in\:C;i\in\:{I}^{{\prime\:}}$$(16)$$\:{\omega\:}_{i}-\sigma\:+\delta\:\ge\:M\cdot\:\left({\beta\:}_{c,i}-1\right),\:\forall\:c\in\:C;i\in\:{I}^{{\prime\:}}$$(17) -
(7)
The constraints for determining whether a tram stops at the intersection or not.
Formulas 18–21 specify that if the consumption time of the signal cycle at the respective intersection exceeds the green time of the tram phase when tram \(\:c\) arrives at intersection \(\:i\), tram \(\:c\) can proceed without halting. Otherwise, it must come to a halt and wait for the signal light to turn green.
$$\:{Z}_{i}\cdot\:\left({x}_{c,i}-1\right)<{t}_{c,i}^{\text{a}\text{r}\text{r}}-{O}_{i}\le\:{Z}_{i}\cdot\:{x}_{c,i},\:\forall\:c\in\:C;i\in\:{I}^{{\prime\:}}$$(18)$$\:{t}_{c,i}^{\text{o}\text{t}}={t}_{c,i}^{\text{a}\text{r}\text{r}}-{O}_{i}-{Z}_{i}\cdot\:\left({x}_{c,i}-1\right),\:\forall\:c\in\:C;i\in\:{I}^{{\prime\:}}$$(19)$$\:{t}_{c,i}^{\text{r}\text{t}}={Z}_{i}-{t}_{c,i}^{\text{o}\text{t}},\:\forall\:c\in\:C;i\in\:{I}^{{\prime\:}}$$(20)$$\:\left({\alpha\:}_{c,i}-1\right)\cdot\:M<{t}_{c,i}^{\text{o}\text{t}}-{T}_{i}^{\text{g}}\le\:{\alpha\:}_{c,i}\cdot\:M,\:\forall\:c\in\:C;i\in\:{I}^{{\prime\:}}$$(21) -
(8)
The total number of delayed vehicles constraints.
When the ASPS is adopted by the tram at intersection \(\:i\), it will cause delays for vehicles. The total number of delayed vehicles is calculated as depicted in formula 22.
$$\:N=\sum\:_{i\in\:I,c\in\:C}{T}_{i}^{\text{g}}\cdot\:{\omega\:}_{i}\cdot\:\left(1-{\alpha\:}_{c,i}\right),\:\forall\:c\in\:C;i\in\:{I}^{{\prime\:}}$$(22) -
(9)
The comfort constraints.
The comfort index is calculated by formula 23, and \(\:n\) is the interval number. The comfort level of a tram is represented by \(\:D\), which is determined by the speed profile chosen for each interval of the tram’s route. Specifically, \(\:{d}_{c,i,j,p}\) denotes the comfort corresponding to the speed profile \(\:p\) of tram \(\:c\) on interval \(\:(i,j)\).
During the tram’s entire journey along the route, the speed, acceleration, and the rate of change of acceleration undergo dynamic variations. For simplicity, the tram can be modeled as a particle, and the entire route is divided into several intervals. The comfort index for the entire route is then described by the average value of the comfort indicators across all these intervals42.
$$\:D=\frac{1}{n}\sum\:_{c\in\:C,p\in\:P}{d}_{c,i,j,p}\cdot\:{\phi\:}_{c,i,j,p},\:\forall\:c\in\:C;p\in\:P;i,j\in\:I$$(23) -
(10)
Tram headways constraints.
The safety headway time is represented by formulas 24–25. The arrival headway and departure headway between two consecutive trains must be greater than the minimum arrival and departure headway.
$$\:{t}_{c+1,i}^{\text{a}\text{r}\text{r}}-{t}_{c,i}^{\text{a}\text{r}\text{r}}\ge\:{H}^{\text{a}\text{r}\text{r}},\:\forall\:c\in\:C\backslash\:\left\{n\right\};i\in\:\stackrel{-}{I}$$(24)$$\:{t}_{c+1,i}^{\text{d}\text{e}\text{p}}-{t}_{c,i}^{\text{d}\text{e}\text{p}}\ge\:{H}^{\text{d}\text{e}\text{p}},\:\forall\:c\in\:C\backslash\:\left\{n\right\};i\in\:\stackrel{-}{I}$$(25)
Solution approach
The objective functions of the proposed model involve minimizing total energy consumption (\(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\)) and minimizing total travel time (\(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\)). However, their units and orders of magnitude are different, making it not feasible to determine the final objective function solely by setting the weight factor. Thus, this paper employs the weighted-sum method for system analysis44 to normalize the objective functions. We denote the optimal solutions for these two objective components as \(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}^{\text{*}}\) and \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}^{\text{*}}\). When our focus is solely on tram energy consumption, we can utilize Eqs. (1), (3)–(25) to address the problem and obtain the minimum total energy consumption (\(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}^{\text{*}}\)). Alternatively, if we only consider train travel time without accounting for energy consumption, we can solve the problem using Eqs. (2), (3)–(25) and determine the minimum total travel time (\(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}^{\text{*}}\)). Subsequently, the objective function for the optimization problem is established as follows:
Where \(\:{{\uplambda\:}}_{1}\) and \(\:{{\uplambda\:}}_{2}\) are the weights of \(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\) and \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\) respectively, and meet \(\:{{\uplambda\:}}_{1}+{{\uplambda\:}}_{2}=1\), \(\:\frac{{{\uplambda\:}}_{1}}{{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}^{\text{*}}}\) and \(\:\frac{{{\uplambda\:}}_{2}}{{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}^{\text{*}}}\) can be considered as normalization factors.
Case study
Description of a real test
The test bed is based on the Lijiang Tram Line 1 in China, with a length of about 20 km. The line comprises 5 stations and 7 intersections. Figure 5 shows the detailed parameters of the line. Notably, the Tourist Distribution Center Station to Yulong Mount Station includes 7 long ramp sections (Gradient ≥ 25‰), as shown in Table 2.
Nodes 1, 3, 6, 8, and 12 correspond to stations, while 2, 4, 5, 7, 9, 10, and 11 represent intersections. The line maintains a speed limit of 70 km/h. The timetable is depicted in Fig. 6 and utilizes an ASPS. The speed profile optimization model42,43 is used to obtain the speed profile set (\(\:P\)) for each interval while considering the relevant parameters of the line (interval length, gradient, curve radius, and tunnel length), the speed limit scheme, and the stop plan. The set \(\:P\) is employed to solve the energy-efficient problem of the tram system.
The real-time road traffic flow at the intersections is presented in Table 3, which is used to determine the signal priority strategy. In this study, we specify that if the road vehicles exceed 800, the NSPS is in effect by the tram at the intersection; otherwise, it adopts the ASPS.
For the ASPS, the tram must pass through the intersections at a speed limit of 20 km/h, and the dwell time is 0. The tram may encounter a red signal light at an intersection when the NSPS is adopted. The upper bound of the dwell time is determined by the duration of the red signal light, while the lower bound is 0. The dwell time ranges of nodes and the timing parameters of signal lights are displayed in Table 4. Trams are subject to a minimum departure headway of 5 min and a minimum arrival headway of 2 min.
As shown in Fig. 6, a total of 17 trams operates between Tourist Distribution Center Station and Yulong Mount Station. The line is subject to a speed limit of 70 km/h, and 45 km/h on long ramps. Cumulatively, the tram travel time is 31,773 s, and the total energy consumption is 2872 \(\:\text{kW}\cdot\text{h}\).
This paper employs the commercial optimization solver IBM ILOG CPLEX 12.10 to solve the mathematical model. The experiments involving numerical analysis are set to demonstrate the effectiveness of the MILP model that we proposed. All the following experiments are carried out on a computer with Intel(R) Core(TM) i5-8265U CPU @ 1.60 GHz 1.80 GHz and 8 GB RAM.
Experimental results
Experimental results, benefits of bi-objective collaborative optimization
The Pareto front is derived by adjusting the weight coefficients of \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\) and \(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\), as illustrated in Fig. 7.
To evaluate the advantages of considering the bi-objective optimization method, two extreme points from the Pareto front are selected, which are used to compare with the experimental results of a single-objective optimization model focused on minimizing either total travel time (\(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\)) or total energy consumption (\(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\)).
As depicted in Table 5, it is evident that compared to the single-objective optimization method,
the bi-objective can reduce the \(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\) by 1.34% when we consider the same \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\) (32215 s). Similarly, under the same \(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\) (2653 \(\:\text{kW}\cdot\text{h}\)), the bi-objective optimization method can reduce the \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\) by 2.72%. This clearly demonstrates that the bi-objective integrated optimization method is more effective than the single-objective optimization.
Benefits of the multi-signal priority strategies
This section analyzes the results of the MSPS and the ASPS, as depicted in Table 6. Here, we solve the integrated optimization MILP model based on the objective functions constructed in Section The constraints of this model. Four evaluation indexes are selected to analyze the experimental results, namely total travel time (\(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\)), energy consumption (\(\:{\text{Z}}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\)), comfort (\(\:D\)), and the total number of delayed vehicles (\(\:N\)). Total travel time (\(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\)), energy consumption (\(\:{\text{Z}}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\)), and the total number of delayed vehicles (\(\:N\)) are used as key metrics to evaluate operational efficiency45.
Table 6 reveals that MSPS has a more pronounced effect on reducing the number of vehicle delays. The total number of delayed vehicles (\(\:N\)) with the MSPS is lower compared to the ASPS regardless of the objective. When the ASPS is applied throughout the entire journey, trams always pass through intersections without stopping, sacrificing green phases, which increases delays for road traffic. In contrast, the proposed approach in this paper can significantly reduce the impact of tram operations on road traffic by utilizing green phases without occupying those allocated for road traffic. This method minimizes the delay for social traffic while ensuring tram efficiency.
Additionally, the outcomes of the two types are different when we employ different objective functions. While setting a specific objective function may minimize the corresponding index value, it generally does not guarantee that other index values can also be minimized. For example, if the objective is set to minimize \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\), the \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\) of the optimization results under MSPS and ASPS are 32,215 s and 32,033 s, respectively. These values are lower than the corresponding total travel time index values when other objective functions are set. When aiming to minimize \(\:{\text{Z}}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\), both the \(\:{\text{Z}}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\) and \(\:N\) are lower under MSPS compared to the other objective functions. However, the comfort index (\(\:D\)) value is relatively higher, indicating that the discomfort of passengers is more obvious. Compared with the initial timetable of the ASPS (actual operation), it is clear that the proposed method significantly reduces total energy consumption and the number of vehicle delays while enhancing passenger comfort. The comfort index (\(\:D\)) under specific objectives is relatively high, primarily due to trams inevitably stopping at intersections under MSPS.
A comparative experiment with the timetable of ASPS (initial timetable)
Here, we keep the same threshold and the objective function weights (\(\:{\sigma\:}_{1}\) >800, \(\:[{\lambda\:}_{1}=0.4,\:{\lambda\:}_{2}=0.6]\)), and compare it with the timetable of the ASPS (initial timetable) to analyze its total travel time (\(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\)), total energy consumption (\(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\)), comfort (\(\:D\)), and total number of delayed vehicles (\(\:N\)).
As shown in Fig. 8, we have successfully reduced energy consumption while ensuring the efficient operation of the trams. Although the tram’s travel time increased slightly (with an average increase of 1 min per tram), this had minimal impact on overall operational efficiency. The total energy consumption under MSPS (our work) is reduced by 144 \(\:\text{k}\text{W}\cdot\:\text{h}\), with reductions ranging from 1.54 to 7.07% per tram. Furthermore, the signal priority strategy is determined by the road traffic flow at intersections to reduce the impact on road traffic. As depicted in Fig. 9, the intersections are represented by the red dotted line, and after train rescheduling, the trams make five stops at the intersections (as indicated by the red circles in Fig. 9), with tram 1 stopping twice, tram 2, tram 3 and tram 4 stopping once each. As presented in Table 6, the number of vehicle delays caused by tram operations under MSPS (our work) is 29,751, which represents a reduction of 11,124 delays compared to the ASPS (initial timetable). The total number of vehicles delayed is reduced by 27.21% and effectively improves the overall traffic operational efficiency.
In addition, we also consider passenger comfort during the tram operation while optimizing the road traffic efficiency at intersections. Therefore, we add the comfort index constraints to this model. According to the international standard ISO 2631-1: 1997, a tram achieves its highest comfort level when the rate is less than 0.315 m/s². Table 6 illustrates that despite the trams stopping 5 times at intersections under MSPS (the objective is min \(\:\text{Z}\)), the comfort rate is lower compared to the ASPS (initial timetable) by \(\:\frac{0.328-0.301}{0.328}\times\:100\text{\%}=8.23\text{\%}\). This indicates that we further enhanced passenger comfort while also optimizing travel time and energy consumption.
Sensitivity analysis
Considering that traffic flow and signal timing affect the model’s outcomes, this section conducts a sensitivity analysis of the above influencing factors.
Experiments on the influence of different traffic flow thresholds (i.e., \(\:{\sigma\:}_{1}\:\)>800, \(\:{\sigma\:}_{2}\:\)>700, and \(\:{\sigma\:}_{3}\:\)>600)
In this section, we compare three experimental groups with identical configurations across different thresholds (\(\:{\sigma\:}_{1}\) >800, \(\:{\sigma\:}_{2}\) >700, \(\:{\sigma\:}_{3}\) >600) to analyze their total travel time (\(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\)), energy consumption (\(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\)), comfort (\(\:D\)), and the total number of delayed vehicles (\(\:N\)). In these three comparison experiments, the tram can adopt NSPS (\(\:{\beta\:}_{c,i}=1\)) only when the road traffic flow at intersections exceeds 800, 700, or 600, respectively. In all cases, we arrive at a similar conclusion. As depicted in Fig. 10, the trend of the Pareto fronts remains identical across different thresholds. Notably, the \(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\) and \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\) of the Pareto solutions in Case 1 (\(\:{\sigma\:}_{1}\) >800) are the lowest.
Three specific node types (i.e., \(\:[{\lambda\:}_{1}\:=\:1,\:{\lambda\:}_{2}\:=\:0]\), \(\:[{\lambda\:}_{1}\:=\:0.4,\:{\lambda\:}_{2}\:=\:0.6]\), and \(\:[{\lambda\:}_{1}\:=\:0,\:{\lambda\:}_{2}\:=\:1]\)) within each Pareto front are identified to provide a detailed analysis in this section. These nodes represent the values of different weights for the two objective functions on one Pareto front, respectively. As shown in Fig. 10, comparing the three left nodes for the weights \(\:[\:{\lambda\:}_{1}\:=\:1,\:{\lambda\:}_{2}\:=0]\), it becomes clear that as the threshold decreases (e.g., Case 1- \(\:{\sigma\:}_{1}\) >800 to Case 3- \(\:{\sigma\:}_{3}\) >600), \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\) increases when we minimize \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\). There is little difference in \(\:{\text{Z}}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\) between Case 2 (\(\:{\sigma\:}_{2}\) >700) and Case 3 (\(\:{\sigma\:}_{3}\) >600). This is because the number of stops at the intersections increases in Case 3 (\(\:{\sigma\:}_{3}\) >600), leading to an increase in both \(\:{Z}_{\text{t}\text{r}\text{a}\text{v}\text{e}\text{l}\:\text{t}\text{i}\text{m}\text{e}}\) and \(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\). When we compare the three right nodes in Fig. 10, where the weights are \(\:[\:{\lambda\:}_{1}\:=\:0,\:{\lambda\:}_{2}\:=\:1]\), it is observed that the total travel time remains consistent across the three cases when minimizing \(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\). However, as the threshold decreases, the \(\:{Z}_{\text{e}\text{n}\text{e}\text{r}\text{g}\text{y}}\) increases. This increase is due to the rise in the number of stops and the running speed of the section.
Comparing the weights of the intermediate nodes \(\:[\:{\lambda\:}_{1}\:=\:0.4,\:{\lambda\:}_{2}\:=\:0.6]\) in Fig. 10, the values of the comparison experiment output are shown in Table 7; Fig. 11. It is noticeable that even if we reduce the thresholds, the total travel time remains nearly unchanged (within a few seconds) while the total energy consumption increases. Additionally, there are substantial differences in the indicators for comfort and the total number of delayed vehicles. This disparity can be attributed to the fact that as the cases decrease in the thresholds (e.g., Case 1- \(\:{\sigma\:}_{1}\) >800 to Case 3- \(\:{\sigma\:}_{3}\) >600), the number of stops at intersections increases for the tram system, resulting in a reduced total number of delayed vehicles for road traffic but increased tram energy consumption. Simultaneously, the heightened number of stops leads to increased discomfort for passengers.
Here, the following conclusions can be drawn. If we want to save energy consumption and improve passenger comfort to the greatest extent, it is advisable to raise the thresholds for determining a tram signal priority strategy (e.g., Case 1- \(\:{\sigma\:}_{1}\) >800). Additionally, we can also infer that in the case of traffic congestion and significant obstruction by road traffic at intersections, besides changing the signal cycle, opting for a lower threshold (e.g., Case 3- \(\:{\sigma\:}_{3}\) >600) can also increase road traffic efficiency.
Experiments on the influence of different signal timing schemes (i.e., \(\:{Z}_{1}\:\)= 60, \(\:{Z}_{2}\:\)= 80, and \(\:{Z}_{3}\:\)= 100)
By keeping other model parameters and constraints fixed, the signal timing settings are adjusted, with specific parameters shown in Table 8. The impact of the signal timing on the optimization results is illustrated in Fig. 12; Table 9.
From Fig. 12, the Pareto frontiers under the three different signal timing schemes exhibit a similar trend. However, as the signal cycle duration increases, both the total travel time and total energy consumption increase for the same weight combination. Comparing the weights of the intermediate nodes \(\:[\:{\lambda\:}_{1}\:=\:0.4,\:{\lambda\:}_{2}\:=\:0.6]\) in Table 9, the total travel time, total energy consumption, comfort index, and total number of tram stops at intersections are positively correlated with signal cycle duration. In contrast, the total number of delayed vehicles is negative.
When the signal cycle duration increases from 60 to 80 s, the total travel time increases from 32,724 to 33,434 s, and the total energy consumption rises from 2728 \(\:\text{k}\text{W}\cdot\:\text{h}\) to 2737.1 \(\:\text{k}\text{W}\cdot\:\text{h}\). Simultaneously, the total number of delayed vehicles decreases from 28,751 to 27,383. The increase in signal cycle duration leads to longer waiting times for trams at red lights at intersections. The increase in tram stops at intersections results in higher stop-start energy consumption, ultimately leading to longer travel times and higher energy consumption. Furthermore, the increase in tram stops at intersections negatively impacts the comfort index, and reduces passenger comfort. However, with the increase in signal cycle duration, the total number of delayed vehicles decreases. This reduction is also related to the increase in tram stops at intersections, which allows road traffic to experience less delay. Therefore, while the signal timing parameters of Case 1 have minimal impact on tram operational efficiency, the signal timing parameters of Case 3 are more beneficial for road traffic.
Experiments on the interaction of signal cycle variations and road traffic flow with energy savings and operational efficiency
By fixing other model parameters and constraints, the signal cycle and road traffic flow are adjusted to analyze their impacts on tram operational efficiency and energy consumption. The experimental results are illustrated in Figs. 13 and 14, and 15.
The trends under different signal cycles and traffic flow thresholds exhibit clear patterns. As the signal cycle increases and the traffic flow thresholds decrease, both the total travel time and total energy consumption increase, while the number of delayed vehicles shows a declining trend. When the signal cycle increases from 60 to 100 s, and the traffic flow threshold decreases from 800 to 600, the total travel time increases from 32,724 to 33,747 s, and the total energy consumption rises from 2728 to 2765.6 \(\:\text{k}\text{W}\cdot\:\text{h}\), while the total number of delayed vehicles decreases. The extended signal cycle leads to increased dwell time for trams at red lights and more frequent stops at intersections, thereby increasing start-stop energy consumption and total travel time. However, the reduction in delayed vehicles is associated with improved traffic flow efficiency at intersections, which benefits road traffic.
Although extended signal cycles and lower traffic flow thresholds generally degrade tram performance, they benefit road traffic by reducing vehicle delays. The optimal balance depends on traffic conditions: shorter signal cycle (60 s) with higher traffic flow thresholds (800) are preferable under low traffic volumes, whereas longer signal cycle (100 s) with reduced thresholds (600) are more appropriate for high traffic volumes, thereby enhancing overall system efficiency.
Conclusions
This paper has studied the energy-efficient optimization problem in tram operations in conjunction with multi-signal priority strategies (MSPS). The main advantage is that the energy-saving tram operation was achieved while enhancing the road traffic efficiency at intersections. We developed a MILP model to resolve the problem. Additionally, the weighted-sum method is used to transform the bi-objective function into a comprehensive objective. We constructed the model based on the principles of signal cycle variation and real-time road traffic flow, and optimized the arrival and departure times of trams at stations and intersections to minimize energy consumption and travel time. Furthermore, the MSPS was employed to reduce the impact of trams on road traffic. The problem of low traffic efficiency at intersections is solved. Moreover, the speed profile was also optimized to improve passenger comfort. Experiments have been conducted based on Lijiang Tram Line 1 in China, the superiority of the model was verified: (1) the bi-objective model was established in this study can further improve the optimization efficiency by 1.34-2.72% under the same objective, compared with the single-objective; (2) the MSPS can reduce the delay of road traffic by 14.79%, compared with the ASPS.
The influences of signal priority strategies, signal cycle, and road traffic were considered in this paper while optimizing the energy consumption and travel time for the tram system. Future research can explore the following three points. Firstly, in order to simplify model solving, we assume that the overall parameters of the trams are fixed in the process of obtaining the speed profile set (\(\:P\)) by utilizing the optimization model. Actually, the number of passengers is the main factor that influences the train’s quality. The fluctuation in passenger load has a direct impact on tram energy consumption and travel time. Therefore, future research should account for the variability in passenger loads by developing dynamic optimization models through methodologies such as stochastic optimization, fuzzy optimization, and robust optimization. These approaches can achieve more precise optimization outcomes while ensuring better alignment with real-world operational conditions. Secondly, collaborative optimization of multiple trams can be achieved by considering the utilization of regenerative braking energy in the model. This approach has the potential to further enhance energy efficiency and operational coordination within the tram network. Future studies should prioritize integrating regenerative braking energy into the optimization model, and explore ways to enhance energy utilization through tram-to-tram cooperative optimization. Thirdly, incorporating both passenger load and collaborative optimization into the model will significantly increase the complexity of the problem, thereby reducing the model’s computational efficiency. To address this challenge, future work will explore the use of heuristic algorithms to simplify the solution process.
Data availability
The date is used in the manuscript can be obtained from the manuscript or supplementary information files.
References
Shi, J., Sun, Y., Schonfeld, P. & Qi, J. Joint optimization of Tram timetables and signal timing adjustments at intersections. Transp. Res. Part. C-Emerg Technol. 83, 104–119. https://doi.org/10.1016/j.trc.2017.07.014 (2017).
Liu, H., Zhang, Y. & Zhang, K. Evaluating impacts of intelligent transit priority on intersection energy and emissions. Transp. Res. Part D Transp. Environ. 86, 102416. https://doi.org/10.1016/j.trd.2020.102416 (2020).
He, J. et al. An optimization model of Tram timetables considering various signal priority strategies. Sci. Rep. 12 (1), 16564–16564. https://doi.org/10.1038/S41598-022-19762-9 (2022).
Górka, A., Czerepicki, A. & Krukowicz, T. The impact of priority in coordinated traffic lights on Tram energy consumption. Energies 11 (01), 53–58. https://doi.org/10.3390/en17020520 (2024).
Feng, J. X. et al. An integrated optimization model for energy saving in metro operations. IEEE Trans. Intell. Transp. Syst. 28 (8), 3059–3069. https://doi.org/10.1109/TITS.2018.2871347 (2019).
Qu, Y. C. et al. Robust optimization of train timetable and energy efficiency in urban rail transit: A two-stage approach. Comput. Ind. Eng. 146 (Aug). https://doi.org/10.1016/j.cie.2020.106594 (2020).
Huang, K. & Liao, F. X. A novel two-stage approach for energy-efficient timetabling for an urban rail transit network. Transp. Res. Pt e-Logist Transp. Rev. 176 (Aug). https://doi.org/10.1016/j.tre.2023.103212 (2023).
Scheepmaker, G. M., Goverde, R. M. & Kroon, L. G. Review of energy-efficient train control and timetabling. Eur. J. Oper. Res. 257 (2), 355–376. https://doi.org/10.1016/j.ejor.2016.09.044 (2016).
Wang, Z. & Luo, X. Research on train energy-saving optimization in urban rail transit line. Comput. Eng. 6 (41), 24–28. https://doi.org/10.3969/j.issn.1000-3428.2015.06.005 (2015).
Mintsis, E., Vlahogianni, E. I. & Mitsakis, E. Dynamic eco-driving near signalized intersections: systematic review and future research directions. J. Transp. Eng. Part. A: Syst. 146 (4), 04020018. https://doi.org/10.1061/JTEPBS.0000318 (2020).
He, D. Q. et al. Energy efficient metro train running time rescheduling model for fully automatic operation lines. J. Transp. Eng. Part. A: Syst. 147 (7), 04021032. https://doi.org/10.1061/JTEPBS.0000546 (2021).
Cao, Y. et al. Trajectory optimization for high-speed trains via a mixed integer linear programming approach. IEEE Trans. Intell. Transp. Syst. 23 (10), 17666–17676. https://doi.org/10.1109/TITS.2022.3155628 (2022).
Liu, S. et al. Optimization of train running time for saving energy in urban rail transit. Urban Rail Transit. 32 (05), 145–150. https://doi.org/10.3969/j.issn.1672-6073.2019.05.024 (2019).
Zhou, W. L. et al. Collaborative optimization of energy-efficient train schedule and train circulation plan for urban rail. Energy 263 (Jan). https://doi.org/10.1016/j.energy.2022.125599 (2023).
Sun, X. B., Hong, L. & Dong, H. R. Energy-efficient train control by multi-train dynamic Cooperation. IEEE Trans. Intell. Transp. Syst. 18 (11), 3114–3121. https://doi.org/10.1109/TITS.2017.2682270 (2017).
Zhang, Z. Y. et al. Pareto multi-objective optimization of metro train energy-saving operation using improved NSGA-II algorithms. Chaos Solitons Fractals 176 (Nov). https://doi.org/10.1016/j.chaos.2023.114183 (2023).
Anh, A. T. H. T. et al. Speed profile optimization of an electrified train in Cat Linh-ha dong metro line based on Pontryagin’s maximum principle. Int. J. Elec Comp. Eng. 10 (1), 233–242. https://doi.org/10.11591/ijece.v10i1.pp233-242 (2020).
Sicre, C. et al. A method to optimize train energy consumption combining manual energy efficient driving and scheduling. WIT Trans. Built Environ. 114, 549–560. https://doi.org/10.2495/CR100511 (2010).
Udriste, C., Tevy, I. & Antonescu, P. Optimal control problem for minimization of net energy consumption at metro. Mathematics 11 (4), 1035. https://doi.org/10.3390/math11041035 (2023).
Shang, M. Y., Zhou, Y. H. & Fujita, H. Energy-saving operation synergy for multiple metro-trains using map-reduce parallel optimization. IEEE Trans. Veh. Technol. 72 (2), 1319–1332. https://doi.org/10.1109/TVT.2021.3133858 (2022).
Su, S. et al. An energy-efficient train operation approach by integrating the metro timetabling and eco-driving. IEEE Trans. Intell. Transp. Syst. 21(10), 4252–4268. https://doi.org/10.1109/TITS.2939358 (2019).
Jeong, Y. & Kim, Y. Tram passive signal priority strategy based on the MAXBAND model. KSCE J. Civ. Eng. 18 (5), 1518–1527. https://doi.org/10.1007/s12205-014-0159-1 (2014).
Zhou, Y. et al. An arterial signal coordination optimization model for trams based on modified AM-BAND. Discrete Dyn. Nat. Soc. 2016 (1), 5028095. https://doi.org/10.1155/2016/5028095 (2016).
Zhang, T. et al. Timetable optimization for a two-way Tram line with an active signal priority strategy. IEEE Access. 7, 176896–176911. https://doi.org/10.1109/ACCESS.2019.2957437 (2019).
Ji, Y. et al. Coordinated optimization of Tram trajectories with arterial signal timing resynchronization. Transp. Res. Part. C-Emerg Technol. 99 (Feb), 53–66. https://doi.org/10.1016/j.trc.2019.01.008 (2019).
Yan, Y. et al. Operation optimization and control method based on optimal energy and hydrogen consumption for the fuel cell/supercapacitor hybrid Tram. IEEE Trans. Ind. Electron. 68 (2), 1342–1352. https://doi.org/10.1109/TIE.2020.2967720 (2021).
Xiao, Z. et al. Energy-efficient predictive control for trams incorporating disjunctive time constraints from traffic lights. Transp. Res. Part. C-Emerg Technol. 151 (Jun). https://doi.org/10.1016/j.trc.2023.104113 (2023).
Xu, M. J. et al. Energy-efficient control of energy storage tram with signaling constraints. In 37th Chinese Control Conference (CCC), Wuhan, CHINA, 25–27 July 2018. https://doi.org/10.23919/ChiCC.2018.8483267 (2018).
Xing, Z. X. et al. Energy consumption optimization of tramway operation based on improved PSO algorithm. Energy 258 (Nov). https://doi.org/10.1016/j.energy.2022.124848 (2022).
Caramia, P. et al. Energy saving approach for optimizing speed profiles in metro application. In 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, FRANCE, 02–04 November 2016. https://doi.org/10.1109/ESARS-ITEC.2016.7841443 (2016).
Su, R. D., Gu, Q. R. & Wen, T. Optimization of high-speed train control strategy for traction energy saving using an improved genetic algorithm. J. Appl. Math. 2014 (May). https://doi.org/10.1155/2014/507308 (2014).
Hasanzadeh, S., Zarei, S. F. & Najafi, E. A train scheduling for energy optimization: Tehran metro system as a case study. IEEE Trans. Intell. Transp. Syst. 24 (1), 357–366. https://doi.org/10.1109/TITS.2022.3215095 (2023).
Huang, Y. R. et al. Saving energy and improving service quality: bicriteria train scheduling in urban rail transit systems. IEEE Trans. Intell. Transp. Syst. 17 (12), 3364–3379. https://doi.org/10.1109/TITS.2016.2549282 (2016).
Zhang, H. R. et al. Energy-Efficient Timetable Optimization Empowered by Time-Energy Pareto Solution Under Actual Line Conditions. IEEE Trans. Intell. Transp. Syst. early access, 1–19. https://doi.org/10.1109/TITS.2023.3345739 (2024).
Zheng, H., Chen, J., Huang, Z. & Zhu, J. Joint optimization of Multi-Cycle timetable considering Supply-to-Demand relationship and energy consumption for rail express. Mathematics 10 (21), 4164. https://doi.org/10.3390/math10214164 (2022).
Luan, X. J. et al. Integration of real-time traffic management and train control for rail networks-part 1: optimization problems and solution approaches. Transp. Res. Part. B-Methodol 115 (Sep), 41–71. https://doi.org/10.1016/j.trb.2018.06.006 (2018).
Zhang, T. et al. Timetable optimization of Tram considering energy saving goals. J. Traffic Transp. Eng. -Engl Ed. 19 (06), 171–181. https://doi.org/10.19818/j.cnki.1671-1637.2019.06.016 (2019).
Guan, L. A two-stage optimization algorithm of the train traction energy consumption in urban rail transit. IEEE Intell. Transp. Syst. Mag 15 (2), 26–40. https://doi.org/10.1109/MITS.2022.3217076 (2022).
Zhou, W. et al. Integrated optimization of tram schedule and signal priority at intersections to minimize person delay. J. Adv. Transp. 2019, 4802967. https://doi.org/10.1155/2019/4802967 (2019).
Zhang, T. et al. Research on bus signal priority strategy for urban arteries based on real-time vehicle queuing detection. In 4th International Conference on Cloud Computing and Big Data Analysis (ICCCBDA), Chengdu, CHINA, 12–15 April 2019. https://doi.org/10.1109/icccbda.2019.8725719 (2019).
Shang, M. Y., Zhou, Y. H. & Fujita, H. Deep reinforcement learning with reference system to handle constraints for energy-efficient train control. Inf. Sci. 570 (Sep), 708–721. https://doi.org/10.1016/j.ins.2021.04.088 (2021).
He, J. et al. Energy-efficient Tram speed trajectory optimization considering the influence of the traffic light. Front. Energy Res. 10 (Aug). https://doi.org/10.3389/fenrg.2022.963275 (2022).
Long, S. H. et al. Integrated speed modeling and traffic management to precisely model the effect and dynamics of temporary speed restrictions to high-speed railway traffic. Transp. Res. Part. C-Emerg Technol. 152 (Jul). https://doi.org/10.1016/j.trc.2023.104148 (2023).
Hong, X. et al. Integrated optimization of capacitated train rescheduling and passenger reassignment under disruptions. Transp. Res. Part. C-Emerg Technol. 125 (Apr). https://doi.org/10.1016/j.trc.2021.103025 (2021).
Li, J. et al. Coordinated optimization of modern Tram control and timetable for energy saving. J. Railw Sci. Eng. 14 (7), 1552–1558. https://doi.org/10.19713/j.cnki.43-1423/u.2017.07.029 (2017).
Acknowledgements
This work was supported by the Science and Technology Innovation and Demonstration Project of the Department of Transport of Yunnan Province (Yunnan Jiaotong Textbook Ben < 2022 > No. 18), the Yunnan Xing Dian Talents Plan young of China under Grant KKRD202202112, and the Yunnan Fundamental Research Project under Grant 202301AU070033.
Author information
Authors and Affiliations
Contributions
J.H. and F.W. proposed the methodology, all authors conceived the experiment(s), F.W., Y.D., and Z.Y. conducted the experiment(s), J.H. and F.W. wrote the original draft, F.W., Y.D., Z.Y., and J.Y. analyzed the results. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
He, J., Wang, F., Duan, Y. et al. Energy-efficient train timetable optimization for tram system under multi-signal priority strategies. Sci Rep 15, 8123 (2025). https://doi.org/10.1038/s41598-025-91891-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-91891-3