Introduction

With the increasing number of electronic devices, the space electromagnetic environment is becoming more and more complex. The performance of electronic devices decreases or even fails to work properly because of electromagnetic interference. For larger electronic equipment, traditional method for electromagnetic compatibility test results in a time-consuming process which is also limited by the equipment size. The wideband microwave imaging system can quickly identify and locate the electromagnetic interference sources, which has the advantages of large range, wide bandwidth and dynamic real-time1,2. In microwave imaging system the operational frequency range is 1GHz–6 GHz, which can cover most of the equipment’s working frequencies. However, since the imaging system uses focal plane array scanning for signal acquisition3, the response parameters are not consistent for each channel. In addition, there are differences in the detection of response characteristics to radiation sources of different frequencies. As a result, the stripe noise appearing in the acquired electromagnetic image varies with the frequency of the radiation source, which ultimately affects the localization accuracy of the EMS4,5,6.

The array scanning imaging method is widely used in remote sensing satellite earth detection7, infrared imaging system8and Synthetic Aperture Radar imaging system9. However, due to the inconsistency of the devices response in multiple channels, the image contains the stripe noise. To solve this problem, the stripe noise removal methods can be broadly classified into three categories: optimization-based methods, statistical-based methods and deep learning-based methods. The optimization-based stripe noise removal methods can be regarded as an ill-posed inverse problem, the regularization model receives multiple prior information as inputs10 in order to estimate the stripe component well. Chang et al. proposed a low-rank based single image decomposition model (LRSID)11 to remove stripe noise from the image decomposition point of view by using low-rank regularization. Li et al. proposed a non-local mean image denoising method12 to achieve stripe noise removal by capturing the details of the image. He et al. utilized bootstrap filter to calculate the filter output by considering the content of the boot-strap image to achieve stripe noise removal13. A key limitation of prior-based de-striping methods is their tendency to remove both noise and image details indiscriminately, resulting in blurring artifacts.

Among the classical statistical-based methods, Chang et al. dissected the principles and properties of stripe noise generation14. They combined the wavelet transform and matrix matching method to propose a new stripe noise removal method, which can better maintain the image quality and effectively eliminate the stripe noise. Tendero et al. proposed the midway histogram equalization (MHE) method15, which removes stripe noise by introducing redundant information between neighboring columns. Zeng et al. proposed a method16 to remove stripe noise by statistically analyzing the Fourier spectral features of the image. A limitation of these methods is its potential to enhance noise artifacts, thereby degrading image signal quality.

The increasing complexity of emerging applications presents challenges for traditional, mathematically simple models, which may lack the scalability to adequately address these scenarios. Deep learning methods, however, offer the potential to capture intricate underlying structures directly from data. Motivated by recent advancements in deep learning, this study investigates the effectiveness of these techniques for stripe noise removal, specifically within the wideband microwave imaging systems. For example, Guan et al. proposed stripe noise removal Wavelet deep neural network (SNRWDNN)17, which employs a convolutional neural network (CNN) structure from the perspective of the transform ___domain and utilizes wavelet transform coefficients prediction to achieve stripe noise removal. In addition, the study by J. Guan et al. proposed the spatiotemporal stripe noise removal (ST-SNR) method18. This method utilizes a bidirectional gated convolutional recurrent unit (BiGCRU) to take full advantage of the strong correlation of the successive stripe components between columns in the im-age, to effectively remove the stripe noise. These methods exhibit satisfactory performance for low to medium stripe noise, but their effectiveness diminishes significantly when dealing with higher noise contamination, resulting in persistent stripe artifacts. There is also a deep unfolding iterative denoising (DINR) algorithm19 proposed by Fayya et al., which achieves the removal of stripe noise by unfolding the iterative algorithm into the form of a deep neural network. In the proposed method, Recurrent Neural Networks (RNNs) are employed to iteratively remove column noise from images. While RNNs typically generate predictions across numerous time steps, their performance can be enhanced through algorithm unfolding (or unrolling) over the input sequence. This approach allows the network to inherit prior ___domain and structural knowledge, rather than relying solely on extensive training. Deep unrolled networks, leveraging their universal approximation capabilities, are capable of more accurately approximating the target function. Deep unrolled networks offer the flexibility to learn a single model capable of handling multiple degradations non-blindly while effectively capturing spatial patterns and details.

Inspired by deep-unfolding techniques23,24, we propose an innovative wavelet deep unfolding network from the perspective of the transform ___domain for iterative stripe noise removal (WDUNINR) algorithm. The network fully considers the inherent characteristics of stripe noise and the complementary information among the coefficients of different wavelet sub-bands. It utilizes the correlation of adjacent row signals to remove the stripe noise of independent rows. This is achieved through an iterative deep-unfolding algorithm. In this algorithm, the noise estimated in one network iteration serves as the input for the next iteration. During each iteration, the algorithm estimates the noise of each row by using the information of the current row and adjacent rows. The high correlation between adjacent rows in a clean image helps the algorithm better distinguish noise from the original signal. The noise estimated at the end of each iteration is used to gradually clean the image. Thus, our method continuously feeds the output of the network, which is a partially stripe-removed image, back into the network as input. A bidirectional fusion strategy with a spatial attention mechanism is constructed to enhance the long-time correlation. This enables a more thorough separation of scene details from stripe noise and an accurate restoration of details. Additionally, a mathematical model of stripe noise and a broadband dataset are innovatively developed, enabling the algorithm to adapt to noise that varies dynamically with frequency.

Characteristics analysis of Stripe noise

Wideband microwave imaging system

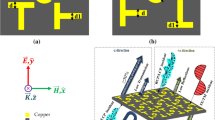
The wideband microwave imaging system comprises a parabolic reflecting surface and a multi-channel ultra-wideband digital signal acquisition system. In microwave imaging system the operational frequency range is 1GHz–6 GHz, which can cover most of the equipment’s working frequencies. Electromagnetic waves are focused onto the imaging surface through the reflective surface. The concentrated electromagnetic waves are then captured by a multi-channel ultra-wideband digitized signal acquisition system and displayed on a computer. This multi-channel ultra-wideband digitized signal acquisition system includes electro-optical sensors, all-eight optical switches, optical circulators, optical couplers, laser pulse source, photodetector and multi-channel data acquisition board. The function of electro-optical sensors is to modulate spatial electric field strength E from the radiation source onto the intensity \(\:{\text{I}}_{\text{in}}\) of the light from the laser pulse source, so the output light intensity can be expressed as:

$$\:{\text{I}}_{\text{out}}\text{=}{\frac{\text{1}}{\text{2}}\text{I}}_{\text{in}}\left(\text{1}{+\upalpha \text{E}}\right)$$
(1)

Where \(\:{\upalpha}\) is the modulation factor. When an optical signal which carried the spatial electric field information pass the photodetector, its output voltage can be expressed as

$$\:{\text{V}}_{\text{out}}\text{=G}{\text{I}}_{\text{out}}\text{=}{\frac{\text{1}}{\text{2}}\text{GI}}_{\text{in}}\left(\text{1}{+\upalpha\text{E}}\right)$$
(2)

\(\:\text{G}\) is the gain of the photodetector. By using the down-conversion characteristics of the laser pulse source, the spatial electric field signal can be moved from the high frequency to the low frequency to realize wide-band imaging. The laser emits very narrow pulses with a low duty cycle, allowing for high peak power within each pulse. These pulses can be treated as an ideal impulse train:

$$\:{\text{I}}_{\text{in}}\text{=c}\sum\:_{\text{n}=-\infty}^{{+\infty}}{\updelta}\left(\text{t-}\frac{\text{n}}{{\text{f}}_{\text{0}}}\right)$$
(3)

Where \(\:c\) is the magnitude of the impulse signal; \(\:{\updelta}\left(\text{t}\right)\) is the Dirac function. The multi-channel data acquisition board is applied to convert the voltage signal from the photodetector into digital signals, which could be processed and uploaded by a computer. For a more detailed process, please refer to20.

As depicted in Fig. 1, the 16 × 1 electro-optical sensors are positioned in the scanning plane for line scanning. The scanning direction covers 80 points per line along the y-axis, denoted as S1-S80. After the acquisition is complete, it returns to the initial acquisition point. The acquired data is saved, and the probe subsequently returns to the origin, marked as P1-P16. Throughout the imaging process of the wideband microwave imaging system, variations in the parameters of the channel devices and non-uniform coupling between the devices give rise to stripe noise in the resulting images. Additionally, each channel sensor responds uniquely to radiation sources of different frequencies. Consequently, the stripe noise in the obtained electromagnetic image fluctuates with the frequency of the radiation source.

Fig. 1
figure 1

Simple diagram of the wideband microwave imaging system.

Full size image

Stripe noise mathematical model

In order to accurately estimate stripe noise in wideband electromagnetic images, it is crucial to analyze the distributional properties of the stripe noise21 and represent them in an appropriate manner. According to references18,19, stripe noise is typically considered as additive noise, and mathematical models are used to describe stripe noise in electromagnetic images. Let \(\:X\), \(\:S\), and \(\:Y\) represent the \(\:\text{n} \times \text{m}\) matrices of the original clean image, the stripe noise, and the degraded image respectively. The noise added to the i-th row can be expressed as follows:

$$\:{\text{y}}_{\text{i}}\text{=}{\text{x}}_{\text{i}}{+}{\text{s}}_{\text{i}}$$
(4)

where \(\:{\text{y}}_{\text{i}}\), \(\:{\text{x}}_{\text{i}}\), and \(\:{\text{s}}_{\text{i}}\) are the i-th rows of \(\:Y\), \(\:X\), and \(\:S\) respectively. The elements of \(\:{\text{s}}_{\text{i}}\) have equal values. That is, \(\:{\text{s}}_{\text{i}}^{\left(\text{1}\right)}\text{=}{\text{s}}_{\text{i}}^{\left(\text{2}\right)}\text{=}{\cdots}\text{=}{\text{s}}_{\text{i}}^{\left(\text{n}\right)}\), and they are distributed as:

$$\:{\text{s}}_{\text{i}}\text{~N}\left(\text{0,}{{\sigma}}^{\text{2}}\right)$$
(5)

Although the noise variance remains constant across different rows within the same image, it can vary from one image to another. Similarly, in wideband electromagnetic images with different electromagnetic source frequencies, the carried stripe-noise intensities can be considered different. Specifically, regarding the stripe matrix S, the intensity follows a distribution of

$$\:{\sigma}\text{~U}{(}{0,}{\upbeta}{)}$$
(6)

Where U is the uniform distribution, and β is the noise intensity.

A wideband microwave imaging system was employed for conducting numerous experiments. Through these experiments, it was observed that the noise intensity varies in relation to the frequency of the radiation source. After analyzing the experimental data, we noted that the striped noise fluctuation within the electric field distribution map of the radiation source spans from 0.02 to 0.22 at different frequencies. The intensity of noise decreases with increasing frequency. The relationship between the noise intensity and the frequency of the radiation source is depicted in Fig. 2. The relationship between the noise intensity \(\: \upbeta\) and the radiation source frequency f can be expressed as:

$$\:\upbeta=\text{0.06633}\text{*}{\text{e}}^{\text{-}\text{1.696}\text{*f}}$$
(7)
Fig. 2
figure 2

The noise intensity changes with the frequency of the radiation source.

Full size image

Methods

Network architecture

The proposed architecture of WDUNINR is illustrated in Fig. 3. The WDUNINR method comprises a Haar discrete wavelet transform, a noise feature extraction module, and a deep unfolding bidirectional gated recurrent unit with spatial attention. The input electromagnetic image undergoes wavelet decomposition, resulting in a series of quarter-sized coefficients. We focus on processing the approximate sub-band coefficients, which primarily capture the distribution of the stripe noise. After passing through the feature extraction module, structured data features are extracted and enhanced. Subsequently, the data flows into the BiSAGRU structure, which engages in recurrent iterations to further attenuate the noise. By utilizing the processed approximate sub-band coefficients and other sub-band coefficients obtained after wavelet decomposition, an inverse wavelet transform is applied to generate decontaminated images.

Fig. 3
figure 3

Overall architecture diagram.

Full size image

Haar discrete wavelet transform (HDWT)

The Haar discrete wavelet transform (HDWT)22 is a widely used signal processing technique. It could decompose the signal into frequency components and spatial ___location information at different scales. Following the discrete wavelet transform, the original image is decomposed into four sets of coefficients: LL, representing the wavelet decomposition approximation sub-band coefficients; HL, representing the horizontal sub-band coefficients; LH, representing the vertical sub-band coefficients; and HH, representing the diagonal sub-band coefficients. Among them, the LL approximation coefficients reflect the low-frequency components and the overall trend of the signal. The other sub-band coefficients describe the high frequency details and local variations of the signal. The output equation of wavelet decomposition given a noisy image Y is denoted as:

$$\:\text{LL,(HL,LH,HH)=HDWT(Y)}$$
(8)

Example results of the HDWT on an electromagnetic image are illustrated in Fig. 4. It is observed that the stripe noise is predominantly concentrated within the approximate components following wavelet decomposition. After the discrete wavelet trans-form analysis of the electromagnetic image, our choice is to exclusively process the LL sub-image, which enables us to retain the original image details.

Fig. 4
figure 4

Stripe noise-contaminated image’s HDWT example: (a) Noisy contaminated image; (b) Approximation coefficients; (c) Horizontal coefficients; (d) Vertical coefficients; (e) Diagonal coefficients.

Full size image

Structural feature extraction module

To further enhance the effectiveness of stripe noise removal while better preserving the original details, a feature extraction module is incorporated. This module processes structured feature data from the image, facilitating both feature extraction and enhancement. The module consists of the convolutional layer, the Rectified Linear Unit (ReLU) layer, the pooling layer, and the fully connected layer. Specifically, a structure comprising two convolutional layers is constructed. In the first layer, 32 convolutional kernels of size 3 × 3 with a stride of 1 are utilized, employing ‘same’ padding. In the subsequent layer, 64 convolutional kernels of size 3 × 3 with a stride of 1 are employed, also utilizing ‘same’ padding. To introduce non-linearity, the ReLU activation function is applied following the convolutional layers. A Max Pooling operation with a window size of 2 × 2 and a stride of 2 is performed after each convolutional layer, as depicted in Fig. 5. Furthermore, batch normalization is applied after each convolutional layer to expedite model convergence and enhance robustness. This can be mathematically expressed as follows:

$$\:{\text{c}}_{\text{FE}}\text{=}{\text{f}}_{\text{FE}}\text{(}\text{W*}\text{LL+b}\text{)}$$
(9)

Where W represents the shared weights of the convolutional channels; LL denotes the input values; * signifies the convolution operation; b represents the bias term of the convolution operation; \(\:{\text{c}}_{\text{FE}}\) represents the outcome of the operation; and \(\:{\text{f}}_{\text{FE}}\) signifies the activation function applied during the convolution process.

Fig. 5
figure 5

Network structure diagram of feature extraction module.

Full size image

Deep unfolded iterative BiSAGRU for noise removal

Motivated by the depth unfolding technique23,24, our proposed algorithm aims to iteratively estimate the residual noise and gradually eliminate the image noise. The overall structure of the depth unfolding is depicted in Fig. 6a. Let \(\:\text{X}\text{(}\text{k}\text{)}\) represent the estimated clean sub-image at the end of the k iteration, with \(\:\text{X}\text{(0)}\text{=}{\text{c}}_{\text{FE}}\). Let \(\:\text{S}\text{(}\text{k}\text{)}\) denote the estimated noise at the end of the k iteration. The estimated contamination-free image after the k iteration is:

$$\:{\text{X}}^{\left(\text{k}\right)}\text{=}{\text{X}}^{\left(\text{0}\right)}\text{-}{\text{S}}^{\left(\text{k}\right)}$$
(10)

During the iteration process, the function \(\:\text{S}\text{(}\text{k}\text{)}\text{=f}\) is utilized to re-estimate the noise from the previous iterations, denoted as \(\:{\text{f}}_{\text{k}}\left({\text{X}}^{\left(\text{k-1}\right)}\right)\). Thus, the output of the k iteration is:

$$\:{\text{X}}^{\left(\text{k}\right)}\text{=}{\text{X}}^{\left(\text{0}\right)}\text{-}{f}_{k}\text{(}{\text{X}}^{\text{(}\text{k-}\text{1)}})$$
(11)

The purpose of designing the \(\:{\text{f}}_{\text{k}}\) function is to estimate the residual noise from the previous step. By exploiting the inherent characteristics of stripe noise, we process the electric field distribution maps of radiation sources at various frequencies, aiming to effectively eliminate this noise from the image. We introduce noise to the image based on a noise model that aligns with real-world scenarios, ensuring an effective noise removal process. To distinguish noise from the actual pixel values of the uncontaminated image within row i, we rely on neighboring row pixel values, which exhibit a strong correlation with row i. By closely examining pixel values from adjacent rows, we can deduce the extent of noise interference in row i, enabling more accurate noise prediction and removal operations. Utilizing these properties, we represent the function \(\:{\text{f}}_{\text{k}}\) using BiSAGRU, a bidirectional gated recurrent unit with the spatial attention mechanism. \(\:{\text{F}}_{\text{k}}\) denotes the k layer of a multilayer BiSAGRU, where the inputs to the entire network architecture are m vectors of length n. The inputs of the entire network architecture are m vectors of length n. Thus, for row i it can be expressed as:

$$\:{\text{f}}_{\text{k}}\text{(}{\text{x}}_{\text{i}}^{\text{(}\text{k-}\text{1)}}\text{)=}{\text{BiSAGRU}}_{\text{k}}\text{(}{\text{x}}_{\text{i}}^{\left(\text{k-}\text{1}\right)}\text{,}{\text{g}}_{\text{k}}\left({\text{x}}_{\text{0}\text{:i-}\text{1}}^{\left(\text{k-}\text{1}\right)}\right)\text{,}{\text{h}}_{\text{k}}\left({\text{x}}_{\text{i+}\text{1}\text{:m}}^{\left(\text{k-}\text{1}\right)}\right)\text{)}$$
(12)

where \(\:{\text{g}}_{\text{k}}\left(\text{.}\right)\) and \(\:{\text{h}}_{\text{k}}\text{(.)}\) are forward and backward hidden states, respectively. These state vectors encapsulate relevant information preceding and succeeding each row. By employing these techniques, the network effectively leverages spatial information from neighboring rows for noise reduction in the given row of the image. The bidirectional gated recurrent unit (BiGRU) is a variant of recurrent neural network (RNN). Unlike traditional RNNs, GRUs combines cell states into hidden states25 and integrates input and forgetting gates into a single update gate. BiGRU possesses the capacity to capture extensive redundant information from both the past and the future, enhancing the estimation of stripe components. Incorporated within the BiGRU structure, we introduce a spatial attention mechanism between the forward and backward GRUs, as illustrated in Fig. 6b. This mechanism comprises an input layer, a hidden layer for the forward GRU, a hidden layer for the backward GRU, a spatial attention feature weighting layer (SAFW), and an output layer. The SAFW module computes spatial attention weights based on the hidden states of both the forward and backward GRUs. Spatial attention feature weighting occurs post feature fusion, as depicted in Fig. 6c. The calculation of spatial attention weights is elaborated in the expanded segment of Fig. 6c. Through this module, distinct spatial locations can be dynamically assigned to varying attentional weights, allowing for the emphasis of critical spatial regions and enhancement of the model’s denoising capability.

Each pixel of the sub-image is input to the first BiSAGRU unit, where the number of units is the number of rows in the image, i.e. 256, and each output is captured by the next BiSAGRU layer. The result of the final sub-image is represented as:

$$\:{\text{LL}}_{\text{BiSAGRU}}\text{=}{\text{f}}_{\text{k}}\left(.\right)$$
(13)
Fig. 6
figure 6

Deep unfolding iterative BiSAGRU specific network structure. (a) Deep unfolded BiSAGRU. (b) BiSAGRU structural. (c) Spatial attention feature weighting (SAFW).

Full size image

Haar discrete wavelet inverse transform (IHDWT)

The Haar discrete wavelet inverse transform aims to recombine the components obtained after the wavelet transform. It restores the original signal image and reconstructs the features extracted from the wavelet transform. We utilize the three original components of HL, LH, and HH after wavelet transform. Additionally, we use the approximate components of \(\:{\text{LL}}_{\text{BiSAGRU}}\) obtained after model processing. These components are used to obtain the pollution-free image after denoising using discrete wavelet inverse transform (IHDWT). Let Z denote the resultant pollution-free image, which can be expressed as:

$$\:{\text{Z}\text{=}\text{IHDWT}\text{[}\text{LL}}_{\text{BiSAGRU}}\text{,(}\text{HL}\text{,}\text{LH}\text{,}\text{HH}\text{))]}$$
(14)

Training dataset

In this paper, we utilize the electromagnetic simulation software FEKO to conduct simulations of the wideband microwave imaging system, as depicted in Fig. 7. The version number of the software FEKO used is 2019. Simulation software allows us to generate electric field distribution images at various frequencies, locations, and with differing numbers of radiation sources. The electromagnetic images are processed using MATLAB software, with the version number R2022a. The radiation source is positioned 10 m away from the parabolic plane, situated within a height of 2.6 m and a width of 5.2 m, mirroring the dimensions of the real imaging system. The parabolic reflecting surface has a projected aperture of 3 m and a focal length of 1.7 m. The image plane is inclined at an angle of 62 degrees to the Y-axis and is positioned 2.05 m from the parabolic plane.

In the electromagnetic simulation, various frequencies, locations and numbers of interference sources are configured for imaging. The image dimensions are set at 256 × 256 pixels. A total of 6000 electromagnetic images are employed as the training dataset. Figure 8. shows a subset of the simulated electromagnetic images. The training comprises 1000 electromagnetic images within the frequency range of 1 GHz to 6 GHz. To enhance training efficiency, the training set undergoes noise reduction based on the previously established noise model. Stripe noise intensity ranging from 0.02 to 0.22 is introduced to the electromagnetic images across the frequency range of 1 GHz to 6 GHz. Figure 9. provides a visual representation of certain image pairs from the training set. For model validation, the dataset is partitioned, with 85% allocated for training and 15% for validating the model’s performance. During the training phase, the learning rate is set to 0.001, the optimization algorithm employed is Adam, and the maximum number of training epochs is capped at 100.

Fig. 7
figure 7

Simulation model of wideband microwave imaging system.

Full size image
Fig. 8
figure 8

Simulation of the electric field distribution of radiation sources at different frequencies, numbers and locations.

Full size image
Fig. 9
figure 9

Some image pairs in the training dataset. (a) The noise intensity is 0.22 for 1 GHz. (b) The noise intensity is 0.08 for 3 GHz. (c) The noise intensity is 0.04 for 5 GHz.

Full size image

Results

To validate the effectiveness of the proposed WDUNINR model, we begin by verifying its structural composition. The validation of the network’s structural composition involves confirming the efficacy of each module within the model. Subsequently, we utilize both simulation data and experimental data to compare the results with those produced by several alternative methods, including DINR, MHE and SNRWDNN. Relevant evaluation metrics are employed to demonstrate that the proposed model proficiently removes stripe noise in wideband microwave imaging system. To ensure the accuracy of the comparison with these methods, we utilize the publicly available original code. When compared with the three methods, the approach presented in this paper not only effectively mitigates stripe noise but also accurately approximates the original electric field distribution map.

Common metrics for evaluating the stripe noise removal effect for unreferenced images are vertical gradient energy (E)26 and residual nonuniformity (Ur)27. The wide-band microwave imaging system images the radiation source, and the resulting electro-magnetic image is a non-referenced image, so these two metrics are chosen to evaluate the noise removal performance.

Horizontal stripe noise exclusively contributes to the increase in vertical gradient energy, while it does not impact the horizontal gradient energy. The assessment of stripe noise removal effectiveness relies on the evaluation of vertical gradient energy (E), with smaller values indicating better denoising outcomes. The vertical gradient energy can be mathematically expressed as follows:

$$\: E = \sum\limits_{{x = 1}}^{m} {{{\sum\limits_{{y = 1}}^{n} {\left| {f(x,y)-f(x,y + 1)} \right|^{2} } } \mathord{\left/ {\vphantom {{\sum\limits_{{y = 1}}^{n} {\left| {f(x,y)f(x,y + 1)} \right|^{2} } } {(m \times n)}}} \right. \kern-\nulldelimiterspace} {(m \times n)}}}$$
(15)

Residual non-uniformity refers to the presence of a non-uniform luminance or color distribution within a digital image. It encompasses undesired spatial variations or deviations that exist in an image, surpassing the intended uniformity. Residual non-uniformity impacts the visual quality of an image and the precision of subsequent image processing tasks. The assessment of stripe noise removal effectiveness involves the evaluation of residual non-uniformity (Ur), where smaller values correspond to better denoising outcomes. Residual non-uniformity can be mathematically expressed as follows:

$$U_{r} = \frac{1}{{\mathop f\limits^{-} }}\sqrt {\frac{1}{{mn}}\sum\limits_{{x = 1}}^{m} {\sum\limits_{{y = 1}}^{n} {\left( {f\left( {x,y} \right)-\mathop f\limits^{-} } \right)^{2} } } }$$
(16)

Validation of network model structure validity

To validate the efficacy of the modules within the network structure, a series of experiments were conducted. We process the electric field distribution maps made by radiation sources from 1GHz to 6 GHz based on an iterative bidirectional gated recirculation unit (BiGRU). Experiments with 6–15 iterations were performed to determine the optimal number of iterations. The experimental outcomes are illustrated in Fig. 10. Among all frequency ranges of the wideband electromagnetic images, the 13-layer BiGRU network structure demonstrates the lowest values for both E and Ur. This structure adeptly mitigates striped noise, thus prompting us to select 13 layers as the optimal number of iterations.

Fig. 10
figure 10

Comparison of vertical gradient energy and residual nonuniformity assessment with different number of iterations. (a) The vertical gradient energy. (b) The residual non-uniformity.

Full size image

Based on this, other modules are added and their effectiveness is verified. The electric field distribution maps are made by testing 1 GHz, 3 GHz, and 5 GHz radiation sources. We add wavelet transform modules, feature extraction module, spatial attention module and evaluated them using vertical gradient energy and residual nonuniformity, respectively. The experimental results are shown in Table 1, where the E-value and Ur-value are optimized by introducing Haar discrete wavelet decomposition. The input electromagnetic image is converted into a series of quarter-sized coefficients using wavelet decomposition. We processed the striped noise by concentrating mainly on the sub-components. This helps in preserving the original signal details of the image and learning the noise intensity and distribution accurately. After wavelet decomposition, we pass the sub-coefficients through a structural feature extraction module. The powerful capability of this module in structured feature data processing and feature extraction is utilized. The experimental results show that the E-value and Ur-value decreases by adding the feature extraction module, indicating the effectiveness of the feature extraction module.

The inclusion of the spatial attention mechanism resulted in a decrease in E and Ur values. Compared to 13BiGRU, our final model improves on average 12.4% in terms of vertical gradient energy and 7.6% in terms of residual nonuniformity in processing wide-band electromagnetic images. Since the spatial attention mechanism enables the network to pay more attention to and emphasize important spatial locations by adaptively learning spatial weights. We incorporated spatial attention into the feature fusion process of the forward GRU and backward GRU within the bidirectional gated recurrent unit (BiGRU). By harnessing global contextual information, important spatial information is identified, thereby addressing the problem of limited global context in convolutional operations. Furthermore, this approach contributes to preserving the original image details. With these optimizations in place, our model demonstrates improved performance and robustness in wideband electromagnetic image denoising tasks.

Table 1 Evaluation of test dataset images involved the comparison of vertical gradient energy (E) and residual non-uniformity (Ur) values across different model structures.
Full size table

Validation and analysis of simulation results

To validate the effectiveness of the proposed model, we conducted simulations involving electric field distribution images from three radiation sources at a frequency of 2 GHz. Normalized images were subjected to the addition of stripe noise with a noise intensity of 0.13. The proposed method was employed and compared against several other methods (MHE, SNRWDNN, DINR). The comparison results are depicted in Fig. 11, where noticeable stripe noise is evident in both SNRWDNN and MHE results. The DINR method exhibits fewer noise residuals but falls short in effectively restoring the details of the original electric field distribution. Conversely, the approach presented in this paper not only adeptly mitigates stripe noise, but also accurately approximates the original electric field distribution map while preserving superior detail representation.

Fig. 11
figure 11

Comparison of denoising effects of multiple algorithms for 2 GHz electromagnetic radiation sources with noise intensity of 0.13. (a) Original Image. (b) Degraded Image. (c) The result of MHE. (d) The result of SNRWDNN. (e) The result of DINR. (f) The result of our method.

Full size image

The electric field distribution of two radiation sources at a simulation frequency for 1 GHz is plotted. Stripe noise with the noise intensity of 0.22 is added to the normalized images. The comparison results are shown in Fig. 12, where the MHE and SNRWDNN methods cannot filter out the noise completely and there is serious noise residue. The DINR method can reduce the presence of the stripe noise more significantly compared to the MHE and SNRWDNN methods. And the method proposed in this paper shows excellent results in dealing with electromagnetic images with severe stripe noise, which is significantly better than several other methods. This indicates that our proposed method can effectively remove the stripe noise and maintain better image quality of electric field distribution in the presence of high noise intensity. The method shows strong performance in processing wideband electromagnetic images with severe wide noise.

Fig. 12
figure 12

Comparison of denoising effects of multiple algorithms for 1 GHz electromagnetic radiation sources with noise intensity of 0.22. (a) Original Image. (b) Degraded Image. (c) The result of MHE. (d) The result of SNRWDNN. (e) The result of DINR. (f) The result of our method.

Full size image

To evaluate the wideband de-striping noise characteristics of the proposed method, we conducted simulations using two sets of electromagnetic images. The first set comprised electromagnetic images with two radiation sources at a frequency of 3 GHz. Stripe noise with a noise intensity of 0.15 was added to these images. The second set contained electromagnetic images with two radiation sources at 5 GHz, with stripe noise having a noise intensity of 0.1. Figure 13 illustrates the distribution of electric field strength in these two sets of electromagnetic images. We merged their incoherences to generate a multi-frequency radiation source electric field distribution map, as shown in Fig. 13c. From Fig. 14, it is evident that the MHE, SNRWDNN, and DINR methods exhibit varying degrees of residual stripe noise when processing these electromagnetic images. The MHE method appears to distort the original electric field distribution. In contrast, our proposed method effectively removes the stripe noise associated with radiation sources at different frequencies, showcasing its wideband denoising capabilities. Notably, the noise intensity in our composite electromagnetic images reaches 0.25, exceeding the range of electromagnetic image training. Nonetheless, the method proposed in this paper adeptly removes noise, underscoring its robustness. These results further underscore the proficiency of our proposed method in handling striped noise within intricate electromagnetic images, particularly under wideband conditions.

Fig. 13
figure 13

Multi-frequency radiation source electromagnetic field distribution images. (a) 3 GHz Two radiation sources. (b) 5 GHz Two radiation sources. (c) Multi-frequency radiation source.

Full size image
Fig. 14
figure 14

Comparison of de-noising effects of multiple algorithms for multi-frequency electromagnetic radiation sources. (a) Original Image. (b) Degraded Image. (c) The result of MHE. (d) The result of SNRWDNN. (e) The result of DINR. (f) The result of our method.

Full size image

Validation and analysis of experimental results

The wideband microwave imaging system mainly consists of a biased parabolic reflecting surface and a wideband receiving system of electro-optical sensors. The electro-magnetic waves are converged through the reflecting surface and then transmitted from the receiving system to the computer. Through the electromagnetic signal processing to get the radiation source of the electric field distribution map. Therefore, we can intuitively and quickly locate and detect the radiation source. The microwave imaging system is applied to carry out experimental measurements in the darkroom. Through experimental data to verify the performance of the stripe noise removal algorithm in practical applications. We built an imaging system in an anechoic chamber and performed imaging experiments on double-ridged horn antennas(1GHz–6 GHz) in a 5.2 m ×2.6 m rectangular area. Figure 15. shows the experimental test configuration of the microwave imaging system [20]. The image coordinate origin is the same height as the reflection surface as shown in Fig. 15c. We used 16 × 1 sensors to scan from the positive direction of the coordinate axis to the negative direction. The imaging reflective surface is applied in the darkroom to image the radiation source as shown in Fig. 15a. The experiments set two and three double-ridged horn antennas (1 GHz ~ 6 GHz) with different frequencies as radiation sources, respectively. They are placed in a rectangular area of 5.2 m × 2.6 m for imaging as shown in Fig. 15b.

Fig. 15
figure 15

Experimental test configuration of microwave imaging system. (a) Physical image of imaging reflector surface. (b) Physical image of horn antenna. (c) Experimental test configuration diagram.

Full size image

To validate the algorithm’s effectiveness, two radiation sources with a frequency of 1 GHz and a separation distance of 35 centimeters are utilized for imaging. The denoising performance is compared against the MHE, SNRWDNN, and DINR methods. The outcomes are presented in Fig. 16, with the red-boxed region indicating the primary distribution area of stripe noise within the electromagnetic image. Observing the experimental results, it becomes evident that the MHE and SNRWDNN methods fail to effectively eliminate the stripe noise, resulting in residual noise. The DINR method demonstrates proficiency in removing the stripe noise. However, its direct utilization of the original image for denoising leads to the compromise of the image’s original signal details, rendering it less advantageous in qualitative assessments. In contrast, our proposed method can filter out the noise as much as possible without destroying the electric field strength distribution of the radiation source. The results in Fig. 16 show that our method maintains the original signal details of the radiation source and removes the stripe noise significantly better than other methods.

To further assess the effectiveness of our proposed algorithm in eliminating stripe noise from electric field distribution maps of high-frequency radiation sources. We conduct tests on the electric field distribution maps of two 3 GHz radiation sources at 35 centimeters. Due to the relatively low intensity of stripe noise in high-frequency radiation sources, we employ a logarithmic plot representation of the electric field distribution. The experimental results are presented in Fig. 17, with the red-boxed area denoting the principal distribution region of stripe noise within the electromagnetic image. Upon analysis of the outcomes, it becomes apparent that both the MHE and SNRWDNN methods fall short in completely eradicating the stripe noise, leaving behind noise residuals. Conversely, the DINR method exhibits an excessive smoothing phenomenon, as evident in the green box in Fig. 17e. In contrast, our proposed method effectively eradicates the stripe noise while achieving superior image denoising outcomes. Our approach excels in dealing with electric field distribution maps of high-frequency radiation sources, successfully preserving original signal details and significantly mitigating the impact of stripe noise. Our algorithm proves notably advantageous in denoising high-frequency radiation source electric field distribution maps.

Fig. 16
figure 16

Comparison of various methods for 1 GHz electromagnetic radiation from two sources. (a) Image without radiation source. (b) Test image. (c) The result of MHE. (d) The result of SNRWDNN. (e) The result of DINR. (f) The result of our method.

Full size image
Fig. 17
figure 17

Comparison of various methods for 3 GHz electromagnetic radiation from two sources. (a) Image without radiation source. (b) Test image. (c) The result of MHE. (d) The result of SNRWDNN. (e) The result of DINR. (f) The result of our method.

Full size image

To assess the effectiveness of stripe noise removal in electromagnetic images containing multi-frequency radiation sources, we set the radiation source frequencies as 1 GHz, 3 GHz and 4 GHz to generate logarithmic representations of the electric field distribution. The outcomes are depicted in Fig. 18, with the red-boxed area indicating the primary distribution region of stripe noise within the electromagnetic image. From the results, it is apparent that the DINR method exhibits excessive smoothing, evident in the green-boxed region in Fig. 18e. This phenomenon arises since detectors respond differently to radiation sources of varying frequencies during electromagnetic wave detection. Consequently, the DINR method unavoidably eliminates signal during the denoising process, leading to the degradation of original signal details from the radiating source. The MHE and SNRWDNN algorithms continue to exhibit incomplete noise filtering in the local edge region of the image. In comparison, our proposed method effectively minimizes noise without compromising the electric field strength distribution of the radiation source, setting it apart from the other three methods.

Fig. 18
figure 18

Comparison of various methods for electromagnetic radiation sources at 4 GHz (Top Left), 3 GHz (Top Right), and 1 GHz (Bottom Left). (a) Image without radiation source. (b) Test image. (c) The result of MHE. (d) The result of SNRWDNN. (e) The result of DINR. (f) The result of our method.

Full size image

To verify the wideband denoising properties of the proposed algorithm, we quantitatively evaluated the above test images and test images at other frequencies using vertical gradient energy (E) and residual nonuniformity (Ur). The test results are shown in Table 2. In addition, we processed the test images from 1 GHz to 6 GHz using each of the four methods and evaluated the processed images, and the results are shown in Fig. 19. We compared the quantitative evaluation results of the original images of the experimental tests. We can observe that compared to the other three methods, our proposed method has the lowest E and Ur values and achieves better stripe noise removal results.

Table 2 Comparison of vertical gradient energy (E) and residual non-uniformity (Ur) values across different algorithms.
Full size table
Fig. 19
figure 19

Comparison of vertical gradient energy (E) and residual non-uniformity (Ur) values across different algorithms. (a) The vertical gradient energy. (b) The residual non-uniformity.

Full size image

In summary, our method shows outstanding advantages in experimental data. Through comparing quantitative and qualitative evaluation results with other methods, we demonstrate the effectiveness and superiority of our proposed algorithm for wideband electromagnetic image denoising. The method can successfully remove striped noise without loss of image details and features. More accurate localization is achieved in wideband microwave imaging systems.

Discussion

In this paper, we propose an innovative wavelet deep unfolding network from the perspective of the transform ___domain for iterative stripe noise removal (WDUNINR) in wideband microwave imaging systems. Unlike existing de-striping methods, WDUNINR consists of Haar discrete wavelet transform, noise feature extraction module, and deep unfolding bidirectional gated recurrent unit with spatial attention. Utilize the wavelet de-composition to convert the input electromagnetic image into a series of quarter-sized coefficients. The model iteratively de-stripes the main concentrated sub-band coefficient of the stripe noise line by line. During each iteration, BiSAGRUs are used to estimate the line noise, using information from adjacent lines to help distinguish between noise and actual pixel values. Through the verification of a large amount of experimental and simulation data, our proposed method outperforms other classical denoising methods in both quantitative and qualitative evaluations. The method can effectively remove the striped noise from wideband electromagnetic images. Enabling fast and accurate localization of interference sources in wideband microwave imaging systems. Although the proposed method has high accuracy, it still has the disadvantage of relatively large computational volume. We will optimize the computation reduction method by application in the future work.