Introduction

The meteoric expansion of the e-commerce sector has markedly accelerated the evolution of the logistics industry within China. This sector is a significant consumer of conventional fossil fuels and a major contributor to substantial carbon emissions. In light of the progressive degradation of the global climate, the adoption of low-carbon logistics strategies has become an imperative adaptation. According to statistics from Greenpeace Organization1, carbon emissions associated with China’s logistics sector are projected to reach 55.65 million tons in 2022 as shown in Fig. 1, reflecting an average increase of 25.1% over the past six years. The carbon emissions within the logistics industry primarily originate from three major areas: warehousing, packaging materials, and transportation. Notably, transportation alone accounted for 62.7% of the total emissions within the logistics sector in 2022. This highlights the urgent need for low-carbon transportation solutions in logistics, which has spurred innovative research initiatives, including energy-efficient intelligent transportation scheduling2, green logistics3 and low-carbon logistics network design4.

Fig. 1
figure 1

Logistics business involved carbon emissions in China (2017-2022).

Full size image

The comprehensive supporting infrastructure and reliable performance of traditional fuel vehicles have established them as the dominant mode of logistics transportation over recent decades. In contrast, electric vehicles (EVs) face several significant challenges, including limited battery capacity, susceptibility to climatic conditions affecting battery performance, and insufficient distribution of charging stations (CSs). It is not uncommon to observe numerous vehicles queuing to charge at these stations. Such issues severely hinder the transportation efficiency within the logistics sector and significantly impede the adoption of EVs in this industry. This is particularly critical in urban logistics, where the timeliness of transportation is a paramount concern. Generally, urban areas tend to have a relatively higher number of CSs. Consequently, a viable strategy to enhance the transportation efficiency of urban logistics involves generating multiple optimal transportation routes for heterogeneous electric logistics vehicles (ELVs) that possess varying load capacities and battery specifications, all while ensuring timely transportation. This approach aims to minimize energy consumption during transit. Each route for an ELV comprises logistics packages (LPs) and CSs, with each vehicle visiting these locations sequentially according to its designated route. Therefore, determining the optimal routes for ELVs for multiple CSs presents a practical and intriguing challenge.

Numerous studies have focused on the formulation of transportation routing optimization models5 and the collaborative logistics of pickup and delivery systems6,7. There is also significant research dedicated to the simultaneous optimization of routing and charging for fleets of ELVs8. Considering elements such as fixed, transportation, and carbon emission costs, a model for optimizing low-carbon logistics routing for cold chains was developed, integrating constraints concerning vehicle load and delivery windows9. Zhang et al.10 proposed a model for low-carbon, flexible, time-sensitive pickup and delivery (LC-FTSP-TW) aimed at minimizing greenhouse gas emissions within logistics frameworks, accommodating fluctuations in traffic conditions, customer delivery timelines, and vehicle energy requirements. The M-NSGA-II algorithm was employed to reduce energy consumption and carbon emissions in urban logistics transportation11. Considering that logistics transportation must account for factors such as energy consumption and the spatial distribution of CSs, the associated optimization problem exhibits high dimensionality and strong nonlinearity, which often struggle to provide efficient and scalable solutions for traditional optimization methods. Therefore, the deep reinforcement learning (DRL) method featuring an attention mechanism was designe to optimize the longest or total travel duration for vehicles of varying capacities. This method includes a vehicle selection decoder and a node selection decoder, facilitating the automated selection of both a vehicle and a node for that vehicle at each decision point12. Furthermore, given the constraints of battery capacity, a novel optimal charging strategy for ELVs on long journeys was introduced, providing drivers with precise charging guidance for specific routes13. However, none of the aforementioned studies have addressed the heterogeneity of ELVs or the presence of multiple CSs concurrently.

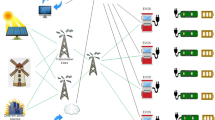
In contrast to existing literature, the proposed LECS system is designed to identify optimal transportation routes for heterogeneous ELVs, each characterized by different load capacities and battery specifications, as shown in Fig. 2. The optimal transportation route is anticipated to be a Hamiltonian tour, representing a permutation of a subset of LPs and CSs. Notably, each LP must be assigned exclusively to the tour of a single ELV and can only be included once. Furthermore, it is assumed that each ELV can achieve a full charge within a reasonable timeframe upon arrival at CS. Unlike traditional logistics scheduling approaches, which primarily focus on vehicle load capacity and routing optimization, the proposed method considers multiple factors, including the heterogeneity of ELVs, the distribution of CSs, and the timeliness of transportation.

Fig. 2
figure 2

Illustration of LECS system in urban logistics.

Full size image

The deployment of a LECS holds the promise of substantially curtailing both energy consumption and carbon emissions in urban logistics transportation. This system is particularly appealing to logistics companies that utilize unmanned ELVs. Notably, improvements in charging efficiency could further diminish carbon emissions across the entire urban logistics transportation sector, thereby facilitating the adoption of new energy vehicles from an economic standpoint. However, the challenges associated with LECS system are considerable. Primarily, it is essential to identify an optimal Hamiltonian transportation tour for each heterogeneous ELV while accommodating multiple CSs and adhering to constraints related to maximum transportation duration. The tour may encompass any subset of all LPs and CSs, indicating that the process of determining the optimal tour may require exponential time for any given ELV. Furthermore, each LP must be assigned precisely once. Due to the high time complexity involved, there currently exists no effective exact algorithm or approximation algorithm capable of addressing LECS problem.

Fortunately, the DRL-based graph attention mechanism dynamically adjusts learnable attention weights, enabling ELVs to focus on critical nodes (such as CSs or key task nodes) at different mission stages while filtering out irrelevant information, which can effectively reduce the interference of noisy nodes and provide efficient and scalable solutions for the associated optimization problem with high dimensionality and strong nonlinearity. Therefore, this paper formulates LECS problem, which aims to minimize the total energy consumption of various heterogeneous ELVs with differing loads and battery capacities, while adhering to the constraints of maximum transportation duration. After analyzing the complexity of LECS problem, it was initially modeled as a Markov decision process (MDP). Subsequently, a heterogeneous attention model based on encoder-decoder architecture (HAMEDA) approach, which is designed to automatically learn a construction policy for solving LECS problem, consisting of an encoding phase and a decoding phase. Finally, HAMEDA is trained using REINFORCE algorithm14. The primary contributions of this study are outlined as follows:

  1. 1.

    A novel LECS framework is introduced, aiming to optimize total energy usage across a network of diverse ELVs. Through rigorous theoretical examination, it is demonstrated that solving the LECS problem is non-deterministic polynomial-time hard (NP-hard).

  2. 2.

    To capture the complex relationships between LPs and CSs, a heterogeneous graph attention network is employed to encode the features of nodes to the embeddings in the encoding phase of HAMEDA model. During the decoding phase, a masking technique is integrated to effectively manage the graph structure, thereby precluding the selection of infeasible nodes and enhancing the overall solution quality. Furthermore, to enhance training stability, proposed model is trained via DRL in an unsupervised manner with the one-agent-per-decoding-step strategy.

  3. 3.

    Extensive simulations demonstrate that the proposed HAMEDA model reduce the total energy consumption by at least 1.64% compared to traditional heuristic and learning-based algorithms, while only 3.5% higher than the optimal solution. Furthermore, HAMEDA offers an optimal balance between execution time and solution quality, making it particularly suitable for large-scale applications requiring prompt decision-making. The scheme has been open-sourced, enabling researchers to utilize it for evaluating auto-scaling methodologies.

The structure of the remainder of this study is organized as follows: Section II surveys pertinent literature. Section III delineates the system model and articulates the LECS problem. Section IV details the HAMEDA model, proposed as a resolution to the LECS challenge. Section V undertakes a performance assessment. Section VI culminates with the conclusions.

Related work

Low-carbon logistics network design

Recently, the design of networks for low-carbon logistics has garnered significant attention from researchers both domestically and internationally15,16. Liang et al.17 developed a dynamic generalized method of moments (GMM) model and a Tobit model to investigate the potential temporal and spatial effects of environmental regulation on the green total factor productivity within the low-carbon logistics sector. For regional multimodal logistics networks, Jiang et al.18 proposed an enhanced adjustable robust optimization method aimed at reducing carbon dioxide emissions. In pursuit of harmonizing the goals of governmental bodies with those of cold chain logistics firms, Zhang et al.19 devised a bilevel programming-based decision-making model that seeks to minimize the aggregate costs within the entire cold chain logistics framework. In subsequent research, the intricacies of a low-carbon integrated forward/reverse logistics network were analyzed, leading to the development of a fuzzy stochastic programming model aimed at reducing costs associated with carbon trading balances20. Additionally, to achieve specific carbon dioxide emission targets in a regional logistics network, a bi-level optimization model was developed, integrating the selection of investments in logistics infrastructure and the allocation of subsidies for sustainable transportation modes21. To facilitate enterprises in reducing carbon emissions during current logistics operations, Wang et al. formulated a green urban closed-loop logistics distribution network model designed to minimize both greenhouse gas emissions and total operational costs22. Li et al.23 proposed an optimization model for the EV routing problem, tailored to the sharing economy, with the aim of minimizing comprehensive costs including operational, penalty, queuing, electricity, and environmental expenses. A Catastrophic Adaptive Genetic Algorithm (CA-GA), based on Monte Carlo sampling, was engineered to solve the low-carbon path optimization issue, accounting for transportation costs, time expenses, and carbon emission costs amidst dual uncertainty24. Furthermore, a multistage planning approach for developing low-carbon charging infrastructure for EVs was introduced, featuring an innovative travel route choice model that allows EV drivers to make multiple charging detours before completing their routes25. Zhang et al.26 crafted a sparrow search algorithm enhanced by an adaptive t-distribution for tackling a multi-objective low-carbon multi-modal transportation planning problem with fuzzy demand and fuzzy time (MOLCMTPP-FDFT), aiming to minimize both costs and time while integrating essential policies on carbon emissions, carbon taxes, carbon trading, and carbon offsets.

The aforementioned methods address the challenges associated with low-carbon path optimization and decision-making in dynamic network environments. In contrast to the studies cited above, this paper introduces an innovative scheduling mechanism aimed at minimizing energy consumption and carbon emissions produced by heterogeneous ELVs during urban logistics transportation.

Cost optimization method design

Challenges within the transportation sector are broadly categorized under generalizations of the vehicle routing problem (VRP) or the traveling salesman problem (TSP), both recognized as NP-hard issues. Consequently, conventional strategies to manage such NP-hard challenges generally fall into three categories: exact algorithms, heuristic algorithms, and methods reliant on DRL. Exact algorithms are designed to yield optimal solutions through enumeration or other techniques. However, they generally exhibit exponential running times27. In contrast, approximate algorithms can deliver feasible solutions within polynomial time and are capable of identifying approximate solutions that are relatively close to the optimal for large-scale cost optimization challenges28,29. Compared to the aforementioned two categories, DRL-based methods tend to produce solutions more rapidly and possess the ability to autonomously learn representations of states and actions. This characteristic diminishes the dependence on ___domain-specific knowledge and may uncover complex patterns that traditional methods fail to capture. To derive an approximate solution for covering salesman problem (CSP), Li et al.30 introduced a novel deep learning approach utilizing multi-head attention (MHA), which was trained using unsupervised DRL techniques. To reduce the overall flight distance of unmanned aerial vehicles (UAVs), this study introduces a DRL-based approach, employing a multi-head heterogeneous attention (MHHA) mechanism. This mechanism supports the strategic sequential formulation of routes with an emphasis on energy efficiency31. Several frameworks leveraging DRL have been developed to address a challenging yet nontrivial variant of TSP32,33. In addressing large-scale problem scenarios to enhance solution quality, Zhao et al. suggested a novel DRL model, which incorporates a local search method aimed at further elevating the quality of solutions. This model is structured around an actor, an adaptive critic, and a routing simulator34. Additionally, an adaptive car-following trajectory control algorithm (e.g., deep adaptive control) was developed to address the challenges associated with adaptive vehicle trajectory control across varying risk levels35. Furthermore, to decrease the total charging time for EVs, the research presented a DRL algorithm focused on reducing not only the overall charging duration for EVs but also achieving significant reductions in the origin-destination distance36.

However, the presence of heterogeneous vehicles and the mixing of CS and LP nodes can negatively affect the convergence and efficiency of optimization models, factors that have not been adequately addressed by the previously mentioned methods. In contrast to the works discussed above, this paper proposes a heterogeneous attention model-based approach HAMEDA for LECS problem utilizing DRL. This approach demonstrates superior performance compared to traditional heuristic methods and other learning-based techniques.

System model and problem formulation

System model

This study examined a low-energy consumption scheduling system composed of a logistics cloud platform, an online community consisting of n users and z CSs, as well as m ELVs with varying load and battery capacities. Each user is associated with an LP that requires collection by an ELV. For clarity, \(N=\{1,2, \cdots ,n\}\) is used to uniformly represent both users and their corresponding LPs. \(Z=\{1,2, \cdots ,z\}\) is employed to denote the collection of CSs, while \(M=\{1,2, \cdots ,m\}\) is used to represent ELVs. All computations for this system are conducted by the logistics cloud platform. Given the presence of multiple CSs, each may be visited by an ELV multiple times or not at all. It is assumed that these CSs have been established within the region of interest, and the ___location information \((x_0^e,x_1^e, \cdots ,x_z^e)\) of CSs has been provided to the platform. Each user \(i \in N\) is also required to submit pertinent information \(U{I_i} = (w{_i^{LP}},x_i^u)\) to the platform, which includes \(w_i^{LP}\) and \(x_i^u\), representing the weight of LP i and its current ___location, respectively. Generally, weight serves as a standard criterion for logistics services37. Additionally, each ELV must submit information \(V{I_m} = (x_m^v,R_m ,R_m^r,r_m ,w_m^{\max },w_m^{ELV})\) to the platform, where \(x_m^v\) is the current ___location of ELV m and \(R_m ,R_m^r,r_m\) are the maximum battery capacity, current battery capacity, and unit battery consumption of ELV, respectively. It is assumed that each CS possesses unlimited energy capacity, ensuring that all arriving ELVs can be fully recharged. \(w_m^{\max },w_m^{ELV}\) are the maximum and current load weight of ELV m’s, respectively.

LECS system represents a complete graph \(G=(X,E)\), whereis a combination of LP set \({X^{LP}} = ({x_1}, \cdots ,{x_n})\), the depot \({x_0}\), and CSs set \({X^{CS}} = ({x_{n + 1}}, \cdots ,{x_{n + z}})\). The node setcan be constructed as \(X = \{ {x_0}\} \cup {X^{CS}} \cup {X^{LP}}\). \(E = (\{ {x_i},{x_j}\} :i < j)\) is the edge set. Each edge \(\{ {x_i},{x_j}\}\)is associated with a non-negative travel time \({t_{i,j}}\) and the shortest route length \(d({x_i},{x_j})\).

A feasible ELV m’s tour \({\pi ^m}\) commences at the depot \({x_0}\), sequentially traverses a series of LPs and CSs, and ultimately returns to \({x_0}\), where each CS may be accessed multiple times. To facilitate the representation of ELV access sequence in the most efficient manner, this study introduce \({\delta _z} - 1\) dummy nodes for each CS, which share their respective locations. The set of dummy nodes is \(X_d^{CS}\). The number \({\delta _z}\) of dummy nodes associated with each CS, is determined by the frequency of visits to the corresponding CS z. It is advisable to minimize \({\delta _z}\) to reduce the overall size of the network38. For convenience, \(I = {X^{CS}} \cup {X^{LP}} \cup X_d^{CS}\) and \({Z'} = {X^{CS}} \cup X_d^{CS}\) is defined. Consequently, the total number of nodes in the resulting augmented graph \(G' = (I,E)\) can be calculated as follows:

$$\begin{aligned} count = n + 1 + \sum \limits _{k = 0}^{\textrm{z}} {{\delta _z}} \end{aligned}$$
(1)

The following section presents the formulation of the problem and an analysis of its complexity. Table 1 provides a list of commonly used notations.

Table 1 Frequently used notations.
Full size table

Problem formulation

In an LECS system, the study aims to identify a maximum of transportation Hamiltonian tours, one for each ELV, that commence and conclude at the depot while visiting a selected subset of nodes, including CSs as necessary, to minimize the total energy consumption associated with transportation. This study defines the arc set \(A = \{ ({x_i},{x_j}):i < j{{ \ }}~and~{{\ }}i,j \in I\}\) within graph \(G'\). Therefore, the edge set E is substituted with an arc set A, where each arc \(({x_i},{x_j}):i < j{{\ }}~and~{{ \ }}i,j \in I\) corresponds to a respective edge \(\{ {x_i},{x_j}\}\). Additionally, the decision variable \({x_{i,j}}\) is expressed as follows:

$$\begin{aligned} {x_{i,j}} = \left\{ {\begin{array}{*{20}{c}} 1& {if~~{{ \ }}{x_i},{x_j} \in {\pi ^m},i < j}\\ 0& {otherwise} \end{array}} \right. \end{aligned}$$
(2)

The duration of the transportation tour for ELV’s can be expressed as follows:

$$\begin{aligned} dist({\pi ^m}) = \sum \limits _{{x_i},{x_j} \in {\pi ^m},i < j} {d({x_i},{x_j}) \cdot {x_{i,j}}} \end{aligned}$$
(3)

where \(d({x_i},{x_j})\) is the shortest route length between node \({x_i}\) and node \({x_j}\).

The remaining load capacity of ELV m is expressed as follows:

$$\begin{aligned} w_m^{ELV} = w_m^{\max } - \sum \limits _{i \in {\pi ^m}} {w_i^{LP}} \end{aligned}$$
(4)

The remaining transportation duration of ELV m is given as follows:

$$\begin{aligned} T_m^{ELV} = {T_{\max }} - \sum \limits _{j \in {\pi ^m}} {{\eta _j}} - \sum \limits _{i,j \in {\pi ^m},i < j} {{t_{i,j}}\left( m \right) {x_{i,j}}} \end{aligned}$$
(5)

and

$$\begin{aligned} {t_{i,j}}\left( m \right) = {{{d({x_i},{x_j})}} \!/ \!{{{v_m}}}} \end{aligned}$$
(6)

where \({T_{\max }}\) is the maximum transportation duration for each EV, which is treated as a constant; \({t_{i,j}}\) is the travel time from node i to node j; \({v_m}\) is the average speed of ELV m. \({\eta _j}\) is also assumed to be constant, signifying the service time when node i is classified as a LP; otherwise, it indicates the recharging time.

The total energy consumption of ELV m can be expressed as follows:

$$\begin{aligned} Q_m \left( {{\pi ^m}} \right) = r_m \cdot dist({\pi ^m}) \end{aligned}$$
(7)

The remaining battery capacity of ELV m is given as follows:

$$\begin{aligned} R_m^r = R_m - Q_m \left( {{\pi ^m}} \right) \end{aligned}$$
(8)

The objective of this study is to minimize the total energy consumption of all ELVs. This issue is defined as LECS problem, which can be articulated as follows:

$$\begin{aligned}&{{\varvec{(LECS )}}}~~~\min {{ \ }}\sum \limits _{m \in M} {Q_m \left( {{\pi ^m}} \right) }\end{aligned}$$
(9)
$${{\varvec{s.t.}}}{{ \ }}\sum \limits _{j:({x_i},{x_j})\in A}{{x_{i,j}}}=\sum \limits _{j:({x_j},{x_i}) \in A}{{x_{j,i}}}=1,\forall i \in {X^{LP}}$$
(9-1)
$$\sum \limits _{j:({x_i},{x_j}) \in A,i \ne j} {{x_{i,j}}} \le 1,{{ \ }}\forall i \in X$$
(9-2)
$$\sum \limits _{j:({x_i},{x_j}) \in A,,i \ne j} {{x_{i,j}}} = \sum \limits _{j:({x_j},{x_i}) \in A,,i \ne j} {{x_{j,i}}} ,{{ \ }}\forall i \in I$$
(9-3)
$$\sum \limits _{i \in I,i \ne j} {{x_{i,0}}} = \sum \limits _{i \in I,i \ne j} {{x_{0,i}}} \le m,\forall j \in M$$
(9-4)
$$\sum \limits _{i \in {\pi ^m}} {w_i^{LP}} \le w_m^{\max },\forall m \in M$$
(9-5)
$$\begin{array}{l} R_m - r_m \cdot d({x_i},{x_j}) \cdot {x_{i,j}} \ge 0, \forall m \in M,i \in N,j \in {Z'} \end{array}$$
(9-6)
$$\begin{array}{l} R_m - r_m \cdot d({x_i},{x_j}) \cdot {x_{i,j}} \ge 0, \forall m \in M,i \in N,j \in {Z'} \end{array}$$
(9-7)
$${\pi ^m} \cap {\pi ^{m'}} = \{ {x_0}\} ,\forall m,m' \in M,m \ne m'$$
(9-8)
$${s_i} - {s_j} + 1 \le \left( {1 - {x_{i,j}}} \right) \left| {{\pi ^m}} \right| ,\forall i,j \in {\pi ^m},i \ne j$$
(9-9)
$$1 \le {s_i} \le \left| {{\pi ^m}} \right| ,\forall i \in {\pi ^m}$$
(9-10)
$$\begin{array}{l} {\tau _j} \ge {\tau _i} + \left( {{t_{i,j}} - {\eta _j}} \right) {x_{i,j}} - {T_{\max }}(1 - {x_{i,j}}),{{ \ }} \forall i \in I,j \in I\backslash \{ 0\} \end{array}$$
(9-11)
$$0 \le {\tau _0} \le {T_{\max }}$$
(9-12)
$${t_{0,j}} \le {\tau _j} \le {T_{\max }} - \left( {{t_{j,0}} + {\eta _j}} \right) ,\forall j \in I\backslash \{ 0\}$$
(9-13)
$${x_{i,j}} \in \left\{ {0,1} \right\} ,{{ \ }}\forall i \in I$$
(9-14)

where \({\tau _i}\) is a time variable that indicates the arrival time of an ELV at node i, which is initialized to zero upon departure from the depot. Constraint (9-1) stipulates that each LP must be accessed only once. Constraint (9-2) ensures that each CS is visited at most once, including the dummy nodes. Constraint (9-3) mandates that each LP possesses a single in-degree and a single out-degree. Constraint (9-4) limits the total number of tours to a maximum of m. Furthermore, each ELV is required to commence and conclude its journey at the depot. Constraint (9-5) guarantees that the cumulative weight of all LPs within ELV m’s tour \({\pi _m}\) does not exceed its maximum load capacity. Constraint (9-6) ensures that each ELV can access the subsequent LP based on its current battery capacity. Similarly, constraint (9-7) confirms that each ELV can reach the nearest CS, also contingent upon its current battery capacity. Constraint (9-8) prohibits the overlap of routes between any two ELVs, with the exception of the depot. Constraints (9-9) and (9-10) prevent the formation of subtours within the route of any ELV. The arrival time at each node for each ELV is monitored through constraint (9-11). Constraint (9-12) establishes an upper limit on arrival times upon return to the depot, specifically the maximum transportation duration \({T_{\max }}\). Constraints (9-13) provide lower and upper bounds on arrival times at LPs and CSs, ensuring that each tour is completed by time \({T_{\max }}\). The final constraint defines the variables as binary.

Hardness analyzing

This study endeavors to identify an exact algorithm for LECS problem. However, as demonstrated by Theorem 1, LECS problem is classified as NP-hard. Subsequently, the complexity associated with LECS problem is investigated.

Theorem 1

LECS problem is NP-hard.

In the realm of logistics optimization, the Green vehicle routing problem (G-VRP)39 is characterized on a comprehensive graph wherein the vertices symbolize the locations of LPs, ELVs, and a central depot. The primary aim of G-VRP is to ascertain a collection of routes for ELVs that optimize efficiency by minimizing the cumulative distance traveled. Each tour commences at the depot, visits a designated set of LPs within a predetermined time constraint, and subsequently returns to the depot, all while adhering to the driving range limitations imposed by the battery capacity of ELVs. Additionally, each tour may incorporate stops at one or more CSs to facilitate recharging of ELVs during the journey. G-VRP can be expressed as follows:

$$\begin{aligned}&{{\varvec{ (G-VRP)}}}~~~\min \sum \limits _{m \in M} {dist({\pi ^m})} ~~~~~~ \nonumber \\&{{\varvec{ s.t.}}}~~~ (9-1)-(9-4)~ and ~(9-6)-(9-14) \end{aligned}$$
(10)

LECS problem presents differences from G-VRP in two main aspects. Firstly, LECS incorporates an additional constraint (9-1) that ensures the heterogeneity of ELVs with varying load weights. Furthermore, the objective function (9) of LECS considers the heterogeneity of ELVs in terms of their different unit energy consumption. Therefore, the G-VRP problem can be seen as the special case of LECS problem, where the ELVs’ load weights are unfinite. Obviously, this problem is a generalization of the well-known NP-hard G-VRP problem39. This indicates that LECS problem is at least as complex as G-VRP. Given that G-VRP is classified as NP-hard39, it follows that LECS problem is also NP-hard.

Reformulation as MDP

Given that LECS problem is classified as NP-hard, obtaining an optimal solution within polynomial time is infeasible. Route formulation within the LECS is envisioned as a series of sequential decision-making tasks. This perspective allows for a natural formulation of the problem as an MDP model, which can be effectively addressed using Encoder-Decoder architecture40.

1) State: The global state \({S_t}\) encompasses comprehensive state information, whereas each ELV m possesses only partial state information \(s_t^m,s_t^m \in {S_t}\). The state \(s_t^m = \left( {\pi _t^m,R_m^r\left( t \right) ,w_m^r\left( t \right) ,T_m^r\left( t \right) } \right)\) comprises the partial solution \(\pi _t^m\), the remaining battery capacity \(R_m^r\left( t \right)\), the remaining load capacity \(w_m^r\left( t \right)\), and the remaining duration limit \(T_m^r\left( t \right)\) at time step t for ELV m. Additionally, \(\pi _t^m\) contains all nodes that have been visited up to time step t.

2) Action: The action space at time step t is \(a_t^m = \left( {N_t^r,{Z_t}} \right) ,m \in M\), where \(N_t^r\) is the set of available LP nodes that have not yet been visited but can be accessed by ELV m at time step t, \({Z_t}\) is the set of available CS nodes that ELV m can reach at time step t. Therefore, the action space for all ELVs can be defined as follows:

$$\begin{aligned} {A_t} = \bigcup \nolimits _{m \in M} {a_t^m} \end{aligned}$$
(11)

The agent must select an action \({A_t}\) from the set at time step t unless it reaches a terminal state.

3) Reward: To minimize the overall energy consumption of all ELVs, the reward is defined as the negative of the objective value. Consequently, the reward function R is computed as follows:

$$\begin{aligned} R = - \sum \limits _{m \in M} {Q_m \left( {{\pi ^m}} \right) } \end{aligned}$$
(12)

4) Transition: The subsequent state \(s_{t + 1}^m=\left( {\pi _{t + 1}^m,R_m^r\left( {t + 1} \right) ,w_m^r\left( {t + 1} \right) ,T_m^r\left( {t + 1} \right) } \right)\) is determined by the node selected at time step t. The partial solution is concatenated with the newly selected node j (i.e., resulting in \(\pi _{t + 1}^m = \left( {\pi _t^m;\left\{ j \right\} } \right)\)). The modifications to \(w_m^r\left( {t + 1} \right)\) and \(T_m^r\left( {t + 1} \right)\) are executed in accordance with Eq. (4) and (5). Specifically, if node j is classified as a LP node, \(R_m^r\left( {t + 1} \right) = R_m^r\left( t \right) - {r_m}\left( {i,j} \right)\) is defined, where \({r_m}\left( {i,j} \right)\) is the energy consumption of ELV m for traversing from the previous node i to the current node j. Conversely, if node j is categorized as a CS node, then \(R_m^r\left( {t + 1} \right) = R_m\) is applicable.

Methods

This section introduces HAMEDA model as a solution to LECS problem, which facilitates the dynamic extraction of additional features from nodes. The HAMEDA model, upon completion of training, facilitates the calculation of the optimal value of the objective function. This calculation leverages the parameters derived from training and specific input instances. As illustrated in Figure  3, the HAMEDA model employs an Encoder-Decoder architecture to parameterize and educate the agent’s policy \(pr{o_\theta }(\pi |X)\). Each decision-making round is divided into \(T\) time steps. At each time step \(t\), the encoder projects and embeds the graph nodes, capturing their spatial and contextual relationships, while the one-agent-per-decoding-step procedure is employed to improve the creation of optimal transportation routes for the decoder. Specifically, this policy strategically selects nodes sequentially for each ELV, culminating in a node permutation that integrates the depot, all LPs, and a subset of CSs, collectively denoted as \(\pi = {\pi ^0}, \cdots ,{\pi ^m}, \cdots ,{\pi ^{\left| M \right| }},m \in M\). Furthermore, is a permutation of the selected nodes for ELV m, which can be defined as follows:

$$\begin{aligned} {\pi ^m} = \pi _0^m\left( { = {x_0}} \right) ,\pi _1^m, \cdots ,\pi _{\left| {{\pi ^m}} \right| }^m\left( { = {x_0}} \right) \end{aligned}$$
(13)

where \(\left| {{\pi ^m}} \right|\) is the total number of nodes selected by ELV m.

Consequently, for the input instance X and the set of learnable parameters \(\theta\), the probability distribution \(pr{o_\theta }(\pi |X)\) of solution \(\pi\) is regarded as the policy for determining \(\pi\) given \(\theta\). The policy function can be expressed as follows:

$$\begin{aligned} pr{o_\theta }(\pi |X) = \prod \limits _{m \in M} {\prod \limits _{t = 1}^{\left| {{\pi ^m}} \right| } {pr{o_\theta }(\pi _{_t}^m|X,\pi _{_{1:t - 1}}^m)} } \end{aligned}$$
(14)

where \(\pi _{_t}^m\) is the node selected by EV at decision step t; \(\pi _{_{1:t - 1}}^m\) is the node selected by m at \(t-1\) time steps. The objective is to identify the optimal parameter set \({\theta ^ * }\) that generates the optimal tour \({\pi ^ * }\) for EVs.

Fig. 3
figure 3

Tour construction of HAMEDA model applied to two ELVs and five target nodes.

Full size image

Model design

The HAMEDA framework is bifurcated into two pivotal phases: encoding and decoding. The encoding phase sees the encoder extracting structural features and embedding each graph node of the input instance X. These embeddings are crucial for generating the key of HAMEDA. During the decoding phase, the framework processes these embeddings along with the step context and a mask denoting infeasible nodes, thereby aiding the node selection process for each ELV. Given the requirement to manage transportation tours for numerous ELVs concurrently, this study introduces an innovative decoding strategy tailored to the multi-agent dynamics of the problem. This strategy effectively mitigates the challenges posed by the combinatorial expansion inherent in the multi-agent action space.

Encoding phase

To construct the key for each node, a heterogeneous graph attention (HGA) network-based encoder is employed to encode the features of the nodes into embeddings that encapsulate the structural patterns of the input instance X. As illustrated in Figure  4, the encoder comprises L identical attention layers. Each attention layer consists of two sub-layers: a multi-head heterogeneous attention (MHHA) sublayer and a simple, position-wise feed-forward (FF) sublayer. MHHA sublayer incorporates both self-attention and cross-attention mechanisms, enabling the identification of relationships among all nodes, including CS nodes and ELV nodes. FF sublayer functions as a fully connected network. A residual connection operation is implemented between every two sublayers, followed by a normalization operation. The \({d_x}\)-dimensional input node \({x_i}\) is initially mapped to the \({d_h}\)-dimensional initial node embeddings \(h_i^{(0)}\). This mapping can be achieved through a linear transformation that incorporates learnable parameters as follows:

$$\begin{aligned} h_i^{(0)} = \left\{ {\begin{array}{*{20}{c}} {W{x_i} + b}& {if~~{{ \ }}i \ne 0}\\ {{W_0}{x_i} + {b_0}}& {if ~~{{ \ }}i = 0} \end{array}} \right. \end{aligned}$$
(15)

where \(W,{W_0} \in {^{{d_x} \times {d_h}}}\) and \(b,{b_0} \in {^{{d_h}}}\) are the learnable parameters; and \({x_0}\) is the starting node when \(i = 0\) is considered. Consequently, this study employs the self-reliant parameters \({W_0},{b_0}\) for \({x_0}\). Given that there are \(count - 1\) nodes in graph \(G'\), excluding the depot, the configuration is denoted as \(\left( {count - 1} \right) {d_h}\) for the initial node embedding.

Fig. 4
figure 4

Illustration of encoding phase in HAMEDA model.

Full size image

To extract features, the self-attention mechanism is employed to compute the key, query, and value vectors for node i, which can be expressed as follows:

$$\begin{aligned} \begin{array}{c} {K_i} = {W^k}h_i^{(L - 1)}\\ {q_i} = {W^q}h_i^{(L - 1)}\\ {v_i} = {W^v}h_i^{(L - 1)} \end{array} \end{aligned}$$
(16)

where \({W^k},{W^q} \in {R^{{d_h} \times {d_q}}}\) and \({W^v} \in {R^{{d_h} \times {d_v}}}\) are the learnable weight parameters; while \({d_q} = {d_v} = {{{d_h}} / \varpi }\) and \(\varpi\) are the number of attention heads. This configuration enables the model to extract a greater number of structural features.

The scaled dot product of the query vector of node i and the key vector of node j is determined to assess the compatibility between the two nodes. This computation can be expressed as follows:

$$\begin{aligned} {u_{i,j}} = \frac{{q_i^T{K_j}}}{{\sqrt{{d_q}} }} \end{aligned}$$
(17)

The node weight is subsequently determined by applying a softmax function, as outlined below:

$$\begin{aligned} {a_{i,j}} = {\textrm{softmax}}({u_{i,j}}) = \frac{{{e^{{u_{i,j}}}}}}{{\sum \limits _{j' = 1}^n {{e^{{u_{i,j'}}}}} }} \end{aligned}$$
(18)

The described methodology facilitates the elucidation of relationships between any two nodes, with particular emphasis on the interaction between charging nodes and their target counterparts. Consequently, the cross-attention mechanism is employed to extract additional structural features. In this model, the key \(K_j^c\), query \(q_i^e\), and value \(v_j^c\) vectors can be articulated as follows:

$$\begin{aligned} \begin{array}{c} K_j^c = {W^{kc}}h_k^c\\ q_i^e = {W^{qe}}h_i^e\\ v_j^c = {W^{vc}}h_j^c \end{array} \end{aligned}$$
(19)

where \(h_i^e\) and \(h_j^c\) are the embeddings of LP node i and CS node j, respectively. All parameters \({W^{kc}},{W^{qe}},{W^{vc}}\) are subject to training. Therefore, the weights assigned to the connections between CS nodes and LP nodes are computed as follows:

$$\begin{aligned} u_{i,j}^{ec} =&\frac{{{{\left( {q_i^e} \right) }^T}K_j^c}}{{\sqrt{{d_q}} }} \end{aligned}$$
(20)
$$\begin{aligned} a_{i,j}^{ec} =&{\textrm{softmax}}({u_{i,j}}) = \frac{{{e^{u_{i,j}^{ec}}}}}{{\sum \limits _{j' = 1}^n {{e^{u_{i,j}^{ec}}}} }} \end{aligned}$$
(21)

This study leverages the cumulative output of all attention heads to enhance the single head vector \(h_i^{\left( \varpi \right) }\), which can be formally expressed as follows:

$$\begin{aligned} h_i^{\left( \varpi \right) } = \sum \limits _j {{a_{i,j}}{v_j}} + \sum \limits _j {a_{i,j}^{ec}} v_j^c \end{aligned}$$
(22)

Notably, while CS nodes might be visited repeatedly, LP nodes are restricted to a single visit. Consequently, the attention mechanisms from LP nodes to CS nodes primarily enhance the embeddings of the LP nodes alone. In contrast, the attention heads associated with CS node embeddings yield a value of zero. Following the concatenation of messages from various heads, the resulting multi-head vector is processed through a skip-connection layer and a batch normalization (BN) layer as follows41:

$$\begin{aligned} h_i^{l'} = BN(h_i^{\left( {L - 1} \right) } + {W^{out}} \cdot concat\left\{ {h_i^{\left( 1 \right) }, \cdots ,h_i^{\left( \varpi \right) }} \right\} ) \end{aligned}$$
(23)

where \(concat\left\{ \cdot \right\}\) is the concatenation operator; \(BN\left( \cdot \right)\) is BN function; and \({W^{out}}\) is a trainable parameter. Subsequently, the output vector from FF sublayer is transmitted through a skip connection and a BN layer, as described below:

$$\begin{aligned} h_i^l = BN(h_i^{l'} + FF\left( {h_i^{l'}} \right) ) \end{aligned}$$
(24)

Through the progressive traversal across L attention layers, refined node embeddings are obtained. Subsequently, a comprehensive graph embedding is calculated, encapsulating overarching graph information.

$$\begin{aligned} \overline{{h^N}} = {{{\sum \limits _{i \in X} {h_i^L} }} \!/ \!{{n + 1 + z}}} \end{aligned}$$
(25)

Both the graph embeddings \(\overline{{h^N}}\) and the advanced node embeddings \(h_i^l\) are utilized as inputs to the decoder.

Decoding phase

During the encoding phase, leveraging both the refined node embeddings and the comprehensive graph embedding, along with the intermediate solution \(\pi _{1:t - 1}^m\) at each construction step \(t \in \left\{ {1, \cdots ,T} \right\}\), this study ascertains the subsequent node \(\pi _t^m\) in the decoding phase. The decoder, at each step, creates a probability distribution over the nodes, informed by the embeddings generated during the encoding phase. However, if multiple ELVs simultaneously make decisions, the dimensionality of the joint action space increases exponentially, leading to a substantial rise in training complexity and computational overhead. To address this challenge, we adopt the one-agent-per-decoding-step strategy, ensuring that only one agent makes a decision per time step. This approach effectively transforms the problem into a sequential optimization process, progressively constructing an optimal solution, thereby improving the stability for creation of optimal transportation routes. A pivotal initial step involves identifying which ELV will make decisions at each time step t as is shown in Figure  3. Thereafter, the current active index \(\ell\) of the ELV is established as follows:

$$\begin{aligned} \ell \leftarrow t\% m \end{aligned}$$
(26)

A context vector \(h_\ell ^{ct}\left( t \right)\) is determined at each decoding step t, incorporating the global graph embedding \(\overline{{h^N}}\), the embedding of the most recently visited node, and the remaining battery capacitie \(R_m^r\left( t \right)\), the remaining load capacity \(w_m^r\left( t \right)\), and remaining time duration \(T_m^r\left( t \right)\). For the initial step of decoding, the embedding of the last visited node is replaced with trainable parameters. The computation of the context vector \(h_\ell ^{ct}\left( t \right)\) is detailed below:

$$\begin{aligned} h_\ell ^{ct} = {W^{graph}} \cdot \overline{{h^N}} + {W^{step}} \cdot concat\left\{ {Inpu{t_t},R_m^r\left( t \right) ,w_m^r\left( t \right) ,T_m^r\left( t \right) } \right\} \end{aligned}$$
(27)

where

$$\begin{aligned} Inpu{t_t} = \left\{ {\begin{array}{*{20}{c}} {{W^d}}& {if~~{{ \ }}t = 1}\\ {h_{\pi _{\left| {{\pi ^\ell }} \right| }^\ell }^L}& {if~~{{ \ }}t > 1} \end{array}} \right. \end{aligned}$$
(28)

where \({W^{graph}},{W^d}\) and \({W^{step}}\) are the matrices of trainable parameters.

In the process of computing node selection \(\pi _t^\ell\), it is essential to take into account not only the previously selected nodes \(\pi _{1 \sim t - 1}^\ell\) but also the compatibility between these selected nodes and the remaining nodes. This study ensures a logical and efficient progression in the selection process, optimizing the overall route based on proximity and compatibility criteria \(\pi _t^\ell\). Therefore, in light of these considerations, an additional attention mechanism42 is incorporated to process \(h_\ell ^{ct}\), which facilitates the acquisition of more comprehensive information.

The query \({q_\ell }\) is constructed as follows:

$$\begin{aligned} {q_\ell } = soft\max (\frac{{h_\ell ^{ct}K_1^T}}{{\sqrt{{d_k}} }}){V_1} \end{aligned}$$
(29)

where \({K_1}\) and \({V_1}\) are linear projections of the node embeddings \(h_\ell ^{ct}\). \({d_k}\) is the scaling factor and \({d_k} = \frac{{{d_h}}}{M}\), with M denoting the number of heads in Scaled Dot-Product Attention mechanism43.

The key vector for node i in the single-head attention mechanism is computed as follows:

$$\begin{aligned} {k_i} = {W^K}h_i^L \end{aligned}$$
(30)

Through the aforementioned operation, the query-key \(({q_\ell },{k_i})\) is derived. The compatibility between the query and the key is subsequently calculated according to the following methodology.

$$\begin{aligned} u_i^\ell = \frac{{q_\ell ^T{k_i}}}{{\sqrt{{d_k}} }} \end{aligned}$$
(31)

During network training, the presence of infeasible nodes in the action space increases the complexity of training and hinders convergence. The masking process improves learning efficiency by dynamically filtering out infeasible nodes to reduce the exploration space, thereby accelerating the convergence of the optimal strategy and enhancing the overall solution quality. Therefore, \(u_i^\ell\) is constrained between \(- R\) and \(+ R\) utilizing the \(\tanh \left( \cdot \right)\) function, while the infeasible nodes are masked. In this masking process, the infeasible nodes are assigned a value of \(- \infty\) to facilitate the updating of \(u_i^\ell\).

$$\begin{aligned} u_i^\ell \leftarrow \tanh \left( {u_i^\ell } \right) \cdot R \end{aligned}$$
(32)

The infeasible nodes consist of the following categories:

  1. 1)

    LP nodes that have been already visited;

  2. 2)

    LP nodes that whose package weight exceed remaining load weight of current ELV;

  3. 3)

    The LP or CS nodes that the ELV cannot reach at the current step due to the insufficient battery capacity or insufficient remaining duration;

  4. 4)

    LP nodes that would cause the ELV to fail to reach any CS nodes at the next step if the ELV visits them at the current step;

  5. 5)

    The depot when there are still remaining target nodes that need to be visited.

To facilitate the normalization of final probabilities within the range [0, 1], this study utilizes the softmax function. Thus, the likelihood of choosing node i at the decoding step t is formulated as follows:

$$\begin{aligned} pro_{_i}^t = {\textrm{softmax}}(u_i^\ell ) = \frac{{{e^{u_i^\ell }}}}{{\sum \limits _{j = 1}^n {u_j^t} }},i = 1, \cdots ,n \end{aligned}$$
(33)

Assuming the application of a greedy strategy to ascertain the pickup tour \(\pi ^\ell\), this study selects the node with the highest probability \(p_{_i}^t\) as \(\pi _t^\ell\) during the decoding step t. Specifically, the decoder generates a probability distribution across all nodes as described by Eq. (33). Subsequently, a node is selected to visit based on a specified strategy and append it to the end of \(\pi _{1:t - 1}^\ell\) at each construction step. This decoding procedure repeats iteratively until all LP nodes are visited, and ELVs return to the depot.

Model training

HAMEDA model is trained to obtain parameters \(\theta\) through policy gradient methods utilizing REINFORCE algorithm14. This approach integrates both the policy network and the baseline network. The policy network \(pr{o_\theta }(\pi |X)\) generates a probability distribution over the action space based on the current state. The baseline network functions to provide a standard reward, aiming to decrease variance with a greedy rollout strategy that selects the action of highest probability. Notably, the baseline network shares an identical architecture with the policy network. Subsequently, this study employs gradient descent to update \(\theta\) , and the gradients of \(\theta\) can be expressed as follows:

$$\begin{aligned} {d_\theta }&= \frac{1}{B}\sum \limits _{\lambda = 1}^B {\left( {{\textrm{R}}\left( \lambda \right) - b(\lambda )} \right) \cdot {\nabla _\theta }pr{o_\theta }(\pi |\lambda )} \end{aligned}$$
(34)
$$\begin{aligned} \theta&\leftarrow {\textrm{Adam}} \left( {{{ \theta ,}}{{\textrm{d}}_{{ \theta }}}} \right) \end{aligned}$$
(35)

where B is the batch size and \(b\left( \cdot \right)\) is a baseline function within the baseline network. The implementation of the baseline function facilitates a significant reduction in computational costs and enhances the rate of convergence. \(\theta\) can be updated utilizing the Adam optimizer44.

The training algorithm employed in the proposed method is delineated in Algorithm 1. The baseline function \(b\left( \cdot \right)\) is instantiated as \(R(\pi _i^ * )\), which is developed through a greedy rollout approach, while \(R(\pi _i )\) is constructed via a sample rollout method. Initially, it is essential to initialize the model parameters \(\theta ,{\theta ^ * }\) with random values for both the policy and the baseline policy, concurrently setting \({\theta ^ * } \leftarrow \theta\) (line 1). Subsequently, HAMEDA model undergoes training based on predetermined epochs and steps (lines 2-16). During the training process, instances are randomly selected from the sample set X (line 4), and the policy is executed through sampling and greedy methods to compute the transportation tours \({\pi _i}\) and \(\pi _i^ *\), respectively (lines 5-6). When the sampled solution \({\pi _i}\) demonstrates superior performance compared to the greedy solution \(\pi _i^ *\), Monte Carlo sampling is employed to iteratively refine the parameters, thereby enhancing the policy model parameters as delineated in lines 7-10, where B represents the batch size. Additionally, a paired t-test is performed at each epoch to determine whether updates are necessary for the baseline parameters, as specified in lines 13-15. Should the policy outperform the baseline, the parameters of the latter are replaced with those of the former. After extensive training iterations within each epoch, the refined policy network is capable of generating effective solutions.

Once HAMEDA model has been trained using Algorithm 1, the optimal Hamiltonian transportation tour \(\pi\) for ELVs can be calculated based on the trained parameters \(\theta\) and the given input instance X.

Algorithm 1
figure a

Training HAMEDA using REINFORCE.

Full size image

Discussion

The study presents a detailed description of the data generation methodology employed for the training and testing datasets, as well as the benchmark algorithms and hyperparameter settings utilized for the proposed HAMEDA model. The experimental setup involves random sampling of the coordinates of depots and LPs within a unit square defined by the interval \({[0,1]}\times {[0,1]}\), employing a uniform distribution. CSs are selected randomly from a discrete grid defined by \({[0,0.25,0.5,0.75,1]}\times {[0,0.25,0.5,0.75,1]}\). The weights of LPs are discrete values randomly chosen from the set \({[1,2,\ldots ,6]}\). It is assumed that the unit energy consumption and speeds remain constant before and after the loading of packages for each ELV. For the purpose of simplification, the vehicle speed is standardized for all ELVs to 1.0. To assess the performance of the proposed model, HAMEDA on instances of varying problem sizes are evaluated, specifically 20 LPs with 2 CSs, and 50 LPs with 5 CSs, which designated as L20C2 and L50C5, respectively. Furthermore, the performance of the proposed HAMEDA is compared against several representative baseline algorithms, which include:

  1. 1.

    OPT: The optimal solution to LECS problem is obtained using the standard Gurobi version 9.0.1 solver45, which is recognized as a state-of-the-art exact solver for combinatorial optimization problems.

  2. 2.

    Pointer Network (Ptr-Net): Ptr-Net is effective in addressing combinatorial optimization problems, utilizing an attention model to select a member from the input sequence as the output46. The hyperparameters employed are consistent with those proposed in HAMEDA.

  3. 3.

    Variable Neighborhood Search (VNS): An effective heuristic approach for addressing VRP and their variants47.

  4. 4.

    Kool-AM: Kool-AM can leverage the graph attention mechanism to effectively capture the relationships between nodes, which is applied to solve combinatorial optimization problems. Following the idea of48, we the model to the multi-agent scenario.

All algorithms were implemented using Python version 3.7.6. Furthermore, the implementations of Ptr-Net and HAMEDA were conducted utilizing PyTorch framework version 1.2.0 in conjunction with CUDA version 9.2. The experimental simulations were performed on a system running Ubuntu 16.04.6, which is equipped with a 32GB Tesla V100S GPU and an Intel\(\circledR\) Xeon\(\circledR\) Gold 5218R CPU with 500GB of storage. Each measurement was averaged over 1,000 iterations. A selection of parameters utilized for training and testing is presented in Table 2.

Table 2 Default parameter settings for HAMEDA model.
Full size table

Performance results

This study initially conducted a comparative analysis of the reward training curves associated with the proposed HAMEDA algorithm across varying node counts to assess its convergence. In Figure 5, the reward function exhibits a marked increase corresponding to the rise in training iterations, indicating a continuous decrease in the value of the objective function. Subsequently, HAMEDA algorithm demonstrates convergence, with L20C2 configuration achieving convergence in approximately 50 iterations, while L50C5 configuration converges in about 90 iterations. Notably, the convergence rate of HAMEDA surpasses that of Ptr-Net algorithm. Furthermore, HAMEDA ultimately attains a higher reward compared to Ptr-Net algorithm. In contrast to L20C2, L50C5 configurations of both algorithms exhibit a certain degree of fluctuation during the training iterations. However, HAMEDA algorithm maintains a relatively higher level of stability. This phenomenon can be attributed to the increasing number of LPs, which enhances the effectiveness of the constraints within the objective function. These observations indicate a significant improvement in the learning efficiency of HAMEDA algorithm, attributable to the implementation of the heterogeneous graph attention mechanism and the newly proposed decoding procedure utilized by HAMEDA network.

Fig. 5
figure 5

Effect of training epochs on convergence and performance of HAMEDA model.

Full size image
Fig. 6
figure 6

The effect of HGA and improved decoder.

Full size image
Fig. 7
figure 7

Effects of LPs and CSs on total energy consumption: (a) Total energy consumption versus LPs; (b) Total energy consumption versus CSs.

Full size image

To validate the effectiveness of proposed HGA network, the one-agent-per-decoding-step strategy and masking process, Fig. 6 illustrates the reward changes over iterations for the HAMEDA algorithm, the HAMEDA without HGA , and the HAMEDA without improved decoding paradigm, i.e. the one-agent-per-decoding-step strategy and masking process, under scenarios with L50C5. The simulation results indicate that, compared to the HAMEDA algorithm without HGA, the proposed algorithm achieves higher rewards but with a slower convergence rate. This suggests that incorporating HGA network into the encoder allows agents to extract more hidden relationships among all nodes, leading the policy iteration closer to the optimal solution. The reason for the slow convergence speed is that the HGA network integrates self-attention and cross-attention mechanisms, extracts more features, leads to an increase in the dimensionality of the state and joint action space, and requires more iterations. Additionally, compared HAMEDA algorithm without improved decoding paradigm, the proposed algorithm demonstrates faster and more stable learning speeds and higher rewards. This is because the masking process effectively filters out infeasible nodes to reduce action space that proposed algorithm needs to learn and explore, thereby enhancing the algorithm’s learning speeds and rewards. The one-agent-per-decoding-step strategy can enhance training stability. Thus, the HGA network, the one-agent-per-decoding-step strategy and masking process can effectively improve the performance of the HAMEDA algorithm.

Fig. 8
figure 8

Effects of different constraints on total energy consumption in ELVs: (a) Maximum load capacity; (b) Maximum battery capacity; (c) Maximum transportation duration.

Full size image

The research subsequently analyzed the variations in total energy consumption across all algorithms with respect to different node configurations. The parameters are established as follows: a maximum travel time of 65, a maximum energy consumption of 15, and a maximum load constraint of 150. In order to intuitively show the impact of different numbers of LPs and CSs, we set different scales for the y-axis in Figure 7a and 7b. Figure 7a demonstrates that an increase in the number of LPs is correlated with a rise in the total energy consumption, as measured across all algorithms, with the number of CSs held constant at 5. This increase can be attributed to the fact that the total length of transportation routes typically expands with the increase in the number of users. Notably, the energy consumption reported by the proposed algorithm remains lower than that of the other algorithms. In Figure 7b, an increase in the number of CSs results in a decrease in the total energy consumption outputted by all algorithms, with the number of LPs maintained at 50. This reduction can be explained by the enhanced recharging strategy afforded by the additional CS nodes, which allows ELVs to extend their service range more effectively. Under the constraints of limited load and duration capacity, ELVs can cover a broader area, thereby facilitating the servicing of more LP nodes and significantly reducing overall system energy consumption. In comparison to Ptr-Net and Kool-AM, HAMEDA demonstrates superior performance in optimizing the objective function, attributable to the heterogeneous graph attention mechanism that adeptly extracts dynamic features and relationships among all nodes, including both CS and ELV nodes.

This study conducted an analysis of the effect of varying constraint values on total energy consumption in Figure 8 with the number of LPs and CSs set at 50 and 5, respectively. The results indicate that as the values of several constraints, including maximum transportation duration, maximum battery capacity, and maximum load capacity, increase, the total energy consumption of the different algorithms tends to decrease. This reduction in energy consumption among all ELVs can be ascribed to higher constraint settings, which enable the vehicles to service an increased number of LP nodes.

Table 3 details the execution times of the OPT, HAMEDA, VNS, Ptr-Net and Kool-AM algorithms, noting that the duration required by each algorithm extends as the node count rises. Notably, the runtime of OPT and VNS algorithms exhibits an almost exponential growth as the problem size escalates, whereas the runtime of the learning-based methods demonstrates a linear growth pattern. Specifically, the runtimes of OPT and VNS methods are significantly longer than those of the learning-based approaches, which consistently remain approximately 1s. Furthermore, HAMEDA consistently yields a solution that is comparable in quality while requiring relatively less execution time for large-scale instances.

Table 3 Comparative running times of OPT, HAMEDA, Ptr-Net and VNS.
Full size table

Comparatively, the HAMEDA algorithm consistently demonstrates at least a 1.64% lower total energy consumption than other DRL-based algorithms, i.e. Ptr-Net and Kool-AM, yet it shows 3.5% higher when compared to OPT. Moreover, HAMEDA significantly outperforms other baseline algorithms in execution speed for large-scale scenarios, thus enhancing timely decision-making capabilities. The experimental findings underscore HAMEDA’s ability to strike an effective balance between quick execution and high-quality solutions, alongside marked improvements in optimization efficacy and system scalability.

Conclusion

This paper addresses LECS problem in urban logistics, where multiple CSs are available for recharging ELVs. LECS problem is formulated to minimize the total energy consumption of heterogeneous ELVs, each with different load capacities and battery sizes, under the constraint of maximum transportation duration. Given the NP-hard nature of LECS problem, it was modeled as an MDP and proposed HAMEDA approach, based on an Encoder-Decoder architecture. HAMEDA incorporates a heterogeneous graph attention network to capture advanced representations of the relationships between LPs and CSs during the encoding phase. In the decoding phase, a novel procedure that utilizes a one-agent-per-decoding-step routine and a masking strategy is introduced to enhance solution quality in tour generation, thereby improving learning efficiency. HAMEDA model is trained through DRL in an unsupervised manner. Extensive experiments demonstrate that HAMEDA reduces total energy consumption by at least 1.64% compared to traditional heuristic and learning-based algorithms. Furthermore, HAMEDA consistently delivers comparable solutions with significantly reduced execution times, making it an optimal choice for large-scale tasks that require rapid decision-making.

Our current research focuses on low energy consumption scheduling in scenarios with fixed CSs. However, in regions where fixed CSs are sparsely deployed or nonexistent, the coordinated scheduling of mobile CSs and ELVs remains an open challenge for future exploration. Additionally, the proposed centralized approach relies on the logistics cloud platform for all computations, potentially leading to significant data exchange between ELVs and the cloud. To further enhance efficiency and scalability, future research will explore advanced distributed methodologies, such as decentralized federated learning49, to reduce communication overhead and improve overall system performance.