Introduction

Power plants and automobiles currently rely on conventional combustion-based technology. However, global warming, significant increases in oil and natural gas prices, and growing air pollution have paved the way for more sustainable energy options1,2,3. One of the newest renewable energy conversion technology developments is fuel cells, or FCs. The proton exchange membrane fuel cell (PEMFC) has proved impressive promise and robust competitiveness among various FC types in portable, automotive, and distributed applications due to its solid-state electrolyte, low operating temperature, excellent transient performance, high energy concentration, superior energy effectiveness, compact design with scalability, minimal noise, and no environmental emissions.4. The fuel cells are categorized depending on the selection of fuel and electrolyte. Currently, six main various types of fuel cells are existing: Proton exchange membrane fuel cell (PEMFC)5. Phosphoric acid fuel cell (PAFC)6. Alkaline fuel cell (AFC)7. Direct methanol fuel cell (DMFC)8. Molten carbonate fuel cell (MCFC)9. Solid oxide fuel cell (SOFC)10.

In this sense, FCs components are considered electrochemical energy conversion devices used in AC and DC grids11. These devices use hydrogen and oxygen as fuel, transforming chemical energy into electrical energy and heat. It is a low-temperature version where noble metal catalysts like platinum occupy reaction sites. Moreover, energy is released as a consequence of the reaction. A fuel cell’s internal chemical processes produce heat, liquid water, and DC power. One of the most promising technologies in this area is PEMFCs, which convert chemical energy molecules into electrical energy via electrochemical processes12,13.

A sequence of PEMFCs is linked to raising the terminal voltage to the required level since the temperature and supply pressure may impact the terminal voltage, which can vary from 0.9 to 1.23 V/cell14,15,16. A stack is a group of PEMFCs linked in parallel or series for a given application. Due to polarization losses, its terminal voltage presents a non-linear characteristic with the drawn load current. Additionally, the PEMFCs’ output voltage primarily drops speedily because of the activation voltage drop, then linearly due to the ohmic voltage drop, and last, excessively due to concentration losses17.

On the other hand, data-driven modelling techniques have no explicit equations and instead use black-box models that have been extensively trained on vast quantities of data to roughly approximate test scenarios18. However, the training and testing of these models need a large amount of experimental data, which leads to expensive experiments and a drawn-out model building process. Equivalent Circuit model is developed using electrical components to examine output characteristics and evaluate PEMFC dependability. In the field of electrical design, these models are very important. The user may effectively assess the PEMFC performance under a range of operating conditions thanks to empirical modelling, which easily predicts the voltage-current characteristics using semi-empirical equations19. However, because inadequate data and model parameter information limit PEMFC modeling, the most challenging aspect of Amplette’s suggested PEMFC modeling technique is accurately estimating unknown modeling parameters20.

In its mathematical form, the PEMFC model has a set of unknown parameters that are not included in the fabricators’ datasheets. Optimization techniques have been developed due to the increasing significance of PEMFCs model parameters extraction in research. The starting values have an important influence on the quality of the findings of mathematical and analytical procedures, and simplified concepts are often used, which ultimately leads in substantial inaccuracies in the methods’ output. The research community is dedicated to creating innovative methods for determining the precise and reliable model parameters of PEMFCs. To increase precision, dependability, and efficiency and support the sustainable production of solar energy, researchers improve current methods and create new ones. The main goal of the optimization process frequently entails diminishing the sum of squared variance between the projected data points and the observed output current of PEMFC units, according to the literature collected in Table 1. Minimizing the frequently utilized SQE is essential to address this issue. The techniques mentioned above have confirmed operative in several pursuits, completing roles counting providing precise findings, enhancing convergence speed, improving the synergy between local and global search, and avoiding stagnation in local minima21,22,23.

Probabilistic in nature, optimization approaches generate solutions for a particular optimization problem from a population. As a result, they are excellent at solving complex engineering optimization problems and may be used for a variety of purposes, such as; butterfly optimization algorithm (BOA)24, bat algorithm (BA)25,26,27, grasshopper optimization algorithm (GOA)28, hybrid brown-bear and hippopotamus algorithms (BOHA)29, improved mayfly optimization algorithm (IMOA)30, harris hawk optimizer (HHO)31, moth flam optimizer (MFO)32, whale optimization algorithm (WOA)33. One such special application where a numerous metaheuristic optimization techniques were applied in the early literature is PEMFC parameter estimation, specifically: harmony search (HS)34, particle swarm optimization (PSO)35, coyote optimizer (CO)36, artificial bee swarm optimization (ABSO)37, cuckoo search algorithm (CS)38, bonobo optimizer (BO)39, bird mating optimizer (BMA)40, firefly optimization algorithm (FOA)41, remora optimizer (RO)42, grasshopper optimizer (GSO)43, bird mating optimizer (BMO)44, gorilla troops optimizer (GTO)45, biogeography optimization (BBO)46, backtracking search algorithm (BSA)47, artificial bee colony DE optimizer (ABCDEO)48, teaching–learning based optimization (TLBO)49, marine predators and political optimizers (MPO)50, grey wolf optimizer (GWO)51, shark smell optimization (SSO)52, hunger games search algorithm (HGSA)53, monarch butterfly optimizer (MBO)54, shuffled frog-leaping algorithm (SFLA)55, equilibrium optimizer (EO)56, henry gas solubility optimizer (HGSO)57, neural network optimizer (NNO)58, jellyfish search algorithm (JSA)59. chaotic fluid search optimizer (CFSO)60, hybrid artificial bee colony (HABC)37, bird mating optimizer (BMO)44, chicken swarm optimizer (CSO)61, multi-verse optimizer (MVO)62, whale optimization algorithm (WOA)63, developed teamwork optimizer (TWO)64, JAYA algorithm65, chaotic harris hawks optimization (CHHO)66, improved artificial ecosystem optimizer (IAEO)67, two-stage differential evolution (TDE)68.

Table 1 Numerous optimizers for PEMFCs model parameters identification.
Full size table

Contributions to the work

This study centers on the Proton Exchange Membrane Fuel Cell (PEMFC) as the primary system of interest, given its importance and extensive use in clean energy applications, especially in transportation and stationary power generation. The membrane electrode assembly (MEA) in PEMFCs typically employs Nafion as the proton exchange membrane. Nafion is a commercially available and well-established material, renowned for its exceptional proton conductivity, mechanical durability, and resistance to chemical degradation under standard operating conditions. Furthermore, PEMFCs are highly sensitive to changes in operating parameters, rendering them an excellent platform for evaluating and validating optimization algorithms. In this paper, the estimate of unknown parameters is treated as a difficult nonlinear optimization issue that necessitates a robust optimization strategy, introducing a novel approach to the complicated problem of optimum parameter identification in PEMFC models. Two significant enhancements have been made to the fundamental Parrot Optimizer (PO) to address the mentioned problem. The improved Parrot Optimizer (IPO) incorporates two significant advancements to the original algorithm: Opposition-Based Learning (OBL) and the Local Escaping Operator (LEO). OBL simultaneously assesses the current solution and its opposite, enabling the algorithm to explore a broader range of possibilities and retain the superior solution, thereby enhancing both exploration and convergence. LEO, functioning as a local search mechanism, generates new solutions by integrating the best-known solution with randomly chosen solutions from the population. This introduces diversity and randomness, allowing the algorithm to escape local optima and investigate unexplored areas of the search space. Together, these enhancements strengthen the algorithm’s capacity to balance exploration and exploitation, resulting in a more robust and efficient approach for addressing complex optimization challenges. The combination of OBL and LEO ensures faster convergence and higher-quality solutions by preventing stagnation in local optima and promoting thorough exploration of the search space. The NedStackPS6, BSC 500 W, and Ballard Mark V PEMFC stacks are employed to experimentally assess the improved proposed parrot optimizer technique. Comparing the findings of the enhanced PO with those of a number of analytical, numerical, and combination methods that have been reported in the literature demonstrates its exceptional performance and accuracy. Figure 1 shows the main overview of paper. This research’s principal contribution is summed up in the list below:

  • A new optimization method, the Improved Parrot Optimizer (IPO), is proposed to solve the problem of optimal parameter identification in PEMFC models, treating this as a challenging nonlinear optimization issue that requires a strong optimization technique.

  • The fundamental PO algorithm receives two significant improvements: Local Escaping Operator (LEO), which is integrated with PO to improve exploration, avoid local optima, and enhance overall convergence, and Opposition-Based Learning (OBL), which speeds up the search process and improves the generation of candidate solutions.

  • Using three different PEMFC stacks (NedStackPS6, BSC 500 W, and Ballard Mark V), the suggested IPO strategy is experimentally evaluated and contrasted with a number of well-known modelling approaches from the literature to show its effectiveness and dependability.

Fig. 1
figure 1

Main overview of article.

Full size image

This article is divided into five sections: The introduction is presented in "Introduction" section. The explanation of the issue and the PEMFC model that has to be optimized are shown in "PEMFC modelling and characteristics" section. "Improved parrot optimizer (IPO)" section provides description of the IPO algorithm. In "Results and interpretation on benchmark functions test" section, the simulation results and comparisons are discussed, and the conclusion is presented in “Conclusion and future work” section.

PEMFC modelling and characteristics

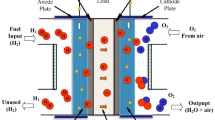
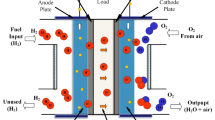
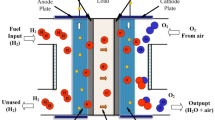
Numerous modelling approaches are available in the field of proton exchange membrane fuel cells (PEMFCs) to comprehend its properties behavior. Figure 2 illustrates the fundamental construction and operating principle of a PEMFC. The open circuit voltage of PEMFC is lower than the cell reversible voltage because of activation losses, concentration losses, and ohmic losses1. Consequently, the overall output voltage that controls fuel cell performance:

$$V_{cell} = E_{Nernst} - V_{act} - V_{ohm} - V_{conc}$$
(1)
Fig. 2
figure 2

Clarified model of PEM fuel cell.

Full size image

Nernst voltage

The potential found in an open circuit thermodynamic balance under no load constraints is the cell reversible voltage, or \({E}_{Nernst}\). This potential is computed using the fundamental Nernst formula with an additional component to account for temperature variations. The following is the equation for the cell’s reversible voltage:

$$E_{Nernst} = 1.229 - 8.5 \times 10^{ - 4} \left( {T - 298.15} \right) + 4.308 \times 10^{ - 5} T(ln\left( {P_{H2} + 0.5 lnP_{{O_{2} }} } \right)$$
(2)

where T denotes temperature in Kelvin and \({P}_{{O}_{2}}\) and \({P}_{H2}\) stand for the partial pressures of oxygen and hydrogen, respectively.

Activation losses

The entire slowness of the processes occurring on the electrode surface is characterized by the activation potential \({V}_{act}\). Additionally, a portion of the voltage produced is lost during the chemical reaction’s drive, as shown by semi-empirical characteristics like:

$$V_{act} = - \left( {\zeta_{1} + \zeta_{2} T + \zeta_{3} T ln\left( {C_{{O_{2} }} } \right) + \zeta_{4} T ln\left( {I_{FC} } \right)} \right)$$
(3)

where \(i\) denotes the cell current, \({C}_{{O}_{2}}\) indicates the oxygen concentration at the cathode’s catalytic interface (mol/cm-3) as expressed below, and \({\zeta }_{i}\) (\(i\) = 1…4) stands for the semi-empirical parametric factors.

$$C_{{O_{2} }} = \frac{{P_{{O_{2} }} }}{{\left( {5.08 \times 10^{6} } \right) \times exp\left( { - \frac{498}{T} } \right)}}$$
(4)

Ohmic loss

Ohmic voltage loss (\({V}_{ohm}\)) represents the combined resistance to ion flow through the electrolyte and the resistance to electron passage through the substance. The described voltage that occurs in PEMFC may be quantitatively expressed as follows since this voltage drop is largely linear and proportionate to the current density:

$$V_{ohm} = I_{FC} \left( {R_{M} + R_{C} } \right)$$
(5)

where the resistance in electrical conductors and membranes is indicated by \({R}_{M}\) and \({R}_{C}\), respectively. Because it is not affected by slight changes in voltage or current, the electron resistance is calculated using Eq. (6), while the resistivity for a generally employed Nafion membrane is defined by Eq. (7).

$$R_{M} = \frac{{r_{m} l}}{A}$$
(6)
$$r_{m} = \frac{{181.6\left[ {1 + 0.003\left( {\frac{{I_{FC} }}{A}} \right) + 0.0062\left( \frac{T}{303} \right)^{2} \left( {\frac{{I_{FC} }}{A}} \right)^{2.5} } \right]}}{{\left[ {\lambda_{m} - 0.634 - 3\left( {\frac{{I_{FC} }}{A}} \right)} \right] \times exp\left( {4.18\left( {T - \frac{303}{T}} \right)} \right)}}$$
(7)

where the parametric coefficient is denoted by \({\lambda }_{m}\) and the membrane specific resistivity (Ω Cm) by \({r}_{m}\).

Concentration loss/mass transport voltage drop

The fuel cell’s output voltage decreases based on the current extracted from it and other physical factors. The partial pressure of hydrogen and oxygen decreases due to the voltage drop brought on by mass movement, which also alters their concentrations. Therefore, the following formula may be employed to estimate the voltage drop caused by mass movement or concentration loss:

$$V_{conc} = - \frac{RT}{{nF}} ln\left( {1 - \frac{{I_{FC} }}{{I_{max} A}}} \right)$$
(8)

where \({I}_{max}\) shows the limiting current’s destiny and n is the number of electrons.

Problem formulation

The experimental results should be consistent with the PEMFC mathematical model designated in the preceding part. It is necessary to estimate the seven parameters [\({\zeta }_{1}\), \({\zeta }_{2}\), \({\zeta }_{3}\), \({\zeta }_{4}\), \(\lambda\), \({R}_{C}\), and B] that affect the PEMFC stack’s performance in the mathematical model. When using experimental data to determine the PEMFC’s unknown parameters, the objective function is essential. An objective function should be designed before determining the unknown parameter \(X =[{\zeta }_{1}, {\zeta }_{2}, {\zeta }_{3}, {\zeta }_{4}, \lambda , {R}_{C}, B]\). This article’s optimization goal, in contrast to earlier works, is to determine a set of best parameter values that achieve the smallest sum of the squared errors (SQE) between the experimental voltage (\({V}_{exp}\)) and the simulated voltage (\({V}_{sim}\)), which is obtained from Eq. (9). This can be expressed as

$$F\_obj = \mathop \sum \limits_{i = 1}^{N} \left( {V_{sim} - V_{exp} } \right)^{2}$$
(9)

where N denotes the number of samples collected from the experimental data.

Improved parrot optimizer (IPO)

This part describes the general overview of the improved PO and the developed optimization frameworks. The improved PO has undergone two significant enhancements to address the problem: Opposition-Based Learning to increase candidate solutions and convergence speed, and the Local Escaping Operator to prevent the algorithm from being trapped in local optima and enhance exploration capabilities. The IPO operators are explained in the following sections. The flowchart of the improved PO is shown in Fig. 3.

Fig. 3
figure 3

Flowchart of the improved PO.

Full size image

The parrot optimizer (PO)

This subsection provides an overview of the PO and its main operations.

Inspiration

The popular parrot species Pyrrhura Molinae is a favourite among pet owners because of its appealing appearance, strong attachment with its owners, and simplicity of training82. Prior research and breeding initiatives have identified four unique behavioral characteristics of Pyrrhura Molinae: foraging, staying communicating, and a dread of strangers83.

Mathematical model

Population initialization

The suggested PO’s initialization development may be shown as follows, taking into account a swarm size of N, maximum generations of \({Max}_{iter}\), and search space restrictions of \(ub\) (upper bound) and \(lb\) (lower bound):

$$X_{i}^{0} = lb + rand\left( {0, 1} \right) \cdot \left( {ub - lb} \right)$$
(10)

where the ___location of the \({i}^{th}\) Pyrrhura Molinae in the first phase is indicated by \({X}_{i}^{0}\), and \(rand(0, 1)\) represents a random number in the interval [0, 1].

Foraging behavior

As part of their foraging behaviour, POs fly in the direction of the food after estimating its approximate ___location mostly by looking at the food’s ___location or by taking the owner’s position into account. The positional movement obeys the following equation:

$$X_{i}^{t + 1} = (X_{i}^{t} - X_{best} ) \cdot Levy\left( {dim} \right) + rand\left( {0,1} \right) \cdot \left( {1 - \frac{t}{{Max_{iter} }}} \right)^{{\frac{2t}{{Max_{iter} }}}} \cdot X_{mean}^{t}$$
(11)

In Eq. (11), the current position is indicated by \({X}_{i}^{t}\), and the ___location of the subsequent update is shown by \({X}_{i}^{t+1}\). \(Levy(D)\) indicates the Levy distribution, which is used to characterise parrot flying, and \({X}_{mean}^{t}\) indicates the average position within the current population. In addition to representing the host’s current ___location, \({X}_{best}\) indicates the optimal ___location that has been sought from start to the present. The symbol indicates the number of iterations \(t\). \(rand(\text{0,1}).{\left(1-\frac{t}{{Max}_{iter}}\right)}^{\frac{2t}{{Max}_{iter}}}.{X}_{mean}^{t}\) signifies monitoring of the population’s position overall to further target the food’s direction, whereas \({(X}_{i}^{t}-{X}_{best}).Levy(dim)\) implies movement depending on one’s ___location in respect to the owner.

The present swarm’s average position, represented by \({X}_{mean}^{t}\), is determined by using the procedure in Eq. (12).

$$X_{mean}^{t} = \frac{1}{N}\mathop \sum \limits_{k = 1}^{N} X_{k}^{t}$$
(12)

Using the formula in Eq. (13), where γ is given the value of 1.5, the Levy distribution may be derived.

$$\left\{ {\begin{array}{*{20}l} {Levy\left( {dim} \right) = \frac{\mu .\sigma }{{\left| v \right|^{{\frac{1}{\gamma }}} }}} \hfill \\ {\mu \sim N\left( {0,dim} \right)} \hfill \\ {\begin{array}{*{20}c} {v\sim N\left( {0,dim} \right)} \\ {\sigma = \left( {\frac{{\Gamma \left( {1 + \gamma } \right).sin\left( {\frac{\pi \gamma }{2}} \right)}}{{\Gamma \left( {\frac{1 + \gamma }{2}} \right).2^{{\frac{1 + \gamma }{2}}} }}} \right)} \\ \end{array} } \hfill \\ \end{array} } \right.$$
(13)
Staying behavior

The staying habit of the sociable Pyrrhura Molinae mainly consists of abruptly flying to any region of its owner’s body and then remaining still for a predetermined amount of time. This procedure may be shown as follows:

$$X_{i}^{t + 1} = X_{i}^{t} + X_{best} \cdot Levy\left( {dim} \right) + rand\left( {0,1} \right) \cdot ones\left( {1,dim} \right)$$
(14)

where the all-1 vector of dimension dim is indicated by \(ones(1,dim)\). The procedure of randomly halting at a portion of the host’s body is shown by \(rand(\text{0,1}).ones(1,dim)\), while \({X}_{best}.Levy\left(dim\right)\) indicates the flying to the host.

Communicating behavior

Close group communication is a characteristic of the naturally sociable Pyrrhura Molinae parrots. Both communicating without flying to the flock and flying to the flock are included in this communication behavior. The average ___location of the present population is used to represent the flock’s center in the PO, where the two behaviors are expected to take place with balanced odds. This operation can be depicted as:

$$X_{i}^{t + 1} = \left\{ {\begin{array}{*{20}l} {0.2.rand\left( {0,1} \right) \cdot \left( {1 - \frac{t}{{Max_{iter} }}} \right).\left( {X_{i}^{t + 1} - X_{mean}^{t} } \right), P \le 0.5} \\ {0.2.rand\left( {0,1} \right) \cdot exp\left( { - \frac{t}{{rand\left( {0,1} \right).Max_{iter} }}} \right), P > 0.5} \\ \end{array} } \right.$$
(15)

where \(0.2.rand(\text{0,1}) \cdot exp\left(-\frac{t}{rand(\text{0,1}) \cdot {Max}_{iter}}\right), P>0.5\) means that an individual quickly takes off after communicating, and \(0.2.rand(\text{0,1}) \cdot \left(1-\frac{t}{{Max}_{iter}}\right) \cdot \left({X}_{i}^{t+1}-{X}_{mean}^{t}\right)\) means that an individual joins a parrot’s surrounds in order to converse. Since both actions are possible, they are realised via a randomly selected \(P\) in the interval [0, 1].

Fear of strangers’ behavior

Birds often have an innate mistrust of strangers, and Pyrrhura Molinae parrots are no exception. The following describes how they behave when they are looking for a safe environment, avoiding strangers and finding refuge with their owners:

$$X_{i}^{t + 1} = X_{i}^{t} + rand\left( {0,1} \right) \cdot cos\left( {0.5\pi .\frac{t}{{Max_{iter} }}} \right) \cdot \left( {X_{best} - X_{i}^{t} } \right) - cos\left( {rand\left( {0,1} \right) \cdot \pi } \right) \cdot \left( {\frac{t}{{Max_{iter} }}} \right)^{{\frac{2}{{Max_{iter} }}}} .\left( {X_{i}^{t} - X_{best} } \right)$$
(16)

where \(cos\left(rand(\text{0,1}).\pi \right).{\left(\frac{t}{{Max}_{iter}}\right)}^{\frac{2}{{Max}_{iter}}}.\left({X}_{i}^{t}{-X}_{best}\right)\) illustrates the process of separating from strangers and \(cos\left(0.5\pi .\frac{t}{{Max}_{iter}}\right).\left({X}_{best}-{X}_{i}^{t}\right)\) illustrates the procedure of reorienting to fly towards the owner.

Opposition-based learning (OBL)

The suggested technique that evaluates a current solution’s cost function is opposition-based learning (OL). In order to get closer to the global optimum, OL investigates a solution and its corresponding opposing solution at the same time84. As a result, the inverse solution of a solution symbolized by (Ki) in the improved KO can be written as (Kbi) and given as84:

$$\overline{{X_{i} }} = ub_{i} + lb_{i} - X, i = 1:NP$$
(17)

The lowest and maximum values, represented as (ubi and lbi), respectively, define the search area for the present population’s (i) dimension in this case. After comparing the fitness functions of the two solutions (Ki) and (Kbi), the better solution is retained and the worse one is eliminated. In particular, if ((K) >  = f(Kb)) (In circumstances when maximizing is the goal), (f(K)) is kept; if not, (Kbi) is maintained.

Local escaping operator (LEO)

A supplementary local search technique, the Local Escaping Operator (LEO), was first presented in85. Its main goal was to improve the exploration capabilities of the PO by making it easier to explore new areas, especially in challenging real-world applications. This enhances the quality of the solution as a whole. By updating the placements of solutions according to predetermined criteria, LEO improves the convergence behavior of the optimization algorithm and successfully keeps it from being stuck in local optima86.

The LEO aims to increase the suggested PO algorithm’s effectiveness in handling the mentioned issue. The ___location of the solution \({X}_{n}^{t+1}\) may be considerably altered by this operator. The LEO uses many solutions, counting the optimal ___location (\({x}_{best}\)), the solutions \({X1}_{n}^{t}\) and \({X2}_{n}^{t}\), two random solutions \({x}_{r1}^{t}\) and \({x}_{r2}^{t}\), to provide a solution with a greater performance (\({X}_{LEO}^{t+1}\)). The following strategy generates the solution:

$$\begin{aligned} & {\varvec{if}} \,rand < pr \\ & {\varvec{if}}\, rand < 0.5 \\ & X_{LEO}^{t + 1} = X_{n}^{t + 1} + f_{1} \times (v_{1} \times x_{best} - v_{2} \times x_{n}^{t} ) + f_{1} \times \sigma_{1} \times \left( {v_{3} \times \left( {X2_{n}^{t} - X1_{n}^{t} } \right) + v_{3} \times \left( {x_{r1}^{t} - x_{r2}^{t} } \right)} \right)/2 \\ & X_{n}^{t + 1} = X_{LEO}^{t + 1} \\ & X_{LEO}^{t + 1} = x_{best} + f_{1} \times (v_{1} \times x_{best} - v_{2} \times x_{n}^{t} ) + f_{1} \times \sigma_{1} \times \left( {v_{3} \times \left( {X2_{n}^{t} - X2_{n}^{t} } \right) + v_{3} \times \left( {x_{r1}^{t} - x_{r2}^{t} } \right)} \right)/2 \\ & X_{n}^{t + 1} = X_{LEO}^{t + 1} \\ & {\varvec{End}} \\ & {\varvec{End}} \\ \end{aligned}$$
(18)

A uniform random number in the interval [-1,1] is denoted by \({f}_{1}\), a random number from a typical distribution with a mean of 0 and a standard deviation of 1 by \({f}_{2}\), the probability by pr, and three random numbers, \({v}_{1}\), \({v}_{2}\), and \({v}_{3}\), which are defined as follows:

$$\begin{aligned} v_{1} = & \left\{ {\begin{array}{*{20}l} {2 \times rand} \hfill & {if\sigma_{1} < 0.5} \hfill \\ 1 \hfill & {Otherwise} \hfill \\ \end{array} } \right. \\ v_{2} = & \left\{ {\begin{array}{*{20}l} {rand} \hfill & {if\sigma_{1} < 0.5} \hfill \\ 1 \hfill & {Otherwise} \hfill \\ \end{array} } \right. \\ v_{3} = & \left\{ {\begin{array}{*{20}l} {rand} \hfill & {if\sigma_{1} < 0.5} \hfill \\ 1 \hfill & {Otherwise} \hfill \\ \end{array} } \right. \\ \end{aligned}$$
(19)

In this case, \({\sigma }_{1}\) is a number in the interval [0, 1], while rand is a random value in the interval [0, 1]. The formulas above can be simplified as follows

$$\begin{aligned} v_{1} = & R_{1} \times 2 \times rand + \left( {1 - R_{1} } \right) \\ v_{2} = & R_{1} \times rand + \left( {1 - R_{1} } \right) \\ v_{3} = & R_{1} \times rand + \left( {1 - R_{1} } \right) \\ \end{aligned}$$
(20)

where the binary parameter \({R}_{1}\) takes a value of either 0 or 1. The value of \({R}_{1}\) is 1 if parameter \({\sigma }_{1}\) is less than 0.5, and 0 otherwise. The following approach is proposed to find the solution for \({x}_{k}^{t}\) in Eq. (21).

$$\begin{aligned} x_{k}^{t} = & \left\{ {\begin{array}{*{20}l} {v_{rand} } \hfill & { if\sigma_{2} < 0.5} \hfill \\ {x_{p}^{t} } \hfill & {Otherwise} \hfill \\ \end{array} } \right. \\ x_{rand} = & X_{min} + rand\left( {0,1} \right) \times \left( {X_{max} - X_{min} } \right) \\ \end{aligned}$$
(21)

In this case, \({x}_{rand}\) denotes a novel solution, \({x}_{p}\) signifies a randomly chosen solution of the population (\(p \in [1, 2,\dots ,N]\)), and \({\sigma }_{2}\) indicates a random value between [0–1]. It is possible to simplify Eq. (21) as:

$$x_{k}^{t} = R_{2} \times x_{p}^{t} + \left( {1 - R_{2} } \right) \times x_{rand}$$
(22)

where the value of the binary parameter \({R}_{2}\) is either 0 or 1. The value of \({R}_{2}\) is 1 if \({\sigma }_{2}\) is less than 0.5, and 0 otherwise. By choosing the values of parameters \({v}_{1}\), \({v}_{2}\), and \({v}_{3}\) at random, the population becomes more diverse and escapes local optimum solutions.

Results and interpretation on benchmark functions test

A thorough performance analysis of our newly concepted IPO using both multi-modal and unimodal benchmark functions is the main objective of this section. We choose to combine unimodal and multi-modal benchmark functions in order to offer an equitable and thorough assessment of the IPO’s performance. While unimodal functions help evaluate the algorithm’s convergence efficiency, multi-modal functions look at the algorithm’s ability to balance exploration in identifying a range of solutions with exploitation in fine-tuning solutions. A variety of distinct benchmark tasks are included in the study, as shown in Tables 2 and 3. A thorough evaluation of the efficacy attained by including Opposition-based Learning and Local Escaping Operator strategies into the original PO framework is made possible by the diverse features and degrees of complexity of these assignments. Out of this large set of benchmark functions, two main groups have been distinguished: functions F1 through F7, which exhibit unimodal behavior, and functions F8 through F13, which are known for their complex multimodal properties. Within a 30-dimensional search space, each experiment in this assessment is designed with 30 people iterated across 500 generations. For every test scenario, we conducted 30 independent runs in order to improve the robustness and dependability of our results. The mean and standard deviation of the fitness error were used to carefully examine the algorithm’s performance, giving a clear indication of its consistency and efficiency.

Table 2 Description of unimodal benchmark functions.
Full size table
Table 3 Description of multimodal benchmark functions.
Full size table

To assess the effectiveness of the proposed approach, we carried out a comprehensive comparison study, contrasting it with a variety of heuristics. They include more recent, well-known algorithms like PO, BA, WOA, and SCA. The control parameters of these employed methods, as detailed in Table 4, critically influence the attainment of optimal or near-optimal solutions. Performance metrics including Worst (Worst), Best (Best), Standard Deviation (Std), and Average (Average) were computed for every technique that was analyzed. With strong emphases highlighting the best findings, Table 5 provides a comprehensive summary of the trial outcomes, including the best options.

Table 4 Control parameters values of the proposed algorithm.
Full size table
Table 5 Optimization results of proposed algorithms.
Full size table

Unimodal test functions can be used to evaluate an algorithm’s capacity to find and employ the optimal answer. Nonetheless, the algorithm’s ability to explore and navigate away from local optima is reliably measured by multimodal functions, which include many local minima. A detailed examination of Table 5's data reveals that the IPO approach consistently yields extremely competitive results, with advances on functions F1-F5, F7, and F11-F13 being particularly noteworthy. This study shows that the IPO method works exceptionally well when looking at the optimal solution zone, mostly because to its strong added enhancement. On the other hand, the other methods, standard PO, SCA and BA, have less success doing a thorough and extensive search. The table, which shows IPO’s outstanding performance on multimodal functions, provides more proof of its powerful exploratory capability when compared to the standard PO approach. According to the presented results, the PO framework’s usage of additional operators improves exploration and successfully reduces the chance of local minima. On the other hand, the OBL mechanism expands the search scope by evaluating both the current solution and its opposite, enhancing exploration and convergence. LEO improves local search by combining the best solution with random and selected candidates, promoting diversity and helping the algorithm escape local optima. These two enhancements refine the balance between exploration and exploitation, making the algorithm more robust and efficient in tackling complex optimization problems, as will be demonstrated in the next section on parameter estimation of PEMFC.

The exploratory skills of an algorithm may be best assessed using multi-modal test functions, which are appropriate for testing IPO’s capacity to balance exploration and exploitation while avoiding local optima. As shown in Table 4, the findings show that IPO routinely performs better than other algorithms on all composite functions, F8-F13. The reason is that OBL mechanism evaluates both the current solution and its opposite simultaneously, broadening the search space and retaining superior solutions to enhance exploration and convergence in IPO. Meanwhile, the LEO acts as a local search tool, generating new solutions in IPO by integrating the best-known solution with random and selected population solutions. This introduces diversity and randomness, aiding the algorithm in escaping local optima and exploring uncharted regions of the search space. Together, these mechanisms strengthen the algorithm’s ability to balance exploration and exploitation, boosting its robustness and effectiveness in tackling these complex optimization challenges.

As shown in Fig. 4, the convergence patterns of IPO are assessed and contrasted with those of rival algorithms. The best solutions for a collection of unimodal and multimodal functions at each iteration are shown in the convergence profiles, which were obtained from 30 separate runs. The graphs show the evolution of IPO’s convergence, which is characterized by notable oscillations in the initial iterations and less variances in subsequent phases. By continually improving locations, the combination of LEO and OBL tools improves results as the number of generations rises, producing better results. The population’s collective effort is reflected in the falling curves. The study emphasizes how proposed improvement increase PO’s efficacy, especially in exploitation, but IPO continuously shows better convergence patterns. This shows that IPO may successfully strike a balance between exploration and exploitation, beating competing algorithms over the course of the iterations.

Fig. 4
figure 4

The convergence profiles of applied methods.

Full size image

Numerical results and interpretation

This section examines how well the suggested IPO performs while extracting parameters from four PEMFC stacks, known as NedStackPS6, BCS500W, and Ballard Mark V. Table 6 displays these stacks’ technical details and operational circumstances. The first three stacks were chosen for testing largely because their experimental V-I data are publicly available and repeatable in the literature, allowing readers to verify our findings easily. These datasets have been exploited for fuel cell designing examination owing to their varied limit of functionality circumstances and efficiency data they include, making them well-suited for evaluating the precision and resilience of fuel cell models across multiple situations. Additionally, the humidity at the cathode and anode for the vapor is always maintained at \(100 \%\). It is important to emphasize that the entire number of parameters found is reflected in the input dimension D, which is comparable to 7. The maximum number of iterations and population size counts for each method are 500 and 30, respectively. The PEMFC parameter extraction limit bounds are obtained from existing research works to ensure impartial comparisons. By specifying the search ranges of \({X=[\zeta }_{1}, {\zeta }_{2}, {\zeta }_{3}, {\zeta }_{4}, {\lambda }_{m}, {R}_{C}, \beta ]\), Table 7 presents a full perspective of the search limit for PEMFC discovered parameters. IPO is used to determine the total of the squared errors between the PEMFC stack’s computed output voltage (\({V}_{Calculted}\)) and actual output voltage \({(V}_{actual})\) at various current instances, using the fitness function provided in Eq. (9), up to the total number of generations. A range of commercial PEMFC are presented in the numerical experiments outlined below. It is important to highlight that the optimal results of the IPO, derived from a total of 20 separate trials, are summarized and discussed in the subsequent text.

Table 6 Technical details of employed PEMFC units.
Full size table
Table 7 Upper and lower bounds of the optimized parameters.
Full size table

Test case 1: NedStackPS6

This test case reveals the results of further tests conducted to evaluate the stability of the suggested IPO when used with an efficient PEMFC stack, namely the NedStackPS6, which has unique properties. The NedStackPS6 has a rated power of 6 kW and consists of 65 cells, featuring a membrane thickness of 178 µm and a surface area of 240 \({\text{cm}}^{2}\). 1.125 \(\text{A}/{\text{cm}}^{2}\) is its maximum current density. Table 6 presents experimental data obtained from64 at a temperature of 70 C and an oxygen and hydrogen pressure of 1 atm.

Table 8 illustrates SQE values and best parameters for PEMFCs units in recent literature. A multiple comparison examination is employed to investigate the variations in mean ranks between IPO and the rival optimization algorithms to further confirm IPO’s efficacy. Table 9 compares the SQE values and calculated parameters from the NedStackPS6 stack’s best run. The suggested IPO approach, with the lowest IPO values of around 2.065816V, continuously obtains the lowest SQE when compared to other methods. Algorithms with similar fitness values are almost identical. A collection of SQE-related statistical results is shown in Table 10. The designd method constantly attains lower values for the best (2.065816V), mean (2.489416V), Std (0.438577V), and worst (3.314078) SQE, which also show that IPO’s mean rank is much better and different from all other algorithms. Table 11 presents a collection data of the IPO’s measured and calculated voltage values. The statistical analysis reveals a remarkably close correlation between the simulated and experimental voltages. The key reason for this outcome is the extra algorithm components’ synergistic action. These operators, which comprise an effective Local Escaping Operator and an Opposition-Based Learning, contribute collectively to produce superior outcomes by iteratively adjusting their locations in search of best solutions.

Table 8 Performance of IPO against other advanced optimizers for PEMFC units in recent literature.
Full size table
Table 9 Statistical analysis results of employed optimizers.
Full size table
Table 10 SQE values and optimized parameters of PEMFC units using proposed optimizers.
Full size table
Table 11 Collection data of the IPO’s measured and calculated voltage values.
Full size table

The development of SQE averages is exposed in Fig. 5a, which contrasts the developed IPO with other algorithms, to highlight the enhanced efficiency of the IPO. In this instance, IPO yields the best result under (SQE = 2.065816V). Local minima are reached via the IPO method, which starts off with a fast convergence speed that gradually drops and stabilizes at the conclusion. Also, it is evident from the convergence plot that IPO performs quite well in terms of convergence, especially when compared to methods such as PO, TSO, and BA. Profoundly, The IPO consistently exhibits advanced convergence patterns, especially in exploitation, as emphasized by the study, which highlights how the proposed improvements enhance PO’s efficiency. The downward trends illustrate the collective contribution of the population, while the combination of LEO and OBL techniques improves solutions through ongoing ___location refinements, leading to better results as generations advance. Characterized by notable oscillations in the initial phases and diminished variations in later stages, the graphs illustrate the IPO’s convergence progression. This demonstrates the IPO’s ability to effectively balance exploration and exploitation, surpassing other algorithms over multiple iterations. Figure 6a shows the algorithmic ranking radar graphic. Importantly, the evaluation repeatedly shows that the suggested approach is preferable to alternative approaches by producing lower SQE values.

Fig. 5
figure 5

Convergence curves of IPO against its competitive algorithms for employed stacks.

Full size image
Fig. 6
figure 6

Algorithmic ranking radar chart for employed PEMFC stacks.

Full size image

The research aimed to estimate the voltage-current characteristics of a PEMFC by integrating the optimally extracted parameters into a computational model. Figure 7a displayed the voltage-current curves in the NedStackPS6 unit produced by different optimization algorithms, compared with experimental results. The IPO exhibited remarkable precision, with its predictions aligning closely with the experimental data throughout the operational range. In comparison, other advanced algorithms displayed noticeable deviations, especially in the zoomed-in portions of the graphs. This enhanced performance of the improved PO stems from its efficient exploration of the parameter space and its capability to escape local optima, establishing it as a reliable tool for PEMFC modeling. The results underscore the significance of the IPO in delivering accurate predictions for the PEMFC stack.

Fig. 7
figure 7

IV curves using proposed methods.

Full size image

The contrast between the computed and experimental models of the voltage-current relationship is shown in Fig. 8a, while the internal voltage drops in the NedStackPS6 unit are illustrated in Fig. 8b. Twenty-nine data points are experimentally included in this specific testing. It can be seen that the measured and calculated voltages align closely with each other. To evaluate the influence of pressure and temperature on NedStackPS6 efficiency, the designed stack model is updated and tested at a constant pressure under varying temperatures of 45, 60, and 75 °C. The stack efficiency testing is shown in Fig. 8c at a fixed temperature of 343 K while varying the partial pressures (\({P}_{H2}/{P}_{O2}=1/1\), (\({P}_{H2}/{P}_{O2}=2/1\), and \({P}_{H2}/{P}_{O2}=3/2)\). The stack’s final voltage increases in harmony with the pressure. Besides, the graphical potential of the mentioned stack is illustrated in Fig. 8d under the temperature effect. The voltage increases simultaneously with the rising temperature.

Fig. 8
figure 8

The main efficiency of NedStackPS6.

Full size image

Test case 2: BCS500W

This section reports the results of further testing to evaluate the suggested IPO’s stability when combined with the BCS500W unit. This stack comprises 32 cells with a membrane thickness of 178 μm and a surface area of 64 cm2. The maximum current density achieved by the stack is 0.469 A/cm2. According to4, the experimental data shown in Table 6 were collected at 60 °C and 1 atm of pressure, with the partial pressures of hydrogen and oxygen fixed at 0.2095 atm.

The optimized parameters and SQE values for this unit from recent investigations are shown in Table 11. The efficacy of the IPO approach was verified by comparing the mean rankings of IPO and other optimization strategies using a statistical comparison. SQE values and optimal parameters from the best trial of the BCS500W unit are illustrated in Table 12. The suggested IPO strategy consistently yields the lowest SQE, at around 0.012457 V. Table 6 summarizes the SQE-related statistical findings. The findings indicate that the proposed approach consistently achieves superior outcomes, with the best value at 0.012457 V, a mean of 0.095174 V, a standard deviation of 0.115875 V, and a worst value of 0.447771 V. These results highlight that IPO’s rank is significantly better and distinct from those of all competing algorithms. A collection data of the IPO’s measured and calculated voltage values is exposed in Table 11. These data show an exceptionally strong match between the simulated and experimental voltages. The enhanced results are attributed to integrating additional components in the standard PO algorithm, which enhances the search process and results in better solutions.

Table 12 Sensitivity analysis results.
Full size table

Figure 5b shows the convergence of SQE averages, drawing comparisons between the designed IPO and other algorithms to underline its superior effectiveness. under identical simulated circumstances. In this case, the optimal outcome under (SQE = 0.012457 V) is achieved via IPO. The IPO approach steadily drops and regulates towards the end, achieving local minima with a rapid convergence speed. Compared to other algorithms such as PO, TSO, and BA, it has good convergence performance. Additionally, the effectiveness of suggested enhancements is demonstrated by the IPO’s constant advanced convergence trends, especially in exploitation. The research emphasizes how the effective populations as a whole contributes and how LEO and OBL strategies are used to provide better solution. The graphs, which exhibit oscillations in the early stages and less variance in the latter stages, indicate how the IPO can balance exploration and exploitation, outperforming competing algorithms over a number of iterations. A similar observation can be made about the algorithmic ranking radar graph shown in Fig. 6b.

By incorporating the optimal parameters into a computer model, the study sought to determine the voltage-current characteristics of a PEMFC. The voltage-current curves generated by several optimization techniques in the BCS500W unit were shown in Fig. 7b and contrasted with the experimental findings. Throughout the operational range, the IPO’s predictions nearly matched the experimental data, demonstrating its exceptional accuracy. Other employed algorithms, in contrast, showed observable variations, particularly in the graphs’ zoomed-in areas. The IPO is an effective method for PEMFC modeling because of its effective parameter space exploration and capacity to avoid local optima, which contribute to its increased performance. The outcomes highlight how important the IPO was in providing exact estimations for the PEMFC stack.

Figure 9a compares the voltage-current relationship between the experimental and calculated models, and Fig. 9b illustrates the internal voltage dips in the BCS500W unit. This case includes several experimental data points, revealing a close alignment between the measured and calculated voltages. Using the same process as in Case 1, the stack unit is reconfigured and assessed at a constant pressure across 45, 60, and 75°C temperatures to examine how temperature and pressure influence the efficiency of the BCS500W. At a constant temperature of 333 K, Fig. 9c displays the stack efficiency trials with various partial pressures. The results show that the partial pressure causes the final voltage of the stack to increase. Additionally, Fig. 9d illustrates the potential variation of the stack with temperature, demonstrating a consistent increase in voltage with temperature.

Fig. 9
figure 9

The main efficiency of BCS500W.

Full size image

Test case 3: Ballard Mark V

The Ballard Mark V Stack uses the IPO approach in this section to determine the optimal stack cell properties and juxtapose them with the experimental conditions. Each membrane in the 35 cells that make up the stack has a surface area of 50.6 cm2 and a thickness of 178 µm. The maximum current density it can achieve is 1.5 A/cm2. In Table 6, experimental results from72 are presented. These measurements were made at 70°C and 1 atm of pressure for both hydrogen and oxygen.

Recent studies show that the IPO strategy performs better than other optimization techniques. Tables 8–10 demonstrate that it achieved the lowest SQE value of 0.814325 V with a mean of 0.979013 V and a standard deviation of 0.209104 V. The proposed IPO outperforms all estimated components, demonstrating its superior ability to accurately locate optimal spots and its continuous performance, demonstrating robustness and flexibility. Table 11 compiles the IPO’s measured and calculated voltage values. The obtained data confirm a highly accurate match between the simulated and experimental currents.

Figure 5c shows IPO method’s superior performance in achieving optimal SQE averages, with a steady decrease and rapid convergence compared to other algorithms like PO, TSO, and BA. Integrating additional operators into the PO framework improves exploration, reduces the risk of local minima, and accelerates convergence. The OBL mechanism expands the search scope by assessing both current and opposite solutions, enhancing convergence efficiency. At the same time, LEO strengthens local search by merging the best solution with random candidates, promoting diversity and helping to avoid local optima. These enhancements fine-tune the balance between exploration and exploitation, resulting in a more robust, efficient, and faster-converging algorithm. The algorithmic ranking radar graph in Fig. 6c shares a similar finding.

Figure 7c illustrated the voltage-current curves generated by different optimization algorithms for the Ballard Mark V stack, alongside experimental data. The IPO demonstrated remarkable precision, with its predictions closely matching the experimental results throughout the operational range. Other methods, on the other hand, showed notable variations, particularly in the magnified part of the graphs. The IPO’s enhanced performance is attributed to its effective exploration of the parameter space and its capability to escape local optima, establishing it as a dependable tool for PEMFC modeling. In Fig. 10a, internal voltage dips of the stack unit are highlighted, and experimental and computed voltage-current relationships are compared in Fig. 10b. The results demonstrate a tight agreement between observed and expected values. The effect of temperature and pressure on efficiency is evaluated by testing the stack unit at different temperatures. The findings show that the increase in partial pressures at 343 K results in an increase in voltage as illustrated in Fig. 10c. Furthermore, Fig. 10d illustrates how the stack voltage consistently rises with the increase in temperature.

Fig. 10
figure 10

The main efficiency of Ballard Mark V.

Full size image

Sensitivity analysis

Sensitivity analysis measures how changes in parameters affect the outcomes. To support the continuous development of more dependable and effective PEMFCs, it seeks to rank, filter, and detect areas that provide extreme output values. The influence of changing the uncertain variables by \(\pm 5\%\) is exposed in Table 12. As shown by a significant rise in the SQE, the findings show that the model exhibits great sensitivity to the parameters \({\zeta }_{1}\) and \({\zeta }_{2}\). Additionally, the model has a considerable sensitivity to \({\zeta }_{3}\), \({\zeta }_{4}\), and \({\lambda }_{m}\), but a decreased sensitivity to \({R}_{C}\) and \(\beta\). Because of the considerable nonlinearity of the model, even minor departures from the IPO best values of the variables might provide noticeably inaccurate results.

Conclusion and future work

In this study, we tackle the challenges of nonlinear optimization by introducing an improved version of the Parrot Optimizer (PO) to identify seven unknown parameters in PEMFC models accurately. By adding a Local Escaping Operator and opposition-based learning, the enhanced PO algorithm performs better at exploring different solutions and avoiding local optima. The IPO was extensively tested through the use of benchmark functions to evaluate its performance. Its ability to optimize the PEMFC model was demonstrated using three distinct PEMFC stacks: NedStackPS6, BCS Stack, and Ballard Mark V. A thorough comparison with several well-established modeling approaches from the literature further validated the method’s effectiveness and reliability. The resulting SQE values for the NedStackPS6, BCS Stack, and Ballard Mark V units were 2.065816V, 0.012457V, and 0.814325V, respectively. Notably, the IPO showed a 12.87% improvement in the best performance metric and an 88.37% reduction in standard deviation when compared to the original PO. The sensitivity analysis shows the dependability and efficacy of the enhanced PO approach for parameter estimation, which verifies that the optimized model appropriately depicts the PEMFC systems. These findings underscore that the developed approach, along with sensitivity analysis, accurately captures the dynamics of the PEMFC model, delivering the lowest SQE values and ensuring stable convergence. All things considered, this work greatly improves the accuracy and effectiveness of PEMFC models, which makes it a major advancement for fuel cell system optimization in renewable energy applications.

The present study identifies numerous promising avenues for future works via the enhanced PO. It recommends broadening the application of IPO to include areas such as: optimizing energy management within microgrids, Maximum Power Point Tracking for better photovoltaic system efficiency, solving Optimal Power Flow issues, and parameters extraction for photovoltaic models.