Introduction

Rolling bearings are essential components in power transmission within mechanical systems and are critical to the operation of various rotating machinery1,2,3,4. During operation, factors such as misalignment, imbalance, rubbing, and overload can cause wear, potentially leading to bearing component faults. Bearing faults are among the primary causes of failures in rotating machinery5,6. Bearing fault diagnosis is crucial for the reliability of real-world platforms such as heavy-lift vehicles, elevators, power converters, and bearing systems7,8,9,10. Recently, data-driven approaches for bearing fault diagnosis have garnered significant attention11. Bearing fault diagnosis approaches typically fall into two categories: model-driven and data-driven. Model-driven approaches rely on prior knowledge to build accurate diagnosis models. Techniques like fast Fourier transform, wavelet analysis, and empirical modal decomposition can extract time-frequency features and analyze instantaneous frequency for fault diagnosis. However, these methods excessively depend on expert judgment and pre-existing knowledge. In contrast to traditional model-driven approaches, data-driven fault diagnosis methods depend less on expert knowledge and instead focus more on extracting reliable insights from mechanical equipment data. These methods are gaining recognition in academia and industry due to their universality in establishing relationships between data and fault types.

Traditional data-driven fault diagnosis usually uses a shallow model for data processing and training. Shallow models have been widely utilized in rolling bearing fault diagnosis, leveraging their simplicity and effectiveness in scenarios with limited data. Traditional approaches such as k-Nearest Neighbors (kNN)12,13, Support Vector Machines (SVM)14,15, and Principal Component Analysis (PCA)16,17,18,19 focus on extracting time, frequency, or time-frequency ___domain features manually. However, these approaches require manual feature extraction and are constrained by limited network depth.

Deep learning techniques have been widely studied for fault diagnosis applications as they are increasingly applied to overcome the limitations of shallow models in fault diagnosis20, demonstrating their potential in contactless fault detection21. Tong et al.22 developed an intelligent fault diagnosis method for rolling bearings using advanced deep learning techniques, which could enhance diagnostic accuracy in similar bearing fault detection scenarios. Zhang et al.23 proposed a method combining ensemble empirical mode decomposition and an optimized SVM for the multi-fault diagnosis of rolling element bearings. Shao et al.24 introduced an adaptive deep belief network with a dual-tree complex wavelet packet for fault diagnosis. Cheng et al.25 compared the performance of the back propagation neural network (BPNN) and other neural networks for rolling bearing fault diagnosis, finding BPNN achieved the highest accuracy despite computational burden. Zhu et al.26 proposed a genetic algorithms (GA) and BPNN algorithm to enhance fault diagnosis accuracy for industrial rolling bearings. In addition to these approaches, recent studies on fault diagnosis techniques in other mechanical systems, such as the optimization design for journal-thrust coupled bearings using particle swarm optimization (PSO)27, and multi-cavitation state diagnosis in vortex pumps28, suggest that similar strategies could be adapted to enhance bearing fault diagnosis accuracy. Furthermore, models such as the Jiles-Atherton and nonlinear autoregressive exogenous neural network for modeling hysteresis29 and methods based on rough set theory for reliability optimization30 show potential for further improving the interpretability and efficiency of fault diagnosis in bearing systems. Zhi et al.31 introduced a novel gearbox localized fault detection method based on meshing frequency modulation (MFM) analysis, which directly identifies faults by observing changes in the meshing frequency bandwidth. Liu et al.32 presented an improved dual-microphone Active Noise Cancellation (ANC) method, IM-RM-LMS, which effectively cancels noise from two moving sound sources by assimilating Doppler distortion laws for TADS applications. Elik et al.33 introduced reconfigured single- and double-diode models (Reconfig-SDM and Reconfig-DDM) for more accurate photovoltaic (PV) cell/module modeling by adding small series resistances, optimized through the Squirrel Search Algorithm (SSA), and experimentally tested, showing improved performance over existing approaches. Tejani et al.34 presented the 2-Archive Multi-Objective Cuckoo Search (MOCS2arc), an advanced multi-objective optimization algorithm that enhances solution diversity and optimization performance for truss structures and test functions, demonstrating superior results compared to other established algorithms.

In recent years, deep learning, particularly the Autoencoder (AE) theory, has been applied to intelligent fault diagnosis (IFD). Studies such as those in35,36,37,38,39,40,41,42,43,44,45,46 have developed various AE-based methods for tasks including vibration signal processing, rotating machinery fault diagnosis, unbalanced fault diagnosis, semi-supervised fault diagnosis, and bearing fault detection, demonstrating AE’s powerful capabilities in feature extraction and fault diagnosis. Lu et al.47 also investigated the effectiveness of a SDAE for health state identification in signals containing ambient noise and working condition fluctuations. However, while single AE models excel at dimensionality reduction, their shallow structure often hinders the efficient processing of large-scale data. In addition, handling noisy data is also crucial48,49,50,51. To overcome these limitations, this paper proposes integrating the SDAE model, leveraging its stacked network structure and noise reduction capabilities for enhanced performance in bearing fault diagnosis.

Although deep learning techniques demonstrate outstanding diagnostic capabilities, they often necessitate iterative fine-tuning during gradient optimization. Conversely, the extreme learning machine (ELM) is extensively applied in recognizing motion states and diagnosing faults due to its rapid learning, simplicity in training, and overall efficiency52. Vashishtha et al.53 proposed an intelligent method for bearing defect identification using Swarm Decomposition and ELM optimization. Researchers have also explored combining ELM with kernel functions to handle nonlinear characteristics in vibration signals, resulting in kernel ELM (KELM) for improved fault diagnosis accuracy54. Additionally, Kasun et al.55 introduced an ELM-based auto encoder (ELM-AE) for feature representation learning, enhancing the multi-layer extreme learning machine performance. The deep ELM model with multiple hidden layers performs better than the original ELM model.

Metaheuristic algorithms are also applied in deep learning models, particularly in the automatic selection of optimal parameters, where swarm intelligence optimization algorithms iteratively determine the best hyperparameters for deep networks56,57,58,59. For instance, Chauhan et al.60 introduced a crayfish optimization algorithm for adaptively optimizing wavelet filters in machine fault diagnosis, improving accuracy in extracting fault-related frequencies despite challenges like low signal-to-noise ratios and background noise, while Zhang et al.61 proposed an anomaly detection method for wind turbines using long short term memory-SDAE and extreme gradient boosting. Zhu et al.62 proposed a bearing fault diagnosis method based on hierarchical entropy and support vector machine optimized by particle swarm optimization. Hu et al.63 proposed a rolling bearing fault diagnosis based on variational mode decomposition and genetic algorithm-optimized wavelet threshold denoising. Li et al.64 an intelligent bearing fault diagnosis of rotating machinery using wavelet transform and ant colony optimization. Vashishtha et al.65,66 proposed methods for detecting faults using optimized SVM and MED filtering with the Aquila optimizer. In engineering, data collected from projects may suffer from incompleteness and noise, which hinders the effectiveness of KELM in learning typical features, especially when working with large-scale datasets. Thus, this paper introduces a novel fault diagnosis model, SDAE-adaptive hierarchical hybrid KELM (AHHKELM), which utilizes SDAE for noise mitigation and deep feature extraction. To improve KELM’s capabilities, this paper combines polynomial and radial basis function kernels to create hybrid KELM (HKELM), further stacked into HHKELM. Aquila Optimizer (AO)67 is employed for hyper-parameter selection in HHKELM. The resulting adaptive HHKELM serves as the ultimate fault classifier. The proposed stacked denoising autoencoder-adaptive hierarchical hybrid kernel extreme learning machine (SDAE-AHHKELM) method effectively extracts meaningful feature information and mitigates noise interference with adaptive hyper-parameter selection, demonstrating its superiority in bearing fault diagnosis through two illustrative examples.

The main contributions are summarized as follows:

  1. 1.

    We introduce an enhanced Aquila Optimizer to improve the performance and stability of the HHKELM model. By incorporating chaos mapping, a new balanced search strategy, and adjusting the parameter \(G_2\), the algorithm becomes more effective in avoiding local optima and improving global search capabilities. These improvements enhance the robustness of the model during parameter optimization, leading to better fault diagnosis accuracy and reliability.

  2. 2.

    We propose the SDAE-AHHKELM model, which integrates the SDAE feature extractor with the HHKELM classifier. SDAE performs noise reduction and deep feature extraction, which are crucial for dealing with noisy data in industrial applications. The innovative combination of SDAE and HHKELM enhances fault diagnosis performance, going beyond the results achievable by simply combining these existing techniques.

  3. 3.

    Experimental results on the CWRU, MFPT, and JNU datasets demonstrate the model’s flexibility, reliability, and robustness in engineering applications. The SDAE-AHHKELM model shows significant improvements in fault diagnosis accuracy and stability compared to traditional methods, effectively addressing complex fault diagnosis tasks through better feature extraction, model structure, and parameter optimization.

The remainder of this article is organized as follows. Section 2 presents a brief review of the key principles behind both SDAE and KELM. Section 3 focuses on the introduction of the SDAE-AHHKELM diagnosis model. Section 4 demonstrates the effectiveness of the SDAE-AHHKELM approach using three bearing case studies, CWRU, MFPT and JNU. Finally, Section 5 summarizes the findings and suggests avenues for future research.

Related Knowledge

Stacked denoising auto-encoder (SDAE)

Within the ___domain of mechanical fault diagnosis, raw oscillation signals often suffer from significant noise interference, making it challenging to achieve optimal performance for the Autoencoder (AE). To bolster the AE’s resilience and expand its usability, Vincent et al.68 proposed the addition of random noise to create altered data \(x'\). This altered data then acts as the input for the Denoising Autoencoder (DAE). These ’noise’ data serve as the Denoising Autoencoder input. The novel variant model adeptly captures both the original and degraded features resulting from noise introduction, thereby substantially improving the AE’s robustness and generalization performance. This approach effectively addresses the issue of overfitting.

Two common approaches exist for adding noise to the DAE: firstly, the input data \(x\) undergoes random zeroing based on a specific mapping function, followed by filling and noising the zeroed data bits during network training; secondly, noise is directly incorporated into the data. Consequently, the transformations and updates for the encoder and decoder mappings are defined as follows:

$$\begin{aligned} \varvec{h}= & S\left( \varvec{W} \varvec{x}' + \varvec{b}_1\right) , \end{aligned}$$
(1)
$$\begin{aligned} \varvec{z}= & S\left( \varvec{W}^{\prime } \varvec{h}+\varvec{b}_2\right) , \end{aligned}$$
(2)

where the activation function \(S\) utilizes the sigmoid function; \(\varvec{W}\) and \(\varvec{W'}\) denote the weight matrices, while \(\varvec{b_1}\) and \(\varvec{b_2}\) are the bias vectors.

The DAE loss can be expressed in the following form:

$$\begin{aligned} L_{\textrm{DAE}}=\frac{1}{n} \sum _{j=1}^n \left( \frac{1}{2}\left\| \hat{x}_j - y_j \right\| ^2 \right) , \end{aligned}$$
(3)

where \(n\) represents the number of input samples, \(y_j\) denotes the \(j\)th input sample, \(\hat{x}_j\) is the reconstructed output for the \(j\)th sample, and \(\Vert \cdot \Vert\) represents the norm operation.

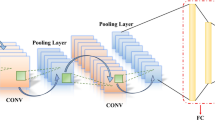
The DAE model employs an iterative process to refine the network’s weight matrix and bias vector. This is accomplished using the backpropagation algorithm, aiming to minimize the reconstruction error. However, the DAE faces a common limitation of shallow networks: a restricted learning capacity that hinders the extraction of deeper characteristics. Multiple DAE units are interconnected to construct an SDAE model to augment the feature extraction capability of a single DAE model. The features derived from the hidden layer of the previous DAE are sequentially passed as inputs to the next DAE, aiding in the acquisition of valuable characteristics. SDAE embodies deep network traits, greatly boosting its generalization capability. It is capable of learning more robust and deeper meaningful features from the data, leading to better outcomes in feature extraction compared to a shallow network. The architecture of the SDAE is illustrated in Figure 1.

Fig. 1
figure 1

SDAE network structure.

Full size image

Kernel extreme learning machine

In the context of ELM, feature representation can be divided into direct and indirect mapping approaches. A key operation in ELM is the calculation of the dot product between feature vectors. Indirect mapping achieves this computation through kernel methods69,70, bypassing the need for an explicit definition of the feature space and mapping functions, which makes it a versatile method extensively employed across different domains. Consequently, Huang et al.71 proposed the KELM, a method that incorporates kernel functions to enhance the generalization capabilities and accelerate the learning efficiency of ELM. The kernel matrix in KELM, defined in accordance with Mercer’s condition, is represented as:

$$\begin{aligned} \varvec{\Theta }_{\textrm{KELM}}=\varvec{H} \varvec{H}^\textrm{T}, \quad \Theta _{\textrm{KELM}_{i, j}}=\varvec{h}(\varvec{x}_i) \varvec{h}(\varvec{x}_j)=K(\varvec{x}_i, \varvec{x}_j) . \end{aligned}$$
(4)

Thus, the output function expression of KELM is:

$$\begin{aligned} \beta= & \varvec{H}^\textrm{T}\left( \frac{\varvec{I}}{C}+\varvec{H} \varvec{H}^\textrm{T}\right) ^{-1} \varvec{Y}, \end{aligned}$$
(5)
$$\begin{aligned} f(\varvec{x})= & \varvec{h}(\varvec{x}) \varvec{\beta } = \varvec{h}(\varvec{x}) \varvec{H}^\textrm{T}\left( \frac{\varvec{I}}{C} + \varvec{H} \varvec{H}^\textrm{T}\right) ^{-1} \varvec{Y} = \left[ \begin{array}{c} K\left( \varvec{x}, \varvec{x}_1\right) \\ \vdots \\ K\left( \varvec{x}, \varvec{x}_N\right) \end{array}\right] \left( \frac{\varvec{I}}{C} + \varvec{\Theta }_{\textrm{KELM}}\right) ^{-1} \varvec{Y}. \end{aligned}$$
(6)

where \(C\) and \(\varvec{I}\) represent the regularization parameter and the identity matrix, respectively, while \(K(x_i, x_j)\) denotes the kernel function. This formulation clearly demonstrates that the size of the feature space has no influence on the effectiveness of the mapping, thereby effectively mitigating the curse of dimensionality72,73.

Method

The SDAE-AHHKELM framework is designed to address the challenges of rolling bearing fault diagnosis by integrating advanced feature extraction, adaptive hybrid kernel learning, and optimized parameter tuning. This model consists of three core components: a Stacked Denoising Autoencoder , an Adaptive Hierarchical Hybrid Kernel Extreme Learning Machine (AHHKELM), and an Improved Aquila Optimizer (IAO). The SDAE is employed to extract robust and noise-resilient features from vibration signals through a multi-layer architecture that reduces noise impact by introducing random corruption during training and reconstructing clean signal representations, effectively preserving key fault information. The AHHKELM combines polynomial and Gaussian radial basis kernels to address the limitations of single-kernel methods, enabling the classifier to capture both linear and nonlinear relationships within the data, thereby significantly enhancing fault classification accuracy and scalability for complex scenarios. Additionally, the IAO algorithm fine-tunes the hyperparameters of the AHHKELM by incorporating chaos mapping and adaptive parameter adjustment, which improves its ability to escape local optima and achieve global convergence. Together, these components ensure the framework is efficient, robust, and reliable, making it well-suited for industrial applications in bearing fault detection and predictive maintenance.

Aquila optimizer

The Aquila Optimizer (AO) is a nature-inspired meta-heuristic optimization algorithm inspired by the hunting behavior of eagles. The optimization process of the AO algorithm is characterized by four main strategies: (1) utilizing a vertical perch to select the high-soaring search space, (2) employing short gliding attack profiles to explore the divergent search space, (3) using low-flying slow descent attacks for convergence in the search space, and (4) using walking to dive for prey.

(a) Expanded search (\(Y_1\)): The Aquila begins by flying from a high altitude to explore the search space. The formula is given by:

$$\begin{aligned} Y_1(t+1)= & Y_{\text{ opt }}(t) \times \left( 1 - \frac{t}{T}\right) + \left( Y_{\mu }(t) - Y_{\text{ opt }}(t) \times \text{ rand }\right) , \end{aligned}$$
(7)
$$\begin{aligned} Y_{\mu }(t)= & \frac{1}{P} \sum _{k=1}^P Y_k(t), \end{aligned}$$
(8)

where \(Y_{1}(t+1)\) is the position of the solution at the next iteration; \(Y_{\text {opt}}(t)\) is the best solution found before the t-th iteration; \(Y_{\mu }(t)\) is the mean position of the current population; \(\text {rand}\) is a random number in the interval (0, 1); t is the current iteration number; T is the maximum number of iterations.

(b) Narrowing the scope of exploration (\(Y_2\)): The Aquila narrows down the selected area to explore the target prey and prepare for an attack. The formula is given by:

$$\begin{aligned} Y_2(t+1) = Y_{\text {opt}}(t) \times \operatorname {Levy}(d) + Y_\rho (t) + (y - x) \cdot \text {rand}, \end{aligned}$$
(9)

where d denotes the dimensional space; \(Y_{\rho }(t)\) is a random solution within the range [1, P]; and \(\text {Levy}(d)\) is the Levy flight distribution function.

(c) Expanded development (\(Y_3\)): The Aquila selects a target area to approach its prey and initiates an attack. The formula is given by:

$$\begin{aligned} Y_3(t+1) = \left( Y_{\text {opt}}(t) - Y_{\mu }(t)\right) \times \beta - \text {rand} + \left( (UB - LB) \times \text {rand} + LB\right) \times \gamma \end{aligned}$$
(10)

where \(\beta\) and \(\gamma\) are adjustment parameters in the range (0, 1); LB is the lower bound of the problem; and UB is the upper bound of the problem.

(d) Reducing the scope of development (\(Y_4\)): As the Aquila closes in on its target, it maneuvers randomly and launches attacks based on the prey’s position. The formula is given by:

$$\begin{aligned} \begin{aligned} Y_4(t+1)&= Y_{\text {opt}}(t) \times QG - \left( G_1 \times Y(t) \times \text {rnd}\right) - G_2 \times \operatorname {Levy}(d) + \text {rand} \times G_1, \\ QG(t)&= t^{\frac{2 \times \text {rand} - 1}{(1 - T)^2}}, \\ G_1&= 2 \times \text {rand} - 1, \\ G_2&= 2 \times \left( 1 - \frac{t}{T}\right) . \end{aligned} \end{aligned}$$
(11)

where QG is the quality function used to balance the search strategy; \(G_1\) represents different strategies employed by Aquila to pursue the prey; and \(G_2\) represents the decreasing value from 2 to 0, symbolizing the flight slope of Aquila.

IAO Algorithm

The AO algorithm, when applied to complex problems, is prone to getting stuck in local optima, leading to premature convergence. To address this issue, tent chaotic mapping, nonlinear inertia weights, and nonlinear convergence factors have been incorporated. These enhancements aim to balance the global and local search capabilities, improve the algorithm’s ability to escape local optima, and boost global search efficiency.

Chaos mapping The initial population of the first generation of the AO algorithm was randomly generated. However, compared to random initialization, utilizing chaotic mapping to generate the first-generation population results in a more uniform distribution across the search space. This distribution aids in steering the algorithm away from local optimization and premature convergence. The improved logistic mapping (ILM) was employed to initialize the population distribution in this study. ILM performs better in initializing population distributions than the classical logistics chaotic map. Therefore, the improved logistic chaotic map was chosen to initialize the Skyhawk population. The formula is expressed as follows:

$$\begin{aligned} & \left\{ \begin{array}{l} x_{n+1}^{\prime } = 4 x_n^{\prime } (1 - x_n^{\prime }) \\ y_n^{\prime } = \frac{1}{\pi } \arcsin (2 x_{n+1}^{\prime } - 1) - \frac{1}{2} \\ x_{n+1} = 4 y_n^{\prime } (1 - y_n^{\prime }) \\ y_n = \frac{1}{\pi } \arcsin (2 x_{n+1} - 1) - \frac{1}{2} \end{array} \right. \end{aligned}$$
(12)
$$\begin{aligned} & \quad X_{ij} = y_n (B_{\textrm{U}_{jj}} - B_{\textrm{L}_j}) + B_{\textrm{L}_j}, \end{aligned}$$
(13)

where \(B_{\textrm{U}_{jj}}\) and \(B_{\textrm{L}_j}\), respectively, are the upper and lower bounds in the j-dimensional search space, \(i \in [1, N]\), \(j \in [1, D]\), N and D are the population size and the number of dimensions of the algorithm, respectively.

The resulting chaotic sequence \([y_n]\) is inserted into equation (13) to obtain the initial position of the Skyhawk population.

New balanced search strategy In AO, if the current iteration number \(t \le \frac{2}{3} T\), the algorithm transitions to the global search stage; otherwise, it proceeds to the local search stage. This paper proposes a new balancing method to achieve a better balance between the two stages and mitigate the influence of local optima. The formula is expressed as follows:

$$\begin{aligned} E=\frac{1}{2} \sin \left( 8 \pi \frac{t}{T}\right) +\left( 1-\frac{t}{T}\right) , \end{aligned}$$
(14)

where E is the oscillatory-type parameter varying with the number of iterations. When \(E > 0.2\), the algorithm performs global search, otherwise it performs local search. To determine the threshold \(E = 0.2\), we substitute \(t = \frac{2}{3}T\) into the balancing formula, yielding \(E \approx 0.23\). The value of \(E = 0.2\) is a practical adjustment based on both theoretical derivation and empirical optimization, ensuring a smoother transition between global and local search stages.

As shown in Figure 2, with improvements, the algorithm can now perform local searches during the middle of the iterations, ensuring a more thorough exploration of the search space. By incorporating global search while retaining the local search mode during the later iterations, the algorithm maintains its comprehensive search capability towards the end of iterations, thus helping to avoid local optimization.

Fig. 2
figure 2

The iteration curve of E value.

Full size image

Adjustment strategy of the parameter \(G_2\) \(G_2\) is a linearly decreasing parameter from 2 to 0, representing the flight slope from the first position to the last position when the Skyhawk tracks its prey. In this paper, a nonlinear decline parameter is proposed. \(G_2\) in equation (11) is adjusted to equation (15).

$$\begin{aligned} G_2=2\left[ 1-\sin \left( 0.7 \frac{t}{T}\right) ^2 \pi \right] . \end{aligned}$$
(15)

The value \(0.7\) in the sine function is an empirically chosen parameter based on both theoretical analysis and experimental validation. It ensures that the algorithm transitions smoothly from global search to local search by maintaining a larger \(G_2\) value during the middle iterations, thereby enhancing the exploration capability. Meanwhile, it allows \(G_2\) to decrease effectively in later iterations, prioritizing local search and improving convergence accuracy.

Figure 3 shows the iteration curve of the \(G_2\) value, comparing the performance of the original and improved algorithms. Based on the new equilibrium method, the algorithm conducts a local search in the middle of the iteration. At this time, the improved \(G_2\) has a larger value, making the algorithm more dependent on Levy flight to search the solution space more thoroughly. In the later iteration, the improved \(G_2\) is small and is less affected by Levy flight random large-scale search. Therefore, the optimal solution \(X_{\text {best}}(t)\) and historical solution X(t) obtained in the previous step will affect the search results of this step and improve the local search capability in the later iteration.

Fig. 3
figure 3

The iteration curve of \(G_2\) value.

Full size image

However, when the number of iterations exceeds a certain threshold, \(G_2\) may become negative, which could interfere with the algorithm’s convergence performance.

To balance the influence of \(G_2\) on the global search and local search, this paper incorporates the improved opposition-based learning (IOBL) strategy into the adjustment of \(G_2\). During the local search phase of the algorithm, the introduction of opposite solutions enriches the population diversity. This enables the algorithm to utilize useful prior knowledge before the development phase, enhancing its ability to escape from local optima.

Opposition-Based Learning (OBL) refers to the process during the evolutionary algorithm’s selection phase, where an opposite position is generated based on the current position. Then, the fitness of the current position and its opposite position is compared. If the fitness of the opposite position is better than the current position, the opposite position is used to replace the current one. Otherwise, the opposite position enters the next iteration of optimization.

The formula for improved opposition-based learning is as follows:

$$\begin{aligned} x_j^{'k} = a_j^k + \left( k_b x_j^b(t) - x_j^a(t) \right) \end{aligned}$$
(16)

where \(x_j^a(t)\) is the current position, \(x_j^b(t)\) is the opposite solution, \(a_j^k, b_j^k\) are the position bounds, \(k_1, k_2\) are the mean weights of the current and opposite positions.

If \(x_j^{'k} \notin [a_j, b_j]\), then it is updated using the following formula:

$$\begin{aligned} x_j^{'k} = {\left\{ \begin{array}{ll} 2a_{max} - x_j^{'k}, & \text {if } x_j^{'k} > b_j \\ 2a_{min} - x_j^{'k}, & \text {if } x_j^{'k} < a_j \end{array}\right. } \end{aligned}$$
(17)

This approach enriches population diversity by introducing opposite solutions and effectively utilizes prior evolutionary knowledge. It helps to accelerate convergence to the global optimum and enhances the algorithm’s robustness.

Comparison To clearly and intuitively demonstrate the practicality and superior performance of the Improved Aquila Optimizer (IAO), this study employs a complex high-dimensional benchmark function, \(f_{\text {test}}\), for comparison. Specifically, the accuracy of three swarm intelligence algorithms-Particle Swarm Optimization (PSO), Grey Wolf Optimizer (GWO), and Aquila Optimizer (AO)-is evaluated alongside the IAO to assess their effectiveness in locating the optimal value67. The expression of the function is as follows:

$$\begin{aligned} f_{test}(x) = -20 \exp \left( -0.2 \sqrt{\frac{1}{30} \sum _{i=1}^{30} x_i^2}\right) - \exp \left( \frac{1}{30} \sum _{i=1}^{30} \cos 2 \pi x_i\right) + 20 + e, \, -32 \le x_i \le 32, \, \min (f_{10}) = f_{10}(0, \ldots , 0) = 0. \end{aligned}$$
(18)
Fig. 4
figure 4

Convergence comparison diagram of three population intelligent algorithms.

Full size image

The fundamental parameters are consistently defined as follows: the problem dimensionality is fixed at 30, and the iteration count is set to 500. PSO algorithm utilizes a fully connected topology. It employs cognitive and social constants (C1, C2) set to 2 each. Additionally, PSO employs an inertia weight that linearly reduces from 0.9 to 0.1 during optimization. The velocity of particles is limited to 10% of the dimension range. The GWO algorithm utilizes a convergence parameter that undergoes a linear reduction from 2 to 0 during optimization. Figure 4 depicts the performance comparison and convergence behavior of the different evaluation algorithms.

The test function contains numerous local extreme values, necessitating the algorithm to possess the ability to escape from local optima. In Figure 4, 30 random numbers are selected from the specific range of [-50, 50], and the iteration cycle is repeated 500 times. Observations reveal that both the AO and IAO algorithms quickly converge to the optimal value early in the iteration process.The results, as shown in the convergence curve comparison, highlight the performance differences between the algorithms. Specifically, the IAO algorithm consistently outperforms AO, GWO, and PSO in terms of achieving a lower objective function value, with the best value found by IAO being 3.0706e-06, which is a significant improvement compared to AO’s best value of 4.6102e-06. The relative improvement in the objective function value by IAO is approximately 33.4%.As shown in the convergence curves, IAO converges much faster and more effectively than the other algorithms. Its fitness value stabilizes at 3.0706e-06 after just 100 iterations and remains consistent throughout the rest of the iterations. In contrast, AO stabilizes at 4.6102e-06 after 400 iterations, while GWO and PSO struggle to approach a similar level of optimization, with final objective function values of 0.60282 and 0.39193, respectively. This further demonstrates IAO’s ability to escape local optima and achieve a better global solution.Compared to PSO and GWO algorithms, both AO and IAO algorithms exhibit significantly enhanced iteration convergence efficiency and optimization performance. They effectively address local optimization issues and offer superior solutions to multi-dimensional optimization problems. Furthermore, the IAO algorithm demonstrates superior local search capabilities in later iterations, thus mitigating the risk of falling into local optima and presenting additional advantages over the AO algorithm.

Hierarchical hybrid kernel extreme learning machine

Choosing the kernel function along with its parameters significantly influences KELM’s performance, underscoring the importance of selecting a suitable kernel. Furthermore, an individual kernel function may not be appropriate for every scenario. Therefore, employing multiple kernel-based learning strategies, including both linear and nonlinear combinations, to merge two kernel functions as basis functions can assist in creating a novel hybrid kernel. Although the KELM framework utilizing a polynomial kernel exhibits robust generalization abilities, its learning capacity may be limited. In contrast, the Gaussian kernel greatly enhances KELM’s approximation capability and provides superior smoothness along with strong classification performance74. The formulas for the Gaussian radial and polynomial kernel functions are presented as follows:

$$\begin{aligned} K_{\text{ rbf } }\left( \textrm{x}, \textrm{x}^{\prime }\right)= & \textrm{e}^{-\frac{\left\| x-x^{\prime }\right\| ^2}{2 \delta ^2}}, \end{aligned}$$
(19)
$$\begin{aligned} K_{\text{ poly } }\left( \textbf{x}, \textbf{x}^{\prime }\right)= & \left( \left( \textbf{x}_i \cdot \textbf{x}_i^{\prime }\right) +p\right) ^q, \end{aligned}$$
(20)

where x represents the sample of the normalized training set, \(x^{\prime }\) represents the transpose of the sample of the normalized test set, \(\sigma\) is the bandwidth used to control the local scope of the Gaussian kernel function, p and q are the kernel parameters of the polynomial kernel function.

Hence, to enhance KELM’s generality and approximation capability, this study integrates the two functions above to create a new composite function as the kernel function for KELM. Subsequently, a novel hybrid kernel learning machine model is formulated, and its computational procedure is outlined as follows:

$$\begin{aligned} K_{\text{ hybrid } }\left( \textbf{x}, \textbf{x}^{\prime }\right) =\omega \cdot K_{p o l y}+(1-\omega ) \cdot K_{r b f}, \end{aligned}$$
(21)

where, \(\omega\) denotes the weight parameter, and it is constrained within the interval [0, 1].

By leveraging the unique properties of the combined kernel function, the developed HKELM framework exhibits enhanced abilities in both learning and generalization. Nevertheless, the impact of these improvements may be constrained in specific real-world scenarios, owing to the relatively shallow nature of its network structure.

Multi-layer ML-ELM achieves excellent performance while maintaining the fast learning rate typical of ELM. Deep neural architecture are constructed by iteratively layering multiple ELM-AEs55 .The weight \(\beta _i\) produced by the i-th ELM-AE is considered as corresponding to the i-th layer in the ML-ELM. This process is repeated to build a deep ELM structure. The interactions between adjacent hidden layers within the ML-ELM are described as follows:

$$\begin{aligned} \varvec{H}^i=h\left( \left( \beta _i\right) ^{\varvec{T}} \varvec{H}^{i-1}\right) , \end{aligned}$$
(22)

where the output weight \(\beta _i\) can be calculated according to formula (23).

$$\begin{aligned} \beta =\varvec{H}^\textrm{T}\left( \frac{\varvec{I}}{\varvec{C}}+\varvec{H}\varvec{H}^\textrm{T}\right) ^{-1} \varvec{Y}. \end{aligned}$$
(23)

Through the implementation of the previously discussed ML-ELM, an ELM-based deep network structure is achieved. In this work, the developed HKELM serves as the top-level classifier within the ML-ELM framework. By combining the strengths of deep network architectures with those of kernel methods, the HHKELM is established. Figure 5 offers a visual representation of the HHKELM structure.

Fig. 5
figure 5

HHKELM network structure diagram.

Full size image

If the hidden layers in the HHKELM model are denoted by n, the corresponding kernel matrix can be represented as:

$$\begin{aligned} \begin{aligned} \varvec{\Theta }_{\text{ HHKELM } }&= \varvec{H_n} \varvec{H_n}^{\varvec{T}}, \\ \varvec{\Theta }_{\text{ HHKELM } M_{i, j}}&= \varvec{h}\left( x_i\right) \varvec{h}\left( x_j\right) = \varvec{K}_{\text{ hybrid } }\left( x_i, x_j\right) . \end{aligned} \end{aligned}$$
(24)

Thus, the HHKELM’s classification output for an input x is represented as:

$$\begin{aligned} \beta _{\text {HHKELM}}= & \varvec{H_n}^{\varvec{T}} \left( \frac{\varvec{I}}{C} + \varvec{H_n} \varvec{H_n}^{\varvec{T}}\right) ^{-1} \varvec{Y} = \varvec{H_n}^{\varvec{T}} \left( \frac{\varvec{I}}{C} + \varvec{H_n} \varvec{H_n}^{\varvec{T}}\right) ^{-1} \varvec{Y}. \end{aligned}$$
(25)
$$\begin{aligned} f(x)= & \varvec{h_n}(x) \beta = \varvec{H_n}(x) \varvec{H_n}^{\varvec{T}}\left( \frac{\varvec{I}}{C}+\varvec{H_n} \varvec{H_n}^{\varvec{T}}\right) ^{-1} \varvec{Y} = \left[ \begin{array}{c} \varvec{K}_{\text {hybrid}}(x, x_1) \\ \vdots \\ \varvec{K}_{\text {hybrid}}(x, x_N) \end{array}\right] \left( \frac{\varvec{I}}{C}+\varvec{\Theta }_{\text {HHKELM}}\right) ^{-1} \varvec{Y}. \end{aligned}$$
(26)

IAO-HHKELM

Despite the HHKELM demonstrating superior learning capabilities and improved generalization performance, the use of multiple kernel functions and a deep network architecture introduces additional hyperparameters compared to the original model. These additional hyperparameters encompass the quantity of nodes in each layer, the \(L_2\) regularization term for the ELM-AE during pre-training, the penalty coefficient \(C\) for the upper-level HKELM, the hidden layer weights, and the kernel parameters \(K_{\text {poly}}\) and \(K_{\text {rbf}}\). Manual selection of these hyperparameters often fails to yield optimal results. To overcome this challenge, the IAO is utilized to iteratively search for the best hyperparameter values in the HHKELM. This iterative approach aims to determine the optimal configuration and develop an adaptive AHHKELM fault classifier.

The HHKELM leverages the IAO for optimizing its extensive hyperparameters, with the objective of minimizing the classification error rate on the HHKELM training set. This adaptive search aims to identify the optimal hyperparameter combination. The flowchart depicting the IAO’s process for optimizing the HHKELM is presented in Figure 6.

Fig. 6
figure 6

Flow chart of the intelligent optimization algorithm based on the IAO-HHKELM.

Full size image

The specific procedure for optimizing the HHKELM model with the IAO is outlined as follows:

Step 1: Extract high-level features from raw data utilizing the SDAE method. Use the quantified samples as input for the HHKELM, and separate them into training and testing sets.

Step 2: Generate the initial population using Tent Chaos mapping along with other relevant settings, and specify the necessary parameters and ranges for HHKELM optimization.

Step 3: Calculate the individual fitness function for Aquila using Equation (26). To determine the initial fitness value, input the training dataset into the equation:

$$\begin{aligned} \text{ fitness } =1-\frac{a c c}{100}, \end{aligned}$$
(27)

where \(acc\) represents the training data’s classification accuracy. The objective is to find the optimal hyperparameter combination by minimizing the fitness function;

Step 4: Utilize the improvement strategy based on formulas (7) to (14) to find the optimal hyperparameter combination;

Step 5: Check if the stopping condition for iterations has been satisfied. If it has, finalize the training and produce the best hyperparameter combination. If not, return to Step 3 and proceed with the loop.

Framework for rolling bearing fault diagnosis and integration process of SDAE with IAO-HHKELM

Consequently, an SDAE-AHHKELM diagnostic framework for bearings is introduced, integrating an SDAE with an IAO-optimized HHKELM. The model comprises four main steps:

  1. (a)

    Collect and preprocess the original signal from the bearing, followed by partitioning it into training and testing sets based on a predefined ratio.

  2. (b)

    Feed the spectral signal, obtained post-FFT, into the SDAE model to learn defect characteristics, enabling the extraction of deep and relevant features from the data.

  3. (c)

    Employ the IAO to fine-tune the hyperparameters for the HHKELM training process by feeding in the deep and meaningful features obtained from the extraction.

  4. (d)

    Utilize the HHKELM model to diagnose faults by feeding in the meaningful features derived from the deep analysis of the test sample subset.

The proposed SDAE-AHHKELM enhances the parameter performance of both the original DAE and ELM models through the use of a stacked deep network, iterative refinement with IAO, and the incorporation of a kernel-based approach. Additionally, the fault diagnosis framework efficiently captures deep feature information. In fault classification, the original model’s generalization ability is significantly enhanced by employing a multi-layered structure and integrating an advanced composite kernel function. Finally, experimental data are employed to evaluate and validate the effectiveness of the SDAE-AHHKELM model.

Experimental

Datasets description

The proposed SDAE-AHHKELM fault diagnosis framework was validated using two benchmark datasets: the Case Western Reserve University (CWRU) fault datasets and the Society for Machinery Failure Prevention Technology (MFPT) fault datasets.

The experimental conditions of the CWRU dataset (depicted in Figure 7) are as follows: the motor load is 0 hp, the frequency is 48 kHz, and the rotational speed is 1797 r/min\(^{-1}\). The rolling bearing data are categorized into three fault classes: 0.007 mm (minor fault), 0.014 mm (medium fault), and 0.021 mm (serious fault). In total, ten health states of the bearing are selected for the experiment, including slight fault of ball (BS), slight fault of outer ring (ORS), slight fault of inner ring (IRS), moderate fault of ball (BM), moderate fault of outer ring (ORM), moderate fault of inner ring (IRM), large fault of ball (BL), large fault of outer ring (ORL), large fault of inner ring (IRL), and normal state (N). Each health condition comprises 1024 vibration signal points across 100 randomly sampled groups of samples. The original signals were converted into frequency-___domain signals using the FFT method, which were then used as the sample set and split in a 7:3 ratio.

The MFPT dataset from the United States serves as a widely recognized standard dataset for testing machine learning algorithms in fault diagnosis. Managed by the Machinery Failure Prevention Technology Working Group at the National Institute of Standards and Technology (NIST), this dataset provides a standardized benchmark for researchers, engineers, and students to evaluate fault diagnosis algorithms. Researchers and engineers utilize the MFPT bearing datasets for various purposes, including algorithm development, predictive maintenance modeling, performance evaluation of monitoring techniques, and more. By leveraging this dataset, they gain valuable insights into industrial equipment performance, reducing production downtime, lowering maintenance costs, and improving equipment reliability and efficiency75.

The data made available by the MFPT uses a NICE bearing. The MFPT dataset includes but is not limited to, 3 baseline conditions, 3 outer race fault conditions, and 7 outer race fault conditions. This work investigates nine distinct fault categories, as outlined in Table 1. For the MFPT dataset, 1024 vibration signals in each group of 100 samples were randomly selected for each fault. The original signals were converted into frequency ___domain signals using the FFT method as the sample set. Subsequently, the data was split with a 7:3 ratio.

The Jiangnan University (JNU) bearing datasets were provided by Jiangnan University. These datasets consist of three bearing vibration datasets collected at different rotating speeds. The data were collected at a sampling frequency of 50 kHz. The JNU datasets include one healthy state and three fault modes: inner ring fault(IR), outer ring fault(OR), and rolling element fault(RE). The datasets cover the following rotating speeds: 600 RPM, 800 RPM, and 1,000 RPM. For the JNU dataset, we tested each group of bearing faults using bearing signals of three speeds of 600RPM, 800RPM, and 1000RPM, obtaining nine fault types, and randomly selected 1024 vibration signals from 100 samples for each group of faults. The FFT method was used to convert the original signal into frequency ___domain signal as the sample set. Subsequently, the data were split in a 7:3 ratio.

Fig. 7
figure 7

CWRU bearing fault simulation test bench.

Full size image
Table 1 Overview of Fault Types in Rolling Bearings from the MFPT Dataset.
Full size table

Model construction and parameter settings

In this subsection, we start by presenting an SDAE algorithm for feature extraction, which leverages deeply effective features from the hidden layers as input to the IAO-HHKELM fault classification model. The IAO-HHKELM model’s hyperparameters are iteratively optimized via IAO to achieve the desired outcomes. Detailed configurations are provided in Table 2.

The hyperparameters of CWRU dataset refined by IAO in AHHKELM model are shown in Table 3. The hyperparameters of MFPT dataset refined by IAO in AHHKELM model are shown in Table 4. The hyperparameters of JNU dataset refined by IAO in AHHKELM model are shown in Table 5. Additionally, Figure 11 depicts the fitness function curve for the HHKELM model, refined using IAO.

Regarding the sensitivity of performance to the kernel weighting parameter \(\omega\), the optimization results show that the choice of \(\omega\) significantly affects the performance of the hybrid kernel. The optimal \(\omega\) values for the CWRU, JNU, and MFPT datasets were determined through experimentation, as shown in Figure 8, 9, and 10: For the CWRU dataset, the best performance was achieved at \(\omega\) = 0.8, with an accuracy of 0.99. For the MFPT dataset, the best performance was found at \(\omega\) = 0.9, with an accuracy of 0.87407. For the JNU dataset, the optimal performance was achieved at \(\omega\) = 0.8, with an accuracy of 0.83333.

Fig. 8
figure 8

Performance and Kernel Weighting Parameter (\(\omega\)) in CWRU dataset.

Full size image
Fig. 9
figure 9

Performance and Kernel Weighting Parameter (\(\omega\)) in MFPT dataset.

Full size image
Fig. 10
figure 10

Performance and Kernel Weighting Parameter (\(\omega\)) in JNU dataset.

Full size image

To comprehensively evaluate the superior performance of the SDAE-AHHKELM model, various comparison methods are employed, including KELM, SDAE-KELM, HHKELM, IAO-HHKELM, and SDAE-HHKELM.

Within this set of algorithms, KELM is considered a shallow learning model, while HHKELM is regarded as a deep learning model. The optimal regularization coefficient for KELM is consistently set to 40, with a kernel parameter of 10 and a linear kernel for training.

By considering both shallow and deep network models and incorporating the impact of the SDAE method and the intelligent optimization algorithm IAO, the comparison highlights the effectiveness and superiority of the SDAE-AHHKELM fault diagnosis model.

Fig. 11
figure 11

The fitness curve of the SDAE-AHHKELM.

Full size image
Table 2 Configuration of SDAE-AHHKELM Parameters.
Full size table
Table 3 AHHKELM hyper-parameter settings in CWRU dataset.
Full size table
Table 4 Configuration of AHHKELM Hyperparameters in MFPT dataset.
Full size table
Table 5 Configuration of AHHKELM Hyperparameters in JNU dataset.
Full size table

Performance evaluation metrics

To comprehensively evaluate the performance of the SDAE-AHHKELM model, this paper utilizes recall, precision, and F1-score metrics.

  1. (a)

    True positive (TP): The positive sample is correctly classified as positive.

  2. (b)

    True negative (TN): The negative sample is correctly classified as negative.

  3. (c)

    False positive (FP): The negative sample is incorrectly classified as positive.

  4. (d)

    False negative (FN): The positive sample is incorrectly classified as negative.

Precision is defined as the ratio of true positive classifications to all positive classifications76,77. The formula for precision is expressed as follows:

$$\begin{aligned} \text {Precision} = \frac{\text {True Positive}}{\text {True Positive} + \text {False Positive}}. \end{aligned}$$
(28)

The recall represents the proportion of true positive samples correctly classified among all positive samples. The recall formula is as follows:

$$\begin{aligned} \text {Recall} = \frac{\text {True Positive}}{\text {True Positive} + \text {False Negative}}. \end{aligned}$$
(29)

The F1-score indicates a harmonic average of precision and recall, falling within the range [0, 1]. The F1-score formula is as follows:

$$\begin{aligned} \text {F}_{1}\text {-score} = 2 \times \frac{\text {Recall} \times \text {Precision}}{\text {Recall} + \text {Precision}}. \end{aligned}$$
(30)

Discussion

Case 1: CWRU fault datasets

Figure 12 presents the confusion matrix of classification for various fault diagnosis methods. The SDAE-AHHKELM method achieves the highest accuracy, outperforming SVM, KELM, and HHKELM by effectively capturing complex fault patterns through deep feature extraction. While SVM and KELM show good performance, their ability to distinguish subtle fault differences is limited compared to the SDAE-based models. Among the SDAE-enhanced models, SDAE-SVM also improves fault classification but still lags behind SDAE-AHHKELM, which excels in both precision and recall. The IAO-HHKELM method benefits from optimization algorithms but does not match the comprehensive performance of SDAE-AHHKELM, which demonstrates superior effectiveness in fault separation and diagnosis.

Fig. 12
figure 12

Confusion matrix diagram of different fault diagnosis methods for the CWRU datasets. (a) SVM, (b) SDAE-SVM, (c) KELM, (d) SDAE-KELM, (e) HHKELM, (f) SDAE-HHKELM, (g) IAO-HHKELM, (h) SDAE-AHHKELM.

Full size image

To further assess the effectiveness of the SDAE-AHHKELM method, t-distributed stochastic neighbor embedding (T-SNE)78 was employed to visualize the trained results, as depicted in Figure 13. In these figures, the SDAE-AHHKELM model shows distinct and well-separated clusters for different fault types, which indicates effective fault differentiation.

The clear separation of fault categories in the t-SNE plot indicates that the SDAE-AHHKELM model effectively extracts meaningful features and captures the underlying patterns in the data. The separation effect is particularly strong for subtle fault categories, such as minor faults in the ball or outer ring, which are difficult for other models to distinguish. This enhanced feature extraction capability is mainly due to the combination of noise reduction and deep feature extraction by stacked denoising autoencoders. This observation suggests that employing SDAE for hierarchical feature extraction from raw input data results in improved separation and clarity among different fault feature types. Consequently, the SDAE method demonstrates robust fault feature extraction and classification capabilities.

Fig. 13
figure 13

Confusion matrix diagram of different fault diagnosis methods for the CWRU datasets. (a) Raw input data visualization diagram, (b) Visualization of Data after SDAE Training.

Full size image

The performance metrics of recall, precision, and F1-score for all approaches are summarized in Table 6. Remarkably, the proposed SDAE-AHHKELM model surpasses the other five methods across all three evaluation criteria, underscoring its significant superiority and capability to produce satisfactory outcomes.

Due to the inherent randomness present in each iteration of the intelligent optimization algorithm, the final fault classification accuracy may exhibit significant variation. To mitigate this variability, 20 independent repetitions were performed for both the SDAE-AHHKELM model and the other seven models. Figure 14 illustrates a comparison between the average and best classification accuracies.

Based on the findings illustrated in the aforementioned figure, the SDAE-AHHKELM method surpasses other combined diagnosis models, showcasing superior average classification accuracy and diagnostic effectiveness.

To replicate a more realistic industrial scenario for fault diagnosis, Gaussian white noise with varying signal-to-noise ratios (SNR) was introduced into the original signal to generate noisy data. Specifically, slight Gaussian white noise with SNR levels of -5 dB, -2 dB, 0 dB, 2 dB, and 5 dB was added to the dataset to create a noise-enhanced version. This dataset was then used to evaluate the performance of SDAE-ADHKELM in noisy fault classification tasks. The SNR is computed using the following equation:

$$\begin{aligned} \text {SNR} = 10 \log _{10} \left( \frac{PE_r}{PE_n} \right) \end{aligned}$$
(31)

where \(PE_r\) and \(PE_n\) denote the power of the original signal and the noisy signal, respectively.

Figure 15 is the classification accuracy diagram of test samples of different algorithms. When SNR = 0 dB, it is found that the SDAE-AHHKELM and SDAE-KELM can maintain an accuracy rate of about 80%, and the accuracy rate of other methods is far lower. With the continuous decrease of SNR, the fault recognition accuracy of all methods is decreased. But on the whole, the SDAE-AHHKELM still maintains the highest accuracy among the ten methods, with good robustness and classification.

Table 6 Evaluation Index of Each Model in CWRU
Full size table
Fig. 14
figure 14

Best and average classification accuracy of different fault diagnosis methods in CWRU.

Full size image
Fig. 15
figure 15

The fault classification accuracy of different fault diagnosis methods under different SNR conditions in CWRU.

Full size image

Case 2: MFPT fault datasets

Figure 16 presents the confusion matrix of classification for various fault diagnosis methods. The SDAE-AHHKELM approach achieves the highest fault classification accuracy, reaching 98.15%. When compared to SVM and KELM, the performance of SDAE-based methods, such as SDAE-KELM and SDAE-SVM, shows a marked improvement in feature extraction and fault classification. Although SVM performs well, its accuracy is lower than that of SDAE-SVM, which benefits from the integration of SDAE for better feature representation. The comparison between HHKELM and IAO-HHKELM highlights the significant role of the IAO optimization algorithm in fine-tuning hyperparameters and enhancing classification accuracy. Among all the hybrid methods, SDAE-AHHKELM demonstrates the superior capability for fault separation, providing the most robust and accurate classification results.

Fig. 16
figure 16

Confusion matrix diagram of different fault diagnosis methods for the MFPT data set. (a) SVM, (b) SDAE-SVM, (c) KELM, (d) SDAE-KELM, (e) HHKELM, (f) SDAE-HHKELM, (g) IAO-HHKELM, (h) SDAE-AHHKELM.

Full size image
Fig. 17
figure 17

Confusion matrix diagram of different fault diagnosis methods for the MFPT data set. (a) Raw input data visualization diagram, (b) Visualization of Data after SDAE Training.

Full size image

To further assess the effectiveness of the SDAE-AHHKELM method, t-distributed stochastic neighbor embedding (T-SNE)78 was employed to visualize the trained results, as depicted in Figure 17.

This observation suggests that employing SDAE for hierarchical feature extraction from raw input data improves separation and clarity among different fault feature types. As a result, the SDAE approach exhibits strong capabilities in extracting and classifying fault features.

To comprehensively evaluate the effectiveness of the SDAE-HHKELM framework, this case study also utilizes recall, precision, and F1-score metrics mentioned in the above section. The performance metrics of recall, precision, and F1-score for all approaches are summarized in Table 7. The SDAE-AHHKELM model proposed in this study surpasses the other seven methods across all three evaluation criteria, underscoring its significant superiority and capability to produce satisfactory outcomes.

Due to the inherent randomness in each iteration of the intelligent optimization algorithm, the final fault classification accuracy may exhibit significant variation. A total of 20 independent repetitions of the SDAE-AHHKELM model, along with the other seven models, were performed to mitigate variability. Figure 18 illustrates a comparison between the average and best classification accuracies.

Based on the findings illustrated in the figure above, the SDAE-AHHKELM method surpasses other combined diagnosis models, showcasing superior average classification accuracy and diagnostic effectiveness.

Figure 19 presents the fault identification accuracy of test samples under noisy conditions, comparing the SDAE-AHHKELM with other diagnostic algorithms. The fault classification accuracy for the MFPT dataset under noisy conditions is generally lower than that of the CWRU dataset. The accuracy rates of SVM, KELM, HHKELM, and IAO-HHKELM are significantly lower than those of models incorporating SDAE methods. The results indicate that the SDAE demonstrates superior performance and excellent effectiveness under noisy conditions. Overall, the SDAE-AHHKELM achieves the highest accuracy across different SNR conditions, exhibiting stronger noise resistance and enhanced classification performance.

Table 7 Evaluation Index of Each Model in MFPT.
Full size table
Fig. 18
figure 18

Best and average classification accuracy of different fault diagnosis methods in MFPT.

Full size image
Fig. 19
figure 19

The fault classification accuracy of different fault diagnosis methods under different SNR conditions in MFPT.

Full size image

Case 3: JNU fault datasets

Figure 20 presents the confusion matrix of classification for various fault diagnosis methods. The SDAE-AHHKELM approach achieves the highest fault classification accuracy, reaching 97.50%. When compared to SVM and KELM, the performance of SDAE-based methods, such as SDAE-KELM and SDAE-SVM, shows a significant improvement in feature extraction and fault classification. While SVM performs adequately, its accuracy is lower than that of SDAE-SVM, which benefits from the integration of SDAE for better feature representation. The comparison between HHKELM and IAO-HHKELM highlights the important role of the IAO optimization algorithm in fine-tuning hyperparameters and improving classification accuracy. Among all the hybrid methods, SDAE-AHHKELM demonstrates the superior capability for fault separation, providing the most reliable and precise classification results.

Fig. 20
figure 20

Confusion matrix diagram of different fault diagnosis methods for the JNU data set. (a) SVM, (b) SDAE-SVM, (c) KELM, (d) SDAE-KELM, (e) HHKELM, (f) SDAE-HHKELM, (g) IAO-HHKELM, (h) SDAE-AHHKELM.

Full size image
Fig. 21
figure 21

Confusion matrix diagram of different fault diagnosis methods for the JNU data set. (a) Raw input data visualization diagram, (b) Visualization of Data after SDAE Training.

Full size image

To further evaluate the performance of the SDAE-AHHKELM method, t-distributed stochastic neighbor embedding (T-SNE) was employed to visualize the trained results, as shown in Figure 21.

This observation suggests that using SDAE for hierarchical feature extraction from raw input data enhances the separation and clarity among different fault feature types. Consequently, the SDAE approach demonstrates strong capabilities in extracting and classifying fault features.

To thoroughly evaluate the performance of the SDAE-HHKELM framework, this case study also employs recall, precision, and F1-score metrics as discussed in the previous section. The performance metrics of recall, precision, and F1-score for all methods are summarized in Table 8. The SDAE-AHHKELM model presented in this study outperforms the other seven methods in all three evaluation criteria, highlighting its significant superiority and capacity to deliver outstanding results.

Due to the inherent randomness in each iteration of the intelligent optimization algorithm, the final fault classification accuracy may exhibit considerable variation. A total of 20 independent repetitions of the SDAE-AHHKELM model, along with the other seven models, were conducted to reduce variability. Figure 22 presents a comparison between the average and best classification accuracies.

Based on the results shown in the figure above, the SDAE-AHHKELM method outperforms other hybrid diagnosis models, demonstrating superior average classification accuracy and diagnostic performance.

Figure 23 presents the fault identification accuracy of test samples under noisy conditions, comparing the SDAE-AHHKELM with other diagnostic algorithms. The fault classification accuracy for the JNU dataset under noisy conditions is generally lower than that of the CWRU dataset. The accuracy rates of SVM, KELM, HHKELM, and IAO-HHKELM are considerably lower than those of models incorporating SDAE methods. The results suggest that SDAE demonstrates superior performance and robustness under noisy conditions. Overall, the SDAE-AHHKELM achieves the highest accuracy across different SNR conditions, showing stronger noise resistance and improved classification performance.

Table 8 Evaluation Index of Each Model in JNU.
Full size table
Fig. 22
figure 22

Best and average classification accuracy of different fault diagnosis methods in JNU.

Full size image
Fig. 23
figure 23

The fault classification accuracy of different fault diagnosis methods under different SNR conditions in JNU.

Full size image

As shown in Table 9, we summarize the key differences between the proposed approach and several existing methods in terms of model formulation, algorithmic techniques, and performance metrics. The comparison highlights the strengths of our method, including its accuracy in fault detection, as well as the improved precision and recall in bearing diagnostics, among other aspects.

Table 9 Comparison of the Proposed Method with Existing Approaches
Full size table

As shown in Table 10, we highlight the inherent trade-offs between cost minimization and risk mitigation, two key aspects in decision-making processes, especially in industrial and engineering applications. By comparing our approach with related work, we can better understand how these trade-offs are handled in different contexts. The table summarizes the key differences between cost minimization and risk mitigation, as well as their implications in the context of our proposed method and other relevant studies.

Table 10 Trade-offs between Cost Minimization and Risk Mitigation.
Full size table

In line with the findings of recent studies, we explore the challenges posed by data uncertainty and operational variability in fault diagnosis. For instance, He et al.84 present a method for improving fault diagnosis in Permanent Magnet Synchronous Machines (PMSMs) by integrating multisource information to address the inherent data uncertainty. This aligns with our approach, where we employ hierarchical models optimized by the Aquila Optimizer, which enhances the robustness of our system when exposed to fluctuating and noisy data. Similarly, Hang et al.85 introduce a robust diagnostic technique for detecting partial demagnetization faults in PMSMs under complex working conditions, focusing on the use of radial air-gap flux density. Our model also tackles similar challenges by adapting to fluctuations in demand and system disruptions, using an optimization framework that ensures accurate fault diagnosis despite operational variations.

Conclusions

This study presents a pioneering approach to bearing fault diagnosis, employing the SDAE-AHHKELM network. Notably, the SDAE’s deep network architecture adeptly captures critical features from vibration signals emitted by bearings. Additionally, this paper introduce a novel HHKELM model that combines polynomial and Gaussian kernel functions. To enhance the performance and stability of the HHKELM model, this paper introduce the Aquila optimizer algorithm. By incorporating chaos mapping, implementing a refined, balanced search strategy, and fine-tuning parameter \(G_2\), the effectiveness of the AO algorithm is enhanced in escaping local optima and conducting global searches. These enhancements bolster the robustness of our model during parameter optimization, thereby improving fault diagnosis accuracy and reliability. Finally, the AHHKELM fault classifier is specifically tailored to accurately discern various fault types.

To assess the effectiveness of the proposed SDAE-AHHKELM model, experiments were conducted using all the CWRU, MFPT and JNU bearing datasets. The findings revealed a notable enhancement in overall performance metrics, including precision, recall, and F1-score, when comparing SDAE-AHHKELM against other state-of-the-art methods across all datasets. Although the performance of SDAE-AHHKELM may not demonstrate significant superiority in individual fault categories within the CWRU, MFPT and JNU datasets, the best classification accuracy and the average classification accuracy in all nine overall fault categories are always more excellent than other methods, showing superior performance. This comprehensive improvement underscores the effectiveness and reliability of the proposed approach in bearing fault diagnosis.

Nevertheless, in industrial environments, data often arrives without categorical labels, complicating the classification and annotation of mechanical equipment data. Semi-supervised learning approaches for fault diagnosis offer a blend of supervised and unsupervised learning advantages, leveraging both labeled and unlabeled bearing data to enhance generalization capabilities and classification accuracy.

Additionally, other advanced methods, such as deep learning techniques, are also gaining traction for bearing fault diagnosis. These approaches, particularly convolutional neural networks and recurrent neural networks, have shown significant promise in automatically learning hierarchical feature representations from raw data. Incorporating these methods into the fault diagnosis process may further improve diagnostic accuracy, especially in complex and noisy environments.

Future research will focus on integrating semi-supervised learning into the SDAE-AHHKELM model to achieve semi-supervised rolling bearing fault feature extraction and diagnosis.