Introduction

Seedling transplanting is a crop planting method with multiple advantages, including high yield, stable production, climate compensation, and improved land utilization1,2. Currently, the commonly used transplanting machinery in China is mainly semi-automatic transplanters, among which the hanging cup transplanter meets the requirements for crop film-covered transplanting and is therefore widely applied3,4,5. However, in actual operation, the seedlings inevitably interact with the planter itself, and as the transplanting speed increases, the relative motion between the seedlings and the planter changes, leading to a decrease in seedling uprightness and damage to the seedling pot body, which in turn affects the transplanting quality and fails to meet the operational requirements6,7,8.

Many scholars have researched the interactions between seedlings and planters. Wang et al.9, through a combination of theoretical derivation and experiments, applied Hertz contact theory and the kinetic energy theorem to establish a collision contact mechanics model for seedlings, and through field planting experiments, determined the optimal parameter combination for mechanical planting of seedlings. Chen et al.10 explored the relative motion between seedlings and the planter during the planting process based on motion differential equations. Liu et al.11 used goal programming to optimize the collision contact force of seedlings and the differential equation of the collision motion, resulting in an optimal transplantation parameter combination that reduces seedling collision damage. However, existing studies often fail to intuitively analyze the dynamic changes in the interaction between seedlings and planters, lacking in-depth analysis of the process, which is often costly to analyze in practice. Therefore, the introduction of simulation has become an important tool for studying this issue. Many scholars have used the Discrete Element Method (DEM) to simulate interactions between materials and working components12,13. Yang et al.14 utilized the EDEM analysis software to establish a discrete element model of the collision process between the potted seedlings and the wall of the seedling guide tube, obtaining the collision forces and motion patterns of the seedlings. Deng, et al.15 used EDEM software based on the DEM to simulate and analyze the interaction characteristics when potatoes fall onto a separation sieve. Bao, et al.16 applied the DEM for numerical simulation of the blueberry mechanical harvesting process and obtained the movement characteristics of blueberries during harvesting operations. However, existing simulation studies have not yet addressed the simulation of the interaction between seedlings and planters during the operation of cup-type transplanting machines.

Furthermore, how to more accurately predict the complex interactions during transplantation remains an urgent challenge. Due to the numerous factors influencing the interaction characteristics of the seedlings and the complexity of the seedlings’ movement trajectories, the entire operation process exhibits strong nonlinear features. In recent years, with the development of machine learning technologies, Artificial Neural Networks (ANNs) have been widely applied in research on fitting nonlinear problems17,18. Traditional response surface methodology (RSM) analysis may face challenges related to complexity and sample size constraints, which can potentially compromise its fitting performance19. Compared to traditional mathematical modeling methods, neural networks are better suited to handle complex nonlinear interactions, demonstrating stronger adaptability and predictive capabilities20,21. Marey, et al.22 developed a prediction model based on a multilayer feed-forward neural network combined with a back propagation algorithm (BP algorithm) using plowing speed, plowing depth, soil moisture content, and soil bulk density as inputs, and chisel plough operational performance as outputs. Additionally, some researchers have combined BP neural networks with other technologies, such as genetic algorithms, for model optimization studies19,23. Zhang et al.24 optimized a BP neural network using a genetic algorithm (GA-BP) to create a predictive model for walnut shell rupture force, with results showing significant improvements in both training speed and prediction accuracy.

Therefore, this study aims to address the aforementioned issues. A discrete element simulation model is constructed for the pot seedling-planter system to analyze the interaction characteristics during the transplanting process. At the same time, an artificial neural network (ANN) combined with the BP and GA-BP algorithms is used to develop a pot seedling collision damage model under varying parameter conditions. The predictive performance and fitting stability of the machine learning regression models, specifically BP and GA-BP, are then compared. The research results can provide a basis for exploring the interaction mechanism between pot seedling-planter and serve as a fundamental reference for the construction of planting quality prediction models in complex field environments.

Materials and methods

Structure and working principle of transplanter

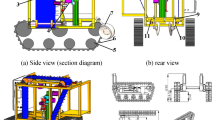
As shown in Fig. 1, the hanging cup transplanter mainly consists of a seedling feeding mechanism, a three-point suspension device, a planting mechanism, a planting depth adjustment mechanism, ground wheels, soil covering wheels, feeding cups and seats, etc. The planting mechanism is mainly composed of an installation plate and a planter (to be introduced in “Planting mechanism simplified model establishment” section). During the transplanting process, the tractor pulls the transplanting machine forward through the three-point suspension device. The ground wheels transmit the power to the seeding feeding mechanism and the planting mechanism, and there is a motion matching relationship between the two. The staff place pot seedlings into the feeding cup. When the planters rotate to the receiving position, the feeding cup throws pot seedlings, and the planters complete the receiving process. As the planter carrying the pot seedlings rotates to the lower planting position, the planter performs hole punching. The pot seedlings fall into the prepared holes, and then the soil covering wheels cover and compact the soil, completing the transplanting operation.

Fig. 1
figure 1

Three-dimensional model diagram of hanging cup transplanter. (1) Seedling feeding mechanism; (2) Three point suspension device; 3. Planting mechanism; 4. Planting depth adjustment mechanism; 5. Ground wheels; 6. Soil covering wheels; 7. Feeding cups; 8. Seats. Image was performed using Creo 6.0 (https://www.ptc.com/cn).

Full size image

Simulation of pot seedlings-planter interaction

Pot seedling model establishment

In the simulation of pot seedlings-planter interaction, establishing an accurate model for the pot seedling is the basis for ensuring the effectiveness of the simulation results. Since the quality of pot seedlings is mainly focused on the pot body, the effect of stems and leaves above the pot body on the quality of pot seedlings is ignored, and this study focuses only on the modeling simulation study of the pot body itself7. At the same time, the seedling pot body is a composite of the root system and substrate. To improve computational efficiency, the root system and the substrate are modeled with the same particle model to establish the pot body model for simulation. The pot body is modeled using Creo 6.0 (PTC, Massachusetts, USA) three-dimensional software according to the geometric dimensions of the physical pot body. The length of the upper side of the pot body model is 35 mm, the length of the lower side is 15 mm, and the height of the pot body is 45 mm. The model was imported into EDEM software (Altair, Michigan, USA), a discrete elemental model of the pot body was generated using the natural sedimentation particle filling method14. The pot body particle model consists of individual spherical particles with a radius of 1 mm. The contact model between the seedling pot body particles is the Hertz-Mindlin with bonding model, where the bonding force inside the pot body is replaced by bonded bonds between particles. The seedling simulation model is shown in Fig. 2. The simulation model parameters are shown in Table 125.

Fig. 2
figure 2

Discrete element model of pot body.

Full size image
Table 1 Discrete element simulation parameters of pot body.
Full size table

Planting mechanism simplified model establishment

Figure 3 shows a simplified model of the planting mechanism. The material of the planting mechanism is Q235 steel. Due to the specific motion matching relationship between the seeding feeding mechanism and the planting mechanism, it is necessary to determine the spatial positioning relationship between the feeding cup and the planter before starting the simulation. Based on the previous research of group26, the seedling throwing position is set to the position where the center plane of the feeding cup coincides with the center plane of the planting mechanism. Through the preliminary seedling throwing test and the ratio of the transplanter driving system, it was determined that when the distance from the feeding cup to the seedling throwing position L is 11.95 mm, and the angle between the planter and the center surface of the planting mechanism is 32.67°, it can meet the normal seedling throwing requirements of the transplanter. A discrete element method (DEM) and multi-body dynamics (MBD) combined simulation approach was used to conduct pot seedling-planter interaction experiments. The simplified models of the planting mechanism were imported into ADAMS and EDEM software, where material properties were set, and connection constraints were applied. According to the agronomic requirements of transplantation, a planting frequency of 20–50 plants/min was sufficient to meet the transplantation needs. To comprehensively study the collision dynamics between the seedling pots and the transplanter, representative transplanting frequencies of 22, 34, and 46 plants/min were selected for simulation experiments based on preliminary test results.

Fig. 3
figure 3

Schematic diagram of transplanting mechanism simulation model.

Full size image

Predictive modeling dataset establishment

The transplanting process is characterized by a complex operational environment and inherent randomness in the falling posture of pot seedlings when released by the feeding cup27. Additionally, the interaction between pot seedlings and the planter involves multiple influencing factors, leading to strong nonlinearity and uncertainty throughout the process. Given the capability of artificial neural networks (ANNs) in simulating complex nonlinear problems, this study employs a neural network model to treat the collision damage of pot seedlings as a nonlinear problem driven by multiple factors, thereby establishing a collision damage model under various parameter conditions.

Test design

The accuracy and generalization ability of a neural network model depend on the quantity and quality of the training data. Studies show that neural network models can be effectively established with relatively small datasets after appropriate experimental design21,28. To ensure model reliability, the dataset in this study is generated using the results from a Response Surface Design experiment20.

Existing research has shown that planting frequency, seedling falling posture, and the physical mechanical properties of seedlings significantly impact their collision damage during the pot seedling-planter interaction9,11. Among them, the falling posture is mainly influenced by the height of the seedlings. The physical mechanical properties of the pot seedlings are mainly related to the pot body moisture content and volume. Therefore, the experimental factors chosen are the pot body volume (X1), pot body moisture content (X2), seedling height (X3), and planting frequency (X4). The damage rate of pot seedlings is taken as the experimental indicator, and a Box-Behnken experimental design method is used to design an orthogonal experiment. The planting frequencies selected are 22, 34, and 46 plants/min, respectively. The seedling heights are obtained at different seedling ages, corresponding to 11.8 ± 9.61 mm, 15.8 ± 10.61 mm, and 20.3 ± 8.61 mm for seedling ages of 20, 25, and 30 days, respectively (mean ± standard deviation, the same below). The pot body moisture content is measured using a drying method, with three levels selected: approximately 43%, 52%, and 61%. The pot body volume is determined by using different cell tray specifications, namely 50, 72, and 105. Table 2 shows the level coding table for the experimental factors.

Table 2 Level coding table of test factors.
Full size table

Test conditions and environment

The experiment was conducted at the Intelligent Soil Trough Laboratory of the College of Mechanical and Electrical Engineering, Inner Mongolia Agricultural University. The main equipment used includes an electronic balance (model HZW-3002), universal angle ruler, a soft brush, adhesive labels, a soil compaction tester (model TYD-2), an electric hot air-drying oven (model DHG-9245 A), a hanging cup transplanting machine, and a TCC electric four-wheel drive soil trough test cart. The soil used in the experiment is sandy loam. To ensure the soil conditions in the trough meet transplanting operation requirements, the soil was plowed, leveled, and compacted before the experiment. The soil moisture content was measured at 10 different locations in the trough, resulting in a moisture content of 14.52 ± 1.33% and a compaction of 97.5 ± 6.55 N/cm². The pot seedlings used were of the Tonghui 562 variety of oil sunflower, supplied by Inner Mongolia He Yuan Agricultural Technology Co., Ltd., as shown in Fig. 4.

Fig. 4
figure 4

Test oil sunflower pot seedlings.

Full size image

Test indicator

Each experimental group involves continuously transplanting 40 oil sunflower seedlings. The planting process is shown in Fig. 5. Before each experiment, the seedlings are weighed using an electronic balance (accuracy: 0.1 g), and labeled. After each experiment, the seedlings are weighed again to calculate the substrate loss rate (PB) and record the number of damaged seedlings (damage is defined as a substrate loss rate exceeding 15%)29,30. The seedling damage rate (PD) is then calculated using the following formula.

$${P_{\text{B}}}=\frac{{M - {M_1}}}{M} \times 100\%$$
(1)
$${P_{\text{D}}}=\frac{{{N_{\text{D}}}}}{N} \times 100\%$$
(2)

Where PD represents the damage rate of pot seedlings, %; ND represents the number of seedlings with damage, plant; N represents the total number of seedlings, plant; PB represents the substrate loss rate, %; M and M1 represent the mass of the pot seedlings before and after transplantation, respectively, g.

Fig. 5
figure 5

Transplanting test process.

Full size image

Based on the principle of zero absolute velocity, when the seedlings fall into the hole, their horizontal velocity is 0 m/s, and their vertical velocity is small, mainly influenced by gravity31. Therefore, this study does not consider the interaction between the seedlings and the planting soil when the seedlings enter the hole. Additionally, when weighing the seedlings after transplantation, the loose soil on the surface of the pot needs to be removed using a soft brush to ensure the accuracy of the experimental results. The process of weighing the pot seedlings is shown in Fig. 6.

Fig. 6
figure 6

Weighing process of oil sunflower pot seedlings.

Full size image

Regression modeling using machine learning algorithms

Feedforward ANNs and error-backpropagation (BP) algorithms are common in the field of agricultural engineering. A multilayer perceptron-based network was selected for this study. The network was developed based on three layers: the input layer, hidden layer, and output layer. Each layer is connected to another layer through neurons, which process information using a structure similar to synaptic connections in the brain. Figure 7 illustrates a typical neuron structure where each input (x) coming from other neurons is multiplied by their respective weights (wi, 1 \(\leqslant\) i \(\leqslant\) n), and then subtracted by the bias vector (β). This summed inputs (h) or information is passed through an activation function (f) to obtain the output (y) of a specific neuron, as shown in Eqs. (3) and (4)32. Using the Response Surface Design experimental results as the dataset, BP, GA-BP regression models were constructed for fitting. The dataset (29 sets) was randomly divided into training sets (21 sets, 70%), testing sets(4 sets, 15%), and validation sets(4 sets, 15%).

$$y=f\left( {wx - \beta } \right)$$
(3)
$$wx=\left( {{x_1}{w_1}+{x_2}{w_2}+\cdots+{x_{\text{n}}}{w_{\text{n}}}} \right)$$
(4)
Fig. 7
figure 7

A typical structure of neuron32. Image was performed using Office 16 (https://www.office.com/).

Full size image

BP (Backpropagation)

In the process of constructing the BP neural network, key parameters such as the number of nodes in each layer, activation function, and the number of hidden layers need to be carefully considered. The number of nodes in the input layer is determined by the number of input parameters, which is 4 in this study. The number of nodes in the output layer is determined by the number of output parameters, which is 1 in this study. Between the input and output layers, one or more hidden layers are often added. As the number of hidden layers increases, the accuracy improves, but the network structure becomes more complex and the learning efficiency decreases. Therefore, for the number of hidden layers, it is generally better to have as few as possible while meeting the requirements. Based on Hecht-Nielsen’s research33, a network with a single hidden layer can approximate any multivariate function. This study adopts a single hidden layer structure. According to research, when the number of input nodes in a BP artificial neural network is n, the number of nodes in the hidden layer is often selected as 2n + 134. The BP network model can effectively reflect reality, so the number of nodes in the hidden layer is chosen as 9. Based on this, the BP network model in this study adopts a 3-layer network with a structure of 4-9-1. The network topology diagram is shown in Fig. 8.

Fig. 8
figure 8

Neural network topology diagram. Image was performed using Office 16 (https://www.office.com/).

Full size image

During the training process, the transfer function from the input layer to the hidden layer was chosen as the Sigmoid function, while the transfer function from the hidden layer to the output layer was chosen as the linear function. The training algorithm used the LM algorithm, and the mapminmax function was applied to normalize the input and output data to eliminate the influence of dimensions. The target error for training was set to 0.001, and the learning rate was set to 0.001, with a maximum of 50 training steps.

GA-BP (genetic algorithm–backpropagation)

The GA-BP algorithm fully leverages the global search capability of the genetic algorithm. By integrating the genetic algorithm, GA-BP optimizes the structure and parameters of the BP neural network. The genetic algorithm evolves individuals (i.e., the BP network parameter sets) towards higher fitness through operations such as selection, crossover, and mutation35. According to the practical considerations, the chromosome length of the genetic algorithm is set to 76, the population size is 200, the number of evolutions is 100, the crossover probability is 0.8, and the mutation probability is 0.2.

Data analysis and processing

In this study, the Matlab R2020a (MathWorks Corporation, Massachusetts, USA) software was chosen as the operating platform for the algorithm. The predictive performance of the machine learning model was evaluated using the coefficient of determination (R2), mean squared error (MSE), and mean absolute deviation (MAD). A higher R2 indicates a better fit of the model, while lower MSE and MAD values indicate better accuracy and stability of the model20.

Results and discussions

Collision motion characteristics of pot seedlings

Figure 9 illustrates the entire motion process of pot seedlings inside the planter under different planting frequencies. It can be observed that when the planting frequency is 22 plants/min, the motion process of the pot seedling in the planter can be divided into seven stages. Stage 1: The pot seedling is in the process of free fall before coming into contact with the planter (Fig. 9a-1). Stage 2: Collision occurs between the pot seedling and the edge of the planter’s mouth (Fig. 9a-2). Stage 3: After the collision, the pot seedling is bounced upwards. It is observed that during the upward motion, the pot seedling undergoes a certain rotation relative to the planter. The motion direction and posture of the pot seedling change (Fig. 9a-3). Stage 4: The pot seedling continues its descent inside the planter, following a parabolic trajectory (Fig. 9a-4). Stage 5: The pot seedling reaches the planting nozzle, and a second collision occurs between the pot seedling and the inner wall of the planting nozzle (Fig. 9a-5). Stage 6: After the second collision, the pot seedlings start rotating around the contact point with the planting nozzle. At the same time, they slide along the inner wall of the planting nozzle until they tightly adhere to it (Fig. 9a-6). Stage 7: Once the pot seedlings are firmly attached to the inner wall of the planting nozzle, they slide down along the wall until they reach the bottom of the planting nozzle (Fig. 9a-7). The collision between the seedling-planter is marked with a black circle in the figure.

Fig. 9
figure 9

Pot seedling transplanting drop process at different planting frequencies. Image was performed using EDEM 2022.3 (https://altair.com/).

Full size image

The motion process of pot seedlings inside the planter at planting frequencies of 34 and 46 plants/min (Fig. 9b,c) is similar to the analysis mentioned above. However, the collision position or number of collisions between the pot seedling-planter may vary.

Mechanical variation laws of pot seedlings

Figure 10 shows both the variation curves of collision contact force and accumulative number of broken cohesive bonds of pot body under different planting frequencies. It can be observed that the collision contact force generated by the first collision between the pot seedling-planter is relatively maximum. Consequently, the number of broken cohesive bonds increases sharply. In groups a, b, and c, the collision contact forces are 2.368 N, 2.689 N, and 2.565 N, respectively, and the numbers of broken cohesive bonds are 437, 520, and 494. Among them, when the planting frequency is 34 plants/min, the pot seedlings are subjected to the largest collision contact force and the largest number of broken bonds. This is because the center of the pot seedling is close to the center of the planter when the feeding cup throws pot seedlings. In the falling process, the collisions between the pot seedling-planter are less, and the throwing time of the pot seedling is prolonged, so that the collision contact force of the pot seedling is relatively large at the first collision.

After the first collision, as the pot seedlings rebound and fall, under the planting frequencies of 22 and 46 plants/min, a second collision occurs. The collision contact force at this point is significantly lower than that of the first collision, and the corresponding number of broken cohesive bonds shows a gradual increasing trend. In groups a and c, the collision contact forces are 1.353 N and 1.446 N, and the numbers of broken bonds are 221 and 279, respectively. It can be seen that during the process of transplanting, the second collision between the pot seedling-planter also causes collision damage to the pot body. To achieve the required transplanting quality, it is necessary to reduce the number of collisions between the pot seedling-planter as much as possible27.

Fig. 10
figure 10

Variation laws of collision contact force and broken bond number. Image was performed using Origin 2021 (https://www.originlab.com/).

Full size image

Figure 11 shows the contact forces distribution between the pot seedling-planter during the first collision at different planting frequencies. Under the planting frequency of 22 plants/min, the bond color at the collision contact points of the seed tray changed, with some bonds turning red, indicating that the force was transmitted from the contact area to adjacent particles and gradually diminished. When the planting frequency increased to 34 plants/min, the number of red bonds at the contact area significantly increased, and the force transmission covered a wider range, affecting more adjacent particles. At a planting frequency of 46 plants/min, the force exerted at the contact point was significantly smaller compared to the previous two collision scenarios, with some bond colors turning green. However, observing the force transmission inside the seedling tray reveals that the force is transmitted from the contact point to almost the entire tray, with the transmission range being the largest. This indicates that at different planting frequencies, the interaction between the seedlings and the planter varies, leading to different force transmission ranges inside the seedlings. As a result, this causes varying degrees of bonding reduction between the particles inside the seedlings and different levels of collision damage.

Fig. 11
figure 11

Contact force distribution of first collision between the pot seedling-planter. Image was performed using EDEM 2022.3 (https://altair.com/).

Full size image

Simulation verification tests

To validate the accuracy and reliability of the simulation model, verification experiments were conducted using seedlings with a substrate moisture content of 61%, a seedling age of 30 days, and a pot volume of 105 cells (Consistent with the simulation model of seedling pot body). These experiments were performed at different planting frequencies (22, 34, and 46 plants/min). The experimental conditions and environment were consistent with those described in “Test conditions and environment” and “Test indicator” sections. The substrate loss rate (PB) after planting was used as the evaluation metric and compared with the simulation results. In the simulation experiments, the substrate loss rate (PB′) was defined as the percentage of broken bonds between the particles of the pot seedlings after simulation relative to the total number of bonds before simulation. The calculation formula is shown in Eq. (5).

$${P_B}^{\prime }=\frac{{{N_2}}}{{{N_1}}} \times 100\%$$
(5)

where PB′ is the simulated substrate loss rate, %; N1 is the number of bonds in the pot before simulation; N2 is the number of broken bonds in the pot after simulation.

Fig. 12
figure 12

Comparison of simulated and measured substrate loss rates. Image was performed using Origin 2021 (https://www.originlab.com/).

Full size image

The validation results are shown in Fig. 12. At each planting frequency, the differences between the experimental data and the predicted values fall within an acceptable range, with errors of 10.3%, 3.6%, and 6.4%, respectively, confirming the accuracy of the simulation model.

BP neural network model

The experimental design for training the network and the corresponding experimental results are presented in Table 3.

Table 3 Scheme and result of experiments.
Full size table

The predicted results of the BP neural network model are shown in Table 4. The relative error rates between the predicted values and the target values for the test samples range from 0.08 to 16.93%, with an average relative error rate of 10.71%. The evaluation indicators of the BP network model are as follows: R2 = 0.955, MSE = 6.499, and MAD = 6.180.

Table 4 Prediction result of neural network model.
Full size table

Genetic optimization BP ( GA-BP ) neural network model

Table 5 shows the predicted results of the genetic BP neural network model. It can be observed that the relative error rates between the target values and the predicted values range from 2.25 to 10.54%, with an average relative error rate of 5.14%. The evaluation indicators of the genetic BP model are as follows: R2 = 0.992, MSE = 0.951, and MAD = 0.631. By comparing the two network models, it is found that the evaluation indicators of the GA-BP model are superior to those of the BP model, with an increase of 3.87% in R2, and a decrease of 86.37% and 89.79% in MSE and MAD, respectively. This indicates that the prediction accuracy and fitting effect of the BP neural network model optimized by the genetic algorithm are superior to those of the BP neural network model, which is consistent with other process optimization conclusions36.

Table 5 Prediction result of neural network model.
Full size table

As shown in Fig. 13, the performance of the mean square error (MSE) was evaluated for the training set, validation set, and test set. MSE measures the average error of the data based on the degree of variation. A smaller MSE indicates a higher accuracy of the model in describing the experimental results. The best validation performance was achieved at the 4th step of training, with an MSE of 0.00174, indicating the completion of training for the GA-BP neural network. Therefore, the GA-BP network exhibits fast convergence and high stability. Figure 14 presents the performance of the GA-BP network model on training, validation, testing, and all data. The correlation coefficients (R) for these datasets are as follows: 0.982, 0.989, 0.998, and 0.947, respectively. These coefficients indicate a strong correlation between the predicted and actual data.

Fig. 13
figure 13

GA-BP neural network performance curve. Image was performed using Matlab R2020a (https://ww2.mathworks.cn/products/matlab.html).

Full size image
Fig. 14
figure 14

Regression analysis. (a) for training, (b) for validation, (c) for testing, (d) for all data. Image was performed using Matlab R2020a (https://ww2.mathworks.cn/products/matlab.html).

Full size image

Conclusions

This study constructs a discrete element model for the seedling-planter interaction system and adopts the DEM-MBD coupling simulation method to investigate the interaction characteristics between the seedling and the planter during the operation of a cup-type transplanting machine. As the transplanting frequency changes, both the collision contact position and the interaction force between the seedling and the planter also vary accordingly. During the initial collision, the collision force reaches its maximum value, resulting in the most severe damage to the seedling pot body. Additionally, using artificial neural network (ANN) techniques, a seedling collision damage model under different parameter conditions was constructed by combining BP and GA-BP algorithms. The predictive capability and fitting stability of these two machine learning regression models were compared. Comparative, The GA-BP network model significantly outperforms the BP network model in terms of prediction accuracy and fitting performance. The findings not only provide theoretical support for understanding the interaction mechanism between the cup-type planter and seedlings but also offer practical guidance for constructing planting quality prediction models in complex field environments.

Future research will focus on expanding the sample size, optimizing experimental design, and broadening the parameter range to enhance the generalization capability of the model. Additionally, other machine learning techniques will be explored, including the development of neural network models suitable for small-sample datasets, such as lightweight convolutional neural networks (CNNs) or pre-trained models based on transfer learning. These approaches are expected to maintain high predictive performance even with limited data availability.