Introduction

Porosity plays a critical role in oil and gas exploration and development, influencing the identification of favorable zones and guiding development strategies1,2,3,4. Currently, porosity characterization primarily relies on experimental methods such as helium expansion, nitrogen adsorption, high-pressure mercury injection, scanning electron microscopy, and nuclear magnetic resonance5,6. While effective, these approaches are limited by the availability of core samples and the high costs of conducting the experiments, hindering the comprehensive analysis of entire wells or larger regions7. Moreover, these techniques are costly, time-consuming, and challenging to implement for continuous assessment, with their accuracy often affected by external factors like experimental conditions and the operator’s technical expertise.

Traditional porosity calculation methods are limited by geological heterogeneity, incomplete logging data, and excessive reliance on specific physical assumptions. Additionally, these methods often suffer from challenges such as complex mathematical modeling, low computational efficiency, and suboptimal prediction accuracy. To overcome these limitations, researchers have proposed a novel approach that integrates well-scale analysis with core measurements to develop a more accurate porosity model. This method enhances both the precision and reliability of porosity estimation, addressing the shortcomings of conventional techniques. Well-log analysis is the primary method employed in the oil and gas sector to determine petrophysical properties8,9, which can be used to make indirect predictions10. Historically, porosity prediction models have included single-parameter prediction models, multiple linear regression models, and empirical methods11. However, although these mathematical models allow for continuous evaluation, their prediction accuracy remains limited12,13.

Recently, machine learning (ML) algorithms have emerged as a powerful tool for improving prediction accuracy. ML models have surpassed traditional statistical methods in various fields, including drilling, reservoir performance, geological mechanics, and reservoir characterization1,2,14,15,16,17,18,19,20,21. Machine learning excels at handling complex data patterns, non-linear relationships, and multivariable problems, offering unmatched capabilities in big data analysis, regression, and prediction tasks22,23,24,25,26,27. Numerous studies have validated the potential of ML in enhancing subsurface evaluations28,29,30,31,32,33. For instance, Lammoglia et al.34 applied fuzzy logic (FL) and neural network (NN) methods to evaluate lithology using GR, RHOB, NPHI, and DT logging data in the Namorado oil field. Cao et al.35 predicted missing sonic logging curves using data from four wells. Yasin et al.36 employed support vector machine and particle swarm optimization algorithms to predict the porosity of the Lower Goru reservoir in the Sawan gas field, Pakistan. Zhou et al.37 and Li et al.38 proposed enhanced lithology recognition methods using feature decomposition, selection, and transformation of logging data. Subasi et al.39 predicted reservoir permeability using gradient boosting regression models based on standard logging data. Hussain et al.8 applied FL and NN to predict the porosity of the Gular sandstone reservoir, while Gholami and Ansari40 developed an optimized Alternating Conditional Expectation (ACE) model for predicting porosity from logging and seismic data, finding that ACE minimized prediction errors. Other studies, such as those by Subasi et al.39 and Li et al.41, further demonstrated the superiority of ML models like stochastic gradient boosting (SGB) and artificial neural networks (ANN) in porosity estimation.

Mkono et al.42 introduced the GMDH-DE method to predict the permeability based on a total of 3516 data from three wells of the Wangkwar formation in the Gunya oilfield, and established a permeability prediction model with an accuracy of 95%; Zhang et al.43 used K-means and XGBoost to train 94 wells with 3389 monolayer data in the southern Ordos Basin, and the fitting accuracies were 73% and 85% respectively; Zhao et al.44 used the optimized XGBoost permeability prediction model to analyze the linear relationship between the logging parameters and the measured permeability of the cores based on the carbonate reservoir parameters of the four wells, which improved the calculation accuracy and efficiency of the model; Hassaan et al.45 utilized two straight well logging parameters from the Middle East, used three machine learning algorithms, RF, SVM, and DT, to predict the permeability, and preferred the RF model with an accuracy of more than 91% to predict the permeability; Kumar et al.46 used the logging data of four wells from the Upper Assam basin to apply the XGBoost and RF machine learning algorithms to train the prediction model to obtain the porosity of the missing layer section, and the prediction accuracy is between 80 and 90%; Davari and Kadkhodaie47 used five machine learning algorithms ELM, RF, GB, KNN, and MLP to predict the porosity and permeability of two wells in the NW oil field of the Persian Gulf, and the RF model with an accuracy of 92.5% was finally selected as the preferred model.

A review of recent research highlights significant challenges in porosity estimation using machine learning: (1) most datasets used in model construction are limited to a few wells, (2) current studies focus predominantly on single lithology types, such as sandstone or mud stone, without addressing more complex lithology, and (3) existing ML algorithms could be further optimized to enhance prediction accuracy.

To address these challenges, seven logging data from the Ordos Basin were used in this study as the optimal set of logging curves3. We trained and tested four machine learning models—random forest (RF), XGBoost, multilayer perceptron (MLP), and gradient boosting decision tree (GBDT)—using a data set of 105,411 samples collected from 72 exploration wells in the southwestern basin. Each sample set consisted of seven-dimensional log curves and a one-dimensional porosity measurement. On the basis of the GBDT model, we globally optimized the model’s hyperparameters by introducing the particle swarm optimization (PSO) algorithm, thus constructing the GBDT model based on the PSO optimization (PSO-GBDT model for short). This model was validated using two randomly selected, unseen wells from the basin, achieving a high prediction accuracy of 99%. The use of machine learning significantly reduces costs and improves prediction accuracy compared to traditional laboratory testing methods.

Geologic setting

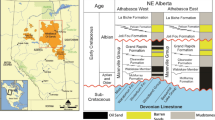
The study area is located in the southwestern part of the Ordos Basin48, stretching from Huachi in the north to Ningxian in the south, and from Tarim Bay in the east to Qingyang in the west (Fig. 1). This region lies on the Qingyang plunging anticline structure belt, in the lower part of the Yishan slope, covering approximately 2170 square kilometers49,50,51,52. Based on sedimentary cycles, the area is divided into 10 oil-bearing formations, from bottom to top, known as the Chang 10 to Chang 1 formations49,53,54,55,56. The main marker layer, K1, at the base of the Chang 7 formation, comprises black mudstone, shale, carbonaceous mudstone, and tuffaceous mudstone57,58,59. Similarly, the K9 marker layer at the base of the Chang 1 formation consists of black mudstone, shale, carbonaceous mudstone, and tuffaceous mudstone. The Chang 3 formation is a lithological oil reservoir reservoir with medium porosity, averaging 15.8%. Auxiliary marker layers such as T3y1 are characterized by developed sandstone with coarse lithology, containing turbid zeolite and loose cementation. The Chang 4 + 5 formations have been studied in greater detail due to the well-developed sandstone in the Chang 2, Chang 3, and Chang 6 formations60. The porosity of the Chang 8 reservoir varies between 8 and 11%. The lithology of the Chang 9 formation consists primarily of dark mudstone, black mudstone, and sandstone. The porosity of the Chang 8 reservoir ranges from 4.5 to 17.5%, predominantly between 6 and 10%, with an average value of 8.6%. The Chang 10 formation consists primarily of sandstone and siltstone, with miscellaneous rocks such as claystone and chert present in some areas, and porosity generally ranges from 10 to 25%.

Fig. 1
figure 1

Division of geological units in the Ordos basin48.

Full size image

Methods

Dateset

The primary methods for obtaining porosity include laboratory core analysis, well logging data interpretation, and seismic data prediction. Of these, core analysis and well logging interpretation are relatively well-established, while seismic data prediction remains less explored. Common well logging techniques used to calculate porosity include nuclear magnetic resonance, resistivity, neutron, density, velocity, and micro-electrode methods61.

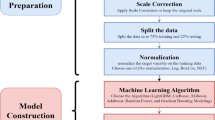
In this study, after removing missing and anomalous data, the dataset was preprocessed using min–max normalization. This method scales features to a specific range, reducing discrepancies between feature scales and preventing certain features from disproportionately influencing the model due to differences in magnitude during training.

Finally, 105,411 sample data points were collected from core experiments in 72 exploration and appraisal wells within the study area. The formations sampled range from the Chang 10 to Chang 1 oil-bearing formations. Seven types of well logs—acoustic time (AC), caliper (CAL), compensating neutrons (CNL), densities (DEN), natural gamma (GR), resistivity (RT), and spontaneous potential (SP)—were selected as input logs, as they best reflect the formation characteristics. Each sample data set comprises an eight-dimensional vector, consisting of the seven types of logging data and one-dimensional porosity measurement data.

The dataset used in this study comprises conventional logging data, which is readily available and ensures data sufficiency and completeness. Spontaneous Potential (SP), Natural Gamma (GR), and Well Diameter (CAL) primarily indicate mud content, while Acoustic Wave (AC), Density (DEN), and Neutron (CNL) serve as key porosity measurement curves. When integrated with resistivity (RT) logs, these parameters effectively support reservoir delineation, porosity estimation, and hydrocarbon identification, including saturation assessment.

Machine learning algorithms

Random forest (RF)

Random forest (RF) is an ensemble learning algorithm that integrates multiple decision trees. Its basic unit is the decision tree, which falls under the ensemble learning category in machine learning, designed to improve the generalization ability of individual decision trees62.

Random forest (RF) achieves robustness through its random selection of both samples and features. Specifically, each tree in the forest is constructed by randomly choosing a fixed number of samples and features from the entire training dataset. The term “forest” emphasizes the model’s composition of multiple decision trees, as illustrated in Fig. 2. Each decision tree serves as an independent predictor, and for any given input, the N trees produce N predictions. In regression tasks, the random forest aggregates these predictions by averaging the outputs of all trees, resulting in a robust and stable estimate62.

Fig. 2
figure 2

Schematic diagram of random forest63.

Full size image

RF is widely acknowledged for its high predictive accuracy across a broad range of machine learning tasks. It performs well on large datasets and can accommodate high-dimensional feature inputs without the need for dimensionality reduction. Additionally, RF offers valuable insights into feature importance, which aids in identifying key predictors in regression analysis. It also provides an unbiased estimate of internal generative errors during model training and efficiently handles missing data. Despite its strengths, RF has some limitations, including the potential for over-generalization and difficulty in accurately modeling highly complex or non-linear relationships.

Extreme gradient boosting (XGBoost)

XGBoost is a boosting tree model within the family of boosting algorithms, designed to combine multiple weak classifiers into a strong classifier64. Its core components are decision trees, which serve as weak learners that are sequentially constructed, with each tree informed by the errors of its predecessor. This sequential approach corrects the misclassified training samples from the previous tree, progressively refining the model with each iteration65.

XGBoost builds its model around an objective function that guides the weighting of leaf nodes, calculates information gain after node splits, and determines feature importance. A greedy algorithm selects the optimal feature at each node by maximizing the gain of the objective function, after which branching conditions for the left and right subtrees are established. The weighted quantile sketch method efficiently computes split points, while the leaf node weights are derived from the objective function. This process repeats until all features are used or the pre-defined tree depth is reached, completing the decision tree65. During testing, input features are passed through each decision tree in XGBoost, with each tree contributing prediction weights at its nodes. The final prediction is the aggregate of these weights across all trees65.

Compared to other machine learning algorithms, XGBoost improves precision by applying a second-order Taylor expansion of the loss function. It supports both classification and regression trees (CART) and linear models. Regularization terms are incorporated into the objective function to reduce overfitting. Additionally, XGBoost supports subsampling during tree construction and is optimized for parallel computing, making it effective at handling missing data65. However, its disadvantages include relatively high time and space complexity during the pre-sorting phase.

Multilayer perceptron regression (MLP)

Multilayer perceptron (MLP) is a type of artificial neural network (ANN) that can be used for both regression and classification problems. It is composed of multiple layers, including an input layer, one or more hidden layers, and an output layer. The structure of MLP for regression tasks is illustrated in Fig. 3.

Fig. 3
figure 3

Schematic diagram of multilayer perceptron regression.

Full size image

An MLP consists of three types of layers. The input layer receives data, with each node representing a feature. The hidden layers, comprising one or more layers, process inputs through activation functions and transmit the results to the next layer. The number of hidden layers and nodes determines the model’s complexity and learning capacity. The output layer structure depends on the task: classification problems have multiple nodes corresponding to categories, whereas regression problems typically have a single node representing the predicted value63,66.

MLP offers several advantages. It models nonlinear relationships through activation functions, handles high-dimensional data irrespective of type, and optimizes parameters efficiently via backpropagation to enhance performance. However, MLP has limitations. Its high computational complexity demands substantial resources. Excessive hidden layers may lead to overfitting, resulting in strong performance on training data but poor generalization. Additionally, MLP is sensitive to data preprocessing, and improper standardization or normalization may hinder convergence.

Gradient boosting decision tree (GBDT)

Gradient boosting decision tree (GBDT) is an iterative algorithm that generates a weak classifier using a CART regression tree in each round, where each classifier is trained based on the residuals of the previous one67. Description of the mathematical language: Utilizing the learner \(f_{t - 1} \left( x \right)\) from the previous iteration along with the loss function \({\text{L}}\left( {{\text{y}},f_{t - 1} \left( x \right)} \right)\) to construct a CART regression tree weak learner model \(h_{t} \left( x \right)\), minimizing the loss for this iteration \({\text{L}}\left( {{\text{y}},f_{t} \left( x \right)} \right) = {\text{L}}\left( {{\text{y}},f_{t - 1} \left( x \right) + h_{t} \left( x \right)} \right)\)67. In regression problems, if the loss function is the mean squared error, the residual is computed as the difference between the true value and the predicted value. For other loss functions, the negative gradient of the loss function is used as an estimate for the residual. The inputs, outputs, and calculation steps for GBDT are as follows:

Inputs: Training dateset \({\text{T}} = \left\{ {\left( {x_{1} ,{\text{y}}_{1} } \right)\left( {x_{2} ,{\text{y}}_{2} } \right), \ldots \left( {x_{{\text{N}}} ,{\text{y}}_{{\text{N}}} } \right)} \right\},\) \(x_{{\text{i}}} \in {\text{X}} \subseteq {\text{R}}^{{\text{n}}} ,x_{{\text{i}}} \in {\text{X}} \subseteq {\text{R}}^{{\text{n}}}\) loss function \({\text{L}}\left( {{\text{y}},f\left( x \right)} \right)\);

Outputs: Regression Tree \(f\left( x \right)\).

(1) Initialization \(f_{0} \left( x \right) = argmin\sum\nolimits_{i = 1}^{N} {\text{L}} \left( {{\text{y}}_{{\text{i}}} ,c} \right)\).

(2) m = 1, 2, …, M

(a) \({\text{i}} = 1,2, \ldots ,{\text{N}},\) count

$$r_{mi} = - \left[ {\frac{{\partial L\left( {y_{i} ,f\left( {x_{i} } \right)} \right)}}{{\partial f\left( {x_{i} } \right)}}} \right]_{{f\left( x \right) = f_{m - i} \left( x \right)}}$$

(b) For \(r_{mi}\) fitting a regression tree, get the leaf node region of the \(m\) tree \(R_{mij}\), \(j = 1,2, \ldots ,J\)

(c) \(j = 1,2, \ldots ,J\), count

$$c_{mj} = argmin\mathop \sum \limits_{{x_{i} = R_{mj} }} L\left( {y_{i} ,f_{m - 1} \left( {x_{i} } \right) + c} \right)$$

(d) Update \(f_{m} \left( x \right) = f_{m - 1} \left( x \right) + \sum\nolimits_{j = 1}^{J} {c_{mj} } I\left( {x \in R_{mj} } \right)\).

(3) Obtain a regression tree

$$f\left( x \right) = f_{M} \left( x \right) = \mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{j = 1}^{J} c_{mj} I\left( {x \in R_{mj} } \right)$$

This method offers several advantages, including fast computation speed during the prediction phase, with the ability to perform parallel computation across trees. It demonstrates excellent generalization and expressive power, particularly on densely distributed datasets. The use of decision trees as weak classifiers provides GBDT with strong interpretability and robustness. Additionally, GBDT can automatically discover high-order relationships between features without the need for special data preprocessing, such as normalization67.

Particle swarm optimization (PSO)

The particle swarm optimization (PSO) algorithm, also known as the Bird Flocking Algorithm, was introduced in 1995 as an evolutionary computation technique inspired by the study of bird flocking behavior68.

$$\begin{aligned} v_{i} \left( {t + 1} \right) & = \omega v_{i} \left( t \right) + c_{1} r_{1} \left( {P_{best,i} \left( t \right) - x_{i} \left( t \right)} \right) + c_{2} r_{2} \left( {g_{best} \left( t \right) - x_{i} \left( t \right)} \right) \\ x_{i} \left( {t + 1} \right) & = x_{i} \left( t \right) + v_{i} \left( {t + 1} \right) \\ \end{aligned}$$

where \(v_{i} \left( t \right)\) represents the velocity of the ith particle at iteration t, and \(x_{i} \left( t \right)\) denotes its current position. \(r_{1}\) and \(r_{2}\) are random numbers between 0 and 1, \(c_{1}\) is the self-learning coefficient, \(c_{2}\) is the social-learning coefficient, and \(\omega\) is the inertia factor, which reflects the tendency of a particle to maintain its current velocity. \(P_{best,i} \left( t \right)\) and \(g_{best} \left( t \right)\) represent the best solution experienced by the ith particle and the global best solution across all particles before iteration t. After updating the velocity and position of each particle, velocity and position constraints are applied. The updated particles are then used to evaluate the objective function and update \(P_{best,i} \left( t \right)\) and \(g_{best} \left( t \right)\). These steps are repeated until the convergence criterion is met69.

The algorithm models bird flocking behavior using swarm intelligence principles, where individuals within a group share information to optimize their movements collectively. By simulating the collective behavior of animals, PSO allows the swarm to evolve from a state of disorder to order in the solution space, ultimately converging on the optimal solution68. The main process of the algorithm is depicted in Fig. 4:

Fig. 4
figure 4

Steps of particle swarm optimization algorithm.

Full size image

Step 1 Initialize the random positions and velocities of the particles in the swarm, and set the number of iterations.

Step 2 Calculate the fitness value for each particle.

Step 3 For each particle, compare its fitness value with the fitness value of the best position it has encountered. If it is better, update its current best position.

Step 4 For each particle, compare its fitness value with the fitness value of the best position encountered by the entire swarm. If it is better, update the global best position.

Step 5 Update the velocity and position of each particle based on velocity and position formulas, optimizing their positions.

Step 6 If the termination condition is not met (usually the maximum number of iterations or minimum error requirement), return to Step 2.

The particle swarm optimization (PSO) algorithm offers several advantages. It avoids the use of crossover and mutation operations, instead relying on particle velocity to explore the search space. During its iterative process, only the most successful particles share information, which results in a rapid convergence rate. Additionally, PSO features a memory capability that enables it to recall and share historical optimal positions within the swarm. With a minimal set of adjustable parameters, its straightforward structure simplifies implementation in engineering contexts. PSO also uses real-number encoding, which is directly aligned with the problem solution, with the number of variables in the solution corresponding to the dimensions of the particles.

Results and discussions

Measured porosity and its characteristics

The original well logging data were collected from 72 exploration wells located in the southwestern part of the Ordos Basin. The distribution of measured porosity is illustrated in Fig. 5, which includes both a histogram and a density plot. The porosity data range from 0 to 30%, with an average value of 11.80%, a minimum value of 0.20%, and a maximum value of 31.65%. The first density peak is observed between 5 and 12%, with a density exceeding 0.08. The second peak occurs between 18 and 21%, with a relatively lower density of approximately 0.06.

Fig. 5
figure 5

Density plot of measured porosity distribution (The two peaks with the highest porosity distribution density are between 5–12% and 18–21%, respectively).

Full size image

Well logging data and its characteristics

Descriptive data analysis is a crucial step in the machine learning modeling process. After standardizing the data, an analysis was conducted on 105,411 sample sets from 72 exploration wells using various graphs and charts. Figure 6 displays the distribution density of the model parameters. AC data is normally distributed between 200 and 275 μs/m, with an average value of 243.90 μs/m, a minimum of 169.24 μs/m, and a maximum of 437.89 μs/m. CAL data ranges from 20 to 25 cm, with an average of 22.37 cm, a minimum of 19.61 cm, and a maximum of 58.89 cm. CNL data is normally distributed between 10 and 25%, with an average of 17.67%, a minimum of 0.97%, and a maximum of 81.34%. DEN data is unevenly distributed between 2 and 3 g/cm3, with an average of 2.50 g/cm3, a minimum of 1.42 g/cm3, and a maximum of 2.76 g/cm3. GR data is primarily concentrated between 25–75 API and 125–175 API, with an average of 78.27 API, a minimum of 18.64 API, and a maximum of 541.29 API. RT data is concentrated between 25 and 75 Ωm, with some scattered values, an average of 31.13 Ωm, a minimum of 1.95 Ωm, and a maximum of 2000.00 Ωm. SP data is normally distributed between 0 and 100 mV, with an average of 57.03 mV, a minimum of − 42.44 mV, and a maximum of 121.45 mV. The main purpose of data correlation analysis is to provide a scientific basis for modeling, help identify key variables and optimize the model structure.

Fig. 6
figure 6

Density plot of model input parameter distribution (acoustic time (AC), well logging (CAL), compensating neutrons (CNL), densities (DEN), natural gamma (GR), resistivity (RT), and natural potential (SP)).

Full size image

Relevance analysis

This article employs the Pearson correlation coefficient method to evaluate the relationships between different parameters and the target parameter. The Pearson correlation coefficient, denoted by r, is a statistical measure used to quantify the degree of linear correlation between two variables. It is calculated based on the sample size (n), observed values (x and y), and means of the two variables. r indicates the strength of the linear relationship between two variables. The absolute value of r represents the ratio of the covariance of two feature variables to the product of their standard deviations. A larger absolute value suggests a stronger correlation. Several conditions must be met for valid correlation analysis: the relationship between the features is linear, both features are continuous data, the overall distribution of the features is normal or close to a unimodal distribution, and the observed values appear in pairs with each pair of observations being independent. The strength of correlation is categorized based on the range of the correlation coefficient: 0.8–1.0 indicates extremely correlated, 0.6–0.8 is strongly correlated, 0.4–0.6 is moderately correlated, 0.2–0.4 is weakly correlated, and 0.0–0.2 is very weakly correlated or not correlated. Positive coefficients denote positive correlation, while negative coefficients indicate negative correlation. Figure 7 presents the Pearson correlation coefficient heat map analysis, revealing that DEN exhibits an extremely strong correlation with porosity, AC is strongly correlated with porosity, CNL, SP, GR, and CAL show weak correlations with porosity, and RT exhibits a very weak correlation with porosity. The main purpose of data correlation analysis is to provide a scientific basis for modeling, help identify key variables and optimize the model structure.

Fig. 7
figure 7

Heat map of Pearson correlation (The color depth indicates the strength of the correlation, such as AC and DEN have a strong correlation with the measured porosity, and the color is darker).

Full size image

Machine learning model building

This study employs GBDT, RF, XGBoost, and MLP for porosity prediction. Tree-based models (GBDT, RF, XGBoost) excel in regression tasks, feature importance assessment, and complex relationship modeling, while MLP enhances nonlinear modeling. These methods offer strong generalization, practical validation, and easy parameter tuning.

Other methods like SVM perform well on small datasets but struggle with scalability and parameter tuning. k-NN, though simple, suffers from the “dimensionality catastrophe” in high-dimensional data and noise sensitivity. Linear models, despite their interpretability, fail to capture the nonlinear nature of porosity prediction. These four selected algorithms balance performance, efficiency, and interpretability, making them well-suited for porosity prediction.

After processing the data and conducting correlation analysis, the well logging data from 72 exploration wells were selected as input parameters for the machine learning model, with porosity serving as the corresponding output parameter for model training. In this study, the coefficient of determination R2 was used to evaluate the performance of the machine learning model. It is calculated using the following formula:

$$R^{2} = 1 - \frac{SSE}{{SST}} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i} - y_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i} - \overline{y}} \right)^{2} }}$$

To ensure comprehensive coverage and avoid overlap between the training and testing sets, the processed data was randomly divided into a training set (80%) and a testing set (20%). Four distinct machine learning models—GBDT, RF, XGBoost, and MLP—were trained. Figure 8 present a comparison of the fitting accuracy among these models. The optimal prediction outcome was achieved by the RF model, with GBDT following closely behind.

Fig. 8
figure 8

GBDT, RF, XGBoost, and MLP Porosity machine learning prediction model fitting diagram.

Full size image

Table 1 shows the fitting accuracy values for these models. The RF model achieves the best prediction results for both training and test set accuracy, with GBDT following closely and more closely.

Table 1 Comparison of machine learning model fitting accuracy.
Full size table

Machine learning model optimization

When comparing the outcomes of GBDT, RF, XGBoost, and MLP, RF emerges as the most effective predictor. However, a significant disparity between the training and test sets suggests a potential overfitting issue. Although GBDT’s prediction results are inferior to those of RF, its accuracy remains consistent across training and testing sets, indicating robust performance. In contrast, XGBoost and MLP exhibit overall poorer prediction results. This analysis highlights an opportunity for further optimization of model accuracy. Consequently, the PSO algorithm is introduced to refine the models and enhance prediction accuracy.

The PSO algorithm primarily optimizes four parameters: N-estimators, Learning Rate, Max-depth, and Alpha. N-estimators: This parameter specifies the number of decision trees in the ensemble, directly affecting model accuracy. While a higher number of estimators generally improves performance, beyond a certain threshold, it may lead to overfitting without further accuracy gains. Learning Rate: The learning rate must be carefully selected. A high learning rate can cause instability, while a low rate may extend training time. Max-depth: This parameter determines the maximum depth of decision trees, impacting model performance in both high-dimensional and low-sample scenarios. It is crucial for evaluating whether increasing tree depth enhances effectiveness. Alpha: Alpha denotes the weight of the L1 regularization term, which can accelerate computations, especially in high-dimensional contexts. Table 2 presents the ranges and optimal values of these four hyperparameters used in the PSO algorithm for the experiment.

Table 2 The hyperparameters found by the PSO used in the experiment.
Full size table

After optimizing the fitting accuracy of the four machine learning models—GBDT, RF, XGBoost, and MLP—Table 3 reveals the following improvements:

  • GBDT: The training set accuracy increased by 4.16%, and testing set accuracy improved by 2.32%.

  • RF: The training set accuracy decreased by 1.19%, while testing set accuracy increased by 0.5%.

  • XGBoost: This model showed notable gains, with training set accuracy rising by 10.45% and testing set accuracy increasing by 4.05%.

  • MLP: Training set accuracy saw a modest improvement of 1.88%, accompanied by a 1.92% increase in testing set accuracy.

Table 3 Optimization comparison of prediction accuracy of four machine learning models.
Full size table

These enhancements reflect the effectiveness of optimization in improving model performance across different machine learning approaches.

In order to ensure the fairness of the model evaluation and avoid overfitting, we did not use the same test set as the model generalization performance evaluation when performing hyperparameter tuning. The generalization ability of the model is mainly evaluated by using an independent test set after the data division and hyperparameter tuning are completed, which ensures the independence of the hyperparameter tuning process and the final model evaluation, and thus avoids the possible bias caused by using the same test set for tuning and evaluation.

The PSO algorithm optimizes hyperparameter combinations by systematically tuning four key parameters: N-estimators, learning rate, maximum depth, and alpha. This optimization significantly enhances the model’s predictive accuracy, generalization ability, and computational efficiency, allowing PSO-GBDT to perform more effectively in porosity prediction tasks. Additionally, PSO not only improves the efficiency of hyperparameter optimization but also enables the GBDT model to better adapt to data characteristics, resulting in higher performance and greater robustness in porosity prediction.

Experimental validations demonstrate that the PSO algorithm exhibits strong global search capabilities in hyperparameter optimization. By leveraging diverse initial particle positions, velocity and position updates, local optimum escape mechanisms, and parameter tuning strategies, PSO effectively mitigates the risk of converging to local optima. This capability is particularly advantageous for complex high-dimensional problems, where PSO maintains high stability and optimization efficiency. The model’s high final prediction accuracy further confirms the effectiveness of PSO’s tuning strategy in avoiding local optima.

After comparing the predicted results of the models, it was observed in Table 3 that the optimized GBDT regression and XGBoost exhibited increased fitting accuracy without signs of overfitting. In contrast, MLP did not show a significant increase in accuracy following optimization. Although RF demonstrated high accuracy prior to optimization, the test set results showed no substantial improvement after optimization, coupled with a decrease in training set accuracy. This suggests that overfitting was reduced for RF during the PSO optimization process. Consequently, the PSO-GBDT model was selected as the preferred porosity prediction model. The predicted results of this model are illustrated in Fig. 9.

Fig. 9
figure 9

Prediction results of PSO-GBDT porosity model.

Full size image

Compared to PSO-GBDT, RF suffers from suboptimal parameter tuning and insufficient prediction accuracy in certain cases. XGBoost requires complex manual tuning and is prone to overfitting when handling noisy data. MLP is highly sensitive to input data scaling, feature selection, and sample distribution, leading to an unstable training process. In contrast, PSO-GBDT outperforms these methods in nonlinear modeling, parameter optimization, and generalization ability.

The PSO-GBDT model demonstrates greater reliability than traditional physical methods in complex geological environments, particularly when dealing with noisy data or intricate geological conditions, enabling more accurate porosity predictions. While traditional physical methods offer stronger interpretability, especially in simple geological settings, they often struggle with complex environments. Although the PSO-GBDT model has slightly lower interpretability, it provides insights into its decision-making process through techniques such as feature importance analysis.

Application of predicting the unseen porosity data

The PSO-GBDT-based porosity prediction model was applied to two randomly selected wells, Well-1, Well-2, Well-3, Well-4, in the Ordos Basin. The results are illustrated in Fig. 10. For Well-1, which spans from 1100 to 1985 m, the model demonstrated excellent fitting with training set and testing set accuracies of 99.95% and 99.42%, respectively. Similarly, Well-2, ranging from 1035 to 2270 m, showed strong fitting, with training set and testing set accuracies of 99.99% and 99.77%, Well-3, ranging from 1070 to 2280 m, showed strong fitting, with training set and testing set accuracies of 99.14% and 97.58%, Well-4, ranging from 950 to 2150 m, showed strong fitting, with training set and testing set accuracies of 99.56% and 98.57%, respectively. The porosity fitting results for these single wells are presented in Fig. 11, where the predicted porosity values generated by the PSO-GBDT model closely align with the measured porosity data.

Fig. 10
figure 10

Based on PSO-GBDT, the predicted porosity of the whole well section of four wells in Ordos Basin is compared with the real value.

Full size image
Fig. 11
figure 11

Single well porosity fitting results of four random wells in Ordos based on PSO-GBDT.

Full size image

The high R2 values of 99.95% and 99.42% for the training and testing sets in Well-1, 99.99% and 99.77% in Well-2, 99.14% and 97.58% in Well-3, and 99.56% and 98.57% in Well-4, indicate an excellent fit of the PSO-GBDT model. These results suggest that the model has successfully captured the underlying patterns in the data without significant overfitting, as evidenced by the close alignment between training and testing set accuracies. Additionally, the predicted porosity values generated by the PSO-GBDT model align well with the measured data, as illustrated in Fig. 11.

In summary, the PSO-GBDT algorithm demonstrates exceptional accuracy and effective application in porosity prediction. It addresses the challenge of incomplete porosity distribution due to the inability to continuously sample cores and facilitates accurate porosity prediction across the entire region and all well sections.

SHAP global explanation

SHAP (SHapley Additive exPlanations) is a method for interpreting prediction results based on Shapley values theory. It provides both global and local interpretability by decomposing prediction outcomes into the contributions of each feature. The core concept of SHAP involves calculating the Shapley value for each feature, which represents its contribution to the prediction. This value is then multiplied by the feature value to determine its impact on the prediction.

The PSO-GBDT model has been analyzed using SHAP, as illustrated in Fig. 12. The interpretation results reveal that DEN (density) has the most significant influence on the model’s predictions. AC (acoustic time) also exerts a substantial impact, followed by RT (resistivity), GR (natural gamma), and SP (natural potential). In contrast, CAL (well logging) and CNL (compensating neutrons) have the least influence on the model results.

Fig. 12
figure 12

SHAP global interpretation PSO-GBDT model results bar chart.

Full size image

Application prospects and limitations

Noise in logging data can distort input values, reducing prediction accuracy and potentially causing overfitting. Uncertainty impacts feature selection and model performance, complicating the optimization process and hindering the discovery of optimal solutions. Both noise and uncertainty increase data volatility, undermining decision-making accuracy.

The PSO-GBDT model is cost-effective, utilizing logging data for porosity prediction without the need for expensive laboratory analyses or extensive sampling, significantly reducing data acquisition costs. Its simple structure and efficient optimization enable rapid adaptation to varying reservoir properties, meeting real-time demands. Automated prediction reduces human error, improving overall exploration and development efficiency.

The study’s predictive data is limited to the Ordos Basin, where the PSO-GBDT model demonstrates high accuracy. Future work will focus on validating its scalability and applicability to other basins with more complex geological conditions, enhancing its performance in diverse reservoirs. Ongoing optimization will further improve its robustness and reliability across various environments.

During model development, raw data underwent filtering, transformation, and feature engineering. Statistical methods were applied to handle outliers, and Min–Max normalization ensured consistent scaling across logging parameters, improving model stability and accuracy. The PSO-GBDT model’s fast prediction speed and low computational requirements make it suitable for integration into real-time logging operations, optimizing oilfield operations and decision-making efficiency.

The PSO-GBDT model outperforms traditional methods by providing faster, more accurate predictions. Unlike techniques such as seismic inversion or NMR analysis, which require specialized equipment, PSO-GBDT only requires conventional logging data and has lower computational costs than other deep learning models.

The PSO algorithm optimizes the hyperparameter search space and avoids excessive iterations, offering a cost-effective solution for large-scale reservoir assessments. Training takes only a few hours on a medium-sized cluster, which is practical for most scenarios. Future optimizations through distributed computing and parallelization will further enhance computational efficiency.

Machine learning techniques in resource extraction require careful consideration of potential biases and their environmental impact. Data variability may lead to overfitting specific geological environments, compromising generalization. This study incorporates data selection diversity and cross-validation to improve model robustness. Accurate porosity predictions are key to reducing resource wastage and minimizing environmental impact. Future work will enhance the model’s interpretability by integrating geological knowledge and constraints.

Conclusions

This article presents a case study on reservoirs in the southwestern part of the Ordos Basin, focusing on the application of machine learning optimization algorithms, particularly PSO-GBDT, to investigate the correlation between conventional well logging data and porosity. The study aims to develop a novel method for constructing reservoir porosity models with high predictive accuracy. The following conclusions are drawn.

The GBDT model offers strong generalization capabilities, high accuracy, and automatic handling of missing values. Combined with the PSO optimization algorithm, which is known for its adaptability and ease of implementation, the model addresses challenges such as the high cost associated with conventional experimental characterization and the low precision of porosity calculations from logging data. The PSO-GBDT model is highly effective for predicting porosity, addressing the limitations of discontinuous coring, and enabling cost-effective and rapid porosity estimation. The model achieves high precision and efficiency in porosity prediction, providing valuable guidance for oil and gas exploration in the Ordos Basin. This approach also offers potential for predicting other critical reservoir parameters.