Introduction

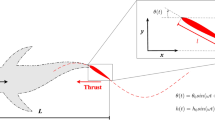
Natural selection favors the survival of the fittest. After billions of years of evolution, some diving beetles have developed unique propulsion organs and swimming methods, such as Dytiscus marginalis, Micronecta scholtzi, and Notonecta triguttata. Their hind legs are strong and powerful, covered with numerous swimming hairs (as shown in Fig. 1), flat and paddle-shaped, enabling them to propel themselves by paddling1,2,3,4.

Fig. 1
figure 1

The diving beetle and the swimming hairs on the hind legs.

Full size image

In 1961, Nachtigall’s research demonstrated that the hind legs of diving beetles are highly efficient propulsion organs, with the tarsus and the swimming hairs distributed on it generating 81.8% of the total thrust during propulsion5. Extensive research has shown that the densely distributed swimming hairs on the tarsus provide the main propulsive force for swimming6,7,8,9. In nature, many organisms rely on seamless webbed feet to generate swimming thrust, such as frogs, geese, and platypuses, all of which use webbed feet to create forward motion. However, organisms like diving beetle, which generate thrust using evenly distributed swimming hairs, are uncommon. Unlike continuous webbed feet, there are micro gaps between each swimming hair. In our conventional understanding, the presence of these gaps would allow water to flow through the plate, reducing pressure drag and consequently leading to a loss of thrust.

Based on bionics, organisms have gradually adapted to their living environments through long-term evolution, and this biological characteristic of diving beetle must have evolved to better adapt to the underwater environment. The small size of diving beetle demands higher efficiency in the paddling propulsion of their hind legs. The swimming hairs of diving beetle have diameters of approximately 10–21 μm, with gaps between the hairs ranging from about 6–23 μm. Whether this unique structure of uniformly distributed microcylinders and microgaps provides a fluid dynamics advantage is a question worthy of in-depth study. Currently, most research related to diving beetles focuses on their biological characteristics10,11, swimming performance12,13, and bionic robots14,15,16. However, fluid dynamics studies related to swimming hairs have not been reported.

The flow around circular or prismatic cylinders is often considered a typical problem in the phenomenology of blunt body flow17. Cylindrical structures are common in engineering applications and nature, such as bridge piers, heat exchanger tubes, high-rise buildings, chimneys, power lines, and oil and gas pipelines17,18,19,20,21, which has led to extensive researches on the flow around cylinders. The vortex shedding of a single cylinder is closely related to engineering applications and fundamental fluid mechanics and has been extensively studied and deeply understood22. These studies have revealed the flow characteristics transformations resulting from the interaction of viscous and inertial forces. Since multi-cylinder structures are more common than isolated ones in engineering practice, researchers have gradually shifted their focus to the flow around multiple cylinders. Currently, research on the flow around two cylinders19,20,21,23,24,25, three cylinders26,27,28, four cylinders22,29,30,31, and cylinder arrays32,33,34,35,36,37,38 arranged in different ways is quite extensive. These studies mainly investigate the effects of Reynolds number, cylinder gap, and arrangement on the wake structure and vortex shedding mechanism, vortex-induced vibration characteristics and suppression, and heat exchange characteristics of cylinder arrays. Numerous experimental and numerical simulation methods have also been developed.

In experimental research, visualization methods mainly include Particle Image Velocimetry (PIV)18,39,40,41,42, Laser Doppler Velocimetry (LDV)29,43, and Laser-Induced Fluorescence (LIF)18,26,42,44. These methods primarily obtain characteristics of flow around cylinder such as the wake structure and vortex shedding mechanism through experimental means. In numerical simulations, traditional CFD methods generally choose laminar models at low Reynolds numbers19,20,25,35,36, while turbulence models are chosen at high Reynolds numbers, such as RANS (Reynolds-averaged N-S)21,28,38 and LES (Large-eddy simulation)29,33,38. Sometimes, the DNS (Direct Numerical Simulation) method is also used24,31. This method does not rely on models and has high computational accuracy, but it requires high mesh quality and is not suitable for large-scale or highly turbulent situations. For some special cases, such as flow through porous media or high Reynolds number flows, the LBM (Lattice Boltzmann Method)26,34,37,45 and DVM (Discrete-Vortex Method)46,47 have certain advantages. Unlike traditional CFD methods, LBM is a mesoscopic-scale computational fluid dynamics method with the advantages of simple fluid interaction description, easy setup of complex boundaries, parallel computation feasibility, and ease of implementation, making it suitable for solving flow and mass transfer problems in porous media. DVM replaces the continuous distribution of vorticity in local rotational regions with a finite number of discrete vortices, calculating their interactions and evolution to achieve numerical simulation of the entire flow field. In applications involving flow around cylinders, the discrete vortex method can significantly improve computational efficiency while maintaining the accuracy of results consistent with traditional CFD methods.

Although the aforementioned problem of flow around cylinder arrays is similar to the research content of this paper, the minimum sizes of the cylinders and gaps reach only the millimeter scale, whereas the diameters and gaps of the swimming hairs are both on the micrometer scale. All of this leads to significant difference in flow characteristics, making the paddling process of swimming hairs a new research area. The open-source software OpenFOAM can be adapted to actual research problems encountered to achieve numerical simulations that match experimental results. Therefore, this paper selects OpenFOAM 4.1 for numerical simulation analysis of this process.

icoFoam is a transient solver in OpenFOAM, based on the finite volume method, designed to solve incompressible laminar flows. It is based on the PISO algorithm. Since it was originally designed for laminar flow, it does not inherently include a turbulence model. Under the conditions that high-resolution meshes and small time-step, it can be used for quasi-DNS. Quasi-DNS is a numerical simulation method that directly solves the Navier–Stokes (NS) equations, with computational accuracy falling between direct numerical simulation (DNS) and large eddy simulation (LES). Komen et al. studied turbulent flow inside a pipe and concluded that, with sufficient mesh resolution, the finite volume method can also achieve high-quality mean velocity and fluctuating velocity fields48. Komen et al. further used the finite volume method for quasi-DNS and calibrated it against large-eddy simulation with the finite volume method, noting that the latter can introduce certain numerical dissipation49. Axtmann and U. Rist also used OpenFOAM for quasi-DNS, studying the characteristics of the compiler and parallel computing50. Liu et al. conducted quasi-direct simulations of lid-driven cavity flow using icoFoam51, further validating the feasibility of using OpenFOAM for quasi-direct simulations. Compared to direct numerical simulation (DNS), icoFoam requires fewer mesh elements, which can speed up simulations and shorten the computation cycle. Additionally, the flow states in this study are all laminar and the fluid is incompressible. Therefore, this paper uses the icoFoam solver for numerical simulation of the paddling process of swimming hairs.

This paper establishes a two-dimensional model of a flat plate with multiple microcylinders arranged in gaps (multi-microcylinder seam plate that mimics the swimming hairs) to study the drag characteristics of the seam plate using numerical simulation. The study explores the flow field characteristics during the paddling process of the multi-microcylinder seam plate and investigates the influence of gaps on pressure drag and viscous drag. The results reveal that the unique arrangement of the swimming hair exhibits excellent drag-enhancing performance, which has significant implications for the development of small underwater vehicles using paddling propulsion systems. Future underwater vehicles will evolve towards low-noise and miniaturized designs, where paddling propulsion could be a promising option. Implementing micro-gaps on paddling propulsion components through advanced techniques could further enhance propulsion efficiency. Similarly, for certain microfluidic devices, arranging micro-gaps on key power components can also improve overall efficiency.

Results analysis and discussion

Variance analysis and optimization of the maximum value of the drag increase rate

To achieve the best regression analysis accuracy, power function transformation tests were applied to \(\varepsilon_{tf}\), \(\varepsilon_{vf}\) and \(\varepsilon_{pf}\). It was found that all three parameters required power function transformations. The detailed transformation parameters are shown in Table 1. After transformation, the parameters \(\varepsilon_{tf}{\prime}\), \(\varepsilon_{vf}{\prime}\) and \(\varepsilon_{pf}{\prime}\) were obtained.

Table 1 Power function transformation parameters for \(\varepsilon_{tf}\), \(\varepsilon_{vf}\) and \(\varepsilon_{pf}\).
Full size table

Variance analysis was conducted on the parameters \(\varepsilon_{tf}{\prime}\), \(\varepsilon_{vf}{\prime}\) and \(\varepsilon_{pf}{\prime}\) with the results shown in Table 2. The data indicate that the coefficients of determination R2 for the regression equations of the three parameters are 0.9691, 0.9473 and 0.9684, respectively. This demonstrates that the regression equations for all three parameters have good confidence levels.

Table 2 Variance analysis results for \(\varepsilon_{tf}{\prime}\), \(\varepsilon_{vf}{\prime}\) and \(\varepsilon_{pf}{\prime}\).
Full size table

From the significance ranking of the factors, it can be seen that flow velocity (X3) has a highly significant impact on the drag increase rate \(\varepsilon_{tf}\), viscous drag increase rate \(\varepsilon_{vf}\), and pressure drag decrease rate \(\varepsilon_{pf}\). Additionally, X22 and X1X2 also have significant effects on all three parameters. Since both X22 and X1X2 are related to the microgap width, this indicates that the microgap width is also a key factor affecting the drag-increasing characteristics. Relatively speaking, the variables related to microcylinder diameter X1 and X12 are less significant, suggesting that the microcylinder diameter is a secondary factor affecting the drag-increasing characteristics. Notably, X22 has a greater significance than X3 in affecting the viscous drag increase rate \(\varepsilon_{vf}\), indicating that the gap to diameter ratio plays a crucial role in viscous drag. This is related to the underlying cause of viscous drag. As shown in Table 2, viscous drag is the primary source of the increased drag of the seam plate with multiple microcylinders, hence the gap to diameter ratio is a critical parameter for drag increase.

Using the regression model, optimization was performed for the drag increase rate \(\varepsilon_{tf}\), with the results shown in Table 3. The data indicate that the 9 sets of optimization results basically cover the entire range of microcylinder diameters. The optimal gap to diameter ratio varies for different microcylinder diameters, but the actual gap size is approximately in the range of 22–35 μm. Considering that the diameter of the diving beetle’s swimming hairs is 10–21 μm, and the gaps between the hairs are about 6–23 μm. Therefore, this is similar to the optimization result of group 9. This indicates that the swimming hairs of diving beetle have excellent hydrodynamic performance for increasing paddling drag, which is crucial for such small-sized organisms. Compared to continuous webbed feet, the gap-distributed swimming hairs minimize energy loss for the organism, while providing better paddling performance than seamless webbed feet. The only drawback is the limited stiffness of the swimming hairs, which cannot withstand excessive loads. The excellent performance of swimming hair has important reference and guidance significance for small biomimetic underwater vehicles. Under the premise of ensuring sufficient paddling performance of underwater propulsion components, their weight should be reduced as much as possible for the purpose of reducing additional energy loss during the paddling process. With limited battery energy storage, it is of great significance for the endurance of small underwater vehicles.

Table 3 Optimization results for drag increase rate \(\varepsilon_{tf}\).
Full size table

Drag variation characteristics of the multi-microcylinder seam plate

The proportion of viscous drag \(r_{v}^{G}\) (viscous drag/total drag × 100%) of the multi-microcylinder seam plate has a certain correlation with the viscous drag proportion \(r_{v}^{SC}\) of a single microcylinder. When the gap to diameter ratio is relatively small, the flow field on both sides of the microcylinders are not fully developed due to the constraint of the gaps. At this time, the viscous drag proportion of the seam plate is relatively small, i.e., \(r_{v}^{G}{ < }r_{v}^{SC}\). As the gap to diameter ratio continues to increase, \(r_{v}^{G}\) gradually converges to \(r_{v}^{SC}\). When the gap to diameter ratio increases to the point where the flow fields between the microcylinders no longer interfere with each other, that is, when each microcylinder is completely independent, \(r_{v}^{G} = r_{v}^{SC}\). Therefore, the range of \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) (defined as the ratio of the viscous drag percentage) is (0,1], which is applicable to all multi-microcylinder seam plates. Based on the analysis in the previous section, viscous drag is the main reason for the increased drag of the multi-microcylinder seam plate. Hence, this study uses the dimensionless number \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) as the independent variable to investigate its intrinsic relationship with the drag characteristics of the multi-microcylinder seam plate.

As shown in Fig. 2, which illustrates the drag characteristics curve of the multi-microcylinder seam plate. Figure 2a indicates that the viscous drag proportion \(r_{v}^{{G_{\max } }}\) of the multi-microcylinder seam plate is significantly smaller than the pressure drag proportion \(r_{p}^{{G_{\max } }}\), where, \(r_{v}^{{G_{\max } }} = {{G_{vf} } \mathord{\left/ {\vphantom {{G_{vf} } {(G_{vf} + G_{pf} )_{\max } }}} \right. \kern-0pt} {(G_{vf} + G_{pf} )_{\max } }}\) and \(r_{p}^{{G_{\max } }} = {{G_{pf} } \mathord{\left/ {\vphantom {{G_{pf} } {(G_{vf} + G_{pf} )_{\max } }}} \right. \kern-0pt} {(G_{vf} + G_{pf} )_{\max } }}\). As \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) continues to increase, the viscous drag proportion of the multi-microcylinder seam plate is in a continuous rising state, while the pressure drag proportion is in a slow declining state. The growth rate of the viscous drag proportion is faster, resulting in improved drag-increasing effectiveness of the multi-microcylinder seam plate.

Fig. 2
figure 2

Drag characteristics curve of the multi-microcylinder seam plate. (a) variation curves of the pressure drag (Gpf), viscous drag (Gvf), and drag increase rate (εtf) relative to the seamless plate of the multi-microcylinder seam plate with respect to the ratio of the viscous drag percentage. (Gpf + Gvf)max is the maximum total drag of the multi-microcylinder seam plate under the same flow field conditions; (b) variation curves of the average pressure drag (\(\overline{{G_{pf} }}\)) and average viscous drag (\(\overline{{G_{vf} }}\)) on each microcylinder in the multi-microcylinder seam plate with respect to the ratio of the viscous drag percentage. SCpf and SCvf are the pressure drag and viscous drag on an isolated microcylinder under the corresponding flow velocity conditions, respectively.

Full size image

When \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) increases to around 0.9, if the value of \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) continues to increase, it will cause both the viscous drag proportion \(r_{v}^{{G_{\max } }}\) and the pressure drag proportion \(r_{p}^{{G_{\max } }}\) of the multi-microcylinder seam plate to drop rapidly, ultimately leading to a swift decline in the drag increase rate of the multi-microcylinder seam plate.

Overall, the drag increase rates of the three groups of multi-microcylinder seam plates all peak when \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) is between 0.85 and 0.9. Changes in microcylinder diameter and flow velocity did not cause large fluctuations in the \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) values corresponding to the peak drag increase rates. The increase in flow velocity only significantly raised the peak drag increase rate of the multi-microcylinder seam plate. Compared to microcylinder diameter, flow velocity has a more noticeable impact on the drag increase rate. All of these have important guiding value for future engineering applications. Given the known drag composition of a single microcylinder, i.e., \(r_{v}^{SC}\) is known, it is possible to roughly estimate the drag composition relationship \(r_{ve}^{G}\) of the multi-microcylinder seam plate when the drag increase rate peaks. By using numerical simulation methods to obtain the drag composition relationships of the multi-microcylinder seam plate under two different gap to diameter ratios (i.e., viscous drag proportions \(r_{v1}^{G}\) and \(r_{v2}^{G}\)), and selecting as large a range of gap to diameter ratios as possible to ensure that \(r_{v1}^{G}{ < }r_{ve}^{G}{ < }r_{v2}^{G}\), the bisection method can be used to iteratively narrow down the gap to diameter ratio range. This allows for quickly identifying the gap to diameter ratio corresponding to the optimal drag increase effect.

As shown in Fig. 2b, the average pressure drag and viscous drag acting on a single microcylinder in the multi-microcylinder seam plate continue to increase until \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) is approximately 0.93. This indicates that as the gap to diameter ratio increases, it results in an increase in both the pressure drag and viscous drag acting on a single microcylinder.

The reduction in pressure drag exhibited by the multi-microcylinder seam plate is caused by the decrease in the number of microcylinders, meaning that the loss of pressure drag due to the loss of solid area is greater than the gain in pressure drag resulting from the enlargement of the gaps. At the same time, the enlargement of the gaps also leads to an increase in viscous drag, both of which together compensate for the loss of pressure drag due to the loss of solid area. In the initial stages, the gains in both viscous and pressure drags can completely offset the loss of pressure drag, resulting in the multi-microcylinder seam plate demonstrating drag-increasing mechanical characteristics.

As the gap to diameter ratio continues to increase (i.e., the viscous drag proportion ratio \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) continues to increase), the cumulative gain effects of both viscous and pressure drags enhance the drag-increasing effect of the multi-microcylinder seam plate. When \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) is approximately 0.9, the gains from both drags can essentially offset the pressure drag loss due to the loss of solid area. At this point, the drag-increasing effect of the multi-microcylinder seam plate reaches its optimal level.

When \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) continues to increase beyond this point, although the average pressure drag and viscous drag acting on a single microcylinder continue to rise, they can no longer compensate for the pressure drag loss due to the reduction in solid area. As a result, the drag-increasing effect of the multi-microcylinder seam plate diminishes and quickly transitions to a drag-reducing state. Compared to the pressure drag and viscous drag on a single microcylinder, the average pressure drag and viscous drag on each microcylinder in the multi-microcylinder seam plate are smaller in the initial stages (with the values of the pressure drag proportion curve and the viscous drag proportion curve both being less than 0). This means that when there are more microcylinders, the gaps will be very small, and the average pressure drag and viscous drag distributed on a single microcylinder are relatively small.

As \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) continues to increase, the average pressure drag proportion first exceeds 0, meaning that the average pressure drag on a single microcylinder becomes greater than the pressure drag on an isolated microcylinder, while the average viscous drag remains less than the viscous drag on an isolated microcylinder. The reason for this is that viscous drag primarily depends on the development of the flow field within the gaps. At the same time, the uniformly spaced arrangement of the multi-microcylinders creates a certain frontal area, which, compared to an isolated microcylinder, results in a pressure drag advantage. This causes the pressure drag proportion to be significantly greater than the viscous drag proportion in the initial stages.

When \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) exceeds 0.85, the average viscous drag proportion for the single microcylinder in the multi-microcylinder seam plate gradually becomes greater than 0. At this point, the drag increase rate of the multi-microcylinder seam plate is already nearing its peak. After \({{r_{v}^{G} } \mathord{\left/ {\vphantom {{r_{v}^{G} } {r_{v}^{SC} }}} \right. \kern-0pt} {r_{v}^{SC} }}\) exceeds 0.9, the average pressure drag and viscous drag on each single microcylinder continue to increase. However, due to the reduction in the number of microcylinders, the total drag of the multi-microcylinder seam plate begins to decrease. Subsequently, the average pressure drag and viscous drag on each single microcylinder start to decrease and eventually converge to the pressure drag and viscous drag of an isolated microcylinder.

Comparative analysis of the overall pressure field and velocity field between the multi-microcylinder seam plate and the seamless plate

To analyze the characteristics of each part of the flow field, we selected the flow field data under the conditions of a microcylinder diameter of 40 μm and a flow velocity of 0.3 m/s. All flow field-related analyses in this paper are based on these conditions.

As shown in Fig. 3, when the gap to diameter ratio is 0.27 and the viscous drag proportion ratio is 0.53, the pressure field of the multi-microcylinder seam plate is similar to that of the seamless plate. Both form an "8"-shaped negative pressure zone behind the plate, with an elliptical pressure concentration zone forming behind the "8"-shaped negative pressure zone. The high-pressure zone in front of the plate is also basically similar. As the gap to diameter ratio increases, the "8"-shaped negative pressure zone behind the seam plate gradually weakens and shifts further back, while the area of the high-pressure zone near the front of the plate decreases. When the gap to diameter ratio reaches 0.73, the "8"-shaped negative pressure zone is no longer clearly visible.

Fig. 3
figure 3

Pressure contours of multi-microcylinder seam plate and seamless plate.

Full size image

When the gap to diameter ratio reaches 1.11, the "8"-shaped negative pressure zone completely disappears, and a rectangular low-pressure zone with relatively uniform pressure forms near the rear of the plate. This indicates that the pressure field formed by the fluid passing through the gaps tends to become uniform, and the influence between the gaps is gradually weakening. At this point, the drag increase rate of the multi-microcylinder seam plate has already started to decrease. A trapezoidal low negative pressure zone forms further away from the plate. From the velocity contours of the flow field, it can be seen that a velocity circulation still forms at this ___location, resulting in a concentration of negative pressure in this area.

When the gap to diameter ratios are 1.71 and 2.17, the pressure values of the negative pressure zone behind the plate decrease (the decrease in pressure values refers to a reduction in the absolute value of the negative pressure). Although the area of the high-pressure zone near the front of the plate decreases, the area of the secondary high-pressure zone slightly further from the plate increases, reducing the drag of the fluid passing through the gaps.

As shown in Fig. 3h, as the gap to diameter ratio increases, the pressure drag of the multi-microcylinder seam plate continuously decreases and remains consistently lower than the pressure drag of the seamless plate. In the initial stage, the pressure drag decreases slowly. When the viscous drag proportion ratio exceeds 0.85, the pressure drag drops rapidly, causing the drag-increasing effect of the seam plate to begin to weaken and eventually transition to a drag-reducing state. The average pressure drag on a single microcylinder in the multi-microcylinder seam plate continues to increase until the viscous drag proportion ratio reaches 0.9, and it is generally higher than the pressure drag on an isolated microcylinder under the same flow field conditions. This is because when multiple microcylinders are arranged with gaps between them, the outer cross-sectional area formed between them provides a certain shape drag. This portion of the drag increases the average pressure drag on each single microcylinder.

As the viscous drag proportion ratio further increases, the amount of fluid passing through the gaps increases, leading to a gradual reduction in the shape drag of the seam plate, and the average pressure drag on each single microcylinder begins to decrease. When the state is reached where each microcylinder no longer influences the others (viscous drag proportion ratio equals 1), the average pressure drag on each single microcylinder converges to the pressure drag of an isolated microcylinder. Although the average pressure drag on each single microcylinder generally increases, the pressure drag of the seam plate continuously decreases. The primary reason for this is that the outer dimensions of the multi-microcylinder seam plate are fixed, and an increase in the gap to diameter ratio results in a reduction in the number of microcylinders, which in turn reduces the pressure drag of the seam plate.

As shown in Fig. 4, when the gap to diameter ratio is 0.27, the velocity field of the multi-microcylinder seam plate is similar to that of the seamless plate. Two velocity circulations form behind the plate, which is the reason for the formation of the "8"-shaped negative pressure zone. The velocity of the fluid behind the plate is relatively low, while the fluid in front of the plate accelerates to the sides after being obstructed by the plate. This causes the velocity of the fluid on both sides behind the plate to be much higher than that of the fluid in the middle. As a result, the fluid on both sides exerts a backward dragging effect on the fluid in the middle, forming a clockwise circulation on the upper half and a counterclockwise circulation on the lower half.

Fig. 4
figure 4

Velocity contours of multi-microcylinder seam plate and seamless plate.

Full size image

The two circulations converge at the middle position behind the plate, increasing the flow speed in the middle, which is opposite in direction to the velocity of the main flow field. Consequently, two velocity stagnation points are formed at the front and rear convergence points of the two circulations, and the central areas of the circulations form low-speed regions, which are the "8"-shaped negative pressure zones. The two circulations create low-speed closed-loop regions that surround the high-speed fluid in the middle. As the gap to diameter ratio increases, the low-speed zone close to the back of the plate is elongated, indicating that the velocity of the fluid passing through the gaps is relatively low. The low-speed closed-loop region formed by the circulation zones gets narrower, and the flow speed in the central high-speed fluid region decreases. This suggests that the accelerating effect of the high-speed fluid on both sides of the plate on the middle fluid weakens, reducing the speed difference between them. The two circulations become weaker, leading to a decrease in the speed of the high-speed fluid on both sides behind the plate.

When the gap to diameter ratio reaches 1.11, the velocity of the fluid passing through the gaps further increases, forming a “parabolic” shaped low-speed transition zone near the back of the plate. Subsequently, the velocity further decreases, forming a narrower low-speed closed-loop region at the rear. The flow speed at the center is not much different from the speed in the surrounding low-speed region. The intensity of the two circulations is very weak, and the flow speed of the fluid on both sides also decreases.

When the gap to diameter ratios are 1.71 and 2.17, no velocity circulation zones form behind the seam plate. The flow speed in the low-speed region behind the plate continues to increase, indicating a reduction in the plate’s blocking effect on the fluid. The flow speed of the fluid passing through the gaps further increases, and the speed of the fluid on both sides of the plate are nearly equal to the speed of the main flow field.

As shown in Fig. 4h, before the viscous drag proportion ratio reaches 0.9, the viscous drag of the multi-microcylinder seam plate continuously increases, indicating that the friction between the fluid and the microcylinders is intensifying. Afterward, the viscous drag begins to decrease.

However, based on the average viscous drag of a single microcylinder in the seam plate, it is observed that the average viscous drag mentioned above continuously increases throughout the entire range of changes. In the later stages, it gradually exceeds the viscous drag of an isolated microcylinder under the same flow field conditions, indicating that the friction effect of the fluid within the gaps on the microcylinders is continuously intensifying. Similar to the pressure drag of the seam plate, the primary reason for the decrease in viscous drag in the later stages is the reduction in the number of microcylinders in the multi-microcylinder seam plate, leading to a decrease in the viscous drag of the total seam plate. The velocity contours reveal that the flow field of the multi-microcylinder seam plate is laminar in all cases, so the viscous drag of the fluid has a significant impact on the total drag.

Analysis of the pressure field and velocity field inside the gaps of the multi-microcylinder seam plate

To analyze the characteristics of the flow field within the gaps, flow field data from specific locations were extracted. As shown in Fig. 5, the main focus was on the flow field data along the line A-A, which is perpendicular to the flow direction and passes through the center of the microcylinder, and the line B-B, which is along the flow direction and passes through the center of the gap (trying best to ensure that the gap where the data extracted from is located at the center of the multi-microcylinder seam plate. If the number of microcylinders is even, the gap is exactly at the center, and if the number of microcylinders is odd, the center of the multi-microcylinder seam plate is a microcylinder. To ensure uniformity, the gap adjacent to the center microcylinder with an x-coordinate greater than the center microcylinder was selected). Additionally, the circumferential tangential velocity of the central microcylinder in the multi-microcylinder seam plate (circumferential line C–C) was also extracted, as well as the pressure data on the front and rear sides of both the seam and seamless plates (lines D–D and E–E).

Fig. 5
figure 5

Schematic diagram of the ___location of each data extraction line. (a) Data extraction line locations for the seamless plate; (b) data extraction line locations for the seam plate when the number of microcylinders is even; (c) data extraction line locations for the seam plate when the number of microcylinders is odd.

Full size image

As shown in Fig. 6, the curves represent the variations in velocity and pressure along the line A-A. When the gap coordinates take integer values, these locations correspond to the center positions of the gaps. Transitioning forward and backward by 0.5 units gives the coordinates corresponding to the edges of a single gap, with each integer coordinate representing a gap.

Fig. 6
figure 6

Flow field data of multi-microcylinder seam plate at line A-A. (a) Variation curves of the velocity at line A-A; (b) variation curves of the pressure at line A-A.

Full size image

As shown in Fig. 6a, with the continuous increase in the gap to diameter ratio, the velocity of the fluid within the gaps also continuously increases, and the velocity differences between the gaps decrease, indicating that the seam plate’s blocking effect on the fluid is weakening. Before the gap to diameter ratio reaches 0.73, the velocity increases significantly. However, after exceeding 0.73, the rate of velocity increase begins to diminish. This means that in the early stages, the expansion of the gaps led to a rapid development of the internal flow field, but further expansion of the gaps did not result in corresponding changes in the flow field. This indicates that as the gaps continue to enlarge, their restrictive effect on the fluid weakens. Specifically, when the gap to diameter ratios are 1.71 and 2.17, the velocity no longer shows a significant increase. However, compared to an isolated microcylinder, the velocity within the gaps is still higher than that of around the isolated microcylinder, indicating that the gaps still have an accelerating effect on the fluid, although the multi-microcylinder seam plate is already in a drag-reducing state. With the further increase in the gap to diameter ratio, the velocity within the gaps will gradually converge to the velocity around the isolated microcylinder.

As shown in Fig. 6b, when the gap to diameter ratio is less than 0.46, the pressure inside the gaps is positive, indicating that the fluid inside is in a state of mutual compression. At this time, the multi-microcylinder seam plate exhibits a certain drag-increasing effect. When the gap to diameter ratio reaches 0.73, negative pressure starts to appear within the gaps, allowing the fluid to pass smoothly through them. The compressive effect of the gaps weakens, and the multi-microcylinder seam plate achieves its optimal drag-increasing effect. As the gap to diameter ratio further increases, the negative pressure inside the gaps increases and gradually transitions to the pressure around an isolated microcylinder. The restrictive effect of the gaps on the internal fluid further weakens, and the multi-microcylinder seam plate transitions to a drag-reducing state.

As shown in Fig. 7a, the gaps in the seam plate have a significant accelerating effect on the fluid. As the fluid passes through the gaps, the velocity first increases to a peak value and then begins to decrease. The position that the peak velocity appears is generally located on the cross-sectional line passing through the center of the microcylinder. As the gap to diameter ratio increases, this position shifts backward. This indicates that the narrowest part of the gap is no longer where the peak velocity occurs, suggesting that the compressive and accelerating effects of the gaps on the fluid are weakening, and the drag-increasing effect of the multi-microcylinder seam plate begins to diminish. After the fluid passes through the gaps, two velocity stagnation points form behind the multi-microcylinder seam plate. As the gap to diameter ratio increases, the positions of these stagnation points move further back, and the reverse peak velocities also decrease. When the gap to diameter ratio reaches 1.71, the velocity stagnation points no longer appear, and the multi-microcylinder seam plate transitions to the drag-reducing state.

Fig. 7
figure 7

Flow field data of multi-microcylinder seam plate at line B-B. (a) Variation curves of the velocity at line B-B; (b) variation curves of the pressure at line B-B.

Full size image

As shown in Fig. 7b, when the gap to diameter ratio is relatively small, the pressure difference across the gap is basically similar to that of the seamless plate. As the gap to diameter ratio increases, the pressure in front of the gap starts to decrease, and the negative pressure behind the gap increases, indicating that the compressive effect of the fluid in front of the gap weakens, while the suction effect of the fluid behind the gap strengthens. When the gap to diameter ratio reaches 1.11, the pressure in front of the gap further decreases, and the negative pressure behind it begins to decrease. At this point, the drag-increasing effect of the multi-microcylinder seam plate starts to weaken. As the gap to diameter ratio further increases, the pressure in front of the gap continues to decrease, and the negative pressure behind the gap gradually converges to the pressure behind the seamless plate. The multi-microcylinder seam plate no longer exhibits a drag-increasing effect.

As shown in Fig. 8, the circumferential tangential velocity of the central microcylinder in the multi-microcylinder seam plate is depicted. The tangential velocity is defined as negative in the clockwise direction and positive in the counterclockwise direction. When the gap to diameter ratio is small, the tangential velocity around the circumference reaches its maximum negative value at the 90° position and its maximum positive value at the 270° position, with both positions being at the narrowest part of the gap. As the gap to diameter ratio increases, these positions gradually shift towards 60° and 300°. According to the angular definition in the figure, these two positions are symmetrical to each other and continuously move forward, gradually converging to the positions where the maximum tangential velocities (negative and positive) of an isolated microcylinder appear. The difference from the isolated microcylinder’s tangential velocity gradually diminishes.

Fig. 8
figure 8

Circumferential tangential velocity of the central microcylinder of the multi-microcylinder seam plate.

Full size image

In the initial stages, the tangential velocity around the central microcylinder does not change in positive and negative values near 180° position. When the gap to diameter ratio reaches 1.71, changes in positive and negative values of the tangential velocity start to appear around the 180° position for the central microcylinder. This indicates that fluid circulations have already been formed around the 150°–180° and 180°–210° regions of the central microcylinder, that is, slight velocity separations have occurred, resulting in changes in positive and negative values of the tangential velocity. At this point, the multi-microcylinder seam plate is in a drag-reducing state.

As shown in Fig. 9, the pressure curves of the front and rear surfaces of the multi-microcylinder seam plate and the seamless plate are displayed (pressure data at the lines D–D and E–E). The figure shows that when the gap to diameter ratio is small, the pressure of the front surface of the multi-microcylinder seam plate fluctuates around the pressure curve of the seamless plate’s front surface. As the gap to diameter ratio increases, the pressure fluctuations of the front surface of the multi-microcylinder seam plate become more pronounced, with the pressure increasing at the microcylinders and decreasing at the gaps. The pressure decrease at the gaps is more significant, indicating that more fluid passes through the gaps, the impact on the microcylinders strengthens, and the blocking effect of the gaps on the fluid weakens, reducing the conversion of fluid kinetic energy to pressure.

Fig. 9
figure 9

Pressure curves of the front and rear surfaces of the multi-microcylinder seam plate and seamless plate.

Full size image

As the gap to diameter ratio further increases, the pressure loss at the gaps becomes severe, leading to a drag reduction phenomenon in the multi-microcylinder seam plate. The pressure of the rear surface of the multi-microcylinder seam plate is generally lower than that of the seamless plate, showing as negative pressure. This indicates that the negative pressure of the rear surface is also a key factor in increasing drag. In the early stages of increasing the gap to diameter ratio, this negative pressure value continuously increases, and the pressure fluctuations between the gaps and microcylinders also increase, improving the drag-increasing effect of the multi-microcylinder seam plate. As the gap to diameter ratio further increases, the negative pressure at the gaps decreases significantly, while the negative pressure at the microcylinders does not change much. The pressure loss of the front and rear surfaces at the gaps leads to a severe loss of drag in the entire multi-microcylinder seam plate. Consequently, the total drag becomes less than that of the seamless plate, resulting in a drag-reducing phenomenon.

Conclusion

In this study, a bionic structure that mimics the swimming hairs of the hind legs of the diving beetle was established, which has multiple micro-cylinders arranged in uniform gaps. Using the OpenFOAM open-source platform and employing the quasi-DNS method, the motion of this bionic structure in water was numerically simulated to investigate its drag characteristics. The following conclusions were drawn:

  1. (1)

    Under low flow velocity conditions, the multi-microcylinder seam plate exhibits excellent drag-increasing hydrodynamic performance. This indirectly demonstrates the advantage of swimming hairs, which can improve swimming propulsion efficiency while reducing the energy consumption of themself. The unique hydrodynamic performance of swimming hairs provides valuable insights for the propulsion of small underwater vehicles.

  2. (2)

    Variance analysis indicates that the micro-gap size and the gap to diameter ratio are the key factors influencing drag enhancement, while the effect of microcylinder diameter on drag characteristics is relatively weak.

  3. (3)

    The analysis of the drag characteristics of the multi-microcylinder seam plate shows that viscous drag is the primary source of the drag increase. When the viscous drag proportion ratio is less than 0.85, the viscous drag rapidly increases, while the pressure drag slowly decreases, enhancing the drag-increasing effect of the seam plate. When the ratio exceeds 0.9, both viscous drag and pressure drag rapidly decrease, causing the seam plate to quickly transition to a drag-reducing state.

  4. (4)

    Flow field analysis of the multi-microcylinder seam plate and the seamless plate shows that when the gap to diameter ratio is small, two velocity vortices form behind both types of plates. As the gap to diameter ratio increases, the vortices move downstream, become narrower, and weaken, indicating an increase in fluid passing through the gaps. With a further increase in the gap to diameter ratio, the flow field behind the plate gradually becomes more uniform, the gaps’ blocking effect weakens, and the seam plate loses its drag-increasing capability.

  5. (5)

    The analysis of flow field inside the gaps shows that when the gap to diameter ratio is small, the maximum velocity occurs at the narrowest part of the gap, indicating a strong restrictive effect of the gaps on the fluid, with little pressure fluctuation in front of and behind the plate. As the gap to diameter ratio increases, the ___location of the maximum velocity shifts backward, and the pressure fluctuation in front of and behind the plate becomes more pronounced, showing as the absolute value of pressure increases at the microcylinders and decreases at the gaps. The pressure loss at the gaps leads to a drag-reducing phenomenon in the multi-microcylinder seam plate.

  6. (6)

    According to the research results, the primary source of the drag increase in seam plates with multiple microcylinders is viscous drag. Therefore, the influence of plate thickness on the drag- increasing performance requires further investigation. As the flow velocity increases, the pressure drag on the plate also rises, and whether the plate will lose its drag-increasing capability remains an open question for future research.

Numerical simulation process and methods

Governing equations

This numerical simulation targets the flow process around multiple microcylinders arranged with uniform gaps, ensuring that the entire flow field satisfies the laws of mass conservation and momentum conservation. The governing equations for this simulation include the mass conservation Eq. (1) and the momentum conservation Eq. (2).

$$\frac{\partial \rho }{{\partial t}} + \frac{{\partial (\rho v_{x} )}}{\partial x} + \frac{{\partial (\rho v_{y} )}}{\partial y} + \frac{{\partial (\rho v_{z} )}}{\partial z} = 0$$
(1)
$$\begin{aligned} \rho \left( {\frac{{\partial v_{x} }}{\partial t} + v_{x} \frac{{\partial v_{x} }}{\partial x} + v_{y} \frac{{\partial v_{x} }}{\partial y} + v_{z} \frac{{\partial v_{x} }}{\partial z}} \right) & = \rho f_{x} - \frac{\partial p}{{\partial x}} + \mu \left( {\frac{{\partial^{2} v_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} v_{x} }}{{\partial y^{2} }} + \frac{{\partial^{2} v_{x} }}{{\partial z^{2} }}} \right) \\ \rho \left( {\frac{{\partial v_{y} }}{\partial t} + v_{x} \frac{{\partial v_{y} }}{\partial x} + v_{y} \frac{{\partial v_{y} }}{\partial y} + v_{z} \frac{{\partial v_{y} }}{\partial z}} \right) & = \rho f_{y} - \frac{\partial p}{{\partial y}} + \mu \left( {\frac{{\partial^{2} v_{y} }}{{\partial x^{2} }} + \frac{{\partial^{2} v_{y} }}{{\partial y^{2} }} + \frac{{\partial^{2} v_{y} }}{{\partial z^{2} }}} \right) \\ \rho \left( {\frac{{\partial v_{z} }}{\partial t} + v_{x} \frac{{\partial v_{z} }}{\partial x} + v_{y} \frac{{\partial v_{z} }}{\partial y} + v_{z} \frac{{\partial v_{z} }}{\partial z}} \right) & = \rho f_{z} - \frac{\partial p}{{\partial z}} + \mu \left( {\frac{{\partial^{2} v_{z} }}{{\partial x^{2} }} + \frac{{\partial^{2} v_{z} }}{{\partial y^{2} }} + \frac{{\partial^{2} v_{z} }}{{\partial z^{2} }}} \right) \\ \end{aligned}$$
(2)

where, ρ represents the fluid density/kg·m−3; t is the time/s; p denotes the pressure/pa; μ is the dynamic viscosity of the fluid/Pa·s; \(v_{x}\),\(v_{y}\) and \(v_{z}\) are the velocity components of the fluid at the point (x, y, z) at time t/m·s−1; \(f_{x}\),\(f_{y}\) and \(f_{z}\) are the components of the body force unit vector.

The paddling process of swimming hairs involve viscous incompressible three-dimensional flow. Direct numerical simulation of this process can yield precise dynamic data about the paddling, but the number of swimming hairs is large, with diameters ranging from 10 to 21 μm and gaps of approximately 6 to 23 μm. Although the area covered by the swimming hairs is not large, obtaining detailed information about the flow field around the hair requires refining the mesh in the regions of the hairs and gaps, resulting in an exceptionally large number of mesh elements in the computational ___domain. Therefore, it is necessary to simplify the paddling process reasonably. According to studies on the flow around two parallel cylinders19, when the Reynolds number Re < 200, the flow can be considered laminar and simplified to two-dimensional flow. For the diving beetle’s hind leg paddling, the linear velocity of the swimming hairs ranges from approximately 0.28 m/s to 0.54 m/s. According to Eq. (3), the Reynolds number Re < 15, indicating laminar flow. Thus, the process can be simplified to two-dimensional flow.

$${\text{Re}} = \frac{\rho vd}{\mu }$$
(3)

where ρ represents the fluid density/kg·m−3; v is the far-field velocity of the fluid/m·s−1; d is the characteristic length, taken as the diameter of the swimming hair/m; μ denotes the dynamic viscosity of the fluid/pa·s; At a temperature of 25 °C, the density and dynamic viscosity of water are 997 kg·m−3, 890.3 × 10–6 pa·s, respectively52.

Since the paddling process involves incompressible flow, ρ is constant. Additionally, as the process can be simplified to two-dimensional flow, the mass conservation Eq. (1) and the momentum conservation Eq. (2) can be simplified to Eqs. (4) and (5).

$$\frac{{\partial v_{x} }}{\partial x} + \frac{{\partial v_{y} }}{\partial y} = 0$$
(4)
$$\begin{aligned} \rho \left( {\frac{{\partial v_{x} }}{\partial t} + v_{x} \frac{{\partial v_{x} }}{\partial x} + v_{y} \frac{{\partial v_{x} }}{\partial y}} \right) & = \rho f_{x} - \frac{\partial p}{{\partial x}} + \mu \left( {\frac{{\partial^{2} v_{x} }}{{\partial x^{2} }} + \frac{{\partial^{2} v_{x} }}{{\partial y^{2} }}} \right) \\ \rho \left( {\frac{{\partial v_{y} }}{\partial t} + v_{x} \frac{{\partial v_{y} }}{\partial x} + v_{y} \frac{{\partial v_{y} }}{\partial y}} \right) & = \rho f_{y} - \frac{\partial p}{{\partial y}} + \mu \left( {\frac{{\partial^{2} v_{y} }}{{\partial x^{2} }} + \frac{{\partial^{2} v_{y} }}{{\partial y^{2} }}} \right) \\ \end{aligned}$$
(5)

In OpenFOAM, quasi-DNS is a high-accuracy numerical simulation method that directly solves the governing equations through time and space discretization to improve simulation accuracy. Therefore, the discretization schemes for time and space are critical components when performing quasi-DNS in OpenFOAM. In this study, the time discretization method adopted the Runge–Kutta method, while the space discretization was based on the finite volume method (FVM). The discretization method for the convection and diffusion terms adopted second-order central differencing. The pressure–velocity coupling solution method adopted PISO algorithm.

Moreover, numerical dissipation error is an unavoidable issue in quasi-DNS, primarily arising from the discretization scheme, mesh resolution, and time step selection. Numerical dissipation can affect the accuracy of the turbulence energy spectrum, flow statistics, and flow structures. To enhance simulation accuracy, all discretization schemes in this study employed high-order methods, and strict constraints were imposed on both mesh quality and time step (see details in the following contents).

Geometric model

To study the drag-increasing characteristics of the swimming hairs paddling process, we simplified the swimming hairs to microcylinders with a constant diameter. We established models of a seam plate and a seamless plate, both with identical shapes and sizes, to investigate the drag-increasing characteristics of the seam plate by comparing their drag forces. To ensure a sufficient number of microcylinders, and to avoid an excessively large number of mesh elements under the condition that the mesh size is small enough, the theoretical length of the plate was set to 800 μm, resulting in 6–43 microcylinders.

The seam and seamless plate models and their computational domains are shown in Fig. 10. Both models share the same computational ___domain and boundary conditions. Since the seam plate consists of microcylinders and microgaps arranged in sequence, and both the microcylinder diameter and microgap size are variable, it is difficult to ensure that the length of the seam plate is exactly 800 μm. Given the values of the microcylinder diameter and the gap to diameter ratio (gap size/microcylinder diameter), the relationship between the two parameters and the length of the seam plate is expressed in Eq. (6).

$$nd + (n - 1)\lambda d = L$$
(6)

where n represents the number of microcylinders, rounded to the nearest integer; d is the microcylinder diameter/μm; λ is the gap to diameter ratio; L is the theoretical length of the seam plate /μm.

Fig. 10
figure 10

Geometric models and computational domains. (a) Seamless plate model and computational ___domain; (b) seam plate model and computational ___domain.

Full size image

As shown in Fig. 10. By setting L = 800 μm, we can determine the number of microcylinders n using this equation, and then substituting n back into Eq. (6) yields the actual length of the seam plate La.

This length is close to 800 μm, with an error of ± 0.5d(1 + λ). The length of the seamless plate is also set to La. The dimensions of the fluid computational ___domain are 12 mm × 7.2 mm. The distance between the velocity inlet and the model is 4L, the distance between the pressure outlet and the model is 11L, and the distances from the rear and front walls to the model are both 4L. Preliminary trial calculations indicated that the walls had no impact on the flow field around the model, and the computational ___domain met the calculation requirements.

Computational ___domain mesh division and independence verification

The geometric model construction and computational ___domain meshing were performed using ICEM CFD 19.2. The mesh was generated according to the refinement rule shown in Fig. 11. The mesh size growth rates were set to 1.01 and 1.02 for distances of 0–1.5L and 1.5L–3L from the microcylinder, respectively. Beyond a distance of 3L, the mesh size remained constant in the inlet, front wall, and back wall directions. To capture the flow field behind the microcylinder, the computational ___domain was extended significantly longer downstream than upstream. To control the total number of elements, the mesh size growth rate was set to 1.03 in the range of 3L–4.5L downstream of the microcylinder, and beyond 4.5L, the mesh size remained unchanged. Since the multi-microcylinder seam plate consists of multiple microcylinders arranged in sequence, its model unit is the microcylinder. To ensure that the mesh around the microcylinders fit the model more closely, an O-block is established around each microcylinder, generating a layer of mesh in the circumferential direction and extending outward to form additional mesh layers. The mesh is dense and uniform, as shown in Fig. 12e.

Fig. 11
figure 11

Mesh refinement rules for the computational ___domain around the model.

Full size image
Fig. 12
figure 12

Computational ___domain mesh. (a) The mesh of the symmetric computational ___domain for the seam plate model; (b) the mesh of the symmetric computational ___domain for the seamless plate model; (c) mesh around the symmetric seam plate model; (d) mesh around the symmetric seamless plate model; (e) local mesh of the seam plate model; (f) local mesh of the seamless plate model.

Full size image

In general, the boundary layer thickness is around 200 μm, while the width of the gaps in the seam plate does not exceed 100 μm. Therefore, no boundary layer is added around the microcylinders. The computational ___domain meshes for the seam and seamless plate models, as well as the meshes around the models, are shown in Fig. 12. After mesh generation, mesh quality checks are performed, the overall mesh quality ranges from 0.93 to 1, with the aspect ratio between 1.1 and 18.8, the determinant between 0.75 and 1, the orthogonal quality between 0.64 and 1, and the skew between 0.53 and 1. Except for the aspect ratio, where lower values are generally preferable, the closer the other quality parameters are to 1, the better the mesh quality. Therefore, the mesh quality can be considered satisfactory, meeting the computational requirements.

Generally, while ensuring computational accuracy, it is important to control the number of mesh elements. Before dividing the mesh for the seam plate model, we conducted a mesh independence analysis. The computational ___domain mesh was refined according to the \(\sqrt 2\) growth principle. As shown in Fig. 13a–c represent sparse, medium, and dense meshes, with mesh counts of approximately 2.13 million, 3.05 million, and 4.34 million, respectively.

Fig. 13
figure 13

The seam plate model local mesh used for mesh independence analysis. (a) Sparse mesh; (b) medium mesh; (c) dense mesh.

Full size image

By setting the inlet velocities to 0.35 m/s and 0.6 m/s, numerical simulations were conducted using three different mesh densities. Selecting the viscous drag calculation results of the dense mesh as the true value, the relative errors of the viscous drag for the sparse and medium meshes were calculated, as shown in Table 4. The relative error of the viscous drag for the sparse mesh does not exceed 3%, and for the medium mesh, it does not exceed 1.3%. This indicates that the medium density mesh already provides sufficient computational accuracy. Therefore, the number of mesh elements in the computational ___domain is controlled to be around 3 million.

Table 4 Mesh independence analysis.
Full size table

Boundary conditions

The inlet is defined as a velocity-inlet with the velocity direction set to the positive Y-axis. The outlet is set as a pressure-outlet. The rear and front walls are set as symmetry plane. Since OpenFOAM supports only three-dimensional meshes, for two-dimensional calculations, the third dimension not involved in the computation needs to be set to empty. Therefore, the two walls in the Z-axis direction are set to empty. The model surfaces are set as no-slip walls. The convergence criterion is set to 10–6, and the simulation time is set to three times the fluid ___domain flow period. To ensure the convergence of the calculations, the time step is adjusted according to Eq. (7).

$$0.3\frac{\delta }{v} \le \Delta t{ < }\frac{\delta }{v}$$
(7)

where \(\Delta t\) is the time step/s; δ is the minimum mesh size/m; v is the fluid velocity/m·s−1.

Numerical simulation scheme

Inspired by the swimming hairs of the hind legs of the diving beetle, this study established a flat plate model with multiple microcylinders arranged evenly. To verify whether this kind of special structure possesses drag-increasing characteristics, a well-designed simulation scheme is required. The drags experienced by the seam plate with multiple microcylinders moving underwater mainly include pressure drag and viscous drag. The main influencing factors are the cross-sectional area of the seam plate, microcylinder diameter, microcylinder spacing, and water flow velocity. Given that the cross-sectional area of the seam plate is constant, a three-factor, second-order orthogonal rotational combination simulation scheme was designed, with the remaining three factors as the independent variables. The levels and codes of each factor are shown in Table 5.

Table 5 Levels and codes of the factors.
Full size table

This study conducts an analysis of variance on the drag increase rate (\(\varepsilon_{tf}\)), viscous drag increase rate (\(\varepsilon_{vf}\)), and pressure drag decrease rate (\(\varepsilon_{pf}\)) of the seam plate relative to the seamless plate to investigate the influence of each factor on these three mechanical parameters. These parameters are calculated using Eqs. (8)–(10). The simulation results of the mechanical parameters for each group are shown in Table 6. Due to the particularity of numerical simulations, it is impossible to conduct zero-level repeatability experiments. Therefore, values at different times within the last simulation cycle are selected as the results for the zero-level repeatability experiments.

$$\varepsilon_{tf} = \frac{{(G_{pf} + G_{vf} ) - (SL_{pf} + SL_{vf} )}}{{SL_{pf} + SL_{vf} }} \times 100\%$$
(8)
$$\varepsilon_{vf} = \frac{{G_{vf} - SL_{vf} }}{{SL_{pf} + SL_{vf} }} \times 100\%$$
(9)
$$\varepsilon_{pf} = - \frac{{G_{pf} - SL_{pf} }}{{SL_{pf} + SL_{vf} }} \times 100\%$$
(10)

where \(G_{pf}\) and \(G_{vf}\) are the pressure drag and viscous drag of the seam plate/N; \(SL_{pf}\) and \(SL_{vf}\) are the pressure drag and viscous drag of the seamless plate/N.

Table 6 Simulation results of drag for multi-microcylinder seam plate and seamless plate.
Full size table

To further elucidate the variation patterns in the drag of the seam plate, we designed three groups of comparative numerical simulations, as shown in Table 7. Detailed studies were conducted on the drag variation patterns, pressure fields, velocity fields, and the flow fields inside the gaps.

Table 7 Three groups of numerical simulations for comparative analysis.
Full size table