Introduction

In recent years, staggered segment lining has been widely applied in tunnel construction, serving as an effective measure to alleviate urban traffic congestion, in line with the rapid urbanization and escalating population density in cities. As joints exist, changes in the external environment can disrupt the equilibrium of staggered lining segments, causing deformation and internal force accumulation1. When these internal forces exceed the allowable stress levels of the concrete and bolts, separation and dislocation of tunnel segments may occur2,3,4, significantly reducing the tunnel’s load-bearing capacity and potentially leading to severe issues like lining cracks and water leakage5,6. These defects further deteriorate the overall structural performance7,8, posing a long-term risk to tunnel safety and operational integrity. Consequently, this issue has garnered considerable attention from researchers. However, given its underground ___location, staggered segmental tunnel linings experiences deformation due to soil pressure on the cross-sectional lining. The lining structure counters this deformation through its inherent stiffness and strength, resulting in an interaction with the surrounding soil. Existing studies have devoted limited focus to this crucial interaction.

Several studies have explored the deformation characteristics of interleaved segments under surrounding soil pressure, utilizing field investigations9,10, physical model tests11,12,13,14,15, numerical simulations16,17, full-scale tests18, and theoretical analyses19,20,21. Although field surveys and full-scale tests are deemed the most dependable, they face limitations due to complex construction environments22and constraints in size and cost23. Moreover, due to the complexity of boundary conditions and lining-soil interaction, it is extremely challenging to develop precise numerical models23 and rigorous analytical solutions for evaluating tunnel response under surrounding soil pressure. This limits the accuracy of numerical simulations and theoretical analyses.

On the whole, the physical model test stands out as a pivotal methodology in underground engineering research, offering a direct and effective means to assess tunnel structure deformation under surrounding soil pressure. Existing studies on lining-soil interaction can be broadly categorized into two approaches. The first category focuses on analyzing tunnel structure deformation or ground settlement through model soil prepared based on similarity criteria. For instance, Fang et al.11, for example, conducted model tests in sandy soil to explore how tunnel depth and surface volume loss affect surface settlement during tunnel construction, concluding that longitudinal surface settlement in sandy soil is linearly related to buried depth and surface volume loss. Hu et al.12 used aluminum as lining material and studied soil deformation around the model tunnel via micro-shield excavation and manual lining assembly, finding narrower surface settlement troughs in both transverse and longitudinal directions compared to clay or sandy soil, with the deformation zone width decreasing almost linearly with depth relative to underground deformation. The second category employs a ground spring model to account for confining pressure, such as Standing et al.13who used brass as lining material for the model tunnel and investigated single-ring lining mechanical properties with additional bolting. However, the first method is hindered by model testing apparatus size limitations, making it difficult to accurately reflect real-world buried depths and foundation reactions. The second method, studies predominantly focus on single-ring linings, with limited investigation of multi-ring staggered structural lining deformation under lining-soil interaction. Indeed, multi-ring linings exhibit distinct interaction forces, load distribution, and deformation characteristics compared to single-ring linings. Staggered segment linings, composed of prefabricated segments joined by bolts, often possess lower joint stiffness25,26,27, making them more prone to longitudinal factors like uneven settlement and dislocation deformation compared to uniform structures28,29,30. Moreover, these tests typically maintain constant surrounding pressure, which fails to accurately capture the dynamic interaction between lining and surrounding soil during deformation.

In summary, further investigation is warranted into the deformation characteristics of staggered lining segments under surrounding soil pressure. Given the limitations of current research, this study designed a physical model testing apparatus and a scaled down tunnel model for testing. The tunnel model comprises fifteen linings, each with six segments. Using similarity principles, resin material was employed to make the segments, connected by model bolts. Special springs were utilized to simulate soil pressure on the pipe section, reflecting the dynamic deformation interplay between soil and lining. The results were verified through numerical simulations. Furthermore, this study explored the transverse and longitudinal deformation of staggered lining segments under soil pressure, and their interrelations. The research results hold significant implications for the protection of pipe sections subjected to surrounding soil pressure.

Design of the test scheme

The loading conditions in this experiment are strictly static. The physical and mechanical parameters related to tunnel stress and deformation are listed in Table 1, with subscripts “s” and “b” denoting parameters for the segment and bolt, respectively. Geometric similarity and elastic modulus similarity are utilized as the primary similarity criteria30 in the design of the model tunnel. Force and length are chosen as the fundamental dimensions. Employing dimensional analysis, nine similarity criteria (π1 to π9) are derived, as detailed in Table 2.

Consider the elastic modulus similarity ratio (Cls=lsp/Dsm) and geometric similarity ratio (CEs=Esp/Esm) as fundamental. Based on similarity theory and the equal π values principle, Table 3 summarizes the derived similarity relationships. Herein, “p” represents the prototype, and “m” represents the model.

Table 1 Physical parameter.
Full size table
Table 2 Similarity criterion.
Full size table
Table 3 The general law of similarity of the model test.
Full size table

Design of segments

Based on statistical analysis of model tests reported in existing literature, as outlined in Table 4, the most commonly used lining size for urban subways has been selected. The dimensions feature an outer diameter of 6.2 m, an inner diameter of 5.5 m, and a thickness of 0.35 m. Each segment is made up of one fundamental, two adjacent, and three standard blocks. After comprehensive comparison and material performance tests, plexiglass was selected for the segment structure model due to its isotropic nature, high transparency, light weight, and superior tensile, bending, and compression properties at room temperature, as utilized in various studies1,30,37,38. The stress–strain curve of the segment material, obtained from tensile testing, is shown in Figs. 1 and 2, with Fig. 2 indicating an elastic modulus of 2.78 × 103 MPa for plexiglass.

Finally, as shown in Table 5, the relevant parameters of the model segment are summarized, based on the aforementioned preliminary preparations.

Table 4 Summary of tunnel model tests.
Full size table
Fig. 1
figure 1

Tensile test of segment material.

Full size image
Fig. 2
figure 2

Stress–strain curve of segment material.

Full size image
Table 5 Relevant parameters of model segment.
Full size table
Fig. 3
figure 3

Detailed diagram of model segment structure.

Full size image
Fig. 4
figure 4

Model tunnel and segments.

Full size image

Bolt design

The prototype tunnel is connected with 16 M30 bolts at ring joints and 12 M30 bolts at each longitudinal joint. The physical parameters of bolts include diameter (ld), length (lt), elastic modulus (Et), and Poisson ratio (µt). As per the geometric similarity ratio (Clt = 15.5), the stiffness ratio for joints in the prototype tunnel (αij)p is equivalent to that in the model tunnel (αij)m. Here, i = 1 denotes the lateral joint, i = 2 the longitudinal joint, j = 1 bending condition, j = 2 tensile condition, and j = 3 shear condition. The joint stiffness expressions are outlined in Table 6.

Table 6 Joint stiffness expression.
Full size table

According to Table 6, a calculation method that can simultaneously consider the bending similarity, shear similarity, and tensile (compressive) similarity at the joint is presented in this study.

The model tunnel consists of a total of a longitudinal and c transverse connecting bolts. These bolts have an elastic modulus of b× 104 Pa and a Poisson ratio denoted by d. As a result, the stiffness ratios at the joints can be determined for both the prototype tunnel (αij)p and the model tunnel (αij)m.

The stiffness ratio of the transverse joint can be expressed as follows:

$$\:\left\{\begin{array}{c}\frac{{\left({E}_{\text{s}}{I}_{\text{s}}\right)}_{\text{p}}}{{\left(n{E}_{\text{b}}{I}_{\text{b}}\right)}_{\text{p}}}=\frac{{\left({E}_{\text{s}}{I}_{\text{s}}\right)}_{\text{m}}}{{\left({n}^{{\prime\:}}{E}_{\text{b}}{I}_{\text{b}}\right)}_{\text{m}}}={\alpha\:}_{11}\\\:\frac{{\left({E}_{\text{s}}{A}_{\text{s}}\right)}_{\text{p}}}{{\left(n{E}_{\text{b}}{A}_{\text{b}}\right)}_{\text{p}}}=\frac{{\left({E}_{\text{s}}{A}_{\text{s}}\right)}_{\text{m}}}{{\left({n}^{{\prime\:}}{E}_{\text{b}}{A}_{\text{b}}\right)}_{\text{m}}}={\alpha\:}_{12}\\\:\frac{{\left({G}_{\text{s}}{A}_{\text{s}}\right)}_{\text{p}}}{{\left(n{G}_{\text{b}}{A}_{\text{b}}\right)}_{\text{p}}}=\frac{{\left({G}_{\text{s}}{A}_{\text{s}}\right)}_{\text{m}}}{{\left({n}^{{\prime\:}}{G}_{\text{b}}{A}_{\text{b}}\right)}_{\text{m}}}={\alpha\:}_{13}\end{array}\right.$$
(1)

where Is=bt3/12, Ib = πd4/64, As=bt, and Ab = πd2/4.

The stiffness ratio of the longitudinal joint can be expressed as follows:

$$\:\left\{\begin{array}{c}\frac{{\left({E}_{\text{s}}{I}_{\text{s}}^{{\prime\:}}\right)}_{\text{p}}}{{\left(n{E}_{\text{b}}{I}_{\text{b}}\right)}_{\text{p}}}=\frac{{\left({E}_{\text{s}}{I}_{\text{s}}^{{\prime\:}}\right)}_{\text{m}}}{{\left({n}^{{\prime\:}}{E}_{\text{b}}{I}_{\text{b}}\right)}_{\text{m}}}={\alpha\:}_{11}\\\:\frac{{\left({E}_{\text{s}}{A}_{\text{s}}^{{\prime\:}}\right)}_{\text{p}}}{{\left(n{E}_{\text{b}}{A}_{\text{b}}\right)}_{\text{p}}}=\frac{{\left({E}_{\text{s}}{A}_{\text{s}}^{{\prime\:}}\right)}_{\text{m}}}{{\left({n}^{{\prime\:}}{E}_{\text{b}}{A}_{\text{b}}\right)}_{\text{m}}}={\alpha\:}_{12}\\\:\frac{{\left({G}_{\text{s}}{A}_{\text{s}}^{{\prime\:}}\right)}_{\text{p}}}{{\left(n{G}_{\text{b}}{A}_{\text{b}}\right)}_{\text{p}}}=\frac{{\left({G}_{\text{s}}{A}_{\text{s}}^{{\prime\:}}\right)}_{\text{m}}}{{\left({n}^{{\prime\:}}{G}_{\text{b}}{A}_{\text{b}}\right)}_{\text{m}}}={\alpha\:}_{13}\end{array}\right.$$
(2)

where Isʹ = π(D4-r4)/64, Ib = πd4/64, Asʹ = bt, and Ab = πd2/4.

The similarity ratio βij for tensile (compressive), bending, and shear stiffness between the model tunnel and prototype tunnel bolt joints is determined by (αij)p/(αij)m. Ensuring an equal similitude ratio for various physical quantities in model tests is vital, yet achieving this in practice can be difficult. Studies by Ye et al.37and Guo39 suggest that if βij exceeds 80%, the joint stiffness similarity between the models meets the testing requirements. In this study, to guarantee consistent and significant physical quantities, the joint stiffness similarity exceeds 85%. The βij results were obtained using Eq. (3), as shown in Table 7. Thus, the method adopted in this study effectively meets the design criteria for bending, shear, and tensile (compressive) similarity of joints.

$$\:{\beta\:}_{\text{i}\text{j}}=1-\frac{\left|{\left({\alpha\:}_{\text{i}\text{j}}\right)}_{\text{p}}-{\left({\alpha\:}_{\text{i}\text{j}}\right)}_{\text{m}}\right|}{{\left({\alpha\:}_{\text{i}\text{j}}\right)}_{\text{m}}}$$
(3)
Table 7 Results of joint similarity.
Full size table

To guarantee bolt connections between adjacent segments of the model tunnel, while taking into account practicality and ease of segment assembly, six longitudinal and one lateral connection bolt were selected. These bolts have dimensions that satisfy 3.28 ≤ b ≤ 4.51 and 2.33 ≤ b/(1 + d) ≤ 3.39. For the model test, pure aluminum wire (HS301) was chosen as the bolt material30,38. The photos of model bolt and design parameters are shown in Fig. 5; Table 8, respectively.

Fig. 5
figure 5

The setting of the staggered lining bolt.

Full size image
Table 8 Related parameters of bolt.
Full size table

Design of loading device reflecting soil–segment interaction

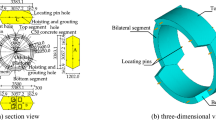
The test device comprises a loading system and a reaction frame, as depicted in Fig. 6. The loading system includes 15 steel rings, each with an inner diameter of 0.57 m and an outer diameter of 0.70 m. These rings are welded to six steel channels, all matching the width of segment. These channels are equipped with specialized equipment to simulate soil pressure, including a full-thread screw (ϕ20 × 100 mm), spring, gasket, plexiglass sleeve, and pressure sensor, as depicted in Fig. 7.

During the test, the screw rotates to compress the spring, transmitting the compressive force to the segment in a stepwise manner to simulate confining pressure from surrounding soil. An outer sleeve surrounds the spring to ensure vertical deformation and prevent displacement when pushed by the bolt head, ensuring accurate force transmission. Additionally, each steel ring features six displacement meters to measure lining ring deformation and longitudinal joint dislocation. The spring-segment interaction produces deformations that reflect segment-soil interaction during lining ring convergence.

Fig. 6
figure 6

Photos of the equipment.

Full size image
Fig. 7
figure 7

Single ring loading device.

Full size image

In designing spring elements, the soil foundation bed coefficient for practical engineering is first determined. Subsequently, using similarity theory, the elastic coefficient required for the model test springs is calculated. The analytical formula for the foundation reaction coefficient of a long beam on the surface, derived by Attewell40 is employed and listed in Table 9. Initially, the actual engineering foundation coefficient is computed to determine the size and stiffness of the springs in the loading element. Then, based on similarity theory, the ratio of the elastic coefficient between actual engineering and the model is obtained. From this ratio, the model tunnel’s foundation coefficient is inversely derived, considering the actual project’s foundation coefficient. Finally, the spring size and stiffness are designed accordingly.

Table 9 Spring parameters.
Full size table

Meanwhile, Kmt can be expressed as:

$$\:{K}_{\text{m}\text{t}}=\frac{G\times\:{d}_{\text{m}}^{4}}{8\times\:{N}_{\text{c}}\times\:{D}_{\text{m}}^{3}}$$
(4)

where G is the shear modulus of steel wire, typically 70,000 MPa; dm is the diameter of the steel wire in mm; D0 is the outer diameter of the spring in mm; Dm is the middle diameter of the spring in mm; N is the total number of spring coils; and Nc is the number of effective spring coil, N− 2.

The design parameters of the spring can be obtained from Table 8 and Eq. (4), as shown in Table 10.

Table 10 Spring design parameters.
Full size table

Loading test scheme

Confining pressure design

The surrounding soil pressure of a single-segment prototype tunnel was obtained based on an actual project in Zhengzhou, China, as shown in Table 11.

Table 11 Surrounding soil pressure of single segment of prototype tunnel.
Full size table

According to the theory of similarity, it can be inferred that:

$$\frac{{F}_{\text{c}\text{p}}}{{F}_{\text{c}\text{m}}}={C}_{\text{E}\text{c}}{C}_{\text{l}\text{c}}^{2}$$
(5)
$${P}_{K}=\frac{{F}_{\text{m}\text{K}}}{{A}_{\text{t}}}$$
(6)

According to Table 9, the concentrated forces on the outboard of the K and B blocks of the prototype segments are 124.1 kN and 372.3 kN, respectively. The initial surrounding soil pressures PK and PM on the outboard of the corresponding blocks of the model segments, calculated using Eqs. (5) and (6), are 34 kPa and 99 kPa, respectively. As shown in Fig. 7, the area At of the test loading platform is 1.26 × 10−3m2. During testing, the spring pressures were calibrated to match the theoretical values by simultaneously rotating the screws on the springs of the 15 steel rings.

Loading progress

An additional load was applied to the bottom sealing block of the eighth ring in this test, as shown in Fig. 7. During the loading process, no adjustments were made to the bolts on the steel rings. The maximum generalized extra load was set at 600 N, incrementally increased in six steps, each lasting at least 10 min. The next load level was applied once the data change rate under the current load was less than one-hundredth of that in the previous step30. Each lining segment is equipped with ten displacement meters in total. Specifically, the displacement meter at the crown records the vertical displacement and ring joint dislocation, while the one inside the lining assesses the convergence deformation. Paired displacement meters at the longitudinal joints measure the longitudinal joint dislocation.

Monitoring arrangement

The measurements in this test encompass the crown vertical displacement Vd, convergence deformation C, ring joint dislocation CJ, and longitudinal joint dislocation LJ of the staggered assembled model tunnel, as illustrated in Fig. 8, under the combined effects of an additional load and confining pressure. Due to space constraints within the K block steel frame, installation of displacement meters in that area was not feasible. Along the model longitudinal direction of tunnel, rings numbered 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15 were monitored for vertical displacement, rings numbered 3, 5, 7, 8, 9, 11, and 13 were monitored for convergence deformation and longitudinal joint dislocation. Circumferentially, longitudinal joint dislocation was measured at positions 101.25°, 168.75°, 236.25°, and 303.75° from the tunnel crown clockwise, as depicted in Fig. 9(a). For the eighth odd-numbered lining rings, measurements were taken at positions 56.25°, 123.75°, and 258.75° on the ring, as shown in Fig. 9(b). The detailed layout, numbering, and quantity of monitoring points are outlined in Table 12.

Fig. 8
figure 8

Monitoring of tunnel deformation.

Full size image
Fig. 9
figure 9

Monitoring of longitudinal joint dislocation.

Full size image
Table 12 Content of monitoring.
Full size table

Test results

Verification of test results

Establishment of numerical model

The prototype tunnel was modeled using the finite element analysis software ABAQUS, as depicted in Fig. 10. This three-dimensional discontinuous finite element model of the shield tunnel comprises multiple parts connected by bolts. For simplicity, gaskets and grooves were excluded, and solid elements were used to build the segments and bolts. The seam contact primarily encompasses surface-to-surface and embedded contacts between concrete and bolts. These contacts exhibit normal and tangential interactions, governed by hard contact and penalty function-based relations, respectively. Friction parameters, with a coefficient of 0.5, simulate realistic deformation behavior41. Surrounding soil pressure is represented by uniform pressure distribution around the tunnel. This study aims to predict tunnel deformation during normal operation, hence employing elastic constitutive modeling for analysis. Considering segment configuration and bolt dimensions, the model employs C3D8R eight-node linear solid elements, with each node having three degrees of freedom.

Fig. 10
figure 10

Numerical analysis model.

Full size image

Material parameter

The finite element model consists of concrete segments—standard blocks (67.5°), adjacent blocks (67.5°), and keystones (22.5°)—along with connecting bolts. These components are the primary stress-bearing elements during tunnel deformation. Hence, when selecting the constitutive model, material nonlinearity must be thoroughly considered. Additionally, computational efficiency and convergence are essential factors. In this study, elastoplastic models are employed for both segments and bolts38. The calculation parameters for each component are outlined in Tables 5 and 8.

Loading conditions and boundary constraints

Considering the specific engineering scenario, the cover layer was determined to have a thickness of 5 m and an average unit weight of 17 kN/m³. The initial soil pressure state without longitudinal deformation was used to calculate tunnel lining loads (P1, P2, …, P5), as shown in Table 13. This load distribution is depicted in Fig. 11. To mimic external loads on the structure, concentrated loads are applied at specified points on the tunnel’s exterior, mimicking the arc-shaped pad from the model test. This load increase linearly until the tunnel reaches its ultimate capacity. Furthermore, displacement constraints are imposed at both tunnel ends, restricting X, Y, and Z displacements on the first and fifteenth ring surfaces of segments to zero.

Fig. 11
figure 11

Calculation model for soil pressure and surrounding stress field of tunnel.

Full size image
Table 13 Soil pressure acting on tunnel.
Full size table

Comparison of numerical simulation results with test results

The numerical results are compared with the maximum values derived from experimental data. During this comparison, the model test measurement results are scaled up according to the geometric similarity ratio to match those of the prototype tunnel.

The vertical displacement comparison is depicted in Fig. 12, showcasing substantial alignment between numerical simulation results and experimental data. For the 8 th ring lining, the difference between test results and numerical simulation is about 0.51 mm. The maximum discrepancy, occurring in the 7 th ring, is approximately 1.75 mm.

The comparison of convergence deformation is depicted in Fig. 13, where numerical simulation results show substantial accord with experimental data. For the 8 th ring lining, the difference between test results and numerical simulation is approximately 0.92 mm. The maximum discrepancy, occurring in the 3rd ring, is around 3.01 mm.

In summary, the experimental results align well with the numerical simulation outcomes, thereby confirming the reliability of the experimental findings.

Fig. 12
figure 12

Comparison of vertical displacement results.

Full size image
Fig. 13
figure 13

Comparison of convergence deformation results.

Full size image

Deformation of linings

The data from this test were normalized, and the pertinent parameters are presented in Table 14. Notably, Fi/F1 represents the ratio of the load at the ith level to the load at the first level, where i = 1,2,3… For instance, if the load at the sixth level is 600 N and the load at the first level is 100 N, then F6/F1 = 6. Variations in test results at identical positions during loading may stem from assembly errors, manual screw rotation inaccuracies for spring compression, and friction between the model lining and reaction frame.

Table 14 Relevant parameters of test data.
Full size table

Under additional loads, the staggered segmental tunnel linings structure undergoes material deformation, including nonlinear behavior under high loading and physical deformations like misalignment and opening. Generally, the staggered segmental tunnel linings structure experiences minimal material deformation under external loads, much less than the deformation caused by joint displacements. Consequently, joint displacements are primarily used to assess the bearing capacity of staggered segmental tunnel linings structure. In other words, if substantial material deformation occurs in the pipe section under external forces, this signifies considerable deformation of the joints in the staggered segmental tunnel linings structure, thereby markedly reducing its load-bearing capacity. In summary, most existing studies have overlooked the deformation of the material itself under external loads1,30,37,42,43.

Deformation of loading ring

The variations in vertical displacement at the crown and bottom, vertical convergence deformation, and ring joint dislocation on both sides of the segment at the tunnel crown are depicted in Fig. 14. As the load increases, the tunnel bottom vertical displacement under additional loads becomes more significant than that of the crown, with this difference widening linearly. Additionally, for each load increment, the bottom vertical displacement increase surpasses that of the tunnel crown. The ratios C/Vd and C/B slightly rise throughout loading. Under hierarchical loading conditions, slight variations in ring joint dislocation are observed between the eighth ring and its adjacent seventh and ninth rings at the crown. Both curves feature two inflection points at varying load levels.

Fig. 14
figure 14

Deformation characteristics of the eighth ring lining under extra loads.

Full size image

Deformation of rings along the longitudinal direction

The vertical displacement in tunnel crown, convergence deformation, and tunnel crown ring joint dislocation for each lining segment along the tunnel longitudinal direction during staged loading are depicted in Figs. 15, 16 and 17. With the tunnel center serving as the origin of the horizontal coordinate system, the distance (H) from the loading point is normalized to the width of segment (W), denoted as H/W. Similarly, for vertical coordinates, the vertical displacement (Vd) and vertical convergence deformation (C) are normalized to the tunnel outer diameter (D), expressed as Vd/D and C/D, respectively. Moreover, the ring joint dislocation (CJ) is normalized by the lining thickness (T), represented as CJ/T.

The vertical displacement of the tunnel displays normal distribution. Below a load of 100 N, the displacement remains negligible, peaking at 0.2(10−4) D. As the load intensifies, the vertical displacement rises sharply. Notably, for all rings except the eighth, a nonlinear distribution emerges in both vertical displacement and crown ring joint dislocation with increasing additional load. For example, at H/W = 0, as the load increases from 100 N to 600 N, the displacement increases nearly linearly: 0.28(10−4) D, 0.28 (10−4) D, 0.39(10−4) D, 0.40(10−4) D, and 0.40(10−4) D, respectively. In contrast, at H/W = 2.0, the displacement increases nonlinearly: 0.14(10−4) D, 0.05(10−4) D, 0.21(10−4) D, 0.28(10−4) D, and 0.49(10−4) D, aligning with the research of Ding et al.1. This indicates that the inter-ring shear force, primarily driving non-loading point lining ring displacement, progressively enhances the transfer effect between rings as the load increases.

The analysis of ring joint dislocation in the staggered segmental tunnel linings shows that at the loading point, the dislocation is notably higher than in other rings, and this disparity becomes more pronounced with increasing load. Greater ring joint dislocation indicates higher shear forces on the bolts. Thus, under extra loading, closely monitoring the performance of ring joint bolts in the loaded lining is crucial.

The results of the convergent deformation analysis show a linear decrease in deformation from the loading position towards both sides. As the load rises, each measurement point exhibits an approximately linear growth trend in deformation. Due to the surrounding soil pressure on the tunnel crown, crown displacement is constrained, leading to a notable increase in lining convergence deformation relative to vertical displacement. Additionally, when compared to existing experimental studies without surrounding soil pressure1, the convergent deformation observed in this study is relatively smaller, indicating that the surrounding soil pressure effectively reduces the elliptical deformation of the lining edges.

The fitting outcomes for the vertical displacement and convergence deformation are displayed in Table 15. The correlations between H/D, Vd/D, and C/D are depicted by exponential and linear functions, respectively. The coefficients a1, b2, a2, b1, and Fi/F1 are approximated as nonlinear (with a1 and Fi/F1 being quadratic polynomial functions, and b2 being exponential), while a2 and b1 are linear. These functional relationships can be employed to estimate missing values in practical engineering scenarios, like vertical displacement of tunnel crowns or bottoms in contact with truncated pile ends, as observed in a viaduct shield machine cutting pile project. This monitoring provided data for calculating F (the additional external force exerted by the truncated pile end on the segment) and convergence deformation. Note that the fitting function relationships outlined in Table 15 are based on specific conditions and may require further refinement through additional engineering research. Ring joint dislocation signifies the vertical displacement variance between adjacent lining, measurable by monitoring each tunnel crown vertical displacement.

Fig. 15
figure 15

Vertical displacement distribution curve along the longitudinal direction of the tunnel.

Full size image
Fig. 16
figure 16

Ring joint dislocation distribution curve along the longitudinal direction of the tunnel.

Full size image
Fig. 17
figure 17

Convergence deformation distribution curve along the longitudinal direction of the tunnel.

Full size image
Table 15 Fitting function.
Full size table

Longitudinal joint dislocation

Distribution characteristics of longitudinal joint misalignment in a circular direction

The longitudinal joint dislocation distribution of the eighth ring lining subject to extra load is depicted in Fig. 18. As the load intensifies, LJ1 at 258.75° displays a linear growth trend, whereas LJ3 at 123.75° and LJ4 at 56.25° exhibit nonlinear growth. Since LJ3 is located in the segment directly impacted by the load, its value surpasses those of LJ1 and LJ4. For example, at a load of 600 N, LJ3 is roughly 2.48 times and 1.72 times larger than LJ1 and LJ4, respectively, with a notably faster rate of increase. Considering the positions of LJ3 and LJ4, special attention should be given to joint deformation at the loading point and adjacent lining segments when extra loads are applied to the staggered segmental tunnel linings. Additionally, the longitudinal joint dislocation results show that for segments directly loaded, shear transfer diminishes progressively from the tunnel bottom to the tunnel crown.

Longitudinal joint dislocation can significantly impair joint performance and jeopardize structural safety, necessitating its monitoring. In practical projects, monitoring each longitudinal joint dislocation within a lining ring is often challenging, and in more constrained projects, even measuring a single dislocation can be difficult. Therefore, for projects allowing partial longitudinal joint dislocation measurement, the dislocation of other joints can be estimated by establishing relationships among segments within the ring, using one dislocation of segment dislocation as a baseline. For projects where direct measurement is infeasible, vertical convergence measurements can be employed to estimate the dislocation of each longitudinal joint. Based on this concept, Fig. 19 presents correlations between longitudinal joint dislocation and convergence deformation under various loads, and the relationship between LJ3/LJ1 and LJ4/LJ1 during loading, using LJ1 as a reference. Analysis results show that LJ1, LJ3, and LJ4 positively correlate with loading and convergence deformation. However, the ratios LJ3/LJ1 and LJ4/LJ1 initially decline but later increase as loading and convergence deformation values rise.

Fig. 18
figure 18

Distribution curve of longitudinal joint dislocation of the eighth lining under a graded load.

Full size image
Fig. 19
figure 19

Variation in longitudinal joint dislocation of the eighth lining under a graded load.

Full size image

Longitudinal joint dislocation under maximum load

The distribution of longitudinal joint dislocation in the odd-numbered lining segments under the maximum additional load is depicted in Fig. 20. Similar to the longitudinal fault stage distribution in Fig. 18, LJ3, being directly impacted by longitudinal loads, exhibits notably larger dislocations compared to other positions. The self-load application points for longitudinal faults decrease clockwise: LJ3 (168.75°) > LJ2 (236.25°) > LJ1 (303.75°) > LJ4 (101.25°). Segments directly under the load show more pronounced longitudinal joint faults than adjacent ones, specifically, at H/W = 1, LJ2 is roughly 88% of LJ3, and LJ4 is about 30% of LJ3. This difference stems from the direct load impact on the bottom segment of the lining arch, contrasting with deformation-induced displacement in adjacent segments. Segments near the loading points (H/W = 1 and H/W = − 1) have the largest longitudinal joint faults. Odd-numbered rings at the same lining position, distant from the loading point (H/W = 0), exhibit approximately equal longitudinal faults, for instance, H/W = 3 and H/W = − 3 are nearly equivalent. Moreover, the longitudinal fault stage decreases nonlinearly towards both tunnel sides: as H/W increases from 1 to 2, LJ3 decreases by about 74.81 μm, and from 2 to 3, it decreases by around 40.58 μm.

Additionally, by real-time tracking and monitoring longitudinal joint dislocation at specific positions on each lining, as per the analysis concept in Sect. 3.3.1, additional data on joint dislocation at various lining positions can be obtained. If validated through extensive applications in adjacent shield tunnel projects, this method could significantly reduce segment longitudinal joint dislocation in affected areas without increasing risks, especially in shield machine-based viaduct pile cutting projects. The test compared LJ2, LJ3, LJ4with LJ1, as illustrated in Fig. 21, to explore the relationship between longitudinal joint dislocation of each lining and their longitudinal distribution. Results showed LJ4/LJ1 and LJ2/LJ1 remained constant, while LJ3/LJ1 increased symmetrically and nonlinearly along the longitudinal direction of tunnel.

Fig. 20
figure 20

Distribution curve of longitudinal joint dislocation of odd ring under the maximum extra load.

Full size image
Fig. 21
figure 21

Proportional relationship between longitudinal joints on odd ring under maximum extra load.

Full size image

Discussions and conclusions

The staggered segmental tunnel linings structure, made up of segments and bolts, boasts significantly less joint stiffness than the segments themselves. Under usual circumstances, when exposed to surrounding soil pressure, the joints are more likely to deform than the segments, causing physical distortions like dislocation and convergence within the staggered segmental tunnel linings structure. These deformations can lead to lining cracks, leaks, and other issues. To analyze the deformation characteristics of the staggered segmental tunnel linings structure under surrounding rock pressure, a multi-ring staggered segmental tunnel linings loading device was designed, considering the impact of surrounding soil pressure. The surrounding soil pressure is commonly modeled as a foundation spring across various theoretical frameworks, such as the equivalent continuous model44,45and beam-spring model46, shell-spring model47, and load-structure model48,49. Based on these frameworks, a specialized spring element is designed to simulate the soil pressure on the lining. Unlike prior studies focusing on single-ring lining structures, this device holistically reflects the co-deformation of lining and soil during tunnel excavation as external conditions evolve. Compared to existing research on multi-ring lining structures, it more precisely obtains the interaction forces, load transfer, and deformation features. Furthermore, due to urban sprawl often necessitating new facility construction near or directly above existing staggered segment linings, such as pile foundations50,51,52, foundation pits53,54,55, and tunnels56,57,58, these new structures often impose extra loads on the staggered linings. Hence, this study includes an extra concentrated load to simulate potential loads from new facility construction.

The test results reveal that when an external concentrated load impacts the surrounding soil and interlaced lining, the vertical displacement, dislocation, and convergence deformation of the directly affected ring are notably larger than those of other rings. As the load intensifies, the vertical displacement and convergence deformation show roughly linear growth, whereas lining deformation at other positions increases nonlinearly. The longitudinal joint dislocation diminishes progressively from the loading point to the tunnel crown, maintaining a consistent distribution pattern along the tunnel. These relationships offer useful reference and predictive understanding for deformation behavior in staggered segmental tunnel linings structure, particularly in projects with limited monitoring.

In this study, valuable optimization potential exists for both the test device and the testing procedure. When applying surrounding rock pressure, controlling the contact between the pressure sensor and spring is difficult, especially due to the spring’s high stiffness, complicating manual loading of confining pressure. Future research aims to employ a linkage loading device to resolve these issues. Moreover, the current test employs 2 mm diameter bolts, leading to minor preload during assembly and introducing errors in test results. In future studies, bolts with greater stiffness will be used to overcome this limitation. Due to test condition constraints, the stress and deformation state of the bolts were not analyzed. Future research will develop micro-stress testing elements for a comprehensive analysis of bolt behavior.