Introduction

The impact of reflection dispersion resulting from mesoscopic flow is significant and deserves attention, as conventional quantitative seismic interpretations can be misleading. Local flow-induced phase variations may introduce uncertainty in the seismic imaging of geological formations. The implications of reflection dispersion for characterizing heterogeneous reservoir rocks are promising, suggesting the potential to utilize frequency-dependent seismic attributes to uncover geological heterogeneity and fluid mobility characteristics. In various geological contexts, multiple distinct fluids can partially saturate porous rocks. In the upper sections of gas-capped reservoirs, gas, oil, and brine often coexist within the available pore space. Additionally, contaminants can infiltrate subterranean aquifers. Groundwater levels may fluctuate due to earthquakes, and subsequent aftershocks are associated with changes in pore fluid distribution. To effectively interpret seismic data for hydrocarbon detection, monitor saltwater intrusion into groundwater aquifers, or analyze reported earthquake waveforms, it is essential to understand how partial fluid saturation influences elastic wave propagation.

The comprehensive model for elastic wave propagation in porous, fluid-saturated media is described by Biot’s equations, as outlined in1,2,3. These equations were formulated using the Lagrangian approach, which defines generalized coordinates based on the average displacements of both solid and fluid components. A dissipation function, dependent on the relative velocity between the solid and liquid phases, was integrated into this framework. In the static or low-frequency limit, Biot’s equations reduce to Gassmann’s equation4, which determines the undrained static bulk modulus of porous materials by considering the properties of the dry framework and the saturating fluid. Both sets of equations assume a single Newtonian fluid (liquid or gas) saturating the porous medium. Subsequent studies have reproduced Biot’s equations using alternative mathematical methods, including volume averaging techniques proposed by Pride et al.5 and homogenization approaches for periodic structures6,7,8. These methods yield similar macroscopic equations, thereby validating Biot’s original formulation. Recently, numerous fluid flow problems have been addressed by researchers and published in the open literature (see Babu et al.9, Zhao et al.10, Kommaddi et al.11, Kodi et al.12 -13).

Biot’s theory, however, is limited to fully saturated media containing a single fluid. Modeling wave propagation in porous materials with multiple immiscible fluids presents significant challenges. Immiscibility refers to the property of fluids that prevents them from mixing, resulting in distinct boundaries between different fluids14. Porous rock formations, such as sandstone, limestone, and shale, can be saturated with various pore fluids, including gas, water, and oil. Since the 1960s, researchers have increasingly focused on elastic wave propagation in partially saturated media. Brutsaert15 pioneered the extension of Biot’s theory by employing mixture theory to account for the effects of two immiscible pore fluids on elastic wave propagation. This mixture theory approach, initially developed for two-fluid systems, has since been refined and expanded by numerous researchers (Brutsaert and Luthin16; Bedford and Drumheller17; Garg and Nayfeh18; Berryman et al.19; Santos et al.20,21; Corapcioglu and Tuncay22; Tuncay and Corapcioglu23; Wei and Muraleethara24,25; Hanyga26; Lu and Hanyga27; Lo28; Lo et al.29). In materials with voids occupied by two immiscible fluids, capillary forces become significant, leading to the prediction of a third compressional wave, specifically a second slow wave. These slow waves are present and attenuate the primary compressional wave through mode conversion. Multiphase poroelasticity theory reveals the existence of four elastic wave modes: three longitudinal waves and one shear wave, which are solutions to coupled differential equations of motion. The extensive analysis of wave propagation in porous materials containing multiphase fluids is credited to Corapcioglu and Tuncay22 as well as Tuncay and Corapcioglu23. Lo et al.30 formulated a complex set of interconnected partial differential equations to elucidate the propagation of dilatational waves in an elastic porous medium containing two immiscible fluids. These equations illustrate the behavior of acoustic waves in porous media with multiple fluid phases, enhanced by the fundamental principles of poroelasticity. Lo et al.31 analyzed various types of dilatory motion by determining the normal coordinates for the three longitudinal waves. They derived equations that describe the relationship between the modes of motion and the saturation level. The hydrologic models of subsurface multiphase flow discussed earlier do not account for the impact of viscous resistance caused by the relative velocity of two adjacent fluids on the behavior of elastic waves in partially saturated porous media. Lo et al.32 introduced a mathematical model that utilizes continuous mixture theory to address the viscous cross-coupling between two immiscible pore fluids. Consequently, all the models mentioned above can be derived as specific instances of this framework. Furthermore, if only one fluid is present in the medium, this model can be simplified to Biot’s theory1,2. The mathematical model established by Arora et al.33 examined wave propagation in a porous medium composed of two solids saturated with two immiscible fluids. The equations for complementary energy and the linear stress-strain relationships of the medium were developed using the concept of virtual complementary work. The Lagrangian motion equation generates a network of interrelated partial differential equations. Xiong et al.34 analytically demonstrated that the model presented by Tuncay and Corapcioglu23, utilizing the volume averaging method, may exhibit instability due to potential structural deficiencies in the wave equations. To address this issue, they established an innovative mathematical framework for wave propagation in partially saturated porous media based on their findings.Wang et al.35 provide a modeling framework designed to simulate wave propagation in heterogeneous, partially saturated porothermoelastic materials. Sun et al.36 presented wave equations for the Biot-patchy-squirt mechanism based on Lagrangian equations, mass conservation equations, and constitutive equations for double-porosity media. For partially saturated porous media, Solazzi et al.37 developed an analytical model to calculate frequency-dependent relative permeability functions that account for viscous coupling effects. Deng et al.38 established a methodology for assessing compaction and monitoring liquefiable soils in mine dumps with fluctuating saturation due to rising groundwater levels. The behavior of waves propagating in non-isothermal poroelastic materials saturated with two-phase fluids was described by a model presented by Santos et al.39. The dynamic differential equations incorporate poroelasticity and heat equations, which integrate the solid, fluid, and thermal fields through coupling terms. A plane wave analysis demonstrated that five distinct waves could propagate.

As seismic waves propagate through rocks, they create pressure differentials at various depths, inducing fluid motion. Wave-Induced Fluid Flow (WIFF) can be classified into three categories based on pressure gradient length scales: mesoscopic, global, and squirt flows. The relationship between wave dispersion and attenuation across a broad frequency spectrum is closely linked to the WIFF process. Developing theoretical models that connect multiscale WIFF with wave propagation may enable the establishment of quantitative characteristics and precise assessments of reservoirs. The WIFF induced by waves is a primary factor contributing to wave dispersion and attenuation, which is significantly influenced by pore structure, fluid properties, and rock type (Yao et al.40; Müller et al.41; Quintal et al.42; Khalid and Ahmed43). However, this critical mechanism is not considered in all the multiphase fluid models mentioned in the previous paragraph. Recognizing the significance of this mechanism, Shi et al.44 introduced a rock seismic model that incorporates three wave-induced fluid flow (WIFF) processes at varying scales, from the size of pores to the wavelength. The model examines a three-phase porous medium that includes two immiscible fluids within its pores. Shi et al.44 focused exclusively on the dispersion and attenuation of seismic waves-specifically, velocity and attenuation-resulting from WIFF in unsaturated porous media. Reflected seismic data is frequently employed in exploratory geophysics to evaluate rock properties such as porosity, fluid saturation, and permeability. Therefore, we extend the study by Shi et al.44 to investigate wave-induced fluid dynamics and the characteristics of seismic wave reflection in partially saturated porous media. First, we present a mathematical model for the propagation of a planar harmonic wave. The solution to the Christoffel equation reveals the presence of four waves in the medium: three compressional waves and one shear wave. Additionally, we calculate the poroelastic reflection coefficients from the boundary surface of sealed holes in porous media at various angles. These poroelastic reflection coefficients are subsequently utilized to compute wave-induced fluid flow and to separate energy contributions. We examine the behavior of energy share curves and wave-induced fluid flow (WIFF) curves at different frequencies of incident waves and angles of incidence, as well as elastic parameters such as porosity, inclusion radius, and liquid saturation. The numerical results demonstrate a significant dependence of energy shares of distinct reflected waves on the incident direction, saturation, porosity, inclusion radius, wave frequency, and WIFF.. The findings of this study fill a critical gap in understanding how these factors influence the propagation of seismic waves in unsaturated porous media, which is essential for reservoir interpretation, physical property inversion, and sediment type classification.

Field equations and constitutive relations

Following Shi et al.44, the equations of motion in the absence of body force for each particle in an unsaturated porous solid are as follows:

$$\begin{aligned} \sigma ^{(0)}_{ij,j}= & \rho _{11}\ddot{u}_i+\rho _{12}\ddot{U}_{i}^{(1)}+\rho _{13}\ddot{U}_{i}^{(2)}-(m_1-m_{12})(\dot{U}_{i}^{(1)}-\dot{u}_i)-(m_2-m_{12})(\dot{U}_{i}^{(2)}-\dot{u}_i),~~~~~\end{aligned}$$
(1)
$$\begin{aligned} \sigma ^{(1)}_{,i}= & \rho _{12}\ddot{u}_i+\rho _{22}\ddot{U}_{i}^{(1)}+\rho _{23}\ddot{U}_{i}^{(2)}+m_1(\dot{U}_{i}^{(1)}-\dot{u}_i)-m_{12}(\dot{U}_{i}^{(2)}-\dot{u}_i),\end{aligned}$$
(2)
$$\begin{aligned} \sigma ^{(2)}_{,i}= & \rho _{13}\ddot{u}_i+\rho _{23}\ddot{U}_{i}^{(1)}+\rho _{33}\ddot{U}_{i}^{(2)}-m_{12}(\dot{U}_{i}^{(1)}-\dot{u}_i)+m_{2}(\dot{U}_{i}^{(2)}-\dot{u}_i), \end{aligned}$$
(3)

where the superscripts 0, 1, and 2 denote the porous solid’s three phases: solid matrix, liquid, and gas. The indices are limited to the values 1, 2, and 3. Repeating an index signifies the involvement of a summation.The inclusion of a dot in the middle of a variable indicates partial differentiation in respect to time, while the inclusion of a comma in the head of an index signifies partial differentiation regarding space. The expressions of various elastic constants are described as

$$\begin{aligned} \begin{aligned} \rho _{11}&=\rho -2(\rho _{f1}S_{1}+\rho _{f2}S_{2})\phi +(g_{12}+g_{13}+2g_{23})\phi ^2,\\ \rho _{12}&=\phi (\rho _{f1}S_{1}-g_{12}\phi -g_{23}\phi ),\\ \rho _{13}&=\phi (\rho _{f2}S_{2}-g_{13}\phi -g_{23}\phi ),\\ \rho _{22}&=g_{12}\phi ^2,\\ \rho _{23}&=g_{23}\phi ^2,\\ \rho _{33}&=g_{13}\phi ^2,\\ \rho&=(1-\phi )\rho _s+\phi S_{1} \rho _{f1}+\phi S_{2} \rho _{f2},\\ g_{12}&=S_{1}\rho _{f1}F_{s}/\phi ,\\ g_{13}&=S_{2}\rho _{f2}F_{s}/\phi ,\\ g_{23}&=0.1\sqrt{g_{12}g_{13}},\\ F_{s}&=((1/\phi )+1)/2,\\ m_{1}&=\tilde{b}_{1}\phi ^2,\\ m_{2}&=\tilde{b}_{2}\phi ^2,\\ m_{12}&=\tilde{b}_{12}\phi ^2,\\ k_{r1}&=\frac{(S_{1}-R_{1})^2}{(1-R_{1})^2},\\ k_{r2}&=\frac{(S_{2}-R_{2})^2}{(1-R_{2})^2},\\ k_{r12}&=\sqrt{0.1k_{r1}k_{r2}},\\ \tilde{b}_{1}&=S_{1}^2\eta _{f1}/(\kappa k_{r1}),\\ \tilde{b}_{2}&=S_{2}^2\eta _{f2}/(\kappa k_{r2}),\\ \tilde{b}_{12}&=S_{1}S_{2}k_{r12}\sqrt{\eta _{f1}\eta _{f2}}/D,\\ D&=\kappa (k_{r1}k_{r2}-k_{r12}^2) \end{aligned} \end{aligned}$$

, \(S_1 + S_2 = 1\), \(\phi =\phi _1+\phi _2=\phi _{10}S_1+\phi _{20}S_2\).

The constitutive relations (Shi et al.44) incorporating global flow and mesoscopic flow in the distinct phases of the porous medium are described in the following form:

$$\begin{aligned} \sigma ^{(0)}_{ij}= & \left[ a_{11}u_{k,k}+a_{12}U^{(1)}_{k,k}+a_{13}U^{(2)}_{k,k}\right] \delta _{ij}+N(u_{i,j}+u_{j,i}),\end{aligned}$$
(4)
$$\begin{aligned} \sigma ^{(1)}= & \left[ a_{12}u_{k,k}+a_{22}U^{(1)}_{k,k}+a_{23}U^{(2)}_{k,k}\right] \delta _{ij},\end{aligned}$$
(5)
$$\begin{aligned} \sigma ^{(2)}= & \left[ a_{13}u_{k,k}+a_{23}U^{(1)}_{k,k}+a_{33}U^{(2)}_{k,k}\right] \delta _{ij},\end{aligned}$$
(6)
$$\begin{aligned} \zeta= & \gamma _1u_{k,k}+\gamma _2U^{(1)}_{k,k}+\gamma _3U^{(2)}_{k,k}, \end{aligned}$$
(7)

where \(\zeta\) specifies the multiscale WIFF in unsaturated porous solid. The coefficients expressed in the aforementioned equations are delineated as

$$\begin{aligned} a_{11}= & A+\gamma _{1}\gamma _{1}/\gamma _{0},\\ a_{12}= & Q_{1}+\gamma _{1}\gamma _{2}/\gamma _{0},\\ a_{13}= & Q_{2}+\gamma _{1}\gamma _{3}/\gamma _{0},\\ a_{22}= & R_{1}+\gamma _{2}\gamma _{2}/\gamma _{0},\\ a_{23}= & R_{3}+\gamma _{2}\gamma _{3}/\gamma _{0},\\ a_{33}= & R_{2}+\gamma _{3}\gamma _{3}/\gamma _{0},\\ A= & \lambda _c-2B_{1}\phi -2B_{2}\phi +(M_{1}+M_{2}+2M_{3})\phi ^2,\\ \lambda _c= & K_{c}-(2 N_m/3),\\ R_{1}= & M_{1}\phi ^2, \\ R_{2}= & M_{2}\phi ^2, \\ R_{3}= & M_{3}\phi ^2,\\ Q_{1}= & \phi (B_{1}-M_{1}\phi -M_{3}\phi ),\\ Q_{2}= & \phi (B_{2}-M_{2}\phi -M_{3}\phi ),\\ B_{1}= & ((S_{1}+\beta )\gamma -\beta +(\gamma -1)\eta )\vartheta K_{c},\\ B_{2}= & (S_{2}+(1-\gamma )\eta )\vartheta K_{c},\\ r= & (S_{1}+\beta )/K_{s}+(q B_{2}+(S_{1}+\beta )(1-(K_{c}/K_{s})))/(K_{c}-K_{m}),\\ M_{1}= & -\left( B_{1}/\delta K_{m}+M_{3}\right) ,\\ M_{2}= & (B_{2}r+\eta )/q,\\ M_{3}= & -(1/K_{m}\delta +r/q)B_{2}-\eta /q,\\ \delta= & \frac{1}{K_s}-\frac{1}{K_m},\\ \phi _{10}= & \phi _{20}=\phi ,\\ \phi _1= & \phi S_1,\\ \phi _2= & \phi S_2,\\ q= & \phi ((1/K_{f1})+(1/P'_{ca}S_{1}S_{2})),\\ \gamma= & (1+P'_{ca}S_{1}S_{2}/K_{f2})/(1+P'_{ca}S_{1}S_{2}/K_{f1}),\\ \alpha '= & 1+(\gamma -1)(S_{1}+\beta ),\\ K_{f}= & \alpha '((\gamma S_{1}/K_{f1})+(S_{2}/K_{f2}))^{-1},\\ G= & (K_{m}-K_{s})K_{f}/(\phi (K_{f}-K_{s})),\\ K_{c}= & (K_{m}+G)K_{s}/(K_{s}+G),\\ \vartheta= & ((1/K_{s})-(1/K_{m})+\phi ((1/K_{m})-(1/K_{c})))/(\alpha '((1/K_{s})-(1/K_{m})+\phi ((1/K_{m})-(1/K_{f})))),\\ P_{ca}= & A[(S_1+S_{r2}-1)^{-2}-((S_{r1}/S_{1})^2)(1-S_{r1}-S_{r2})^{-2}),\\ P'_{ca}= & \frac{dP_{cp}}{dS_1},\\ \beta= & P_{ca}/P'_{ca}, \eta =P_w/P'_{ca},\\ \gamma _{0}= & -((1/3)R_0^2\phi _1^2\phi _2\phi _{20}((\rho _{f1}\omega ^2/\phi _{10})+(\iota \omega \eta _{f1}/\kappa ))+R_{1}\phi _2^2+R_{2}\phi _1^2-2R_{3}\phi _1\phi _2),\\ \gamma _{1}= & (Q_{1}\phi _2-Q_{2}\phi _1),\\ \gamma _{2}= & (R_{1}\phi _2-R_{3}\phi _1),\\ \gamma _{3}= & (R_{3}\phi _2-R_{2}\phi _1). \end{aligned}$$

Utilising constitutive relations inside the equations of motion, we formulate the equations of motion by means of the displacement components. The equations are expressed as follows:

$$\begin{aligned} (a_{11}+N)u_{j,ij}+a_{12}U^{(1)}_{j,ij}+a_{13}U^{(2)}_{j,ij}+Nu_{j,ij}= & \rho _{11}\ddot{u}_i+\rho _{12}\ddot{U}_{i}^{(1)}+\rho _{13}\ddot{U}_{i}^{(2)}\nonumber \\- & (m_1-m_{12})(\dot{U}_{i}^{(1)}-\dot{u}_i)(m_2-m_{12})(\dot{U}_{i}^{(2)}-\dot{u}_i),\nonumber \\ a_{12}u_{j,ij}+a_{22}U^{(1)}_{j,ij}+a_{23}U^{(2)}_{j,ij}= & \rho _{12}\ddot{u}_i+\rho _{22}\ddot{U}_{i}^{(1)}+\rho _{23}\ddot{U}_{i}^{(2)}\nonumber \\+ & m_1(\dot{U}_{i}^{(1)}-\dot{u}_i)-m_{12}(\dot{U}_{i}^{(2)}-\dot{u}_i),\nonumber \\ a_{13}u_{j,ij}+a_{23}U^{(1)}_{j,ij}+a_{33}U^{(2)}_{j,ij}= & \rho _{13}\ddot{u}_i+\rho _{23}\ddot{U}_{i}^{(1)}+\rho _{33}\ddot{U}_{i}^{(2)}\nonumber \\- & m_{12}(\dot{U}_{i}^{(1)}-\dot{u}_i)+m_{2}(\dot{U}_{i}^{(2)}-\dot{u}_i). \end{aligned}$$
(8)

Plane harmonic wave propagation

To examine the propagation properties of planar harmonic waves in the specified medium, we postulate the assumption

$$\begin{aligned} \left\{ u_j, U^{(1)}_j, U^{(2)}_j\right\} =\left\{ \bar{S}_j, \bar{L}_j, \bar{G}_j\right\} e^{\left\{ \iota \omega \left( p_kx_k-t \right) \right\} }, \end{aligned}$$
(9)

where the slowness vector is denoted by the expression \(\left( p_1, p_2, p_3\right)\) and the angular frequency is depicted by the symbol \(\omega\). When the phase velocity V is considered, the concept of slowness may be described as \(\left( p_1, p_2, p_3\right) ={\bf{N}}/V\). It is possible to use the row matrix \({\bf{N}} =(n_1, n_2, n_3)\) to represent the direction of phase propagation. The vectors \((\bar{S}_1, \bar{S}_2, \bar{S}_3)\), \((\bar{L}_1,\bar{L}_2,\bar{L}_3)\), and \((\bar{G}_1, \bar{G}_2,\bar{G}_3)\), respectively, constitute the representations of the polarisations of the solid and fluid particles that are present in the composite medium. By inserting (9) into the equation (8), we have a set of equations, which are as follows:

$$\begin{aligned} \left[ (a_{11}+N)n_in_j+(N-b_{11}V^2)\delta _{ij} \right] \bar{S}_j+\left[ a_{12}n_in_j-b_{12}V^2\delta _{ij} \right] \bar{L}_j+\left[ a_{13}n_in_j-b_{13}V^2\delta _{ij} \right] \bar{G}_j=0,~\end{aligned}$$
(10)
$$\begin{aligned} \left[ a_{12}n_in_j-b_{12}V^2\delta _{ij} \right] \bar{S}_j+\left[ a_{22}n_in_j-b_{22}V^2\delta _{ij} \right] \bar{L}_j+\left[ a_{23}n_in_j-b_{23}V^2\delta _{ij} \right] \bar{G}_j=0,~\end{aligned}$$
(11)
$$\begin{aligned} \left[ a_{13}n_in_j-b_{13}V^2\delta _{ij} \right] \bar{S}_j+\left[ a_{23}n_in_j-b_{23}V^2\delta _{ij} \right] \bar{L}_j+\left[ a_{33}n_in_j-b_{33}V^2\delta _{ij} \right] \bar{G}_j=0,~ \end{aligned}$$
(12)

where

$$\begin{aligned} b_{11}= & \rho _{11}+\frac{\iota }{\omega }(m_{1}+m_{2}-2m_{12}),\quad b_{12}=\rho _{12}-\frac{\iota }{\omega }(m_{1}-m_{12}),\quad b_{13}=\rho _{13}-\frac{\iota }{\omega }(m_{2}-m_{12}),\\ b_{22}= & \rho _{22}+\frac{\iota }{\omega }m_{1},\quad b_{23}=\rho _{23}-\frac{\iota }{\omega }m_{12},\quad b_{33}=\rho _{33}+\frac{\iota }{\omega }m_{2}. \end{aligned}$$

In order to establish a connection between the three types of displacements, namely \({\bf{u}}\), \({\bf{U}}^{(1)}\), and \({\bf{U}}^{(2)}\), the Eqs. (10), (11) and (12) are solved as follows.

$$\begin{aligned} \bar{L}_i=\Gamma _{ij}\bar{S}_j;\qquad \Gamma =\frac{b_0}{a_0}\left( {\bf{I}}-{\bf{N}}^T{\bf{N}} \right) +\frac{b_0V^4+b_1V^2+b_2}{a_0V^4+a_1V^2+a_2}{\bf{N}}^T{\bf{N}},\end{aligned}$$
(13)
$$\begin{aligned} \bar{G}_i=\Delta _{ij}\bar{S}_j;\qquad \Delta =\frac{c_0}{a_0}\left( {\bf{I}}-{\bf{N}}^T{\bf{N}} \right) +\frac{c_0V^4+c_1V^2+c_2}{a_0V^4+a_1V^2+a_2}{\bf{N}}^T{\bf{N}}. \end{aligned}$$
(14)

In this context, the depiction \({\bf{N}}^T\) signifies the transpose of the row matrix \({\bf{N}}\), whereas the description \({\bf{I}}\) is a three-dimensional identity matrix. The aforementioned equations establish a number of constants, and the different constants are provided by

$$\begin{aligned} a_{0}= & b_{22}b_{33}-b_{23}^2, a_{1}=2a_{23}b_{23}-a_{22}b_{33}-a_{33}b_{22}, a_{2}=a_{22}a_{33}-a_{23}^2,\\ b_{0}= & b_{23}b_{13}-b_{12}b_{33}, b_{1}=a_{12}b_{33}+a_{33}b_{12}-a_{13}b_{23}-a_{23}b_{13}, b_{2}=a_{13}a_{23}-a_{12}a_{33},\\ c_{0}= & b_{12}b_{23}-b_{13}b_{22}, c_{1}=a_{13}b_{22}+a_{22}b_{13}-a_{12}b_{23}-a_{23}b_{12}, c_{2}=a_{12}a_{23}-a_{13}a_{22}. \end{aligned}$$

When we put equations (13) and (14) into equation (10), we get a set of three equations, which are as follows:

$$\begin{aligned} \left[ a_3{\bf{N}}^T{\bf{N}}+b_3\left( {\bf{I}}-{\bf{N}}^T{\bf{N}} \right) \right] \mathbf {\bar{S}}=0, \end{aligned}$$
(15)

which are the Christoffel equations that describe the propagation of harmonic plane waves in a porous material. Following is a description of the coefficients that are utilised in a number of relations are as follows:

$$\begin{aligned} a_3= & \left( a_{11}+2N-b_{11}V^2\right) \left[ a_0V^4+a_1V^2+a_2\right] +(a_{12}-b_{12}V^2)[b_0V^4+b_1V^2+b_2]\\ & \quad \quad +(a_{13}-b_{13}V^2)[c_0V^4+c_1V^2+c_2],\\ b_3= & N-\left[ b_{11}+b_{12}\frac{b_0}{a_0}+b_{13}\frac{c_0}{a_0}\right] V^2. \end{aligned}$$

It is possible to determine the determinant of the coefficient matrix, which is provided by \(a_3{\bf{N}}^T{\bf{N}}+b_3({\bf{I}}-{\bf{N}}^T{\bf{N}})\). This determinant may be expressed as \((b_3a_3^2)\). It is essential that the determinant \((b_3a_3^2)\) be equal to zero in order to ensure that the Christoffel equations (15) need a solution that is not trivial. In the case whenever the value of \(a_3\) is equal to zero, we are able to deduce the following mathematical relationship:

$$\begin{aligned} d_3V^6+d_2V^4+d_1V^2+d_0=0, \end{aligned}$$
(16)

where

$$\begin{aligned} d_{3}= & b_{11}a_{0}+b_{12}b_{0}+b_{13}c_{0},\\ d_{2}= & b_{11}a_{1}+b_{12}b_{1}+b_{13}c_{1}-(a_{11}+2N)a_{0}-a_{12}b_{0}-a_{13}c_{0},\\ d_{1}= & b_{11}a_{2}+b_{12}b_{2}+b_{13}c_{2}-(a_{11}+2N)a_{1}-a_{12}b_{1}-a_{13}c_{1},\\ d_{0}= & -(a_{11}+2N)a_{2}-a_{12}b_{2}-a_{13}c_{2}. \end{aligned}$$

In this particular circumstance, the polarisations \(\bar{\textbf{S}}\) align themselves in a manner that is complementary to the phase direction \({\bf{N}}\). This demonstrates that the equation presented before has accurately described the propagation of dilatational waves. An unsaturated porous medium is characterised by the presence of three dilatational waves, and the propagation of these waves is characterised by three roots of the cubic equation (16) in terms of \(V^2\). Because of the existence of viscous pore fluids, a medium is believed to be dissipative. In light of this, equation (16) has complex roots, which suggests that dilatational waves in the medium are subject to attenuation. The four dilatational waves with velocity order \(\Re (V_1)> \Re (V_2)>\Re (V_3)\) are referred to as \(P_1,~P_2,~P_3\) waves, respectively, for the purpose of making the discussion more convenient.

Another equation, namely \(b_3 = 0\), produces

$$\begin{aligned} V=\sqrt{N/\left[ b_{11}+b_{12}\frac{b_0}{a_0}+b_{13}\frac{c_0}{a_0}\right] }. \end{aligned}$$
(17)

n this scenario, the polarisation \(\bar{\textbf{S}}\) is orientated perpendicular to the propagation direction \({\bf{N}}\). This equation will define the velocity of a transverse wave in a medium that sustains attenuation as a result of the viscosity of the fluid contained beneath its pores. The solitary transverse wave is considered to be the SV wave.

Reflection at plane boundary

The purpose of the investigation is to explore the consequences of porosity, water saturation, wave frequency, and inclusion radius on the fluid flow and energy distribution of reflected waves at the stress-free surface of a unsaturated porous material.

Definition of the problem

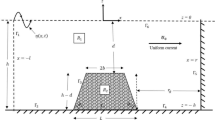
Consider a rectangular coordinate system (x, y, z), where the region \(z>0\) consists of a porous medium saturated with two immiscible viscous fluids that permeate farther in the z-direction. The plane described by the equation \(z=0\) is regarded as the stress-free surface of this material (Fig. 1). The substantial attenuation of a seismic wave may be more explicitly shown by its irregular propagation. Thus, the extensive propagation of an attenuated wave in a dissipative medium is regarded as inhomogeneous. This is determined by the alignment of the propagation vector and the divergence of the attenuation vector from the propagation vector. Consequently, two angles, namely \(\theta _0\) and \(\gamma _0\), are necessary to describe an inhomogeneous incident wave (Fig. 1). As stated by Borcherdt45, horizontal slowness may be determined through \(\theta _0\) (angle of propagation), \(\gamma _0\) (angle of attenuation), \({\textbf {A}}\) (attenuation vector), and \({\textbf {P}}\) (propagation vector).

Fig. 1
figure 1

Schematic diagram of the problem.

Full size image
$$\begin{aligned} s=|{\textbf {P}}|\sin \theta _0-\iota |{\textbf {A}}|\sin (\theta _0-\gamma _0). \end{aligned}$$
(18)

Consequently, for an incident wave with velocity \(V_0\), we have

$$\begin{aligned} |{\textbf {P}}|^2= & \frac{1}{2}[\Re (\frac{\omega ^2}{V^2_0})+\sqrt{(\Re (\frac{\omega ^2}{V^2_0}))^2+(\Im (\frac{\omega ^2}{V^2_0}))^2/\cos ^2\gamma _0}],\end{aligned}$$
(19)
$$\begin{aligned} |{\textbf {A}}|^2= & \frac{1}{2}[-\Re (\frac{\omega ^2}{V^2_0})+\sqrt{(\Re (\frac{\omega ^2}{V^2_0}))^2+(\Im (\frac{\omega ^2}{V^2_0}))^2/\cos ^2\gamma _0}]. \end{aligned}$$
(20)

The dissipative characteristics of the porous medium need the specification of the incident wave at the boundary \(z=0\) about its propagation direction (\(\theta _0\)) and attenuation direction (\(\gamma _0\)). The vector (\(s,0,q_0\)) depicts the slowness vector of the incident wave, with \(q_0 (=\pm \sqrt{1/V_0^2-s^2})\) indicating the vertical slowness of the incident wave. For the incident wave to propagate towards the boundary in the negative z-direction, the real part of \(q_0\) must be negative. Snell’s law stipulates that the horizontal slowness (s) of both incident and reflected waves is invariant. The vector (\(s,0,q_k\)) depicts the slowness vector for reflected waves, where \(q_k=\pm \sqrt{1/V_k^2-s^2}, (k=1,2,3,4)\). To ensure the dissipation of reflected waves travelling away from the boundary in the positive z-direction, the imaginary part of \(q_k\) must be greater than zero.

In the subsequent step, the aggregate displacement of material particles in the medium is equal to the combination of the displacements corresponding to the wave that strikes the medium and the four waves that reflect off of it. Consequently, the depiction of the overall displacement of material particles in the \(xz-\)plane for two dimensions motion may be represented as follows:

$$\begin{aligned} u_j= & [ \bar{S}_j^{(0)}\exp (-\iota \omega q_0 z)+\sum _{k=1}^{4}\epsilon _k \bar{S}_j^{(k)}\exp \left\{ \iota \omega (sx+q_{k}z-t)\right\} ], \nonumber \\ U^{(1)}_j= & [\bar{L}_j^{(0)}\exp (-\iota \omega q_0 z)+\sum _{k=1}^{4}\epsilon _k \bar{L}_j^{(k)}\exp \left\{ \iota \omega (sx+q_{k}z-t)\right\} ],\nonumber \\ U^{(2)}_j= & [\bar{G}_j^{(0)}\exp (-\iota \omega q_0 z)+\sum _{k=1}^{4}\epsilon _k \bar{G}_j^{(k)}\exp \left\{ \iota \omega (sx+q_{k}z-t)\right\} ],\quad (j=x,z),~~~~~~ \end{aligned}$$
(21)

The excitation factors for reflected waves are denoted by the \(\epsilon _k\) symbol. These factors are related to the incident wave. The index ‘0’ is used to signify the wave that is incident. In this context, the index ‘k’\((=1,2,3,4)\) is used to denote the reflected waves \((P_1,P_2,P_3,SV)\) simultaneously. There is a possibility of defining the polarisation of a longitudinal and transverse waves by using the unit vector \({\textbf {n}}\), which may be computed as \({\textbf {n}}=(s,0,q_k)V_k\).

Boundary conditions

The current geometry incorporates boundary constraints for particle motion at the stress-free planar surface at \(z=0\). This study considers impermeable boundary conditions, namely sealed holes, at the plane defined by \(z=0\). At an impermeable barrier consisting of sealed pores, there is no flow of interstitial fluid permitted at the surface when waves pass through the plane at \(z=0\). Therefore, the appropriate boundary conditions that must be fulfilled at the plane \(z=0\) are as follows:

$$\begin{aligned} i)~\sigma ^{(0)}_{zz}= & 0,\nonumber \\ ii)~\sigma ^{(0)}_{zx}= & 0,\nonumber \\ iii)~U^{(1)}_z= & 0,\nonumber \\ iv)~U^{(2)}_z= & 0. \end{aligned}$$
(22)

Reflection coefficients

To formulate an array of four contemporaneous non-homogeneous linear equations, we must first resolve the four boundary conditions (22) using the displacement articulated in Eq. (21). The following expressions represent the system of four equations:

$$\begin{aligned} \sum _{k=1}^{4}f_{lk}\epsilon _{k}=-f_{l0},\qquad (l=1,2,3,4). \end{aligned}$$
(23)

For \((k=1,2,3,4)\), we have

$$\begin{aligned} f_{1k}= & a_{11}[s\bar{S}_{x}^{(k)}+q_k\bar{S}_{z}^{(k)}]+a_{12}[s\bar{L}_{x}^{(k)}+q_k\bar{L}_{z}^{(k)}]+a_{13}[s\bar{G}_{x}^{(k)}+q_k\bar{G}_{z}^{(k)}]+2Nq_kS_z^{(k)},\\ f_{2k}= & N[q_k\bar{S}_x^{(k)}+s\bar{S}_z^{(k)}],\quad f_{3k}=\bar{L}_z^{(k)},\quad f_{4k}=\bar{G}_z^{(k)}. \end{aligned}$$

The system of equations, represented by the variables \(\epsilon _k\) (where \(k=1,~2,~3,~4\)), is solved employing the Gauss elimination technique. These unknown entities might be referred to as reflection coefficients.

Wave-induced fluid flow

With the aid of the relations (13) and (14) in equation (7), the WIFF in pores can only be discovered as a result of the dilation of solid particles, and it is described as follows:

$$\begin{aligned} \zeta =[\lambda _1+\lambda _2\Gamma (V)+\lambda _3\Delta (V)](u_{x,x}+u_{z,z}). \end{aligned}$$
(24)

By applying equation (21) to the equation that came before it, we could derive

$$\begin{aligned} \zeta (V_k)=\iota \omega \epsilon _k[\lambda _1+\lambda _2\Gamma (V_k)+\lambda _3\Delta (V_k)](sA_x^{k}+q_kA_z^{k})e^{\iota \omega (sx+q_{k}z-t)}, (k=1,2,3,4). \end{aligned}$$
(25)

We can verify that \(\zeta (V_4)=0\) by integrating the shear wave existence condition into the equation as mentioned above. It suggests that three longitudinal waves regulate the movement of WIFF inside pores. Hence, the functions \(\varsigma (V_1), \zeta (V_2),\varsigma (V_3)\) represent the individual contribution of \(P_1,P_2,P_3\) to the overall fluid flow. Since \(V_k\) is a complex number, it follows that \(\varsigma (V_k)\) is also a complex number. The fluid flow caused by longitudinal waves, denoted as \(\zeta _k\), is a physical quantity that may be determined as the real component of its complex form, which is represented as \(\zeta _k=\Re (\zeta (V_k))\). The sum of \(\zeta _1\), \(\zeta _2\), and \(\zeta _3\) represents the overall fluid flow that occurs in a partly saturated porous solid when a \(P_1\) (or SV) wave is placed to the stress-free surface of a partially saturated porous solid comprising two viscous fluids (immiscible).

Energy partition

This article seeks to analyse the partitioning of energy from incident wave into distinct reflected waves. The energy transferred per unit area in the plane \(z=0\) is determined by computing the scalar product of the surface traction and particle velocity as outlined by Achenbach46. The existence of a dissipative porous medium results in energy dissipation, necessitating the consideration of interaction energy (Borcherdt45; Krebes47) or interference energy (Ainslie and Burns48) between two waves with distinct characteristics. Consequently, the total energy flow comprises the energy flux transmitted by reflected waves and the interaction energy between two distinct types of waves. The medium now enables the transmission of five waves: one incident and four reflected. Consequently, an energy matrix is formulated to delineate the distribution of incoming energy at the surface \(z=0\).

$$\begin{aligned} E_{lk}=\Re (P_{lk}\epsilon _{l}\bar{\epsilon _k})/\Re (P_{55}),\quad \quad (l,k=1,2,3,4,5); \end{aligned}$$
(26)

where \(\epsilon _5=1\). A bar above a complex number signifies its conjugate. The components \(P_{lk}\) in Eq. (26) are defined by

$$\begin{aligned} P_{lk}= & \left[ a_{11}[s\bar{S}_{x}^{(l)}+q_{l}\bar{S}_{z}^{(l)}]+a_{12}[s\bar{L}_{x}^{(l)}+q_{l}\bar{L}_{z}^{(l)}]+a_{13}[s\bar{G}_{x}^{(l)}+q_{l}\bar{G}_{z}^{(l)}]+2Nq_l S_z^{(l)}\right] \bar{S}_{z}^{(k)}\nonumber \\+ & G\left[ s\bar{S}_{z}^{(l)}+q_{l}\bar{S}_{x}^{(l)}\right] \bar{\bar{S}}_{x}^{(k)}+X_l\bar{\bar{L}}_{z}^{(k)}+Y_l\bar{\bar{G}}_{z}^{(k)}, \end{aligned}$$
(27)

where

$$\begin{aligned} X_l=a_{12}[s\bar{S}_{x}^{(i)}+q_k\bar{S}_{z}^{(l)}]+a_{22}[s\bar{L}_{x}^{(l)}+q_k\bar{L}_{z}^{(l)}]+a_{23}[s\bar{G}_{x}^{(l)}+q_k\bar{G}_{z}^{(l)}]\\ Y_l=a_{13}[s\bar{S}_{x}^{(i)}+q_k\bar{S}_{z}^{(l)}]+a_{23}[s\bar{L}_{x}^{(l)}+q_k\bar{L}_{z}^{(l)}]+a_{33}[s\bar{G}_{x}^{(l)}+q_k\bar{G}_{z}^{(l)}]. \end{aligned}$$

When dealing with porous media, the energy matrix \(E_{ij},~(i,j=1,~2,~3,~4,~5)\) is used to ascertain the energy proportions of four reflected waves, which are represented by the symbols \(P_1\), \(P_2\), \(P_3\), and SV accordingly. It is possible to differentiate the energy proportions of the reflected waves \(P_1\), \(P_2\), \(P_3\), and SV by referring to the diagonal entries \(E_{11}\), \(E_{22}\), \(E_{33}\), and \(E_{44}\). In order to determine the interaction energy that results from the interference of the incident wave with each reflected wave, the equation \(E_{IR}=\sum _{i=1}^{4}(E_{5i}+E_{i5})\) becomes applicable. It is possible to determine the interaction energy between every pair of reflected waves by using the expression \(E_{RR}=\sum _{i=1}^{4}(\sum _{j=1}^{4}E_{ij}-E_{ii})\). It is necessary for the aggregate bulk energies of the reflected waves and the overall interaction energy to be equal to the bulk energy of the incident wave at the stress-free surface to satisfy the law of energy conservation requirements.

$$\begin{aligned} \sum _{i=1}^{4}E_{ii}+E_{RR}+E_{IR}=-E_{55}=1. \end{aligned}$$
(28)

During the whole process of reflection, it is essential that the energy balance law at the stress-free surface be maintained at each and every angle of incidence. This law is known as the energy balance law. As a consequence, relation (28) guarantees the preservation of energy at the surface that is free of stress.

Numerical example

We employ a numerical model of an unsaturated porous solid to examine the impact of wave frequency, incidence direction, and elastic properties like porosity, inclusion radius, and liquid saturation on reflection characteristics and WIFF. A reservoir rock (sandstone) saturated with water and \(CO_2\) is chosen for the numerical model of porous medium. Table 1 contains information on the sandstone’s elastic and dynamic constants.

Table 1 The parameters of sandstone that has been saturated with gas and water.
Full size table

Numerical discussion

Partitioning of incident energy among reflected waves

\(P_1\)-wave incidence

Figure 2 illustrates how porosity affects the distribution of energy in reflected waves at the stress-free surface of closed pores. It has been seen that the energy share of the \(P_1\) waves is increasing as the porosity (\(\phi\)) increases. The phenomenon is also seen in all other refracted waves, however these waves experience a decrease in energy distribution as porosity increases. The energy partitions clearly indicate that the bulk of the energy is distributed between the \(P_1\) and SV waves. The \(P_1\) wave energy decreases as the angle rises from normal incidence. Following a minimum at around \(40^0\), the energy progressively rises until it reaches grazing incidence. The reflected SV wave exhibits contrasting behavior, indicating the conversion of energy at the surface. The graphs of bulk energy shares for various reflected waves exhibit that at normal and grazing incidence, only the reflected \(P_1\) wave remains. In contrast, the SV wave does not survive at any angle [Yang and Sato49]. The energy proportions of reflected \(P_2\) and \(P_3\) waves are minimal. This is attributable to the fact that the phase speeds of these waves are much lower than those of all other wave modes. The energy shares of slower waves diminish as the angle of incidence rises. The calculations have been validated against the principle of energy conservation. The graphs of bulk energy shares for various reflected waves clearly indicate that energy conservation is observed at every angle of incidence. This proves the validity of the energy balance law as articulated in Eq. (25). It confirms that the numerical computations are analytically accurate.

Figure 3 illustrates the effect of wave frequency on the allocation of incident energy among four reflected waves in a partly saturated porous medium. The image displays that the \(P_1\) wave first intensifies with increasing frequency. However, the influence of frequency becomes negligible upon attaining an angle of \(\theta _0=45^\circ\). The increasing \(\omega\) amplifies the energy contribution of the SV wave. The energy dispersion is more significant for slower waves, substantially diminishing the \(P_3\) wave at low frequencies. Further, there is a substantial increase in the energy distribution of the \(P_2\) wave with rising frequency. The correlation between energy shares and frequency may enhance fluid content prediction in seismic data interpretation and facilitate the development of novel processing techniques for evaluating fluid characteristics from seismic data.

The effect of water saturation, denoted by the symbol \(S_2\), on the energy distributions of reflected waves is seen in Figure 4. Figure 3 illustrates that the energy shares at the stress-free surface of an unsaturated poroelastic material may go through considerable changes depending on its frequency. A change in the saturation of the fluid may bring about a substantial change in the frequency-dependent behaviour of the fluid, which in turn brings about a significant change in the energy shares associated with the fluctuations in water saturation. An increase in \(S_2\) decreases the strength of the \(P_1\) wave. On the contrary, the rest of the waves showed a substantial rise when \(S_2\) grew. The faster waves exhibit an opposing behavior compared to the incidence direction (\(\theta _0\)). The energy ratios of slower waves exhibit comparable fluctuations. The interference energy is notably enriched when the value of \(S_2\) grows, mainly when the incidence is normal.

Fig. 2
figure 2

Energy shares as a function of the incidence direction \((\theta _0)\) with different porosity (incident \(P_1\) wave).

Full size image
Fig. 3
figure 3

Energy shares as a function of the incidence direction \((\theta _0)\) with different frequency (incident \(P_1\) wave).

Full size image
Fig. 4
figure 4

Energy shares as a function of the incidence direction \((\theta _0)\) with different water saturation (incident \(P_1\) wave).

Full size image

The radius of spherical inclusions embedded in a partially saturated porous media plays a significant role in determining the heterogeneity scale of the rock. Consequently, it has a direct impact on the way seismic waves propagate. Figure 5 demonstrates how altering the value of \(R_0\) impacts the energy distribution among the four reflected plane waves. It is evident from this figure that the inclusion radius has a substantial impact on the reflection coefficients. As \(R_0\) grows, the contrast in \(P_1\) wave impedance increases, resulting from a more significant magnitude of the reflected \(P_1\) wave. Consequently, the energy distribution of the reflected waves is altered correspondingly. The rise in \(R_0\) greatly intensified the \(P_1\) wave. However, when the value of \(R_0\) grows, the SV wave becomes less prominent. In proportion to the rise in \(R_0\), the energy shares of slower waves are decreasing.

Fig. 5
figure 5

Energy shares as a function of the incidence direction \((\theta _0)\) with different inclusion radius (incident \(P_1\) wave).

Full size image

The impacts of WIFF on the ways in which incident energy is distributed across four reflected waves are seen in Fig. 6. In the presence of WIFF, the \(P_1\) wave is enhanced between the values of 0 and \(25^0\), while it is diminished between the values of \(\theta _0\) and \(25^0\). For values of 0 to \(90^0\), the existence of WIFF results in the enhancement of the \(P_2\) and SV waves. The existence of WIFF, on the other hand, causes the \(P_3\) wave to be weakened throughout the whole spectrum of incidence directions.

Fig. 6
figure 6

Energy shares as a function of the incidence direction \((\theta _0)\) in the presence and absence of WIFF (incident \(P_1\) wave).

Full size image

SV-wave incidence

To determine the incidence of a SV wave, we will analyze the distribution of incident energy among many reflected waves. The differences in the energy distribution of the reflected waves are shown in Fig. 7, which plots the variances as a function of frequency and incidence angles. On all of the waves, a reversal effect of porosity is noticed, which is in contrast to the wave with the incidence \(P_1\) shown in Fig. 1. A critical angle is regularly seen during the reflection of elastic waves. When the angle of incidence is exceeded, the energy flow vector of the associated wave mode begins to propagate in a direction parallel to the contact. A critical angle of around \(45^\circ\) is found for the reflected \(P_1\) wave. In the vicinity of \(45^\circ\), the energy ratio of the reflected \(P_1\) wave becomes unimportant. The \(P_1\) wave undergoes degeneration and transforms into an interface wave, which does not convey vertical energy flow. Concerning other reflected waves outside the critical angle, the reflected SV wave is given precedence. The contribution of the \(P_1\) wave to the total energy is reduced as the value of \(\phi\) increases. The energy shares of slower waves show similar variations. The slower waves beyond the critical incidence become more significant as \(\theta _0\) increases. The influence of interference energy from the interaction between incoming and reflected waves on energy preservation is negligible at all angles of incidence. Nonetheless, energy conservation is substantially affected by the interference energy between reflected waves.There is a strong indication from the graphs of bulk energy shares for the different reflected waves that the only wave that survives at both normal and grazing incidence is the reflected SV wave, while the \(P_1\) wave does not survive at either angle (Yang and Sato49).

The influence of frequency on the distribution of incident energy among the four reflected waves is seen in Fig. 8. According to the data shown in this figure, the energy proportions of the \(P_1\) wave grow as the frequency of the wave increases. In the same vein, the rising \(\omega\) increases the energy share of the SV wave. Nevertheless, when \(\theta _0\) is less than or equal to \(25^0\), this increase loses its significance. The energy dispersion is more visible for slower waves, which leads to an extensive weakening of the \(P_3\) wave at low frequencies. Furthermore, as the frequency rises, there is a discernible reduction in the proportion of energy that goes into the \(P_2\) wave. As the angle of incidence, denoted by \(\theta _0\), grows, the significance of the contribution made by slower waves going beyond the critical incidence becomes more significant.

Fig. 7
figure 7

Energy shares as a function of the incidence direction \((\theta _0)\) with different porosity (incident SV wave).

Full size image
Fig. 8
figure 8

Energy shares as a function of the incidence direction \((\theta _0)\) with different frequency (incident SV wave).

Full size image

Figure 9 illustrates the effect of saturation on the energy distribution via incidence angles. Just as in the case of incident wave \(P_1\) shown in Fig. 4, changes in water saturation have a substantial impact on the distribution of energy. The energy shares of longitudinal waves were significantly enhanced when \(S_2\) increased. Furthermore, the slower \(P_2\) wave experiences a significant rise in strength as water saturation increases, especially for \(S_2=0.9\) beyond the critical incidence. On the contrary, the SV wave is weakened as \(S_2\) increased.

Fig. 9
figure 9

Energy shares as a function of the incidence direction \((\theta _0)\) with different water saturation (incident SV wave).

Full size image

Figure 10 illustrates the effect of changing the value of \(R_0\) on the energy distribution among the four reflected plane waves. The graphic demonstrates that the inclusion radius significantly affects all the reflection coefficients. As \(R_0\) increases, the proportion of energy attributed to longitudinal waves decreases. On the contrary, the SV wave diminished as the value of \(R_0\) increased. Like the incident wave \(P_1\) in Fig. 5, slower waves became stronger as \(R_0\) increased. However, the quicker waves are affected differently by the inclusion radius in comparison to the incident \(P_1\) wave.

Fig. 10
figure 10

Energy shares as a function of the incidence direction \((\theta _0)\) with different inclusion radius (incident SV wave).

Full size image

In Fig. 11, we illustrate the impact that WIFF has on the distribution of incident energy among four reflected waves. The \(P_1\) wave is strengthened in the presence of WIFF below their critical incidence. The SV wave is weakened for \(0\le \theta _0\le 55^0\) and strengthened for \(\theta _0>35^0\) in the presence of WIFF. Figure 6 depicts similar behavior for \(P_2\) and \(P_3\) waves, and thus, it may be deduced that a similar impact of WIFF on \(P_2\) and \(P_3\) waves appeared for both incident waves (i.e., \(P_1\) and SV).

Fig. 11
figure 11

Energy shares as a function of the incidence direction \((\theta _0)\) in the presence and absence of WIFF (incident \(P_1\) wave).

Full size image

Longitudinal waves contribution to WIFF

\(P_1\)-wave incidence

In this study, we investigate the function that longitudinal waves play in the flow of fluids at the stress-free surface of a partly saturated porous material. The investigation takes into account three distinct measures of porosity, denoted by \((\phi )\), water saturation, denoted by \((S_2)\), and inclusion radius, denoted by \((R_0)\), as seen in Figs. 12, 13 and 14. From these figures, it is possible to conclude that waves \(P_1\) and \(P_2\) are the primary contributors to fluid flow throughout the system. Since the porosity, water saturation, and inclusion radius are all increasing, the fluid flow caused by these waves may decrease. On the other hand, the contribution of wave \(P_2\) diminishes as the angle of incidence rises. Wave \(P_3\) has minimal impact on the fluid flow induced. It is seen that the fluid flow that is produced by waves \(P_2\) and \(P_3\) diminishes when the incidence gets closer to the direction of grazing. On the other hand, the fluid flow caused by the \(P_1\) wave may be detected at both normal and grazing incidence temperatures. Each factor considerably impacted the wave-induced fluid flow when taken together.

Fig. 12
figure 12

WIFF as a function of the incidence direction \((\theta _0)\) with different porosity (incident \(P_1\) wave).

Full size image
Fig. 13
figure 13

WIFF as a function of the incidence direction \((\theta _0)\) with different inclusion radius (incident \(P_1\) wave).

Full size image
Fig. 14
figure 14

WIFF as a function of the incidence direction \((\theta _0)\) with different water saturation (incident \(P_1\) wave).

Full size image

SV-wave incidence

Following this, we will analyze the occurrence of the SV wave. The WIFF is affected by porosity \((\phi )\), water saturation \((S_2)\), and inclusion radius \((R_0)\), as can be seen in Figs. 15, 16 and 17. This is comparable to the situation shown in Figures 12, 13 and 14, which depicts the incident wave \(P_1\). As can be observed in the case of the incident wave \(P_1\), these properties also influence WIFF, which is analogous. However, when compared to the incident \(P_1\) wave, the influence of the incident direction on WIFF is not comparable. When the waves strike the surface at normal and grazing angles, the fluid flow created by these waves is no longer there. Waves \(P_1\) and \(P_2\) are the key elements that influence fluid flow, and the scenario is quite similar to the one with the incident wave. However, when the wave is incident at a grazing angle, it does not contribute to the WIFF. Except for the normal and grazing angles, the \(P_2\) wave contributes to the WIFF over the whole spectrum of incidence angles.

Fig. 15
figure 15

WIFF as a function of the incidence direction \((\theta _0)\) with different porosity (incident SV wave).

Full size image
Fig. 16
figure 16

WIFF as a function of the incidence direction \((\theta _0)\) with different inclusion radius (incident SV wave).

Full size image
Fig. 17
figure 17

WIFF as a function of the incidence direction \((\theta _0)\) with different water saturation (incident SV wave).

Full size image

Conclusions

The purpose of this study is to evaluate the characteristics of wave-induced fluid flow (WIFF) in unsaturated porous media, as well as the properties of the seismic waves that are reflected. An eigensystem is generated, and the Christoffel equations clarify the existence of three longitudinal waves and one transverse wave within the medium, along with their propagation characteristics. The porous media is considered dissipative due to the viscosities present in the saturated fluids. The incident and reflected waves are classified as inhomogeneous waves due to the dissipative nature of the medium. We calculate the poroelastic reflection coefficients for every angle of incidence at the boundary surface of sealed pores in the porous media. Subsequently, these poroelastic reflection coefficients are used to compute the fluid flow induced by the longitudinal waves. Additionally, we calculate the distribution of incident energy among the reflected waves at the boundary of the reflecting medium. From the numerical example, several findings emerge that are insightful and relevant, as listed below.

  1. i.

    No critical angle is observed when a faster dilatational wave strikes the surface. In contrast, a critical angle is noted whenever a shear wave encounters a stress-free surface.

  2. ii.

    The graphical representations of bulk energy shares associated with various reflected waves clearly demonstrate that, for both normal and grazing incidences, only one type of reflected wave physically persists among all the reflected waves. This type of reflected wave is identical to the incident wave.

  3. iii.

    The energy shares associated with distinct energy types are functions of incident direction, water saturation, porosity, inclusion radius, WIFF, and wave frequency.

  4. iv.

    For the incidence of the \(P_1 (SV)\) wave, an increase in porosity and inclusion radius strengthens (weakens) the reflected \(P_1\) wave but weakens (strengthens) the refracted SV wave. Other reflected waves may weaken slightly with the increase in porosity and inclusion radius in both cases.

  5. v.

    For the incidence of the \(P_1 (SV)\) wave, an increase in water saturation weakens (strengthens) the reflected \(P_1\) wave but strengthens (weakens) the refracted SV wave. Other reflected waves may strengthen slightly with the increase in water saturation in both cases.

  6. vi.

    The increase in wave frequency weakens the reflected \(P_2\) wave for both incident waves. In contrast, all other refracted waves may strengthen with the increase in frequency.

  7. vii.

    The energy partition remains unchanged near grazing incidence for longitudinal waves despite variations in porosity, inclusion radius, water saturation, and frequency for the incidence of the \(P_1\) wave. In contrast, the SV wave is unaffected at both normal and grazing incidences.

  8. viii.

    It has been demonstrated that the conservation law for incident energy is upheld at all angles of incidence during the reflection process. To accurately account for the distribution of energy among the various reflected waves, it is essential to consider the energy dissipated during the interference process that occurs between different pairs of waves in the dissipative medium. This further substantiates the correctness of the numerical calculations from an analytical perspective.

  9. ix.

    For the incidence of the \(P_1~(SV)\) wave, the reflected \(SV~(P_1)\) wave is amplified across the entire range of incident directions in the presence of WIFF. A similar behavior is observed for the \(P_2\) and \(P_3\) waves in the presence of WIFF for both incident waves (i.e., \(P_1\) and SV).

  10. x.

    The \(P_1\) and \(P_2\) waves significantly contribute to WIFF for both types of incidence (i.e., \(P_1\) and SV incidence). The faster wave, \(P_1\), contributes to WIFF at both grazing and normal incidences when the \(P_1\) wave is incident. In contrast, the slower waves do not contribute at grazing incidence. However, none of the waves contribute to WIFF at either grazing or normal incidences in the case of an incident SV wave.

In practical applications, the petroleum industry commonly employs seismic reflection techniques to investigate sedimentary basins for hydrocarbon-trapping structures. This method is utilized to explore water, oil, and gas resources. Additionally, the ___location of high-saturation areas can be identified through the analysis of reflected seismic waves. In today’s world, water, oil, and gas are essential to our daily lives; without them, our existence would be significantly challenged. The seismic reflection technique provides valuable structural information and has become the primary strategy for conducting comprehensive investigations of the deep crust. The model under evaluation represents a realistic scenario that may arise during the search for water or hydrocarbons. The search methodologies utilizing WIFF may yield significant insights into the reservoir’s productivity. Therefore, the authors believe that researchers in structural engineering and exploration may be inclined to adopt the proposed model in their simulation studies.