Introduction

As a key component of robotic actuators, manipulators have received intensively academic attention in the field of spatial grasping and object manipulation1,2,3. A powerful and adaptable manipulator is of great significance to perform a specific task in robotics. As humanoid robots gain prominence in recent years, grippers are supposed to be more intelligent and anthropomorphic. However, the complicated structure brought by anthropomorphic design deny traditional control strategy. As a practice of embodied intelligence4, the emerging intelligent control approach is adopted to realize versatile functionalities owing to its outstanding feature learning and pattern recognition. Generally, these intelligent behaviors arise from the interaction between structure, perception, and action. Combined with vision5,6, force7, and haptic8,9 perception, deep neural networks are successfully applied in various robotic end-grasping scenarios2,10,11,12,13. However, computational costs by these intelligent approaches are usually too expensive14 along with excess heat dissipation and no real-time response by limited manipulator processors. Hence, achieving optimal grabbing quality necessitates a delicate balance between structural design and intelligent control approach. As a critical factor to the performance of a manipulator15,16, the grabbing quality is highly relevant to a wide range of aspects, including a manipulator’s stability, accuracy and safety, as well as its ability to adapt to objects of various sizes and shapes. Therefore, state-of-the-art structural design is another new trending to improve grabbing quality due to the computational limitations17.

An outstanding case of the structural design is the anthropomorphic dexterous hand18,19,20. The integrated linkage-driven dexterous anthropomorphic (ILDA) robotic hand21 features superior tactile sensing capabilities through an integrated linkage drive, 15 degrees of freedom across 20 joints and a mass of 1.1 kg. Nevertheless, the control strategy is severely challenged by the complicated structure of ILDA, which only some gestures are presented. In spite of adaptive wrapping, soft grippers22,23,24,25,26,27 are designed to be flexible and lightweight, but may not hold heavy load. The planar linkage gripper28 is most widely used for general tasks with a two-finger or multi-finger design. However, it is short of dealing with irregularly shaped objects. The underactuated and multi-jointed manipulators29,30,31,32 have emerged to address the poor adaptability of planar gripping, which are typically in three-finger31,33 or four-finger34,35 configurations. Multi-joint manipulators with mode switching33,35 have shown greater adaptability for various grasping tasks. However, these designs are confined to only a few grasping tasks and lack of rigidity due to the series structures of multi-joint. Besides, many novel grippers have been developed, such as miniature grippers36,37, reconfigurable grippers38, tendril-like grippers39, trap-like grippers40, jellyfish-like grippers41, entangling grippers42, twist grippers43, origami grippers44,45,46, resilient seashell grippers47, suction cup grippers48, inanimate spider grippers49 and bionic bird grippers for drone landing50. These exotic gripping designs are hardly adopted on a wide scale considering the maintenance.

In 1913, a patent was granted to Paulin Karl Kunze for the invention of ‘Fractal Vise’51. The original ‘Fractal Vise’ design divided each jaw into four tiers, featuring a sliding rotating dovetail joint with two movable jaws controlled by a screw. Each tier possessed a similar structure and function with sectors and partial rotation. Rotation was facilitated by sliding slots, ensuring that each sector could rotate back and forth within a certain angle. This design can be applied in clamping frames (such as pliers and lathe chucks), clamping devices (like limb and head clamps, and foot clamps for surgical and similar instruments), support devices (circular bearings, brackets, chair seats and backrests, surgical and handicapped chairs), sheet metal straightening machines, or other equipment51. Nevertheless, due to the complicated structure of the ‘Fractal Vise’, the cost of machining and manufacturing was prohibitively expensive at that time. Therefore, the ‘Fractal Vise’ has few application scenarios till now.

In the past three decades, many cutting-edge manufacturing techniques have been developed and commercialized, which makes complicated structures easy to obtain. Moreover, fractal structure inspires a novel design paradigm in robotics. In this study, the main focus lies on the structural design to upgrade the grabbing quality. Inspired by the ‘Fractal Vise’, a fractal gripper with mode-switching is proposed, which can achieve excellent robust holding in both grasping and gripping modes. Featuring the multi-scale adaptivity, the fractal design enables the gripper to accommodate objects of wide-ranged sizes and shapes. The design philosophy combines the adaptivity of fractal geometry52 and the principle of lever53. The core of the fractal gripper design lies in its unique fractal structure, which achieves multi-level linkage grasping through a series of self-similar geometric units. In the fractal structure, each fractal unit can be regarded as an independent lever, and these units are arranged according to different size levels, collectively forming the multi-level lever system of the fractal finger. The fractal units are sequentially arranged along a tree-like topological structure, forming a complex multi-level linkage lever network. This design, by superimposing the mechanical effects of levers at different scales, enables the hierarchical topological characteristics of the fractal gripper to achieve efficient multi-level force transmission and distribution, thereby significantly enhancing its grasping performance and adaptability. The fractal gripper optimizes the force transmission and distribution through the geometric characteristics of its fractal structure. The fractal gripper proposed in this paper distributes the input force evenly across multiple contact points through the collaborative action of multiple fractal units, enabling stable and adaptive grasping functionality.

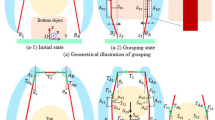
Based on the minimum potential energy principle, the fractal gripper redistributes force according to the morphology of targeted object. Each sectorial part in the fractal structure can be rotated, which make the finger adaptable to any geometrical morphology. The design concept and adaptive mechanism of fractal gripper is illustrated in Fig. 1. Kunze’s original patent for a ‘Fractal Vise’ is characterized by having only one degree of freedom for actuation, relying on a screw-drive mechanism for clamping, and featuring 2n+1 − 1 joints, where n is the design parameter defining the fractal structure, analogous to the structural depth of a binary tree. In Kunze’s ‘Fractal Vise’, a fractal structure design parameter of n = 3, results in a total of 15 joints. This finding implies that the size of contact element is reduced with the number of fractals. For the fractal gripper, the fractal structure design parameter is set to be n = 2, resulting in a total of 7 joints (Fig. 1a).

Fig. 1
figure 1

The design concept and adaptive mechanism of fractal gripper. (a) A simplified two-dimensional planar diagram of a fractal structure, corresponding to a binary tree structure with a depth of two, possesses good adaptability and force redistribution characteristics. (b) For objects of different geometric scales, three cases of planar gripping using fractal structures are presented. Relying on the adaptive characteristics of the fractal structures, the geometric surface of the objects can be fully enveloped.

Full size image

The adaptive mechanism of the fractal design is unveiled in Fig. 1b. When holding various shapes, the contact force and pressure will redistribute and re-equilibrate according to the minimum potential energy principle. This mechanism will avoid local high contact stress from deforming severely or damaging the targeted object. The fractal design enables the gripper to hold objects of various shapes more safely, leading to a more robust and reliable grasping capacity. Additionally, the wear-resistant (redundant) nature of fractal grippers can ensure continuous proper functionality, because even if one contact element (the last layer of finger) is damaged, the other parts will continue to function properly. This feature enhances the reliability and durability of the fractal gripper. The design inspiration and physical prototype of the fractal gripper is shown in Supplementary Fig. S1. Considering the above-mentioned superiority of fractal design, we will make full use of it in the proposed fractal gripper, which will be clearly illustrated in the following sections.

The fractal gripper designed in this study differs significantly from the “Fractal Vise” designed by Pauline Karl Kunze in several aspects. Firstly, our fractal gripper has a mode-switching function, allowing flexible transitions between grasping and gripping modes, thereby enabling more diverse object grasping approaches. Secondly, the fractal gripper features a self-recovery function for spatially stable grasping, which can trigger continuous robust grasping, further enhancing the grasping efficiency. Additionally, unlike the “Fractal Vise”, which is limited to grasping objects in a two-dimensional plane, our design extends the grasping capability into three-dimensional space, enabling more complex object grasping tasks. However, the overall structural design of the current fractal gripper prototype is slightly more complex compared to the “Fractal Vise”.

The fractal gripper achieves passive grasping adaptability through its unique tree-like fractal structure. When in contact with uneven surfaces, the underactuated characteristics of the fractal units allow the joints of each finger to autonomously adjust the contact posture based on the object’s contours. This process is achieved through two key mechanisms:

Passive compliance The reaction torque generated by contact with the environment triggers a cascade of motion adjustments in the fractal joints, thereby forming a contact point distribution that matches the geometric features of the object’s surface.

Joint motion coupling The kinematic constraints between fractal levels ensure the coordinated response of each finger unit, preventing stress concentration caused by local over-constraining.

The spring constraint in the fractal structure, combined with the self-locking feature of the driving module, provides dual safety protection. The spring system achieves a spatially uniform distribution of contact forces through preload balance. The screw-drive mechanism in the driving module (self-locking feature) ensures that each fractal hand does not open in reverse during stable grasping, enabling envelope grasping of non-uniform surface objects and ensuring that the contact point position does not slip in a stable state.

The main contributions of this paper include:

  1. (1)

    Fractal gripper design with switchable modes. The proposed fractal gripper combines fractal geometry and lever principles to improve adaptability and grasping performance. The switchable mode feature allows the gripper to alternate between grasping and gripping, enhancing its functionality for handling different object types.

  2. (2)

    Self-recovery and force redistribution. The fractal gripper’s resilient structure enables self-recovery, allowing for stable and continuous grasping. Its fractal design redistributes force and balances pressure, making it suitable for handling irregularly shaped objects.

  3. (3)

    Theoretical and experimental analysis. A formulated description and compliance effects analysis were carried out to evaluate the fractal gripper’s performance. The theoretical analysis aims at concluding the local compliance stability between fractal gripper and target system. For the equilibrium grasp condition of fractal gripper, the stability of fractal grippers in grasping objects is analyzed by Jacobi matrix and compliance effects. The fingertip pressure data is measured to prove the smooth force distribution under grasping mode. Through theoretical and experimental analysis, it is demonstrated that the fractal gripper exhibits excellent adaptability and stability when handling various shapes and sizes, along with smooth force distribution features.

Methods

The structural design of the fractal gripper

This section outlines the detailed structural design of the proposed fractal gripper, which is depicted in Fig. 2. In the structural design of the fractal gripper, a single drive motor and fractal structure are utilized to grab almost any irregularly shaped target object safely. To achieve successful grasping, the object must conform to the design space defined by the fractal gripper. An exploded view of the overall structure of the fractal gripper is clearly presented in Fig. 2a. The fractal gripper consists of three main parts: the fractal finger, the driving module and the mode-switching module. On the grasping surface of the fractal finger, a flexible polymer layer, specifically PDMS54, is attached, which is referred to as the flexible body. The flexible body will help to avoid any scratching and protect the object’s geometric surface. Details of the fabrication method can be found in Supplementary Fig. S2. A flange is integrated with both the motor bracket and the support plate, which allows the fractal gripper to be attached to the robotic arm.

Fig. 2
figure 2

The overall structure design of the fractal gripper. (a) An exploded view of the overall structure of the fractal gripper. (b) A schematic diagram of the driving module of the fractal gripper, which achieves the opening and closing of three fractal structures through spiral transmission and has a self-locking feature. (c) A half-and-half design diagram of the fractal finger, dividing each part into two halves, assembled using screws and nuts. Between each T-slot, a spring is used to achieve the self-recovery effect of the sectorial parts.

Full size image

The driving module of the fractal gripper is illustrated in Fig. 2b, which is actuated by a micro-gear motor. The driving module features reciprocating movement with single degree of freedom, utilizing a rocker in conjunction with a screw to achieve a fixed constraint on the fractal structure. The bottom end of the rocker, fixed by the screw and locking nut, achieves rotational cooperation with a floating gear seat on the support plate. This setup enables switchable mode via the floating gear seat. The rotation of the rotary screw, driven by a micro-gear motor, facilitates the linear movement of the movable nut and its fitting. The screw drive will actuate the rocker to control the movement of the three fractal fingers. Finally, the end of the rotary screw, along with the coupling, is fastened by a locking nut. A cylindrical bore is centrally located in the support plate and the motor bracket, forming a clearance fit with the movable nut. The micro-gear motor and screw support are installed on the motor bracket. The role of screw support is to ensure the axial running of the rotary screw under excessive clamping force during movement. It also prevents its detachment from the coupling. Another cylindrical bore is created in the middle section of the rocker to establish the linkage with the oscillating rod. The other end of the oscillating rod rotates with the floating support seat on the movable nut fitting, allowing the floating support seat to rotate around the movable nut fitting. The screw-drive mechanism possesses a self-locking characteristic, which is triggered when the helical rise angle is less than the equivalent friction angle between the thread faces. It ensures the gripper remains secure after the object has been grasped and the motor has stopped in the event of a power failure. Meanwhile, the self-locking characteristic prevents rocker slackening due to the excessive load.

Additionally, the switching between grasping and gripping mode is realized by a worm-and-gear biaxial microform motor. This motor drives the rotary screw with the movable nut and linkage to achieve an adaptive grasping effect on the targeted object.

Fractal structure adopts a half-and-half design, where each part is divided into two halves with mirror symmetry and assembled using screws and nuts. Differing from the ‘Fractal Vise’, the original dovetail groove is replaced with a T-slot, and a restraining structure on the edges of the sectorial part prevents it from rotating out of the T-slot. The resilient design facilitates the self-recovery effect of the sectorial parts between each T-slot (Fig. 2c). The orange circle marks the screw bore’s position, while the blue circle indicates the fixed needle roll’s ___location, which is utilized to fix the end of the spring. Additionally, each sector of fractal structure is allowed to rotate around its center. This guarantees that a non-zero torque will remains if the contact element isn’t in full contact with the targeted object. As a result, the rotation will continue until the full contact with the targeted object is reached.

In the structural design of fractal gripper, the design of the kinematic parameters is presented in Table 1. As shown in Fig. 2b, the screw-drive can be achieved through the use of a micro-gear motor and a coupling, with the motor revolutions being recorded as φ. The travelling distance of the movable nut L is designed to be 15 mm. The movable angle θ of the rocker is defined as the angle between the center axis and the rotary screw. In this work, the upper bound of the movable angle θ is θmax ≈ 32°. The performance parameters for the micro-gear motor, which is utilized in both the driving module (screw-drive) and the mode-switching module, are presented in Supplementary Table S4.

Table 1 Kinematic parameters of the fractal gripper.
Full size table

In the screw-drive component of the driving mechanism, a single shaft output micro-gear motor is employed, with a load velocity nload = 40 rpm. The rotary screw, being a single-threaded screw (Z = 1), has a pitch (P) set to 7 mm. The velocity of the movable nut is V = nload × P × Z = 4.67 mm/s, which determines the opening velocity of the fractal gripper. In the case of constant motor velocity, the velocity of the movable nut (V) increases with the pitch of screw. The motor revolution (φ) is defined as φ = L/(P × Z) = 2.14 revolutions, where the travelling distance of the movable nut L is set to be 15 mm.

In addition, the screw-drive mechanism possesses a self-locking characteristic, which is triggered when the helical rise angle is less than the equivalent friction angle between the thread faces. Actually, the self-locking behavior in the screw-drive mechanism is designed to prevent uncontrolled backward or reverse motion in the absence of an external force. The motion mechanism of the fractal gripper is shown in Fig. 3. The operational mechanism of the fractal gripper mainly includes the driving module and the mode-switching module, as shown in Fig. 3a. The motion mechanism of the driving module is represented by the state change from ① to ②, illustrating the movement of the movable nut by 10 mm from its initial position. The motion mechanism of the mode-switching module is represented by the state change from ③ to ④. After switching from the grasping mode to the gripping mode, the movable rod travels at a distance of s = 19 mm (Fig. 3a), and the floating support seat rotates by 50° as well as the floating gear seat.

Fig. 3
figure 3

The motion mechanism of the fractal gripper. (a) The motion mechanism of the driving module and mode-switching module of the fractal gripper is demonstrated by using the state diagram. (b) The mode-switching process of the fractal gripper is shown, where ③ is the grasping mode and ④ denotes the gripping mode.

Full size image

Switchable mode of the fractal gripper

The mode-switching functionality is realized by a specific-designed module, including worm-and-gear biaxial microform motor, axle drive bevel pinion, idler, floating gear seat, floating support seat, movable rod and movable rod fitting (Fig. 2a). The design of mode-switching module is depicted in Fig. 3b.

During the mode-switching process, the worm-and-gear biaxial microform motor is utilized to actuate the axle drive bevel pinion, which delivers the idler to actuate the floating gear seat, achieving the state of bilateral reverse rotation. The floating gear seat then causes the rocker to rotate. Cylindrical bores within the floating support seat can accommodate the movable rod and its fittings to facilitate relative movement of the rocker. The mode-switching of the fractal gripper is dynamically demonstrated in Supplementary Movie S1.

Switchable mode is achieved by using a single motor. Figure 3b illustrates the switching process, which is realized by the cooperation between the movable rod and its fitting to ensure a smooth transition. Three rockers are involved in the mode switching, which two of them are rotatable and the other one is non-rotatable. The rotation of rocker is controlled by the floating gear seat and the fixed support seat. Combining with the oscillating rod and the floating support seat, the fixed support seat enables only one rocker to swing back and forth. While, integrating with the floating gear seat, the movable rod, the movable rod fittings and the floating support seat, the other two rockers are designed to be compatible with both rotating and swinging.

In the switchable mode, the micro-gear motor is of a dual-axis output type, featuring a symmetrical gear transmission structure with mirror symmetry on both sides. Its output shaft is matched with the active bevel gear, allowing the idler to drive through the active bevel gear. The idler, comprising a combination of the driven bevel gear and the straight-tooth cylindrical gear, interacts with the floating gear holder to facilitate the rotation of the rocker. The active bevel gear is specified with Z1 = 20, the driven bevel gear with Z2 = 30, the straight-toothed cylindrical gear within the idler gear with Z3 = 18, and the floating gear seat with Z4 = 30. The loading velocity of the output shaft of the switchable mode motor is given as n1 = 14 rpm, and the velocity of the floating gear seat, denoted as n4, can be derived based on the gearing ratio formula that relates the number of teeth to rotational velocity, as per Eq. (1).

$$\frac{{z_{2} \cdot z_{4} }}{{z_{1} \cdot z_{3} }} = \frac{{n_{1} }}{{n_{4} }}$$
(1)

The rotational velocity of the floating gear seat is found to be n4 = 5.6 rpm, which contributes to the safety and stability of the mode-switching process by maintaining low velocity. Every gear should have enough teeth to ensure that the transmission mechanism possesses adequate bearing capacity.

Grasping mode involves more comprehensive contact to envelop or encircle the targeted object, which is usually applied to handle with soft objects, such as fruits, vegetables and so on. While gripping mode makes use of the opposing force to directly clamp onto an object, which requires the object to have stable points that can be gripped. To this end, gripping is typically used for harder objects that require a smaller contact area. The operation is simple, primarily relying on direct force opposition to keep the object stable. The switchable mode enables the fractal gripper to deal with more objects in different shapes and sizes.

Printing of the fractal gripper

The fractal gripper prototype developed in this manuscript is fabricated using the fused deposition modelling (FDM) process and Polylactic acid (PLA) material. The prototype is fabricated using 3D printing technology and the Bambu Lab X1-Carbon 3D printer for structural printing. The manufacture process is realized by 3D printer, which converts our designed models to physical prototypes and accelerates the design-to-realization cycle. Polylactic acid (PLA) is selected as printing material owing to its reliable strength and low cost, which is very helpful to conceptualize, validate and iterate the design of the fractal gripper. In the future, the ultimate design can be printed with high-performance materials, such as carbon fiber-reinforced plastics or metal alloys, to cater to practical demanding scenarios. Currently, the total mass of the PLA fractal gripper is 0.445 kg, assembled with screws, nuts, springs, and the motor. The fabrication details of the fractal gripper can be found in the Supplementary Materials. Supplementary Tables S1 to S3 list the parts of the fractal gripper and the STL file names for these parts. All STL files and 3D models of the fractal gripper are shown in Supplementary Data file S1 to S2.

Addition of springs for self-recovery

The self-recovery functionality of the fractal finger is achieved by attaching springs to the assembled structure. The cylindrical pin or wire is used at the outer side of the fractal structure to secure one end of the spring and lap the other end to inner side. The size of the springs is selected according to the dimensions of the T-slots. It is recommended that two springs of the same type can be placed side by side in each T-slot. This arrangement helps to prevent the torsional entanglement of individual spring during relative rotation of the fractal parts. The self-recovery feature of the fractal gripper is demonstrated in Supplementary Movie S2.

In practical grasping, the presence of springs introduces additional elastic forces, particularly in the equilibrium grasp state. However, these elastic forces do not significantly affect the distribution and magnitude of the contact force. This is because, in the equilibrium grasp state, the spring enhances the applied force of the fractal fingers through its restoring force, improving the reliability of the grasp without altering the contact force distribution or compliance effect. This feature is attributed to the driving module in the fractal gripper design, which achieves the linkage of the three fractal fingers through screw-drive mechanism. The spring constraints in the fractal structure and the self-locking characteristics of the driving module together provide a dual safety guarantee. Specifically, the spring system achieves a balanced distribution of contact force in space through preload force equilibrium. Meanwhile, the screw-drive mechanism, with self-locking characteristics, ensures that the fractal fingers do not reverse open during stable grasping. This mechanism maintains the balanced stability of the grasped object and prevents the contact points from slipping during the stable state. During the closing contact between the fractal gripper and the object, the fractal structure automatically adjusts its shape due to compression, and the spring adapts accordingly. Meanwhile, the restoring force of the spring helps maintain stability during the grasping process. When the object undergoes slight displacement disturbance, the spring’s elastic force can quickly adjust the finger’s position, thus maintaining the grasping stability.

Assembly of the mode-switching module

The assembly of the mode-switching module requires contains the following steps:

  1. (1)

    The axle drive bevel pinion is installed first on the output shaft of the worm-and-gear biaxial microform motor, using a transition fit;

  2. (2)

    The floating gear seat is assembled on the support plate;

  3. (3)

    The idler is assembled;

  4. (4)

    The worm-and-gear biaxial motor is assembled.

Attention should be paid to the fit between the gears. Additionally, ensure the mirror image arrangement of the floating gear seat on both sides. The driving torque is passed on from the axle drive bevel pinion to the idler and to the floating gear seat. Based on this process, the switchable mode is realized with the help of the floating support seat and the movable rod. The remaining assembly details for the fractal gripper can be found in the Supplementary Information.

Results

Formulated description of the fractal finger

Burdick and Tisdale55 laid the theoretical groundwork for fractal finger and fractal hand in two-dimensional planes. Building on this foundation, we extend these theories to three-dimensional grasping with fractal gripper, providing a detailed explanation of the motion mechanisms of fractal finger and fractal gripper presented. First, we present an in-depth description of the geometric structure of fractal finger and the contact theory between the fingertip and object, as illustrated in Fig. 4. This paper assumes that there is only a single point of contact between the fractal finger’s fingertip and the object. This assumption implies that at the point of contact, the relative curvature between the fingertip and the object is positive.

Fig. 4
figure 4

Geometry and description of the fractal finger. (a) Diagram of the geometrical structure of the fractal finger and the fingertip Link. (b) Diagram of the torque balance condition. (c) Diagram of the overlap model of the fingertip with the object.

Full size image

A single-plane fractal finger is composed of rigid links connected by revolute joints, which are arranged in a binary tree structure. The base joint serves as the root node of the tree, and a fractal finger with t-level consists of (t-1) levels of sub-joints below the base joint, resulting in a total of (t-1) revolute joints55.

The base joint angle and joint axis are defined as η1 and J1, respectively. For the sub-joints, both the joint and rotation angles are denoted with two subscripts: i ∈ {2, …, t} represents the level of the joint in the joint tree, and j ∈ {1, …, 2i-1} indexes the joints in order within each level. The joint angle vectors of the fractal finger are organized by hierarchical levels, as per Eq. (2).

$$\vec{\eta } = \left[ {\eta_{1} ;\eta_{2,1} ,\eta_{2,2} ;\eta_{3,1} , \ldots ,\eta_{3,4} ; \ldots ;\eta_{t,1} , \ldots ,\eta_{{t,(2^{t} - 1)}} } \right]^{T}$$
(2)

At the ith-level (for i = 1, …, t-1), each finger segment li, j is connected to its parent segment in the (i-1) level via a single revolute joint and is connected to its two child segments at the (i + 1) level through revolute joints. Connections at the same level are sequentially indexed using the subscript j. The base joint is connected to the base link and the rocker. A finger base frame, denoted as Bi for i ∈ {1, 2, 3}, is attached to the base of each finger (see Figs. 4b and Fig. 5a).

Fig. 5
figure 5

Coordinate system establishment of the fractal gripper and fingertip pressure measurement experiment. (a) Diagram of the reference coordinate system and the base frame of the fingers for the fractal gripper. (b) Layout diagram of the sensor attachment sequence at the fingertips of the fractal finger. (c) Fingertip pressure measurement experiment for the fractal gripper in the grasping mode. (d) Processed 12-channel fingertip pressure curves under equilibrium grasp conditions.

Full size image

The origin of each link’s body fixed reference frame coincides with the axis of the parent joint, and its x-axis bisects the sub-joint. All links at the same level have uniform dimensions, defined as follows (see Fig. 4a): The finger link width, \(d_{w}^{i}\) for i = 1, …, t − 1, refers to the distance between the axes of the sub-joints at joint level i. The link pitch, \(d_{p}^{i}\) for i = 1, …, t − 1, is equal to the height of the isosceles triangle formed by the ith-level links.

The distal fingertip links are connected to their parent links through revolute joints at the tth-level. The reference frame Fk is located at the center of the fingertip. The distance from joint Jn, k to the origin of frame Fk is r, and all contact surfaces have a curvature κ. The thickness of the flexible body is h, and it satisfies the relation \(r = h + d_{p}^{i}\).

A fractal gripper is composed of three fractal fingers, each of which is connected to a movable nut through a rocker. A single drive motor combined with a screw transmission mechanism can enable the synchronized movement of the three fractal fingers. We model this motion as a prismatic joint, where the movable nut performs linear movement. The composite vector representation of the fractal gripper joint angles is given by Eq. (3). Where L is the Travelling distance of the movable nut, see Fig. 2b and Table 1.

$$\Phi = (\eta_{1} ,\eta_{2} ,\eta_{3} ,L)^{T}$$
(3)

The fractal finger and fractal gripper Jacobian

The derivation of the Jacobian matrix for the fractal finger and fractal gripper serves the following purposes: (1) Describing Kinematic Relations: The Jacobian matrix is used to characterize the relationship between the joint velocities of the fractal structure and the end-effector velocity (e.g., fingertip). With the Jacobi matrix, it can analyze the end-motion characteristics of the fractal gripper under different joint motions. (2) Analyzing Force and Torque Transmission: The transpose of the Jacobian matrix maps the forces and torques on the end-effector to the joint space, enabling the analysis of force and torque distribution during the grasping process. (3) Studying Equilibrium Grasp Condition: The Jacobian matrix allows the analysis of the equilibrium grasp condition of the gripper during object grasping.

A t-level fractal finger has 2t−1 fingertip links. Let \(V_{k} = (x_{i,k} ,y_{i,k} ,\dot{\phi }_{i,k} )^{T} ,k = 1, \ldots ,2^{t - 1}\), denote the rigid body velocity of the kth fingertip frame Fk in Bi. The fractal finger Jacobian JF, i (ηi), of the ith finger maps the 2t − 1 joint velocities to the velocity triplets of the 2t−1 fingertip frames. Let \(\vec{\xi }_{i,j}\) denote the vector, as per Eq. (4).

$$\vec{\xi }_{i,j} = \left[ {\begin{array}{*{20}c} {M\overrightarrow {s}_{ij,k} } \\ 1 \\ \end{array} } \right],\,M = \left[ {\begin{array}{*{20}c} 0 & { - 1} \\ 1 & 0 \\ \end{array} } \right]$$
(4)

where \(\vec{\xi }_{i,j}\) is a vector formed by combining the displacement vector from the jth joint of the ith level to the fingertip and the corresponding rotation matrix. The vector \(\vec{s}_{ij,k}\) represents the vector from joint Ji, j​ to the origin of Fk​. The fractal finger Jacobian matrix is a (3 × 2t−1) × (2t − 1) matrix.

The rigid body velocity of the kth fingertip frame Fk in Bi, as per Eq. (5).

$$V_{k} \, = J_{F,i} (\eta_{i} )\dot{\eta }_{i}$$
(5)

where JF, i (ηi) is the Jacobian matrix corresponding to the fractal finger. \(\dot{\eta }_{i}\) is the vector of joint angular velocities. The specific form of the Jacobian matrix JF, i (ηi) is given in Supplementary Equation (S.1).

The matrix \(J_{F}^{T}\) maps the torques of the 2t−1 fingertip frames to the torques of the 2t − 1 joints. The origin of each fingertip contacts frame Ci, j is located at the contact point, with its x-axis defined as the outward unit normal vector of the fingertip surface (see Fig. 4a).

The corresponding contact frame on the object, denoted as \(C_{i,j}^{O}\), also has its origin at the contact point. Its x-axis is an outward-pointing unit vector from point O, and it is parallel but in the opposite direction to the x-axis of Ci, j. The vector \(\vec{c}_{i,j} (\eta_{i} )\) points from the origin of the coordinate frame Bi to the origin of the coordinate frame Ci, j for the jth fingertip of the ith finger. Let \(\vec{f}_{i,j}\) denote the contact force between the jth fingertip of the ith finger (i ∈ {1,2,3}) and O. Let Wi, j denotes the wrench basis of the contact model for the jth fingertip, which describes the forces that can be supported at the contact point in frame Ci, j. The matrix Wi, j reflects the direction and possible magnitudes of contact forces under a given contact model, and it is used to compute the stability and force distribution when the finger is in contact with an object. The matrix Wi, j takes the form of either a frictionless point contact model and a point contact with friction model:

$$W_{i,j} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ \end{array} } \right],W_{i,j} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ 0 & 0 \\ \end{array} } \right]$$

Let \(\vec{f}_{i}\) denote the vector of all finger i contact forces, as per Eq. (6).

$$\vec{f}_{i} = (\vec{f}_{i,1} ,\vec{f}_{i,2} , \cdots ,\vec{f}_{{i,2^{t - 1} }} )^{T}$$
(6)

The block diagonal matrix \(\widetilde{W}_{i}\) organizes all the contact models of the ith finger (i = 1, 2, 3), as per Eq. (7).

$$\widetilde{W}_{i} = \left[ {\begin{array}{*{20}c} {W_{i,1} } & 0 & \cdots & 0 \\ 0 & {W_{i,2} } & \cdots & 0 \\ \vdots & \cdots & \ddots & \vdots \\ 0 & \cdots & 0 & {W_{{i,2^{t - 1} }} } \\ \end{array} } \right]$$
(7)

Let \(\vec{f} = \left[ {\vec{f}_{1} ,\vec{f}_{2} ,\vec{f}_{3} } \right]\) denote the contact force vector for all the fractal gripper fingertips.

The fractal gripper Jacobian matrix JH (Φ) relates the joint velocities of the hand to the fingertip velocities that can be transmitted to point O. It includes the effect of the movable nut. In most analyses, under the equilibrium grasp conditions, the contact frame Ci, j and the fingertip frame Fi, j are coincident55. The matrix \(T_{{CB_{i} }}^{i}\) transforms the velocities of all 2t-1 contact frames from the representation in the Bi frame to their respective contact frames, as shown in Eq. (8).

$$T_{{CB_{i} }}^{i} = \left[ {\begin{array}{*{20}c} {\left( {T_{{B_{i} C_{i,1} }}^{i} } \right)^{ - 1} } & \cdots & {\left( {T_{{B_{i} C_{{1,2^{t - 1} }} }}^{i} } \right)^{ - 1} } \\ \end{array} } \right]^{T}$$
(8)

Equilibrium grasp conditions of the fractal gripper

In the equilibrium grasp of a three-finger fractal gripper, the fingertip contact force, \(\vec{f}^{eq}\), applied to O must result in a zero net torque at O: \(G\vec{f}^{eq} = \vec{0}\). Here, G is the grasp mapping matrix, which has the form G = [G1, G2, G3]. Each submatrix Gi (i ∈ {1, 2, 3}) represents the contact mapping for each finger. The grasp mapping matrix Gi for each finger is defined in Supplementary Equation (S.2). To simplify the analysis, we examine the case of frictionless contact. A similar conclusion can be drawn for the case of contact with friction.

As shown in Fig. 4(b), the line of action of the contact force applied to the jth frictionless fingertip must pass through the axis of joint Jt, j; otherwise, an unbalanced torque will be generated at Jt, j. Let τt, j represent the torque around joint Jt, j. Consider two adjacent t-level fingertip links, lt, j ​and lt, j+1, which are connected to the same parent link. The lines of action of the contact force vectors \(\vec{f}_{t,j}\) and \(\vec{f}_{t,j + 1}\) must pass through the axes of the joints to which their respective fingertips are connected. The magnitude and direction of the contact forces must satisfy the net zero-force equilibrium condition at the (t-1) level parent joint, as per Supplementary Equation (S.3). Under frictionless contact, the angles ηt, j for all j in the equilibrium grasp are determined by the shape of the object and its orientation within the hand. Supplementary Equation (S.4) is solely a function of the scalar forces ft, j and ft, j+1. Similar constraints must be recursively applied to the parent joints, ultimately applying to the base joint (see Fig. 4b).

The fractal gripper can securely grasp objects in space while in the equilibrium condition. Even if the finger joints are undriven, the hand can still stably hold the object. Consider a three-finger fractal gripper grasping a rigid object O under frictionless contact conditions, with the grasp in the equilibrium state q0. When the object O is slightly perturbed from its equilibrium state by a small displacement \(\dot{q}\), the joints η1, η2​, η3 of the fractal finger remain momentarily stationary. The velocity of the object-side contact frame associated with the ith finger is defined in Eq. (9).

$$V_{{C_{i}^{O} }} = T_{{OC_{i}^{O} }}^{ - 1} \dot{q}$$
(9)

where the matrix \(T_{{OC_{i}^{O} }}^{ - 1}\) transforms the velocity of the object into the velocities of the 2t-1 contact frames.

The velocity of the corresponding fingertip contact frame is transmitted through the contact normal line, as described in Eq. (10).

$$V_{{C_{i} }} = \widetilde{W}_{i}^{T} T_{{C_{i} C_{i}^{O} }} V_{{C_{i}^{O} }}$$
(10)

where the matrix \(T_{{C_{i} C_{i}^{O} }}\) converts the velocities of the contact frames on the object into the coordinate frame of the finger contact frames. The velocity of the finger contact frames can be expressed in terms of the joint velocities of each finger, as shown in Eq. (11).

$$V_{{C_{i} }} = J_{F,i} (\eta_{i,0} )\dot{\eta }_{i}$$
(11)

By combining the above equations (Eqs. 9–11), the following relationship can be derived, as shown in Eq. (12).

$$J_{F,i} (\eta_{i,0} )\dot{\eta }_{i} = \widetilde{W}_{i}^{T} T_{{C_{i} C_{i}^{O} }} T_{{OC_{i}^{O} }}^{ - 1} \dot{q}$$
(12)

where the joint velocities \(\dot{\eta }_{i}\) that satisfy Eq. (12) correspond to the kinematic joint responses to the displacement perturbation of object O. The set of all possible solutions to Eq. (12) can be seen in Supplementary Equation (S.5).

Analysis of compliance effects and fingertip pressure

Although the fingertips and the body of the object may be rigid, in reality, their materials are elastically deformable. When the object and the fingertips are pressed against each other, their surfaces will deform according to the magnitude of the contact forces. This approach assumes that the shapes of the rigid fingertips and the object can virtually penetrate each other when pressed together, with the net interaction force modeled as a function of this virtual overlap (see Fig. 4c). The overlap δj (Φ, q) between fingertip j and object O is defined as the minimum translation required to separate the undeformed shape of the fingertip from the undeformed shape of the object.

The Hertz contact model can accurately capture the interaction using the contact force function fj = kδj3/2, where the constant k depends on the geometry and material properties at the contact point. The contact force model fj = kδj is a good approximation of a linear spring compliance relationship55,56,57.

The stiffness matrix of a single finger can be derived from the expression for the potential energy Π(⋅), as shown in Eq. (13). This energy arises when the finger deviates from its equilibrium posture (q0, Φi,0) due to disturbances affecting both the object and the finger mechanism.

$$\Pi (u) = \mathop \sum \limits_{j = 1}^{{2^{t - 1} }} \mathop \smallint \nolimits_{{\delta_{j} (u_{0} )}}^{{\delta_{j} (u)}} f_{j} (\delta_{j} )\frac{{d\delta_{j} }}{dt}dt = \mathop \sum \limits_{j = 1}^{{2^{t - 1} }} \mathop \smallint \nolimits_{{\delta_{j} (u_{0} )}}^{{\delta_{j} (u)}} f_{j} (\delta_{j} )d\delta_{j}$$
(13)

where the contact force fj (δj) is generated by the compliant interaction between the jth fingertip (flexible body) and object O, and u is a simplified notation representing u = (q, η)T. The scalar normal force fj acts along the normal Nj to the contact surface, and δj represents the virtual overlap (see Fig. 4c). The integrand in Eq. (13) represents the work done by the normal force through the differential displacement of the contact surface.

Assuming there are no losses in the finger mechanism (e.g., joint friction) and no losses during material deformation (e.g., heat dissipation), the integral in Eq. (13) is independent of the specific path followed by the fingertip55. Therefore, Π(u) is conservative and can be evaluated using the following rules, as per Eq. (14).

$$\frac{d}{du}\mathop \smallint \nolimits_{g(u)}^{h(u)} \vec{f}_{j} (\sigma_{j} )d\sigma_{j} = \vec{f}_{j} (h(u)) \cdot \frac{dh(u)}{{du}} - \vec{f}_{j} (g(u)) \cdot \frac{dg(u)}{{du}}$$
(14)

Using this rule, the gradient of Π(u) takes the form, as per Eq. (15).

$$\nabla_{u} \Pi (u) = \mathop \sum \limits_{j = 1}^{{2^{t - 1} }} f_{j} (u)\nabla_{u} \delta_{j} (u)$$
(15)

The Hessian matrix of Π(u) at the equilibrium grasp point defines the stiffness matrix of the finger, as per Eq. (16).

$$\nabla_{u}^{2} \Pi (u_{0} ) = \mathop \sum \limits_{j = 1}^{{2^{t - 1} }} \underbrace {{\frac{{df_{j} }}{{d\delta_{j} }}(\nabla_{u} \delta_{j} \nabla_{u} \delta_{j}^{T} )}}_{{1^{st} - order,K^{1} }}|_{{u_{0} }} + \underbrace {{f_{j} \nabla_{u}^{2} \delta_{j} }}_{{2^{nd} - order,K^{2} }}|_{{u_{0} }}$$
(16)

To analyze the equilibrium grasp, we assume that the movable nut of the fractal gripper is locked in place when in equilibrium. In the case of three fingers, for small instantaneous perturbations of the fingers and the object, the potential energy of the fractal gripper and object system is expressed by Eq. (17).

$$PE = \dot{u}_{1}^{T} (K_{1}^{1} + K_{1}^{2} )\dot{u}_{1} + \dot{u}_{2}^{T} (K_{2}^{1} + K_{2}^{2} )\dot{u}_{2} + \dot{u}_{3}^{T} (K_{3}^{1} + K_{3}^{2} )\dot{u}_{3}$$
(17)

Equation (17) represents the total elastic energy of the three fingers under their respective stiffness matrices. See Supplementary Equation (S.6) for the corresponding matrix equation. The potential energy of each finger is determined by both its linear stiffness and nonlinear stiffness. The linear stiffness components (e.g., \(K_{1}^{1} ,K_{2}^{1} ,K_{3}^{1}\)) describe the linear elastic response of the fingers under small displacements. The nonlinear stiffness components (e.g., \(K_{1}^{2} ,K_{2}^{2} ,K_{3}^{2}\)) describe the nonlinear elastic response of the fingers under large displacements or complex contact conditions.

The stiffness matrix \(K_{i}^{1} + K_{i}^{2}\)( i ∈ {1, 2, 3}) represents how each finger resists deformation during contact. Understanding the stiffness matrix of each finger can help optimize the finger design to enhance the stability and adaptability of the grasp.

The potential energy function PE is the sum of the potential energies of all the fingers. This means that PE encompasses the energy state of the entire system under small perturbations, describing the local stability of the system. If PE is positive definite with respect to the velocities of each finger (i.e., PE is a positive definite function of \(\left( {\dot{q},\dot{\eta }_{1} ,\dot{\eta }_{2} ,\dot{\eta }_{3} } \right)^{T}\)), then the gripper and object system is locally compliantly stable. We are only concerned with the gripper and object response to perturbations of O.

The form of the 1st-order stiffness term in Eq. (16) is:

$$K_{i}^{1} = \mathop \sum \limits_{j = 1}^{{2^{t - 1} }} f^{\prime}_{j} \left[ {\begin{array}{*{20}c} {\nabla_{q} \delta_{j} \nabla_{q} \delta_{j}^{T} } & {\nabla_{q} \delta_{j} \nabla_{{\eta_{i} }} \delta_{j}^{T} } \\ {(\nabla_{q} \delta_{j} \nabla_{{\eta_{i} }} \delta_{j}^{T} )^{T} } & {\nabla_{{\eta_{i} }} \delta_{j} \nabla_{{\eta_{i} }} \delta_{j}^{T} } \\ \end{array} } \right]_{{u_{0} }}$$

where \(K_{i}^{1}\)(i ∈ {1, 2, 3}) is used to quantify the changes in contact forces and torques caused by small variations in the object position q and finger joint angles ηi near the equilibrium position. The individual blocks of the matrix represent the different effects of object position and finger joint angles on the displacement of the contact points. By calculating the outer product of these gradients, the stability and compliance of each fractal finger in the fractal gripper during grasping tasks can be analyzed.

The quadratic form \(u^{T} (K_{1}^{1} + K_{2}^{1} + K_{3}^{1} )u\) is given by:

$$u^{T} (K_{1}^{1} + K_{2}^{1} + K_{3}^{1} )u = \dot{q}^{T} (\mathop \sum \limits_{i = 1}^{3} \mathop \sum \limits_{j = 1}^{{2^{t - 1} }} f^{\prime}_{i,j} \nabla_{q} \delta_{i,j} \nabla_{q} \delta_{i,j}^{T} |_{{u_{0} }} )\dot{q}$$

For a hardening spring model, fj′ = dfj/dδj is always positive, thus the 1st-order stiffness matrix is positive definite. Since the 1st-order stiffness term is positive definite, to ensure the stability of the grasp on the object, it is sufficient to show that the 2nd-order stiffness contributions \(K_{1}^{2} ,K_{2}^{2} ,K_{3}^{2}\) do not undermine the stability of the 1st-order term. The quadratic contribution to the potential energy is given by:

$$u^{T} (K_{1}^{2} + K_{2}^{2} + K_{3}^{2} )u = \dot{q}^{T} (\mathop \sum \limits_{i = 1}^{3} \mathop \sum \limits_{j = 1}^{{2^{t - 1} }} f_{i,j} \nabla_{q}^{2} \delta_{i,j} |_{{u_{0} }} )\dot{q}$$

For the frictionless fingertip contact model, the form of \(\nabla_{q}^{2} \delta_{j}\) is:

$$\nabla_{q}^{2} \delta_{i,j} = \frac{1}{{r_{F} + r_{{O_{i,j} }} }}\left( {\begin{array}{*{20}c} {\vec{n}_{i,j} \vec{n}_{i,j}^{T} - I} & {(r_{{O_{i,j} }} - \rho_{i,j} )M\vec{n}_{i,j} } \\ {(r_{{O_{i,j} }} - \rho_{i,j} )(M\vec{n}_{i,j} )^{T} } & {(r_{F} + \rho_{i,j} )(r_{{O_{i,j} }} - \rho_{i,j} )} \\ \end{array} } \right)$$

where \(\vec{n}_{i,j}\) is the unit normal vector at the boundary of the jth contact point of the ith finger. The scalars \(r_{{O_{i,j} }}\) and \(r_{F}\) are the radii of curvature at the contact points on the object and the fingertip, respectively, while \(\rho_{i,j} = \vec{n}_{i,j} \cdot \vec{p}_{i,j}\) represents the projection of the vector \(\vec{p}_{i,j}\), which points from the origin of frame O to the jth contact point of the ith finger, onto the direction of \(\vec{n}_{i,j}\).

\(\vec{p}_{i,j}\) is the vector from the origin of frame O to the jth contact point of the ith finger. The matrix M is defined in Eq. (4). For most practical designs, it is unlikely that the 2nd-order terms will destabilize the system. First, note that for most engineering materials, fi,j′ >  > fi,j. This means that the 1st-order stiffness terms play a dominant role in the overall stiffness contribution. Compared to the 2nd-order stiffness terms, the 1st-order stiffness terms have a more significant impact on system stability55. Therefore, the potential destabilizing effect of the 2nd-order terms becomes relatively unimportant. Secondly, if the curvature radii of the fingertips are relatively flat, then rF >  > 1, so 1/(rF + rOi,j) <  < 1. Therefore, with appropriate design constraints, the fractal gripper can be ensured to be compliantly stable when performing equilibrium grasp.

Based on the above analysis, it is concluded that the fractal gripper and object system is locally compliantly stable. Based on the grasping model of the fractal gripper, we conducted fingertip pressure measurement experiments. Measurements were conducted using a 12-channel thin-film pressure sensor. Diagram depicting the reference coordinate system and the base frame of the fingers in the fractal gripper, as shown in Fig. 5a. The attachment sequence of the 12-channel pressure sensors at the fingertips is shown in Fig. 5b.

The hardware setup for the fingertip pressure measurement experiment of the fractal gripper in the grasping mode is detailed in Fig. 5c. It specifically illustrates the configuration of the sensors, gripper structure, and associated measurement devices used in the experiment. This setup is designed to accurately capture the pressure distribution at the fingertip during the grasping process, providing a reliable experimental foundation for subsequent data analysis.

The thin-film pressure sensors are attached to the flexible bodies of each finger, and the object being grasped in the experiment is a water bottle. In the equilibrium grasp state, we recorded a set of 2-s pressure curves from the fingertip pressure sensors (labeled A0 to A11), as shown in Fig. 5d. From these 12 pressure curves, it can be observed that the stabilization of the closing and balancing process of the three fractal fingers occurs after approximately 1.75 s, with pressure values showing minimal fluctuations thereafter. The fluctuations in the pressure curves are largely due to the assembly precision of the mechanical structure and the force-balancing process during the fractal gripper’s operation. Additionally, it is evident that when the fractal gripper maintains equilibrium while grasping the water bottle, the contact pressures exerted by the fingertips are well-distributed, effectively protecting the geometric surface of the object.

This paper primarily focuses on the performance of the fractal gripper during the stabilization process of grasping. We have analyzed the stability of the equilibrium grasp and provided supporting arguments. It is evident from the fingertip pressure measurement experiments of the fractal gripper that, in the equilibrium grasp condition, the fingertip pressures remain stable without significant fluctuations. Each fingertip sensor shows pressure feedback, indicating that the contact pressure is evenly distributed at the fingertips, which is a unique characteristic of fractal fingers. Additionally, the screw transmission mechanism in the fractal gripper has a self-locking feature that helps maintain the stability of the grasp, preventing the object from loosening even if the drive motor loses power.

A detailed analysis of the 12-channel fingertip pressure data shown in Fig. 5d was conducted, and the results are presented in Fig. 6.

Fig. 6
figure 6

Bar chart analysis results corresponding to the fingertip pressure curves of the fractal gripper. (a) Peak pressure. (b) Average pressure. (c) Pressure change rate. (d) Pressure variability (standard deviation).

Full size image

During the fingertip pressure tests, the performance metrics of the fractal gripper include peak pressure, average pressure, pressure change rate, and pressure variability. Peak pressure refers to the maximum pressure detected by each sensor, with the highest recorded by sensor A4 (2.6460 N) and the lowest by A8 (0.7056 N). Average pressure reflects the mean pressure over time, with sensor A4 showing the highest (2.3006 N) and A8 the lowest (0.6055 N). The pressure change rate, indicating the speed of pressure variation, is highest in A6 (0.0039 N/ms) and lowest in A8 (0.0014 N/ms). Pressure variability, representing the standard deviation of pressure readings, is greatest in A10 (0.1361 N) and lowest in A8 (0.0571 N). Analysis of peak pressure, average pressure, pressure change rate, and pressure variability reveals that sensors A1, A4 and A10 experienced higher sustained pressures, indicating their ___location in primary force-bearing areas. Supported by the other fingertips, the fractal gripper achieves effective pressure distribution during equilibrium grasp. Additionally, the self-locking mechanism and synergy between the three fractal fingers ensure local compliant stability of the gripper and object system under small perturbations.

In the fingertip pressure measurement experiments of the fractal gripper, we primarily tested the grasping mode and have demonstrated its ability to achieve stable enveloping grasps of complex objects. It should be noted that in the gripping mode of the fractal gripper, not all fingertips necessarily make contact with the object’s surface. Some edge fingertips of the fractal fingers may not touch the geometric surface of the object, resulting in the main grasp force being concentrated in the central parts of the fractal fingers. Therefore, the force distribution in the gripping mode is not as optimal as in the grasping mode. The analysis of this experimental phenomenon is as follows: The different modes of the fractal gripper exhibit variations in selecting the surfaces of the object to grasp, and the grasp postures also differ. For example, in the water bottle grasp experiment, a brief analysis of the force distribution is provided in Supplementary Fig. S6. In the grasping mode, four flexible bodies in each fractal gripper come into contact with the surface of the bottle, resulting in a more pronounced force distribution effect.

Comparative experiment of fractal gripper and planar gripper

To highlight the force distribution characteristics of the fractal gripper, we conducted a comparative experiment. The pressure curves for the comparative experiment were standardized over a unified time interval, and all data were collected during the equilibrium grasping state. Note that all fingertip pressure data were collected under the motor’s gridlock torque of the drive module. The subjects of the experiment were the fractal gripper and the planar gripper, and the object being grasped was a water bottle. The geometric design of the planar gripper is identical to that of the fractal gripper, but the contact surface is a plane. The physical comparison of fractal finger and planar finger is shown in Supplementary Fig. S7. Soft materials were attached to the contact surfaces of each finger, with pressure sensors placed in the same locations on both the planar and fractal fingers. Both grippers were made from the same material, using 3D printing for fabrication. In the planar gripper experiment, only contact points A1, A5 and A9 exhibited surface pressure. Therefore, the comparative data analysis focuses on the fingertip pressure of these three points, as shown in Fig. 7. In this data analysis, the planar gripper is simplified as ‘Planar’, and the fractal gripper is simplified as ‘Fractal’.

Fig. 7
figure 7

The experimental results of the comparison between the fractal gripper and the planar gripper (groups A1, A5 and A9).

Full size image

The specific comparison of fingertip pressure curves (12-group fingertip pressure data) between the Fractal and Planar grippers is visualized in Supplementary Fig. S8. In the data sets from A0 to A11, groups A1, A5 and A9 show distinct differences. Under the Planar condition, the pressure is significantly higher. Group A1 records 4.94 N, group A5 records 3.54 N, and group A9 records 3.52 N. The standard deviations are minimal, indicating high data concentration. Conversely, under the Fractal condition, the pressure is much lower. Group A1 measures 2.13 N, group A5 measures 0.71 N, and group A9 measures 0.69 N. The standard deviations are also relatively small, reflecting a concentrated data distribution. These results suggest that, in groups A1, A5 and A9, the pressure under the Planar condition is considerably higher than under the Fractal condition.

The statistical analysis of the 12-group fingertip pressure data from the comparative experiment is shown in Fig. 8. See Supplementary Table S7 for detailed comparison of fingertip pressure data.

Fig. 8
figure 8

Comparative analysis of fingertip pressure of fractal gripper and planar gripper. In the bar chart, a bold line is placed at data where the mean pressure is zero, and 0 is labeled above this position. Error bars are included in the bar chart where the mean pressure is not zero, representing the standard deviation (std) for each data set.

Full size image

Among the data sets from A0 to A11, groups A1, A5 and A9 exhibit significant differences. Under the Planar condition, the pressure is higher, with 4.94 N in group A1, 3.54 N in group A5, and 3.52 N in group A9. The standard deviations are minimal, indicating a high concentration of data. In contrast, under the Fractal condition, the pressure is lower, with 2.13 N in group A1, 0.71 N in group A5, and 0.69 N in group A9. The standard deviations are also small, reflecting concentrated data distributions. These findings suggest that in groups A1, A5 and A9, the pressure under the Planar condition is much higher than that under the Fractal condition. The fractal gripper effectively distributes pressure when gripping objects, resulting in a more secure grasp on geometrically complex surfaces.

The experimental results show that the fractal gripper can effectively ensure the stability of grasping a regular contour and axisymmetric object. In addition, when grasping is in an unbalanced state, the stability of grasping non-axisymmetric targets primarily relies on the self-locking feature of the driving module in the three-finger linkage closure mechanism and the synergistic effect of the elastic constraints. The spring system achieves a spatially uniform distribution of contact forces through preload balance. When in contact with the non-uniform surface of an object, the underactuated characteristics of the fractal units allow each finger joint to autonomously adjust the contact posture based on the object’s contours, enabling the fractal units to continuously match the local curvature features of the object’s non-uniform surface. Therefore, as long as each finger maintains at least one contact point with the object’s surface during the grasping closure process, grasping stability can still be ensured, even if the contact targets of the fingers vary. The grasping stability of the fractal gripper primarily stems from its unique adaptive mechanism and the coupling constraint effects of multiple physical fields. During the multi-finger linkage closure process of the fractal gripper, when the fractal topological structure forms a geometrically conformal contact with the object’s surface, the system achieves stable grasping through the self-organizing distribution of contact stresses. This mechanical characteristic is attributed to the self-locking feature of the drive mechanism, which effectively suppresses the decoupling of reverse kinematics of the fractal gripper through friction angle constraints; simultaneously, the elastic components in the fractal configuration further suppress the non-equilibrium displacements of the fractal units by applying a prestress force field, ensuring dynamic balance responses at the contact interface and thereby guaranteeing the grasping stability.

Performance evaluation of the grasping space

In the fractal gripper, the grasping space is measured by the volume of triangular pyramid, which is defined by four vertices including the far end of each connecting rod (three in total) and the bottom end of the rotary screw shared by three connecting rods. The travelling distance of the movable nut L is 15 mm, which defines the size of connecting rods. Therefore, the lengths of connecting rods (oscillating rod and movable rod) are 24.67 mm and 21.12 mm, respectively.

When the mode switching process is triggered, the movable rod travels at a distance of s = 19 mm (Fig. 3a and Table 1) and the floating support seat rotates by 50° as well as the floating gear seat. The opening and closing bounds in dual modes are depicted in Supplementary Fig. S3. Besides, an axonometric diagram of the opening and closing bounds in dual modes is presented (see Supplementary Fig. S4). Meanwhile, an actualized prototype of the fractal gripper, demonstrating the opening and closing bounds in dual modes, is depicted (see Supplementary Fig. S5).

As shown in Supplementary Figs. S3 and S4, the closing state of the gripper in dual modes is indicated by the blue volume, while the opening state of that is indicated by the pink volume. A comparison of the triangular pyramid volume between the opening and closing states is presented in Supplementary Table S5. It is found that gripping mode has more opening state volume but lower increased percentage of volume than grasping mode. With the travelling distance of L = 15 mm for the movable nut, it can be seen that the triangular pyramid volume in the opening state of the grasping mode compared to the closing state is enlarged by 98.03%, and the triangular pyramid volume in the opening state of the gripping mode compared to the closing state is enlarged by 95.26%. To achieve a superior grasping space, the compactness of the overall structure must be ensured. This is achieved by rationalizing the arrangement and layout of the individual components. In design process of the fractal gripper, it is necessary to balance the strength of the grasping space with its compactness to provide stable and reliable grasping capability. Therefore, optimizing the design for superior grasping space necessitates a balance between the strength of the grasp and the compactness of the structure.

The design of the fractal gripper is based on fractal geometry, where the fingers are composed of multiple self-similar geometric units. By adjusting the depth of the fractal structure (i.e., design parameter n), the number of fingers and joints of the gripper can be controlled, thereby affecting the size range of objects it can grasp. By optimizing the joint design (such as joint angles and link lengths), the workspace of the manipulator can be expanded, enabling it to grasp objects of larger sizes.

Physical testing of the fractal gripper

To characterize the grasping capability of the fractal gripper, a physical prototype was constructed to validate its performance. The fractal gripper jaw prototype for this work was fabricated by 3D printing technology and the structure was printed on a Bambu Lab X1-Carbon 3D printer using PLA material. The dimensions of the gripper were maximized to a length of 235.7 mm, a width of 151.8 mm, and a height of 215.2 mm, with a total mass of 0.445 kg. Subsequently, a series of grasping tests were performed in versatile scenarios. In these tests, the fractal gripper is hanged from a fixed bracket and triggered by a wireless remote-control module to conduct physical grasping tasks. As shown in Fig. 9, well-designed grab experiments with objects of diverse shapes and sizes demonstrate the multi-scale adaptability and superior dual grasping stability of the fractal gripper, which implies its wide practical applications in various scenarios. Experimental records of physical grasping by the fractal gripper are enclosed in Supplementary Movies S3–S5. In addition, see Supplementary Information Movies S6 and S7 for the specific assembly process of the fractal gripper.

Fig. 9
figure 9

Physical object grasping tests of the fractal gripper. (a) In the physical grasping test, different objects with relatively symmetrical structures were grasped. The light background means gripping mode, while dark background indicates grasping mode. (b) Grasping test for objects with small dimensions and hard geometric surfaces. (c) Selects medium-sized fruits and vegetables for stable grasping without damaging the skin of the object. (d) Grasping soft dolls of different sizes and asymmetrical structures for test. (e) The fractal gripper successfully suspends the water-filled bottle with a total weight of 865 g. A larger weight was not tested, as slippage occurs at this load, potentially leading to instability.

Full size image

In the physical grasping tests with the fractal gripper, we considered differences in object soft, hard, size, shape, and performed a maximum and minimum grasping weight and size test. Figure 9a illustrates the performance of the fractal gripper in grasping relatively symmetrical objects under different modes, consistently achieving stable grasping. In order to reflect the adaptability of the gripper, more grasping experiments have been conducted. Figure 9b presents experiments involving small-sized objects in physical grasping. Among them, the egg and gourd have regular shapes, while the conch and toy exhibit irregular shapes. In Fig. 9c, medium-sized fruits and vegetables are selected for stable grasping without damaging the skin of the object. Figure 9d presents an experiment involving the grasping of large-sized objects with irregular shapes, all of which are dolls with soft surfaces. The specific measurements of each doll can be found in the Supplementary Fig. S9.

In Fig. 9d, under equilibrium grasping conditions, the height of each doll exceeds the contact surface length of the fractal fingers (95.58 mm). For example, the height of the doll-3 is 120 mm, resulting in a length ratio to the fractal fingers of 1.26 > 1. Despite the large sizes and diverse shapes of these dolls, the fractal gripper still achieves stable and adaptive grasping in the experiments. In Fig. 9e, the water-filled bottle is successfully suspended below the fractal gripper, supporting a total weight of up to 865 g. We did not challenge larger weight because the slippage occurs at that weight, which may lead to instability.

Based on our assessment and testing, the upper limit of the minimum feature scale for the grasped object is defined as 90 mm, and the weight limit is 865 g. The minimum feature scale is defined as the length of the angular bisector corresponding to the apex angle of the isosceles triangle. This isosceles triangle is located at the base of the triangular pyramid volume (see Supplementary Fig. S9b). Additionally, the Supplementary Fig. S9b shows that the maximum grasping volume accommodated by the fractal gripper in the grasping mode is 134.76 cm3. For the grasping experiments on objects with minimal weight and size using the fractal gripper, see Supplementary Fig. S10. Each test object weighs less than 5 g, and the fractal gripper achieves stable grasping relying on the fingertips of its three fingers. The smallest grasped object is a 0.2 g (dog tail grass), with a corresponding minimum diameter of 0.08 mm.

Additionally, owing to the distinctive adaptive properties inherent in the grasping mechanism of the fractal gripper, stable grasping is ensured. This capability is further strengthened by its smooth force distribution mechanism, which efficiently disperses contact pressure. Therefore, the geometric surface of soft objects, such as grapes, can be effectively protected during the grasping process. Because we attach a layer of flexible polymer, namely, polydimethylsiloxane (PDMS), to the grasping surface of the fractal fingers. The flexible layer helps prevent any scratches during the closing process of the fractal gripper, thereby protecting the geometric surface of the object. When the fractal gripper enters a fully enveloping state, all contact points of the fingers with the object work synergistically, uniformly applying compressive forces to the soft object’s surface. The deformation of the PDMS material absorbs localized stress, aligning with the mechanical properties of the grape skin. This results in a relatively smooth normal contact pressure gradient at the fingertip contact points. This prevents localized stress concentration and effectively prevents the rupture of the soft object’s surface. Moreover, even without the addition of PDMS, the current fractal gripper can still successfully grasp grapes without damaging their skin, relying solely on its adaptive functionality. To demonstrate this, we have Supplementary Information Movies S9 and provided a state diagram of the fractal gripper stably grasping grapes (see Supplementary Fig. S11).

Conclusion

In this work, a fractal gripper with switchable mode is developed. Owing to the well-designed mechanism, a multi-joint underactuated structure is proposed, which significantly improves the grabbing quality and robustness. Specifically, it perfectly demonstrates that the inherent multi-scale adaptability, the self-recovery function of the resilient design and the self-locking characteristics of the screw drive enable stable and efficient grasping of the targeted object. Meanwhile, the fractal gripper is equipped with a mode-switching functionality, which can switch between grasping and gripping mode, leading to a wider applicability.

The fractal gripper can be low-cost replicated by desktop-grade 3D printer and easily assembled due to the half-and-half design of each fractal part. Based on the analysis of compliance effects, it is concluded that the fractal gripper and object system is locally compliantly stable. Experiments demonstrate that in an equilibrium grasp, the fractal gripper maintains stable, evenly distributed pressures, with its self-locking mechanism preventing slippage even if power is lost. Inspiring from the century-old ‘Fractal Vise’ mechanism, we provide a powerful actuator for a robotic arm based on numerous physical tests. The philosophy of fractal design is anticipated to advance the structural innovation of cutting-edge robotics.

The current control system design of the fractal gripper employs an open-loop control scheme, where a wireless remote-control module regulates both the driving module and the mode-switching module, with the motor’s direction being controlled via remote control buttons. In the future, the structure and control system of the fractal gripper will undergo a comprehensive upgrade. The gripper will be mounted at the end of an industrial robotic arm, with the addition of tactile sensors to enable stable closed-loop control for grasping.