Introduction

Shale gas, a type of natural gas found in shale reservoirs, primarily resides in natural fractures and pores in both free and adsorbed states. Predominantly composed of methane, it is celebrated as a clean and efficient energy source1. As per the International Energy Agency (IEA), unconventional natural gas reserves globally surpass those of conventional natural gas, with shale gas constituting 63% of these unconventional reserves. However, the unique characteristics of shale gas reservoirs, including low porosity, low permeability, and heterogeneity, result in suboptimal production and extraction efficiency2. Consequently, improving the extraction efficiency of shale gas, especially through a deeper understanding of its gas content - the quantity and distribution of natural gas in shale, has emerged as a significant and challenging research area3.

China’s shale gas resources are predominantly found in the Upper Ordovician Wufeng Formation - Lower Silurian Longmaxi Formation, primarily located in the South China region near the Sichuan Basin4. Years of exploration have led to the industrial extraction of marine shale gas in the Sichuan Basin, with significant advancements in understanding reservoir characteristics, formation conditions, exploration evaluation, and factors controlling high yield5. Presently, seismic technology is the primary tool for shale gas exploration research. However, in the Sichuan Basin and surrounding areas, the application of seismic technology is limited and hindered by challenging surface conditions, complex underground geological conditions, significant terrain variations, complex high-steep structures, and highly developed interference waves. As a result, electromagnetic exploration is employed to offset the limitations of seismic exploration. This technology offers several benefits, including large exploration depth, no shielding by high-resistance layers, sensitive resolution to low-resistance layers, high efficiency, and low cost6. Moreover, a significant resistivity difference exists between the marine shale gas reservoir in the Sichuan Basin and the surrounding rocks, typically exhibiting low resistivity7,8. Hence, electromagnetic exploration technology has yielded promising results in shale gas exploration in southern Sichuan9. Currently, the study of shale gas content primarily involves analysis through logging parameters, seismic parameters, and rock physics parameters2. While these methods offer certain advantages in analyzing shale gas content, few studies consider the impact of resistivity and do not analyze resistivity comprehensively with logging and core parameters. This omission reduces the accuracy of the gas-bearing characteristic model and the precision of shale gas exploration. Therefore, this article addresses this issue by conducting electromagnetic exploration work in the southern Sichuan area and applying resistivity to the construction of the gas-bearing characteristic model.

Given that logging, core, and electromagnetic parameters represent different physical quantities and have intricate relationships with each other, it is not suitable to merely integrate these parameters using traditional statistical methods. Consequently, it becomes essential to identify a method capable of effectively distinguishing these parameters and constructing their inherent relationships for the creation of a gas-bearing characteristic model10. Kernel Principal Component Analysis (KPCA) holds significant application potential in the field of geophysics, primarily in areas such as dimensionality reduction, feature extraction, prediction model optimization, and data visualization. KPCA can effectively reduce the dataset’s dimensionality and extract its most crucial features11. Compared to traditional PCA, KPCA offers substantial advantages when dealing with non-linear relationships12.

Emerging machine learning methods, including Support Vector Regression (SVR), Random Forest, and Linear Regression, offer superior learning capabilities and predictive performance, providing fresh perspectives and tools for studying shale gas content. Indeed, machine learning has found extensive applications in the field of geophysics. For instance, some researchers employ machine learning methods to interpret and analyze seismic data, thereby enhancing the efficiency and accuracy of seismic data processing13. In addition, machine learning has been used for geological modeling and prediction of subsurface fluid flow, which offer new possibilities for the study of shale gas gas content14, however, despite some achievements in the application of machine learning in the geophysical field15, its application in the prediction of shale gas content is still in its infancy and needs further research and exploration.

Recent studies have highlighted the potential of combining well-log derivative attributes with machine learning for improved lithofacies classification. For example, Al-Mudhafar et al. (2022) demonstrated how boosting machine learning algorithms can significantly enhance the classification of lithofacies in heterogeneous carbonate reservoirs, improving prediction accuracy and addressing the inherent heterogeneity in reservoir properties (Al-Mudhafar et al., 2022)16. Similarly, Wood (2022) utilized a combination of well-log derivatives, volatility, and sequence boundary attributes, along with machine learning techniques, to classify carbonate/siliciclastic lithofacies, showcasing the potential of multi-attribute analysis for better subsurface characterization (Wood, 2022)17. Furthermore, Al-Mudhafar et al. (2022) evaluated the performance of boosting techniques for lithofacies classification, emphasizing their success in heterogeneous carbonate reservoirs and the improvement of prediction robustness (Al-Mudhafar et al., 2022)16.

This study aims to tackle the challenges associated with the low prediction accuracy of shale gas reservoirs and the complexities of fulfilling exploration requirements. To achieve this, we have developed a quantitative prediction method for reservoir gas content, employing Kernel Principal Component Analysis and Support Vector Regression (KPCA-SVR). The procedure begins with the normalization and preprocessing of well logging, core, and electromagnetic parameters, followed by an examination of gas-sensitive parameters. The KPCA-SVR model parameters are then optimized, and the model is trained using well logging, core, and electromagnetic data. This approach enables intelligent, high-precision predictions of gas content parameters. Ultimately, we have applied this method to predict gas content parameters in the Wufeng-Longmaxi shale gas field in the Changning area of the Sichuan Basin. Our goal is to significantly improve the efficiency of shale gas extraction and resource utilization.

Methodology

Wide-field electromagnetic method principle (WFEM)

The Wide Field Electromagnetic Method (WFEM) is an innovative approach to artificial-source frequency-___domain electromagnetic depth measurement6, first introduced by academician ‘He Jishan’. This method skillfully incorporates the advantages of CSAMT’s use of artificial fields to mitigate field randomness, while also integrating the benefits of MELOS’s non-far-field measurements. It meticulously defines the formula for calculating apparent resistivity, applicable across the entire field, thereby expanding the observational range of the artificial-source electromagnetic method and enhancing the speed, precision, and efficiency of fieldwork. Over a uniform surface, the rigorous and precise expression for the Ex of a horizontal electric dipole source is defined as follows:

$$\:{E}_{x}=\frac{I\text{d}L}{2\pi\:\sigma\:{r}^{3}}\left[1-3{sin}^{2}\phi\:+{e}^{-ikr}(1+ikr)\right]$$
(1)

The apparent resistivity over a wide field is defined as:

$$\:{\rho\:}_{a}={K}_{E-{E}_{x}}\frac{{\Delta\:}{V}_{MN}}{I}\frac{1}{{F}_{E-{E}_{x}}\left(ikr\right)}$$
(2)
$$\:{K}_{E-{E}_{x}}=\frac{2\pi\:{r}^{3}}{\text{d}L\cdot\:MN},\:{\Delta\:}{V}_{MN}={E}_{x}\cdot\:MN$$
(3)

Where: ‘I’ denotes the supply current; ‘dL’ is the length of the electric dipole source; ‘i’ represents the imaginary unit; ‘k’ is the wavenumber of the uniform half-space; ‘r’ is the transmission and reception distance, which is the distance from the observation point to the center of the dipole; ‘σ’ is the conductivity; ‘φ’ is the angle between the direction of the electric dipole source and the radius vector from the source’s midpoint to the reception point; ‘ΔVMN’ is the observed potential difference; ‘MN’ is the measurement electrode distance; ‘KE−Ex’ is the device coefficient; ‘FE−Ex’ is the electromagnetic response function.

As can be inferred from the above formulas (1), (2), and (3), by conducting measurements over a vast area, including the far-field and parts of the non-far-field, and observing a component of the artificial source electromagnetic field, we can apply iterative calculation to extract information about the underground apparent resistivity. This constitutes the fundamental principle of the Wide Field Electromagnetic Method.

Principle of kernel principal component analysis and kernel function parameter optimization (KPCA)

Kernel Principal Component Analysis (Kernel PCA), a sophisticated variant of Principal Component Analysis (PCA), adeptly handles non-linear relationships through the use of kernel methods11. Often, the non-linear characteristics of data can render PCA ineffective for dimension reduction. In such cases, Kernel PCA can be utilized to address this issue. As illustrated in Fig. 1, Kernel PCA projects the data into a higher-dimensional space using non-linear mapping, and then applies PCA within this space. This process effectively captures the non-linear structure of the data. Therefore, when dealing with parameters that exhibit non-linear relationships, Kernel PCA is a more effective choice for data dimension reduction.

Fig. 1
figure 1

KPCA principle analysis diagram.

Full size image

The procedure for Kernel PCA is delineated as follows:

Initially, we establish the original data matrix X=[POR, RHO, GR, U,TOC]^T. Here, we have n samples and five variables. The expression of matrix X is:

$$X={({X_{POR}},{X_{Ro}},{X_{GR}},{X_U},{X_{TOC}})^T}=\left| {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}&{{x_{13}}}&{{x_{14}}} \\ {{x_{21}}}&{{x_{22}}}&{{x_{23}}}&{{x_{24}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{x_{n1}}}&{{x_{n2}}}&{{x_{n3}}}&{{x_{n4}}} \end{array}\begin{array}{*{20}{c}} {{x_{15}}} \\ {{x_{25}}} \\ \vdots \\ {{x_{n5}}} \end{array}} \right|$$
(4)

Subsequently, we normalize Eq. (4). For an n-dimensional feature vector x, the normalized vector x’ can be expressed as:

$$x^{\prime}=(x - \mu )/\sigma$$
(5)

Here, µ represents the mean of the feature vector, while σ denotes the standard deviation. Furthermore, this study employs mean and median statistics to fill missing values in the data set.

Kernel Function Selection: The choice of kernel function is pivotal for Kernel PCA. In this study, we use a Radial Basis Function (RBF), cross-validation, and grid search to calculate the optimal parameter γ. We set a γ range from 0.01 to 100. We perform cross-validation for each set of parameters by dividing the data set into five subsets. Each time, we designate one subset as the testing set and the remaining subsets as training sets. For each parameter set, we calculate the average performance across the five tests.

Kernel Matrix Calculation: The kernel matrix is the core of Kernel PCA, encapsulating the similarity between samples. For kernel function K(x, y), the kernel matrix K can be expressed as:

$$K=\left| {\begin{array}{*{20}{c}} {K({x_1},{x_1})}&{K({x_1},{x_2})}&{K({x_1},{x_3})}&{K({x_1},{x_4})} \\ {K({x_2},{x_1})}&{K({x_2},{x_2})}&{K({x_2},{x_3})}&{K({x_2},{x_4})} \\ \vdots & \vdots & \ddots & \vdots \\ {K({x_n},{x_1})}&{K({x_n},{x_2})}&{K({x_n},{x_3})}&{K({x_n},{x_4})} \end{array}\begin{array}{*{20}{c}} {K({x_1},{x_5})} \\ {K({x_2},{x_5})} \\ \vdots \\ {K({x_n},{x_5})} \end{array}} \right|$$
(6)

Here, xi, xj are samples in the dataset, and n is the total number of samples. Principal Component Extraction: The extraction of principal components is essentially an eigenvalue decomposition process of the kernel matrix, where the largest eigenvalue and its corresponding eigenvector—the principal component—must be identified. The eigenvalue decomposition for the kernel matrix K can be presented as:

$$K=V\Lambda {V^T}$$
(7)

Here, V represents the eigenvector matrix, Λ is the eigenvalue matrix, and VT is the transpose of V.

Data Projection: The final step involves projecting the original data onto the principal components to obtain the transformed dataset. For each sample xi, its projection onto the principal components can be represented as:

$${z_i}={V^T} * {x_i}$$
(8)

Here, V is the eigenvector matrix, xi represents the original sample, and zi is the transformed sample.

Support vector regression principle (SVR)

Support Vector Regression (SVR), a variant of the Support Vector Machine (SVM), is utilized for regression analysis. As Fig. 2 illustrates, the underlying philosophy of SVR involves the projection of data into a higher-dimensional feature space via non-linear mapping, followed by the construction of a linear model within this space. This is accomplished via a hyperplane that projects the predicted output. The optimal hyperplane is the one possessing the maximum margin from the nearest points, known as the support vectors.

The procedure for SVR is delineated as follows:

Initially, we establish a training dataset where X represents the principal component PC1 after Kernel PCA dimension reduction, and Y denotes the gas content (Vg). With sample parameters as n, X=[x1,x2,…,xn]^T, and Y=[y1,y2,…,yn]^T, the objective of SVR is to discover a function f(x) such that for all training data, the maximum deviation between f(x) and the actual target yi is ε, while simultaneously being as smooth as possible. The mathematical representation is:

$${z_i}={V^T} * {x_i}{\text{min \{ w,b,\varvec{\upxi},\varvec{\upxi}*\} 1/2 * ||w||2 + C \varvec{\Sigma}(}}{{\text{\varvec{\upxi}}}_{\text{i}}}{\text{+ }}{{\text{\varvec{\upxi}}}_{\text{i}}}{\text{*)}}$$
(9)
$${\text{Constraints:}}{{\text{y}}_{\text{i}}}{\text{ - }}{{\text{w}}^{\text{T}}}\varphi {\text{(}}{{\text{x}}_{\text{i}}}{\text{) - b }} \leqslant \varepsilon {\text{+ }}{{\text{\varvec{\upxi}}}_{\text{i}}}$$
(10)
$${w^T}\varphi ({x_i})+{\text{ }}b{\text{ }}-{\text{ }}{y_i}{\text{ }} \leqslant {\text{ }}\varepsilon +{\text{ }}{\xi _i}^{*}$$
(11)
$${\text{ }}{\xi _i},{\text{ }}{\xi _i}^{*} \geqslant {\text{ }}0$$
(12)

Here, ||w||²denotes the tube width, ξi and ξi* are the slack variables allowing error, while C > 0 signifies the penalty parameter for the error term. The goal is to minimize the cost function that incorporates both the margin size and the error penalties to ensure the model is both accurate and generalizable.

Fig. 2
figure 2

(a) shows the original spatial nonlinear data, (b) shows the mapped data, and (c) shows the hyperplane display of the data.

Full size image

KPCA-SVR model Building process

The process of predicting shale gas content using the KPCA-SVR model involves several key steps: data preprocessing, principal component extraction via Kernel PCA, model training, and validation. First, missing data (less than 2% of the dataset) was imputed using the median value within each geological unit. Noise in the resistivity data was reduced by applying a 5-point median filter, followed by a smoothing algorithm. Outliers were identified using Grubbs’ test (α = 0.01) and removed to ensure model accuracy. Feature sensitivity analysis was performed to select the most relevant parameters, such as porosity and resistivity, based on their correlation with the target variable (gas content). The data was then normalized using Z-score normalization to ensure uniformity across features. For model training, the dataset was split into training and validation sets, with hyperparameters for the Support Vector Regression (SVR) model optimized through grid search and cross-validation. The model’s performance was evaluated based on error rates (RMSE) and R² values, ensuring that only the best-performing models were validated. This process is summarized in the flowchart in Fig. 3.

Fig. 3
figure 3

Flow chart of KPCA-SVR model construction.

Full size image

Applications

Reservoir structure and gas content

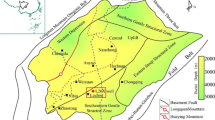
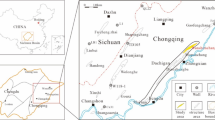
Figure 4a depicts the Sichuan Basin, a significant inland basin located in the southwestern part of China. Covering an area of roughly 165,000 square kilometers, the basin extends from 102°E to 108°E longitude and 28°N to 34°N latitude, positioned on the eastern edge of the Qinghai-Tibet Plateau. Geographically, the Sichuan Basin, situated west of the Qinling-Huaihe line and in the midstream region of the Yangtze River, serves as a crucial area linking the towering mountains and deep valleys of western Sichuan with the plains and hillocks of the central and eastern regions. The basin is a product of the collision between the Indian and Eurasian tectonic plates and features a diverse underground geological structure, with a crustal thickness typically varying from 30 to 40 km. This rich underground structure houses abundant resources, including oil, natural gas, and coal.

Figure 4b outlines the Changning region, located on the southwestern edge of the Sichuan Basin. This region, positioned east of the Kangdian ancient landmass, south of the Le Mountain-Longnusi ancient uplift Longmaxi formation erosion line, and north of the Qianbei depression, lies within the low-steep dome belt of southern Sichuan. Characterized by a vast expanse of structurally stable areas, it contains complete sedimentation records in the Wufeng formation and the Longmaxi formation, the latter currently having a burial depth ranging from 3000 to 6000 m. The terrestrial detritus of the Longmaxi formation in the Changning region primarily originates from the nearby Qianzhong ancient uplift.

Figure 4c illustrates our deployment of 12 broadband electromagnetic survey lines, six oriented east to west and six north to south, spanning a total length of 72 km. With a measuring point distance of 0.1 km, the deployment includes 720 data points and 30 checkpoints, focusing on the bottom of the Silurian Longmaxi formation and the Ordovician Wufeng formation as the main target layers. The study aims to delineate the electrical response characteristics of the stratigraphy within the designated region, mapping the resistivity distribution features of the target layers and the influence range of major faults on the low-resistance variations of the Longmaxi formation. Figure 4d shows the Changning block containing multiple well logs, with the exploration block covering wells X1, X2, and X3, each possessing several faults of varying sizes. Figure 4e presents the conventional well logging and lithologic characteristics of the Longmaxi formation in well X2, which can be divided into two sections: Long-1 and Long-2. In the GR, AC, and DEN well logs, Long-1 exhibits a funnel shape, while Long-2 displays a bell shape. The Long-1 and Long-2 sections, composed primarily of gray-black calcareous shale and black shale, with interbedded pyrite and calcareous bands, are the main exploration targets in the region. In the Changning area, the total thickness of Long-1 and Long-2 ranges from 140 to 240 m, exhibiting excellent preservation and regional continuity.

Fig. 4
figure 4

(a) presents the geographical ___location of the region, (b) provides an enlarged representation of the research block, (c) illustrates the layout of the regional broadband electromagnetic survey lines, (d) displays the geological structure of the block, (e) offers interpretation diagram of Well X2.

Full size image

Data acquisition and analysis of shale gas-bearing sensitivity parameters

In this study, we gathered and analyzed data from three distinct categories: well logging parameters (porosity (POR), acoustic transit time (AC), compensated neutron (CNL), density (DEN), natural gamma (GR), potassium-uranium-thorium ratio (U), permeability (PERM)), core parameters (total organic carbon content (TOC), gas content (Vg)), and electromagnetic parameters (resistivity (ρ)). These data were sourced from a 36 square kilometer wide-area electromagnetic exploration profile, three well logs (X1, X2, X3), and 120 core samples from the same well logs.

Given the inherent instability and uncertainty associated with resistivity (ρ) data due to the influence of lithological variations, environmental noise, and equipment errors, specific preprocessing steps were undertaken to improve data quality and reduce uncertainty. First, noise was removed from the resistivity data using a median filter, which effectively reduced high-frequency noise and minimized the impact of random fluctuations. Following noise reduction, a smoothing algorithm was applied to the resistivity curves to generate more consistent profiles, thereby mitigating the influence of abrupt changes that could skew the interpretation. Additionally, statistical outlier detection was employed to identify and remove data points that deviated significantly from expected resistivity ranges, ensuring that the dataset used for modeling was both reliable and representative of the actual geological conditions. These preprocessing steps were essential for stabilizing the resistivity data, thus enhancing its reliability as a sensitive parameter in shale gas content prediction.

The data acquisition and processing proceeded as follows: Initially, we preprocessed and interpreted the data from the 36 square kilometer wide-area electromagnetic exploration profile, yielding interpreted resistivity profiles for 12 survey lines. The primary profile analyzed was the L2 line, which intersects wells X1 and X2. As shown in Fig. 5a, the wide-area resistivity inversion profile of the L2 line effectively reflects the complete structural morphology, with distinct electrical layer markers and significant longitudinal resistivity variations. This profile indicates approximately seven primary electrical layers from the surface to the target layer and identifies one major fault (Gong 88) and one medium fault (F1). As depicted in Fig. 5b, the average resistivity of the Longmaxi reservoir at depths of 3400–3700 m in wells X1 and X2 is 12Ω.m.

Subsequently, we collected a variety of well logging parameters from three well logs (X1, X2, X3). Using well X2 as an example, Fig. 4e illustrates that the well logging parameters include POR, AC, CNL, DEN, GR, and U, each reflecting different characteristics of the rock.

Finally, we obtained core parameters from 120 core samples. The core parameters include TOC and Vg, each serving as key indicators of the organic carbon content and natural gas reserves in the rock, respectively. After pre-processing, which included the steps of processing missing values, anomalies, and duplicate values, we summarized the above logging, core, and electromagnetic parameters, as shown in Table 1.

Fig. 5
figure 5

(a) L2 line resistivity inversion interpretation section. (b) L2 line Longmaxi Formation reservoir section.

Full size image
Table 1 X2 well multi-parameter summary table (partial data).
Full size table

Crossplot identification technology is crucial in oil and gas exploration, particularly for assessing data quality and determining sensitive parameters. Using Well X2 as an example, we first define reservoir and non-reservoir zones based on stratigraphic interpretation information. We then use the labeled data from Table 1 to construct crossplots. As shown in Fig. 6, we start with an analysis of correlation magnitude, calculating the correlation coefficient (Corr) and R2 for each data set. Higher Corr and R2 values indicate a stronger correlation. Parameters that satisfy |Corr| > 0.8 and R2 > 0.6 are considered sensitive to Vg.

In the process of selecting sensitive parameters, we chose POR, DEN, ρ, U, TOC, and PERM as input features for shale gas content prediction. This selection is based on their significant physical relationships with gas content, detailed as follows: POR (Porosity): Porosity directly determines the available storage space for gas within the rock, and thus shows a strong positive correlation with gas content. DEN (Density): For rocks of the same type, higher porosity usually corresponds to lower density, resulting in a negative correlation between density and gas content.ρ (Resistivity): The presence of gas reduces the electrical conductivity of the rock, thereby reducing resistivity, which establishes a negative correlation between resistivity and gas content. U (Uranium Content): Uranium content indicates the proportion of radioactive elements in the rock, which correlates with organic richness, a key source of natural gas, leading to a positive correlation with gas content. TOC (Total Organic Carbon): Total organic carbon content is directly related to the availability of organic material, which is a key source of natural gas, thus showing a positive correlation. PERM (Permeability): Permeability determines the capacity of gas to flow through the rock; therefore, permeability is positively correlated with gas content.

Although these sensitive parameters show a clear physical relationship with gas content, it is important to note that the sensitivity of these parameters may vary across different geological settings. Geological environments, mineral composition, and reservoir characteristics differ significantly between regions, potentially affecting the relationship between these parameters and gas content. Therefore, the selection of these sensitive parameters has been optimized specifically for the geological conditions of the southern Sichuan Basin to ensure the model’s effectiveness in this region.

As Fig. 6a,d,f,g,h,i illustrate, POR, DEN, ρ, U, TOC, and PERM are sensitive to Vg and effectively distinguish between reservoir and non-reservoir zones. Conversely, AC, CNL, and GR are less effective in this delineation. From the perspective of positive and negative correlation, despite some outliers, the general trend of the crossplots indicates that POR, U, TOC, and PERM are positively correlated with Vg, while DEN and ρ are negatively correlated.

An in-depth discussion of Vg and its related parameters reveals that the relationships between Vg and each parameter have significant physical foundations. The relationship between Vg and POR is positive, as porosity provides storage space for natural gas. The relationship between Vg and DEN is negative, as in the same type of rock, greater porosity results in lower density. The relationship between Vg and ρ is also negative, as more gas in the rock pores reduces resistivity. The relationship between Vg and U is positive, as U usually represents the proportion of radioactive elements in the rock, which are related to the content and type of organic matter, the main source of natural gas. The relationship between Vg and TOC is positive, as TOC is the content of organic matter in the rock, and organic matter is the main source of natural gas. Lastly, the relationship between Vg and PERM is positive, as higher permeability allows more natural gas to flow out of the rock.

In summary, POR, U, TOC, PERM, DEN, and ρ are the preferred input features for predicting gas content (Vg). However, relying on a single parameter cannot accurately predict gas content. Therefore, we need to perform principal component analysis on these six parameters to construct parameter variables that can reflect the trend of gas content changes.

Comparison of dimensionality reduction methods: PCA vs. KPCA

To evaluate the effectiveness of dimensionality reduction, both Principal Component Analysis (PCA) and Kernel Principal Component Analysis (KPCA) were applied to the input parameters, including resistivity (ρ), porosity (POR), density (DEN), potassium (U), total organic carbon (TOC), and permeability (PERM). The key objective of this comparison was to determine which method better captures the underlying relationships between the features for subsequent modeling.

Experiments were conducted using both PCA and KPCA to reduce the dimensionality of the input parameters. The reduced features were then used to train several machine learning models: Linear Regression, SVR (Linear), SVR (Non-linear), and Random Forest. The performance metrics, Mean Squared Error (MSE) and R² score, were computed to assess the effectiveness of each model in predicting gas content.

Table 2 Presents the results of the comparison between PCA and KPCA.
Full size table

As shown in Table 2, KPCA generally outperformed PCA across multiple evaluation metrics. Specifically, the Linear Regression model improved significantly when using KPCA, as demonstrated by an increase in R² (from 0.873 to 0.890), reduction in RMSE (from 0.591 to 0.551), MAE (from 0.285 to 0.253), and MAPE (from 7.32 to 6.45%). Similarly, the SVR (Linear) model showed noticeable improvements across all metrics when KPCA was applied. These additional metrics confirm KPCA’s enhanced capability to effectively capture the nonlinear relationships present within the dataset, thus providing a more robust prediction model.

Modeling gas content using KPCA-SVR

In the process of parameter dimension reduction, the primary task is to determine whether the relationship between parameters is linear or nonlinear. This study uses resistivity (ρ) as the research object, separately establishing linear and nonlinear models for ρ with POR, DEN, U, TOC, and PERM, setting the model parameters as test_size = 0.5, random_state = 42. As shown in Fig. 7, through a comprehensive assessment of scatter prediction diagrams and Mean Squared Error (MSE) histograms, the MSE of the nonlinear model is smaller, suggesting that ρ has a nonlinear relationship with other parameters. To further quantify this, Spearman rank correlation analysis was conducted, which demonstrated a statistically significant nonlinear correlation between resistivity and other features (p < 0.01). This provides strong evidence supporting the conclusion that resistivity (ρ) exhibits a nonlinear relationship with other parameters.

Fig. 6
figure 6

Crossplot analysis, (a) Vg versus POR, (b) Vg versus AC, (c) Vg versus CNL. (d) Vg versus DEN, (e) Vg versus GR, (f) Vg versus ρ, (g) Vg versus U. (h) Vg versus TOC, (i) Vg versus PERM.

Full size image

When parameter variables exhibit nonlinear relationships, Kernel PCA is a more effective choice for data dimension reduction.

Subsequently, we use the Z-score standardization method for input parameters ρ, POR, DEN, U, TOC, and PERM. Based on formulas (4) and (5), we obtain standardized data, then calculate the optimal kernel function γthrough cross-validation and grid search. In this process, the γ parameter grid is set to take 5 geometric sequence values from 0.01 to 100, and the number of folds for cross-validation is set to 5. This implies that the dataset is divided into 5 parts, one of which is used as the validation set and the rest as the training set. This process is repeated 5 times, and the optimal kernel function γ is determined to be 0.01. Then, based on formulas (6), (7), and (8), the kernel matrix is calculated, and three principal components PC1, PC2, and PC3 are extracted. As depicted in Fig. 8, PC1 closely resembles Vg in terms of data histogram distribution characteristics and depth change morphology, hence PC1 is chosen to participate in the training of the nonlinear SVR model.

Fig. 7
figure 7

Plots of linear characteristics for determining ρ vs. other parameters. (a) ρ vs. POR, (b) ρ vs. DEN, (c) ρ vs. U, (d) ρ vs. TOC, (e) ρ vs. PERM. (f) Error analysis plots for linear and nonlinear models.

Full size image
Fig. 8
figure 8

(a) Histograms of PC1, PC2, PC3, Vg, (b) Variation with depth.

Full size image

In this study, we select PC1 as the input variable to establish a nonlinear SVR model, with the model training parameters set as test_size = 0.5, random_state = 42. To determine the kernel function γ and penalty coefficient C of the nonlinear SVR model, we use cross-validation and grid search, setting γ to take 6 geometric sequence values from 0.001 to 100, and C to take 5 geometric sequence values from 0.1 to 1000. The optimal solution is found to be C = 10, γ = 1. Then, based on formulas (9), (10), (11), and (12), we construct the nonlinear SVR model.

To better demonstrate the superiority of the model, we construct linear SVR, linear regression, and random forest models respectively with PC1 as the input variable, keeping the model training parameters consistent. As depicted in Fig. 9a,b,c,d, the prediction effect of the nonlinear SVR is the best, followed by linear regression, with linear SVR relatively lower, and the random forest effect being the worst. As shown in Fig. 9e, by comparing the Mean Squared Error (MSE), Root Mean Squared Error (RMSE), R2 Score, and Mean Absolute Error (MAE) of the four models, it is evident that the MSE, RMSE, and MAE of the nonlinear SVR model are the smallest, and R2 is the largest. As depicted in Fig. 9f, the residual plot intuitively shows that the nonlinear SVR is closer to the 0 value line, and in combination with Fig. 10, it can be comprehensively deduced that the nonlinear SVR provides the best gas content prediction effect.

Fig. 9
figure 9

(a) Nonlinear SVR, (b) Linear SVR, (c) Linear regression, (d) Random forest. (e) Model comparison results, (f) Model residual plots.

Full size image
Fig. 10
figure 10

Illustrates the comparison between the MSE and R² scores for each model when using PCA and KPCA.

Full size image

Validation of the KPCA-SVR gas-bearing feature model

In this study, we use the KPCA-Nonlinear SVR model to predict the full-section log gas content of the Longmaxi Formation reservoir in wells X1, X2, and X3. As shown in Fig. 11, the KPCA-Nonlinear SVR model successfully predicts the full-section log gas content of the reservoirs in these wells. Core-measured data is used as the validation criterion to evaluate the consistency between the predicted and measured values.

To assess the practical application of the model, we performed a comprehensive error analysis based on field data from three wells: X1, X2, and X3. The absolute error distributions between predicted and measured values were analyzed, providing key statistics such as maximum error, minimum error, and average error. These results further validate the reliability of the model in real-world shale gas exploration.

The results of the validation with measured data show a remarkably high fit between the predicted and measured values. This not only validates the effectiveness of the model but also demonstrates its stability in practical applications. Furthermore, a residual distribution analysis was conducted, revealing that the model’s predictions fall within a 95% confidence interval. This suggests a controlled level of uncertainty in the predictions, indicating that the model is robust and its results are reliable. The error distribution showed a normal distribution pattern, with a mean close to zero, further confirming the model’s consistency.

To further explore the practical implications, we also compared the model’s predicted gas content with production data (e.g., initial gas production rates). The analysis demonstrated a strong correlation between predicted gas content and early production rates, highlighting the model’s direct contribution to shale gas development.

These findings strongly suggest that the KPCA-Nonlinear SVR model performs exceptionally well in the challenging task of predicting the full-section log gas content of the Longmaxi Formation reservoir in southern Sichuan, with an acceptable level of uncertainty.

Fig. 11
figure 11

Validation plots with results from wells X1, X2, X3.

Full size image

Discussion

This study aimed to refine the accuracy of gas content prediction by developing a gas-bearing characteristic model for the southern Sichuan area using Kernel Principal Component Analysis (KPCA) and Support Vector Regression (SVR). While this model demonstrates strong performance in the study region, its generalization to other geological areas or conditions may face challenges, particularly due to the reliance on resistivity data, which may not be available in all regions. In areas lacking sufficient electromagnetic survey data, the model’s applicability could be limited. To address this, future research could explore integrating alternative geological parameters, such as seismic or well logging data, and develop adaptive data fusion techniques to improve model generalizability across different geological settings.

Additionally, the complexity of KPCA and SVR models presents challenges when applied to large datasets. The computational demands of the KPCA-SVR method could hinder its scalability, especially in cases with extensive datasets or limited computational resources. Optimizing the dimensionality reduction process, for instance, by employing more efficient algorithms or utilizing parallel computing methods, could enhance the model’s computational efficiency and enable its application to larger datasets. This would make it more feasible for use in real-world, large-scale shale gas exploration projects.

Another consideration is the inherent uncertainty in the prediction results. While the model shows promising results, the residual distribution analysis indicates that the predictions fall within a 95% confidence interval, suggesting a controlled and acceptable level of uncertainty. However, incorporating further uncertainty analysis could help quantify the potential variability of the predictions and refine the model’s reliability, providing a more robust framework for gas content estimation.

In addition to these challenges, improving the accuracy of gas content prediction has significant environmental and economic implications. More reliable predictions can reduce exploration costs and mitigate environmental impacts, contributing to more sustainable shale gas development. As a result, the enhanced predictive capabilities of this model not only benefit exploration efforts but also play a crucial role in ensuring energy supply security in a rapidly evolving global energy landscape.

Conclusion

This investigation effectively devised a shale gas content characteristic model employing Kernel Principal Component Analysis (KPCA) and Support Vector Regression (SVR), aimed at refining the accuracy of shale gas reserve estimations in the southern Sichuan area. We identified pivotal parameters impacting gas content, including porosity, density, resistivity, potassium-uranium-thorium ratio, total organic carbon (TOC), and permeability. Based on the KPCA-Nonlinear SVR methodology, we constructed a gas content characteristic model, and the predictive outcomes were corroborated through three well logs.

Our study successfully established a model for forecasting shale gas content, with significant theoretical and practical implications for the development and exploitation of shale gas. We introduced an innovative methodology using resistivity data, which supports the application of electromagnetic detection technology in shale gas exploration. Additionally, we incorporated a machine learning-oriented approach to construct a gas content characteristic model, enabling more precise predictions of shale gas reserves.

Improving shale gas exploration efficiency using this model has considerable environmental and economic benefits. Enhanced predictive accuracy reduces the need for extensive drilling operations, thus minimizing the environmental impact of shale gas exploration. By providing more reliable estimates of gas reserves, this model can help optimize resource extraction, reducing the costs and energy consumption associated with traditional exploration methods. Economically, the model could contribute to a more cost-effective and sustainable shale gas industry, promoting long-term energy security while minimizing the environmental footprint of exploration activities.