Introduction

Optimizing plant fertilizer use has become an urgent requirement for food security and agricultural sustainability1,2,3. On one hand, under-fertilization results in ‘yield gaps’4 and can increase land-use demands to offset production shortfalls5,6. On the other, overfertilization increases farm costs, drives biodiversity loss7, pollutes freshwater, and exacerbates N2O emissions8,9. So-called “precision fertilization” seeks to optimally navigate these trade-offs, fertilizing when and where biomass yield increases with nutrients (i.e. areas that are ‘ ‘fertilizer responsive’ or ‘nutrient limited’) while eliminating inputs that have no benefit (e.g., areas more limited by drought, such that biomass is unchanged by fertilization)10,11. Precision fertilization is increasingly urgent for global food production, with nutrients in industrialized agriculture constituting up to 35% of farm costs12,13,14. Successfully implementing precision fertilization requires spatially and temporally explicit information on the causal factors that determine when and where nutrients increase biomass. However, these factors remain difficult to quantify.

Variability in fertilizer responsiveness often results from interacting edaphic, climatic, and biotic processes that operate across multiple scales. Regionally, variability can derive from gradients of soil fertility15,16, aridity, and or plant species richness, where niche complementarity mediates nutrient uptake17. Locally, within-field differences in soil physicochemical conditions (e.g., particle size, pH) can generate spatial heterogeneity in plant productivity18. Similarly, within-field turnover in species richness and composition19 can lead to differences in resource uptake that, in turn, alter biomass. Temporally, intra- and interannual fluctuations in moisture availability20 often affect fertilizer responsiveness, and indeed yearly nutrient-climate covariation has become central to forecasting nutrient limitation21,22. In combination, these scale-dependent factors may explain why fertilizer responsiveness varies widely, and why predicting and managing for its occurrence is so difficult. They also explain why industrialized agriculture typically employs a default bet-hedging strategy of ‘adding everywhere and all the time’ despite its sizeable environmental impacts, economic costs, and failure to increase yield in certain contexts. A key to achieving ‘sustainable intensification’4,23 in global food systems, where food production is balanced with reduced nutrient pollution, will depend on determining the drivers of yield variation with fertilization.

Here, we conduct a globally distributed field experiment with standardized rates of fertilization over multiple years to test when, where, and at what scale the annual application of essential macronutrients (combined nitrogen [N], phosphorus [P], and potassium [K]) fails to increase annual peak aboveground biomass. We quantified “responsiveness” relatively, based on the difference in biomass between replicated fertilized and unfertilized one m2 plots within the same year. Responses were paired by year to minimize the impacts of the wide among-year variability in climate and biomass that characterizes many grasslands15. We then conducted a retrospective modelling exercise, parameterized with our field data, to determine the precision fertilization scenarios that would best maximize yield while avoiding situations where fertilization is wasted because plants do not respond. This work occurred on 61 rangelands from six continents with sites spanning global gradients of climate, edaphic fertility, and species richness (Table S1). With data for up to 15 years of fertilization, we target rangelands - defined here as uncultivated grass-dominated areas capable of supporting native or domesticated grazers24,25,26,27—because they are commonly resource-limited19, often fertilizer-responsive28,29,30, and typically moisture limited15,31. Rangelands are rarely fertilized, allowing us to quantify biomass responsiveness without the confounding influence of past nutrient use. Rangeland responses should also mirror nutrient limitation in croplands given that many of the world’s cultivated farmlands were once part of the global grassland biome. Using exclosures to remove the influence of grazer-offtake on annual yield, we assessed drivers of variability in aboveground biomass at three levels: among sites (“site scale”), within-sites (“plot scale”), and over time (“temporal scale”). Our globally and longitudinally distributed data allow us to untangle the covarying relationships among climatic, edaphic, and richness-related factors on fertilizer responsiveness, while our parameterized modelling allows us to explore how different management scenarios for fertilizer cessation affects yield.

Results

Global inefficiencies in fertilization

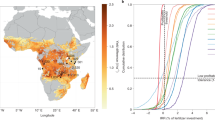
Globally, fertilization increased annual aboveground peak plot-level biomass (hereafter “biomass”) by 43%, from an average of 348 g m2 year−1 in unfertilized plots to 499 g m2 year−1 in NPK treatment plots. However, this global trend concealed widespread inefficiencies in responsiveness. Across the experiment, 393 of 1,518 (26%) treatment units (plots*years) failed to respond positively to fertilization relative to controls (Fig. 1). In total, 57 of 61 sites had at least one plot in one year that was unresponsive. Among sites, the probability of non-responsiveness ranged from 12 to 49% (Fig. 1; Tables S2, S3). Unexpectedly, sites with a high frequency of non-responsiveness were not confined to any global region (Fig. 1). Relatedly, moisture-limitation did not unilaterally predict the likelihood of yield responding to fertilization despite our sites having a mean annual precipitation range of 226 to 1,744 mm year−1 (see below).

Fig. 1
figure 1

The global distribution of variation in the probability that biomass will not respond to NPK fertilization. (a) Mapped points show the ___location of the 61 sites included in our study, ranging from a low (blue) to high (red) probability of no yield increase with fertilization. (b) Among-site variation in the probability that biomass will not respond to NPK fertilization, with “non-responsiveness” indicating biomass in a fertilized plot was equal to or less than control plot biomass, suggesting biomass was not nutrient limited. Points are conditional modes from a random intercept-only model with site as a random grouping factor. Error bars show 95% confidence intervals associated with the site-specific conditional modes. The dashed red line depicts the global intercept and gives the expected probability across all sites.

Full size image

Large-scale spatial variability in nutrient limitation

We used generalized linear mixed effects models with group-mean centered explanatory variables to test how variability in climatic, edaphic, and biotic factors at three levels (among-sites, within-sites, and over time) contributed to the probability that yield would be unresponsive to fertilization (“Methods”). Among sites, we tested if biomass responsiveness was influenced by aridity (the ratio of annual precipitation to annual potential evapotranspiration [PET]), species richness, and pre-treatment levels of soil and biomass (“Methods”). The probability that a site would not respond to fertilization was generally higher at sites with below average plot-level species richness, with this effect interacting significantly with the mean daily aridity (Fig. 2, Table S4). Specifically, the likelihood that fertilizer would not produce a positive biomass response was highest at sites that were both species poor and dry (See also32. In contrast, at more mesic sites, the relationship between richness and non-responsiveness was reversed, such that biomass in mesic sites with lower plot-level richness was more likely to respond than mesic sites with higher plot-level richness. Overall, the probability of not responding was unaffected by among-site variability in aridity outside of its interaction with species richness (Table S4).

Fig. 2
figure 2

The effect of average plot-level species richness at multiple scales on the probability that grassland biomass will be non-responsive to fertilization. Panel (a) shows the effect of among-site variability and panel (b) shows the effect of interannual variability in species richness regardless of site- or block-level variability (i.e., blocks = replicated pairs of treated and untreated plots). Colored lines characterize the interaction between species richness and site-level mean daily aridity. Lines correspond to z-scores where 0 is the mean across sites, − 1 is one standard deviation below the mean, and 1 is one standard deviation above the mean. Measures of error associated with these model estimates are presented in Table S4.

Full size image

Fine-scale spatial variability in nutrient limitation

At the plot scale (i.e., plots within a single site), we tested if non-responsiveness was influenced by deviations from the site mean for pre-treatment soil nutrient concentrations, species richness, and pre-treatment biomass production (Tables S5, S6). We found that pre-treatment soil conditions did not determine the probability of responsiveness at the site level; however, plots with higher pretreatment soil pH were less responsive than neighboring plots with lower pH, regardless of the site-level value of the variable (Fig. 3a, Table S6). Plots with higher pre-treatment soil P were less responsive to fertilization (Fig. 3) than plots with lower P, but there was no effect of among-plot variability in pretreatment soil N or K concentrations (Table S6). Similarly, fertilizer responsiveness was not significantly affected by the pre-treatment biomass or species richness of sites or plots (Table S6).

Fig. 3
figure 3

The effect of within-site variability in initial plot soil conditions on the probability that grassland biomass will be non-responsive to fertilization. Non-responsiveness was more likely in replicated pairs of plots (i.e., blocks) with higher pH than the mesite-average pH (a) and in blocks with soil phosphorus at higher concentration than the site average (b). Measures of error associated with these estimates are presented in Table S6.

Full size image

Temporal variability in nutrient limitation

We evaluated cumulative responsiveness over time based on the number of years that fertilizer had been applied. Globally, the probability of non-responsiveness did not change significantly over time (Fig. 4, Table S7). However, we observed substantial among-site variability in this temporal change, with the probability increasing at some sites while decreasing at others (Fig. 4, Table S7). We also tested if nutrient limitation responded to interannual variability in aridity or species richness. The probability that a plot would fail to respond in a given year (i.e., no difference in plot biomass between treatment and controls) was influenced by interannual variation in plot species richness, regardless of the average richness of its respective plot or site, and its interaction with the contextual effect of site-level aridity (Fig. 2; Table S4). Across the entire species richness gradient captured by our experiment (ranging from 1 to 40 species per plot and 25–128 species per site), the probability of not responding increased in dry sites in years with below-average species richness.

Fig. 4
figure 4

Change in the responsiveness of grassland biomass to NPK + over increasing yearly fertilization. The dashed black line shows the global mean trend while the solid colored lines show site-specific changes. Error associated with these estimates are presented in Table S7.

Full size image

Modelling trade-offs between yield reductions and overfertilization

With intensive agriculture, universal fertilizer inputs produce high average yield33 but likely overfertilize in many instances34,35,36. We leveraged the spatial and temporal resolution of our data to retrospectively evaluate how modifying inputs affects yield and overfertilization according to different criteria (Table 1). To achieve this, we designed a range of hypothetical management scenarios for fertilizer cessation using control plot data to approximate the degree to which yields might decline in the year following fertilizer not being applied (see “Methods”). Critically, while the various cessation scenarios were able to reduce overfertilization from 9 to 60%, they always led to yield declines ranging from 1 to 20% (Table 1). In short, no precision fertilization scenario was able to match the biomass yield achieved by ‘adding everywhere and all the time’ because of the difficulty in predicting when a plot would not respond. All benefits of cessation were strictly derived from the reduced use of nutrients, which would reduce costs and environmental impacts but be unable to maintain maximum yield.

Table 1 The projected effect of fertilizer cessation according to different management scenarios on mean grassland biomass production and fertilizer-use.
Full size table

Land sparing approaches that prioritize cropping on productive soils while ceasing management of low-yielding areas6,37 may be implemented over large spatial scales (e.g., ceasing fertilization of entire sites) or at finer spatial scales (e.g., considering within-site heterogeneity). We trialed land sparing approaches at both the site- and plot-scale based on the average yield response at each level. Our projections suggested that ceasing fertilization in sites after observing non-responsiveness at both the plot and site scales could reduce overfertilization (Table 1). Meanwhile, fertilization cessation at the plot scale was highly effective in reducing overfertilization (i.e., preventing fertilization of plots that did not respond by increasing biomass), but led to greater yield reductions (Table 1). As these decisions require observation of yield responses to fertilization over one or more growing seasons, we also evaluated decisions made based on the first year of fertilization and over the first three years of fertilization. Basing responsiveness on three years instead of one saved yield but was less effective at reducing overfertilization.

Another cessation scenario is to modify inputs according to a site’s management history; for example, reducing inputs to sites that have a longer history of fertilization but maximizing them in historically low-input areas to close potential yield gaps38,39. We evaluated how yield and overfertilization would respond to fertilizer cessation after different temporal cut-offs. Only fertilizing for three years caused large reductions in yield relative to the intensive ‘everywhere all the time’ scenario (Table 1). Increasing the number of years that plots were fertilized reduced yield loss but at the expense of more overfertilization. However, ceasing fertilization after 10 years appeared a more efficient strategy - it only reduced yield by 3.4% relative to the intensive scenario, while reducing overfertilization by 11.8% (Table 1).

Precision fertilization increasingly utilizes technology to measure fine-scale spatial and temporal variability in the climatic, edaphic, and biotic factors that may regulate nutrient limitation, and then modifies the addition of nutrients accordingly10,40. We tested how ceasing fertilization affected yield and overfertilization, given the factors identified as important in our explanatory analyses. At the site-scale, not fertilizing species-poor sites led to marginal reductions in yield but reduced overfertilization by 11% and, similarly, not fertilizing the most arid sites caused minor yield loss but reduced overfertilization by 17% (Table 1). Within sites, not fertilizing plots where pre-treatment soil pH greatly exceeded the site-average pH (irrespective of absolute site pH) reduced yield by 1.2% and decreased overfertilization by 10%. Similarly, not fertilizing plots that greatly exceeded the site-average pre-treatment soil phosphorus concentration reduced yield by 2.7% and decreased overfertilization by 10%. At the annual scale, not fertilizing in years when species richness was below the plot average, irrespective of the absolute richness of the site or plot, was projected to reduce yield by 4.4% and decrease overfertilization by 12% (Table 1).

Discussion

Our study demonstrated substantial variability in the responsiveness of rangeland plant biomass to fertilization, with plots unresponsive 26% of the time. Previous investigations have considered site-level limitations, classifying rangelands as either ‘nutrient limited’ or ‘not nutrient limited’ based on average biomass change with fertilization over multiple sampling times and points28,29,30. We found that all sites contained areas that were nutrient limited in at least one year but also that most sites had areas that were not nutrient limited in one or more years. This quantification of global-scale spatial and temporal variability in nutrient limitation has important implications. Principally, it confirms the likelihood of frequent overfertilization under intensive agricultural scenarios while also clarifying opportunities for targeted cessation of fertilization that would reduce economic and environmental costs even if yield loss appears inevitable. Overall, this demonstrates how understanding and monitoring factors associated with variability in nutrient limitation will be critical for optimally balancing agricultural yield with reduced fertilization - a key goal of sustainable intensification23,41,42.

Variability in nutrient limitation

Among sites, the chance of nutrient limitation did not display directional change over time. While it may be expected that repeated annual fertilization would progressively increase the stoichiometric limitation of other factors43,44,45 thereby reducing fertilizer responsiveness, this trend may be more likely to occur for single-nutrient inputs that exacerbate limitation by other nutrients43,44,46. In contrast, we simultaneously fertilized with three essential plant macronutrients, thereby reducing the likelihood of this occurring. Additionally, while nutrient enrichment generally reduces rangeland plant richness30,44, there may be adjustments in species composition by fast-growing taxa that would allow nutrient uptake to keep pace with inputs thereby maintaining a state of limitation (that is to say, fertilization continues to increase yield, despite richness declining). This aligns with recent work demonstrating increasing biomass production over time under annual fertilization19. More broadly, the absence of a temporal trend means variability in nutrient limitation is likely guided by spatial and interannual variability in key covariates.

We found that species richness, aridity, soil pH, and soil phosphorus had the strongest impacts on fertilizer responsiveness, but that they acted at different scales. Higher plot-level species richness generally increased the chance that yield would increase with fertilization. This effect operated at both the site level and over time, where sites or years with higher species richness were associated with better responsiveness. One explanation may be that species-rich communities contain a broader set of complementary traits, allowing greater capture of added resources and subsequent conversion to biomass47,48. Promoting species richness may be a possible strategy for increasing rangeland fertilizer responsiveness or, alternatively, helping to maintain higher biomass when fertilization is halted.

We expected climatic fluctuations to drive variability in fertilizer responsiveness, especially if moisture limitation exceeds nutrient limitation in arid rangelands15,16,25,32. Our models indicated that aridity influenced nutrient limitation only when it interacted with species richness. We found that sites that are both dry and species-poor were the most susceptible to overfertilization. However, the probability of nutrient limitation not being directly influenced by aridity, despite the gradient captured in our study ranging from extremely arid to highly mesic, aligns with other work showing that rangeland nutrient limitation exists across precipitation gradients with only the magnitude of limitation varying with aridity31. The chance of not being nutrient limited was generally higher in plots with higher pre-treatment soil phosphorus, (i.e., fertilizing was less likely to increase yield if soil P was already high) or plots with higher pH, but it was not influenced by pre-treatment soil N or K+. Interestingly, pH and soil P influenced nutrient limitation via within-site heterogeneity (plot-level variability) but had no effect among sites.

Unlike most work on growth limitation by elemental nutrients24, the current study assessed nutrient limitation in the absence of large herbivores. This study design provides a new lens on growth limitation by ruling out consumption by large herbivores as an unseen driver of plant nutrient response patterns49,50. While other consumers may still play a role in the observed plant responses, the localized effects of plot-scale pH and species richness suggest that the soil and plant community likely play a stronger role. Most notably, this design provides clear insights into nutrient limitations on plant available biomass for rangeland grazing.

Precision fertilization in rangelands

The value of rangelands is partly dependent on forage production, which correlates positively with livestock yield51 and the delivery of ecosystem services such as carbon sequestration25,52. A key finding of our analysis is that while nutrient limitation varied within sites, almost all contained areas that were limited in at least one year. This result echoes previous findings28 but advances understanding by demonstrating that nutrient limitation is not only a site-level signal, but rather is a widespread within-site phenomenon that depends on a multitude of factors including plot-scale soil pH and nutrient availability, water availability, and species richness. Precision fertilization thus can be valuable to maximize yield, which is often desirable for supporting livelihoods and enhancing food security51. However, the many areas that were not nutrient limited across sites pose the risk of overfertilization that would, in real-world situations, reduce farmer profit and contribute to eutrophication-driven diversity loss7,19 thereby impairing long-term rangeland sustainability47. This emphasizes that precision fertilization schemes, if deemed necessary53,54, should prioritize precision application especially at finer scales within sites53,55.

Lessons for optimizing fertilizer use

Some general inferences emerged from our data concerning the critical dichotomy between using nutrients to maximize food production while reducing the costs and environmental impacts of industrialized farming. From the perspective of maximizing biomass irrespective of other factors, the best outcome always arose from intensive fertilization (i.e., fertilizing all plots in all years). All fertilizer cessation scenarios sacrificed some degree of yield, which is problematic given that global food production may need to double by 205011. In theory, yield could have been maintained if we were able to avoid fertilizing areas that were not nutrient limited while precisely targeting areas that were. However, the scenarios we designed frequently failed to identify these locations correctly. Even when armed with substantial prior knowledge of the conditions under which fertilizer worked in our system, it remained difficult for any cessation scenario to match the yield benefits of intensive fertilization.

Given these considerations, the greatest benefits of precision fertilization appear to be the reduction of farm costs and environmental impacts. Neither of these benefits are trivial. Global fertilizer costs are rising significantly12,14 and projections on when we will reach “peak phosphorus production” range from one to several decades13. Accordingly, the ability to maintain yield while minimizing fertilizer inputs will become increasingly critical for food security towards 2050. Concurrently, agricultural nutrient pollution is exacerbating greenhouse gas emissions9, biodiversity loss7, and the eutrophication of freshwater and marine systems globally56. These interacting demands support the need for precision fertilization, but also highlight greater risks associated with trying-but-failing to effectively reduce inputs. Our analysis shows that precision fertilization is difficult to implement due to variability in nutrient limitation (which changes locations within sites and over time) and uncertainty in parameter estimates for explanatory variables associated with limitation. This reveals that further work is required to improve our ability to accurately predict dynamic nutrient limitation so that strategies for fertilizer cessation can more effectively maintain yield while cutting inputs.

Methods

Experimental design and data

We assessed the responsiveness of aboveground peak annual biomass production (hereafter “biomass”) to fertilization in 61 rangeland sites on six continents (Fig. 1; Table S1). By rangelands, we refer to uncultivated non-forested and often grass-dominated plant communities that are capable of supporting native or domesticated grazers. Some rangelands can be forb-dominated at all or parts of the year, although this is uncommon among our sites. We confined our work to enclosed fenced areas to isolate biomass responses to nutrient addition without grazer offtake. Each of the 61 sites support one or multiple species of grazers including native and/or domesticated ungulates, with the level of grazing intensity varying widely49,57. The most intensely grazed sites include rangelands in climates that are both mesic (e.g., UK [sheep], Scandinavia [reindeer]) and arid (e.g., central and western Australia). All included rangelands are part of the globally distributed Nutrient Network experiment58 and span a latitudinal gradient from − 52o to + 69o. These sites range in elevation from 8 m to 4241 m, with wide differences in long-term (50 year) mean annual precipitation (MAP: 226 to 1745 mm) and mean annual temperature (MAT: -3.2 °C to 24.1 °C)58.

To test how edaphic, climatic, and biotic factors altered fertilization responsiveness, we followed a globally standardized nutrient addition protocol58. Fertilized plots received equal yearly additions of pelletized nitrogen (N; 10 g m−2 year-1 as time-release urea [CH₄N₂O]), phosphorus (P; 10 g m−2 year−1 as triple-super phosphate [Ca(H2PO4)2·H2O]), and potassium (K; 10 g m−2 year−1 as potassium sulphate [K2SO4]). In addition, in the first treatment year only, all fertilized plots received 100 g m−2 of an essential nutrient mix, including: 15% Fe, 14% S, 1.5% Mg, 2.5% Mn, 1% Cu, 1% Zn, 0.2% B and 0.05% Mo. This combined multi-factor fertilizer prescription was designed to maximize the likelihood of detecting nutrient limitation on aboveground biomass, given that such responses can be prone to Type II error (i.e., a rangeland is nutrient limited, but the nutrient limitation is not detected). For example, the addition of NPK fertilizer is likely to produce a biomass response in rangelands limited by P and K that would not be detected if only N fertilizer was added43,44,59. We also added nutrients at high levels typical of industrialized agriculture, as this similarly increases the odds of triggering a limitation response. All control and treatment plots included in our analysis were surrounded by 230 cm high metal fencing including a 1 cm mesh around the base to prevent biomass offtake by both medium and large herbivores (full detail provided previously58). All sites contained a minimum of three blocks of paired plots (ranging from three to six blocks per rangeland) and between three and fifteen years of biomass measurements (Table S1).

Live aboveground biomass in each 25 m2 plot was harvested annually from two 10 × 100 cm strips at the time of peak biomass production and dried at 60 °C. Henceforth, biomass refers to the sum of aboveground vascular and nonvascular live mass in g dry mass m−2. We created a binomial response variable in which \(y=0\) indicates that biomass increased relative to unfertilized fenced plots in response to fertilization in the same block and \(y=1\) indicates that biomass failed to respond positively. Annual plant litter accumulation was recorded as the sum of dead biomass in g dry mass m−2 in each plot in the same strip from which live mass was obtained. All sites re-locate biomass sampling strips each year to prevent a harvesting effect. Species richness was measured annually in a fixed 1 m2 quadrat within each of the fertilized 25 m2 plots. Pretreatment soil conditions including soil percent nitrogen, phosphorus (ppm), potassium (ppm), and pH were obtained from soil cores of 10 cm depth (detailed soil sampling methods are provided in19,44,58). Site specific precipitation (mean daily mm) and potential evapotranspiration (PET) were obtained from the Climatic Research Unit60 and used to calculate mean daily aridity as \(\frac{mean daily precipitation}{mean daily PET}\). This gives an overall metric of moisture availability for plant growth, where values of one indicate precipitation is matched by evapotranspiration, values lower than one indicate arid sites, while values greater than one indicate mesic sites. Arid sites constitute 70% of the Nutrient Network grasslands, with the remainder being mesic (MacDougall, unpublished data) – this 70:30 ratio is comparable to all grasslands globally61.

Evaluation of variability in nutrient limitation

We fit a series of generalized linear mixed effects models (GLMMs) to evaluate how variability in fertilizer-responsiveness is distributed spatially and temporally. All models were fit with a logit link, where the log-odds that \(y=1\) dependent on \(z\) (a linear combination of regression coefficients) is given as: \(log\left(\frac{\pi }{1-\pi }\right)=z\), and the probability that \(y=1\) (\(\pi\)) is given as: \(\pi = \frac{\text{e}\text{x}\text{p}\left(z\right)}{1+\text{e}\text{x}\text{p}\left(\text{z}\right)}\). Estimates are presented on the log-odds scale in the model summary tables of the supporting information but are presented as probabilities in figures to aid interpretation. All models were fit using the glmmTMB package62 in R version 4.2.163.

Our data are organized in a three-level structure, with repeated yearly measurements of a plot (ij\(k\); level 1 units) nested in plots (\(jk\); level 2) that, in turn, are nested in sites (\(k\); level 3). To test how the responsiveness of biomass varied between these levels, we fit a random intercept-only model of the form:

$$log\left(\frac{{\pi }_{ijk}}{1-{\pi }_{ijk}}\right)= {\beta }_{0}+ {u}_{0k}+ {u}_{1jk}+ {e}_{ijk}$$

Here, the left side of the equation denotes the log-odds that \(y=1\) in the \({i}^{th}\) year in the \({j}^{th}\) plot of the \({k}^{th}\) site. The \({\beta }_{0}\) coefficient is the global intercept, representing the estimated log-odds that \(y=1\) at the global scale, \({u}_{0k}\) is a random intercept that measures between-site variability in \({\beta }_{0}\), \({u}_{1jk}\) is a random intercept that measures between plot variability in \({\beta }_{0}+ {u}_{0k}\), and \({e}_{ijk}\) is residual error associated with within-plot variability in the log-odds that \(y=1\). We also included a first order autoregressive term for year to account for the fact that observations in years that are closer in time (e.g., observations in years one and two) may be more similar than those that are distant in time (e.g., observations in years one and fifteen). This model performed best in AIC comparisons of different random effects structures (Table S2). We extracted conditional modes from this model that show the expected probability of non-responsiveness at each site and in each plot.

Evaluation of temporal change in nutrient limitation

To test the hypothesis that the probability of non-responsiveness would increase over time, we fit the quadratic model:

$$\begin{aligned} log\left(\frac{{\pi }_{ijk}}{1-{\pi }_{ijk}}\right) &= {\beta }_{0}+ {u}_{0k}+ {u}_{1jk}+ \left({\beta }_{1}+ {u}_{2k}+ {u}_{3jk}\right){year}_{ijk} \\ &+ \left({\beta }_{2}+ {u}_{4k}+ {u}_{5jk}\right){year}_{ijk}^{2}+ {e}_{ijk}.\\ \end{aligned}$$

As described for model 1, this gives a global fixed intercept and random intercepts for site and plot-in-site. In addition, this model provides fixed slopes (\({\beta }_{1}\), \({\beta }_{2}\)) and random slopes for site (\({u}_{2k}\), \({u}_{4k}\)) and plot-in-site (\({u}_{3jk}\), \({u}_{5jk}\)) associated with both the linear and quadratic forms of the year variable. This structure allows for the probability of non-responsiveness to change over time in a non-linear form and for the nature of that change to vary between sites and plots. The inclusion of random slopes is expected to account for autocorrelation. Inferences about the significance of change in probability over time were based on a likelihood ratio test for the null hypothesis that \({\beta }_{1}=0\).

Assessing factors regulating nutrient limitation

To evaluate mechanisms contributing to variability in fertilizer responsiveness we fit mixed-effects models with the same random effects as above whilst also including fixed effects for multiple explanatory variables. To assess how these mechanisms operate across the multiple spatial and temporal scales that characterize our data, explanatory variables were included at three levels using group-mean centering64. Explanatory variables at the site level (\(k\)) were centered and z-score standardized relative to the mean of the variable across all the data (grand-mean centering). Coefficients associated with grand-mean centered variables estimate the effect of among-site variability in an explanatory variable; for example, the coefficient associated with grand-mean centered species richness provides a specific estimate of how fertilizer-responsiveness varies along an among-site richness gradient, from species-poor to species-rich sites. Explanatory variables at the plot-in-site level (\(jk\)) were centered (most sites had three 25 m2 plot replicates per treatment [three replicates x two treatments = 6 plots per site], with each replicate considered a block) and z-score standardized relative to the site mean (group-mean centering) to characterize how much the plot mean deviates from the site mean. For example, the coefficient associated with site-mean centred species richness estimates how fertilizer-responsiveness varies in response to within-site heterogeneity in plot species richness, irrespective of the site’s position on the global richness gradient. Finally, variables were included at the yearly scale (\(ijk\)) by group-mean centering values around the plot-in-site mean. Coefficients associated with variables at this level show how interannual variability contributes to the responsiveness of biomass. For example, the coefficient associated with plot-mean centered species richness estimates how fertilizer-responsiveness varies in response to interannual changes in plot species richness, regardless of the mean relative richness of the plot or site. Including each variable at multiple scales allows explicit estimation of the within and among group effects that are central to our hypotheses.

For the 61 sites that had sufficient observations, we used centered variables to assess the influence of aridity and species richness on biomass responsiveness. Here, we fit the model:

$$\begin{aligned} log\left( {\frac{{\pi _{{ijk}} }}{{1 - \pi _{{ijk}} }}} \right) & = \beta _{0} + u_{{0k}} + u_{{1jk}} + \beta _{1} SpeciesRichness_{k} + \beta _{2} Aridity_{k} \\ & + \beta _{3} SpeciesRichness_{{jk}} + \beta _{4} Aridity_{{ik}} + \beta _{5} SpeciesRichness_{{ijk }} \\ & + \beta _{6} (SpeciesRichness_{k} *Aridity_{k} ) + \beta _{7} (SpeciesRichness_{{ijk}} *Aridity_{k} ) \\ & + \beta _{8} (SpeciesRichness_{k} *SpeciesRichness_{{ijk}} ) + e_{{ijk}} . \\ \end{aligned}$$

We took a multi-model inference approach to determine the best set of these factors for explaining variation in biomass responsiveness. We used the ‘dredge’ function in the MuMIn package65 to rank models with different subsets of parameters, then averaged coefficients over all models within 2 AIC of the best model. We present full averages of parameter estimates in the main text and both full and conditional averages in the supporting information.

For the 48 sites that had pre-treatment observations of species richness and biomass, we fit the model:

$$\begin{aligned} log\left(\frac{{\pi }_{ijk}}{1-{\pi }_{ijk}}\right) &= {\beta }_{0}+ {u}_{0k}+ {u}_{1jk}+ {\beta }_{1}{SpeciesRichness}_{jk} + {\beta }_{2}{Biomass}_{jk} \\ &+ {\beta }_{3}{SpeciesRichness}_{k} + {\beta }_{4}{Biomas}_{k} + {\beta }_{5}{Aridity}_{k}+ {e}_{ijk}.\\ \end{aligned}$$

Note, this model only operates at the site and plot-in-site level as pre-treatment data do not vary at a yearly scale. Finally, for the 33 sites with pre-treatment soil conditions, we fit the model:

$$\begin{aligned} log\left(\frac{{\pi }_{ijk}}{1-{\pi }_{ijk}}\right) &= {\beta }_{0}+ {u}_{0k}+ {u}_{1jk}+ {\beta }_{1}{Litter}_{jk} + {\beta }_{2}{N}_{jk} + {\beta }_{3}{P}_{jk}+ {\beta }_{4}{K}_{jk} \\ &+ {\beta }_{5}{pH}_{jk}+ {\beta }_{6}{SpeciesRichness}_{jk} + {\beta }_{7}{Biomass}_{jk }+ {\beta }_{8}{Litter}_{k} \\ &+ {\beta }_{9}{N}_{k} + {\beta }_{10}{P}_{k}+ {\beta }_{11}{K}_{k} + {\beta }_{12}{pH}_{k}+ {\beta }_{13}{SpeciesRichness}_{k} \\ &+ {\beta }_{14}{Biomass}_{k } + {\beta }_{15}{(N}_{jk}*{pH}_{jk})+ {\beta }_{16}{(K}_{jk}*{pH}_{jk}) \\ &+ {\beta }_{17}{(pH}_{jk}*{SpeciesRichness}_{jk}) + {e}_{ijk}. \\ \end{aligned}$$

Sites included in each subset are noted in Table S1. Variables were centered and standardized separately for each subset to avoid skewing means with missing variables.

Evaluating precision fertilization scenarios

We used empirically measured biomass from 61 rangeland sites to explore the trade-off between maximizing yield while minimizing ‘overfertilization’ (i.e., when adding nutrients does not increase biomass). The boundaries of this exploration range from one extreme with repeated annual fertilization of all plots (NPK + plots), to the other, where no plots are fertilized (control plots). We then evaluated 13 intermediate scenarios based on varying (i) the duration of fertilizer application including our estimated measure of cessation, (ii) fertilizer cessation when informed by baseline factors of species richness, pH, aridity, and site fertility (e.g., P levels prior to P addition), or (iii) the spatial application of nutrients when armed with the knowledge of locations where responsiveness to fertilization within-sites is low or nil. Our goal was to rank outcomes within these boundaries based on ratios between maximizing yield but preventing over-fertilization as much as possible. The scenarios described in Table 1 were defined based on a three-step process:

  1. 1.

    For each scenario, we calculated average plot yield across all experimental units in g m−2 year−1, and overfertilization, measured as the number of experimental units in which yield did not increase with fertilization.

  2. 2.

    We then considered how different precision fertilization scenarios would alter average plot yield and inefficiency if the experiment was conceptually re-run while modifying fertilizer inputs according to different guiding principles. Under these scenarios, we conditionally substituted the treatment plot yield value with its corresponding control plot value if it met the specified criteria then set overfertilization to zero in that unit. This assumes that control plot biomass would approximate the decline in biomass in the following year that would occur if a fertilized plot became unfertilized, recognizing that fertilizer ‘legacy’ effects on biomass can sometimes persist after cessation66,67,68.

  3. 3.

    We contrasted scenarios in which fertilization was modified based on the responsiveness of subsets of experimental units at different spatial and temporal scales (‘scale-dependent’ scenarios) with scenarios based on not fertilizing units with values of climatic, edaphic, or biotic covariates that surpass thresholds identified in earlier modelling (‘context-dependent’ scenarios). Under the ‘optimal’ scenario, we projected average yield across the experiment if only nutrient limited plots were fertilized. Under four spatial scale-dependent scenarios, we substituted control values in (1) plots that were not limited in the first year of fertilization, (2) plots that were not limited on average over the first three years of fertilization, (3) sites that were not limited in the first year of fertilization, or (4) sites that were not limited on average over the first three years of fertilization. In three scenarios, we considered the role of a site’s fertilization history, substituting control values to project the effect of ceasing fertilization after three, five, or ten years. Under five ‘context-dependent’ scenarios, we used thresholds for covariates identified as important in our explanatory modelling to project the impact of not fertilizing in (1) sites where average plot-level species richness was more than one standard deviation below the global mean, (2) sites where average aridity was more than one standard deviation below the global mean, (3) plots where average pre-treatment soil pH was more than 1.3 standard deviations above the site mean, (4) plots where average pre-treatment soil phosphorus was more than 1.3 standard deviations above the site mean, and (5) years where plot species richness was more than one standard deviation below plot average species richness.