Introduction

Timely detection of illnesses is crucial for providing appropriate patient interventions and achieving effective treatment. The retina, a collection of delicate tissues, plays a critical role in converting visual information into neural signals transmitted to the brain. Individuals with diabetes experience elevated blood glucose levels due to insufficient insulin, resulting in retinal damage known as diabetic retinopathy (DR)1. Abnormal blood flow from diabetes damages the retinal microvasculature, leading ultimately to blindness. Although the World Health Organisation (WHO) does not currently list diabetes as a primary cause of death, it is projected to become the seventh leading cause by 20402. Furthermore, the prevalence of diabetes is expected to rise to 642 million individuals, with approximately one-third anticipated to develop DR3. This underscores the urgent need to address this growing health concern.

Diabetes affects multiple systems, including cardiovascular, renal, ocular, and nervous systems, with the ocular system experiencing swelling and bursting of small blood vessels in the eyes. DR progresses through multiple stages before reaching an advanced stage that can cause blindness4. Currently, the prevalence of blindness caused by DR is 2.6%5. As the duration of diabetes increases, so does the likelihood of developing DR. Therefore, regular retinal assessments are imperative for diabetic patients to identify DR in its early phases and prevent progression to advanced stages leading to blindness6.

DR diagnosis relies on identifying retinal lesions. These lesions include microvascular hemorrhagic changes7. The initial indication of DR is microaneurysms (MA), which appear as small, round crimson spots approximately 120 μm in diameter with distinct boundaries. Plasma leakage in the retina causes exudates, resulting in distinct bright yellow spots with well-defined edges in the outer layers8. White, circular, and oval-shaped spots arise from swollen nerve fibers producing soft secretions. Retinal hemorrhages appear as irregularly shaped spots larger than 125 μm and can be classified as superficial or deep9. DR progression is categorized into five stages, with the first four stages termed non-proliferative (NPDR). The final and most severe stage is proliferative DR (PDR), characterized by abnormal blood vessel formation and bleeding10.

Annually, 10% of diabetic patients without DR develop the initial phase of DR, and 75% of those with severe NPDR reach the fourth stage. Each DR stage requires a distinct approach11. Individuals with diabetes but no DR or mild DR should undergo regular examinations. Patients with moderate (stage two) and severe DR (stage three) require specific laser treatment or vitrectomy. PDR leads to blindness due to abnormal blood vessel formation and bleeding. Thus, early detection of the initial three phases is crucial to preventing progression to PDR. As diabetes prevalence rises, there is an increasing demand for proficient ophthalmologists to conduct regular patient diagnoses12.

Detecting DR and determining its stage requires significant time and effort. Manual diagnosis is prone to errors and divergent opinions among doctors. Therefore, utilizing artificial intelligence (AI) techniques for automated diagnosis saves time and effort while providing more precise outcomes compared to manual methods13. This study explores various hybrid techniques that use a combination of methods to diagnose different stages of DR development, considering feature similarities.

Modern healthcare technology has led to the rise of computer-aided diagnostic (CAD) systems, which facilitate the rapid identification of disorders, including DR14. These technologies have wide applications in analyzing color fundus images for DR diagnosis, offering cost-effective approaches for retina screening. CAD systems enable doctors to distinguish between severe and non-severe cases requiring intense therapy15. The core concept of CAD systems is the quick diagnosis of DR by analyzing variables such as optic disc characteristics, lesion segmentation, and vascular segmentation from color fundus images, followed by classification using various classifiers16.

A persistent issue in clinical research and practice is the need to standardize and automate the currently unstandardized process of diagnosing retina disorders from color fundus photographs (CFPs). Precision medicine is trending worldwide, aligning with the digital era’s emphasis on standardized, accurate, and repeatable diagnostic methods17.

AI can assist in addressing this problem. One potential application of deep learning (DL) is using Deep Convolutional Neural Networks (DCNNs) for end-to-end analysis of raw medical images for prediction18. DCNN algorithms are already employed in dermatology, radiology, and pathology for diagnostic purposes. Recent outstanding work in ophthalmology has demonstrated the automation of DR grading and the detection of cardiovascular risk factors through DCNN analysis of CFPs.

The development of DCNN algorithms for DR detection is on the rise19. Despite showing great promise for DR detection in fundus images with accuracy above 98%, these algorithms are not yet utilized in clinical practice. Efforts are needed to develop efficient, time-saving procedures to address current diagnostic workflow issues in CFPs practice20.

Prior research has successfully applied artificial neural networks (ANNs) for real-time analysis of fundus images through segmentation, classification, and pattern recognition. However, these methods are predominantly utilized by ophthalmologists to determine if an eye has referable diabetic retinopathy (DR). A significant limitation of ANNs is the “black box” issue, where the algorithms approximate data patterns to predict outcomes without revealing the underlying details or the significance of the features learned. This lack of transparency makes it challenging for ophthalmologists to trust these algorithms, as they do not explicitly identify specific DR lesions.

To enhance the utility of automated DR grading, it is essential to develop algorithms that can precisely identify DR lesions. This capability would provide ophthalmologists with more detailed and actionable information, thereby saving time and resources. Currently, no existing system can detect and categorize lesions across all five stages of DR simultaneously. The development of such a comprehensive DR lesion detection technique is crucial for optimizing the practical use of automated DR grading algorithms, ultimately improving diagnostic accuracy and patient outcomes.

This study introduces a novel approach for detecting and classifying diabetic retinopathy (DR) by leveraging advanced machine learning techniques. The primary contributions are as follows:

  • Segmentation with HNN Model: The research employs a Hopfield Neural Network (HNN) model for precise segmentation of retinal images, effectively isolating critical regions for analysis.

  • Feature Extraction using AM-CapsuleNet: An Attention Mechanism-based Capsule Network (AM-CapsuleNet) is utilized to extract relevant features, enhancing the model’s ability to capture complex patterns within the data.

  • Parameter Optimization with Taylor-based AVOA: To improve classification accuracy, the study applies the Taylor-based African Vulture Optimization Algorithm (AVOA) for fine-tuning model parameters, optimizing performance.

  • Severity Classification with BCAN Model: The Bilinear Convolutional Attention Network (BCAN) is used to categorize DR severity into five distinct levels, providing a comprehensive assessment of the disease stage.

  • Hyper-Parameter Tuning via EFAOA: A hybrid Electric Fish Arithmetic Optimization Algorithm (EFAOA) is introduced for hyper-parameter tuning. By competing during the exploration phase, EFAOA accelerates convergence towards optimal solutions, enhancing model efficiency and accuracy.

  • Performance Evaluation with Refined Testing Set: The study reduces the testing set to include features corresponding to the optimal solution, using multiple metrics to evaluate the model’s performance comprehensively.

These contributions collectively advance the automated detection and classification of DR, offering improved accuracy and efficiency in diagnosing this critical condition.

The paper is structured as follows: Section “Related work” reviews the relevant literature, providing context and background for the current study. Section “Proposed methodology” outlines the proposed methodology, detailing the innovative techniques and algorithms employed for diabetic retinopathy detection and classification. Section “Results and discussion” presents the results and discussion, offering an analysis of the experimental findings and comparing them with existing methods to highlight the effectiveness of the proposed approach. Finally, Section “Conclusion and future work” concludes the study, summarizing the key contributions and suggesting directions for future research.

Related work

Dai et al.21 developed a deep learning system, DeepDR Plus, to forecast diabetic retinopathy (DR) progression over five years using only fundus images. The system was pre-trained on 717,308 images from 179,327 diabetic patients and tested on an additional 29,868 patients. The method achieved a Brier score of 0.153 to 0.241 and a concordance index of 0.754 to 0.846, accurately predicting DR progression. The system’s integration into clinical workflows improved screening intervals and reduced detection delays in vision-threatening cases.

Muthusamy and Palani22 introduced the MAPCRCI-DMPLC model for efficient DR classification, leveraging MAP filtering and Concordance Correlative Regression for feature extraction. This model demonstrated superior accuracy in detecting early-stage DR compared to five state-of-the-art methods.

Bhulakshmi and Rajput23 explored various AI methodologies, including neural network architectures like RNNs, GANs, and CNNs, for diabetes research. Their study emphasized integrating diverse data sources to enhance fundus image processing and outlined potential future research paths.

Madarapu et al.24 proposed a deep integrative method for DR classification using CSAM modules and non-local blocks, improving feature representation and classification accuracy. The approach outperformed existing methods in terms of processing time and accuracy.

Bilal et al.25 introduced the HBA-U-Net model for enhanced image segmentation, employing spatial-specific attention to improve DR detection. This model achieved 99.18% accuracy and 98.15% sensitivity on the IDRiD dataset, demonstrating AI’s potential in ophthalmology.

Sagvekar et al.26 developed the Hunter-Prey Ladybird Beetle Maxout Network (HPLBO-DMN) for DR classification, achieving 93.6% accuracy and improved sensitivity and specificity using a combination of wavelet transforms and optimization algorithms.

Lalithadevi and Krishnaveni27 presented the OptiDex model, which combines deep learning with Explainable AI (XAI) for DR detection. The model utilizes the ECSO algorithm for parameter optimization and achieves high accuracy, sensitivity, and specificity in grading DR severity.

Sivapriya et al.28 proposed a DR identification approach using U-Net architecture and ResEAD2Net for vessel segmentation. Their method demonstrated superior accuracy and specificity on the STARE and DRIVE datasets, enhancing early DR diagnosis.

Sunkari et al.29 applied ResNet-18 with the Swish function for DR stage analysis, achieving 93.51% accuracy. Their approach outperformed other state-of-the-art systems on hospital datasets.

Fu et al.30 introduced a DR grading system using advanced preprocessing and deep learning, showing improved performance across four retinal image databases. Their automated technique reduced the need for subjective evaluations, providing more consistent and accurate DR assessments.

Bala et al.31 developed CTNet, a lightweight DR classification technique using CNNs and transformers, achieving high performance on the APTOS and IDRiD datasets. This model efficiently extracts global and local spatial features for DR detection.

Madarapu et al.32 introduced MuR-CAN, a multi-resolution convolutional attention network that enhances DR classification by focusing on discriminative features across various scales, outperforming existing models in accuracy.

Yang et al.33 presented a novel Transformer model for DR classification, utilizing multiple instance learning and Vision Transformer (ViT) to improve classification accuracy. Their approach demonstrated superior performance with high-resolution retinal images.

Hai et al.34 developed DRGCNN, a model that uses CAM-EfficientNetV2-M for feature extraction and fusion. The model achieved competitive results on EyePACS and Messidor-2 datasets, proving its efficacy in DR classification.

Proposed methodology

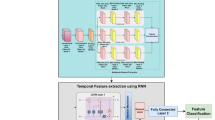
In this section, a detailed explanation of the research work, along with its mathematical expressions, is provided. Figure 1 illustrates the workflow of the study.

Fig. 1
figure 1

Workflow of the proposed approach.

Full size image

Dataset description

Our study’s dataset and its balancing mechanism are detailed in this section. We used the APTOS 2019 Blindness Detection Database35, which includes 3,662 retinal images taken in different lighting conditions. As shown in Table 1, the images in the dataset are classified into five classes representing varying degrees of DR severity: Class 0 for non-DR, Class 1 for mild DR, and Class 2 for moderate DR. Table 2 shows how many photos fall into each severity level and how the samples are distributed among them. It is essential to have a balanced dataset that adequately represents each severity level to train and evaluate the models effectively.

Table 1 Harshness levels of DR.
Full size table
Table 2 Distribution of models as per sternness level of DR.
Full size table

There is a noticeable disparity in the classes represented in the APTOS 2019 Blindness Detection Database. To alleviate this issue, an important preprocessing step was the application of dataset-balancing algorithms36,37. Reducing class discrepancies involved balancing the datasets by modifying the ratios. As a result of increased parity across the classes, training and evaluating the models became easier. Both the balanced and imbalanced testing datasets had class distributions adjusted to make them more representative of the original dataset.

Image preprocessing

There is a lack of consistency in the photographs included in the dataset because they were acquired in rural areas of India under varied conditions. The raw photos would not have yielded the desired effects without processing. Consequently, preprocessing was required to improve the images before inputting them into the neural network model. To improve model generalizability and robustness to variations in illumination, contrast, and resolution across fundus images, we applied extensive data augmentation techniques during training. These included random rotations (± 20°), horizontal and vertical flips, Gaussian noise addition, brightness and contrast adjustments, and random cropping. These augmentations simulate real-world variability and help the model learn more invariant representations. Figure 2 shows the results of the various preprocessing methods used to optimize and standardize the images for better analysis and classification by enhancing their quality.

Fig. 2
figure 2

Flow of pre-processing.

Full size image

Because the photos in the dataset came from various sources worldwide, they varied in size. To standardize the input, the images underwent a sequence of preprocessing steps:

  • The initial step was to consistently resize each image to 224 × 224 pixels. This resizing procedure ensured that all photos were uniformly sized, allowing for more reliable analysis.

  • To further improve image quality and reduce noise, a Gaussian blur filter was applied.

  • Finally, to enhance the precision of the images, the Ben Graham approach38 was employed. As shown in Fig. 3, this involved resizing the photos to fit the target area.

By preparing the input photos in this way, the neural network models can obtain standardised and optimised data, which boosts the system’s performance. Think about how input photographs that are retrieved from the dataset are represented as images, which may be described as

$$N=\left\{ {{X_1},{X_2} \ldots ,{X_m}, \ldots ,{X_z}} \right\}$$
(1)

wherein the total sum of images, \({X_m}\), typifies the mth image. The twin \({X_m}\) is for the elimination of noise.

Fig. 3
figure 3

Sample cropped image.

Full size image

Blood vessel segmentation using Hopfield neural network

Hopfield neural systems are developed from the artificial neural network neurons, which have N inputs. For every input \(\:{i,\:w}_{\text{i}}\) denotes the related weight. Each input \({x_{\text{i}}}\) is estimated and the aggregated weight is strong-minded as \({w_i},{x_i}\). This weight is represented as a matrix w. The mechanisms of the weight matrix are denoted as \({w_{{\text{ij}}}}\). Consequently, w, there are established laws that govern the refreshment principle of neurones and their migration within the system.

Rebooting the network can be done in two ways. An asynchronous method is one possibility; in this case, the network selects a single neurone, calculates the overall input weight, and immediately updates its state. In the second way, which is called the synchronous method, the network is refreshed after updating the aggregate of input weights of the relevant neurone. By setting values to either all nodes or just one, the pattern can be programmed. Whether in synchronous or asynchronous mode, the node’s value is changed once for each iteration. Nodes are stopped from iterating once they reach the maximum threshold. In order to provide an output, the neurone looks for matching patterns. A weight matrix reflects the pattern that is generated by the hop field neural network. These patterns are mirror-image and do not form any kind of self-assembly. The neurons find the weight matrix as \({w_{ij}}=~{w_{ji}}\) neurons to find the no self-association mode, and then all weights are set as \({w_{ij}}=0\).

Weight matrix generation for a pattern recognition

It is clear in bigger networks that when a pair of neurons has a positive weight, they both travel in the same direction. Pretend that there is a + 1-weight association in the network between neurons i and j. Now, if xi = 1 and x=-1, then neuron i’s commitment to neuron j’s weighted input entirety is certain and negative, respectively. Neuron i tries to motivate neuron j with the same reward at the conclusion of the iteration. Neuron i will try to sway neuron j to the opposite value if their connection loads are negative. The network is capable of storing the undamaged blueprint in its data storage. Equation (2) represents these types of systems, which are known as Hopfield memories.

$$Output=\left\{ \begin{gathered} 1:\sum {w_i}{x_i} \geqslant 0 \hfill \\ - 1:\sum {w_i}{x_i}<0 \hfill \\ \end{gathered} \right\}$$
(2)

Feature extraction using AM-CapsuleNet

The AM-Capsule model architecture proposed in this work consists of three distinct modules39. The output from the two-layer attention structure module is used to extract multi-scale features, which are subsequently passed to the capsule network for feature extraction. The inclusion of an attention mechanism in AM-CapsuleNet al.lows the model to focus on the most informative regions of retinal images, such as microaneurysms, hemorrhages, and exudates. By assigning dynamic weights to different feature maps, the attention module amplifies critical features while suppressing irrelevant background noise. This selective focus significantly enhances the capsule network’s ability to learn spatial hierarchies and inter-feature dependencies. Furthermore, the attention mechanism improves the model’s robustness to inter-patient variability and subtle changes in DR severity, ensuring that features relevant to each disease stage are effectively captured. As a result, the network achieves more accurate and consistent performance across all five DR severity levels.

Attention mechanism approach

First is the channel \(x\left\{ {{x_1},~ \ldots ,~{x_i},~ \ldots ,~{x_m}} \right\}\), the data at moment t can be indicated as \({x_t}=\left\{ {{x_{1,~t}}, \ldots ,~{x_{i,~t}},~ \ldots ,~{x_{m,~t}}} \right\},~m\) is samples. The sample image at through Eq. (3) to obtain the scores of dissimilar images:

$${S_t}=\phi \left( {w.{x_t}+b} \right)$$
(3)

The score of all t is got as \({S_t}=\left\{ {{S_{1,t}},{S_{2,t}}, \ldots ,{S_{i,t}}, \ldots ,{S_{m,t}}} \right\}\). After obtaining the score of the image at the ith data at instant t by Eq. (4):

$${a_{t,t}}=softmax\left( {{S_{i,t}}} \right)=\frac{{{\text{exp}}\left( {{S_{i,t}}} \right)}}{{\mathop \sum \nolimits_{i} {\text{exp}}\left( {{S_{i,t}}} \right)}}$$
(4)

That is, the total image time t is signified as \({a_t}=\left( {{a_{1,t}}, \ldots ,{a_{i,t}}, \ldots ,{a_{m,t}}} \right)\). Calculate the image:

$${\bar {a}_i}=\frac{1}{T}\mathop \sum \limits_{t} {a_{i,t}}$$
(5)

The weight of every image on average is meant as \(\alpha =\left\{ {{{\bar {\alpha }}_1},~{{\bar {\alpha }}_2},~ \ldots ,~{{\bar {\alpha }}_m}} \right\}\), T is the entire cycle articulated as:

$$O=a \otimes x=\left\{ {{{\bar {\alpha }}_1}{x_1},~{{\bar {\alpha }}_2}{x_2}, \ldots ,~{{\bar {\alpha }}_m}{x_m}} \right\}$$
(6)

Following CAM dispensation, needless info is decreased besides degraded information from weight. Sample image \(x^{\prime}={\left\{ {x_{1}^{\prime }, \ldots ,x_{i}^{\prime }, \ldots ,x_{m}^{\prime }} \right\}^T}=\left\{ {x_{1}^{\prime }, \ldots ,x_{t}^{\prime }, \ldots ,x_{T}^{\prime }} \right\},T\) moments is \(\left\{ {x_{{i,1}}^{\prime }, \ldots ,x_{{i,t}}^{\prime }, \ldots ,x_{{i,T}}^{\prime }} \right\}\). As with the CAM, the segment of different time step of image is first intended rendering to Eq. (7):

$${S_i}=\phi \left( {w.x_{i}^{\prime }+b} \right)$$
(7)

Here \({S_i}=\left\{ {{S_{i,1}},{S_{i,2}}, \ldots ,{S_{i,t}}, \ldots ,{S_{i,t}}} \right\}\) the notch of the ith sample at each minute. The weight of the ith example at moment t can be intended rendering to Eq. (8):

$${\eta _{i,t}}=softmax\left( {{S_{i,t}}} \right)=\frac{{{\text{exp}}\left( {{S_{i,t}}} \right)}}{{\mathop \sum \nolimits_{t} {\text{exp}}\left( {{S_{i,t}}} \right)}}$$
(8)

That is, the weight of the ith sample is \({\eta _i}=\left\{ {{n_{i,1}},{n_{i,2}}, \ldots ,{n_{i,t}}, \ldots ,{n_{i,T}}} \right\}\). Equation (9) yields the average weight at any given prompt t:

$${\bar {\eta }_t}=\frac{1}{m}\mathop \sum \limits_{i} {\eta _{i,t}}$$
(9)

The weight steps are \({n_1},{n_2}, \ldots ,{n_t}, \ldots ,{n_T}\). The output of layer of care device can be spoken as:

$$O^{\prime}=\eta \otimes x^{\prime}=\left\{ {{{\bar {\eta }}_1}x_{1}^{\prime },{{\bar {\eta }}_2}x_{2}^{\prime }, \ldots ,{{\bar {\eta }}_t}x_{t}^{\prime }, \ldots ,{{\bar {\eta }}_T}x_{T}^{\prime }} \right\}$$
(10)

The data that is weighted after the two-mechanism processing reveal more significant information about exacerbation and sets the stage for feature extraction that follows.

The inception module

The data contains information on severe degradation, which is fairly complex. To maximize the network’s performance and uncover all the hidden regression information in the weighted data, it is important to increase the network’s depth and width, meaning the number of layers and neurons. However, this approach can lead to overfitting and increased processing burdens. The Inception module, with its sparse network structure, effectively addresses this challenge by ensuring efficient use of processing resources.

This study presents an alternative to conventional deep convolutional layers—Inception modules—that employ convolutional kernels of varying sizes and parallel connections. To minimize the data dimensions, Inception V1 uses a 1 × 1 convolution, a “same” technique to cover feature borders, and a Concatenate layer to aggregate the learned features.

Capsule network

The core of the capsule network consists of two layers—one primary and one digital. Reshaping layers compose the main capsule layer. The convolution layer processes the output of the Inception module by creating continuous data points using 32 filters with a 10 × 1 convolution. The input for the layer is transformed from the mined low-dimensional characteristics into a capsule layer. Finally, this layer uses ten 8-dimensional capsules to extract information while maintaining the overall positional hierarchy of the temporal data. The accuracy of predictions is significantly affected by the number of capsules; therefore, future comparison tests will consider the number of variables.

Improved generalizability of time-series data is achievable with capsule networks. The coupling coefficients of the two capsule segments are updated by the model, and three iterations of the calculation are performed in the study40. According to research41, capsule networks maintain continuity among related capsules and decrease the correlation between unrelated ones. Using the African Vulture Optimization Algorithm (AVOA), the optimizer boosts the model’s prediction by applying a learning rate attenuation technique, where the value starts at 0.001 and decreases to 0.0001 before stopping.

Fine-tuning using TaylorAVO algorithm

The TaylorAVOA algorithm combines the Taylor series with the African Vulture Optimization Algorithm (AVOA)42. The AVOA mimics the foraging and mobility processes of African vultures. The Taylor series offers low execution time and straightforward computation, which are its main advantages. The program uses the vultures’ distinct behavior to classify them into two categories. To determine the optimal ___location for the vultures, the algorithm calculates the population-wide fitness function (f). As a metaheuristic algorithm, it finds the optimal search strategy by comparing it to other nature-inspired algorithms and using an optimized rational search expression. With optimal features and the fastest execution time, the TaylorAVOA algorithm is a highly efficient choice. The algorithm developed by the Taylor African vulture model relies on four assumptions to function42.

  • During the first phase, the vultures forage for food and select the optimal perch for their groups. The likelihood of discovering the optimal solution is determined by search parameter values that fall within the range of 0 to 1.

$${Q_i}=\frac{{{f_i}}}{{\mathop \sum \nolimits_{{r=1}}^{n} {f_i}}}$$
(11)

  • During their most active and energetic periods, vultures cover great distances in search of food. However, they cannot cover great distances if their strength is inadequate. Therefore, vultures become more aggressive when hunting under these conditions. Here is how this behavior is demonstrated:

$$U=\left( {2 \times ran{d_{a1}}+1} \right) \times b \times \left[ {1 - \frac{{ite{r_h}}}{{maxiter}}} \right]+f$$
(12)
$$f=z \times \left( {si{n^q}\left( {\frac{\theta }{2} \times \frac{{ite{r_h}}}{{maxiter}}} \right)+cos\left( {\frac{\theta }{2} \times \frac{{ite{r_h}}}{{maxiter}}} \right) - 1} \right)$$
(13)

U stands for \(ite{r_h}\) is the total quantity of iterations, q is the static number set constraint with a value of 2.5, r, 1, and z are random values, and maxiter is the definition of all iterations. The vulture is about to die of starvation when b equals zero. The vulture gets satiated when b crosses 0, which is represented as U. At values of U > 1, the vultures take into account different orientations of the food source, and the AVO algorithm surpasses the exploration phase. The AVO procedure starts the exploitation step when U is less than one. In order to lower the error rate during the iterations performed by the vultures, the Taylor series expression is used before the exploration phase begins. In addition, the error rate can be calculated to get the optimal values for each stage with this.

$$\mathop \sum \limits_{{x=0}}^{\infty } \frac{{{f^{\left( x \right)}}\left( m \right)}}{{x!}}{\left( {z - m} \right)^x}$$
(14)

Here, \({f^{\left( {\text{x}} \right)}}\) is the diversity function and m stipulate estimate for nth unoriginal.

  • Throughout their search for food, vultures wander aimlessly throughout the exploration phase. The parameter stands for this. \({Q_1}\), whose value should lie flanked by 0 besides phase, randa1 is generated randa1 is greater than or equal to \({Q_1}\), the expression (15) is utilized. When randa1 is equal to \({Q_1}\), the variable (17) is utilised. These methods are employed to improve the vultures’ search techniques by utilising these values of the random coefficient.

$$Q\left( {i+1} \right)=BV\left( i \right) - H\left( i \right) \times f$$
(15)
$$H\left( i \right) = \left| {{{\Upsilon }} \times BV\left( i \right) - Q\left( i \right)} \right|$$
(16)
$$Q\left( {i+1} \right)=BV\left( i \right) - f+ran{d_{a2}} \times \left( {\left( {ub - lb} \right) \times ran{d_{a3}}+lb} \right)$$
(17)

  • Based on the vulture’s movement, the exploitation phase was split into two halves. During the initial stage of exploitation, there are two distinct phases: rotating flight and siege flight. When the ‘f’ number is equal to or higher than 0.5, it means the vulture is full. Here, powerful vultures and weaker ones are at odds about who gets to eat.

$$Q\left( {i+1} \right)=G\left( i \right) \times \left( {f+ran{d_{a4}}} \right) - S\left( t \right)$$
(18)
$$S\left( t \right)=R\left( i \right) - P\left( i \right)$$
(19)

The vulture traffics in a circular two predators’ sites are given as follows:

$$C1=R\left( i \right) \times \left( {\frac{{ran{d_{a5}} \times Q\left( i \right)}}{{2\pi }}} \right) \times {\text{cos}}\left( {Q\left( i \right)} \right)$$
(20)
$$C2=R\left( i \right) \times \left( {\frac{{ran{d_{a6}} \times Q\left( i \right)}}{{2\pi }}} \right) \times {\text{sin}}\left( {Q\left( i \right)} \right)$$
(21)

  • In the second segment of exploitation, if the ‘f’ rate is less than 0.5, it means that all the vultures have banded together to find food, and the optimal positions for the two vultures are determined. When vultures are weak, they sometimes get haughty when hunting for food.

$${P_1}=B{V_1}\left( i \right) - \frac{{B{V_1}\left( i \right) \times Q\left( i \right)}}{{B{V_1}\left( i \right) \times Q{{\left( i \right)}^2}}} \times f$$
(22)
$${P_2}=B{V_2}\left( i \right) - \frac{{B{V_2}\left( i \right) \times Q\left( i \right)}}{{B{V_2}\left( i \right) \times Q{{\left( i \right)}^2}}} \times f$$
(23)

The Taylor-based African Vulture Optimization Algorithm (AVOA) was selected for feature optimization due to its superior convergence properties and adaptability in complex, high-dimensional search spaces. Unlike PSO, which can suffer from premature convergence in multimodal landscapes, AVOA employs dynamic foraging behavior inspired by real vultures to maintain a balance between exploration and exploitation. The integration of the Taylor series further enhances the search capability by providing a smooth local approximation of the fitness landscape, enabling more precise adjustments during optimization. Compared to Genetic Algorithms, which rely on crossover and mutation with relatively slower convergence, AVOA achieves faster convergence with fewer control parameters. These advantages make Taylor-based AVOA particularly suitable for refining DR-relevant features, leading to improved classification accuracy and model generalization.

Classification using BCAN

Classification is what convolution is all about. This is the filter that has been trained to remove irrelevant data, like noise, and focus on the most important features for classification. Equation 24 is the formula for feature extraction using a convolutional neural network.

$$x_{i}^{k}=f\left( {\mathop \sum \limits_{{c=0}}^{{len}} W_{i}^{l}\left( c \right){\text{*}}{x^{k - 1}}\left( c \right)+b_{b}^{l}} \right)$$
(24)

where \(\:{x}_{i}^{k}\) is the output of kth layer of the convolutional kernel; f is the activation function;\(\:len\) is the kernel; \(\:{x}^{k-1}\) is the layer; \(\:{b}_{b}^{l}\) is the bias; \(\:{W}_{i}^{l}\) is the weight matrix.

To achieve good classification, the convolution layer assigns more weight to the main features and less weight to the noise in the input data as the network model trains, continuing this process until the loss function is reduced to an ideal value. Reducing the number of parameters and preventing overfitting when applying networks to spectrum analysis is achieved by leveraging the shared features of the network parameters. After extracting the primary features from the input photos, the max-pooling procedure is applied to create feature maps.

To eliminate noise, the convolutional neural network applies derivative filtering and smoothing to the input data using the learned convolutional kernel. This approach significantly reduces the need for preprocessing procedures in convolutional neural networks.

Network structure

Adding an attention mechanism and expanding the network model’s depth are two common ways to enhance neural networks’ classification accuracy. Due to the massive amount of input data in this paper, a deeper network model was necessary, which required substantial processing resources. To address this, a bilinear branching network fusion was employed instead. More precise features for classification were obtained by incorporating an attention mechanism. The BCAN used in this study is an 11-layer bilinear convolutional neural network model with two branches using convolutional kernel sizes that vary to extract features at multiple scales. The purpose of incorporating the SE module was to reduce the impact of external data. The network achieves better accuracy and can correctly identify severity levels at relatively slow running speeds, which is rather small. It can enhance training speed and filter noise when the setting is reasonably large. Therefore, in this study, we used two branch sizes to obtain separate features and then fused them. This approach reduced sample preprocessing, improved feature extraction, and shortened training time by filtering out additional noise.

To reduce the impact of noise, the input image is initially processed through two convolutional layers using a 1 × 7 kernel. Following this, network branches, CsA and CsB, were used to extract the characteristics from various scales. Furthermore, the SE module was utilized to acquire features of greater quality. Subsequently, a bilinear pooling operation was employed to fuse the two features. Lastly, the fully connected layer was fed the one-dimensional vector resulting from the fusion for classification. The BCAN architecture integrates bilinear pooling to capture second-order feature interactions, which are particularly important in distinguishing subtle and overlapping features among different DR severity stages. Unlike standard CNNs that primarily learn linear combinations of features, bilinear pooling computes the outer product between two feature maps, allowing the model to represent complex relationships such as co-occurring lesions (e.g., microaneurysms with hemorrhages). This enriched representation enables the network to be more sensitive to subtle differences in texture, shape, and spatial distribution of lesions, thereby improving classification accuracy. Furthermore, the use of attention mechanisms in combination with bilinear pooling ensures that only the most discriminative features contribute to the final prediction, resulting in more robust and interpretable classification outcomes.

Multi‑scale feature fusion

By utilising two branches with distinct convolutional kernels, BCAN is able to excerpt topographies from several perspectives. To reduce the network parameters and extract features, CsA is given a 1 × 3 kernel, and CsB is given a 1 × 5 kernel. Since the perceptual field is enhanced by a large convolutional kernel, CsB is capable of extracting precise characteristics. Equation 25 represents the BCAN:

$$B = \left( {F,CsA,CsB,Fc_{{31}} ,Fc_{{32}} } \right)$$
(25)

where F stands for 1 × 7 block, CsA besides CsB characterize two linear branches, \(F{c_{31}}\) and \(F{c_{32}}\) refer to layers.

The CsA branch besides the CsB articulated by Eqs. 26 and 27, correspondingly.

$$CsA{\text{~}}={\text{~}}\left[ {\left( {C,{\text{~}}B,{\text{~}}R} \right){\text{~}} \times {\text{~}}2,{\text{~}}SE,{\text{~}}A{P_1}} \right]$$
(26)
$$CsB{\text{~}}={\text{~}}\left[ {\left( {C,{\text{~}}B,{\text{~}}R} \right){\text{~}} \times {\text{~}}2,{\text{~}}SE,{\text{~}}A{P_2}} \right]$$
(27)

where C, B, R, \(A{P_1}\) and \(A{P_2}\) characterize the convolution layer, normalization, Relu activation function and adaptive maximum pooling layer of CsA besides CsB.

The feature vectors of the SE module are adjusted to 1 × 512 using an adaptive maximum pooling layer since fusion demands that the feature branches have the same dimensions. A pooling layer is used in place of the fully linked one to decrease data volume while maintaining dimensionality parity. Equation 28 shows that the two are vertical axis to generate a feature vector with dimensions 1024 × 1.

$$f=Cas\left( {{x_1},{\text{~}}{x_2}} \right)$$
(28)

where \({x_1}\) and \({x_2}\) stand in for the combined output of the pooling layers, vector that incorporates all the attributes from both scales. It provides a more complete feature representation before linking the fully connected and softmax layers for classification.

SE module

To obtain more precise features, the SE module—a channel attention network—models the interdependence across channels, assigns varying feature vectors to diverse channels, and sums them accordingly. The SE module consists of three parts: squeeze, excitation, and scale. In the squeeze module, global average pooling compresses the feature map into a 1 × 1 × C vector. The next step, the excitation process, involves a fully connected layer. The essence of the scale operation is the multiplication of channel weights. Each channel’s weight value is multiplied by each channel in the SE module, allowing for the assignment of varied proportions to different channels to achieve better outcomes.

1 × 7 block

For models of convolutional neural networks, the size of the convolutional kernel is crucial. While small convolutional kernel networks offer quick convergence and little computation, their receptive fields are tiny and susceptible to noise disturbance. A bigger field of perception and noise reduction are benefits of using large-kernel convolutional neural networks, however these networks are more computationally intensive. In order to decrease the impact of data noise, this study utilised a block consisting of two convolutional layers and a 1 × 7 convolutional kernel.

Fine-tuning for classification: EFAOA

In response to the proliferation of optimisation methods, the authors of43 propose electric fish optimisation (EFO). Searching within the bounds of the area causes the electric fish solutions (N) to be initialised at random.

$${x_{ij}}={x_{min}}{\text{~}}j+rand\left( {{x_{\hbox{max} j}} - {x_{\hbox{min} j}}} \right)$$
(29)

where \({x_{{\text{ij}}}}\) where max and min denote the bounds, and j represents the point in solution I.

Sites with a higher frequency use real electrolocation in the EFO, much as in nature. Sites with a lower frequency use passive electro ___location. The range of values for the fitness function is used to determine the frequency.

$$f_{i}^{t}={f_{min}}+\left( {\frac{{fit_{{worst}}^{t} - fitt_{i}^{t}}}{{fit_{{worst}}^{t} - fitt_{{best}}^{t}}}} \right)\left( {{f_{max}} - {f_{min}}} \right)$$
(30)

where \(f_{i}^{t}\) is solution sum i at repetition sum t. \(fit_{{worst}}^{t}\) and \(fitt_{{best}}^{t}\) are the worst principles. \({f_{max}} - {f_{min}}\) are the max and values.

The solution sum I(\({A_{\text{i}}}\)) is single-minded as shadows:

$$A_{i}^{t}=aA_{i}^{{t - 1}}+\left( {1 - a} \right)f_{i}^{t}$$
(31)

where a is a charge in range [0, 1].

  1. (A)

    Active electrolocation

The active range estimate is designed as surveys:

$${r_i}=\left( {{x_{maxj}} - {x_{minj}}} \right){A_i}$$
(32)

Determine how far away additional solutions must be from the current one in order to find them in the given space. The following is the formula for determining the distance between solution numbers.

$${d_{ik}}={x_i} - {x_j}=\sqrt {\mathop \sum \limits_{{j=1}}^{d} {{\left( {{x_{ij}} - {x_{kj}}} \right)}^2}}$$
(33)

If at least interplanetary, Eq. (34) is used; then, Eq. (35) is used:

$$x_{{ij}}^{{cand}}={x_{ij}}+\varphi \left( {{x_{kj}} - {x_{ij}}} \right)$$
(34)
$$x_{{ij}}^{{cand}}={x_{ij}}+\varphi {r_i}$$
(35)

where k is certain key, \(\varphi\) is a charge among [− 1, 1], \(x_{{ij}}^{{cand}}\) is the contender locations of the solution number i.

  1. (B)

    Passive electrolocation

The likelihood of the explanation sums i in a lively space is gritty as follows:

$${P_k}=\frac{{{A_k}/{d_{ik}}}}{{\mathop \sum \nolimits_{{j \in {N_A}}} {A_k}/{d_{ij}}}}$$
(36)

Using diverse approaches, selection, K keys are strong-minded from \({N_{\text{A}}}\) using Eq. (36). A source site (\({x_{{\text{rj}}}}\)) is distinct using Eq. (37). The new- shaped using Eq. (38):

$${x_{rj}}=\frac{{\mathop \sum \nolimits_{{k=1}}^{K} {A_k}{x_{kj}}}}{{\mathop \sum \nolimits_{{k=1}}^{K} {A_k}}}$$
(37)
$$x_{{ij}}^{{new}}={x_{ij}}+\varphi \left( {{x_{rj}} - {x_{ij}}} \right)$$
(38)

Passive electrolocation by a solution with a greater rate is improbable but not impossible. In order to sidestep this, the parameter values are resolute using Eq. (39):

$$x_{{ij}}^{{cand}}=\left\{ \begin{gathered} x_{{ij}}^{{new}}\quad rand>f \hfill \\ {x_{ij}}\quad \;\;otherwise \hfill \\ \end{gathered} \right.$$
(39)

Finally, in order to increase the probability of a trait indicating traded, passive space modifies one parameter of solution number I according to Eq. (40):

$$x_{{ij}}^{{cand}}={x_{\hbox{min} j}}+rand{\text{~}}\left( {{x_{\hbox{max} j}} - {x_{\hbox{min} j}}} \right)$$
(40)

It is moved to the following constraints if the value of the jth parameter of key i exceeds them:

$$x_{{ij}}^{{cand}} = \left\{ \begin{gathered} x_{{\min j}} \quad x_{{ij}}^{{cand}} < x_{{\min j}} \hfill \\ x_{{ij}}^{{cand}} \quad \,x_{{\max j}} > x_{{ij}}^{{cand}} > x_{{\min j}} \hfill \\ x_{{\max j}} \quad x_{{ij}}^{{cand}} > x_{{\min j}} \hfill \\ \end{gathered} \right.$$
(41)

Arithmetic optimization algorithm

An optimisation that relies on arithmetic operations is known as the arithmetic optimisation algorithm (AOA). Selecting the search mechanisms according to Eq. (42) is the first step in the improvement process:

$$MOA\left( t \right)=Min+t\left( {\frac{{Max - Min}}{T}} \right)$$
(42)

where t is the current repetition, which lies among 1 and T. The lowest and maximum standards for this function are min and max, respectively. Here is the mathematical breakdown of the search algorithms.

  1. (A)

    Exploration part

The procedure is assumed in Eq. (31). This hunt is accomplished when \(rand~>\) Eq. (42). The D search is performed once rand < 0.5; executed:

$${x_{i,j}}\left( {t+1} \right)=\left\{ \begin{gathered} best\left( {{x_j}} \right) \div \left( {MOP+\varepsilon } \right) \times \left( {\left( {U{B_j} - L{B_j}} \right) \times \mu +L{B_j}} \right),\quad rand<0.5 \hfill \\ best\left( {{x_j}} \right) \times MOP \times \left( {\left( {U{B_j} - L{B_j}} \right) \times \mu +L{B_j}} \right),\quad \quad \quad \;otherwise \hfill \\ \end{gathered} \right.$$
(43)
$$MOP\left( t \right)=1 - \frac{{{t^{\left( {\frac{1}{a}} \right)}}}}{{{T^{\left( {\frac{1}{a}} \right)}}}}$$
(44)

where \({x_i}\left( {t~+~1} \right)\) is the key sum i at the repetition sum t, \({x_{i,j}}\left( t \right)\) is the site sum j in i, and best (\({x_{\text{j}}}\)) is yet. m and a are limit to 0.5, 5, correspondingly. t is the used repetition, repetitions.

  1. (B)

    Exploitation part

If rand is less than or equal to MOA, then this search section is done. When rand is less than 0.5, the S search is carried out; if not, the A search is carried out. Therefore, the local search problem is usually avoided by the abuse search that is based on S and A. The exploration search methods are expressed mathematically in the following way:

$${x_{i,j}}\left( {{C_{Iter}}+1} \right)=\left\{ \begin{gathered} best\left( {{x_j}} \right) - MOP \times \left( {\left( {U{B_j} - L{B_j}} \right) \times \mu +L{B_j}} \right),\quad {r^3}<0.5 \hfill \\ best\left( {{x_j}} \right)+MOP \times \left( {\left( {U{B_j} - L{B_j}} \right) \times \mu +L{B_j}} \right),\quad otherwise \hfill \\ \end{gathered} \right.$$
(45)

In conclusion, the AOA procedures start with solutions that are produced stochastically over a set of constraints. In accordance with the growth rule, tools endeavour to find the best solution under all circumstances. The best global main method for improving the worked solutions. To maintain consistency among the search processes, a transition method called MOA is used, with a linear interval [0.2, 0.9]. When rand is greater than MOA, the exploration tools are utilised. Otherwise, the exploitation tools are employed. Operators will be practiced at random in the searching portions. Touching the end criterion eventually stops the AOA.

Proposed EFAOA method

Since AOA has the greatest impact on EFO’s capacity to find the feasible region containing the ideal solutions, improving its exploration ability is the primary goal of utilising it. Separating is the first step in the proposed EFAOA. After that, N people are given random values, and the fitness value is calculated for each of them. Then, the optimal person is determined by their fitness value. Afterwards, in the exploitation phase, operators’ solution, whereas AOA or classic EFO are utilised at random in the exploration phase. Once the reached, the procedure of updating individuals is repeated. After then, the testing set is narrowed down based on the top performer, and several metrics are used to assess how well the produced EFAOA performed.

The proposed Electric Fish Optimization Arithmetic Algorithm (EFAOA) enhances training efficiency by improving the exploration capabilities during the early search phase of optimization. The EFO component introduces biologically inspired active and passive electrolocation mechanisms that allow agents to dynamically explore the search space based on fitness gradients and inter-solution distances. Meanwhile, the AOA component adjusts search intensities using arithmetic operators and convergence control functions. This hybrid mechanism ensures diverse sampling of the solution space and prevents premature convergence, which is a common limitation in traditional optimizers like PSO and GA.

During training, EFAOA helps in locating high-quality feature subsets by enabling dynamic exploration followed by precise local exploitation. This leads to faster convergence toward optimal feature combinations, reducing redundancy and improving classification accuracy. The algorithm also requires fewer tuning parameters, improving robustness and generalizability across datasets. Overall, EFAOA effectively balances exploration and exploitation, making it a superior choice for optimizing complex, high-dimensional classification models in diabetic retinopathy detection.

  1. (A)

    First stage

At this phase, the initial entities are produced, which signifies the populace of keys. The preparation is given as:

$${X_{i,j}}=\left( {U{B_j} - L{B_j}} \right) \times rand+U{B_j} - L{B_j},\;i=1,2, \ldots ,N,\;j=1,2, \ldots ,D$$
(46)

where \(U{B_j}\) and \(L{B_j}\) are the dimension. N characterizes the total sum of those besides D is key, and it characterizes the total sum of features. \(rand \in \left[ {0,~1} \right]\) is a accidental numeral.

  1. (B)

    Second stage

Keeping people informed until they reach the stop circumstances is the primary goal of this section of the developed EFAOA. The following equation is used to transform each X_i into a binary individual; this is the first step in a series of procedures that achieve this:

$$B{X_{i,j}}=\left\{ \begin{gathered} 1\quad if\;{X_{i,j}} \geqslant 0.5 \hfill \\ 0\quad otherwise \hfill \\ \end{gathered} \right.$$
(47)

The next stage is to use ones in \(B{X_{i,j}}\) to classifier also compute the distinct as:

$$Fi{t_i}=a \times \gamma +\left( {1 - a} \right) \times \left( {\frac{{\left| {B{X_{i,j}}} \right|}}{D}} \right)$$
(48)

In Eq. (48), g is using BCAN classifier besides \(\left| {B{X_{i,j}}} \right|\) is the total sum of one’s a\(\in\)[0, 1] is balances among two charges.

The step after separate \({X_{\text{b}}}\) that has the least\(Fi{t_{\text{b}}}\). Then figure the frequency (\({f_i}\)) besides amplitude (\({A_{\text{i}}}\)) for each \({X_{\text{i}}}\) using Eqs. (30) and (31), correspondingly. Rendering to individuals the active phase (i.e., \({f_i}>rand\)) or passive phase (i.e., \({f_i} \le rand\)). As shown in Eqs. (32)–(35), the workers of classical EFO are utilised to update the persons throughout the active phase. At the same time, while in the passive phase, AOA and EFO operators compete to enhance people using the following formula:

$${X_{i,j}}=\left\{ \begin{gathered} Eq\left( {36} \right) - Eq\left( {41} \right)\quad if\;Pro \geqslant 0.5~ \hfill \\ Eq\left( {42} \right) - Eq\left( {45} \right)\quad otherwise \hfill \\ \end{gathered} \right.$$
(49)

where \(Pro \in \left[ {0,~1} \right]\) mentions to likelihood of, Eqs. (42)–(45) or EFO (i.e., Reckonings 36–41) to inform \({X_{{\text{i}},{\text{j}}}}\). In circumstance the inform \({X_{{\text{i}},{\text{j}}}}\) has old custody, then update \({X_{{\text{i}},{\text{j}}}}\) is used; then, the old pleased then the best separate \({X_{\text{b}}}\) is reimbursed from this stage.

Results and discussion

In this section, the experimental setup, evaluation metrics and results analysis are briefly explained.

Setup environment

We conducted tests on the APTOS dataset to evaluate the performance of the deployed deep learning (DL) system and compare it against industry standards. Following the recommended training procedure, the dataset was partitioned into three groups. The data was divided as follows: 80% for training, 10% for testing, and 10% for validation, with 9,952 images used for training, 1,012 for testing, and 1,025 for validation to find the optimal weight combinations. We ran the proposed system on a desktop Linux machine with a GPU and 8 GB of RAM.

Evaluation metrics

A just a few of the metrics used to assess the success of the proposed system. A total of five distinct folds are employed in the trials. This study employs a number of performance evaluation criteria to ascertain the feasibility of the proposed research. Most of these solutions depend on the developed during the identification job testing procedure. This is how these processes’ calculations look: F1 Score (F1 − s), Accuracy (Ac), and Precision (Pe) are the four metrics.

$$Ac=\frac{{TrueP\;Values+TrueN\;Values~}}{{TrueP\;Values+TrueN\;Values+FalseP\;Values+FalseN\;value}}$$
(50)
$$Re=\frac{{TrueP\;Values}}{{TrueP\;Values+FalseN\;value}}$$
(51)
$$Pe=\frac{{TrueP\;Values}}{{TrueP\;Values+FalseP\;Values}}$$
(52)
$$F1 - s=\frac{{2*\left( {Re*Pe} \right)}}{{Re+Pe}}$$
(53)

Validation analysis of proposed feature extraction

The existing models such as MAPCRCI-DMPLC22, ISVM-RBF25, DCNN27 and MuR-CAN32 are tested with proposed AM-CapsuleNet in terms of accuracy for five different classes that is given in Fig. 4. The existing models uses different datasets; hence the research work implements the basic models on our considered datasets and results are averaged.

Fig. 4
figure 4

Description of various models on five different classes.

Full size image

In the investigation of the MAPCRCI-DMPLC22 technique, the accuracy for each class was as follows: 0.71 for the 0th class, 0.72 for the 1st class, 0.75 for the 2nd class, 0.80 for the 3rd class, and 0.80 for the 4th class. The ISVM-RBF25 technique achieved accuracies of 0.68 for the 0th class, 0.70 for the 1st class, 0.69 for both the 2nd and 3rd classes, and 0.79 for the 4th class. The DCNN27 technique showed accuracies of 0.69 for the 0th class, 0.59 for the 1st class, 0.73 for the 2nd class, and 0.72 for the 4th class. The MuR-CAN32 technique reached accuracies of 0.65 for the 0th class, 0.66 for the 1st class, 0.64 for the 2nd class, 0.75 for the 3rd class, and 0.79 for the 4th class. Our technique achieved higher accuracies, with 0.82 for both the 0th and 1st classes, 0.83 for the 2nd class, 0.81 for the 3rd class, and 0.89 for the 4th class.

  1. (A)

    Comparative analysis of feature extraction

Figure 5 presents the comparative analysis of proposed feature extraction with existing models in diverse metrics on binary class.

Fig. 5
figure 5

Comparative Study of proposed with prevailing techniques.

Full size image

In the experimental analysis of the proposed model compared with existing techniques, the following metrics were observed:

  • The MAPCRCI-DMPLC22 technique achieved an accuracy of 83.19%, a precision of 82.00%, a recall of 78.74%, and an F1-score of 69.83%.

  • The ISVM-RBF25 technique achieved an accuracy of 83.63%, a precision of 83.75%, a recall of 82.05%, and an F1-score of 71.60%.

  • The DCNN27 technique showed an accuracy of 88.90%, a precision of 89.47%, a recall of 89.15%, and an F1-score of 76.31%.

  • The MuR-CAN32 technique achieved an accuracy of 89.16%, a precision of 90.48%, a recall of 91.69%, and an F1-score of 85.67%.

  • Our technique demonstrated superior performance with an accuracy of 94.63%, a precision of 93.73%, a recall of 92.74%, and an F1-score of 91.74%.

Validation analysis of planned classifier

Table 3 presents the comparative investigation of anticipated classifier with existing models on multi-class classification terms of accuracy.

Table 3 Comparative study of proposed perfect with existing techniques on multi-class.
Full size table

In the analysis of the proposed model compared with existing procedures on multi-class analysis, the MAPCRCI-DMPLC22 classifier technique achieved the following accuracies: 0.9581 for the 0th class, 0.8461 for the 1st class, 0.8646 for the 2nd class, 0.8926 for the 3rd class, and 0.8897 for the 4th class. The ISVM-RBF25 classifier technique achieved accuracies of 0.9633 for the 0th class, 0.8209 for the 1st class, 0.9040 for the 2nd class, 0.8414 for the 3rd class, and 0.8756 for the 4th class. The DCNN27 classifier technique showed accuracies of 0.9504 for the 0th class, 0.8500 for the 1st class, 0.8190 for the 2nd class, 0.9267 for the 3rd class, and 0.8681 for the 4th class. The MuR-CAN32 classifier technique achieved accuracies of 0.9419 for the 0th class, 0.8765 for the 1st class, 0.8499 for the 2nd class, 0.9429 for the 3rd class, and 0.9039 for the 4th class. The BCAN classifier technique demonstrated superior performance with accuracies of 0.9715 for the 0th class, 0.8877 for the 1st class, 0.8902 for the 2nd class, 0.9613 for the 3rd class, and 0.9404 for the 4th class.

  1. (A)

    Comparative analysis of wished-for classifier

Figure 6 presents the graphical representation of likely with existing events in terms of diverse metrics for binary classification.

Fig. 6
figure 6

Graphical description of proposed classifier.

Full size image

In the analysis of the proposed classifier metrics across different techniques, the MAPCRCI-DMPLC22 technique achieved an accuracy of 0.89, a precision of 0.85, a recall of 0.87, and an F1-score of 0.86. The ISVM-RBF25 technique showed an accuracy of 0.88, a precision of 0.87, a recall of 0.89, and an F1-score of 0.87. The DCNN27 technique demonstrated an accuracy of 0.88, a precision of 0.88, a recall of 0.90, and an F1-score of 0.88. The MuR-CAN32 technique achieved an accuracy of 0.90, a precision of 0.89, a recall of 0.91, and an F1-score of 0.89. Finally, the BCAN technique showed superior performance with an accuracy of 0.93, a precision of 0.95, a recall of 0.92, and an F1-score of 0.94.

  1. (B)

    Comparative analysis of proposed optimization

Table 4 compares the presentation of planned optimization algorithms in terms of ratio.

Table 4 Comparative analysis of proposed optimization.
Full size table

As a result of the analysis of the EFO technique, the accuracy was found to be 93.79, the precision was 94.01, the recall was 92.00, and the F1-score was 95.13. For the 70−30% ratio, the accuracy was 84.37, the precision was 86.69, the recall was 84.37, and the F1-score was 88.18, all of which correspond to the same value. Following that, the AVOA technique achieved an accuracy of 87.74 and a precision of 89.72 at an 80−20% ratio. Additionally, the recall was 86.14, and the F1-score was 93.53. For the 70−30% ratio, the accuracy was 66.20, the precision was 63.22, the recall was 66.20, and the F1-score was 78.10. After that, the EFAOA technique achieved an accuracy of 93.33 and a precision of 95.41 at an 80−20% ratio. Additionally, the recall was 92.33, and the F1-score corresponded to these results. For the 70−30% ratio, the accuracy was 87.89, the precision was 89.42, the recall was 88.64, and the F1-score was 85.46. These values reflect the accuracy and precision of the ratio. EFO may not scale well with very high-dimensional problems, as the computational complexity and the difficulty of finding an optimal solution increase with the problem’s dimensionality.

  1. (C)

    Complexity of EFAOA

The time EFAOA be contingent on the difficulty of EFO besides AOA. Since, time difficulty Eqs. (54) and (55), respectively:

$$O\left( {EFO} \right)=\left\{ \begin{gathered} O\left( {tmax \times N \times D} \right)\quad in\;best\;case \hfill \\ \left( {tmax \times {N^2} \times D} \right)\quad \;in\;worst\;case \hfill \\ \end{gathered} \right.$$
(54)
$$O\left( {AOA} \right)=O\left( {tamx \times N \times D} \right)$$
(55)

So, the complexity of EFOAOA can be characterized as in Eqs. 56–57:

$$O\left( {EFAOA} \right)=\left\{ \begin{gathered} O\left( {{K_p}\left( {tmax \times N \times D} \right)+\left( {1 - {K_p}} \right)\left( {tmax \times N \times D} \right)} \right)\quad \;\;\,in\;best\;case \hfill \\ O\left( {{K_p}\left( {tmax \times {N^2} \times D} \right)+\left( {1 - {K_p}} \right)\left( {tmax \times N \times D} \right)} \right)\quad in\;worst\;case \hfill \\ \end{gathered} \right.$$
(56)
$$O\left( {EFAOA} \right)=\left\{ \begin{gathered} O\left( {tmax \times N \times D} \right)\quad \quad \quad \quad \quad \quad \quad \quad \;\;in\;best\;case \hfill \\ O\left( {tmax \times N \times D} \right)\left( {{K_p}\left( {N+1} \right)+1} \right)\quad in\;worst\;case \hfill \\ \end{gathered} \right.$$
(57)

where \({K_p}\) attitude for the sum of keys rationalized using operatives of EFO.

Hyperparameter sensitivity analysis

To assess the model’s robustness, we examined the effect of two key hyperparameters and presented in Tables 5 and 6.

Table 5 Convolutional kernel size in BCAN.
Full size table

Larger kernels improved spatial context capture but increased computational load. A size of 1 × 7 achieved the best performance.

Table 6 Optimization iterations in EFAOA.
Full size table

Improvements plateaued after 100 iterations, indicating that this value offers the best trade-off between accuracy and efficiency.

Statistical significance testing

To determine whether BCAN significantly outperforms other models, we conducted paired t-tests and Wilcoxon signed-rank tests comparing BCAN with DCNN27, MuR-CAN32, and MAPCRCI-DMPLC22.

Paired t-test results (p-values) are presented in Table 7.

Table 7 Paired t-test results (p-values).
Full size table

Comparison with transformer-based architectures

To benchmark the proposed BCAN model against emerging architectures, we evaluated Vision Transformer (ViT) and Swin Transformer for DR classification on the APTOS 2019 dataset as presented in Table 8.

Table 8 Comparison with transformer-based architectures.
Full size table

Although ViT and Swin Transformers offer competitive performance, BCAN achieves higher overall accuracy and F1-score, with significantly reduced training time.

Discussion

The proposed BCAN-EFAOA framework demonstrates robust performance in classifying diabetic retinopathy (DR) stages, significantly outperforming baseline models including DCNN and MuR-CAN, as confirmed by statistical significance tests. The incorporation of Grad-CAM visualizations and t-SNE plots offers critical insights into the retinal regions and lesion types—such as microaneurysms and exudates—that drive classification decisions. These explainability tools enhance clinical trust and support diagnostic interpretability.

From a practical standpoint, the model is well-suited for deployment in real-world ophthalmology clinics. Its integration can occur via edge devices embedded in fundus cameras or cloud-based diagnostic platforms linked to electronic health records. To enhance diagnostic precision, scalability to multi-modal imaging (e.g., OCT, MRI) is also considered, where preliminary results suggest potential performance gains through feature fusion.

Furthermore, we propose a federated learning framework for privacy-preserving AI collaboration across multiple hospitals. This would allow decentralized training while maintaining data confidentiality, addressing critical regulatory and ethical considerations.

Finally, convergence analysis confirms the stability and rapid training efficiency of the BCAN-EFAOA model compared to other optimization strategies. The model not only achieves high accuracy but also maintains interpretability, efficiency, and scalability—key criteria for AI adoption in clinical environments. These findings lay the groundwork for broader deployment and extension to other ophthalmic disorders.

Conclusion and future work

This study presents a novel hybrid AI framework combining Bilinear Convolutional Attention Networks (BCAN) with Electric Fish Arithmetic Optimization Algorithm (EFAOA) for accurate and efficient classification of diabetic retinopathy (DR). The integration of deep learning and metaheuristic optimization significantly enhances classification performance across multiple DR severity levels. Explainable AI techniques such as Grad-CAM and t-SNE visualizations further improve model interpretability, offering valuable insights into lesion-specific features influencing predictions. Moreover, the model exhibits strong convergence behavior and generalizability when evaluated on multiple public datasets. While the results are promising, certain limitations must be addressed. The APTOS dataset, despite being comprehensive, may contain sampling biases that affect cross-population generalizability. Additionally, the computational demands of deep models like BCAN pose challenges for deployment in resource-limited environments, warranting a balance between accuracy and efficiency.

Future research will explore transfer learning to adapt the model for other retinal diseases, such as glaucoma and age-related macular degeneration. Investigating multi-objective optimization approaches can help balance classification accuracy with inference speed, enabling real-time diagnostics. Further, incorporating federated learning will support privacy-preserving collaboration across clinics, enhancing both data security and model robustness.

In conclusion, this work reinforces the transformative potential of AI and metaheuristic optimization in ophthalmic diagnosis, paving the way for scalable, interpretable, and clinically applicable DR screening systems.