Introduction

The Landau-Lifshitz-Gilbert (LLG) equation has been used extensively to model magnetisation dynamics in a wide range of physical systems1. Today, it forms the basis for entire research areas, such as micromagnetics2,3,4,5,6,7,8,9,10,11 and spin-lattice dynamics12,13,14,15,16. It has also predicted many interesting dynamical effects, like chaos17,18 and type-III intermittency19. In refs.20,21,22 it has been used to model a magnetic nanoparticle which behaves chaotically when driven by the effective field. The LLG equation has also found application in various models of anomalous \(\varphi _0\) Josephson junctions, in which the weak link between the two superconductors (S) may be formed by a ferromagnetic (F) material, in the so-called S-F-S \(\varphi _0\) Josephson junction23,24,25,26.

Being nonlinear, analytical solutions of the LLG equation can be obtained only in a few cases27. In most instances, the LLG equation has to be solved numerically. Due to its wide applicability, several studies have specifically focused on developing more accurate and efficient numerical methods for its solution28,29,30,31,32. The main difficulty encountered in solving the LLG equation numerically lies in satisfying the unit length constraint on the magnetisation magnitude32. To overcome this difficulty, d’Aquino et al.28 developed a symplectic numerical integration scheme, based on the midpoint rule. This scheme exactly preserves the magnetisation magnitude. However, due to the implicit nature of the midpoint rule, it requires finding the components of the time-evolved magnetisation vector by solving a system of nonlinear equations via a root finding algorithm (typically, the Newton–Raphson method). Subsequently, it was shown that the use of a suitable quasi-Newton iterative procedure and fast iterative techniques to solve sparse linear systems can significantly reduce the simulation time29. Recently, d’Aquino et al.30 have also suggested the use of a pseudo-symplectic technique to solve the LLG equation, based on the work of Aubry and Chartier33. The pseudo-symplectic technique uses an explicit Runge-Kutta method with coefficients that have been optimised to conserve m.

Within the context of micromagnetics, Albuquerque et al.2 proposed a numerical framework for the solution of the LLG equation using a semi-implicit Crank-Nicholson integration scheme. The same work developed a physically-based self-consistency criterion that allows for a quantitative measurement of error in dynamic micromagnetic simulations. In essence, this criterion involves calculating the Gilbert damping constant from the simulated magnetisation motion and then comparing it to the actual damping parameter that was used in the simulation. In 2014, Rahim et al.34 developed a mixed mid-point Runge-Kutta like scheme for solving the LLG equation. This scheme satisfies the dynamic properties of the LLG equation for time steps up to 1.25 ps34, as was verified by using the \(\mu\)MAG standard problem #435. Recently, Fourier-spectral methods have been employed to solve the LLG equation more accurately32. In order to satisfy the unit length constraint the equations were formulated as a penalty problem32. Semi-implicit finite difference schemes have also been proposed to solve the LLG equation, including inertial effects36. Inertial effects become important for processes that occur on time scales shorter than picoseconds. To model such processes, a second order term is added to the LLG equation, giving rise to the so-called inertial LLG equation (iLLG)31,37. To enforce the unit length constraint in the iLLG equation, an implicit finite element scheme is required31.

Since thermal fluctuations are important in real materials, several different numerical techniques have been devised to solve the LLG equation with added random fluctuations, leading to the stochastic Landau-Lifshitz-Gilbert (sLLG) equation. The sLLG equation was originally developed to study the relaxation of ferromagnetic nanoparticles38. Usually, the thermal fluctuations are included in the sLLG equation via the effective field. Integrating the sLLG equation requires the use of non-Riemann calculus to treat the discontinuous thermal field39,40,41. In the context of the sLLG equation, the problem of conserving the modulus of the magnetisation m is circumvented by transforming the sLLG equation into spherical polar coordinates, before discretisation39. Recently, Leliaert et al.42 have also employed spherical coordinates to extend the use of existing high-order explicit solvers, with adaptive time stepping, to non-zero temperatures.

While the use of the spherical coordinates (\(m,\theta ,\varphi\)) effectively eliminates m from the dynamics (since m can be set to 1), there are many situations in which it is more convenient to use Cartesian coordinates. For micromagnetics, Nakatani et al.43 have developed a mathematical framework for solving the LLG equation, expressed in Cartesian components of magnetisation, by using the backward difference method to conserve m43. In the context of spin-lattice (molecular) dynamics, the lattice structure is also more naturally described in terms of Cartesian coordinates. The parallelisation of large-scale molecular dynamics codes usually takes place by subdividing the volume occupied by the system into smaller cubes (not spheres), making Cartesian coordinates the more efficient choice13.

Despite the availability of accurate numerical techniques for solving the LLG equation2,28,29,30,34,43,44, several works (see, for example, refs.19,20,22), have solved the LLG equation in Cartesian coordinates by using an explicit solver with a fixed time step. Other than having no control over the error, because of the fixed time step, such methods lead to linear deviation in m, as the numerical solution evolves. In some instances, this non-conservation of m could produce numerical artefacts, especially when long simulation times are involved25. The fact that standard solvers are still being used to solve the LLG equation could mean (i) that the specialised techniques are not well known and/or (ii) that there is some reluctance to use them, perhaps because they are more difficult to implement and/or (iii) that the non-conservation of m in the numerical solution does not influence the validity of the obtained results. Notwithstanding the possibilities (i) and (ii), the assumption (iii) has seldom been tested by, for instance, comparing different solvers. Given this situation, there still exits a need for simpler, if not better, methods whereby the LLG equation can be solved easily and with accurate \(m=1\) conservation. In the present work, instead of proposing yet another specialised method to solve the LLG equation, we motivate through theoretical considerations the addition of a phenomenological term to the LLG equation to make it easier to solve by standard methods.

We note that the same phenomenological term is discussed in at least two previous works on numerical micromagnetics (see Eq. (4) of ref.45 and Eq. (2.62) of ref.46). There, it is referred to as the ‘longitudinal relaxation term’46. Despite having been implemented46 in the finite element package finmag46 and in the finite difference package simlib46, a literature search for ‘longitudinal relaxation’ and ‘LLG equation’ did not reveal any other relevant works. Thus, although we are not the first to discover a term of this form, the term is not well documented in the literature surrounding the LLG equation, in general; nor is it well known, even within the micromagnetics community.

Our present discussion thus serves two main purposes: (i) To create a wider awareness of the additional term and show that it is useful for integrating the LLG equation in certain situations – if not in micromagnetics, then at least in several other models that are currently of interest (see, for example, refs.17,18,19,20,21,22,23,24,25,26). (ii) To provide a better theoretical motivation for how this term naturally appears within the context of the numerical solution to the LLG equation.

Theoretical motivation

In this section, we will derive a dimensionless norm-conserving form of the LLG equation that is more suitable for its numerical time integration. The LLG equation for the magnetisation vector \(\textbf{M}\) is given by47,48,

$$\begin{aligned} \frac{\textrm{d}\textbf{M}}{\textrm{d}t}=-\gamma \textbf{M}\times \textbf{H}_{\textrm{eff}}+\frac{\alpha }{M_{\textrm{s}}}\textbf{M} \times \frac{\textrm{d}\textbf{M}}{\textrm{d}t}{,} \end{aligned}$$
(1)

where \(\gamma\) is the gyromagnetic ratio, \(\alpha\) is the Gilbert damping, \(M_{\textrm{s}}\) is the saturation magnetisation, and \(\textbf{H}_{\textrm{eff}}\) is the effective magnetic field. The first term on the right side of (1) causes a precession of \(\textbf{M}\) about the direction of the effective field, while the second term represents damping, which causes the magnetisation spiral inwards towards the direction of the effective field. To solve (1) numerically, it is usually written in the standard form of a system of first order ODEs, i.e.

$$\begin{aligned} \frac{\textrm{d}\textbf{M}}{\textrm{d}t}=\textbf{F}\left( \textbf{M}\right) {.} \end{aligned}$$
(2)

To achieve this standard form, the term \(\textrm{d}\mathbf {M/}\textrm{d}t\), appearing on the right hand side of (1), can simply be replaced by the right hand side of the same equation, i.e.

$$\begin{aligned} \frac{\textrm{d}\textbf{M}}{\textrm{d}t}= & -\gamma \textbf{M}\times \textbf{H}_{\textrm{eff}} +\frac{\alpha }{M_{\textrm{s}}}\textbf{M}\times \overset{\frac{\textrm{ d}\textbf{M}}{\textrm{d}t}\text { substituted from r.h.s. of (1)}}{ \overbrace{\left[ -\gamma \textbf{M}\times \textbf{H}_{\textrm{eff}}+ \frac{\alpha }{M_{\textrm{s}}}\left( \textbf{M}\times \frac{\textrm{d} \textbf{M}}{\textrm{d}t}\right) \right] }} \nonumber \\= & -\gamma \textbf{M}\times \textbf{H}_{\textrm{eff}}-\frac{\alpha \gamma }{M_{\textrm{s}}}\textbf{M}\times \left( \textbf{M}\times \textbf{H}_{\textrm{eff}}\right) +\frac{\alpha ^{2}}{M_{\textrm{s}}^{2}}\textbf{M}\times \left( \textbf{M}\times \frac{\textrm{d}\textbf{M}}{\textrm{d}t}\right) . \end{aligned}$$
(3)

The last term in (3) can then be simplified by using the familiar vector identity, \(\textbf{A}\times \left( \textbf{B}\times \textbf{C} \right) =\left( \textbf{A}\cdot \textbf{C}\right) \textbf{B} -\left( \textbf{A}\cdot \textbf{B}\right) \textbf{C}\), to write it as,

$$\begin{aligned} \frac{\alpha ^{2}}{M_{\textrm{s}}^{2}}\textbf{M}\times \left( \textbf{M}\times \frac{\textrm{d}\textbf{M}}{\textrm{d}t}\right)= & \frac{\alpha ^{2}}{M_{\textrm{s}}^{2}}\left( \textbf{M}\cdot \frac{ \textrm{d}\textbf{M}}{\textrm{d}t}\right) \textbf{M}-\frac{\alpha ^{2}}{M_{\textrm{s}}^{2}}\left( \textbf{M}\cdot \textbf{M}\right) \frac{\textrm{d}\textbf{M}}{\textrm{d}t} \nonumber \\= & \frac{\alpha ^{2}}{M_{\textrm{s}}^{2}}\textbf{M}\left( \textbf{M} \cdot \frac{\textrm{d}\textbf{M}}{\textrm{d}t}\right) -\alpha ^{2}\frac{ \textrm{d}\textbf{M}}{\textrm{d}t} . \end{aligned}$$
(4)

Now, the conservation of the magnitude of the magnetisation vector can be used to argue that the first term in (4) vanishes, since

$$\begin{aligned} \textbf{M}\cdot \frac{\textrm{d}\textbf{M}}{\textrm{d}t} = \frac{1}{2}\frac{\textrm{d}}{\textrm{d}t}\left( \textbf{M}\cdot \textbf{M} \right) = 0 {.} \end{aligned}$$
(5)

In this way the usual form of the LLG equation is obtained:

$$\begin{aligned} \frac{\textrm{d}\textbf{M}}{\textrm{d}t}=A\left\{ -\gamma \textbf{M} \times \textbf{H}_{\textrm{eff}}-\frac{\alpha \gamma }{M_{\textrm{s}}} \textbf{M}\times \left( \textbf{M}\times \textbf{H}_{\textrm{eff} }\right) \right\} {, } \end{aligned}$$
(6)

where \(A=1/\left( 1+\alpha ^{2}\right)\).

We now draw attention to the use of Eq. (5) in the derivation of (6). Although (5) is a valid analytical simplification to make, it complicates the numerical solution of the resulting LLG Eq. (6). In particular, it leads to the non-conservation of the modulus of the magnetisation vector, unless one of the specialised integration techniques is used to ensure that the numerical approximation of the derivative in (5) is strictly zero. For this reason, we prefer not to make use of (5). Instead, we replace (5) with the approximation,

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\left( \textbf{M}\cdot \textbf{M} \right) \approx \lambda \left( M_{s}^{2} -\textbf{M}\cdot \textbf{M}\right) {,} \end{aligned}$$
(7)

where \(\lambda\) is a positive, but otherwise arbitrary, proportionality constant. The form chosen for Eq. (7) is motivated by the differential equation: \({\dot{x}} = \lambda ( 1-x)\), which admits solutions of the form \(x(t) = 1 + (x_0-1)e^{-\lambda t}\). For any initial condition \(x_0\) and \(\lambda > 0\), these solutions decay exponentially towards \(x=1\). Furthermore, the value of \(\lambda > 0\) is arbitrary in the sense that it only sets the exponential decay constant.

Due to the approximation (7), an additional term now appears in the LLG equation, when it is expressed in the form of (2):

$$\begin{aligned} \frac{\textrm{d}\textbf{M}}{\textrm{d}t}= \underset{\text {additional term}}{\underbrace{ A\left\{ \frac{\alpha ^2 \lambda }{2M_s} \textbf{M} \left( M_{s}^{2} -\textbf{M}\cdot \textbf{M}\right) \right\} }} -A \left\{ \gamma \textbf{M} \times \textbf{H}_{\textrm{eff}}+\frac{\alpha \gamma }{M_{\textrm{s}}} \textbf{M}\times \left( \textbf{M}\times \textbf{H}_{\textrm{eff} }\right) \right\} {, } \end{aligned}$$
(8)

For numerical convenience we rewrite (8) in dimensionless form, by using the same characteristic time scale, \((\gamma M_{\textrm{s}})^{-1}\), as in ref.20. Since we are free to choose any \(\lambda > 0\), we make the choice \(\lambda = 2\gamma M_{\textrm{s}}^{3}/\alpha ^2\), so that the coefficient of the additional term in (8), excluding the factor A, is unity. We note that for any system of dimensionless units, \(\lambda\) can always be chosen in this way, without loss of generality. Finally, we normalise the effective field \(\textbf{H}_{\textrm{eff}}\) and magnetisation \(\textbf{M}\), both to \(M_{s}\). With these conventions we obtain a norm-conserving dimensionless form of the LLG equation:

$$\begin{aligned} \frac{\textrm{d}\textbf{m}}{\textrm{d}\tau }=\underset{\text {additional term}}{\underbrace{A\left\{ \textbf{m}\left( 1-\textbf{m} \cdot \textbf{m}\right) \right\} }} \, \, \, \underset{\text {usual LLG equation}}{\underbrace{-\, A\left\{ \textbf{m}\times \textbf{h} _{\textrm{eff}}+\alpha \textbf{m}\times \left( \textbf{m}\times \textbf{h}_{\textrm{eff}}\right) \right\} }}{. } \end{aligned}$$
(9)

The additional term in (9) is self-regulatory in the sense that it is only non-zero when \(\left| \textbf{m}\right|\) deviates from its expected value, \(\left| \textbf{m}\right| =1\). Furthermore, when \(\left| \textbf{m}\right| < 1\), the factor \((1-\textbf{m}\cdot \textbf{m}) > 0\), causing \(\left| \textbf{m}\right|\) to increase. When \(\left| \textbf{m}\right| > 1\), the factor \((1 - \textbf{m}\cdot \textbf{m}) < 0\), causing \(\left| \textbf{m}\right|\) to decrease.

In Methods, we provide a mathematical proof that the additional term does not affect the dynamics of the original LLG equation, other than to impose a stable fixed point at \(\left| \textbf{m} \right| = 1\).

Numerical results

In the previous section we have motivated why a norm-conserving dimensionless form of the LLG equation (see, Eq. (9), may lead to better numerical conservation of the magnitude of the magnetisation vector \(\left| \textbf{m}\right| =1\), without changing the original dynamics. We now present numerical results to test the effect of this additional term on various solutions of the LLG equation. For clarity, the numerical results are presented in two subsections. In the first, comparisons of different solvers are made for the case of a monodomain, while in the second, a standard micromagnetic test calculation is performed.

Comparison of different ODE solvers for the case of a monodomain

In this section we consider the case of a single magnetisation vector, representing a so-called monodomain, as discussed in refs.17,18,19,20,21,22, for instance. We compare the extent to which seven different ODE solvers conserve \(\left| \textbf{m}\right| = 1\), with and without the additional term in Eq. (9). For clarity, details about the seven numerical methods used for our comparisons are provided in the first section of Supplementary Material. For the purposes of these comparisons, we solve (9) for the effective field \(\textbf{h}_{eff} = B \sin \left( \omega t \right) {\hat{y}} + m_z{\hat{z}}\), using the parameters \(B = 0.5\), \(\omega = 0.5\), and \(\alpha = 0.05\), with the initial condition \(m_x = m_y = 0\), \(m_z = 1\), at \(\tau = 0\). At these parameters the solution is chaotic, posing a stringent test for the numerical solvers.

Fig. 1
figure 1

Comparison of the absolute value of the error in \(\left| \textbf{m}\right|\) for the seven different time integration techniques used to solve (9), without (a,c and e) and with (b, d, and f) the additional term. In (a), (b), (e), and (f), the fixed time step was \(\Delta \tau = 0.01\), while for the two adaptive time step methods, shown in (c) and (d), the absolute and relative error tolerances were both equal to \(\varepsilon = 1\times 10^{-12}\). Other parameters: \(B = 0.5\), \(\omega = 0.5\), \(\alpha = 0.05\), and \(\Delta \tau = 0.01\). For additional details, see the main text surrounding this figure.

Full size image

Figure 1, plots, on a log scale, the error \(\left| \left| \textbf{m}\right| -1 \right|\), obtained from the seven different numerical methods, without (left hand column of figures), and with (right hand column of figures) the additional term in Eq. (9). Without the additional term, for the five methods shown in Fig. 1 (a) and (c), we see that \(\left| \textbf{m}\right|\) is not conserved. As expected, for these explicit methods the errors grow linearly with the integration time (even for the RK4GILL method that has been used recently in refs.19,22). On the other hand, for the explicit pseudo-symplectic and implicit Gauss-Legendre methods, shown in (e), we see that the error in \(\left| \textbf{m}\right|\) remains well below \(10^{-13}\), showing no growth over the time ___domain. With the additional term, we see in Fig. 1 (b) and (d), that the error in \(\left| \textbf{m}\right|\) no longer grows linearly, but instead fluctuates randomly below a well-defined threshold, for each case. For the fixed time-step methods shown in (b) we see that the thresholds for the two fourth-order methods (RK4 and RK4GILL) are approximately the same (\(\lessapprox 10^{-10}\)), whereas for the fifth-order method (RK5) it is about three orders of magnitude smaller (\(< 10^{-13}\)). For the two adaptive time step methods shown in (d), we see that the error thresholds are on the same order of magnitude as the chosen error tolerance setting (\(\varepsilon = 10^{-12}\)). For the two methods that are designed to conserve \(\left| \textbf{m}\right|\), we see in (f) that their thresholds are \(< 10^{-10}\) for GL2 and \(< 10^{-11}\) for RK5PS, showing no growth over the time ___domain. We note that the latter two thresholds are significantly higher than for the same two methods without the additional term, as shown in (e). The reason for this will be explained in connection with Fig. 2, which shows the maximum error in \(\vert \left| \textbf{m}\right| - 1 \vert\) as a function of either the step size, \(\Delta \tau\), or error tolerance setting, \(\varepsilon\). For simplicity, in the following description we will refer to this error simply as, ‘the error’.

Fig. 2
figure 2

The maximum error, over the same integration period shown in Fig. 1, for different values of the fixed time step, \(\Delta \tau\), and error tolerance setting, \(\varepsilon\). Other parameters are the same as in Fig. 1. As before, \(\varepsilon\) is the absolute and relative error tolerance settings for the adaptive time step methods (DOPRI5 and DOP853), shown in (c) and (d). For comparison, the horizontal dotted lines in (b, d, e, and f) shows the typical error ( \(\max \left\{ \left| \left| \textbf{m}\right| -1 \right| \right\} \le 10^{-13 \,}\)) obtainable by the two methods (RK5PS and GL2) that do conserve \(\left| \textbf{m}\right|\), without the additional term in (9). The legend in each figure also shows a fitted formula for the CPU time consumed by each calculation, as a function of either \(\Delta \tau\) or \(\varepsilon\).

Full size image

For ease of comparison the sub-figures in Fig. 2 are in one-to-one correspondence with those in Fig. 1, and using the same colours. Here, since the scales vary over several orders of magnitude, we make use of a log-log plot. The various markers refer to the data points, which were calculated for \(\Delta \tau = 1/2048, 1/1024, \ldots , 1/128, 1/64\), in Fig. 2 (a,b, e, and f) and for \(\varepsilon = 10^{-15}, 10^{-14}, \ldots , 10^{-11}, 10^{-10}\), in (c) and (d). Let us first consider the various methods without the additional term, as shown by the left hand column of Fig. 2 (a, c, and e). In (a) we see that the error follows a power law dependence, which shows up on the log-log scale as a linear increase in the error with increasing \(\Delta \tau\). However, this power law dependence breaks down at the smallest time step, for the two fourth-order methods, and at the smallest three time steps, for the fifth-order method. The smallest error that can be achieved in all three cases is on the order of \(10^{-13}\). For the adaptive time step methods shown in (c), there is also a power law dependence of the error, but here the dependence is on \(\varepsilon\). The power law dependence on \(\varepsilon\) persists right down to the smallest error tolerance (\(\varepsilon = 10^{-15}\)), which is close to the machine precision (\(2.22 \times 10^{-16}\) for double precision, i.e. 64 bits). As in (a), the smallest achievable maximal error is also \(\sim 10^{-13}\). The reason the errors do not decrease further in (a) or (c) is due to the fact that none of the explicit methods shown in (a) and (c) conserve m. This gives rise to the linear growth in the error, as we have seen in Fig. 1 (a) and (c). The error thus grows proportionally to the total integration time (here, 10 000 dimensionless time units), irrespective of how small the time step is made. By contrast, the pseudo-symplectic (RK5PS) and implicit (GL2) methods do conserve m, independently of the chosen time step size. In (e), therefore, the errors remain \(\sim 10^{-13}\), irrespective of \(\Delta \tau\). One may ask, why do the errors in (e) not become much smaller, as the time step reduces? The answer to this question differs, depending on the method. In the case of RK5PS, firstly, the conservation is not exact, since the coefficients for this pseudo-symplectic method were optimised to conserve m as best as is possible, while retaining the explicit nature of the method (see, refs.30,49) Secondly, if one looks at the optimised coefficients for the RK5PS method, one sees that several of the coefficients are only specified to 14 or 15 decimal places (two orders of magnitude higher than the machine precision), which means that the method could suffer from numerical round off errors sooner that it should. One can see, from the green dashed line in (e), how these round off errors become more significant (causing the error to increase) as the step size becomes smaller. For the GL2 method, the \(\sim 10^{-13}\) error that we see is purely from round-off errors in the calculation. We have confirmed this by re-coding the GL2 method in quadruple precision, using the Python module gmpy2. With no other changes in the code, the quadruple precision reduces the GL2 errors in (e) to below \(10^{-17}\), for all step sizes (not shown). Of course, the fact that the GL2 method conserves m to a high precision, even for relatively large fixed time steps, should not be confused with the numerical accuracy of the obtained solution. Let us bear in mind that, even the largest time step of \(\Delta \tau = 1/64\) will also conserve m to a high precision, but it may not be sufficiently small to produce a converged numerical solution (see, the second paragraph of Discussion).

We now consider the results with the additional term, as shown in the right-hand column of Fig. 2 (b, d, and f). Once again, we see that the errors for the first three methods, shown in (b), follow a power law dependence on \(\Delta \tau\). With the additional term, however, the power law dependence persists down to the smallest time step, where the error falls between \(10^{-15}\)–\(10^{-14}\). Here again, the error cannot be made any smaller by further reducing the time step, because of the accumulation of round-off errors in the calculations. As one expects, the round off errors start to limit the higher-order method (RK5), at larger time steps than for the two lower-order methods (RK4 and RK4GILL). When comparing (a) and (b), we should appreciate that the smallest achievable errors in (a) are approximately an order of magnitude higher than in (b). More importantly, in (b), the errors do not grow proportionally to the integration time, as they do in (a). Thus, the additional term offers a considerable advantage. In the case of the variable time-step methods, shown in (d), we see a similar behaviour to that of the three fixed time-step methods. In (d) we again see the limiting role played by the round-off errors as \(\varepsilon \rightarrow 10^{-15}\). Here, the higher-order method is less affected by the round-off errors (compared to the RK5 method in (b)) because it makes use of adaptive time stepping. Other than speeding up the calculation, the adaptive time stepping allows larger time steps to be taken, thereby reducing the number of computational operations and reducing the size of the typical numbers involved in each operation. These two factors minimise the influence of the round-off errors.

For convenience, the legends in Fig. 2 also provide approximate expressions for the computational times consumed by the various methods. These expressions were obtained by fitting a power law to the CPU time data for each method. The resulting expressions approximate the CPU times to within 5%. We have used these expressions to compare the efficiency of the various methods by calculating the CPU time taken to integrate (9) for 10 000 dimensionless time units. To make the comparison fair, we choose the \(\Delta \tau\) or \(\varepsilon\) from Fig. 2 (b, d, and f), to give \(\max \left\{ \left| \left| \textbf{m}\right| -1 \right| \right\} \le 10^{-13}\). This value for \(\max \left\{ \left| \left| \textbf{m}\right| -1 \right| \right\}\) was chosen because it is of the same order of magnitude as the typical error for the RK5PS and GL2 methods, without the additional term in (9), as shown by the horizontal dotted line in Fig. 2 (e). The resulting CPU times are listed in Table 1. From Table 1 it is easy to see that the overall winner is the DOP853 method, which is more than three times faster than DOPRI5, and more than eight times faster than RK5. Of the three fixed time step methods, the higher-order RK5 method is almost four times faster than the classic RK4 method, and about six times faster than RK4GILL.

Table 1 CPU times consumed by the different ODE solvers, to integrate Eq. (9) for 10 000 dimensionless time units with the additional term, i.e., as for Fig. 1 (b, d, and f). Here \(\Delta \tau\) and \(\varepsilon\) were chosen, according to the intersections of the horizontal dotted lines in Fig. 2 (b, d, and f), to ensure that \(\max \left\{ \left| \left| \textbf{m}\right| -1 \right| \right\} \le 10^{-13}\) throughout the entire integration time. Other parameters are the same as in Fig. 1. The CPU time refers to an Intel Xeon CPU, model E5-2690 v4 @ 2.60GHz.
Full size table

Comparisons for \(\mu\)MAG standard problem #4

In the case of a monodomain, we have seen that the additional term in Eq. (9) facilitates the use of standard solvers for the numerical solution of the LLG equation, making implementations much easier and saving on CPU time, through use of adaptive, explicit methods, like DOP853. Because the LLG equation lies at the heart of micromagnetic simulations and because the available literature is sparse, it is now worth considering whether the additional term may also offer some advantage in numerical micromagnetics. To this end, a complete Python 3 script has been provided to solve the \(\mu\)MAG standard problem #435, in the second section of Supplementary Material. This script was originally written in Python 2 by Abert et al.8. We have chosen it as the starting point of our micromagnetic simulations, for two reasons: (i) The original code consists of fewer than 70 lines, making it an attractive prospect for pedagogical purposes. (ii) It can reproduce results from other methods, in particular those obtained from the geometric integration method of d’Aquino et al.29.

The original script solved the \(\mu\)MAG standard problem \(\#4\)35 by using a projected explicit Euler scheme for the integration of the LLG equation8. To be more specific, after each fixed first-order Euler time step (dt = 5e-15), all the magnetisation vectors are simply renormalised to unity (see Listing 5 and Eq. (22) of ref.8). After making several syntactical changes to the original script, it ran in Python 3 with identical results. Due to various optimisations that have been made in Python 3, the newer version performed considerably faster than the original Python 2 version. For Field 1 (Field 2), the original Python 2 code solved the \(\mu\)MAG standard problem \(\#4\) in 2023 (1985) CPU seconds per ns of simulated time, while the Python 3 version took only 862 (842) CPU seconds per ns. The results from both versions of the original code were identical and visually indistinguishable from those reported by d’Aquino et al.29.

The Python 3 code was then changed to incorporate the additional term in Eq. (9), and to make use of standard ODE solvers, in place of the projected Euler scheme. As can be seen from the listing in the second section of Supplementary Material, we initially chose the DOP853 solver from scipy.integrate.ode. This choice was motivated by the superior performance of DOP853 for the monodomain case. For the \(\mu\)MAG standard problem \(\#4\), the relative and absolute error tolerances, \(\varepsilon\), were set to 1e-13, leaving all the original parameter settings unchanged. At these settings, the DOP853 solver performed the time integration for Field 1 (Field 2) in 102 (136) CPU seconds per ns, i.e. about 8 times faster than the Python 3 version of the original code by Abert et al.8. The latter increase in speed is due to the adaptive time stepping and higher order of the DOP853 method, as opposed to the original Euler scheme.

Fig. 3
figure 3

(a-b) The time evolution of the averaged magnetisation components \(\overline{m_i}\) for the \(\mu\)MAG standard problem \(\#4\)35 using the two methods discussed in the main text. In (a) the curves from two methods are almost indistinguishable for Field 1 and in (b) they are in good qualitative agreement for Field 2. (c-d) The relative error in the damping, for each field, calculated according to the method described in refs.2,28,29. The insets show the distributions of the fluctuations in \(1- \vert \textbf{m}_i \vert\), accumulated throughout each simulation. Both distributions are more or less symmetrical about zero, as discussed in the main text.

Full size image

Figure 3 compares the results from the modified code with the results obtained via the method of d’Aquino et al.29. For Field 1, shown in Fig. 3 (a), the averaged magnetisation components are almost indistinguishable. For Field 2, shown in Fig. 3 (b), the averaged magnetisation components deviate visibly only after the first zero crossing of \(\overline{m_x}\), but remain qualitatively similar throughout the simulation. Interestingly, in the case of Field 2, one does not get exact agreement between any of the different methods that are shown on the \(\mu\)MAG website35. We believe that such differences are not only related to using different methods, but also due to some frustration that is induced by Field 2, among the constituent magnetic moments: visualisations of the system under Field 2 have shown that the central moments rotate in the opposite direction to those nearer the two ends of the thin film, resulting in a more complex reversal than in the case of Field 1. In the case of Field 2, we therefore suspect that the transient response may be chaotic, while in the case of Field 1, it may be more regular. However, a proper investigation of this question would take us beyond the scope of the current work.

Test for unphysical damping effects

Although it was shown in Methods that the additional term in Eq. (9) only serves to maintain the magnitude of the magnetisation vector close to unity, in a micromagnetic simulation, it is possible that the additional term may also affect the rate at which energy is dissipated, acting as a form of artificial damping in addition to the Gilbert damping imposed by \(\alpha > 0\). To test whether this is the case, the relative error in \(\alpha\) was calculated according to the method described in refs.2,28,29. The relative errors for Fields 1 and 2 are plotted in Fig. 3 (c) and (d), respectively. For both fields, the relative errors are on the order of \(10^{-14}\), throughout most of the simulation. This is about 7 orders of magnitude smaller than the same relative error reported by d’Aquino et al.29 (see Figure 7 of ref. 29). We thus conclude that the additional term does not add significantly to the Gilbert damping in this system. One can understand why the additional term does not interfere with damping by looking at the fluctuations that occur in the magnitudes of the magnetisation vectors during the simulation. These fluctuations are distributed more or less symmetrically about zero and, therefore, on average, contribute very little to the energy lost from the system. The distributions of \(1- \vert \textbf{m}_i \vert\), accumulated throughout the simulations for Fields 1 and 2, are shown by the insets in Fig. 3 (c) and (d), respectively.

Test for stiffness effects

In micromagnetic simulations, the higher strength of the exchange interaction between neighbouring spins, compared to the other interactions, can cause stiffness in the numerical solution of the LLG equation. Such stiffness generally becomes more prevalent as the discretisation cells reduce in volume. When stiffness occurs, explicit integration methods, such as DOP853, can become much slower or fail entirely, because the adaptive algorithm repeatedly reduces the time step in an attempt to resolve high-frequency oscillations in the trajectory due to misaligned neighbouring spins. On the other hand, if some minimum time step is enforced, it causes numerical instability in the solution. Fortunately, since the additional term in Eq. (9) makes it possible to use any standard solver, the problem of stiffness can be easily addressed by simply choosing a solver specifically designed to handle stiff systems.

Although the \(\mu\)MAG standard problem \(\#4\)35 is inherently non-stiff3, it can become stiff when the cell size is reduced. To demonstrate the onset of stiffness in the standard problem we have chosen the following cuboidal meshings: (i) \(N=2500\) (\(5\times 5\times 3\)) \(\hbox {nm}^3\), (ii) \(N=4000\) (\(4\times 3.90625\times 3\)) \(\hbox {nm}^3\), (iii) \(N=5120\) (\(3.125\times 3.90625\times 3\)) \(\hbox {nm}^3\), (iv) \(N=6400\) (\(3.125\times 3.125\times 3\)) \(\hbox {nm}^3\), (v) \(N=10\,000\) (\(2.5\times 2.5\times 3\)) \(\hbox {nm}^3\), (vi) \(N=12\,500\) (\(2\times 2.5\times 3\)) \(\hbox {nm}^3\). Figure 4 shows the simulation times consumed by three different integration methods, for each of the meshings (i)-(vi). The first integration method is the fixed time step used in the Python 3 version of the original code by Albert et al.8. The second method is DOP853, and the third is an implicit multi-step variable-order method based on a backward differentiation formula (BDF). Implicit solvers, such as BDF, typically come with the additional cost of having to solve a nonlinear system at each time step. Nevertheless, for stiff systems in micromagnetics, advanced implicit solvers are frequently needed4. In Python 3 there are in fact a number of stiff solvers to choose from, including also Radau – an implicit Runge-Kutta method of the Radau IIA family, and LSODA – Adams/BDF method with step by step stiffness detection and switching. Both DOPR853 the LSODA are also available from the module called numbalsoda50 (not used in the present work), which makes it possible to call these methods from within numba jit-compiled python functions. The jit-compiled functions are typically much faster than those imported from the scipy.integrate.ode module that we make use of for the present work.

Fig. 4
figure 4

The CPU times consumed in solving the \(\mu\)MAG standard problem \(\#4\)35, using the integrations methods indicated by the legend, for different numbers of cells, for (a) Field 1, and (b) Field 2. The CPU time refers to an Intel Xeon CPU, model E5-2690 v4 @ 2.60GHz. The red dashed line, with circular markers, refers to the projected explicit Euler scheme by Albert et al.8. The blue dotted line, with square markers, refers to our present method, using the DOP853 solver. The black solid line with triangular markers refers to our present method, using the BDF solver, which is specifically for stiff systems. The blue arrows point to results for which the DOP853 solver produced the warning message about stiffness, shown by the inset. See, main text for details.

Full size image

In Fig. 4 we show, for both fields of the \(\mu\)MAG standard problem \(\#4\), the CPU times consumed by the three different methods. Since it is not obvious, we present the results for both Field 1 (a) and Field 2 (b), to show that they are qualitatively the same. For the smallest number of cells (\(N=2500\)), we see that the DOP853 method is approximately 8 times faster than the Python 3 version of the original code by Abert et al.8 (as mentioned previously). At \(N=2500\) DOP853 is only marginally faster than the stiff solver, BDF. However, as the number of cells increases, there is a cross-over point when DOP853 becomes less efficient than BDF. The cross-over point can be seen in Fig. 4 (a) at \(N\approx 4000\), and in Fig. 4 (b) at \(N \approx 6400\). As the number of cells increases further, DOP853 produces a warning about possible stiffness, as shown by the insets and the blue arrows in (a), for \(N=6400, 10\,000, 12\,500\) and in (b), for \(N=10\,000, 12\,500\). Once stiffness sets in, the BDF solver is more efficient at advancing the system trajectory over the same time ___domain, as one would expect. In the present problem, the stiffness at high N remains moderate, in the sense that DOP853 is still able to obtain an accurate solution within a reasonable CPU time. However, in more severe cases of stiffness, DOP853 may become completely ineffective, making the BDF the tool of choice.

Although not shown in Fig. 4, we have also implemented the widely used micromagnetism method whereby all the magnetizations are renormalised after every variable time step. We have done so for both the BDF and DOP853 methods. These results are not shown because the CPU times are practically the same as in Fig. 4. Although renormalisation requires the computation of N square roots per step, this additional cost is almost negligible compared to the cost of even one function call. By using the solout() method of DOP853 we were able to monitor the number of successful steps taken by DOP853. Provided the problem was non-stiff, the two methods took roughly the same number of successful steps (and unsuccessful steps, as deduced from the overall CPU times). Unfortunately, we were not able to make similar comparisons for the stiff systems, using the BDF solver. Try as we may, we were not able to extract the information about the internal steps from the BDF class. In any event, it was clear that neither the additional term nor the renormalisation significantly interferes with the step-size control.

The fact that DOP853 becomes less efficient than BDF at the higher N, even when the renormalisation method is used, leads us to suspect that the onset of stiffness, in this system, may not be related to the use of the additional term. This is consistent with what we have shown at the end of Methods, namely, that the form of the additional term does not admit oscillatory solutions. All our considerations of the \(\mu\)MAG standard problem suggest that, in this case, the additional term merely acts as a continuous version of the stepwise renormalisation method.

Lastly, we comment on the heuristic rule introduced at the end of Sec. 2.4 of ref.46, i.e. for the choice of the longitudinal term’s coefficient, \(1/t_{\textrm{relax}}\). As noted in ref.46, the occurrence of stiffness is related to the choice of this constant, or in our case, the choice of \(\lambda\) in Eq. (8). Clearly, if \(\lambda\) is too small, the additional term may not have a sufficient influence on the numerics to ensure proper norm conservation. On the other hand, if \(\lambda\) is too large, the additional term could make the problem more stiff. In numerical solutions, what is too small and too large really depends on how the equations have been cast into dimensionless form. One first has to define appropriate dimensionless groups for the problem, and this involves choosing an appropriate time scale51, as was done in Theoretical motivation for the case of the monodomain. For other possible choices, see Sec. 1.1 of ref.5. Thus, in a micromagnetic simulation in which the fastest time scale is set by the exchange field, the natural choice for the characteristic time is the relaxation time for the high-frequency precessions of the adjacent spins. Therefore, without loss of generality, we can fix the coefficient of the additional term in Eq. (9) to unity, provided that the LLG equation has been written in the appropriate dimensionless form. Any other choice, much larger or smaller than unity, is inconsistent with the less general heuristic rule given in ref.46.

Discussion

In Table 1, we have also included the two methods (RK5PS and GL2) that conserve \(\left| \textbf{m}\right|\), even without the additional term in (9). A comparison of the fitted formulas given in Fig. 2 (e) and (f) shows that the increased times shown for the RK5PS and GL2 methods in Table 1, are about 39% and 44% longer, respectively. We, therefore, do not recommend the use of the additional term with specialised solvers that already conserve \(\left| \textbf{m}\right|\).

A comparison of Fig. 1 (e) and (f) may lead to the conclusion that the GL2 and RK5PS methods become less accurate when applied to the norm-conserving form of the LLG equation. We may be tempted to reach this conclusion since the errors, shown in (e), are much smaller than those in (f). However, we should appreciate that the real reason that the errors increase, as we go from Fig. 1 (e) to (f), is due to the time step (\(\Delta \tau = 0.01\)), being too large to ensure proper convergence of the numerical solutions. As we have mentioned, these solvers conserve \(\left| \textbf{m}\right|\), even for time steps that are too large to ensure proper convergence of the numerical solution. In the absence of the additional term in (9), the error in \(\left| \textbf{m}\right|\) is not a good measure of the error in the numerical solution. On the other hand, with the additional term, the error in \(\left| \textbf{m}\right|\) provides an excellent estimate of the largest possible time step that will ensure the proper convergence of the solution. These optimal time steps are in fact those that were read off from Fig. 2 (f), and shown in Table 1 for the RK5PS and GL2 methods. To see this more clearly, we estimate the largest possible time step for each method to achieve a local truncation error of \(\le 10^{-13}\). This estimate gives \(\Delta \tau < 6.8 \times 10^{-3}\) for the fifth-order RK5PS method, and \(\Delta \tau < 2.5 \times 10^{-3}\) for the fourth-order GL2 method. Both values are in good agreement with those shown in Table 1. Thus, even if an implicit or pseudo-symplectic method is preferred, the additional term we have proposed in (9) may be used to gauge the most appropriate fixed time step for such methods.

Of the five explicit methods we have used to solve the LLG Eq. (9) with the additional term, DOP853 is clearly the tool of choice. To quote Hairer, Nørsett and Wanner52, “The performance of this code, compared to methods of lower order, is impressive.”. In our present work we have shown that the additional term in (9) effectively plants a stable fixed point at \(\left| \textbf{m}\right| = 1\), thereby facilitating the use of explicit adaptive solvers, like DOP853 and DOPRI5. These are generally much faster than specialised methods, and easier to use. Moreover, we have shown that the additional term does not change the dynamics of the original LLG equation, other than by stabilising the numerical solution toward \(\left| \textbf{m}\right| = 1\). Since the additional term does not play a direct role in the dynamics, as one may expect, it is not coupled to the effective field in the original LLG equation, and is in fact independent of any physical constants. For the purposes of obtaining numerical solutions, however, it plays an important role. It allows the LLG equation to be solved with relative ease, via the standard solvers that are available in popular programming languages like Python (e.g. DOPR853, BDF, LSODA, Radau), Matlab53 (e.g. ODE78 or ODE45), Mathematica54 (NDSOLVE, using the “ExplicitRungeKutta” method with “DifferenceOrder” equal to 8 or 5), etc. Here we have numerically tested the effects of the additional term for a monodomain (a single magnetisation vector) as well as for a lattice of magnetisation vectors coupled according to the micromagnetic approximation. In both cases, the additional term facilitates much simpler implementations for the time integration of the LLG equations – as standard solvers can be used – without inducing unphysical damping effects or stiffness that cannot be overcome by an appropriate solver (such as BDF).

In closing, we have shown how the additional ‘norm conserving’ or ‘longitudinal relaxation’ term appears quite naturally in the numerical solution of the LLG equation (9). For problems involving a single monodomain coupled to another system, the method involving the additional term seems ideally suited, since it can conserve m for very long integration times without requiring a highly specialised integration method(s). In micromagnetics, our preliminary results indicate that the additional term makes it possible to implement a numerical solution of the standard \(\mu\)MAG problem \(\#4\), with no apparent drawbacks. Exactly why the additional term has not found a wider applicability in micromagnetic codes has not been documented, to the best of our knowledge. We hope that our current work will create a wider awareness of the additional longitudinal relaxation term among those who use the LLG equation in various models that could include monodomains that are magnetically coupled to a Josephson junction25,26, micromagnetics5,6, or atomistic spin dynamics14.

Methods

Proof that additional term does not alter the dynamics

It is easy to show that the additional term in (9) does not affect the dynamics of the usual LLG equation, other than to regulate \(\left| \textbf{m}\right|\). To this end, let us transform (9) into the polar coordinates \((m,\theta ,\varphi )\), defined by

$$\begin{aligned} m_{x}= & m\sin \theta \cos \varphi \nonumber \\ m_{y}= & m\sin \theta \sin \varphi \nonumber \\ m_{z}= & m\cos \theta { .} \end{aligned}$$
(10)

Here, we have written \(m=\left| \textbf{m}\right|\). By taking the total time derivatives of (10), we obtain the transformation equations for \({\dot{m}}_{x}, {\dot{m}}_{y}\) and \({\dot{m}}_{z}\). We write these, conveniently, in matrix form as,

$$\begin{aligned} \left( \begin{array}{c} {\dot{m}}_{x} \\ {\dot{m}}_{y} \\ {\dot{m}}_{z} \end{array} \right) =\left( \begin{array}{ccc} \sin \theta \cos \varphi & m\cos \theta \cos \varphi & -m\sin \theta \sin \varphi \\ \sin \theta \sin \varphi & m\cos \theta \sin \varphi & m\sin \theta \cos \varphi \\ \cos \theta & -m\sin \theta & 0 \end{array} \right) \left( \begin{array}{c} {\dot{m}} \\ {\dot{\theta }} \\ {\dot{\varphi }} \end{array} \right) , \end{aligned}$$
(11)

with the inverse transformation,

$$\begin{aligned} \left( \begin{array}{c} {\dot{m}} \\ {\dot{\theta }} \\ {\dot{\varphi }} \end{array} \right) =\frac{1}{m}\left( \begin{array}{ccc} m\sin \theta \cos \varphi & m\sin \theta \sin \varphi & m\cos \theta \\ \cos \theta \cos \varphi & \cos \theta \sin \varphi & -\sin \theta \\ -\frac{\sin \varphi }{\sin \theta } & \frac{\cos \varphi }{\sin \theta } & 0 \end{array} \right) \left( \begin{array}{c} {\dot{m}}_{x} \\ {\dot{m}}_{y} \\ {\dot{m}}_{z} \end{array} \right) , \end{aligned}$$
(12)

provided \(\sin \theta \ne 0\).

We can now easily substitute the Cartesian components from (9) into the right hand side of (12), and then make use of (10) to express everything on the right hand side in terms of m, \(\theta\), and \(\varphi\). However, since we are only interested to see how the additional term transforms, here we need not show this entire transformation. We only need to consider the action of the transformation matrix (12) on the additional term, i.e.

$$\begin{aligned} \frac{1}{m}\left( \begin{array}{ccc} m\sin \theta \cos \varphi & m\sin \theta \sin \varphi & m\cos \theta \\ \cos \theta \cos \varphi & \cos \theta \sin \varphi & -\sin \theta \\ -\frac{\sin \varphi }{\sin \theta } & \frac{\cos \varphi }{\sin \theta } & 0 \end{array} \right) \left( \begin{array}{c} A (1-m^2)m\sin \theta \cos \varphi \\ A (1-m^2)m\sin \theta \sin \varphi \\ A (1-m^2) m \cos \theta \phantom {\sin \varphi } \end{array} \right) = A \left( \begin{array}{c} m\left( 1 - m^2 \right) \\ 0 \\ 0 \end{array} \right) . \end{aligned}$$
(13)

As the right hand side of (13) shows, the additional term does not make any contribution to the equations for \({\dot{\theta }}\) and \({\dot{\varphi }}\). It does however change the form of the usual equation for m; namely, \({\dot{m}}=0\). With the additional term the equation for \({\dot{m}}\) reads,

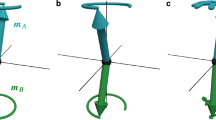
$$\begin{aligned} {\dot{m}} = Am(1 - m^2 ) = f(m). \end{aligned}$$
(14)

It is worth examining the qualitative behaviour of (14). Its vector field, f(m), is plotted in Fig. 5. The right-hand side of (14) has the normal form of the supercritical pitchfork bifurcation51, with two stable fixed points at \(m=\pm 1\). Note that for a one-dimensional equation, such as (14), there can be no oscillatory solutions51. The above analysis shows that, due to the additional term in (9), any perturbations about \(m=1\) will exponentially decrease (if \(1 - m^2 < 0\)) or increase (\(1 - m^2 > 0\)) towards \(m=1\). This mechanism should regulate any perturbations that occur in a numerical solution as the system is evolved in time. In Numerical Results we present various solutions to test the effect of the additional term.

Fig. 5
figure 5

The vector field of Eq. (14). Red arrows point in the directions of flow. There is an unstable fixed point at \(m=0\) (shown by the empty circle), and two stable fixed points at \(m = \pm 1\) (shown by the filled circles). In this Figure \(A=0.95\), but the vector field remains qualitatively the same for any \(A>0\).

Full size image