Introduction

Human capital has a significant positive impact on innovation (Si et al., 2020; Zhang et al., 2017), operational and financial performance (Duodu and Rowlinson, 2021), and growth (Rauch et al., 2005). The emergence of human capital theory (Becker, 1962; Schultz, 1961) provides a theoretical basis for employees to participate in the sharing of an enterprise’s residual value. An increasing number of enterprises have been swept up by this wave of value sharing. In 2020, 632 Chinese A-share listed companies issued plans to implement value sharing (via restricted stocks, stock options, profit sharing, and ESOP), accounting for 16% of the total number of listed companies, with a year-on-year increase of 31% (Dong, 2021).

Value sharing does not always result in higher growth rates or better performance. Evidence from France shows that employee stock options (ESO) do not affect the firm’s long-term financial performance (Triki and Ureche-Rangau, 2012). Even worse, Braam and Poutsma (2015) find a negative relationship between ESO and financial performance analyzing a sample of 195 Dutch-listed companies. In China, 571 of the 678 A-share listed companies that implemented ESOP from June 2015 to September 2018 posted a loss, accounting for 84.22% of the total, with an average loss of 38.02% (Hao et al., 2019). Most of them practiced static value sharing based on initial contribution (SVS), which is a mechanism under which the value-sharing proportion is determined by the initial contribution assessment, and typically will not change for a significant period of time. Employees who have attained a large proportion of value-sharing may demonstrate free-riding behaviors (Kim and Ouimet, 2014). Specifically, once they are assigned their quota of value sharing, the quota remains unchanged for considerable periods; they may obtain high returns regardless of the level of human capital they contribute later on. This may be unfair and weakens incentives. If employees are not rewarded for their human capital, they may lose incentives to contribute more. It would be more effective and fairer if we acknowledge that individual contribution to the value of the company is dynamic and may change over time, and design a system based on that. However, most of the literature on value sharing focuses on the design of the “one-shot” incentive system, and rarely considers the most effective way to update the incentive system over time (Brahm and Poblete, 2018). Huawei’s value-sharing system is an exception.

In practice, it can be observed that Huawei, a world-leading ICT infrastructure and intelligent terminal provider serving more than 3 billion people in over 170 countries and regions, is implementing a mechanism of dynamic value sharing based on contribution (DVS). DVS means that the enterprise estimates the probability that employees are high-capability employees, judges the contribution of employees in value creation, and dynamically adjusts the proportion of value-sharing. Huawei’s ownership structure has undergone four major strategic changes. The first two reforms involved the restructuring of ownership structure due to the urgent demand for funds; subsequently, the last two reforms adopted Saturated Rights Issues (similar to SVS) and Time Unit Plan (similar to DVS) respectively, as shown in Fig. 1. As of 2020, Huawei had 121,269 shareholding employees who collectively held 99.10% of total shares, and more than 105,000 scientific researchers were recruited. Huawei had grown from possessing founding capital of only about $2500 to a renowned global company with a sales revenue of $136.717 billion. It had achieved this without going public. This was closely associated with Huawei’s distinctive value-sharing system that enhanced human capital productivity and firm competitiveness.

Fig. 1: Characteristics of each stage of Huawei’s value-sharing system.
figure 1

Saturated Rights Issues is similar to SVS and Time Unit Plan is similar to DVS.

Full size image

Enterprises urgently need to find a better value-sharing mechanism to accumulate human capital and transfer them into productivity, so as to achieve enterprise growth. Motivated by Huawei’s success, we seek to research how DVS compares to SVS in supporting the growth of enterprises through continuously and steadily improving human capital, profit, and value. How might enterprises that implement DVS quickly evolve to the optimal state? Finally, what external or internal conditions are involved in the process?

To answer these questions, our study intends to reveal the evolutionary mechanism of DVS in enhancing the firm’s human capital, profit, and value by using evolutionary game theory. In real life, participants display bounded rationality. Moreover, they are embedded in social networks and their behavioral choices are affected by legitimacy and imitation (Granovetter, 1985). To better simulate reality, evolutionary game theory effectively explains the decision-making process with bounded rationality and learning mechanisms (Ji et al., 2019).

This paper makes three contributions. First, it enriches the debate on whether value sharing based on contribution is positive for enterprise development, an issue that is seen as a key challenge in value sharing discourse. Second, this paper proposes a mechanism of DVS, which may solve the problem of fairness of benefit distribution, attract and retain high-ability employees, stimulate employees’ creativity, and enable enterprises to create and sustain competitive advantages. Third, this paper studies the conditions for realizing an evolutionarily stable strategy (ESS) considering the bounded rationality and learning mechanism of employees, and provides guidance for enterprises on how to quickly evolve to a stable optimal state.

The remainder of the paper is organized as follows. Related research is reviewed in the section “Literature review”. Section “Model construction” analyzes the competition between enterprises with and without value-sharing plans in the consumer market and then provides the evolutionary analyses between the game players, with SVS and DVS. Subsequently, a simulation analysis is presented in the section “Analysis and discussion”. Section “Conclusions and management implications” concludes the study and highlights related managerial implications.

Literature review

Value sharing

Freeman et al. (2011) propose the concept of “shared capitalism” and define forms of value sharing, including employee ownership, individual employee stock ownership, profit sharing, gain sharing, and stock options. Value sharing refers to sharing the balance of the total income of the enterprise after deducting a charge for depreciation and external fixed contract payments (Zhang et al., 2022).

Theoretical arguments and empirical results of principal-agent theory and human capital theory largely confirm that value-sharing mechanisms have a positive impact on reducing agency costs (Page, 2018) and improving productivity (Kraft and Lang, 2016). Moreover, they can assist in the accumulation of human capital by attracting, screening, and retaining high-capacity workers (Gopalan et al., 2021; Jochem et al., 2018; Oyer and Schaefer, 2005), so as to improve enterprise innovation and performance (Duodu and Rowlinson, 2021; Si et al., 2020). However, some scholars have questioned the effectiveness of value sharing at the employee level. Richter and Schrader (2017) show that ESOP does not have a clear effect on improving productivity. The greater the number of non-management shareholders, the higher the agency cost (Ang et al., 2000); thus highly decentralized ownership leads to serious free-riding problems, which weakens the effectiveness of the incentive (Kim and Ouimet, 2014; Meng et al., 2011). In addition, the relationship between value sharing and organizational human capital accumulation is not clear. Aldatmaz et al. (2018) indicate that the broad-based employee stock option just delays the decisions of employees to resign but does not fundamentally reduce the turnover rate.

The literature provides a basis for explaining the effect of value sharing on enterprises. It is important to note, however, that traditional value sharing at the employee level can be viewed as more of a carrot incentive (Aldatmaz et al., 2018). In Japan, the aggregate number of employee shares held under the ESOP as a percentage of the firm’s total shares was 0.9%; in South Korea, 2.2%; in the United States, 9.2%; in China, 12.9% (Meng et al., 2011). The proportion of human capital to obtain value sharing is low and rarely dynamically adjusted according to the change in the contribution of human capital. Relatively little is known about whether it is helpful to accumulate human capital and improve enterprise performance, if enterprises offer dynamic value sharing based on the contribution of human capital.

Value sharing based on contribution

According to the equity theory, employees’ enthusiasm is not only related to their actual reward but also closely related to whether they feel that this reward has been fairly distributed (Adams, 1965). Unfair compensation contracts consequently reduce employees’ efforts and value creation (Falk and Ichino, 2006). Each participant will be motivated only if they perceive that their reward matches their contribution. Accordingly, Moyer (2012) proposes that the proportion of equity should be divided according to the relative contribution of various types of capital.

Several studies have examined the mechanism of value sharing based on contribution. Narayanan and Levesque (2019) compare the efficiencies of three types of initial equity distribution methods, namely, the venture capitalist’s “gut feeling”, the requested amount of funding, and the contribution-based methods of building principal-agent models. The results suggest that the optimal equity distribution method is the contribution-based method which divides the equity according to their relative contribution to value creation for the new firm. Lab experiments also confirm the effectiveness of the mechanism of value sharing based on contribution. Kagan et al. (2020) compare the efforts and value creation of four types of initial equity distribution contracts by lab experiments, which are equal division, proportional division, threshold vesting and difference vesting contractsFootnote 1. Their study finds that, when participants choose the proportional division contract (i.e., the contract of distributing equity based on contribution), the average effort of participants is always higher than that of other types of contracts. Furthermore, low contributors prefer equal division, while high contributors prefer the contract involving the distribution of equity based on contribution. Therefore, individuals offering high contributions can be screened out by using the contract of distributing equity based on contribution.

We build our research on the aforementioned stream of literature and relax the assumptions to reflect reality better. Narayanan and Levesque (2019) and Kagan et al. (2020) make the assumption that contributions remain unchanged rather than studying the adjustment of the value-sharing proportion with the change in contribution. They also assume that participants are completely rational. However, in practice, the relative and absolute contributions of human capital are constantly changing, and the static value-sharing mechanism may be unreasonable. In addition, participants’ decisions are bounded rational, not completely rational.

Dynamic value sharing based on contribution

The mechanism of value sharing based on contribution is consistent with not only the principle of fairness in the social transaction but also the logic of value creation in production. As enterprises enter the development and maturity stage from the inception, the human capital needed for further growth may be different from what the company possessed in the past. Moreover, individuals’ contribution to the value of the company is dynamic (Fudenberg and Rayo, 2019) due to their changing abilities and the amount of effort they exert. Moreover, through learning about successful working experiences and methods, employees are able to improve their human capital (Prat, 2015). All of these indicate that human capital is dynamic and its contribution to enterprise value appreciation is also dynamic; the value-sharing ratio should change accordingly as well. Therefore, it is more reasonable to study human capital contribution from a dynamic perspective.

In summary, the current body of academic research does not reach a consensus on the effectiveness of value sharing in enhancing firm value and falls short of researching the contribution dynamically. First, scholars have differing views on value sharing: Some scholars believe that it is effective for the growth of enterprises, while others maintain that it is ineffective. There has been a continuing debate on the merits, or otherwise, of value sharing over the last 60 years. Whether the implementation of value sharing based on contribution at the employee level is conducive to enterprise development still needs to be researched. Second, the research of value sharing based on contribution is mostly concentrated on the static aspects of the system without considering the dynamic aspect of the contribution. Therefore, it has strong theoretical and practical significance to study the dynamic change of value sharing with contribution, updating the value sharing proportion over time, and finding the best practice suitable for sustainable enterprise value growth. Finally, previous research based on static or dynamic principal-agent models assumes that participants have not only goal rationality, but also process rationality (i.e., cognitive rationality and instrumental rationality). However, employees’ behaviors are influenced by bounded rationality and learning mechanisms. Thus, further examination is needed as to whether the conclusion drawn by the traditional game is still valid under bounded rationality and learning mechanisms.

To address these dynamics and complexity, and bridge the literature gap with regard to value sharing, this paper integrates the theory of human capital and value creation and compares the impact of SVS and DVS on enterprise human capital, profit, and value using evolutionary game theory. This provides theoretical support for enterprises to formulate value-sharing strategies and has strong practical implications.

Model construction

Nomenclature

Parameters

i the firm with VS (i = 1) and the firm with NVS (i = 2)

r the incentive capacity coefficient of VS and 0 < r < 1

λ the transformation capacity coefficient of VS and 0 < λ < 1

ai the basic value of products produced by firm i

pi prices of products produced by firm i

ci costs of products produced by firm i

z the ___location of consumer on a Hotelling line

e the unit mismatch cost

θ the ratio of profit retention

d the ratio of value sharing received by the employee

w wages received by the employee

n the total number of employees in both companies

Variables

x the ratio of the firm with VS and 0 ≤ x ≤ 1

y the ratio of the staff with high capability and 0 ≤ y ≤ 1

t time

Acronyms

VS the mechanism of value sharing

NVS the mechanism of no value sharing (i.e., salary system)

SVS the mechanism of static value sharing based on the initial contribution

DVS the mechanism of dynamic value sharing based on contribution

HE, LE the high-capability employee and the low-capability employee

Competitive process of enterprises

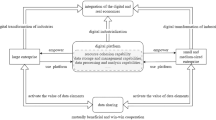
The process of shifting human capital to value creation can be seen to include two transformations. In the first instance, the individual human capital of employees is transferred to the enterprise to form the source of creation; following this, the enterprise is able to transform this capital into innovative products or services that bring utility to consumers. In order to improve market competitiveness, enterprises compete for talent by implementing a series of value-sharing plans. There are two types of enterprises in the market, one seeks to pursue the value-sharing plan (VS), and the other does not adopt the value-sharing plan (NVS).

In the process of attracting talent, the firm could randomly pick a VS or NVS in the talent market. However, the effect may be different because of their characteristics and human capital endowments. The decision on whether or not to implement value sharing will directly affect the degree of accumulation and exploitation of human capital, then influence the utility of products or services to consumers which determines the market share, and finally, the profit of the enterprises is determined, as shown in Fig. 2.

Fig. 2: The interactive influence of enterprise incentive, talent, and market competition strategy.
figure 2

Enterprises take value-sharing mechanisms as a competitiveness-enhancing device to compete in both the talent market and the consumer market.

Full size image

Therefore, an enterprise will play games twice, one between the enterprise and other enterprises, and the other between the enterprise and employees. When making decisions, enterprises should start from consumer demand, focusing on consumer utility, and solving the equilibrium to maximize the enterprise’s profit. Then, by analyzing the evolutionary equilibrium stability strategy, the enterprise decides whether and how to implement the value-sharing plan. The game competition structure is shown in Fig. 3.

Fig. 3: Game competition structure.
figure 3

An enterprise will play games twice, one between the enterprise and other enterprises, and the other between the enterprise and employees.

Full size image

Assume that the incentive capacity of the firm with VS is r, and the firm with NVS is 0.5. The coefficient r measures the incentive capacity, which represents the ability of enterprises to stimulate the transfer of human capital from individuals to enterprises in the initial transformation step. The greater the incentive capacity, the stronger the employees’ willingness to work harder and make greater contributions to the enterprise.

Assume that the transformation capacity coefficient of the firm with VS is λ, and the firm with NVS is 0.5. The coefficient λ measures the transformation capacity, that is, the capacity to absorb and transform human capital into innovation and apply it commercially in the second transformation step.

Assume that there are two kinds of employees in the enterprise: one with high capability and the other with low capability. Consistent with Spence (1973), we assume that the human capital stock of high-capability employees is 1 and that of low-capability employees is 1/2. The firm with VS absorbs human capital and transforms it into innovation, bringing positive utility to consumers. This is referred to as T1.

$$T_1 = \lambda rn\left( {1 + y_1} \right)/2$$
(1)

The firm with NVS absorbs human capital and transforms it into innovation, bringing positive utility to consumers. This is referred to as T2.

$$T_2 = n\left( {1 + y_2} \right)/8$$
(2)

Competition in the consumer market

We use the Hotelling model (Hotelling, 1929) to simplify the process that two types of firms (those who adopt value sharing vs. those who don’t) compete against each other in the consumer market for the following reasons. First of all, we assume one firm goes ahead with VS and the other one goes ahead with NVS. Take China’s mobile phone products as an example. The high-end mobile phone market in China (the mobile phone prices higher than $400) has gradually formed a duopoly competition pattern between Apple and Huawei, with their combined market share accounting for more than 60% of the market (Huang, 2022). This is in line with the characteristics of oligopolistic competition in the Hotelling model. Secondly, the Hotelling model is usually used to construct enterprise competition that considers differences in both consumer preference and products, such as the research of Li and Jain (2016), Ji et al. (2019), and Liu et al. (2006). We focus on a scenario where two horizontally differentiated firms sell their products to consumers. They compete for the marginal consumers and each consumer purchases, at most, one unit of the product. This form of competition, which links consumer preference differences to product differences, is appropriate to use the Hotelling model.

For consumers, they have heterogeneous valuations and are uniformly distributed over a Hotelling line with a range [0, 1] (Li and Jain, 2016). Moreover, the firm with VS is located at 0, and the firm with NVS is located at 1. A consumer’s ___location is denoted by z ∈ [0, 1]. Denote e as the unit mismatch cost which illustrates the magnitude of negative utility incurred from the mismatch between the consumer’s ideal product and the product actually offered by a firm (Ji et al., 2019). Thus, if a consumer purchases the product of the company with VS, it will incur a mismatching disutility of ez. Conversely, if a consumer makes the opposite choice, it will incur a mismatching disutility of e(1−z), as shown in Supplementary Fig. S1 online.

The total utility of products to consumers consists of four parts: the base value of the product, the negative utility brought by the price, the positive utility brought by innovation, and the negative utility brought by the mismatch with their ideal products. The utility of the firm with VS and the firm with NVS to consumers, respectively, is just as follows.

$$u_1 = a_1 - p_1 + T_1 - ez$$
(3)
$$u_2 = a_2 - p_2 + T_2 - e\left( {1 - z} \right)$$
(4)

The profit functions of the firm with VS and the firm with NVS are as follows.

$$\pi _1 = \left( {p_1 - c_1} \right)z$$
(5)
$$\pi _2 = \left( {p_2 - c_2} \right)\left( {1 - z} \right)$$
(6)

Lemma 1 There is game equilibrium in the oligopolistic competition. The equilibrium profit of the firm with VS is \(\pi _1^ \ast\) and that of the firm with NVS is \(\pi _2^ \ast\).

$$\pi _1^ \ast = \frac{{\left( {3e + T_1 - T_2 + g} \right)^2}}{{18e}}$$
(7)
$$\pi _2^ \ast = \frac{{\left( {3e - T_1 + T_2 - g} \right)^2}}{{18e}}$$
(8)

The proof can be found in Supplementary Lemma 1 online.

Observing Eqs. (7) and (8), the equilibrium profit is closely related to the total amount of human capital, so enterprises compete for talented employees in the talent market.

Competition in the talent market

Model framework

The strategy spaces of firms and employees are SF = {VS, NVS} and SE = {HE, LE}, where VS and NVS represent value sharing and non-value sharing (i.e., regular salary), and HE and LE denote high-capability employees and low-capability employees. Participants always give priority to imitating successful strategies, that is, the higher the payoff, the greater the probability of being imitated. Thus, incentives that lead to higher payoff are more likely to survive the process of social evolution (Dong et al., 2019). The next step is to analyze the enterprises’ and employees’ payoffs under different strategies.

Analysis of the enterprise’s payoff

The goal of an enterprise is to maximize its value. The enterprise’s payoff is the value of the enterprise in the evolutionary game. Enterprise value includes physical capital and organizational capital (Juneja and Amar, 2018).

Physical capital: At the end of each accounting period, the firm draws a share θ ∈ (0, 1) of profit as reserved funds for future development, which forms the physical capital at time t. In order to more intuitively reflect the change in enterprise value, the accumulation of physical capital in the early stage of the enterprise is not considered. Then the firm’s physical capital at time t is θπ.

Organizational capital: Organizational capital is built by human capital, and also converts human capital into value (Juneja and Amar, 2018). For the firm with VS, a share λ ∈ (0, 1) of the firm’s human capital is consumed, absorbed, and transformed into product innovation. And a share 1−λ of the firm’s human capital is internalized and transformed into the value of the firm’s acquired institutionalized knowledge and tacit knowledge, such as systems, processes and databases, which constitute the organizational capital of the enterprise. Then the firm’s organizational capital at time t is (1−λ)[ryn + r(1−y)n/2].

The value of enterprises under different strategic choices are as follows.

When enterprises implement VS and employees are high-capability, physical capital is \(\theta \pi _{H1}^ \ast\) and organizational capital is (1−λ)nr, then enterprise value is \(V_{H1} = \theta \pi _{H1}^ \ast + \left( {1 - \lambda } \right)nr\). For \(\pi _{H1}^ \ast\), according to Eqs. (1) and Eq. (7), and let δH1 = λr−(1 + y2)/8, yield \(\pi _{H1}^ \ast = \frac{{\left( {3e + n\delta _{H1} + g} \right)^2}}{{18e}}\).

When enterprises implement VS and employees are low-capability, physical capital is \(\theta \pi _{L1}^ \ast\)and organizational capital is (1−λ)nr/2, then enterprise value is \(V_{L1} = \theta \pi _{L1}^ \ast + \left( {1 - \lambda } \right)nr/2\). For \(\pi _{L1}^ \ast\), according to Eqs. (1) and (7), and let δL1 = [4λr−(1 + y2)]/8, yield \(\pi _{L1}^ \ast = \frac{{\left( {3e + n\delta _{L1} + g} \right)^2}}{{18e}}\).

When enterprises implement NVS and employees are high-capability, physical capital is \(\theta \pi _{H2}^ \ast\)and organizational capital is n/4, then enterprise value is \(V_{H2} = \theta \pi _{H2}^ \ast + n/4\). For \(\pi _{H2}^ \ast\), according to Eqs. (2) and (8), and let δH2 = [2λr(1 + y1)−1]/4, yield \(\pi _{H2}^ \ast = \frac{{\left( {3e - n\delta _{H2} - g} \right)^2}}{{18e}}\).

When enterprises implement NVS and employees are low-capability, physical capital is \(\theta \pi _{L2}^ \ast\) and organizational capital is n/8, then enterprise value is \(V_{L2} = \theta \pi _{L2}^ \ast + n/8\). For \(\pi _{L2}^ \ast\), according to Eqs. (2) and (8), and let δL2 = [4λr(1 + y1)−1]/8, yield \(\pi _{L2}^ \ast = \frac{{\left( {3e - n\delta _{L2} - g} \right)^2}}{{18e}}\).

Analysis of the employee’s payoff

The final earnings of each employee include his or her private payoff gained by using his or her surplus human capital for recreation, leisure, or a second job, and the share of the firm profits when working for a VS firm, or a fixed salary w when working for NVS firm. Moreover, in most job markets, enterprises are uncertain of the employees’ capabilities when enterprises make employment decisions (Spence, 1973). Therefore, enterprises consider the composition of high-capability and low-capability employees to calculate the expected value of the value-sharing proportion d or salary w.

When high-capability employees work in the firm with VS, private payoff is 1−r and sharing payoff is \(d\left( {1 - \theta } \right)\pi _{H1}^ \ast\), then the final payoff is \(S_{H1} = 1 - r + d\left( {1 - \theta } \right)\pi _{H1}^ \ast\).

When low-capability employees work in the firm with VS, private payoff is (1−r)/2, sharing payoff is \(d\left( {1 - \theta } \right)\pi _{L1}^ \ast\), then the final payoff is \(S_{L1} = \left( {1 - r} \right)/2 + d\left( {1 - \theta } \right)\pi _{L1}^ \ast\).

When high-capability employees work in the firm with NVS, private payoff is 0.5 and salary is w, then the final payoff is SH2 = 0.5 + w.

When low-capability employees work in the firm with NVS, private payoff is 0.25 and salary is w, then the final payoff is SL2 = 0.25 + w.

The decision tree for the interest game model is shown in Supplementary Fig. S2 online. The firm implements VS with probability of x ∈ [0, 1] and NVS with probability of 1−x. In addition, denoting with y ∈ [0, 1] and 1−y the shares of high-capability and low-capability employees.

Evolutionary game analysis with SVS

After evaluating human capital and analyzing the relative contribution in value creation by employees, the enterprise with SVS grants employees dividend rights, but excludes rights related to voting, decision-making, ownership transferring, and inheritance. Furthermore, once the value-sharing proportion d is determined, it will not change until the employee leaves the company. Generally, it is common practice not to update d during their time with the enterprise. The payoff matrix for both players under different strategies is shown in Table 1.

Table 1 Payoff matrix for both players.
Full size table

When the firm chooses SVS mechanism, the expected utility is defined as follows:

$$U_{{\rm {SVS}}} = yV_{H1} + \left( {1 - y} \right)V_{L1}$$
(9)

The firm’s average expected utility is as follows:

$$\overline U _{\rm {F}} = x\left[ {{{{\mathrm{y}}}}V_{H1} + \left( {1 - y} \right)V_{L1}} \right] + \left( {1 - x} \right)\left[ {{{{\mathrm{y}}}}V_{H2} + \left( {1 - y} \right)V_{L2}} \right]$$
(10)

According to the Malthusian equation, the firm’s replicator dynamic equation is as follows:

$$\frac{{{\rm {d}}x}}{{{\rm {d}}t}} = \frac{{x\left( {1 - x} \right)}}{6}\left\{ {4g\theta + n\left( {1 + y} \right)\left[ {2\delta \theta + 3\left( {r - 0.5} \right) - 3\delta } \right]} \right\}$$
(11)

In Eq. (11), let g = (a1−c1)−(a2−c2), δ = λr−0.25.

Similarly, when an employee is the type of high capacity, the expected utility is shown in Eq. (12).

$$U_{{\rm {RS}}} = x\left[ {1 - r + d\left( {1 - \theta } \right)\pi _{H1}^ \ast } \right] + \left( {1 - x} \right)\left( {0.5 + w} \right)$$
(12)

The employee’s average expected utility is shown in Eq. (13).

$$\begin{array}{l}\overline U _{\rm {E}} = y\left\{ {x\left[ {1 - r + d\left( {1 - \theta } \right)\pi _{H1}^ \ast } \right] + \left( {1 - x} \right)\left( {0.5 + w} \right)} \right\}\\ \qquad+ \left( {1 - y} \right)\left\{ {x\left[ {\left( {1 - r} \right)/2 + d\left( {1 - \theta } \right)\pi _{L1}^ \ast } \right] + \left( {1 - x} \right)\left( {0.25 + w} \right)} \right\}\end{array}$$
(13)

According to the Malthusian equation, the employee’s replicator dynamic equation is as follows:

$$\frac{{{\rm {d}}y}}{{{\rm {d}}t}} = \frac{{y\left( {1 - y} \right)}}{{72e}}\left\{ \begin{array}{l}18e + x\left[ {36e\left( {0.5 - r} \right) + \delta nd\left( {1 - \theta } \right)\left( {3\delta n + 4g + 12e} \right)} \right]\end{array} \right\}$$
(14)

According to Eqs. (11) and (14), the replicator dynamic system (I) is obtained, which is a two-dimensional nonlinear dynamic system for the firm and employee, as shown in Eq. (15).

$$\left\{ {\begin{array}{l} {F_x = \frac{{{\rm {d}}x}}{{{\rm {d}}t}} = \frac{{x\left( {1 - x} \right)}}{6}\left\{ {4g\theta + n\left( {1 + y} \right)\left[ {2\delta \theta + 3\left( {r - 0.5} \right) - 3\delta } \right]} \right\}} \hfill \\ {F_y = \frac{{{\rm {d}}y}}{{{\rm {d}}t}} = \frac{{y\left( {1 - y} \right)}}{{72e}}\left\{ {18e + x\left[ \begin{array}{l}36e\left( {0.5 - r} \right) + \delta nd\left( {1 - \theta } \right)\left( {3\delta n + 4g + 12e} \right)\end{array} \right]} \right\}} \hfill \end{array}} \right.$$
(15)

Evolutionary game analysis with DVS

An employee’s behavioral choice is affected by imitative learning. If high-capability employees obtain higher payoffs, low-capability employees will imitate the strategies of high-capability employees and actively seek to improve their human capital through learning and training. In the enterprise that implements DVS, the higher the ability of employees, the more contributions they make, and the higher the value-sharing proportion they obtain. That is, generally, an enterprise estimates the probability that employees are high-capability employees, judges the contribution of employees regarding value creation, and dynamically adjusts the sharing proportion, which forms the mechanism of dynamic value sharing based on contribution. Therefore, the value-sharing proportion of high-capability employees is dy.

Following on from the above discussion, and combining the section “Competition in the talent market”, the replicator dynamic system (II) is obtained, as shown in Eq. (16).

Let k = g + 3e, b = 8k2 + 12δnk + 5δ2n2.

$$\left\{ {\begin{array}{l} {\frac{{{\rm {d}}x}}{{{\rm {d}}t}} = \frac{{x\left( {1 - x} \right)}}{6}\left\{ {4g\theta + n\left( {1 + y} \right)\left[ {2\delta \theta + 3\left( {r - 0.5} \right) - 3\delta } \right]} \right\}} \hfill \\ {\frac{{{\rm {d}}y}}{{{\rm {d}}t}} = \frac{{y\left( {1 - y} \right)}}{{72e}}\left\{ \begin{array}{l}18e - 36e\left( {r - 0.5} \right)x + \\ d\left( {1 - \theta } \right)x\left[ {by - \left( {2k + \delta n} \right)^2} \right]\end{array} \right\}} \hfill \end{array}} \right.$$
(16)

Analysis and discussion

Data and parameters

Simulation analysis is a more effective research method in some circumstances and can provide reliable scientific explanations (Ji et al., 2019). Furthermore, more profound management implications can be obtained by sensitivity analysis of different parameters. In order to further test and verify the models, Huawei is taken as an example for simulation analysis. We take China’s mobile phone industry as an example and take Huawei’s enterprise status from 2008 to 2012 as the initial value of numerical simulation. First of all, the total market share of Apple and Huawei in China’s Top smartphone market share exceeds 60%, which is close to oligopoly status (Huang, 2022). Secondly, Huawei began to implement Time Unit Planning (TUP) in 2013, which is a sharing plan close to DVS. A final, important factor is that data on Huawei are available. As a high-profile enterprise both in China and internationally, although not a public company, Huawei manages to be transparent and discloses information periodically. The data used in this paper are from Huawei’s official website, annual reports, China National Intellectual Property Administration, and similar studies.

The data about Huawei from 2008 to 2012 are used as the basis for the initial assignment of relevant parameters. This is because Huawei implemented Saturated Rights Issues from 2008 to 2012. It was similar to SVS. During this time, once an employee’s value-sharing quota was obtained, it would remain unchanged for a significant period, which means future income is not so strongly related to their long-term contribution. We take the average value from 2008 to 2012 as the initial value of the evolutionary game, and these initial parameters represent the initial state of the enterprise. From 2008 to 2012, the average percentage of employee shareholding was about 55%. Put another way, the probability of employees being granted value-sharing rights after entering the enterprise was 55%. Thus, the initial value of x0 is assumed to be 0.55. Those involved in research and development account for 45% of the total number of employees. Therefore, the probability of this group of shareholders being granted value-sharing rights was about 25%, and thus the initial value of y0 is assumed to be 0.25. The average ratio of output to input of intangible assets was 61.79%, and this could characterize the transformation capacity of enterprises to a certain extent, so it is possible to specify that λ = 0.6. Using the compound annual growth rate of the ratio of the added value of intangible assets to employee income to characterize the incentive coefficient, which was about 60%, means r = 0.6. The total number of Huawei shares is about 22.2 billion. In 2020, the dividend per share was 1.86 Yuan, and the enterprise value per share was about 41.3 billion yuanFootnote 2, accounting for about 64% of the total profit. About 36% of the total profit was retained. Therefore, the initial value of θ can be assumed to be 0.4. From 2008 to 2012, more than 60,000 people shared about 98.6% of the equity of the enterprise, with an average shareholding ratio of about 0.0016%, then the initial value of d is set as 0.0016. Around 2008, the average selling price of Huawei’s mobile phone products was about 1400, while that of other manufacturers in the market was about 2500Footnote 3. Therefore, one can set p1 = 1400 and p2 = 2500. With reference to pertinent research, the utility of mobile phone products to consumers is 1.5 times that of mobile phone prices. Thus, the initial value of a1 and a2 are assumed to be 2100 and 3750, respectively. In addition, c1 = 1250 and c2 = 2050Footnote 4. Table 2 shows the key parameters and their initial values.

Table 2 Initial key parameter values.
Full size table

Analysis of the research results

In the present section, numerical simulation is used to analyze the evolution of the proportion of high-capability employees, enterprise profits, and value of firms with SVS and DVS. From Fig. 4, we can conclude that there is no asymptotic ESS between the firm with SVS and high-capability employees. The first observation is that the probability of implementing SVS and the proportion of high-capability employees is unstable, which seriously affects the stability of the team. Furthermore, when the enterprise is sure to implement SVS, the proportion of high-capacity employees gradually decreases over time (e.g. t = 6 to t = 14). Although this appears to be counterintuitive, this does happen in practice. During the period of Saturated Rights Issues, Huawei suffered from brain drain. This was because the proportion of value sharing was static: Some employees enjoyed the generous benefits offered by stock dividends and ignored their income from basic salaries, and consequently, a situation marked by apathy and deteriorating motivation occurred. Really productive employees, especially those in R&D and sales, were not compensated for their contribution. The mismatch between income and contribution led to unfairness, which suppressed work motivation and intensified the turnover of talented employees. This is consistent with the simulation results of the model proposed by this study, which proves its accuracy and reliability.

Fig. 4: Evolution of employees under SVS.
figure 4

There is no evolutionarily stable strategy with the mechanism of static value sharing based on initial contribution.

Full size image

As we can see from Fig. 5a, although the profit of an enterprise with SVS is always higher than that of an enterprise with NVS, the profit fluctuates more sharply. Similarly, Fig. 5b shows that the value of an enterprise with SVS is higher than that of an enterprise with NVS, and the fluctuation range is not as severe as that of the profit but still significant.

Fig. 5: Evolution of profit and value with SVS and NVS.
figure 5

a Evolution of profit with SVS and NVS. b Evolution of firm value with SVS and NVS.

Full size image

Figure 6 indicates that compared to SVS (Fig. 4), the proportion of high-capacity employees is gradually increasing and tends to be stable later, and high-capability employees ultimately dominate the revenue sharing over time for the firm undertaking DVS. That is because the firm with DVS dynamically adjusts the sharing proportion based on contribution, which reduces the possibility of the free-riders and rent-seeking phenomenon, leading to lower returns for low contributors than for the firm with NVS. Following this, low contributors gradually exit and high contributors gradually enter.

Fig. 6: Evolution of employees under DVS.
figure 6

There is an evolutionarily stable strategy with the mechanism of dynamic value sharing based on contribution.

Full size image

Figure 7a demonstrates that the profit of an enterprise with DVS increases rapidly, tends to stabilize, and is much higher than that of an enterprise with NVS. In the early stage of evolution, the profit of the firm with NVS first decreases and then gradually increases, which may be due to the imitative behavior of the talent market. As we can see from Fig. 7b, the value under two revenue sharing schemes exhibits a similar pattern as that of the profit: Compared to an enterprise with SVS, the value of the firm with DVS is increasing sharply, tends to stabilize, and is much higher than that of NVS. Therefore, DVS will benefit enterprise development.

Fig. 7: Evolution of profit and value with DVS and NVS.
figure 7

a Evolution of profit with DVS and NVS. b Evolution of firm value with DVS and NVS.

Full size image

The results of numerical simulation by substituting the initial historical data into models are shown in Figs. 4–7. On the one hand, the above-mentioned results explain why enterprises implement value sharing but are still unable to effectively motivate, attract and retain talent, and cannot significantly improve enterprise performance, which is consistent with the realistic dilemma facing enterprises. On the other hand, DVS can help in the accumulation of high-capacity human capital and the realization of stable and sustainable value creation, which fits well with the rapid development of Huawei after the implementation of TUP (similar to DVS). It also verifies the application and reliability of this study’s models in business practices.

Sensitivity analysis

This section will focus on how to optimize parameters to accelerate the evolution of the system to ESS when enterprises implement DVS. In order to allow for the results of the sensitivity analysis to be comparable with the previous results, the relevant data about Huawei will continue to be used as the basis of the simulation analysis. In the analysis of the sensitivity of one parameter, the values of the other parameters remain consistent with the initial assignment. This study provides guidance for the direction and intensity of efforts of the enterprises to improve their competitiveness.

The influence of initial proportion of high-capability employees on system evolution

Figure 8a shows that with the increase of the initial proportion of high-capability employees, the evolution time for the proportion of high-ability employees to reach equilibrium gradually shortens. Figure 8b indicates that with the increase of the initial proportion of high-capability employees, the speed of maximizing the profits of enterprises similarly accelerates.

Fig. 8: The effect of the initial proportion of high-capability employees (y0) on the proportion of high-capability employees and the profit of the firm.
figure 8

a Evolution of high-capability employees with different y0. b Evolution of profit with different y0.

Full size image

The above occurs because the benefits of high-capability employees are greatly improved through DVS, and other employees will learn and imitate the strategies of the high-capability employees. If the initial proportion of high-capability employees is higher, the diffusion rate of the strategy will be increased and the time for the system to reach evolutionary stability will be shortened. This shows that enterprises with a large number of highly capable employees have unique advantages in using DVS, and can reach the optimal state faster than enterprises with fewer talented workers.

The influence of incentive capacity and transformation capacity on system evolution

Figure 9a compares the impact of low (r = 0.3), medium (r = 0.5), and high (r = 0.7) incentive capacity on the proportion of high-capability employees. As shown by Fig. 9a, with the enhancement of the incentive capacity coefficient, the proportion of high-capability employees reaches the equilibrium value faster. Figure 9b manifests that both the equilibrium value of profits and the speed of reaching equilibrium are affected by the incentive capacity coefficient r. That is, the larger the incentive capacity coefficient is, the greater the equilibrium value of the enterprise’s profit is, and the faster the profit can reach the maximum state.

Fig. 9: The effects of incentive capacity coefficient (r) and transformation capacity coefficient (λ) on the proportion of high-capability employees and the profit of the firm, respectively.
figure 9

a Evolution of high-capability employees with different r. b Evolution of profit with different r. c Evolution of high-capability employees with different λ. d Evolution of profit with different λ.

Full size image

Figure 9c compares the impact of low (λ = 0.3), medium (λ = 0.5), and high (λ = 0.7) transformation capacity on the proportion of high-capability employees. In the section “Model construction”, we assume that the transformation capacity coefficient of the firm with NVS is 0.5. Therefore, λ = 0.3, λ = 0.5, and λ = 0.7 respectively represent three situations where the transformation capacity of the firm with DVS is lower than, equal to, and greater than that of the firm with NVS. In accordance with the enhancement of the transformation capacity (from 0.3 to 0.5), the proportion of high-capability employees reaches the equilibrium value faster. However, when λ = 0.7, although the same number of talented workers in the enterprise can still reach the equilibrium value, the evolution time to reach the equilibrium value is longer than that of λ = 0.5.

Figure 9d reveals that the stronger the transformation capacity of the enterprise is, the greater the evolutionary equilibrium value of the profit will be. But the transformation ability is not linearly related to the time when the profit evolves to the equilibrium. This may be because the enterprise overemphasizes the utilization of human capital and ignores the attraction and accumulation of new human capital, which finally prolongs the time needed for the enterprise to reach the maximum value. Therefore, the value of the transformation capacity should be set appropriately in order to find a balance between the speed and degree of evolution.

The influence of ratio of overall profit-sharing on system evolution

Figure 10a shows the effect of the ratio of overall profit sharing (1−θ) on the proportion of high-capability employees, suggesting that the ratio of overall profit sharing is not linearly related to the evolution speed to the equilibrium. When 1−θ ≤ 0.996, a larger ratio of overall profit-sharing leads to a faster evolution of the proportion of high-capability employees to the equilibrium. When 1−θ > 0.996, increasing the ratio of overall profit sharing greatly prolonged the time taken to reach the equilibrium point. Similarly, Fig. 10b shows that a larger ratio of overall profit-sharing leads to a faster evolution of the profit to the equilibrium when 1−θ ≤ 0.996, and it does not affect the maximum value of the profit. However, when 1−θ > 0.996, the evolution time to the equilibrium is greatly extended.

Fig. 10: The effect of the ratio of overall profit sharing (1−θ) on the proportion of high-capability employees and the profit of the firm.
figure 10

a Evolution of high-capability employees with different 1−θ. b Evolution of profit with different 1−θ.

Full size image

From the employees’ perspective, high-capability employees enjoy greater profit sharing, which will quickly attract highly capable talents in the near term and promote the enterprise’s capacity to obtain short-term competitiveness in the consumer market. However, from a long-term strategic perspective, if enterprises do not reserve enough funds for development, such as R & D investment, it will hinder their resilience in the pursuit of growth and greatly prolong the time for them to reach equilibrium. On balance, the setting of the ratio of overall profit sharing should be moderate without affecting the long-term development of the enterprise. For example, in 2020, Huawei implemented a large-scale value-sharing plan, with a profit-sharing scheme totaling more than 40 billion Yuan. But Huawei undertook this value sharing on the basis of ensuring sufficient R & D investment (about 141.893 billion Yuan) for its continuous development and long-term sustainable growth.

Discussion

Knowledge is one of the most important assets in the 21st century and the bedrock of the new sustainable economy (Russ, 2016). Human capital is the source of knowledge creation and the core capital factor driving the growth of an enterprise’s value and is crucial for creating an organization’s competitive advantage and success (Barney, 1991; Lepak and Snell, 1999). It has become an inevitable trend for human capital to contribute to and share the surplus value. To motivate employees to contribute their valuable human resources to create more value for the firm, the firm wants to tie employees’ pay to firm performance as a means of screening capable and productive employees, and these employees will be willing to invest in firm-specific human capital and work harder (Oyer and Schaefer, 2005). Also, a value-sharing mechanism with higher incentive intensity can help companies attract and retain talented workers (Zenger, 1994). In addition, deferred compensation plans, such as deferred vesting of stock or options have retention effects by increasing the costs to employees when departing the firm (Gopalan et al., 2021; Jochem et al., 2018). Consistent with studies by Duodu and Rowlinson (2021) and Rauch et al. (2005), which find that value sharing is conducive to enterprise performance and growth, our model analysis results show that the value of enterprises implementing value sharing is always higher than the that of enterprises not implementing value sharing. Compared with the research of Duodu and Rowlinson (2021) and Rauch et al. (2005), our research further supports the idea that DVS is a better mechanism than traditional SVS. Under this mechanism, highly capable talents eventually dominate value sharing, while under static revenue sharing, highly capable talents have always been in a state of large fluctuation and the stability of the team is poor. Aldatmaz et al. (2018) indicate that the broad-based employee stock option, which belongs to SVS, just delays the decisions of employees to resign, but does not fundamentally reduce the turnover rate. Our research is helpful to explain why enterprises implementing static value sharing still cannot, in reality, effectively motivate, attract and retain talents, and cannot significantly improve enterprise performance.

Our research is different from the influential Oyer and Schaefer (2005) and the recent Kagan et al. (2020) too. Oyer and Schaefer (2005) show that employees who are optimistic about the enterprise and have advanced abilities tend to choose value-sharing methods linked to the company’s operation, such as stock options. Through model research, we find that the traditional SVS is less attractive to highly competent employees than DVS, and DVS is more stable in attracting and screening highly competent employees. Reinforcing the findings of Kagan et al. (2020), this study further confirms that high-capability employees with high contributions tend to choose contracts of dynamic value sharing based on contribution.

Research limitations and future prospects

Due to basic model assumptions, the Hotelling model does not consider the equilibrium situation when the market is not fully covered. In addition, this study does not consider the impact of other social preferences (such as altruism and reciprocity) and risk preferences (risk aversion) of game participants on the model. Future studies can build evolutionary game models considering different social and risk preferences and explore the impact of these divergent preferences on the effectiveness of enterprise value-sharing mechanisms.

Conclusions and management implications

With the advent of the knowledge economy era, competition among enterprises has been transformed into competition for talent. Enterprises use various types of value-sharing mechanisms to encourage, attract and retain talented workers, but the original intention of value-sharing plans to enhance value creation and competitiveness is often not realized. There has been a heated debate on whether and how to implement value sharing. This study contributes to the debate by comparing the effects of SVS and DVS on enterprise human capital and value creation. The main conclusions and managerial implications are as follows.

First, the profit and value of enterprises with value sharing are higher than those without value sharing. This study further confirms that value sharing, specifically, dynamic value sharing, can help improve enterprise performance. We also find that there is no ESS with the mechanism of static value sharing based on initial contribution. Consequently, the stability of teams of talented individuals is poor, resulting in significant fluctuations in the enterprise’s profit and value creation.

Second, with the mechanism of dynamic value sharing based on contribution, the trajectory of the system stabilizes, and the firm’s profit and value increase more than they would do without this mechanism. This finding indicates that DVS more stably promotes the growth of the enterprise.

Third, the mechanism of dynamic value sharing based on contribution has the function of screening high-capability employees. High-capability employees offering enhanced contributions tend to choose contracts of dynamic value sharing based on contribution, which reinforces the findings of Kagan et al. (2020). High-capability employees ultimately dominate the value sharing under this mechanism in the long run.

Finally, enterprises with a high proportion of high-capability employees have more advantages in implementing the mechanism of dynamic value sharing based on contribution, because it reduces the time taken to achieve equilibrium. This finding implies that the implementation of DVS in high-tech industries may have inherent advantages. In addition, moderately improving the transformation capacity and overall profit-sharing ratio of enterprises is beneficial for the evolution of enterprises when seeking to achieve their optimal state.

Based on these findings, one implication suggests that during the process of improving the transformation ability, there should be a match between ideal talent attraction and retention policies. If the firm simply and intensively seeks to improve its transformation ability, only emphasizes the high-intensity utilization of human capital, and does not align ideal talent attraction and retention policies, it will reduce its capacity to rapidly attract high-capability talents, thus prolonging the evolution time that the profit and value required to reach equilibrium. It is true that more generous sharing of corporate profit with employees can quickly improve the pace of evolution in an enterprise to achieve its optimal state in the short term. However, for the long-term development of the enterprise, sufficient funds should be reserved for its future development. Thus, the proportion of the overall profit to be shared should be set reasonably.