Introduction

Terrorism poses a significant threat to global security and stability (X Sanchez et al., 2018). There have been at least 210,000 terrorist attacks globally since the end of the 1960s. According to the 2024 Global Terrorism Index (GTI), there were almost 3350 terrorist attacks globally in 2023, killing over 8000 people, and resulting in a 56% increase in the average number of people killed per attack (Institute for Economics and Peace, 2024). While the extent and impact of terrorism have fluctuated over time, it remains an important challenge that governments and international organizations seek to counter through intelligence, security efforts, and addressing root causes (Benmelech et al., 2012; Perliger and Pedahzur, 2016). In recent years, terrorism has shown characteristics such as decentralized actors, civilian targets, complex forms, politicized goals, diversified means, and regional focus. It also exhibits trends such as the coexistence of internationalization and localization, the convergence of small-scale and grassroots activities, and the realization of the concept of cyberterrorism. In some countries or regions, terrorist attacks may either merge with separatist organizations, infiltrate by religious extremist groups, or transform into “lone wolf” attacks (Atran, 2021; Luo and Qi, 2021; Manzanero et al., 2021; Shin et al., 2023; Vicent et al., 2021). Without eliminating the soil of hatred, injustice, and inequality, it is difficult to completely eradicate terrorism. Religious extremism, income inequality, and other factors may trigger terrorist attacks. Facing potential terrorist threats, intelligence gathering and early warning measures are crucial, but the anti-terrorism strategies of different countries or regions may vary in emphasis. Typical targets of terrorist attacks include transportation infrastructure, chemical plants, energy facilities, and even virtual online platforms (Al-Dahash et al., 2022; Stewart, 2018; Zuijdewijn and Sciarone, 2021).

At present, the assessment and categorization of the extent of risk caused by terrorist attacks and other catastrophic events are mostly done subjectively (Bridgelall, 2022; Etaywe, 2022). Authoritarian organizations or departments commonly pick several key factors and impose mandatory categorization rules (Gaibulloev and Sandler, 2021; Gibbs, 2020; Hasisi et al., 2020). The risk of a terrorist attack is connected not only to deaths and property damages, but also to the time, ___location, target, and a variety of other elements (Duru et al., 2021). Furthermore, the incidence of terrorism is highly complicated and is influenced by a variety of circumstances, including quantitative ones such as politics, economics, and society, as well as non-quantifiable factors such as religion, history, and culture (Frykberg, 2006; Hao et al., 2019; Hu et al., 2019; Jünger and Gärtner, 2021). Therefore, the categorization technique is overly subjective and one-sided, and it is impossible to address the core issue of assessing the degree of risk caused by terrorist attacks. The existing quantitative study on terrorist attacks around the world is mainly limited to the following issues: (i) The majority of the description is still qualitative, with only a few quantitative analyses (Li et al., 2021; Treistman, 2021). (ii) In terms of research time and area, the time span is brief or limited to a single country or region. (iii) In terms of indicator selection, most of them have only a few study indicators that are fairly simple. (iv) In terms of research methodologies, researchers typically employ an analytic hierarchy process, fuzzy comprehensive evaluation, and K-mean clustering analysis to conduct research, which is subjective and solitary, and lacks evaluation of research results (Davis and Zhang, 2019; Reid, 1997; Wang et al., 2021). Therefore, quantitative analysis and research on terrorist attacks are still in their infancy, and there is still plenty of potential for exploration.

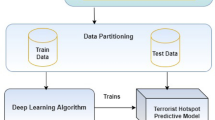
We probe into the risk assessment and categorization of terrorist attacks through quantitative approaches. First, we obtained the terrorist attacks that occurred worldwide from 1970 through 2020 based on the Global Terrorism Database (GTD) and chose 22 indicators related to the risk of terrorist attacks. Then, based on the theory of moment estimation, we combine subjective and objective weighting methods to generate optimal weights and utilize the linear weighted evaluation (LWE), fuzzy comprehensive evaluation (FCE), technique for order preference by similarity to ideal solution (TOPSIS) method, and the particle swarm optimization projection pursuit evaluation (PSO-PPE) method to identify the top 10 riskiest terrorist attacks in the world. Furthermore, the fuzzy c-means (FCM), clustering using representative (CURE), density-based spatial clustering of applications with noise (DBSCAN), clustering in QUEst (CLIQUE) and the Gaussian mixture model (GMM) clustering analysis methods were performed for the classification of terrorist attacks, and the visual analysis was carried out using the kernel density estimation (KDE) method. Finally, we provide three insights and recommendations for anti-terrorism efforts. This work is critical for ensuring national security and social stability in the changing scenario. As a result, an in-depth study of data connected to terrorist attack risk can assist people in better understanding terrorism and give vital information to aid in anti-terrorism and preventative efforts.

We summarize our core contributions are: (i) A more holistic assessment of terrorist attack risk that moves beyond unilateral metrics like casualties and economic damages. We obtained terrorist attacks that occurred worldwide from 1970 through 2020 based on the GTD and selected 22 indicators related to the risk of terrorist attacks. (ii) Robust model evaluation through combining multiple assessment techniques. Based on the LWE, FCE, TOPSIS, and PSO-PPE methods, the normalized comprehensive scores of the four models were averaged to provide the overall comprehensive evaluation value. It addresses the shortcomings of previous related studies, which relied on unilateral assessments of economic losses and casualties from terrorist attacks, and the evaluation methodologies were too subjective and solitary to compare the assessment findings. (iii) Comprehensive risk categorization validated by clustering evaluation criteria and spatial-temporal visualization of risk patterns globally over five decades. This study selects the FCM clustering approach to categorize terrorist attacks based on the FCM, CURE, DBSCAN, CLIQUE, and GMM clustering methods and the outcomes of the three clustering evaluation parameters, which makes the results scientific and reasonable. The findings provide novel insights to enhance understanding of terrorism dynamics and tendencies, with the potential to inform policies and practices for promoting security and stability amidst the evolving terrorist threat landscape.

The remainder of this paper is organized as follows: Section “Methodology” describes the methodology, which includes the datasets, indicator correlation analysis, optimal weight method, and the risk assessment and categorization methods. Section “Results” presents the results of analysis. Section “Conclusion” concludes and provides three insights and recommendations for the current global terrorist attack scenario, anti-terrorism efforts, and stability maintenance.

Methodology

Datasets

The internationally recognized terrorism databases currently available include the Global Terrorism Database (GTD), the International Terrorism: Attributes of Terrorist Events (ITERATE) dataset, the Terrorism in Western Europe: Events Database (TWEED), the RAND Database of Worldwide Terrorism Incident (RDWTI), and the World Incidents Tracking System (WITS). Among them, the GTD has compiled 210,454 terrorist incidents worldwide from 1970 through 2020 (START, 2024), making it one of the most comprehensive terrorism databases available and a widely utilized resource for terrorism research and analysis. However, the GTD also has certain limitations: (i) Like most terrorism datasets, the GTD suffers from selection bias as it relies on media reports and open-source information, which may fail to capture the full scope of terrorist activities, especially in areas with limited media coverage or restricted information flow. Underreporting and spatial–temporal biases are also challenges faced by the GTD, as data availability and quality may vary over time and ___location. (ii) The GTD only captures event-level information about the terrorist attacks themselves. It does not directly consider the broader societal, political, economic, ideological, and other environmental factors that could either enable or constrain terrorism. These contextual factors influencing terrorist activities are not included in the database. Despite these limitations, the GTD remains a valuable resource for quantitative analysis of global terrorism, providing a large structured dataset over an extended time period and broad geographical areas. To detect and evaluate irrelevant data, do a multidimensional analysis of the number of terrorist attacks per year, the weapon type, the attack region, the attacking country, the attack type, and the target/victim type on the obtained data. Then, using the quantification of non-numerical data as the key, we do data cleaning, transformation, classification, and other processing on the data to produce the indicator system of terrorist attack risk.

Data cleaning

We discovered data that was irrelevant to the study during the data exploration and analysis procedure. We concluded that the data follows the following rules: Doubtterr is 1, “unknown” data, the number of records with null values, and the number of records with missing key attributes. The following are the data rules and data cleaning rules:

Doubtterr is 1

In the suspected terrorism (doubtterr) indication, if the ambiguous and uncertain event is a terrorist attack, such an event in GTD will take the value “yes” in this variable. 1 = “Yes” suspects that an event is a terrorist attack; 0 = “No” does not suspect that an event is a terrorist attack, and the database will be recorded as “−9” if this variable is not included in the data collecting procedure while coding. We do not investigate these objective criteria and remove the Doubtterr is 1 and −9.

“Unknown” data

The “unknown” rule for deleting data includes Geocoding Specificity (specificity), Attack Type (attacktype1), Weapon Type (weaptype1), Target/Victim Type (targtype1), Property Damage (property), Extent of Property Damage (propextent), City (city), Name of Entity (corp1), Perpetrator Group Name (gname), Mode for Claim of Responsibility (claimmode), Number of Perpetrators (nperps), Number of Perpetrators Captured (nperpcap), Hostages or Kidnaping Victims (ishostkid), and International-Logistical (INT_LOG).

Number of null records

Latitude (latitude), Longitude (longitude), Total Number of Fatalities (nkill), Total Number of Injured (nwound), Extent of Property Damage (propextent), Name of Entity (corp1), Hostages or Kidnaping Victims (ishostkid), and First Perpetrator Group Suspected/Unconfirmed? (guncertain1) are all included in the total number of null records.

Indicator construction

This article selects as many indicators as possible relevant to the degree of risk caused by terrorist attacks and eliminates certain factors that have no influence on the risk. Second, because the text variables’ descriptions of event characteristics are repeated in other fields, such as the event summary field, which specifies the “time, ___location, person, content, process, and purpose” of the event, these variables are mirrored in other fields. Finally, variable fields with less than 20% completeness should be removed from the GTD database. For example, the second and third weapon type field is about 98% empty. Consequently, removing this variable directly has minimal effect on the statistics. As a result, the indicator system of the risk influencing factors of terrorist attacks is obtained in Table 1.

Table 1 The indicator system of factors affecting the risk of terrorist attacks.
Full size table

Indicator correlation analysis

We conduct an independent analysis of 22 secondary indicators. The correlation analysis methods primarily comprise the Pearson coefficient, Spearman coefficient, and Kendall coefficient (FitzGerald et al., 2023). The Pearson coefficient is appropriate for indicators that follow the normal distribution. Evidently, the sample data does not follow the normal distribution. The Kendall correlation is more robust and efficient than the Spearman correlation in general. As a result, for correlation analysis, we employ the Kendall coefficient. The formula is as follows:

$$\tau =\frac{{n}_{{{c}}}-{n}_{{{d}}}}{\frac{1}{2}n(n-1)}$$
(1)

where \(\tau\) represents the Kendall correlation coefficient between the two indicators. n is the number of terrorist attacks. \({n}_{{\rm {c}}}\) and \({n}_{{\rm {d}}}\) are the number of concordant and discordant pairs. The greater the connection between the two indicators, the bigger the Spearman correlation coefficient.

Optimal weight method based on moment estimation theory

At present, the subjective weighting method primarily relies on the experience and subjectivity of experts to determine the weight and ranking of the evaluation indicators. The objective weighting method determines the weight of the indicators using a mathematical theory approach based on the relationship between the original data, which represents the link between the weight of the evaluation indicators and the change in the original data.

Based on the moment estimation theory of nine indicator-related variables, the subjective and objective weighting methods are combined to achieve the optimal weight. The method considers subjective non-negligibility of events, the internal relationship of each indicator to be assessed, and the weight gradient across time.

Subjective weighting method

Analytical hierarchy process

The analytic hierarchy process (AHP) is a method for subjectively and statistically analyzing the hierarchical nature (Cranmer et al., 2021). It divides the important decision factors into three layers: the goal layer, the criteria layer, and the scheme layer. It determines the benefits and drawbacks of the decision-making scheme based on the experienced judgment of decision-makers. This is the foundation for qualitative and quantitative analysis. The specific procedure is as follows: (i) Build a hierarchy model. (ii) Construct a judgment matrix A. (iii) Hierarchical ranking and testing for consistency. (iv) Hierarchical general ranking and consistency testing.

Order relationship analysis method

The order relationship analysis (ORA) method is a subjective weighting method based on the analytic hierarchy (Miao et al., 2011). The expert’s judgment value on the ratio of a specific indicator to the relevance of all indicators is primarily represented by assessing the elements of each row of the matrix. The specific procedure is as follows: (i) Determine the importance of each of the nine evaluation indicators. (ii) Determine the relative significance of neighboring indications. (iii) Using order synthesis, determine the structural weight of each indication.

Objective weighting method

Entropy weight method

Information entropy is a measure of information uncertainty. The entropy weight (EW) method is a weighting method that generates the indicator weight coefficient based on the effect of each indicator’s relative change degree on the overall system (Xu, 2023). The specific procedure is as follows: (i) Construct a decision matrix X. (ii) Indicator standardization: homogeneity of diverse indicators. (iii) Calculate the characteristic proportion of i evaluation object under indicator j. (iv) Determine the entropy value of indication j. (v) Calculate the coefficient of variation in indicator j. (vi) Determine the weight coefficient of indication j.

CRITIC method

Another objective weighting method for indicators is the CRITIC weight system (Wang et al., 2024). The objective weight of the indicator is determined mostly by the conflict between the contrast intensity and the evaluation indicator. The specific procedure is as follows: (i) Standardization of data Xij. (ii) Determine the linear correlation coefficient between indicators Xi and Xj. (iii) Determine the quantity of data included in indication j. (iv) Determine each indicator’s normalized weight.

Moment estimation theory

The subjective and objective weights are used to generate the optimal weight for the assessment indicators to match the higher education evaluation system (Cui et al., 2021). The subjective weight set of each indicator may be determined using a subjective weighting method based on the concept that subjective weight as

$${W}_{s}=\{{w}_{sj}|1\le s\le k,1\le j\le n\}$$
(2)

Similarly, objective weighting methods are employed to power the assessment indicator and determine the objective weight as

$${W}_{t}=\{{w}_{tj}|k+1\le t\le l,1\le j\le n\}$$
(3)

Assume that k samples are drawn from the subjective weight population and l–k samples from the objective weight population. There are l weight samples for each assessment indicator. If the relative significance coefficients of the subjective and objective weights are α and β, respectively, for the integrated combination weight of each evaluation indicator, the divergence between wj and its subjective and objective weights must be as minimal as feasible. Then the integrated combination weight optimization model is

$$\min H({w}_{j})=\alpha \mathop{\sum }\limits_{s=1}^{k}{({w}_{j}-{w}_{sj})}^{2}+\beta \mathop{\sum }\limits_{t=k+1}^{l}{({w}_{j}-{w}_{tj})}^{2}$$
(4)

where \(0\le {w}_{j}\le 1,1\le j\le n\).

The l samples are drawn from two different populations. The anticipated value of wsj and wtj for each evaluation indicator is

$$\left\{\begin{array}{c}E({w}_{sj})=\frac{\mathop{\sum }\nolimits_{s=1}^{k}{w}_{sj}}{k}\\ E({w}_{tj})=\frac{\mathop{\sum }\nolimits_{t=k+1}^{l}{w}_{tj}}{l-k}\end{array}\right.$$
(5)

Then, for each indicator, the significant coefficients of subjective and objective weights are

$$\left\{\begin{array}{c}{\alpha }_{j}=\frac{E({w}_{sj})}{E({w}_{sj})+E({w}_{tj})}\\ {\beta }_{j}=\frac{E({w}_{tj})}{E({w}_{sj})+E({w}_{tj})}\end{array}\right.$$
(6)

Similarly, using the moment estimation theory for the evaluation indicators in the multi-indicator decision matrix, we can obtain

$$\left\{\begin{array}{c}\alpha =\frac{\mathop{\sum }\nolimits_{j=1}^{n}{\alpha }_{j}}{\mathop{\sum }\nolimits_{j=1}^{n}{\alpha }_{j}+\mathop{\sum }\nolimits_{j=1}^{n}{\beta }_{j}}=\frac{\mathop{\sum }\nolimits_{j=1}^{n}{\alpha }_{j}}{n}\\ \beta =\frac{\mathop{\sum }\nolimits_{j=1}^{n}{\beta }_{j}}{\mathop{\sum }\nolimits_{j=1}^{n}{\alpha }_{j}+\mathop{\sum }\nolimits_{j=1}^{n}{\beta }_{j}}=\frac{\mathop{\sum }\nolimits_{j=1}^{n}{\beta }_{j}}{n}\end{array}\right.$$
(7)

With the aim that the less H(wj) for each evaluation indicator, the better, the optimization model indicated in Eq. (4) may be converted as

$$\begin{array}{c}{{\rm {min}}} H=\left\{H({w}_{1}),H({w}_{2}),\cdots ,H({w}_{n})\right\}\\ {\rm {s.t.}}\left\{\begin{array}{l}\mathop{\sum }\limits_{j=1}^{n}{w}_{j}=1\\ 0\le {w}_{j}\le 1,1\le j\le n\end{array}\right.\end{array}$$
(8)

To convert the multi-objective optimization model into a single-objective optimization model, the linear weighting approach with equal weights is

$$\begin{array}{c}{{\rm {min}}} H({w}_{j})=\mathop{\sum }\limits_{j=1}^{n}\alpha \mathop{\sum }\limits_{s=1}^{k}{({w}_{j}-{w}_{sj})}^{2}+\mathop{\sum }\limits_{j=1}^{n}\beta \mathop{\sum }\limits_{t=k+1}^{l}{({w}_{j}-{w}_{tj})}^{2}\\ {\rm {s.t.}}\left\{\begin{array}{l}\mathop{\sum }\limits_{j=1}^{n}{w}_{j}=1\\ 0\le {w}_{j}\le 1,1\le j\le n\end{array}\right.\end{array}$$
(9)

The optimal weight based on various subjective and objective evaluation indicators may be determined by solving Eq. (9). The importance coefficients based on the subjective and objective weights may be calculated using the model as α and β. The optimal combination of evaluation indicator weights can be determined by solving nonlinear programming.

Risk assessment model

Linear weighted evaluation model

The most widely used simple integrated evaluation model is the linear weighted evaluation (LWE) model (Hu et al., 2022), which essentially finds the weighted sum of each indicator for each terrorist attack once the indicator weights are specified. The formula is as follows:

$${f}_{i}=\mathop{\sum }\limits_{j=1}^{9}{w}_{j}{x}_{ij}(i=1,2,\cdots ,10,166)$$
(10)

where \({f}_{i}\) is the weighted comprehensive evaluation value of the ith terrorist attack.

Fuzzy comprehensive evaluation model

The fuzzy comprehensive evaluation (FCE) model is a decision-making approach that expresses evaluation outcomes using fuzzy sets. Furthermore, it can efficiently and thoroughly assess systems impacted by numerous factors by employing mathematical membership theory to convert qualitative evaluation into quantitative evaluation (Wu and Zhang, 2021). The specific procedure is as follows: (i) Determine the evaluated object’s factor set U and comment set V. (ii) Determine the membership degree vector and form the membership matrix R. (iii) Determine the evaluation indicator’s weight vector W. (iv) Synthesize the FCE model results vector. (v) Analyze the FCE model results.

TOPSIS method

The technique for order preference by similarity to ideal solution (TOPSIS) method arranges the evaluation items using the evaluation problem’s positive ideal and negative ideal solutions (Zhang et al., 2024). Positive ideal solutions are virtual best objects, and each indicator value is the best indicator value among all evaluation objects. While the virtual worst object is another virtual worst object, and each indicator value is. It is the worst value of this indication among all evaluation objects. Each assessment item is graded by its pros and drawbacks by calculating the distance between it and the positive ideal solution and the negative ideal solution. The specific procedure is as follows: (i) employ the vector programming approach to obtain the conventional decision matrix. (ii) Construct a weighted canonical matrix C. (iii) Determine the positive and negative ideal solutions. (iv) Calculate the distance between each evaluation item to the positive and negative ideal solutions. (v) Calculate the relative proximity of each evaluation item and the ideal solution (comprehensive evaluation indicator). (vi) Sort the evaluation objects by superiority and inferiority using the comprehensive evaluation indicator.

Assume that the positive ideal solution’s jth attribute value is \({c}_{j}^{+}\) and the negative ideal solution’s jth attribute value is \({c}_{j}^{-}\), then the distance between each evaluation item to the positive and negative ideal solutions is

$$\left\{\begin{array}{c}{s}_{i}^{+}=\sqrt{\mathop{\sum }\nolimits_{j=1}^{9}{({c}_{ij}-{c}_{j}^{+})}^{2}}\\ {s}_{i}^{-}=\sqrt{\mathop{\sum }\nolimits_{j=1}^{9}{({c}_{ij}-{c}_{j}^{-})}^{2}}\end{array}\right.$$
(11)

Therefore, the relative proximity of each evaluation item and the ideal solution is calculated as

$${f}_{i}=\frac{{s}_{i}^{-}}{{s}_{i}^{-}+{s}_{i}^{+}}$$
(12)

where \({f}_{i}\in [0,1]\), and when\({f}_{i}\to 1\), it indicates that the evaluation object is getting closer to the optimal level.

Particle swarm optimization projection pursuit evaluation method

The projection pursuit evaluation (PPE) method is an efficient statistical approach for dealing with multi-factor complicated problems, and it may be immediately applied to nonlinear and non-normal issues. Its primary premise is to project high-dimensional data into low-dimensional space in a certain combination, and by determining the best projection value, the evaluation value achieved is more referential. The particle swarm optimization (PSO) algorithm is primarily based on adaptive weight computation, which is integrated with the history and present ideal individual ___location, and it gradually approaches the optimal. We employ a novel algorithm, the PSO-PPE method (Du et al., 2023). This approach combines the PSO algorithm and PPE method, which not only speeds up PSO convergence but also solves the problem of discrete random variables. The specific procedure is as follows: (i) Build a linear projection function. (ii) Constructs the projected indicator function. (iii) Optimize the projection direction. (iv) Establish the solution model based on the PSO algorithm.

The objective function of the PPE method is as follows:

$$\begin{array}{c}\max Q(a)=S(a)\cdot B(a)\\ s.t.\left\{\begin{array}{l}a \,>\, 0\\ \mathop{\sum }\limits_{j=1}^{9}{a}_{j}^{2}=1,-1 <\,{a}_{j} \,<\, 1\end{array}\right.\end{array}$$
(13)
$$\left\{\begin{array}{c}S(a)=\sqrt{\frac{1}{10,165}\mathop{\sum }\nolimits_{i=1}^{10,166}{({z}_{i}-\bar{z})}^{2}}\\ B(a)=\mathop{\sum }\limits_{i=1}^{10,166}\mathop{\sum }\limits_{j=1}^{9}(R-{r}_{ij})\cdot I(R-{r}_{ij})\end{array}\right.$$
(14)

where S(a) is the sample standard deviation of the projected eigenvalue \({z}_{i}\), the larger S(a), the more evenly distributed each value is. B(a) is the local density of the projected eigenvalue. \({r}_{ij}\) is the distance between projected eigenvalues, and its value represents the degree of dispersion. The density window width parameter R has a value that depends on the sample data structure. \(I(R-{r}_{ij})\) is the unit step function.

Risk categorization model

Clustering methods

The clustering analysis approach is critical in the mining and processing of big data from terrorist attacks. The partitioning clustering, hierarchical clustering, density-based clustering, grid-based clustering, and model-based clustering are the current dominant clustering analysis approaches (Ali et al., 2023; Bhattacharyya et al., 2022; Yi et al., 2023; Yu and Gui, 2021). The findings of our investigation into the properties and applicability of different clustering approaches are listed in Table 2.

Table 2 The properties and applicability of the five clustering approaches.
Full size table

To quantitatively characterize the global terrorist attacks from 1970 through 2020, we employ the representative approaches corresponding to the five clustering models: FCM, CURE, DBSCAN, CLIQUE, and GMM.

Clustering evaluation

We evaluate five clustering effects using three internal assessment criteria: the Silhouette coefficient, the Calinski–Harabaz Index, and the Davies–Bouldin Index.

Silhouette coefficient (SC) (Peter, 1987)

For a given terrorist attack event, the SC is as follows:

$$s=\frac{b-a}{\max (a,b)}$$
(15)

where a is the mean distance to the other events in the same cluster, and b is the mean distance to the events in different clusters that are closest to it. The higher the SC, the more effective the clustering effect.

Calinski–Harabaz Index (CHI) (Caliński and Harabasz, 1974)

CHI is the ratio of the sum of squared distances between the central events of each cluster and the dataset’s central event (closeness inside a cluster) to the total of squared distances between events in a cluster and the cluster’s central event (separation of the dataset). The formula is as follows:

$$s=\frac{{{tr}}({B}_{k})}{{{tr}}({W}_{k})}\times \frac{{n}_{E}-k}{k-1}$$
(16)
$$\left\{\begin{array}{c}{W}_{k}=\mathop{\sum }\limits_{q=1}^{k}\mathop{\sum}\limits_{x\in {C}_{q}}(x-{c}_{q}){(x-{c}_{q})}^{{{T}}}\\ {B}_{k}=\mathop{\sum }\limits_{q=1}^{k}{n}_{q}({c}_{q}-{c}_{E}){({c}_{q}-{c}_{E})}^{{{T}}}\end{array}\right.$$
(17)

where Bk is the between-clusters dispersion mean and Wk is the within-cluster dispersion. Cq is the set of the terrorist attack events in cluster q, and cq is the center terrorist attack event of cluster q. CE denotes the center of cluster E. nq denotes the number of events in cluster q. The higher the CHI, the more effective the clustering effect.

Davies–Bouldin index (DBI) (Davies and Bouldin, 1979)

DBI calculates the total of the average distances within the class of any two categories divided by the distance between the two cluster centers to get the maximum value. The formula is as follows:

$${R}_{ij}=\frac{{s}_{i}+{s}_{j}}{{d}_{ij}}$$
(18)
$${{DB}}=\frac{1}{k}\mathop{\sum }\limits_{i=1}^{k}\mathop{\max }\limits_{i\ne j}{R}_{ij}$$
(19)

where si the average distance between each terrorist attack in a cluster and the cluster’s centroid. dij represents the distance between the centroids of clusters i and j. The lower the DBI, the more effective the clustering effect.

Kernel density estimation

The Kernel density estimation (KDE) is a method for investigating hotspots in space and time (Campedelli et al., 2021; Onat, 2019). It is used to determine the density of points around elements. It is believed that the probability of a specific geographic event varies depending on where it occurs in space. The kernel density estimation method was utilized to quantify the risk of terrorism in a certain area, considering the temporal and geographical patterns of the agglomeration area. Its approach is based on searching within a circle with a specified radius utilizing the center of each discrete point grid and finding the density values of the remaining grid elements. It is simply a surface interpolation method using discrete sample points. The specific procedure is as follows: (i) Create a search radius’s moving bandwidth and superimpose its center point with the centers of discrete point cells. (ii) Using the kernel density function, compute the density contribution value of each spatial point to each grid in the bandwidth. (iii) Assign a value to each grid’s density value, and that value is the sum of the contribution values of each spatial point inside the grid’s search radius to the grid density. (iv) Output the density value of each grid. The formula is as follows:

$${\hat{f}}_{h}(x)=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{K}_{h}(x-{x}_{i})=\frac{1}{nh}\mathop{\sum }\limits_{i=1}^{n}{K}_{h}\left(\frac{x-{x}_{i}}{h}\right)$$
(20)

where \({\widehat{f}}_{h}(x)\) is the probability density function for estimating kernel density; h is the bandwidth, which is a smoothing parameter; x is the sample points of terrorist attacks; \({K}_{h}\) is the Kernel function described in Silverman’s work (Kemp and Silverman, 1987).

Results

Data exploration and analysis

As seen in Fig. 1, the GTD data enables rich multidimensional exploration of patterns in terrorist attacks globally from 1970 through 2020 across dimensions like time, weapons, geography, tactics, and targets. This allows us to discern important patterns and statistics about how terrorist attacks have manifested historically. Figure 1a shows the number of attacks per year has generally increased over the 50-year period, indicating a growth in the frequency of terrorism incidents globally, with a notable upward trend starting in the early 2000s. This aligns with the shift in the global terrorism landscape following the 9/11 attacks, which marked a pivotal moment in the evolution of terrorist tactics, motivations, and geographic distribution. Figure 1b and e show that explosives, firearms, and bombings/explosions are by far the predominant weapons and tactics used by terrorists, which highlights critical vulnerabilities around systems/policies governing flows of explosive materials and arms that need to be secured. Figure 1c and d reveal that terrorist attacks have been highly concentrated in specific regions like the Middle East, South Asia, and to a lesser extent Sub-Saharan Africa, and at the country level, Iraq, Afghanistan, Pakistan and India top the list. This geographic mapping of historical hot spots is valuable for prioritizing and allocating counter-terrorism resources. Finally, Fig. 1f indicates that terrorists primarily target private citizens/property as well as military and police forces, this insight on typical targeting can inform protective measures for hardening/securing potential high-risk target sets.

Fig. 1: Multidimensional exploration and analysis of data.
figure 1

a The number of terrorist attacks per year. b Weapon type analysis. c The region where the attack occurred. d The country where the attack occurred. e Attack type analysis. f Target/victim type analysis.

Full size image

Indicator correlation analysis

Figure 2 clearly shows that the correlation between the 22 secondary indicators is extremely low, showing that the correlation is not great, and the indicators are independent of each other, indicating that the quality of the selected indicators is relatively high.

Fig. 2
figure 2

The correlation coefficient diagram of the secondary indicator.

Full size image

Optimal weight results

The significance coefficients based on the subjective weight and the objective weight may be calculated using the optimal weight method as α = 0.4711 and β = 0.5289. The optimal combination of evaluation indicator weights can be determined by solving nonlinear programming in Table 3.

Table 3 The optimal weights of nine types of variables in terrorist attacks.
Full size table

From Table 3, in the risk of terrorist attacks, Casualties and Consequences are the most important, with a weight of 38.12%. This is followed closely by the Incident Location, Perpetrator Information, and Target/Victim Information, with weights of 11.07%, 9.43%, and 9.31%, respectively. The GTD ID and date and Attack Information rank fifth and sixth, with weights of 8.35% and 7.81%, respectively. The importance of Incident Information, Additional Information and Sources, and Weapon Information are relatively low, accounting for only 6.57%, 5.70%, and 3.63%, respectively.

Top 10 riskiest terrorist attacks in the world

According to the four risk assessment models, the comprehensive score of each terrorist attack is obtained. We average the normalized comprehensive scores of the four models to acquire the overall comprehensive evaluation value, and then the overall comprehensive score is ranked from high to low in terms of risk. Simultaneously, the related incidents are treated as the same incident, and the top 10 riskiest terrorist attacks from 1970 through 2020 are listed in Table 4.

Table 4 The top 10 riskiest terrorist attacks in the world from 1970 through 2020.
Full size table

Table 4 shows that the top two are 200109110005, and 200109110004, which are the September 11 terrorist attack event with significant casualties. American Airlines Flight 11 crashed into the North Tower of the World Trade Center Complex in New York, killing approximately 3000 people. More than 16,000 others were injured. Two buildings fell, and seven others were partially damaged and collapsed. It is also widely acknowledged as the most serious event of the current terrorist attack. The remaining top 10 terrorist attacks have resulted in a great number of casualties, and the effects have left a significant impact. As a result, in some ways, it demonstrates that the top 10 riskiest terrorist attacks in the world from 1970 through 2020 we have received have a high degree of dependability.

Downward counterfactual events of the top 10 riskiest global terrorist attacks

The top 10 riskiest terrorist attacks identified in this study were significant events that resulted in substantial loss of life and property damage. However, it is crucial to recognize that these events did not occur in isolation and were often preceded by other related plots or attempts that were interdicted or failed due to various reasons (Woo, 2011). Therefore, the 10 most dangerous terrorist attack events obtained in this study can also be found through a downward counterfactual search for extreme events, as these events all generate their own accompanying set of downward counterfactuals (Woo, 2019). Thus, we conducted a Kendall correlation analysis on terrorist attacks, and obtained the highly correlated events for the top 10 riskiest global terrorist attacks in Table 4. Subsequently, based on the Incident Summary and Perpetrator Group Name in the original dataset, we identified the downward counterfactual (DC) events of the top 10 riskiest global terrorist attacks, as shown in Table 5.

Table 5 The downward counterfactual events of the top 10 riskiest global terrorist attacks.
Full size table

Table 5 presents the downward counterfactual events for the top 10 riskiest terrorist attacks globally. The downward counterfactual events refer to related plots or attempts that were interdicted or failed due to various reasons but were highly correlated with the main events in terms of their characteristics, perpetrators, or goals. The downward counterfactual events share similar characteristics with their respective main events, such as involving suicide bombings, car bombings, or attacks targeting specific locations or groups. For each of the top 10 riskiest terrorist attacks, Table 5 lists the corresponding downward counterfactual events, along with their event IDs, correlation coefficients, and brief overviews. To illustrate, we take the September 11 terrorist attack event as an example. Table 5 lists its three major related downward counterfactual (precursor) events as follows:

  1. (i)

    199808070002 (August 7, 1998)—Nairobi, Kenya, US Embassy Bombings

    This event, with a correlation coefficient of 0.9038, involved suicide attackers detonating a vehicle bomb outside the United States Embassy in Nairobi, Kenya. The attack, perpetrated by Al-Qaeda, resulted in 224 fatalities. This event demonstrated Al-Qaeda’s capability and willingness to carry out coordinated attacks against U.S. targets abroad, foreshadowing the scale of the 9/11 attacks.

  2. (ii)

    199302260001 (February 26, 1993)—World Trade Center Bombing

    With a correlation coefficient of 0.8734, this event involved a car bomb detonated by Islamist terrorists in the underground parking garage below Tower One of the World Trade Center in New York City. Although less severe than 9/11 attacks, with 6 fatalities and over 1000 injuries, this attack directly targeted the World Trade Center complex and highlighted its vulnerability to terrorist attacks. It served as a precursor to the subsequent, more devastating 9/11 attacks on the same site.

  3. (iii)

    200107240001 (July 24, 2001)—Bandaranaike International Airport Attack

    This event, with a correlation coefficient of 0.8404, involved 14 militants of the Liberation Tigers of Tamil Eelam (LTTE) launching a suicide attack on the Bandaranaike International Airport in Colombo, Sri Lanka. While not directly linked to Al-Qaeda, this attack demonstrated the use of suicide tactics and the targeting of transportation infrastructure, which were also features of the 9/11 attacks.

These precursor events share several commonalities with the 9/11 attacks, such as the involvement of Al-Qaeda or similar terrorist groups, the use of suicide tactics and vehicle bombings, and the targeting of symbols of power or transportation infrastructure. They provide insights into the evolution of terrorist strategies and capabilities leading up to the unprecedented scale and impact of the 9/11 attacks.

Risk categorization of terrorist attacks

We solve the five clustering techniques in MATLAB software while also obtaining the results of three clustering evaluation parameters for each method under varied cluster numbers and eps neighborhood (for DBSCAN) is shown in Fig. 3.

Fig. 3: Evaluation results of five clustering methods.
figure 3

a Silhouette Coefficient (SC); b Calinski–Harabasz Index (CHI); c Davies–Bouldin Index (DBI).

Full size image

From Fig. 3, we can see that the clustering effect of FCM is better when k = 4, the clustering effect of CURE is better when k = 2, and the clustering effect of CLIQUE and GMM is better when k = 3. Furthermore, the clustering effect of DBSCAN is better when ε = 0.45. We eventually select the FCM clustering approach to categorize terrorist attacks based on the five clustering methods and the outcomes of the three clustering evaluation parameters and then visualize the classification results using ArcMap 10.7 as shown in Fig. 4.

Fig. 4
figure 4

The risk categorization results of global terrorist attacks from 1970 through 2020.

Full size image

Figure 4 shows that the global distribution of terrorist attacks at various levels was unequal from 1970 through 2020. There were 412 Level-I events, with the majority taking place in the Middle East & North Africa, South Asia, Central America & Caribbean, and East Asia. 931 Level-II events occurred primarily in South Asia, Central America & Caribbean, and the Middle East & North Africa. 2224 Level-III events were mostly found in South Asia, the Middle East & North Africa, North America, and Sub-Saharan Africa. While 6599 Level-IV events were mostly concentrated in South Asia, the Middle East & North Africa, Central America & Caribbean, Southeast Asia, and Western Europe.

Spatial distribution of terrorist attacks

The kernel density estimation in the ArcGIS spatial analysis tool is used in this study to visualize the spatial and geographical distribution of global terrorist attacks. The bandwidth in Eq. (20) is 50 km, and the cell size of the output raster data is 0.005 degrees, resulting in a kernel density map of terrorist attacks in countries throughout the world from 1970 through 2020, shown in Fig. 5.

Fig. 5
figure 5

The spatial distribution of terrorist attack risk from 1970 through 2020.

Full size image

Figure 5 illustrates the spatial and geographical distribution of global terrorist attacks, which comprises four “turbulent cores” in the region of Central Asia, Middle East & North Africa, South Asia, and Central America & Caribbean.

  1. (i)

    The region of Central Asia

    The region of Central Asia, particularly Afghanistan and Pakistan, is heavily impacted by Islamic traditions. Terrorists may readily gain the sympathy of local zealots by portraying themselves as national heroes and religious apologists. Terrorist organizations such as the Taliban in Afghanistan, Al-Qaida, and the Islamic State frequently exhibit multinational and cross-border features. In this region, there are three terrible forces of ethnic separatist, religious extremism, and violent terrorism are merging and converging. Both the breadth and intensity of destruction are expanding and intensifying.

  2. (ii)

    The region of Middle East & North Africa

    The region of Middle East & North Africa concentrated on countries such as Syria, Palestine, Arab, and Israel, is one of the world’s most vital security zones. Ethnic conflicts, religious factions, border disputes, ethnic conflicts, wars here, economic backwardness, and other causes have contributed to the region’s rise in terrorism. Terrorist organizations here include the “Hamas” organization, the “Kurdistan Workers’ Party,” the Egyptian Mujahideen organization, and the Pakistani People’s Jihad organization in Palestine, which has contributed to the development of terrorism in the region globally.

  3. (iii)

    The region of South Asia

    The region of South Asia concentrated on countries such as India, Nepal, and Bangladesh, also features racial and ethnic variety, as well as a convoluted political history. For a long period during the Cold War, the region was caught in a geostrategic battle between the United States and the Soviet Union, and the ethnic question was never satisfactorily addressed. Since the Cold War’s end, the development of ethnic conflicts in South Asia has been the primary source of societal instability.

  4. (iv)

    The region of Central America & Caribbean

    The region of Central America & Caribbean concentrated on countries such as Colombia, Peru, Honduras, Nicaragua, and El Salvador. The fundamental reason is because the region has long been impoverished, the government is impotent, and numerous crimes are common. Furthermore, governmental instability, numerous criminal groups, and societal instability all have a role in the occurrence of terrorism in this region.

In addition to the four “turbulent cores”, terrorism in the past five decades has expanded globally, affecting regions such as the Americas and Europe. The “September 11” terrorist attacks took place at the World Trade Center in New York, USA. This catastrophe resulted in over 10,000 deaths, injuries, and property damages. According to a United Nations study, the terrorist assault cost the United States 200 billion yuan in economic losses.

The globalization of the international economy, politics, and social life in the 21st century has aided the growth of the global economy while also strengthening the interdependence of countries and regions, causing certain local, domestic, or regional problems to become global ones. As a result, in the context of globalization, the fundamental causes of terrorism, terrorist organizations’ activities, and the suffering caused by terrorist attacks take on a global hue. Terrorism is becoming more related to the interests of many countries and has become a global concern. Terrorism’s effects and consequences are more widespread. The interconnectedness of countries is growing, as is the relationship of interest, and the effect of terrorism is becoming more widespread.

Conclusion

This study organizes the GTD database’s recorded data from 1970 through 2020, constructs a scientific index system and analytical model, to realize the risk assessment and categorization of terrorist attacks, theoretically enriching the terrorism study material, and reaches the following conclusions:

  1. (i)

    The number of terrorist attacks has steadily increased year after year in the past five decades, with the highest frequency occurring in the Middle East & North Africa, as well as in South Asia and other regions of the world. Among the countries where the attacks occurred, Iraq had the most significant terrorist attacks, implying that most of the countries that were targeted the most were highly inhabited. The most common weapon types globally are Explosives and Firearms. Bombing/Explosion and Armed Assault are the most prevalent forms of attacks across the world, while terrorist organizations mostly target Private Citizens & Property.

  2. (ii)

    The LWE, FCE, TOPSIS, and PSO-PPE methods were utilized to assess the risk of terrorist attacks and the top 10 riskiest terrorist attacks from 1970 through 2020, represented by the September 11 terrorist attack event, and along with their downward counterfactual events. It addresses the shortcomings of previous related studies, which relied on unilateral assessments of economic losses and casualties from terrorist attacks, and the evaluation methodologies were too subjective and solitary to compare the assessment findings.

  3. (iii)

    The FCM, CURE, DBSCAN, CLIQUE and GMM, cluster analysis methods were performed for the classification of terrorist attacks, and we used three evaluation criteria, such as SC, CHI, and DBI, to evaluate the clustering effect, and the visual analysis was carried out using the KDE method. The results demonstrate that the spatial and geographical distribution of global terrorist attacks, which comprises four “turbulent cores” in the region of Central Asia, the Middle East, South Asia, Central America, and the Caribbean.

According to the research, terrorist operations are still mostly concentrated in the Middle East & North Africa, South Asia, and Sub-Saharan Africa, and these regions are primarily represented by the Islamic State as international terrorist groups. The worldwide community has been fighting the Islamic State terrorist forces together in recent years, which has degraded their influence to some extent. Under this strain, they have begun to extend outside to other regions, such as South Africa, North America, Eastern Europe, and Southeast Asia, to survive and grow their power, spreading the forces being fought, and the worldwide terrorist situation remains very critical. In this regard, we have proposed the following constructive recommendations for the four “turbulent cores” in light of the current global situation of terrorist attacks:

  1. (i)

    The region of Central Asia

    First, strengthen border security: Improve intelligence sharing and coordination among regional governments to prevent the movement of terrorists and weapons across borders. Second, invest in economic development: Create economic opportunities in impoverished areas to reduce the appeal of terrorist organizations, especially among youth. Finally, promote dialog among religious leaders: Foster an environment where religious leaders can promote peaceful interpretations of Islam and counter extremist propaganda.

  2. (ii)

    The region of Middle East & North Africa

    First, support political transitions: Encourage and support political transitions to democracy in countries experiencing conflict to reduce the grievances exploited by terrorist groups. Second, address root causes of conflict: Invest in conflict resolution initiatives to address the root causes of conflict and build peace. Finally, strengthen regional cooperation: Enhance intelligence sharing and joint military operations among regional governments to combat terrorist networks.

  3. (iii)

    The region of South Asia

    First, address governance gaps: Strengthen governance, rule of law, and provision of public services in areas with terrorist activity to build trust in government institutions. Second, invest in economic development: Focus economic development efforts on areas with high poverty and unemployment rates to address the socio-economic grievances driving terrorist recruitment. Finally, promote interfaith dialog: Encourage dialog and understanding among different religious communities to counter extremist propaganda.

  4. (iv)

    The region of Central America & Caribbean

    First, target transnational criminal networks: Strengthen law enforcement efforts to dismantle transnational criminal networks that facilitate terrorist activities. Second, address underlying socio-economic issues: Tackle underlying issues such as poverty, inequality, and lack of opportunity through targeted economic and social development programs. Finally, enhance regional cooperation: Improve coordination among regional governments on border security, intelligence sharing, and joint operations against terrorist groups.

While this study offers valuable insights into the risk assessment and categorization of terrorist attacks, it is important to acknowledge several weaknesses and limitations: (i) Although the GTD is a comprehensive dataset, it has inherent weaknesses like selection biases, underreporting, and variability in data quality across time and regions. Using just this single data source restricts the analysis. (ii) Incident-focused data: The GTD only captures details about terrorist attack incidents themselves. It lacks direct data on broader contextual factors like social, political, economic, and ideological environments that enable or constrain terrorism. Future research could explore integrating the GTD data with other structured and unstructured data sources (e.g. economic indicators, opinion polls, social media) to capture broader environmental contexts and downstream impact indicators. Exploring the use of new open-source indicators (such as GDELT, ACLED, etc.) to supplement the limited data also can be pursued, in order to conduct cross-validation and expand perspectives. Furthermore, investigating the root causes, motivations, and underlying sociopolitical dynamics behind terrorism would provide valuable insights for developing more effective counter-terrorism strategies and policies.