Introduction

Amid the increasing globalization and financialization of the world economy, capital markets have emerged as key drivers of global economic growth (Chen et al., 2022). The stock market, as a crucial component of capital markets, is widely regarded as a barometer of a nation’s economic health (Xie et al., 2021). It plays an indispensable role in facilitating capital formation, optimizing resource allocation, serving the real economy, and supporting national development (An et al., 2024). Stock prices are a direct reflection of market trends and have a profound impact on investor decision-making and government macroeconomic regulation (Li & Zhao, 2022; Shen et al., 2011). Therefore, developing effective stock price prediction methods is not only a significant research topic in academia but also an urgent need in the financial industry (Kumar et al., 2024).

The price fluctuation of stock market is affected by various external factors, such as the macroeconomic environment, corporate financial performance, and international political events, leading to highly nonlinear and chaotic characteristics in its behavior (Chen et al., 2024). Traditional statistical models, such as autoregressive moving average (ARMA), autoregressive integrated moving average (ARIMA), generalized autoregressive conditional heteroskedasticity (GARCH), and their variants, have demonstrated certain effectiveness in addressing specific financial time series problems. However, these models typically rely on assumptions such as data stationarity and linearity (Zhao et al., 2023; Lin, 2018; Mondal et al., 2014). In practice, stock market data often deviate from these assumptions, thereby limiting the applicability and performance of traditional models in complex market environments.

In recent years, machine learning methods have become mainstream tools for financial time series forecasting due to their ability to learn patterns from data without requiring strict statistical assumptions. Compared with traditional statistical approaches, machine learning exhibits superior capability in handling nonlinear data, achieving significant advancements in prediction accuracy. However, it is worth noting that these methods still face limitations in capturing long-term dependencies and local information within time series data, particularly when dealing with highly complex temporal datasets (Sharma et al., 2023; Zhou et al., 2019).

To address these challenges, researchers have further advanced deep learning techniques, particularly the long short-term memory (LSTM) network, an improved version of the recurrent neural network (RNN). LSTM has been widely applied in stock market prediction due to its powerful time series modeling capabilities, effectively capturing long-term dependencies, and has become a common approach in financial time series forecasting (Fischer & Krauss, 2018). However, despite its outstanding performance in handling temporal data, LSTM still faces challenges in extracting local feature information, mitigating data noise, and optimizing model generalization. To overcome these limitations, this study proposes a novel hybrid model, BLS-QLSTM, which combines the strengths of the broad learning system (BLS) and quantum neural networks to address the shortcomings of previous models, thereby significantly enhancing the accuracy of stock price predictions.

Inspired by chaotic time series analysis, three stock indices, CSI 300, SSEC and CSI 500, were selected as the experimental data. The Cao method and mutual information method were first employed to determine the embedding dimension and time delay of the original time series data (Zhang Shu-Qing et al., 2010), followed by phase space reconstruction. The data features were then enhanced using BLS to build a quantum long short-term memory model (QLSTM) for prediction. The effectiveness of the proposed model was validated using the above three real stock indices. The main contributions of our work can be summarized as follows:

  1. (1)

    A novel quantum neural network model, called BLS-QLSTM, is proposed for predicting financial time series data. The introduction of BLS and variational quantum circuits (VQCs) significantly improves predictive performance.

  2. (2)

    The BLS-QLSTM model utilizes the cascade structure of BLS to enhance feature representation. Additionally, it exploits the advantages of quantum properties and quantum computation by artfully integrating VQCs with LSTM, effectively mitigating the impact of data noise and rapidly extracting local temporal features.

  3. (3)

    The BLS-QLSTM model is well-suited for chaotic financial time series data prediction. Empirical analysis on CSI 300, SSEC, and CSI 500 stock indices demonstrated excellent results.

The remainder of the paper is structured as follows: “Literature review reviews” the latest research on related methods. “Preliminaries” presents the background theory, providing a brief explanation of the key techniques used in the model. “Framework of BLS-QLSTM modeling” describes the overall framework and computational process of the proposed innovative model. “Experimental results and analysis” discusses the empirical analysis results based on three real stock index datasets. Finally, “Conclusion” concludes the study.

Literature review

Stock price data is inherently high-noise, nonlinear, dynamic, and complex chaotic time series data, making stock price prediction a challenging task. In recent years, researchers have proposed various methods to address this issue, which can be broadly categorized into three types: statistical methods, machine learning methods, and deep learning methods.

Traditional statistical methods rely on systematically observing historical data, performing curve fitting, parameter estimation, and residual analysis to construct models and predict future trends. The ARIMA model, which integrates the advantages of ARMA, transforms non-stationary time series into stationary ones, making it suitable for short-term time series forecasting. Majumder et al. (2019) applied feedforward neural networks, linear models, the Holt-Winter method, and ARIMA to predict the stock index of Bangladesh, where ARIMA demonstrated the highest prediction accuracy. However, the general ARIMA model assumes residuals to be white noise, neglecting the volatility clustering characteristic, leading to the adoption of GARCH model for non-stationary time series forecasting. Lu et al. (2023) applied the GARCH type model to the Chinese nickel industry index, successfully predicting the volatility patterns of this stock index, providing valuable insights for risk management in the nickel market. Nonetheless, some researchers argue that such statistical models rely on specific assumptions and offer limited prediction accuracy, making them unsuitable for modeling and analyzing the complex, non-stationary nature of stock market data.

Machine learning methods exhibit certain advantages in handling nonlinear and non-stationary data, demonstrating strong performance in various prediction tasks, including weather forecasting (Yang et al., 2024), traffic flow prediction (Luo et al., 2023), stock price prediction, and energy prediction (Wang et al., 2023). In stock price prediction, various machine learning algorithms have been applied to real stock indices. Madge and Bhatt (2015) attempted to use support vector machine (SVM) to predict the prices of 34 technology stocks. Their study indicated that while the accuracy of short-term predictions was very low, the long-term prediction accuracy of SVM ranged between 55% and 60%. Parray et al. (2020) converted data from the National Stock Exchange of India’s 50-stock index into a time-series supervised learning format and applied algorithms such as SVM, Perceptron, and Logistic Regression to predict price trends. Compared to trend predictions using unprocessed data, this approach improved prediction accuracy by an average of 2%. Relevant research has focused on enhancing model performance through optimized feature engineering. Nahil and Lyhyaoui (2018) introduced kernel principal component analysis (KPCA) to reduce feature dimensions, integrating it with support vector regression (SVR) to improve stock price prediction. Their results showed that the SVR model with feature extraction using KPCA outperformed SVR model without feature extraction in terms of generalization performance. Yun et al. (2021) proposed using genetic algorithm (GA) as a data optimizer to select optimal features and expand the feature set, with the extreme gradient boosting (XGBoost) model serving as the primary model for stock price prediction. Statistics indicate that multiple techniques such as principal component analysis (PCA) (Chen & Hao, 2018), wavelet transform (WT) (Kao et al., 2013), and particle swarm optimization (PSO) (Rustam & Kintandani, 2019) have also been employed in preprocessing to form integrated models, enhancing the predictive performance of the original machine learning models.

In current research across various fields, employing deep learning models as benchmark methods has become a prevailing trend. Deep learning, a branch of machine learning, has achieved groundbreaking results in numerous tasks (Janiesch et al., 2021). It can identify hidden nonlinear relationships and extract relevant features from complex data without relying on manual processing or statistical assumptions, enabling efficient performance. Consequently, convolutional neural network (CNN), RNN, and LSTM have been widely applied to stock market prediction. CNN employs learnable convolutional layers and downsampling layers as core feature extractors, automatically learning effective feature representations during the training process. Persio and Honchar (2016) used a CNN which took a one-dimensional input for making predictions only based on the historical closing prices while ignoring other possible influencing variables. Ma and Yan (2022) applied CNN to predict stock price changes in the Chinese stock market, and the inclusion of social media sentiment variables effectively improved the model prediction accuracy. However, CNN is unable to use possible correlations between stock price data as a source of predictive information (Hoseinzade & Haratizadeh, 2019). In contrast, RNN and LSTM exhibit greater flexibility in terms of input-output relationships. Their network architectures have the ability to iteratively process time-series data in sequence, allowing them to learn and understand sequential patterns effectively. Rizvi and Khalid (2024) compared various models and concluded that LSTM is the most accurate and reliable model for stock price prediction. Other studies similarly indicate that the improved LSTM model, through the use of memory cells and gates, can effectively learn long-term dependencies. The model largely overcome the challenges of vanishing or exploding gradients, exhibiting superior performance in chaotic time series prediction (Md et al., 2023; Bhandari et al., 2022; Chhajer et al., 2022). However, when dealing with complex time series data, increasing the depth of LSTM network is not always an effective strategy. LSTM still faces challenges in extracting local feature information, addressing data noise, and optimizing model generalization. Jailani et al. (2023) argued that the capability of a single benchmark model is limited. Although hybrid LSTM models require longer training times, they can achieve higher prediction accuracy. The combination of intelligent algorithms or other deep learning networks with LSTM to create hybrid models has become increasingly common, yielding significant improvements (Cai et al., 2024; Yuan et al., 2023).

Quantum computing, leveraging the properties of quantum state superposition and entanglement, possesses powerful parallel computing capabilities. Current literature suggests that research on quantum models primarily focuses on three paradigms: pure quantum machine learning, quantum-inspired machine learning, and hybrid classical-quantum machine learning based on VQCs (Sergioli et al., 2019; Havlíček et al., 2019; Rebentrost et al., 2014). Among these, the use of VQCs to enhance neural networks has emerged as the mainstream development approach. Most quantum neural network models are applied in the field of cryptography (Peral-García et al., 2024; Wang et al., 2023), with only a few utilized for time series prediction. Chen et al. (2020) pioneered the QLSTM architecture, skillfully integrating VQCs with LSTM. This approach utilizes the exponentially growing dimensionality of Hilbert space for data representation and computation, showcasing the potential of hybrid quantum-LSTM models in time series forecasting. Khan et al. (2024) applied a hybrid quantum-LSTM model to forecast solar power generation, while Li et al. (2018) proposed a quantum weighted long short-term memory neural network (QWLSTMNN) for predicting the degradation trends of rotating machinery. Experimental results consistently demonstrate that neural network model incorporating VQCs address certain limitations of classical LSTM model, achieving faster convergence, improved prediction accuracy, and enhanced computational efficiency.

Additionally, BLS with its horizontal expansion capability, effectively enhances feature representation and offers advantages in efficient modeling. BLS has been widely applied across various fields, including image classification (Liu et al., 2021), feature representation (Tang et al., 2021), and fault diagnosis (Fu et al., 2022; Wang et al., 2019). Integrating BLS with other networks results in BLS variants, further improving its efficiency (Zhang et al., 2022). For chaotic time series prediction, Xiong et al. (2024) proposed a novel model based on BLS, which employs a cascade network with frozen weights to rapidly extract features from reconstructed data, thereby maximizing the preservation of chaotic properties and nonlinear relationships. Su et al. (2023) developed a new model framework, which combines the cascade structure of BLS with the attention mechanism of Transformers. This integration enhances feature representation for time series data, achieving superior prediction performance. Some researchers have also applied this approach to stock price prediction. Li et al. (2022) utilized stock price data filtered by the pearson correlation coefficient (PCC) for BLS training to enable rapid extraction of information features. Compared to various machine learning methods, the models built using BLS demonstrated superior performance and fitting capability.

Preliminaries

Phase space reconstruction

Stock data exhibits characteristics of nonlinearity, non-stationarity and high noise, which have been confirmed to be a time series with chaotic properties. The theory of phase space reconstruction (PSR) illustrates the interdependence among the evolution of each component of the system state. The method is based on Takens’ embedding theorem, which states that to ensure the phase space in which the attractor is embedded must reach \(m\ge 2d+1\) if the original attractor resides in an a d-dimensional space (Takens, 1981). It can be further explained that when mapping a one-dimensional chaotic time series from a real-world problem to a higher-dimensional space, the dimensionality of the higher-dimensional space must be greater than or equal to 3 in order to effectively represent the original dynamical system information. For a certain observed time series \(\{x(t),t=1,2,\cdots ,N\}\), once the embedding dimension m and time delay τ are determined, the phase point sequence after phase space reconstruction is given as Eq. (1).

$$X(t)=(x(t),x(t-\tau ),\cdots ,x(t-(m-1)\tau ))$$
(1)

Where \({t}_{i}={N}_{1},{N}_{1}+1,\cdots ,N\); \({N}_{1}=1+(m-1)\tau\). This reconstructed time series can be further defined as {X, Y}, as shown in Eqs. (2) and (3).

$$X=\left[\begin{array}{cccc}x({t}_{1}) & x({t}_{1}-\tau ) & \cdots & x({t}_{1}-(m-1)\tau )\\ x({t}_{2}) & x({t}_{2}-\tau ) & \cdots & x({t}_{2}-(m-1)\tau )\\ \vdots & \vdots & \vdots & \vdots \\ x({t}_{p}) & x({t}_{p}-\tau ) & \cdots & x({t}_{p}-(m-1)\tau )\end{array}\right]$$
(2)
$$Y={[\begin{array}{c}x({t}_{1}+1),x({t}_{2}+1),\cdots ,x({t}_{p}+1)\end{array}]}^{T}$$
(3)

Where the embedding dimension m and time delay τ, calculated using the Cao method and the mutual information method, p correspond to the number of samples. In the reconstructed phase space trajectory, each phase point exists a smooth mapping \({\mathcal F} :{R}^{m}\to R\), denoted as \(Y= {\mathcal F} (X)\), which can then be approximated by building a deep learning model to obtain the mapping \({\mathcal F}\).

Broad learning system

The broad learning system, an enhancement of the random vector functional-link neural network (RVFLNN) (Pao et al., 1994), is an incremental learning method that does not require a deep architecture. The structure of BLS is shown in Fig. 1. BLS exhibits strong generalization capabilities and allows for quick reconfiguration of the network without requiring retraining if expansion is needed (Han et al., 2021). Moreover, its computational speed surpasses that of deep networks. For datasets with limited features and stringent real-time prediction demands, BLS can effectively enhance prediction accuracy through transversal incremental expansion, which enhances feature expression. The specific operation process of BLS is as follows.

Fig. 1: The structure of BLS.
figure 1

BLS is an efficient incremental learning system that does not require deep structures. It initially maps input data to the mapping layer, followed by the augmentation layer. The output layer is connected to both the augmentation and mapping layers.

Full size image

In the initial step, input data \(X\)\((X\in {R}^{p\times m})\) to n mapped node groups (each group has q mapped features), then the mapped feature of the i-th group of mapped nodes is defined as Eq. (4).

$${Z}_{i}=\phi (X{W}_{ei}+{\beta }_{ei}),i=1,\cdots ,n$$
(4)

Where Wei and βei represent randomly generated weights and bias, respectively. ϕ(*) is the activation function of the mapped layer.

In the subsequent step, these mapped features \({Z}_{1},{Z}_{2},\cdots ,{Z}_{n}\) are multiplied by a set of random weights plus the bias and processed with the activation function to create enhanced nodes, denoted as \({H}_{1},{H}_{2},\cdots ,{H}_{m}\), as shown in Eq. (5).

$${H}_{j}=\xi ({Z}_{i}{W}_{hj}+{\beta }_{hj}),i=1,\cdots ,n,j=1,\cdots ,m$$
(5)

Where \({W}_{hj}\) and \({\beta }_{hj}\) represent randomly generated weights and bias, respectively. \(\xi (\ast )\) is the activation function of the enhanced layer.

In the final step, \({Z}_{1},{Z}_{2},\cdots ,{Z}_{n}\) merge with \({H}_{1},{H}_{2},\cdots ,{H}_{m}\) to obtain the enhanced data features, denoted as Eq. (6).

$$A=[Z|H]=[{Z}_{1},\cdots ,{Z}_{{\rm{n}}}|{H}_{1},\cdots ,{H}_{m}]$$
(6)

Meanwhile, the output data of BLS is \(Y=A{W}_{out}\), where \({W}_{out}\) is the weight matrix that needs to be optimized and can be computed through the pseudoinverse.

Variational quantum circuit

Variational quantum circuit (VQC), also known as parameterized quantum circuit, is a kind of quantum gate circuit with free parameters, which is the main part of the quantum computation model. The main process of quantum computing involves using a series of quantum gates to modify the state of qubits (quantum bits, the fundamental units of quantum information), followed by measuring the computation results at the end of the circuit. The structure of the VQC is shown in Fig. 2, which consists of three parts: the encoding layer, the variational layer, and the measurement layer.

Fig. 2: The structure of VQC.
figure 2

VQC is a kind of quantum gate circuit with free parameters. It consists of three main components: the encoding layer, the variational layer, and the measurement layer.

Full size image
  1. (1)

    Encoding layer: classical data is encoded into quantum states and loaded into quantum circuit by changing the states in which the qubits are by \(H\) gate, \({R}_{y}\) gate, and \({R}_{z}\) gate. This study utilizes angle encoding, which demonstrates superior performance compared to base-state encoding and amplitude encoding. Moreover, the method of angle encoding is simpler. Initially, the \(H\) gate transforms the initialized quantum state into an entangled state. Subsequently, classical information \(\overrightarrow{x}={({x}_{1},{x}_{2},\cdots ,{x}_{N})}^{T}\) is applied to the parameters of the rotation gate \({R}_{y}\) and \({R}_{z}\), ultimately converted into a quantum state \(|\overrightarrow{x}\rangle ={\otimes }_{i}^{n}R(\arctan (\theta ))|{0}^{n}\rangle\), where \(\theta ={x}_{i}\) in the rotating gate \({R}_{y}\) and \(\theta ={x}_{i}^{2}\) in the \({R}_{z}\).

  2. (2)

    Variational layer: using multiple \(CNOT\) gates and R gates, these qubits are entangled and rotated to the target state. The parameters of the VQC optimization update are derived from the 3 rotation angles α, β, and γ of the R gate of the variational layer along the x, y, and z axes, respectively, which are iteratively optimized by the gradient descent method.

  3. (3)

    Measurement layer: set at the end of VQC, its main purpose is to measure the expectation value of each qubit by Pauli Z to realize the transformation of quantum information into classical information.

Long short-term memory

RNN is known to suffer from the gradient vanishing or exploding problem and is limited in its capacity to store long-term effective information. To address these issues, Hochreiter and Schmidhuber jointly proposed LSTM in 1997. LSTM builds upon the foundational structure of RNN by incorporating a gating mechanism that controls the information transmission path within the network, thereby enabling the selective forgetting or retention of information (Hochreiter & Schmidhuber, 1997). This functionality has made LSTM extensively applicable in various fields such as natural language processing and time series prediction. In the forward transfer learning process of LSTM, the architecture comprises four crucial components: the forget gate, input gate, output gate, and the cell state, as depicted in Fig. 3. The specific transfer formulas are shown in Eqs. (7)–(12).

$${f}_{t}=\sigma ({W}_{f}\cdot [{h}_{t-1},{x}_{t}]+{b}_{f})$$
(7)

Where \(\sigma\) is the activation function; \({W}_{f}\) is the weight matrix; \({b}_{f}\) is the bias vector; \({f}_{t}\) represents the output of the forgetting gate, whose main purpose is to control whether the state of the memory unit at the previous moment needs to be forgotten or not. The output range is [0,1].

$${i}_{t}=\sigma ({W}_{i}\cdot [{h}_{t-1},{x}_{t}]+{b}_{i})$$
(8)
$$\tilde{{C}_{t}}=\,\tanh\, ({W}_{c}\cdot [{h}_{t-1},{x}_{t}]+{b}_{c})$$
(9)

Where \({W}_{i}\) represents the input matrix; \({W}_{c}\) represents the state matrix; \({i}_{t}\) represents the input gate output, \(\tilde{{C}_{t}}\) represents the temporary state of the memory cell at the current moment. The input gate portion is mainly used to control the extent to which new information is updated by the memory cell.

$${C}_{t}={f}_{t}\circ {C}_{t-1}+{i}_{t}\circ \tilde{{C}_{t}}$$
(10)

Where \({C}_{t}\) is the state output of the current memory cell, which is the superposition of the information of the previous moment and the new information of the current moment.

$${O}_{t}=\sigma ({W}_{o}\cdot [{h}_{t-1},{x}_{t}]+{b}_{o})$$
(11)
$${h}_{t}={O}_{t}\circ \,\tanh ({C}_{t})$$
(12)

Where \({W}_{o}\) is the output matrix, \({b}_{o}\) is the bias vector and \({h}_{t}\) is the hidden state at the current time step.

Fig. 3: The structure of LSTM.
figure 3

LSTM has a chain-like structure with a repeating module. This module consists of four interacting neural network layers, designed in a very special way to manage and maintain long-term dependencies in the data.

Full size image

Framework of BLS-QLSTM modeling

Motivation for modeling

Chaotic time series are different from general time series. In order to recover their original dynamical system, phase space reconstruction is required to map them into a high-dimensional space. However, traditional deep learning models might encounter the curse of dimensionality with increasing data dimensions. In contrast, the capabilities of BLS and VQC can effectively mitigate this issue and enhance model performance.

  1. (1)

    Enhanced feature representation by BLS: BLS employs a simple cascade structure that facilitates information reuse and enriches feature representation. The approach avoids the complex residual connections typical in deep learning models while preserving the integrity of the original information.

  2. (2)

    Quantum State Representation and Quantum Parallel Computing: VQC introduces quantum state representation of the original data, which is instrumental in capturing the microstate of chaotic system. Moreover, VQC leverages the inherent parallelism of quantum computing, enabling more efficient handling of high-dimensional data. It achieves parallel computing through quantum superposition, significantly enhancing the learning capabilities of the model.

Architecture of the QLSTM model

QLSTM is an innovative model that integrates VQCs with classical LSTM network. The QLSTM architecture, as proposed by Chen et al., which comprises six VQC blocks. Experimental results had demonstrated that the hybrid quantum-classical LSTM model not only learns faster but also achieves more stable convergence (Chen et al., 2020). Building on this foundation, Cao et al. (2023) introduced a linear-enhanced quantum LSTM model (L-QLSTM), which added a shared linear embedding layer prior to each VQC within the standard QLSTM framework. This addition enhanced the quantum benefits, improving model learning performance and the accuracy of carbon price predictions. Numerous studies have proved that the introduction of VQCs is beneficial to the performance of classical neural networks. In the study, four VQCs are strategically employed to replace the gates in the recurrent unit of the LSTM network, instead of using the traditional weight matrix. The modification facilitates the construction of a new QLSTM model, whose architecture is illustrated in Fig. 4. The specific operational formula for the QLSTM is provided in Eq. (13).

$$\left\{\begin{array}{ll}{f}_{t}=\sigma (VQ{C}_{1}\cdot [{h}_{t-1},{x}_{t}]+{b}_{f})\\ {i}_{t}=\sigma (VQ{C}_{2}\cdot [{h}_{t-1},{x}_{t}]+{b}_{i})\\ \tilde{{C}_{t}}=\,\tanh (VQ{C}_{3}\cdot [{h}_{t-1},{x}_{t}]+{b}_{c})\\ {C}_{t}={f}_{t}\circ {C}_{t-1}+{i}_{t}\circ \tilde{{ll}_{t}}\\ {O}_{t}=\sigma (VQ{C}_{4}\cdot [{h}_{t-1},{x}_{t}]+{b}_{o})\\ {h}_{t}={O}_{t}\circ \,\tanh ({C}_{t})\end{array}\right.$$
(13)
Fig. 4: The architecture of proposed QLSTM.
figure 4

The QLSTM model integrates Variational Quantum Circuits (VQC) with classical LSTM. In this model, VQCs replace the traditional gates and cell state operations of the LSTM, enhancing the network’s performance and stability.

Full size image

Architecture of the BLS-QLSTM model

Based on the preceding analysis, it is evident that the cascade structure of BLS enhances the feature representation of time series data, while VQC leverage the properties of quantum superposition and entanglement to enhance the learning capabilities of the model through parallel computing. Theoretically, it is feasible to integrate these two approaches to develop a BLS-QLSTM model for predicting chaotic time series. This model would combine the strengths of both components to significantly improve prediction accuracy.

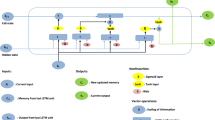
Consequently, this paper proposed a hybrid quantum neural network model, the BLS-QLSTM model, whose framework is depicted in Fig. 5. The model is structured into three primary components: first, the phase space reconstruction module, which reconstructs the phase space of chaotic time series to restore the original dynamical system and convert it into predictable data; second, the broad learning module, where the acquired data is expanded into high-dimensional space through the cascade structure of BLS via random mapping; and third, the VQCs incorporation module, namely, it is the QLSTM module that uses the VQCs to replace the LSTM network gates and memory units in the loop, instead of the original weight matrix, QLSTM then predicts the input data. The operational workflow of the BLS-QLSTM model is detailed as follows:

Fig. 5: The framework of proposed BLS-QLSTM.
figure 5

The BLS-QLSTM model is an innovative composite prediction framework, consisting of three main components: phase space reconstruction, broad learning, and VQCs integration.

Full size image

Step 1: Phase Space Reconstruction (PSR)

For the input original one-dimensional time series data \({x}_{t}\), phase space reconstruction is performed to obtain multidimensional data. Assuming embedding dimension \(m\) and time delay \(\tau\), the phase space reconstructed data \({X}_{t}\) is defined as Eq. (14).

$${X}_{t}=PSR({x}_{t})=[{x}_{t},{x}_{t-\tau },\cdots ,{x}_{t-(m-1)\tau }]$$
(14)

Step 2: Broad Learning System (BLS)

  1. (1)

    Mapped node: define the output \({H}_{i}\) of the mapped node \(i\) as Eq. (15).

    $${H}_{i}=\phi ({W}_{i}{X}_{t}+{b}_{i})$$
    (15)

    Where \({W}_{i}\) and \({b}_{i}\) are the weight and bias of the \(i\)-th mapped node, respectively. \(\phi (\ast )\) is the activation function.

  2. (2)

    Enhanced node: define the output \({E}_{j}\) of the enhanced node \(j\) as Eq. (16).

    $${E}_{j}=\xi ({V}_{j}H+{c}_{j})$$
    (16)

    Where \({V}_{j}\) and \({c}_{j}\) are the weight and bias of the jth mapped node, respectively. \(\xi (\ast )\) is the activation function.

  3. (3)

    Feature merging: merge the outputs of all mapped and enhanced nodes to obtain the output \(F\) of BLS as shown in Eq. (17).

$$F=[{H}_{1},\cdots ,{H}_{{\rm{n}}}|{E}_{1},\cdots ,{E}_{m}]$$
(17)

Step 3: Data Fusion

Splicing and fusing the phase space reconstructed data \({X}_{t}\) with the output of BLS \(F\) to get the multidimensional features to \({Z}_{t}\) in Eq. (18).

$${Z}_{t}=[F|{X}_{t}]$$
(18)

Step 4: QLSTM network prediction

Process the final input data \({Z}_{t}\) using QLSTM to obtain the predicted output \({y}_{t}\) in Eq. (19).

$${y}_{t}=QLSTM({Z}_{t},{h}_{t-1},{C}_{t-1})$$
(19)

Where \({h}_{t-1}\) and \({C}_{t-1}\) represent the QLSTM hidden state and cell state at the previous moment, respectively.

Experimental results and analysis

Data sources

The research objects selected for this paper are three representative stock indices in China: the CSI 300 Index (CSI 300, Index code: 000300), the SSE Composite Index (SSEC, Index code: 000001), and the CSI Smallcap 500 Index (CSI 500, Index Code: 000905), whose time series data are the daily closing prices from January 4, 2013 to December 29, 2023, excluding holidays. Each index has a total of 2,672 data points, which were retrieved from the official Investing website (https://cn.investing.com). The closing price data for these indices are illustrated in Fig. 6, while the statistical description are presented in Table 1.

Fig. 6: Closing price data for stock indices.
figure 6

A graphical representation of the original data for three stock indices: CSI 300 Index, SSEC Index, and CSI 500 Index.

Full size image
Table 1 Statistical description of the closing price data for stock indices.
Full size table

Data processing

Phase space reconstruction of data

The closing price data of the three selected stock indices, CSI 300, SSEC, and CSI 500, have no outliers or missing values. Initially, we employ the Cao method and mutual information method to ascertain the embedding dimension \(m\) and time delay \(\tau\) for each stock index, which are the key parameters for the phase space reconstruction of the data. After calculation, the time delay of the closing price data of the CSI 300 index is \(\tau =16\) and the embedding dimension is \(m=7\); the time delay of the closing price data of the SSEC index is \(\tau =20\) and the embedding dimension is \(m=6\); the time delay of the closing price data of the CSI 500 index is \(\tau =25\) and the embedding dimension is \(m=8\). The time delay \(\tau\) and embedding dimension \(m\) of each stock index data are known, the following phase space reconstruction is performed to recover the original dynamical system information, which helps the short-term prediction of stock index data.

As outlined in “Phase Space Reconstruction”, phase space reconstruction involves converting original one-dimensional time series data into a multidimensional state space. This transformation enables a more profound comprehension of the dynamical characteristics and underlying patterns of the data. After phase space reconstruction, the one-dimensional closing price data of CSI 300 index is reconstructed into a two-dimensional matrix data of 2576 × 7; the one-dimensional closing price data of SSEC index is reconstructed into a two-dimensional matrix data of 2572 × 6; and the one-dimensional closing price data of CSI 500 index is reconstructed into a two-dimensional matrix data of 2497 × 8.

Broad learning of data

Instead of training layer by layer like a deep network structure, BLS uses a cascade structure to quickly learn and expand the feature data. The parameters within the BLS used in this paper are set as follows: the mapped node in the mapped layer is map_num=3, the mapped feature is map_fea_num=2, the enhanced node is enh_num=1 and the enhanced feature is enh_fea_num=10. The feature data obtained from the phase space reconstruction of each stock index is further processed by broad learning as a way to expand the dimension of the features. Finally, the feature data of each stock index is expanded to 16 dimensions.

Data fusion and standardization

In the further analysis process, the feature data derived from phase space reconstruction is concatenated and integrated with the expanded feature data from broad learning. The approach horizontally combines the feature sets obtained from both methods. This way not only increases the dimensionality of the data but also merges information extracted from diverse perspectives, enhancing the expressiveness and accuracy of the final model.

To ensure equitable comparisons among different stock indices and to augment the performance of subsequent models, it is imperative to standardize the fused data. Standardization, a pivotal data preprocessing technique, rescales the data values to achieve a mean of 0 and a standard deviation of 1. This process helps to eliminate the differences in the magnitude of the data, making the learning process more efficient during model training. The standardized formula is Eq. (20).

$${X}_{std}=\frac{X-\mu }{\sigma }$$
(20)

Where \(X\) represents the fused stock index data, \({X}_{std}\) denotes the standardized data. \(\mu\) and σ are the mean and standard deviation of the original data, respectively.

Furthermore, in order to revert the data to its original scale, the output predictions must also undergo inverse standardization, as depicted in Eq. (21).

$$\widehat{y}={X}_{std}\cdot \sigma +\mu$$
(21)

Where \(\hat{y}\) indicates the predicted value post-output and inverse standardization by the QLSTM neural network.

Experimental environment and parameter settings

The processor of the experimental environment in this paper is 12th Gen Intel(R) Core(TM) i5-12500H, the operating system is Windows 11 (64-bit), the deep learning development environment is Pytorch 2.0.1+cpu, and the Python version is 3.10.

In order to verify the predictive ability of the constructed BLS-QLSTM model, this paper selects three real stock index data of the CSI 300 index, SSEC index, and CSI 500 index for experiments and compares the errors with the QLSTM model without introducing BLS as well as the single model LSTM. Due to the chaotic nature of stock index data, the original one-dimensional closing price data must be input after phase space reconstruction. The key parameters in this phase of phase space reconstruction are the embedding dimension \(m\) and the time delay \(\tau\), which can be determined by the Cao method and the mutual information method, respectively, as shown in Table 2. The parameter settings for BLS are shown in Table 3.

Table 2 Main parameter settings of PSR.
Full size table
Table 3 Main parameter settings of BLS.
Full size table

Given the modest dataset size, comprising only 2672 data points per stock index and the relatively low task complexity, thus a single-layer QLSTM was employed. Through continuous trial and error experiments and analyses, the data batch size is 1, the number of iterations is 20, the learning rate is 0.0004. The number of layers of LSTM is also 1 with 16 neurons in a single layer, and the learning rate is 0.00007. All models choose the Adam optimization algorithm for weight and bias adjustments, and use MSE as the loss function. The data partitioning strategy allocates 75% of the samples to training and the remaining 25% to testing.

In the stock index prediction experiment, the labels of up or down were generated based on the percentage change in the daily closing price, setting a threshold of 1%. If the daily price change exceeds 1%, it is labeled as “up”; if the decrease exceeds 1%, it is labeled as “down”; otherwise, it is considered stable. To concentrate on the capacity of models to predict significant movements in different stock indices, the “stable” data points were filtered out, ensuring that the analysis centered on clear upward and downward trends in the indices. Subsequently, the predicted daily closing prices of the model were compared with the actual prices from the previous day to generate up or down prediction labels, and these predictions were analyzed in comparison with the actual outcomes.

Evaluation indicators

In order to explore the accuracy of models, the root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and coefficient of determination (R2) are selected as prediction evaluation indices in this paper to evaluate and compare the predictive effect of models. Additionally, two categorical evaluation metrics, precision and accuracy, were introduced to measure the performance of models in predicting the direction of stock price movements.

  1. 1.

    The formulas for the selected forecasting metrics are as follows as Eqs. (22)–(25).

$$RMSE=\sqrt{\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{({\hat{y}}_{i}-{y}_{i})}^{2}}$$
(22)
$$MAE=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}|\widehat{{y}_{i}}-{y}_{i}|$$
(23)
$$MAPE=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}|\frac{{y}_{i}-\widehat{{y}_{i}}}{{y}_{i}}|$$
(24)
$${R}^{2}=1-\frac{\mathop{\sum }\limits_{i=1}^{n}{(\begin{array}{c}{y}_{i}-\widehat{{y}_{i}}\end{array})}^{2}}{\mathop{\sum }\limits_{i=1}^{n}{(\begin{array}{c}{y}_{i}-\overline{{y}_{i}}\end{array})}^{2}}$$
(25)

In the above formulas, \(\widehat{{y}_{i}}\) is the predicted value, \({y}_{i}\) is the true value, \(\overline{{y}_{i}}\) is the sample mean, \(n\) is the number of samples. Among them, RMSE, MAE, MAPE measure the deviation between the predicted value and the real value. Lower values of these metrics indicate reduced prediction errors, thereby reflecting greater accuracy in the results. The coefficient of determination, R2, when approaching 1, indicates a higher degree of model fit, signifying that the predicted values closely align with the real observations, thereby denoting superior model performance.

2. The formulas for the selected classification indicators are shown in Eqs. (26)–(27).

$$Precision=\frac{TP}{TP+FP}$$
(26)
$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$
(27)

In the aforementioned formulas, TP represents true positives, referring to the number of samples correctly predicted as positive by the model; FP denotes false positives, indicating the number of samples incorrectly predicted as positive by the model; TN stands for true negatives, representing the number of samples correctly predicted as negative; and FN signifies false negatives, referring to the number of samples incorrectly predicted as negative. Precision measures the proportion of true positives among all samples predicted as positive, with a higher value indicating greater reliability of the model in predicting positive cases. Accuracy, on the other hand, assesses the overall predictive accuracy of the model, defined as the proportion of correctly predicted samples out of the total number of samples, with a higher value indicating better overall model performance.

BLS-QLSTM, QLSTM and LSTM comparison experiments

In this section, we conduct experimental comparisons using data from three major stock indices—CSI 300, SSEC, and CSI 500—to thoroughly analyze the predictive performance of three models: LSTM, QLSTM, and BLS-QLSTM. The experiments are primarily evaluated along two dimensions: one focuses on the analysis of forecasting evaluation metrics, while the other centers on the analysis of classification evaluation metrics. Stock index price forecasting is fundamentally a time series prediction problem, typically analyzed using forecasting evaluation metrics. However, in practical applications, investors are concerned not only with the accuracy of price forecasting but also with the ability of models to predict market trends. Therefore, we introduce classification evaluation metrics to comprehensively assess the performance of the proposed model across different stock index datasets.

Experimental results of CSI 300 based on various models

(1) Prediction Evaluation Metrics Results

The BLS-QLSTM model performs best on all four evaluation metrics selected for forecasting the CSI 300 index (See Table 4). Compared to the traditional LSTM model, the BLS-QLSTM achieved a 21.6% reduction in RMSE and demonstrated a 6.3% improvement over the QLSTM model, underscoring its significant advantage in accurately capturing market dynamics. The reduction in MAE further confirms the effectiveness of BLS-QLSTM in minimizing prediction bias, while its robust performance in MAPE highlights the precision of model in reflecting stock market volatility. Additionally, the R2 value increased to 0.99570, indicating a high degree of fit in modeling the overall trend of the stock index. The forecasting results of CSI 300 and the overall model presentation are shown in Fig. 7.

Table 4 Prediction Evaluation Metrics for CSI 300 Index Across Different Models.
Full size table
Fig. 7: The forecasting results of CSI 300 and the overall model presentation.
figure 7

A graphical representation of the forecasting result of the CSI 300 Index using three models: LSTM, QLSTM, and BLS-QLSTM.

Full size image

(2) Classification Evaluation Metrics Results

The classification prediction results for the upward and downward trends of the CSI 300 index demonstrate that the BLS-QLSTM model achieved the best performance in both precision and accuracy metrics (See Table 5). Specifically, the precision of the BLS-QLSTM model reached 0.72505, which is significantly higher than the 0.52401 of the LSTM model and the 0.53579 of the QLSTM model. This indicates that the BLS-QLSTM model has superior accuracy in predicting market uptrends. Additionally, the accuracy of the BLS-QLSTM model was 0.72865, representing an improvement of 23 percentage points compared to the 0.49708 of the LSTM model and an increase of 22 percentage points compared to the 0.51111 of the QLSTM model. These results suggest that the BLS-QLSTM model offers greater reliability and stability in overall trend prediction. A comparison of the confusion matrices for the classification results of the CSI 300 index is illustrated in Fig. 8.

Table 5 Classification Evaluation Metrics for CSI 300 Index Across Different Models.
Full size table
Fig. 8: CSI 300 Index Confusion Matrix Comparison.
figure 8

Visualization of the confusion matrix comparison for predicting the CSI 300 Index’s up and down movements based on LSTM, QLSTM, and BLS-QLSTM models. a LSTM Confusion Matrix; b QLSTM Confusion Matrix; c BLS-QLSTM Confusion Matrix.

Full size image

Experimental results of SSEC based on various models

(1) Prediction Evaluation Metrics Results

The BLS-QLSTM model continues to maintain its leading position in the SSEC forecasting analysis (See Table 6), with a significant reduction in RMSE, being 23.3% lower than that of the LSTM model and 13.3% lower than that of the QLSTM model. This reduction demonstrates the remarkable ability of the model to synthesize market information and enhance the quality of forecasts. The performance of the model on the MAE metric underscores its robustness in reducing mean errors, while the slight variations in the MAPE metric remain within a reasonable range, showcasing the adaptability of the model to specific market conditions. The improvement in the R2 metric to 0.99344 further validates the explanatory power of the BLS-QLSTM model and confirms its utility in market forecasting practice. The forecasting results of SSEC and the overall model presentation are shown in Fig. 9.

Table 6 Prediction Evaluation Metrics for SSEC Index Across Different Models.
Full size table
Fig. 9: The forecasting results of SSEC and the overall model presentation.
figure 9

A graphical representation of the forecasting result of the SSEC Index using three models: LSTM, QLSTM, and BLS-QLSTM.

Full size image

(2) Classification Evaluation Metrics Results

In the classification prediction of the SSEC trend, the performance of different models is presented in Table 7. It is evident that the BLS-QLSTM model significantly outperforms the LSTM and QLSTM models in both precision and accuracy, which are two critical metrics. Specifically, in the SSEC trend classification prediction experiment, the BLS-QLSTM model achieved a precision of 0.82102, compared to 0.55789 and 0.53257 for the LSTM and QLSTM models, respectively. Additionally, the BLS-QLSTM model also attained an accuracy of 0.78933, whereas the LSTM and QLSTM models recorded accuracies of 0.53371 and 0.52809, respectively. These results indicate that the BLS-QLSTM model offers higher accuracy and reliability in classifying the SSEC trend, effectively identifying market changes and reducing the occurrence of misclassifications. A comparison of the confusion matrices for the classification results of the SSEC index is shown in Fig. 10.

Table 7 Classification Evaluation Metrics for SSEC Index Across Different Models.
Full size table
Fig. 10: SSEC Index Confusion Matrix Comparison.
figure 10

Visualization of the confusion matrix comparison for predicting the SSEC Index’s up and down movements based on LSTM, QLSTM, and BLS-QLSTM models. a LSTM Confusion Matrix; b QLSTM Confusion Matrix; c BLS-QLSTM Confusion Matrix.

Full size image

Experimental results of CSI 500 based on various models

(1) Prediction Evaluation Metrics Results

The experimental results of the CSI 500 index highlight the superiority of the proposed BLS-QLSTM model for complex financial data processing (See Table 8). Its RMSE decreases by 36.5% compared to the LSTM model and 19.8% compared to the QLSTM model, this significant reduction not only shows the absolute advantage of the model in reducing the prediction error, but also highlights its insight in mastering the chaotic attributes of the financial market. The significant improvement in MAE and MAPE further confirms the stability and reliability of the BLS-QLSTM model in maintaining the prediction accuracy. The significant improvement in MAE and MAPE further confirms the stability and reliability of the BLS-QLSTM model in maintaining forecast accuracy, and the significant improvement in the R2 of the BLS-QLSTM model to 0.99404 demonstrates the high ability to capture the intrinsic dynamics of the data. The forecasting results of CSI 500 and the overall model presentation are shown in Fig. 11.

Table 8 Prediction Evaluation Metrics for CSI 500 Index Across Different Models.
Full size table
Fig. 11: The forecasting results of CSI 500 and the overall model presentation.
figure 11

A graphical representation of the forecasting result of the CSI 500 Index using three models: LSTM, QLSTM, and BLS-QLSTM.

Full size image

(2) Classification Evaluation Metrics Results

In the classification prediction experiment for the CSI 500 Index trend, the BLS-QLSTM model once again demonstrated its superior performance (See Table 9). From the perspective of two key classification metrics, precision and accuracy, the BLS-QLSTM model significantly outperformed the LSTM and QLSTM models. Specifically, the BLS-QLSTM model achieved a precision of 0.80079, which is considerably higher than the 0.53047 and 0.55935 recorded by the LSTM and QLSTM models, respectively. Moreover, the BLS-QLSTM model also surpassed the other two models in accuracy, reaching 0.77545, showcasing the exceptional capability of the model in accurately classifying the market trends of the CSI 500 Index. A comparison of the confusion matrices for the classification results of the CSI 500 index is shown in Fig. 12.

Table 9 Classification Evaluation Metrics for CSI 500 Index Across Different Models.
Full size table
Fig. 12: CSI 500 Index Confusion Matrix Comparison.
figure 12

Visualization of the confusion matrix comparison for predicting the CSI 500 Index’s up and down movements based on LSTM, QLSTM, and BLS-QLSTM models. a LSTM Confusion Matrix; b QLSTM Confusion Matrix; c BLS-QLSTM Confusion Matrix.

Full size image

Conclusion

Developing efficient and accurate stock price prediction models has long been a central focus in financial research. Previous studies such as Lin (2018) and Mondal et al. (2014) have indicated that statistical models such as ARIMA and GARCH possess certain short-term forecasting capabilities, but they typically rely on assumptions of linearity and stationarity, limiting their adaptability to chaotic financial time series. While machine learning methods exhibit advantages in handling nonlinear relationships, they often fall short in capturing long-term dependencies within time series data and show limited modeling capacity for high-dimensional datasets. In recent years, mainstream studies have increasingly adopted deep learning models such as LSTM to improve the accuracy of time series forecasting. However, challenges remain, including insufficient extraction of local features and weak noise resistance. These limitations suggest that relying solely on a single model is inadequate to fully exploit the complex intrinsic structure of stock index data. Accordingly, we attempt to reform the traditional LSTM and propose a hybrid quantum neural network model, BLS-QLSTM, which incorporates modular design and technological integration to achieve multidimensional enhancements in feature extraction, prediction accuracy, and model robustness.

The BLS-QLSTM model is composed of three main modules: the phase-space reconstruction module, the BLS module, and the QLSTM module. The phase-space reconstruction module employs embedding dimension and time delay techniques to reconstruct chaotic time series data, extracting latent dynamic features and enhancing the nonlinear representational capacity of the data, thus providing higher-quality inputs for subsequent modeling. The BLS module utilizes a cascade structure for efficient feature expansion, enriching stock indices prediction feature space with accurately enhanced features in high-dimensional space, significantly improving the model’s generalization ability. The QLSTM module integrates the parallelism of quantum computing, offering robust noise resistance, and further optimizes the model’s capability to capture short-term and long-term dynamics as well as high-dimensional feature representation efficiency compared to traditional LSTM models. Through the synergistic interaction of these three modules, the BLS-QLSTM model theoretically bridges the research gap in the integration of quantum computing and deep learning for financial time series prediction.

The effectiveness of BLS-QLSTM was validated on three real-world Chinese stock indices: CSI 300, SSEC, and CSI 500. For instance, on the CSI 500 dataset, BLS-QLSTM achieved a 36.5% reduction in RMSE compared to traditional LSTM and a 19.8% reduction compared to QLSTM. The model also showed consistent improvements in MAE and MAPE, while the R2 value reached 0.99404, indicating excellent fit and trend reconstruction ability. In terms of directional classification, the model achieved a classification accuracy of 0.77545 on CSI 500, outperforming LSTM and QLSTM by approximately 24.5% and 21.6%, respectively. Similar performance gains were observed on the CSI 300 and SSEC datasets, further demonstrating the model’s robustness and generalizability across diverse market conditions. These findings confirm that BLS-QLSTM not only enhances numerical prediction performance but also improves the recognition of stock price movement trends, offering a novel and practical approach to modeling chaotic financial time series.

The BLS-QLSTM model demonstrates significant value in both academic research and practical applications. For investors, the model offers precise price forecasting and trend analysis, serving as a scientific tool for optimizing asset allocation, improving investment decisions, and mitigating risks. For market regulators, the model excels in identifying market fluctuations, effectively aiding in the formulation of more precise regulatory policies, enhancing market stability and transparency, and supporting the healthy functioning of financial systems.

Despite the superior performance of the BLS-QLSTM model, there are certain limitations to this study. The maturity of current quantum computing hardware is insufficient to support large-scale applications. Additionally, the high cost of quantum computing restricts the model’s application to small-scale experimental studies. Furthermore, the interpretability of the model requires further enhancement to improve its usability and transparency in practical scenarios. Future research directions include optimizing the model architecture to reduce computational costs and enhance its interpretability and stability; exploring its application potential in other complex domains such as energy, healthcare, and transportation; and leveraging the continuous advancements in quantum computing technology to enable the large-scale implementation of the model in practice.