Introduction

The globally averaged surface temperature has been rising steadily for more than a century, but there is also discernible regional variation. Over recent decades, the highly populated regions of Europe and western North America have experienced extreme summer heatwaves more than most other regions1,2,3. As will be discussed, such regional variation within heatwave trends is, not surprisingly, also evident in the trend of surface temperature. Therefore, understanding the characteristics and mechanisms behind this regional variation of the surface temperature trends is important for climate risk mitigation. One possibility is that the regional variation may originate from short-term intraseasonal timescale processes because much of the zonal variation of the Earth’s surface temperature can be attributed to Rossby wave dynamics4,5 whose intrinsic timescale is intraseasonal6. In fact, the recent land warming was attributed to atmospheric teleconnections which were forced by warming of the ocean surface7. Given these earlier findings, in this study, we test if and to what extent intraseasonal timescale processes can account for the regional, zonally asymmetric component of the long-term trend of the boreal summer surface temperature.

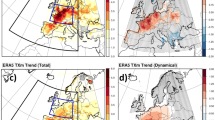
Figure 1a shows the linear trend of the skin temperature (\({T}_{s}\)) during June, July, and August (JJA) from 1979 to 2021. As expected, warming is widespread, but the warming is not spatially uniform. This spatial inhomogeneity can be seen more clearly in Fig. 1b where the zonal-mean component is removed from the total trends. This zonally asymmetric component is reminiscent of a Rossby wave train which occurs on the intraseasonal timescale. For example, positive trends exist over Europe and Mongolia whereas negative trends are located near Kazakhstan and the eastern edge of the Eurasian continent. Western North America has also been warming while eastern North America experienced a relative cooling trend compared to other locations at the same latitude. Another interesting characteristic of this zonally asymmetric \({T}_{s}\) trend pattern is that there are warming hotspots over Europe, western Russia, and western North America (Fig. 1b) where notable summer heatwave events have occurred in recent years. Prior studies attributed the heatwaves that occurred over Europe in 2003 and Russia in 2010 to an anticyclonic atmospheric circulation8,9 and to dry soil moisture10,11. The heatwave that occurred in June 2021 over western North America, which was an unprecedented event in terms of its strong magnitude, was attributed to subsidence under a blocking circulation12 and dry soil conditions13. Therefore, we also examine whether the pronounced trends over Europe and western Russia, and western North America can be attributed to the same processes that caused the extreme heatwave events that occurred over those locations.

Fig. 1: Components of the skin temperature trend pattern.
figure 1

a The linear trend of the JJA mean skin temperature for the period of 1979–2021. b As in (a) but for the zonally asymmetric component of the skin temperature. The dots in (a, b) represent statistically significant points at 95% level as computed by the Mann–Kendall test. The significance levels are only plotted for every two grid points. c Estimated zonal mean removed skin temperature trend contributed by the intraseasonal timescale processes (see text for details). d Difference between observed trend and estimated trend (b, c).

Full size image

It has been shown that the interdecadal trend of the regional temperature and circulation can often be attributed to the long-term trend of intraseasonal timescale processes14,15,16,17. For example, in their study of winter Arctic surface warming, Gong et al.16 combined the regression coefficient between the intraseasonal surface temperature and surface downward longwave radiation (DLR) and the interdecadal surface DLR trend to estimate the surface temperature trend. Using this approach, which will be described in detail in “Methods”, they found that the intraseasonal DLR has a large impact on the interdecadal surface temperature trend. In ref. 17, by applying a similar approach, it was found that the Eurasian circulation trend pattern (Supplementary Fig. 1) can be attributed to an upward trend of an upstream latent heating anomaly which excites the circulation trend pattern on the intraseasonal timescale. In fact, consistent with this study, the wave-like \({T}_{s}\) trend pattern over Eurasia resembles the upper-level circulation trend pattern (cf. Fig. 1b and Supplementary Fig. 1), which again supports the possibility that the wavy, zonally asymmetric \({T}_{s}\) trend pattern is linked to an intraseasonally varying teleconnection pattern. Therefore, motivated by these earlier findings, we apply the method described in the above studies, reconstructing the decadal \({T}_{s}\) trend but only with intraseasonal timescale signals, to test our hypothesis.

Results

\({T}_{s}\) trend reconstructed by intraseasonal timescale processes

Comparing the observed zonally asymmetric \({T}_{s}\) trend pattern (Fig. 1b) with the contribution from intraseasonal processes using Eq. (2) in “Methods” (Fig. 1c), we see that this method captures the key characteristics of the observed trend over land, showing the pronounced positive trends over Europe, Mongolia, and western North America, as well as the negative trends over India and Alaska. This agreement indicates that the intraseasonal timescale processes can explain much of the observed zonal asymmetry in the summer \({T}_{s}\) trend over most NH land areas. Over the ocean, however, there are discernable discrepancies between the two patterns. These discrepancies indicate that intraseasonal timescale processes cannot fully account for the trends over the oceans. In Fig. 1d, we show the difference between the observed trend (Fig. 1b) and the estimated trend (Fig. 1c). Recalling that the estimated trend is entirely due to intraseasonal timescale processes, Fig. 1d can therefore be regarded as the contribution by interannual timescale processes to the zonally asymmetric component of the \({T}_{s}\) trend. Figure 1d shows that the interannual component is notably greater over the ocean and this result is consistent with the fact that the dominant timescales of oceanic processes are longer than the intraseasonal timescale. Over land areas, there are a few locations where the interannual component is larger such as central and eastern North America, the Middle East, and Central Asia. However, its role in the warming of Europe and western North America, which are the main interests of this study, is limited. Therefore, we next investigate which components of (2) contribute to the land warming hotspots.

The intraseasonal timescale regression between \({T}_{s}\) and the shortwave flux shows overall positive coefficients, indicating that \({T}_{s}\) is higher with a stronger net shortwave flux (Fig. 2a). The trend of the zonally asymmetric component of the net shortwave flux indicates that the absorbed shortwave radiation has increased most notably over Europe (Fig. 2b). Other locations including central Asia and southern North America also experienced increasing solar radiation although the trends over these regions are not as strong as the trends over Europe. Figure 2c shows the \({T}_{s}\) trend contributed by the shortwave flux, which is the product between the regression coefficient and the net shortwave flux trend. The shortwave flux most notably contributes to the positive \({T}_{s}\) trend over Europe, western Russia, and Greenland and the negative \({T}_{s}\) trend over India and northern Canada.

Fig. 2: Contributions to the skin temperature trend from the surface energy budget terms.
figure 2

a Regression coefficient between skin temperature and the shortwave flux. b The linear trend of the JJA mean shortwave flux, for the period of 1979–2021. Dots represents statistically significant points at 95% level as computed by Mann–Kendall test. Significance levels are plotted at every other grid point. c The skin temperature trend contributed by the shortwave flux, which is obtained by multiplying panels (a, b). See text for details. d–f As in (a–c) but for sensible heat flux. g–i As in (a–c) but for latent heat flux. j–l As in (a–c) but for surface DLR.

Full size image

The prominent role that the shortwave flux plays in the \({T}_{s}\) trend over Europe is likely to be associated with an upper-level anticyclonic circulation, which was the driver of some of the major European heatwaves8,9. This anticyclonic circulation has indeed been positively trending over Europe, as indicated by the linear trend of the upper-level streamfunction (Supplementary Fig. 1). This finding supports our hypothesis that the dominant contributor to the pronounced \({T}_{s}\) trend over Europe is identical to the mechanism that explained the major extreme heat events that occurred over this ___location. This anticyclonic circulation trend is part of the large-scale Rossby wave trend pattern that extends from the North Atlantic to central Asia1,17,18,19. As mentioned in “Introduction”, this Eurasian circulation trend pattern occurs on the intraseasonal timescale and is effectively forced by a dipole latent heating anomaly (positive anomaly over the North Sea and negative anomaly over the Caspian Sea) which also is trending upward (see Fig. 9 of ref. 17). Therefore, the shortwave flux contribution to the \({T}_{s}\) trend over Europe is likely associated with the more frequent occurrence of those latent heating anomalies and the associated anticyclonic circulation pattern.

The negative regression coefficients between the \({T}_{s}\) and the sensible heat flux corresponds to a warmer surface cooling through an increase in the upward (negative-signed) sensible heat flux to the atmosphere (Fig. 2d). This relationship holds over most of the NH except for the Sahara Desert. The sensible heat flux shows negative trends over both Europe and western North America, and positive trends over India and Canada (Fig. 2e). Given that the JJA climatological sensible heat flux over most of the NH is upward (not shown), the negative sensible heat flux trends over Europe and western North America imply that the cooling due to this process has amplified over time. This negative trend along with the negative regression coefficient has contributed to the strong positive trend in \({T}_{s}\) over western North America (Fig. 2f). This term also has contributed to the positive \({T}_{s}\) trends over Europe and East Asia and negative trends over India.

The regression coefficient between skin temperature and the latent heat flux is negative for most NH land areas while the coefficient is positive over climatologically arid regions such as central Asia/Mongolia and western North America (Fig. 2g). Given the fact that the climatological latent heat flux is negative (evaporative cooling) for most of the NH (not shown), the regression coefficient pattern indicates that when \({T}_{s}\) of land areas is anomalously high the evaporative cooling of the surface is enhanced. The opposite behavior is seen over arid areas where evaporative cooling becomes more muted as \({T}_{s}\) increases. The latent heat flux trend pattern consists of a mixture of both positive and negative trends (Fig. 2h). Once again focusing on land regions, the weak negative trends (enhanced cooling trend) mainly occur over northern Siberia and western Europe, while positive trends (suppressed cooling trend) are prevalent over dry regions such as the Sahara Desert and the Middle East, Mongolia, and, most prominently, western North America (Fig. 2h). The contribution by the latent heat flux to the positive \({T}_{s}\) trend is therefore most notable over western North America, with additional support from various parts of Eurasia (Fig. 2i).

The latent heat flux contribution over western North America may possibly be associated with the drying trend of this region20,21,22,23. Figure 3a, b shows the JJA trend of soil moisture of the topsoil layer (0–7 cm) and precipitation, respectively, both from the ERA5 reanalysis. The precipitation trend from the Global Precipitation Climatology Project dataset (GPCP24) is also presented in Fig. 3c. All three panels show statistically significant declines in precipitation and soil moisture over western North America, although the GPCP precipitation trend is weaker than that of the ERA5. With such a drying trend, evaporative cooling is more limited which would lead to an anomalously warmer \({T}_{s}\), consistent with an earlier finding that hot days in western North America became drier25 and that the heatwave of 2021 was heavily influenced by the dry soil conditions13. This result again shows that the dry conditions which caused the heatwave events of western North America also explain the long-term trend of \({T}_{s}\) at the same ___location. However, such a drought-associated positive skin temperature trend may not be unique to western North America. Mongolia also experienced droughts in recent decades26. Accordingly, there have been long-term declines in soil moisture over Mongolia (Fig. 3a) although the strength of the precipitation decline depends on the dataset (Fig. 3b, c). Such a decline in soil moisture raises the possibility that drought has played an important role in raising the temperature in that region. Consistently, the positive \({T}_{s}\) trend in Mongolia (Fig. 2i) has a contribution from the positive regression coefficient (Fig. 2g) and the positive trend (suppressed cooling trend; Fig. 2h) of the latent heat flux.

Fig. 3: Trends of soil moisture and precipitation.
figure 3

The linear trend of the JJA mean a soil moisture of the top layer (0–7 cm), b ERA5 precipitation, and c GPCP precipitation. All trends are computed for the period of 1979–2021. Dots represent the statistically significant trend at 95% level as computed by the Mann–Kendall test.

Full size image

It is noteworthy that the latent heat flux also contributes to the positive \({T}_{s}\) trend over central Europe albeit with weaker magnitudes compared to the contribution from the shortwave flux (cf. Fig. 2c, l). While a soil moisture anomaly has been reported as an important contributor to notable extreme events such as the 2003 European heatwave10 and the 2010 Russian heatwave11, our analysis shows that for the long-term \({T}_{s}\) trend the enhanced shortwave flux driven by the trending atmospheric circulation is the primary contributor to the rising \({T}_{s}\) in Europe. The point is consistent with a recent study that teleconnection-induced circulation anomalies are a more useful predictor of European heatwaves than is soil moisture27.

The regression coefficients between the surface DLR and the \({T}_{s}\) are positive for most of the NH (Fig. 2j). However, the trends of the surface DLR are relatively weak (Fig. 2k) compared to the trends of other flux terms. Although there are notable positive trends over the Sahara Desert and part of Europe and negative trends over Russia, the zonally asymmetric component of the surface DLR trend did not change much over the last four decades. Thus, while this term contributes to the positive \({T}_{s}\) trends in the Sahara Desert and negative trends over Russia and India, its role is rather negligible over other regions of the NH (Fig. 2l).

Although the role of surface DLR was found to be negligible in generating the zonal asymmetry of the warming pattern, by repeating the same analysis for the total trend (with the zonal mean included), we found that the surface DLR is a major contributor to the \({T}_{s}\) trend (cf. Supplementary Fig. 2d, b), while the regional characteristics of the warming hotspots are contributed by the same processes identified earlier (Supplementary Fig. 2c, e, f). Therefore, it can be concluded that the surface DLR has warmed most of the NH, in addition to the contributions by the shortwave flux and the latent heat flux, which may possibly be associated with an anomalous wavy circulation and droughts, respectively, that have shaped the regional characteristics of the \({T}_{s}\) trend hotspots.

The role of the residual term, which mostly includes heat conduction and oceanic processes, turns out to be negligible over most of the NH (Supplementary Fig. 3). In land areas, the residual term is negative when \({T}_{s}\) is anomalously high, indicating that the surface cools owing to heat conduction in deeper soil layers (Supplementary Fig. 3a). However, the long-term trend of the residual term is small in land areas (Supplementary Fig. 3b). As a result, the heat conduction’s contribution to the warming trend is negligible (Supplementary Fig. 3c). Conversely, over the oceans, while the long-term trend of the residual term is large (Supplementary Fig. 3b), the intraseasonal timescale relationship with ocean \({T}_{s}\) is rather miniscule (Supplementary Fig. 3a), causing the contribution by the residual term to the \({T}_{s}\) trend to be negligible (Supplementary Fig. 3c). The role of this residual term is also negligible when the zonal mean is included (Supplementary Fig. 2g).

Discussion

In this study, we found that intraseasonal timescale processes can explain much of the observed zonally asymmetric \({T}_{s}\) trend pattern over land areas during boreal summer, while it is not the case over the ocean where the dominant timescale is longer than the intraseasonal timescale. Using the surface energy balance equation, we examined the different factors that contribute to the regional characteristics of this zonally asymmetric component of the \({T}_{s}\) trend pattern, which consists of warming hotspots over Europe and western North America where strong heatwave events have occurred in recent decades. Specifically, the shortwave flux contributed to much of the positive \({T}_{s}\) trend over Europe and western Russia while the latent heat flux played a secondary role. However, over western North America, the weakening trend of the latent heat flux (less evaporative cooling) is the primary contributor to the \({T}_{s}\) warming trend while the shortwave contribution is small.

The overall results of this study indicate that the intraseasonal timescale processes, which enabled the extreme heatwave events to be realized, also explain much of the amplitude and spatial extent of the long-term \({T}_{s}\) trend. While various intraseasonal timescale processes have been explored mainly to improve sub-seasonal to seasonal timescale prediction27,28,29, these processes have received less attention in predicting long-term regional climate change. This study shows that intraseasonal timescale variability also plays an important role in shaping the decadal timescale trend. Although internal variability may influence part of the intraseasonal timescale variability, it has also been shown that CO2 forcing can both directly and indirectly impact changes in summertime Rossby wave teleconnections7,30,31,32. The presence of both internal and forced responses complicates the interpretation of circulation change under the influence of anthropogenic warming. Our findings underscore that the accuracy of regional climate projections with climate model simulations is critically dependent on how accurately the models can simulate the teleconnection-associated intraseasonal timescale processes in the presence of global warming.

Methods

Surface energy balance equation and trend reconstruction

To examine the \({T}_{s}\) trend pattern, we analyze each term in the surface energy balance equation. While the energy balance equation may not be used to infer causality, it helps to decompose skin temperature changes into various thermodynamic contributors which allows one to diagnose relevant meteorological processes, such as the quasi-stationary atmospheric circulation33,34. Because the Stefan–Boltzmann law allows the upward longwave radiation at the surface to be written as a function of \({T}_{s}\) only, \({T}_{s}\) trends can be precisely decomposed into contributions from trends in DLR, shortwave and turbulent heat fluxes, and a residual term. The zonal mean removed surface energy balance equation can be written as follows:

$${{\varepsilon }_{s}\sigma {{T}_{{skin}}}^{4}}^{* }={{F}_{{lw}}^{\downarrow }}^{* }+{{F}_{{sw}}}^{* }+{{F}_{{sensible}}}^{* }+{{F}_{{latent}}}^{* }+{R}^{* }$$
(1)

where the asterisk symbol (*) indicates a zonal mean removed quantity. This equation indicates that the upward longwave flux at the surface (the left-hand side of (1)) can be expressed as a summation of the surface DLR (\({{F}_{{lw}}^{\downarrow }}^{* }\)), net shortwave flux at the surface (\({{F}_{{sw}}}^{* }\)), surface sensible heat flux (\({{F}_{{sensible}}}^{* }\)), surface latent heat flux (\({{F}_{{latent}}}^{* }\)), and a residual term (\({R}^{* }\))33,35,36. We assume that the emissivity (\({\varepsilon }_{s}\)) is 1.0 and \(\sigma\) is the Stefan–Boltzmann constant. The residual term (\({R}^{* }\)) accounts for the storage and other processes such as heat conduction, ocean heat transport, ocean vertical mixing, and sea ice influences, and its contribution to the \({T}_{s}\) trend is smaller than the other terms (Supplementary Fig. 3).

We obtained the daily skin temperature and the first four flux terms on the right-hand side of (1) from the European Centre for Medium-Range Weather Forecast ERA5 reanalysis dataset37. For each flux term, we summed 24-hourly accumulation data to obtain the daily data. All data have 1.25° by 1.25° horizontal resolution and the temporal range of 1979–2021. Positive values indicate a downward flux.

We estimate the contribution to the zonal mean removed \({T}_{s}\) trend by each surface flux term with the following expression:

$${\Delta {\hat{T}}_{s}}^{* }\cong \mathop{\sum }\limits_{i}\frac{\partial {T}_{s}^{* }}{\partial {F}_{i}^{* }}\Delta {{F}_{i}}^{* }$$
(2)

where \(\Delta\) indicates the linear trend and \({F}_{i}^{* }\) indicates the four different fluxes from the right-hand side of Eq. (1)16,38. This equation indicates that the estimated zonal mean removed skin temperature trend (\({\Delta {\hat{T}}_{s}}^{* }\)) at each grid point can be obtained from the product of two quantities, the change of skin temperature with respect to the change in the flux on the intraseasonal timescale (\(\frac{\partial {T}_{s}^{* }}{\partial {F}_{i}^{* }}\)) and the linear trend of the flux term (\(\Delta {{F}_{i}}^{* }\)). We obtained the former term, \(\frac{\partial {T}_{s}^{* }}{\partial {F}_{i}^{* }}\), by computing the regression coefficient between the two variables, using the detrended daily JJA data. We detrended the daily data by removing the interannual variability (each year’s JJA mean). This procedure results in each year’s JJA mean value being equal to zero, thereby removing the long-term trend1. Therefore, the quantity \(\frac{\partial {T}_{s}^{* }}{\partial {F}_{i}^{* }}\) only retains the intraseasonal timescale relationship between skin temperature and the flux term, where “intraseasonal” refers to all variations that have a timescale of less than one season, (including, but is not limited to, synoptic scale eddies). The quantity, \(\Delta {{F}_{i}}^{* }\), represents the interdecadal change in the flux obtained by computing the linear trend of the JJA seasonal mean flux for the period of 1979–2021. The significance levels of the trend values were computed with the Mann–Kendall test39. This procedure was applied to all grid points in the Northern Hemisphere (NH).