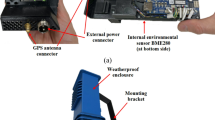
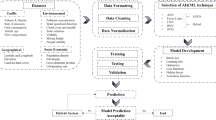
Abstract
Low-cost sensors have revolutionized air quality monitoring, however, precision is questioned compared to reference instruments. Hence, the performance of two widely used PM2.5 Sensors, Purple Air (PA) and ATMOS, were evaluated over a 10-month period in the North Western-Indo Gangetic Plains (NW-IGP). In-field collocation with Beta Attenuation Monitor found low R2 values; 0.40 for ATMOS and 0.43 for PA. To calibrate and improve the accuracy of sensors, five Machine Learning (ML) models and an empirical relative humidity correction methodology were used separately for both sensors. Out of these, the Decision Tree outperformed others, and R2 values improved to 0.996 for ATMOS and 0.999 for PA. Root mean square error reduced from 34.6 µg/m3 to 0.731 µg/m3 for ATMOS and from 77.7 µg/m3 to 0.61 µg/m3 for PA, while using DT as a calibrating model. The study reveals the best-performing ML model for correcting PM2.5 sensor data, enhancing the accuracy of air quality monitoring systems.
Similar content being viewed by others
Introduction
The increasing air pollution in developing nations has been linked to increased adverse health effects on humans1. The rising air pollution levels don’t remain limited to the source region but are also observed to follow long-range transportation due to meteorology2,3. To address this issue, it is essential to conduct high-resolution spatial and temporal monitoring of key air pollutants. For this purpose, ground-based monitoring using high-quality reference-grade instruments (Federal Reference Method (FRM)/Federal Equivalent Method (FEM)) is the most reliable approach. These instruments provide high-quality pollutant data and are recognized as standard instruments by major international air pollution regulatory bodies4,5,6,7.
A major constraint to the widespread use of FRM/FEM instruments is their high initial setup and maintenance costs. As a result, there is a sparse network of such stations in developing countries compared to developed nations. In the past decades, low-cost sensors (LCS) for air quality monitoring have emerged and are now used globally8,9. These sensors play a crucial role in air quality monitoring by providing real-time, high-resolution temporal and spatial data due to their easy and affordable deployment and low maintenance costs. LCS is capable of monitoring gases, Particulate Matter (PM), VOCs, and airborne microorganisms10,11. Gas sensors typically utilize electrochemical and metal oxide technologies, while PM sensors generally operate on light scattering principles. The size-specific signals produced by these sensors are converted into mass concentrations using algorithms12,13,14,15,16.
Despite their various advantages, the use of LCS has limitations. A significant drawback is the quality of data generated compared to FRM/FEM instruments. These discrepancies in PM measurements between LCS and FRM/FEM arise from differences in their operating principles17,18,19. Additionally, LCS is sensitive to meteorological factors, with many studies highlighting the significant impact of Relative Humidity (RH)20,21. Therefore, to enhance the accuracy of air quality data from these sensors, calibration with FRM/FEM instruments is necessary, typically achieved through collocation methods, which include both laboratory and field setups. The laboratory method is often considered to be more reliable, as it allows sensors to be tested under ambient conditions similar to those they will encounter in real-world monitoring22. For calibration, researchers have used various models, ranging from simple linear regression to more complex Machine Learning (ML) models, with ML models generally yielding the best performance in most studies23,24.
The performance of different calibration models varies by ___location, and to date, few studies have explored these models to correct LCS data in India25,26. This study is the first to conduct long-term, in-field calibration of two widely used LCS: PA, which has the largest global network, and ATMOS, which has the largest network in India, specifically in NW-IGP. In this study, we assessed the performance of these sensors in measuring PM2.5 against FEM Beta Attenuation Monitor (BAM) and examined the influence of ambient meteorology on LCS performance.
Five ML models; Multiple Linear Regression (MLR), Decision Tree (DT), Random Forest (RF) Regression Model, Support Vector Machine (SVM), XGBoost (XGB), and an empirical RH correction methodology were employed to calibrate raw measurements from these sensors. These LCS were collocated with the BAM for 10 months, covering all seasons. The study identifies the best-performing ML model, capable of correcting raw sensor measurements in spatial networks across similar urban areas throughout the Indo-Gangetic Plains (IGP) and beyond. The outstanding performance of the model enhances spatial and temporal air quality monitoring, aiding in the identification of local air pollution hotspots, accurate exposure assessment, health risk evaluation, and informed source-oriented policy making. A graphical abstract of the study is presented in Fig. 1.
Results and discussion
Raw ATMOS and PA measurements
The raw PM2.5 measurements from the ATMOS sensor ranged from 0.02 to 328.35 µg/m3, with a mean value of 51.38 µg/m3. In comparison, the raw PM2.5 values from the PA sensor ranged from 1.27 to 537.68 µg/m3, with a mean value of 91.59 µg/m3. The BAM PM2.5 measurements ranged from 0.91 to 213.63 µg/m3, with a mean value of 45.29 µg/m3. A time series comparison of PM2.5 measurements from all these instruments is presented in Fig. 2. Both PA and ATMOS measurements tended to overestimate PM2.5 levels compared to BAM, particularly at higher concentrations, with PA showing a greater degree of overestimation. The root mean square error (RMSE) for raw ATMOS and PA measurements were found to be 77.67 µg/m3 and 34.6 µg/m3, respectively. The mean absolute error (MAE) was 24.19 µg/m3 for ATMOS and 54.52 µg/m3 for PA.
The coefficient of determination (COD) between ATMOS and BAM was 0.40, while it was 0.43 between PA and BAM. Scatter plots and linear fit for these parameters are shown in Fig. 2. In global studies involving long-term field collocations with BAM, higher COD values (ranging from 0.8 to 0.9) have been recorded for PA sensors. However, these results were obtained in locations with very low PM2.5 concentrations27,28. All statistics of raw measurements, including minimum and maximum value and standard deviation, are summarized in Table 1.
Correlation plots of ATMOS PM2.5, PA PM2.5, and their respective RH and Temperature (T) with BAM PM2.5 are presented in Fig. 3. Long-term collocation studies in the IGP region of India using these LCS are limited. A study found lower COD ranging from 0.55 to 0.74 for PA sensors during long-term collocation with BAM in IGP cities, where PM2.5 levels were higher29. Another study reported a COD of 0.32 during a two-month collocation with BAM in Chandigarh30. Research indicates that the composition, and size of PM, along with ambient meteorological conditions, significantly impact LCS performance31. This variability may explain why these sensor’s performance differs from city to city, within the same region. The lower performance of these sensors in this study could also be attributed to discrepancies between the ambient conditions where the sensors were calibrated post-manufacturing and those present in the study area.
Meteorological factors, particularly RH, have been identified as a major contributor to the measurement uncertainty in LCS32. This bias in raw measurements for both LCS is evident in Fig. 2 and is further compared in Table 2. The data in Table 2 shows that the detection of particulates increases with rising RH, for both the ATMOS and PA sensors. However, this effect is negligible in BAM measurements as it has a heater at the inlet, which regulates the RH by maintaining a setpoint33,34.
Performance of calibration models
The performance of each ML model was assessed using RMSE, MAE, and Mean Absolute Percentage Error (MAPE) of the corrected PM2.5 values from the LCS (testing split data). The DT model demonstrates the best performance for both sensors among all the models. Using DT for ATMOS, RMSE decreased from 34.6 µg/m3 to 0.731 µg/m3, the MAE dropped from 24.19 µg/m3 to 0.177 µg/m3, and the MAPE improved from 57.9% to 0.41%. Using DT for PA, RMSE reduced from 77.7 µg/m3 to 0.61 µg/m3, the MAE fell from 54.52 µg/m3 to 0.135 µg/m3 and the MAPE from 125.74% to 0.37%. The DT’s ability to capture non-linear relationships and adapt to complex patterns in the data likely contributed to its superior performance, particularly in predicting PM2.5 concentration.
Additionally, decision trees are valued for their interpretability, making it easier to understand and validate the model’s decision-making process35. While previous studies have indicated that RF models often outperform DT with larger datasets, the DT model performs better for less data36. In this study, the DT model may be performing better by partitioning the feature space37, and efficiently capturing complicated patterns38, while other models may struggle to capture non-linear relationships, resulting in low performance in our dataset for our study region. This finding highlights the advantages of the DT algorithm within R and provides valuable insights for calibrating LCS.
While the performance of the DT model is exceptionally good on the testing/validation dataset, its performance was further evaluated on an unseen dataset, which was not part of the initial training and testing/validation dataset, to assess potential overfitting39. A total of 1,849 raw PM2.5 measurements for ATMOS and 1391 PM2.5 measurements for PA, were used for the analysis. The DT model achieved an R² of 0.986 for PA and an R² of 0.987 for ATMOS on the unseen dataset, indicating strong generalization and minimal overfitting that supports the robustness of the DT model. The evaluation metrics are presented in Table 3, while the linear regression plots and models of corrected LCS measurements (testing with unseen dataset) alongside the corresponding BAM measurements are illustrated in Figs. S1 to S4.
The COD values of corrected PM2.5 measurements from the other models ranged from 0.42 to 0.72 for ATMOS and from 0.52 to 0.79 for PA. While the performance metrics among these models did not significantly differ, the DT model notably outperformed all others. The RH correction methodology performed better than all ML models except for DT. This methodology involved calculating k and m factors in two ways, i.e. for ‘14-day sliding windows’ and ‘constant m and k’ for whole data. The correction equation utilizing the m and k factors derived from 14-day windows improved the R2 to 0.72 for ATMOS and 0.79 for PA (Table 3 and Fig. 4). In contrast, the same equation applied with optimized but constant m and k factors, did not yield satisfactory results (Supplementary Figs. S5 and S6). In a separate study, various ML calibration models were tested on nine LCS over a nine-month collocation period in Chennai, where the SVM model outperformed others26.
This variation in model performance across various regions may be attributed to differences in aerosol morphology, the composition of contributing sources, and meteorological conditions12,40. Detailed performance metrics for all models are provided in Table 3. Scatter plots and statistics of linear regression for corrected LCS measurements (testing data in case of ML models) alongside corresponding BAM measurements are depicted in Fig. 4. Model residuals and comparison of data corrected by models with BAM are given in Supplementary Figs. S7 to S26 for ATMOS and Supplementary Figs. S27 to S46 for PA in the supplementary file.
Effect of RH on LCS measurements
To evaluate the effect of RH on the performance of LCS, raw PM2.5 measurements of both LCS were categorized into four groups based on the corresponding ambient RH levels. These were RH ≤ 25%, 25% < RH ≤ 50%, 50% < RH ≤ 75% and RH > 75%. Further, the COD was then calculated between LCS PM2.5 measurements and corresponding BAM PM2.5 values for each group. The highest COD values for both LCS were found in the highest RH group, i.e., RH > 75 (with COD = 0.59 for ATMOS and 0.63 for PA). Conversely, the lowest COD was recorded for the ≤25 RH group. Scatter plots for these four groups are shown in Fig. 5, while linear regression statistics are presented in Table 4.
a Regression of raw LCS’s PM2.5 measurements and BAM PM2.5 measurements, in different RH groups, i.e., ‘≤25%’, ‘25% < RH ≤ 50%’, ‘50% < RH ≤ 75%’ and ‘>75%’. The scatter, best-fit lines in red color are of Purple Air and BAM. The scatter, best-fit lines in black color are of ATMOS and BAM. b Box plots of relative humidity and temperature, measured by low-cost sensors and reference instruments.
The RH and T readings from these sensors differed from those measured at the reference Continuous Ambient Air Quality Monitoring Station (CAAQM) station. Both LCS recorded higher T and lower RH compared to the reference station (see Figs. 5 and 6). This discrepancy arises because the temperature sensors are placed inside the sensor cabinets, which become heated, leading to inflated temperature readings than the ambient true measurements. Consequently, the RH sensors inside these cabinets also indicate lower RH than the ambient levels measured by the reference instrument. The comparison of these instruments is shown in Figs. 4 and 6. Many studies have reported a low correlation between LCS PM2.5 measurements and reference instruments at low RH levels. This can be attributed to RH effects on the size distribution of PM2.5 particles41,42. Higher RH facilitates hygroscopic growth of aerosols, improving detection by light-scattering devices due to increased particle size, which enhances light scattering and alters the refractive index43.
To curb this bias, some studies have integrated calibration algorithms with hygroscopic factor (k factor derived from Köhler theory) and size distribution correction factor (m factor), resulting in improved calibration outcomes32,44. In the current study, these k and m factors were also derived empirically, following the same methodology, to assess the calibration performance. The correction method utilizing these factors outperformed all the ML models except for the DT model (as shown in Table 3 and Fig. 4). The ML models in this study were trained with RH and temperature variables incorporated into their algorithms, leading to excellent calibration results, particularly with the DT model.
Materials and methods
Study area
The study area for this research is Chandigarh, a city located in northern India (30°45′N 76°47′E) and is one of the union territories of India. It has a total area of 114 km2 with a population exceeding 1 million45. Its climate is characterized as humid subtropical with varying temperatures from season to season (−1 to 45 °C). The majority of the land use pattern of the city is urban, with a few rural pockets on its outskirts. Notably, Chandigarh has the highest vehicle density in the country, contributing significantly to local air pollution. Additionally, its proximity to the states of Punjab and Haryana leads to a seasonal influx of air pollution, particularly from stubble burning in those regions46,47.
Instrumentation and in-field collocation
For the in-field collocation experiment, two LCS, PA and ATMOS, were positioned alongside the BAM (FEM instrument) at the same height (around 12 feet above the ground). Both LCS operate on the nephelometric principle, measuring the light scattered by particles and a laser as the light source. The measurements were conducted from 13th October 2020 to 28th July 2021, covering Post-Monsoon, Winter, Summer, and Monsoon seasons. Hourly averaged PM2.5 data was downloaded from the APIs of the respective sensors, while hourly FEM PM2.5 measurements for the same period were retrieved from the Central Pollution Control Board (CPCB) repository. Data was collected from the BAM (PM101M), which is part of the CAAQMS established by the CPCB. Additionally, both LCSs recorded their own meteorological parameters, including RH and T, which were incorporated into their calibration models. Ambient RH and T data were sourced from the same CAAQMS as mentioned above.
Data processing
A total number of 5222 hourly values from the ATMOS sensor were utilized after excluding data points with erroneous/unrealistic meteorological values for training and testing of model calibration against corresponding BAM measurements. For the PA sensor, 5839 data points were used for training and testing purposes and calibrated with corresponding BAM values. Data points with excessively high values (e.g., temperature readings of 3 data points exceeding 1000 °C), identified as unrealistic (outliers) during plots visualization, were removed from the dataset48. This pre-processing step was crucial to ensure the ML models were trained accurately, thereby enhancing the reliability of the results. This approach follows standard data processing practices as established in previous studies49,50.
Calibration models
Previous studies have demonstrated that models such as Multivariate Linear Regression, Decision Tree, Support Vector Machine, Random Forest, and XGboost have effectively calibrated LCS in various regions worldwide51,52. In this study, the raw data was randomly divided into 70% for calibration and 30% for testing. 70% of the dataset was allocated for model training, while the remaining 30% was used to evaluate the models against different statistical parameters. Recognizing the established relationship between PM2.5, RH, and T, we included these as independent variables and BAM PM2.5 values serving as dependent parameters12,21. A description of all the ML models and their internal characteristics is provided in the following sub-sections.
Multiple linear regression
The MLR model expands upon simple linear regression by accommodating datasets with multiple predictor variables while maintaining a single outcome53. MLR represents a broader form of simple linear regression, encompassing situations with multiple predictor variables54. The MLR model assumes that changes in the independent parameter are associated with consistent changes in the dependent variable, with a linear relationship between them55.
Decision tree
The DT is a non-linear model that recursively splits the dataset into subsets based on the most significant features. Its hierarchical composition enables the efficient handling of complex relationships56. In R, DT is a straightforward and interpretable predictive model that provides easy implementation of complex associations within datasets. We have used the inbuilt library of R to develop a DT ML model57,58,59. In the R library for DT regression, the internal structure involves recursively partitioning the dataset based on selected features to create a hierarchical tree, where nodes represent splitting criteria and terminal leaves contain regression predictions. This design enables the models to efficiently capture non-linear relationships in the data56. The key assumptions made in this model are that the data points are independent and identically distributed, the most important feature is used for splitting the data at each node, and there is a non-linear relationship between dependent and independent variables.
Random forest regression model
RF is highly useful for its high predictive accuracy and in handling complex datasets. It operates by using multiple decision trees through a process called bagging, which incorporates both feature randomness and bootstrap sampling. The internal structure of RF consists of an ensemble of decision trees, each trained on a subset of the data, using a random selection of features. Predictions from these trees are aggregated through a voting or averaging mechanism56,60,61,62. This ensemble approach improves robustness, mitigates bias, and provides a powerful tool for classification and regression tasks. RF regression is practically applied to datasets with complex relationships, non-linear patterns, and a large number of features (datasets with a substantial number of independent variables). We have utilized the inbuilt library of R studio and developed the RF model to calibrate LCS56,63,64. In R’s RF regression (e.g., ‘randomForest’ package. The final prediction is an average or weighted combination of individual tree predictions, leading to improved accuracy and robustness. The key assumptions of this model include that the data points are independent and identically distributed, there is a non-linear relationship between dependent and independent variables, and there is sufficient data availability to construct multiple trees65.
Support vector machine
SVM is an ML model used for regression tasks that identify an optimal hyperplane to minimize the error between predicted and actual values46. This hyperplane can then be used to estimate the label for unseen data29,66, and SVM may effectively capture non-linear relationships30. In the R studio, the internal structure of SVM (e1071 library) focuses on optimizing hyperplane parameters and support vectors to minimize regression errors31,67,68. The assumptions underlying SVM include that the data can be separated by a hyperplane with a maximum margin, that features are scaled when using the kernels function, that the data points are independent, and there is a non-linear relationship between dependent and independent variables67.
XGBoost
XGB is a highly powerful ML algorithm that adds the strengths of gradient boosting and tree-based models, which leads to prediction accuracy69. It operates by iteratively training an ensemble of decision trees, minimizing errors from previous iterations, and adding new trees that correct residual errors70. This algorithm performs gradient boosting with regularization techniques. In the R library for XGB (‘xgboost’ package), the internal structure involves an ensemble of decision trees, and each is sequentially added to minimize the gradient of the loss function71,72,73. The model’s strength lies in its optimization for both predictive accuracy and regularization, achieved by combining weak learners into a robust predictive model. The assumptions made in the model include that the final prediction is an additive combination of all individual trees, that the input features are relevant to the models, and that there is a non-linear relationship between dependent and independent variables74.
Empirical RH correction methodology
This methodology was adopted from a study where, to minimize bias in LCS measurements, occurring due to hygroscopic growth of particles and varying size distribution, k and m factors were introduced63. The following Eq. (1) was used for LCS calibration:
Here k is the hygroscopic growth parameter derived from k-Köhler theory and m is the particle size distribution correction factor. More details are provided in a study by Patel et al.32. The above equation does not apply when RHLCS = 100.
Performance evaluation metrics
To evaluate the calibration performance of these sensors, several metrics were chosen based on the literature review and recommendations from the EPA75. These metrics included the coefficient of determination, root mean square error, mean absolute error, and mean absolute percentage error. RMSE is commonly used to assess the error between two data sets; in this study, it was applied to calculate the error between raw/corrected sensor measurements and corresponding measurements from reference instruments. MAE measures the distance of the raw/corrected values from the reference instrument’s values, while MAPE calculates the predictive accuracy of the model. The analysis was done in R Studio (V-4.2.2). These metrics were applied separately to the raw PM2.5 values of LCS and the corrected PM2.5 values obtained from each model.
Data availability
Data will be made available on request.
Code availability
Code will be available on a knowledge-sharing basis, as it includes intellectual content.
References
Pandey, A. et al. Health and economic impact of air pollution in the states of India: the Global Burden of Disease Study 2019. Lancet Planetary Health 5, e25–e38 (2020).
Kallos, G., Kotroni, V., Lagouvardos, K. & Papadopoulos, A. On the long-range transport of air pollutants from Europe to Africa. Geophys. Res. Lett. 25, 619–622 (1998).
Ravindra, K., Kumar, S. & Mor, S. Long-term assessment of firework emissions and air quality during Diwali festival and impact of 2020 fireworks ban on air quality over the states of Indo Gangetic Plains airshed in India. Atmos. Environ. 285, 119223 (2022).
Noble, C. A. et al. Federal reference and equivalent methods for measuring fine particulate matter. Aerosol Sci. Technol. 34, 457–464 (2001).
Snyder, E. G. et al. The changing paradigm of air pollution monitoring. Environ. Sci. Technol. 47, 11369–11377 (2013).
Taheri Shahraiyni, H., Sodoudi, S., Kerschbaumer, A. & Cubasch, U. The development of a dense urban air pollution monitoring network. Atmos. Pollut. Res. 6, 904–915 (2015).
US EPA, O. EPA Scientists Develop and Evaluate Federal Reference & Equivalent Methods for Measuring Key Air Pollutants. https://www.epa.gov/air-research/epa-scientists-develop-and-evaluate-federal-reference-equivalent-methods-measuring-key (US EPA, O, 2016).
Borghi, F. et al. Miniaturized monitors for assessment of exposure to air pollutants: a review. Int. J. Environ. Res. Public Health 14, 909 (2017).
Kumar, P. et al. The rise of low-cost sensing for managing air pollution in cities. Environ. Int. 75, 199–205 (2015).
Varughese, S. P., Raj, S. M. G., Joel, T. J. & Gautam, S. Detecting airborne pathogens: a computational approach utilizing surface acoustic wave sensors for microorganism detection. Technologies 11, 135 (2023).
Blessy, A., John Paul, J., Gautam, S., Jasmin Shany, V. & Sreenath, M. IoT-based air quality monitoring in hair salons: screening of hazardous air pollutants based on personal exposure and health risk assessment. Water Air Soil Pollut. 234, 336 (2023).
Karagulian, F. et al. Review of the performance of low-cost sensors for air quality monitoring. Atmosphere 10, 506 (2019).
Kim, J., Shusterman, A. A., Lieschke, K. J., Newman, C. & Cohen, R. C. The Berkeley atmospheric CO2 observation network: field calibration and evaluation of low-cost air quality sensors. Atmos. Meas. Tech. 11, 1937–1946 (2018).
Lewis, A. C. et al. Evaluating the performance of low-cost chemical sensors for air pollution research. Faraday Discuss. 189, 85–103 (2016).
Narayana, M. V., Jalihal, D. & Nagendra, S. M. S. Establishing a sustainable low-cost air quality monitoring setup: a survey of the state-of-the-art. Sensors 22, 394 (2022).
Singh, T. et al. Very high particulate pollution over northwest India captured by a high-density in situ sensor network. Sci. Rep. 13, 13201 (2023).
Kushwaha, M. et al. Bias in PM2.5 measurements using collocated reference-grade and optical instruments. Environ. Monit. Assess. 194, 610 (2022).
Shukla, K. & Aggarwal, S. G. A technical overview on beta-attenuation method for the monitoring of particulate matter in ambient air. Aerosol Air Qual. Res. 22, 220195 (2022).
Triantafyllou, E. et al. Assessment of factors influencing PM mass concentration measured by gravimetric & beta attenuation techniques at a suburban site. Atmos. Environ. 131, 409–417 (2016).
Hua, J. et al. Improved PM2.5 concentration estimates from low-cost sensors using calibration models categorized by relative humidity. Aerosol Sci. Technol. 55, 600–613 (2021).
Nakayama, T., Matsumi, Y., Kawahito, K. & Watabe, Y. Development and evaluation of a palm-sized optical PM2.5 sensor. Aerosol Sci. Technol. 52, 2–12 (2018).
Rai, A. C. et al. End-user perspective of low-cost sensors for outdoor air pollution monitoring. Sci. Total Environ. 607–608, 691–705 (2017).
Cordero, J. M., Borge, R. & Narros, A. Using statistical methods to carry out in-field calibrations of low-cost air quality sensors. Sens. Actuators B Chem. 267, 245–254 (2018).
De Vito, S. et al. Calibrating chemical multisensory devices for real-world applications: an in-depth comparison of quantitative machine learning approaches. Sens. Actuators B Chem. 255, 1191–1210 (2018).
Sreekanth, V. et al. Inter-versus intracity variations in the performance and calibration of low-cost PM2.5 sensors: a multicity assessment in India. ACS Earth Space Chem. 6, 3007–3016 (2022).
Srishti S et al. Multiple PM low-cost sensors, multiple seasons’ data, and multiple calibration models. Aerosol Air Qual. Res. 23, 220428 (2023).
Barkjohn, K. K., Gantt, B. & Clements, A. L. Development and application of a United States-wide correction for PM2.5 data collected with the PurpleAir sensor. Atmos. Meas. Tech. 14, 4617–4637 (2021).
Stavroulas, I. et al. Field evaluation of low-cost PM sensors (Purple Air PA-II) under variable urban air quality conditions, in Greece. Atmosphere 11, 926 (2020).
Pisner, D. & Schnyer, D. Support vector machine. in Machine Learning: Methods and Applications to Brain Disorders 101–121 https://doi.org/10.1016/B978-0-12-815739-8.00006-7 (2020).
Christmann, A. & Steinwart, I. Support Vector Machines | SpringerLink. https://link.springer.com/book/10.1007/978-0-387-77242-4 (2008).
Fouodo, C. J. K., König, I. R., Weihs, C., Ziegler, A. & Wright, M. N. Support vector machines for survival analysis with R. R. J. 10, 412–423 (2018).
Patel, M. Y., Vannucci, P. F., Kim, J., Berelson, W. M. & Cohen, R. C. Towards a hygroscopic growth calibration for low-cost PM2.5 sensors. Atmos. Meas. Tech. 17, 1051–1060 (2024).
Schweizer, D., Cisneros, R. & Shaw, G. A comparative analysis of temporary and permanent beta attenuation monitors: the importance of understanding data and equipment limitations when creating PM2.5 air quality health advisories. Atmos. Pollut. Res. 7, 865–875 (2016).
Huang, C.-H. & Tai, C.-Y. Relative humidity effect on PM2.5 readings recorded by collocated beta attenuation monitors. Environ. Eng. Sci. 25, 1079–1090 (2008).
Gao, Y., Wang, Z., Li, C., Zheng, T. & Peng, Z.-R. Assessing neighborhood variations in ozone and PM2.5 concentrations using the decision tree method. Build. Environ. 188, 107479 (2021).
Ali, J. et al. Random Forests and Decision Trees | Semantic Scholar. https://www.semanticscholar.org/paper/Random-Forests-and-Decision-Trees-Ali-Khan/959a8e906ee26b940374b719253c8e188ed78fd3 (2012).
Yin, Q. et al. Interpretable POLSAR image classification based on adaptive-dimension feature space decision tree | IEEE Journals & Magazine | IEEE Xplore. https://ieeexplore.ieee.org/document/9194017 (2020).
Manzella, F. et al. The voice of COVID-19: Breath and cough recording classification with temporal decision trees and random forests—PMC. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9904537/ (2023).
Bush, T. et al. Machine learning techniques to improve the field performance of low-cost air quality sensors. Atmos. Meas. Tech. 15, 3261–3278 (2022).
Kang, Y., Aye, L., Ngo, T. D. & Zhou, J. Performance evaluation of low-cost air quality sensors: A review. Sci. Total Environ. 818, 151769 (2022).
Jayaratne, R., Liu, X., Thai, P., Dunbabin, M. & Morawska, L. The influence of humidity on the performance of a low-cost air particle mass sensor and the effect of atmospheric fog. Atmos. Meas. Tech. 11, 4883–4890 (2018).
Wang, P., Xu, F., Gui, H., Wang, H. & Chen, D.-R. Effect of relative humidity on the performance of five cost-effective PM sensors. Aerosol Sci. Technol. 55, 957–974 (2021).
Zang, L., Wang, Z., Zhu, B. & Zhang, Y. Roles of relative humidity in aerosol pollution aggravation over central China during wintertime. Int. J. Environ. Res. Public Health 16, 4422 (2019).
Malings, C. et al. Fine particle mass monitoring with low-cost sensors: corrections and long-term performance evaluation. Aerosol Sci. Technol. 54, 160–174 (2020).
CensusIndia. Census of India Website: Office of the Registrar General & Census Commissioner, India. https://censusindia.gov.in/2011-common/censusdata2011.html (CensusIndia, 2011).
Mor, S. et al. Impact of COVID-19 lockdown on air quality in Chandigarh, India: Understanding the emission sources during controlled anthropogenic activities. Chemosphere 263, 127978 (2021).
Ravindra, K., Singh, T., Pandey, V. & Mor, S. Air pollution trend in Chandigarh city situated in Indo-Gangetic plains: understanding seasonality and impact of mitigation strategies. Sci. Total Environ. 729, 138717 (2020).
Pengfei, Y., Juanjuan, H., Xiaoming, L. & Kai, Z. Industrial Air Pollution Prediction Using Deep Neural Network. In: Qiao, J. et al. (eds) Bio-inspired Computing: Theories and Applications. BIC-TA 2018. Communications in Computer and Information Science. vol 951. https://doi.org/10.1007/978-981-13-2826-8_16 (Springer, Singapore, 2018).
Shakya, K. M., Peltier, R. E., Shrestha, H. & Byanju, R. M. Measurements of TSP, PM10, PM2.5, BC, and PM chemical composition from an urban residential ___location in Nepal. Atmos. Pollut. Res. 8, 1123–1131 (2017).
Zhao, B. et al. Urban air pollution mapping using fleet vehicles as mobile monitors and machine learning. Environ. Sci. Technol. 55, 5579–5588 (2021).
Hong, G.-H. et al. Long-term evaluation and calibration of three types of low-cost PM2.5 sensors at different air quality monitoring stations. J. Aerosol Sci. 157, 105829 (2021).
Kumar, V. & Sahu, M. Evaluation of nine machine learning regression algorithms for calibration of low-cost PM2.5 sensor. J. Aerosol Sci. 157, 105809 (2021).
Eberly, L. E. Multiple linear regression. Methods Mol. Biol. 404, 165–187 (2007).
Marill, K. A. Advanced statistics: linear regression, part II: multiple linear regression. Acad. Emerg. Med. 11, 94–102 (2004).
Nimon, K. F., & Oswald, F. L. Understanding the results of multiple linear regression: beyond standardized regression coefficients. https://journals.sagepub.com/doi/10.1177/1094428113493929 (2013).
Fratello, M. & Tagliaferri, R. in Encyclopedia of Bioinformatics and Computational Biology (eds. Ranganathan, S., Gribskov, M., Nakai, K. & Schönbach, C.) 374–383 (Academic Press, Oxford, 2019).
Prajwala, T. R. A comparative study on decision tree and random forest using R tool. IJARCCE 196–199 https://doi.org/10.17148/IJARCCE.2015.4142 (2015).
Yadav, K. & Thareja, R. Comparing the performance of naive Bayes and decision tree classification using R. Int. J. Intell. Syst. Appl. 11, 11–19 (2019).
Zhang, Z. Decision tree modeling using R. Ann. Transl. Med. 4, 275 (2016).
Biau, G. & Scornet, E. A random forest-guided tour. TEST 25, 197–227 (2016).
Guo, B. et al. Estimating PM2.5 concentrations via random forest method using satellite, auxiliary, and ground-level station datasets at multiple temporal scales across China in 2017. Sci. Total Environ. 778, 146288 (2021).
Xu, R. Improvements to Random Forest Methodology. Doctoral dissertation, Iowa State University (Iowa State University, 2013).
Garge, N. R., Bobashev, G. & Eggleston, B. Random forest methodology for model-based recursive partitioning: the mobForest package for R. BMC Bioinforma. 14, 125 (2013).
Speiser, J. L., Miller, M. E., Tooze, J. & Ip, E. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst. Appl. 134, 93–101 (2019).
Patwari, N. & Wilson, J. RF sensor networks for device-free localization: measurements, models, and algorithms. Proc. IEEE 98, 1961–1973 (2010).
M. Somvanshi, P. Chavan, S. Tambade and S. V. Shinde, “A review of machine learning techniques using decision tree and support vector machine,” 2016 International Conference on Computing Communication Control and automation (ICCUBEA), Pune, India. pp. 1–7, https://doi.org/10.1109/ICCUBEA.2016.7860040 (2016).
Karatzoglou, A., Meyer, D. & Hornik, K. Support vector machines in R. J. Stat. Softw. 15, 1–28 (2006).
Lee, H. et al. Remote Sensing | Free Full-text | Using Linear Regression, Random Forests, and Support Vector Machine with Unmanned Aerial Vehicle Multispectral Images to Predict Canopy Nitrogen Weight in Corn. https://www.mdpi.com/2072-4292/12/13/2071 (2020).
Chen, T. & Guestrin, C. XGBoost | Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. https://dl.acm.org/doi/10.1145/2939672.2939785 (2016).
Ma, J. & Yu, Z. Application of the XGBoost machine learning method in PM2.5 prediction: a case study of shanghai-aerosol and air quality research. https://aaqr.org/articles/aaqr-19-08-oa-0408 (2019).
Ferreira, L., Pilastri, A., Martins, C. M., Pires, P. M. & Cortez, P. A comparison of AutoML tools for machine learning, deep learning and XGBoost. in 2021 International Joint Conference on Neural Networks (IJCNN) 1–8 (2021).
Noorunnahar, M., Chowdhury, A. H. & Mila, F. A. A tree-based eXtreme Gradient Boosting (XGBoost) machine learning model to forecast the annual rice production in Bangladesh. PLoS ONE 18, e0283452 (2023).
Ramdani, F. & Furqon, M. T. The simplicity of XGBoost algorithm versus the complexity of Random Forest, Support Vector Machine, and Neural Networks algorithms in urban forest classification. https://f1000research.com/articles/11-1069 (2022).
Sagi, O. & Rokach, L. Approximating XGBoost with an interpretable decision tree. Inf. Sci. 572, 522–542 (2021).
Duvall, R. et al. Performance Testing Protocols, Metrics, and Target Values for Fine Particulate Matter Air Sensors: Use in Ambient, Outdoor, Fixed Site, Non-Regulatory Supplemental and Informational Monitoring Applications. U.S. EPA Office of Research and Development (Washington, DC, 2021).
Acknowledgements
The authors acknowledge the support of CPCB for providing CAAQMS data. S.M. and K.R. acknowledge the HCWH for the Climate, Health, and Air Monitoring Project (CHAMP) project. S.M. and K.R. also acknowledge the Ministry of Environment, Forest & Climate Change, for identifying their institute as an Institute of Repute (IoR) under the National Clean Air Program (NCAP). K.R. would like to thank the National Program on Climate Change and Human Health (NPCCHH) under the Ministry of Health and Family Welfare (MoHFW) for designating his institute as a Center of Excellence (CoE) on Climate Change and Air Pollution Related Illness.
Author information
Authors and Affiliations
Contributions
Khaiwal Ravindra: conceptualization, data curation, formal analysis, methodology, resources, validation, visualization, writing—original draft, writing—review & editing. Sahil Kumar: data curation, formal analysis, methodology, software, validation, visualization, writing—review & editing. Abhishek Kumar: data curation, formal analysis, methodology, software, validation, visualization, writing—review & editing. Suman Mor: supervision, data curation, formal analysis, methodology, resources, software, validation, visualization, writing—original draft, writing—review & editing.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ravindra, K., Kumar, S., Kumar, A. et al. Enhancing accuracy of air quality sensors with machine learning to augment large-scale monitoring networks. npj Clim Atmos Sci 7, 326 (2024). https://doi.org/10.1038/s41612-024-00833-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-024-00833-9
This article is cited by
-
Exploration of a practical approach to providing RH corrections to low cost sensor networks
npj Climate and Atmospheric Science (2025)