Abstract
Understanding changes in global ocean heat content (OHC) is essential for investigating Earth’s energy imbalance and climate change. OHC trends are assessed using four state-of-the-art ocean reanalyses and one objective analysis. The spatial OHC trend patterns captured by reanalyses are consistent with each other, but sensitive to the selected time period. A higher proportion of heat uptake in the 100–2000 m sub-surface layer over 2001–2010 than 1994–2000 contributed to the temporary slowdown in global surface warming. The North Atlantic meridional overturning circulation (MOC) and heat transport show better agreement with RAPID observations compared with previous studies. Zonal mean OHC trends in the North Atlantic over 40–60 °N differ for the MOC increasing (2000–2004) and decreasing periods (2005–2010) and OHC increases are more concentrated between 30 and 40 °N in the later MOC increasing period (2011–2022). These results do not support previous studies suggesting that MOC changes are reducing Earth’s mean surface warming.
Similar content being viewed by others
Introduction
The change in global ocean heat content (OHC) plays a key role in Earth’s energy budget and climate change. Because of the relatively small heat capacity of the atmosphere and land surface, the OHC change counts for about 84%–93% of the energy accumulating in the Earth system1,2,3,4,5,6,7. The accurate measurement of Earth’s energy budget imbalance relies on observations of the OHC tendency (OHCT)8. The OHC increase can cause the sea level rise; the heat gain near the ocean surface drives global warming; the heat entering the subsurface ocean will be transported to other places and emerge years later, inducing regional and global climate changes9,10. The heat convergence and divergence in the tropical Pacific is closely associated with the El Niño–Southern Oscillation (ENSO)11,12,13,14 and can be a proxy of the ENSO forecasting. The variation of OHC around the thermocline in the equatorial Pacific can also be a proxy for the forecasting of tropical cyclones landfalling along the coastal areas of China15,16. The increasing oceanic heat transport to the polar region affects the melting of sea ice, contributing to an amplification of acceleration of climate change17. The meridional oceanic heat transport in the Atlantic also determines the mean ___location of the intertropical convergence zone18,19,20 and can affect the global atmospheric and oceanic circulation, and hence the global climate. Therefore, understanding the spatial distribution and uncertainty of the OHC and OHCT, as well as the Atlantic heat transport is of fundamental importance to many aspects of the climate change researches.
Ocean temperature observations are sparse and most of profiles collected by research vessels are above 1000 m before ARGO floats deployment around the early 2000s21. Since the start of the ARGO programme, about 3900 autonomous profiling floats have been in operation so far to provide salinity and temperature profiles every 10 days22. There are a few long term ARGO-based analyses of ocean temperature23,24,25 and a few objectively reconstructed datasets using the spatiotemporal correlations of the ocean temperature available1,26. With the rapid advances in observations and data assimilation technique, several ocean reanalyses from state-of-the-art ocean models are available now, such as the four eddy-permitting ocean reanalyses provided by Copernicus Monitoring Environment Marine Service (CMEMS).
Although the quality of observations and models has been improved greatly, there are still large uncertainties in the OHC, OHCT and ocean heat transport estimations. After examining monthly OHC anomalies in the upper 2000 m of the ocean from six objectively analyzed ocean state products and one ocean reanalysis over 2005–2014, Trenberth et al.27 found that there was a large spread in monthly OHCT computed from OHC of six objective datasets when compared with CERES (Clouds and the Earth’s Radiant Energy System) measurements at the TOA (top of the atmosphere)28,29,30. The OHC month-to-month variability is shown to be spurious and nonphysical, with standard deviations of global monthly changes in OHC about 12 Wm−2 versus 0.64 Wm−2 observed from CERES. Meanwhile, the OHC from the ocean reanalysis ORAP5 (Ocean Reanalysis Pilot v5) from ECMWF (European Centre for Medium-Range Weather Forecasts)31 and its changes from month to month are much more realistic.
A comparative study of OHC in the top 2000 m during the ARGO-era has also been conducted by Liao and Hoteit32 using 12 latest and representative global ocean datasets. They found the global and basins-wide OHC trends were quite consistent among the observation-based datasets but the differences are remarkable among ocean reanalyses, and some ocean reanalyses exhibit much higher or lower basins-wide warming rates than the observation-based datasets. The large-scale warming and cooling patterns in the top 700 m from ocean reanalyses are in agreement with the observation-based datasets, but they are significantly different below 700 m. All datasets suffered from relatively larger uncertainties in the highly dynamic regions.
The uncertainty of oceanic meridional heat transport in the North Atlantic was quantitatively investigated recently by Liu et al.9 using monthly data from three ocean reanalyses. Their results showed substantial differences between reanalysis products. Although the reanalysis products can capture roughly the mean amplitude and the variability of the OMHT (ocean meridional heat transport) to some extent, the mean OMHTs from reanalyses are much lower than that of RAPID (Rapid Climate Change-Meridional Overturning Circulation) observations33. It is also mentioned in their study that variations of the total OMHT are very sensitive to the changes of the corresponding meridional overturning circulation (MOC) as studied previously34,35. Hence, the Atlantic meridional ocean circulation may serve as an indicator of the OMHT change.
Trenberth et al.27 suggested routine examination of the OHCT using the latest datasets. This study revisits the estimations of the global OHC, OHCT and the North Atlantic ocean heat transport using the latest release of four CMEMS ocean reanalyses and one objective analysis from IAP (Institute of Atmospheric Physics)1,36. The variability over the globe and individual basins will be investigated and the ocean heat transport in the North Atlantic will be compared with the RAPID observations. The relationship between MOC and OMHT is investigated at different latitudes in the North Atlantic. The partitioning of the OHC change in different ocean basins over different time periods is conducted to see where the heat goes. The latitude-depth pattern of the zonal mean OHC trend in the North Atlantic is also investigated.
Results
Global mean OHC and OHCT variability
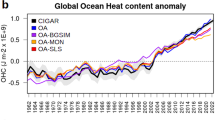
The monthly global area mean time series of OHC and OHCT from five datasets (ORAS5, GLORYS, FOAM, CGLORS and IAP) are plotted in Fig. 1. All lines are 12 month running mean. The OHC lines from ORAS5 (Fig. 1a), GLORYS (Fig. 1b), CGLORS (Fig. 1d) and IAP (Fig. 1e) all show quasi-linear variability over different integration depths. For the FOAM data, while the OHC variability from 0 to 300 m and 0–700 m integrations shows quasi-linear variability, but they are relatively flat before 2005, inconsistent with other datasets. Also the variability of 0–2000 m and full-depth integrations are at odds with other datasets before 2005, with large fluctuations in the 0–2000 m integration of OHC. Further investigations of the OHC mean vertical profiles show large discrepancies of FOAM data from others (Fig. S1), particularly around 1000–2000 m. Linear trends of OHC over different depths and time periods are listed in Table 1 and the observed mean FT (net radiative flux at TOA) and FS from DEEPC are also listed below the table for reference. Trends are significantly positive at the 99% significance level and the trend generally increases with the integration depth, indicating a whole ocean warming during this period. The contribution from the ocean below 2000 m is about 0.02 and 0.04 Wm−2 in ORAS5 over 1993–2017 and 2005–2017, which is smaller than the earlier estimation of 0.07 Wm−2 by Johnson et al.8 over 2005–2015. While the contributions are greater than 0.1 Wm−2 in FOAM and CGLORS over 1993–2017. More observations in the deeper ocean are definitely required to improve these estimations. The trends over 0–2000 m and full-depth are larger than the mean FT of 0.61 Wm−2 and mean FS of 0.58 Wm−2 from DEEPC between 1993 and 2017, and the discrepancy may be from either FT, FS or the OHC, further work is needed to reduce this large discrepancy. However, the trend values of ORAS5 (0.88 ± 0.01 and 0.92 ± 0.01 Wm−2 over 0–2000 m and full-depth, respectively) are closer to the mean FT of 0.79 Wm−2 and mean FS of 0.74 Wm−2 from DEEPC between 2005 and 2017 than that over 1993–2017. The mean OHC trend averaged from five datasets over 0–2000 m between 2005 and 2017 is 0.69 ± 0.12 Wm−2, consistent with the mean FS of 0.74 Wm−2 from DEEPC.
a–e On the left column are OHCs and f–j on the right column are OHCTs. The integration is from the ocean surface to different depths (0–300 m, 0–700 m, 0–2000 m and full depth). The net ocean surface heat flux (FS) from DEEPC is also plotted in the right column for comparison, and its correlation coefficients with OHCT are listed in Table 1. All lines are 12-month running mean and the OHCT time series for GLORYS and FOAM are scaled for clarity by a factor of 0.25 and 0.125.
The global area mean OHCT time series from five datasets over different depths are shown in the right column of Fig. 1, together with the time series of the net surface energy flux FS from DEEPC, and the OHCT time series in Fig. 1g, h are scaled for clarity by a factor displayed at the bottom right of the panel. The correlation coefficients between the global area mean OHCT in different ocean layers and FS are listed in Table 1. For ORAS5 data, OHCT is significantly correlated with FS: r = 0.28–0.44 for 1993–2017, and r = 0.46–0.76 over 2005–2017 across all four integrations, so correlation is higher after 2005 when more observations are available.
For ORAS5 data, the variability of OHCT and FS in the right column of Fig. 1 are in good agreement, particularly in the upper 300 m, except that over 1999–2005 as discovered by Trenberth and Zhang37 and Liu et al.9, when the observing system is transitioning from mainly XBTs (expendable bathythermographs) to mainly ARGO floats38. However, this large discrepancy between OHCT and FS is not shown in other datasets, which may be related to the bias correction methods implied in different datasets. The OHC trends over 1993–2017 are 0.39, 0.67, 1.15 and 1.17 Wm−2 for 0–300 m, 0–700 m, 0–2000 m and full-depth, respectively. The variability of the OHCT time series from GLORYS data (Fig. 1g) has significant positive correlations with FS in general, but the OHCT time series has much larger amplitude than FS, and the negative OHCT trend is opposite to the positive FS trend after 2010. The OHC variability for FOAM data is different when integrated to 700 m or deeper. The overall decrease before 2002 is not expected and the corresponding OHCT has very large inter-annual variability. The OHC variability of CGLORS (Fig. 1d) and IAP (Fig. 1e) are quite consistent, leading to co-variation of the corresponding OHCT for different depth integrations (Fig. 1i, j). The variability correlations with FS are all significant over 2005–2017.
To assess the spatial distribution of the OHC trend patterns captured by the five datasets, we plot the global patterns of the OHC trends over 0–2000 m and 2006–2020 (Fig. 2). Five datasets show basically consistent overall increasing trend of OHC in the eastern Pacific, North Indian Ocean, Atlantic subtropical gyre and south Atlantic, and Southern Oceans, and decreasing trends between about 50–65 °N North Atlantic and tropical western Pacific. The zonal mean OHC trend is shown in Fig. 2f and there is overall good variability agreement except that near north and south poles. In order to compare the spatial patterns with that of Roemmich et al.21, we also calculate and show the OHC trends distributions between 0 and 2000 m and 2006 and 2013 (Fig. S2). There are distinct differences between Figs. 2 and S2, such as the opposite trend signs over the eastern tropical Pacific and the Pacific warm pool. This sensitivity may be related to the OHC redistribution during the El Niño cycle in 2015. Compare Fig. S2 with Fig. 3a of Roemmich et al.21, it is noticed there is similar spatial pattern distribution of the OHC trend, such as the negative trend over the eastern tropical Pacific and North Atlantic, and positive trend over the Southern Ocean and north Indian Ocean. All three plots (Figs. 2f, S2f and 3b of21) show similar local maxima and minima positions in zonal mean variations with latitude, such as the maxima around 35 °N and 40–45 °S and the minima around 30 °N. However, the obvious local minima around 20 °N in Roemmich et al.21 is not shown in both Figs. 2f and S2f.
The above comparison of OHC trends over different periods shows consistent warming in the south oceans and North Indian Ocean, however the heat gain in the Pacific shows different patterns, with strong cooling in the western Pacific and warming in the eastern Pacific over 2006–2020 (Fig. 2), but the patterns reverse over 2006–2013 (Fig. S2), and this feature is consistent across five datasets. To examine the sensitivity of the OHC trend dependence on the selected time period, we plot area-averaged OHC and OHCT variations in the western Pacific Warm Pool (110E-150E, 0-20 N) and the Equatorial Eastern Pacific (EEP, 160W-80W, 10S-10N) (Fig. 3). For the Warm Pool area, all five datasets show the warming trend before 2010 over different depths, then there is a sharp cooling around 2014–2016, which can explain the western Pacific cooling pattern during 2006–2020 in Fig. 2. In contrast, the tropical eastern Pacific shows a weak cooling trend before 2012, but a rapid warming after 2012 (Fig. 3e–h). These changes are consistent across datasets and for different ocean layers. This may be a reflection of the relationship between OHC and El Niño events (such as 2009/2010, 2014–2016 events) (11,39,40). When the surface layer is anomalously warm (El Niño), OHC in EEP rapidly increases and the warm pool OHC decreases sharply, and vice versa for La Nina events. It is noticed that there is a spread of OHC variation over different layers before 2005, particularly in FOAM data, which shows large differences between upper (0–700 m) and lower (>700 m) layers.
OHC and OHCT variability in different ocean basins
In order to investigate contributions to the global mean OHC uncertainties from different basins, we show time series of area-averaged OHCs over the North Pacific, South Pacific, North Atlantic, South Atlantic, Indian Ocean, Southern Ocean (south of 35 °S), tropical (10 °S–10 °N) Pacific and tropical Atlantic (shorted as NP, SP, NA, SA, IO, SO, TP and TA, respectively (Fig. S3) and for different depths and datasets (Fig. 4). For the upper 300 m layer (left column of Fig. 4), the OHC in NP shows a steady warming trend during the study period accompanied by year to year variations relating to the ENSO signal, especially in the two strong El Niño years of 1997/1998 and 2015/2016, indicating NP as a whole loses heat when El Niño occurs. Similar changes can be seen in SP, where the upper 300 m ocean experiences a warming first and then sharply loses heat during the El Niño event. It is noteworthy that SP displays a stronger reaction to the 1997/1998 El Niño and more weakly to the 2015/2016 event, while NP reacts more to the 2015/2016 El Niño and less to the 1997/1998 event. The NA shows warming with fluctuations over 1993–2005, a weak decline to 2015, and then warming again after that, consistent with the finding of Liu and Xie41. The variation in SA is very similar to that in NA, but becomes flat after reaching the peak around 2006. Relatively weak IO warming can be seen during 1993–2006, but the warming rate accelerates after that and peaks at 2016 with sharp decline after 2016. The OHCs from ORAS5 and CGLORS show steady linear increases in SO from 1995 to 2015, while GLORYS and IAP show large fluctuations before 2005. The FOAM generally follows ORAS5 and CGLORS except for the large amplitude variation between 2002 and 2008. For the tropical Pacific, the impact from the 1997/1998 ENSO event on 0–300 m OHC is more profound than that in 2015/2016 as shown in SP, and the OHC change is much larger than that in SP. All datasets show a jump of OHC around 2002–2003 in TA, and the OHC peaks have opposite phases between TP and TA after 2008.
Mean OHC time series for NP (the first row), SP (the second row), NA (the third row), SA (the fourth row), IO (the fifth row), SO (the sixth row), TP (the seventh row), TA (the eighth row) for layers of 0–300 m (the first column), 300–700 m (the second column), 700–2000 m (the third column) and full-depth (the fourth column). All lines are 12-month running mean.
Fluctuations in NA, SA, IO indicate that El Niño events will heat the Atlantic and Indian Ocean, which is opposite to that of NP, SP or TP. This agrees with Cheng et al.11, which stated that the warming of the tropical Indian and Atlantic Oceans during the El Niño events largely offsets the Pacific cooling. The ENSO related signal affects Atlantic and Indian oceans mainly through the mechanisms of Indian Ocean capacitor42 and Atlantic ocean capacitor43. By comparing results from different datasets, ORAS5, GLORYS, CGLORS and IAP agree well with each other in NP, SP, IO, but discrepancies in SA and SO are relatively large compared to other basins. FOAM results agree with other datasets better in NP, SP, NA than in IO. All datasets agree with each other much better after 2006 than before, indicating that ARGO profiles have greatly reduced the biases. The OHC variations for other layers (0–700 m, 0–2000 m and full-depth) are very similar to results of 0–300 m, but the deviations of FOAM OHC from other datasets are large before 2006 and the main deviation is between 700–2000 m in North and South Pacific. The corresponding OHCT variations are plotted in Figure S4. There is good agreement of OHCT between different datasets in different basins over 0–300 m, again the OHCT magnitude from FOAM data is much larger than that from other datasets.
Although the atmospheric greenhouse gas concentration has continued to increase44,45 from 1998 to 2012, there is no statistically significant increase in global surface temperature over this period21. Nieves et al.46 found that over this period, the surface Pacific Ocean has cooled but the upper Indian Ocean and Southern Oceans have warmed, and suggested that the “hiatus” in surface warming appears to be the result of a redistribution of heat within the ocean, rather than a change in the whole Earth warming rate47. To investigate the warming rates in different ocean layers, the global mean and basin-mean OHC trends in eight ocean layers, including 0–100 m, 100–300 m, 300–500 m, 500–700 m, 700–1000 m, 1000–1500 m, 1500–2000 m and 2000 m-bottom, are calculated (Fig. 5) for three periods (1993–2020, 2006–2020 and 1998–2012). Trends have been normalised by 100 m water depth (e.g., the trend in 300–500 m is divided by 2) for comparison purpose. Comparing the global mean with individual basin means over 1993–2020 (left column of Fig. 5), it can be seen that the warming generally peaks at the surface except in TA where it peaks in the 100–300 m layer, and the warming rate decreases with depth. However, the vertical warming patterns are different between basins over 2006–2020 (the middle column in Fig. 5). There is a distinct warming surface layer and a cooling subsurface layer in NP. The warming in the surface layer in NP, SP and TP is much greater than layers below 100 m. The trends from the surface to about 500 m in NA are quite spread between datasets. The surface layer in SA shows a weak warming, and the warming keeps increasing to 300–500 m layer. In the Indian Ocean, a distinct warming mainly occurs in the surface and subsurface layers between 0–300 m, and the warming below 300 m is much weak. The 1998–2012 period (the right column of Fig. 5) is considered as a period of global warming hiatus. The surface layer warming is very weak compared with the evident subsurface warming in the global mean and all eight basins.
Linear OHC trends in different ocean layers (0–100 m, 100–300 m, 300–500 m, 500–700 m, 700–1000 m, 1000–1500 m, 1500–2000 m, 2000–bottom, marked as 1–8 on the x-axis) over three time periods 1993–2020 (left column), 2006–2020 (middle column) and 1998–2012 (right column). The trends are displayed for the global (a–c) and eight basins: NP (d–f), SP (g–i), NA (j–l), SA (m–o), IO (p–r), SO (s–u), TP (v–x) and TA (y, z, zz). Please note the trend is scaled for 100 m water depth (e.g., the trend in 300–500 m is divided by 2).
Following Chen and Tung48, we also partitioned the ocean energy change into different ocean basins and different time periods, in order to check the reliability of some existing results (Fig. 6). The left column of Fig. 6 is the global OHC variability relative to year 2000. The yellow line is the 0–100 m OHC and red line 0–2000 m. The black line is the SSTA from ERSST v5. As expected, the variability of the SSTA and 0–100 m OHC are highly correlated due to mixing in the top ocean layer. The correlation coefficients between them are r = 0.96 for ORAS5, 0.92 for GLORYS, 0.90 for FOAM, 0.94 for CGLORS and 0.96 for IAP. The hiatus period is evident from 2001 to 2007 in all datasets; both the SSTA and 0–100 m OHC are very flat and even the overall 0–2000 m OHC is still increasing, implying increased heat subduction to the deep ocean. The accumulated 0–100 m and 0–2000 m OHCs over 1994–2000, 2001–2010 and 2011–2020 are listed in Table S2 and the annual mean 0–2000 m OHC increases over these three periods are plotted in Fig. 7. The annual mean OHC increase over 2001–2010 is more than 1994–2000 in ORAS5, GLORYS and CGLORS, but it is slightly lower in IAP. The result from FOAM is not displayed in Fig. 7 due to its unrealistic OHC changes over 1993–2010 (Fig. 1c), but it is displayed in Fig. S6 for reference. The largest increase is from ORAS5, but it is not reliable as discussed earlier; this large change is not seen in other datasets and it occurred when the observing system was transitioning from mainly XBTs to mainly ARGO floats38. The annual mean OHC increase over 2011–2020 is less in ORAS5, GLORYS (Fig. 7) and FOAM (Fig. S6) but more in CGLORS and IAP than 2001–2010, consistent with the OHCT trends in Fig. 1. Because the 0–100 m OHC is much less than 0–2000 m OHC, the distribution patterns (not shown) of the 100–2000 m OHC increase over these three periods are similar to that of Fig. 7. Figure 1 of Chen and Tung48 is reproduced in Fig. S5 for reference using datasets employed in this study.
The left column is the global OHC variation relative to year 2000. The yellow line is the 0–100 m OHC and red line for 0–2000 m. The black line is the SSTA from ERSST v5. All lines are 12-month running mean. The right column is the 100–2000 m OHC change for different ocean basins over three time periods 1993–2000, 2001–2010 and 2011–2020. The datasets displayed are ORAS5 (a, f), GLORYS (b, g), FOAM (c, h), CGLORS (d, i) and IAP (e, j).
In order to see where the global OHC change is redistributed, the accumulated 100–2000 m OHC changes (in ZJ) over three time periods (1994–2000, 2001–2010 and 2011–2020) in different ocean basins are computed and listed in Table 2 and displayed in the right column of Fig. 6. The OHCs in the Atlantic, Pacific and Indian Ocean are only integrated to 35 °S here for comparison with Chen and Tung48. The OHC distribution patterns vary with datasets (Fig. 6f–j). Since there are 7 years from 1994 to 2000 and 10 years over the last two periods, the annual mean 100–2000 m OHC over each period is computed for comparison (Fig. 8). It shows that the annual mean OHC over 2001–2010 is much more than that over 1994–2000 in the Atlantic (Fig. 8a) and Indian Ocean (Fig. 8d) across datasets. It is mixed in the Southern Ocean where both ORAS5 and CGLORS show more OHC storage over 2001–2010. In the Pacific, only ORAS5 has more OHC storage over 2001–2010 than the preceding period (1994–2000); other three datasets show less OHC storage. In the Indian Ocean, all datasets show less OHC storage over latter period (2011–2020) than the preceding period (2001–2010), but both CGLORS and IAP have more OHC storage over latter period (2011–2020) than the preceding period (2001–2010) in Atlantic and Pacific.
Oceanic heat transport in the North Atlantic
The MOC and ocean heat transport (OMHT) in the North Atlantic is a major driver of the global redistribution of heat which modulates climate variability over Western Europe and the whole of Eurasia on time scales from seasonal to multi-decadal49,50,51. For example, the strengthening of the northern hemisphere summer monsoon circulation and rainfall during the weakening of the South Atlantic meridional heat transport at 30 °S52 and the enhancement of the ocean heat uptake and the southward shift of the intertropical convergence zone during the subpolar North Atlantic MOC slowdown9. Therefore, quantifying the variability and trends of the MOC and OMHT is essential to advance our knowledge of their influences on the weather and climate system50. Figures 9a, b show the time series of OMHT and MOC at 26 °N and all lines are 12 month running mean. Except for CGLORS having larger OMHT, other three datasets have good agreement with RAPID observations in both amplitude and variability. The 2009 low and the upward trend after that are captured by all datasets. The multiannual mean (April 2004–March 2018) OMHTs are 1.17, 1.24, and 1.21 PW (1 PW = 1015 W) for ORAS5, GLORYS and FOAM, respectively, which are close to the RAPID observation of 1.20 PW. The OMHT of 1.42 PW from CGLORS has larger bias relative to the observation. These reanalyses show better mean value agreement with observations than previous versions where all reanalysis products underestimate the OMHT at 26 °N in the Atlantic compared with the RAPID observations (9). Similar to the results of Karspeck et al.53 who used six ocean reanalysis products in their study, the MOC variability from reanalyses are self consistent. The correlation coefficients with RAPID observations (r) are 0.82 (ORAS5), 0.87 (GLORYS), 0.78 (FOAM) and 0.78 (CGLORS), respectively, from the monthly OMHT data, and 0.75 (ORAS5), 0.82 (GLORYS), 0.58 (FOAM) and 0.86 (CGLORS) for twelve month running means. These correlation coefficients are all significant. The MOC has similar variability characteristics with the OMHT and the scatter plot between them are also shown in Fig. 9c. All correlation coefficients are significant and high (r ≥ 0.88) implying that the variability of the heat transport is dominated by the MOC variation. The regression slopes are 0.064, 0.070, 0.075, 0.070 and 0.076 PW/Sv for ORAS5, GLORYS, FOAM, CGLORS and RAPID, respectively, so within 20% of each other.
Time series of a OMHT and b MOC at 26°N and all lines are 12-month running mean. c is the scatter plot between MOC and OMHT and the correlation coefficients between them from different datasets are also displayed. d Shows the correlation coefficient between MOC and OMHT over 1993–2020 at different latitudes in North Atlantic.
The correlation coefficients between MOC and OMHT over 1993–2020 are also calculated and the variations with latitude are plotted in Fig. 9d. All products have consistent variability and the correlation coefficients are generally greater than 0.8 between 10 and 34 °N. The amplitudes from GLORYS and FOAM drop faster than the other two products after 34 °N, and then they become stable between 44 and 60 °N and the amplitudes oscillate around r = 0.5. The decrease of r with the increasing latitude is possibly due to the loss of heat from the ocean surface to the atmosphere54. Since the OMHT calculation is sensitive to the accuracy of the grid, it is also computed on the native grid (NEMO grid) and the results are plotted in Fig. S7. The variations between the correlation coefficients calculated from the interpolated regular grid (Fig. 9d) and native grid (Fig. S7) are similar; both plots show that ORAS5 has higher correlation coefficients than the other datasets and the amplitude drop is primarily around 34 °N, but the correlation coefficients from the regular grid are slightly higher than that from the native grid.
Considering that both MOC (Fig. 9a) and OMHT (Fig. 9b) have increasing trends during 2000–2004 and 2011–2020, and a decreasing trend for 2005–2010, which are consistent between reanalyses and RAPID observations, the relations between the OHC trend and MOC or OMHT are investigated for ORAS5 (Fig. 10). This shows the contrast between periods when MOC is increasing (2000–2004, Fig. 10a) and decreasing (2005–2010, Fig. 10b) in the North Atlantic. The OHC trend in the upper layer is generally positive when the MOC is increasing and negative when it is decreasing. The spatial distribution patterns (latitude-depth section) between 40 and 60 °N are also different, which is consistent among datasets (Figs. S8–11) and with the result of Chen and Tung48, even though the two time periods here are shorter than theirs. However, for the MOC increasing period 2011–2020, the OHC trend spatial pattern between 30 and 60 °N has changed compared with the earlier increasing MOC period 2000–2004, with concentrated positive OHC trends in the water column between 30 and 40 °N and weak decreasing trends between 40 and 60 °N.
The ocean energy budget in the North Atlantic (26–65 °N) is quantified in Fig. 11 for four reanalyses. The heat transport represented by ΔOMHT (the OMHT at 26 N minus that at 65 °N), together with the surface energy flux FS, should be balanced ideally by the OHC change rate ΔOHC. Since the four ocean reanalyses are forced by ERAI (ERA-Interim) surface fluxes and the DEEPC data are observation-based, the FS from both datasets have been used here to check the energy balance between 26 and 65 °N in North Atlantic. Three lines are FS(ERAI) + ΔOMHT (black), FS(DEEPC) + ΔOMHT (red) and ΔOHC (blue), respectively. They vary in both magnitude and variability across datasets, and the FS + ΔOMHT is not balanced by the ΔOHC across datasets. For the variability, the best correlation between FS(DEEPC) + ΔOMHT and FS(ERAI) + ΔOMHT is r = 0.73, and the best one for ΔOHC and FS(ERAI) + ΔOMHT is r = 0.41, both from ORAS5. The best correlation between ΔOHC and FS(DEEPC) + ΔOMHT is r = 0.49 from CGLORS. The partition of the ΔOHC change into the heat transport and FS merits further investigation using the method of Li et al.55 in a future study, in order to check the sources for both the ΔOHC change and uncertainty.
Energy budget for a ORAS5, b GLORYS, c FOAM and d CGLORS. The FS is the net surface energy flux, ΔOMHT is the OMHT at 26°N minus that at 65°N, ΔOHC is the change rate of OHC in the selected basin. The correlation coefficients displayed are between FS(DEEPC)+ΔOMHT and FS(ERAI)+ΔOMHT (black), ΔOHC and FS(ERAI)+ΔOMHT (red), as well as the ΔOHC and FS(DEEPC)+ΔOMHT (blue).
Discussion
The global mean OHC variations show a consistent substantial upward trend during 1993–2020 over different depths with considerable fluctuations which are reduced after 2005. The trends of ORAS5 (0.84 ± 0.01 and 0.88 ± 0.01 Wm−2 over 0–2000 m and full-depth, respectively) over 2005–2017 are closer to the mean FT of 0.79 Wm−2 and mean FS of 0.74 Wm−2 from DEEPC than that over 1993–2017. The MOC and OMHT in the North Atlantic display good agreement with RAPID observations in both amplitude and variability except for CGLORS having larger values than others. The 2009 low and the upward trend between 2010 and 2017 are captured by all datasets. The multiannual mean (April 2004–March 2018) OMHTs from ORAS5, GLORYS and FOAM are close to the RAPID observation. These reanalyses show better mean value agreement than previous studies where all reanalysis products underestimate the OMHT at 26 °N in the Atlantic basin compared with the RAPID observations (Liu Y et al.56). The mean regression gradients of 0.070 PW/Sv from four ocean reanalyses and 0.076 PW/Sv from RAPID are consistent. All these results indicate the improved estimation of the OHC, OHCT and OMHT from reanalyses.
The heat storage and its partition into different ocean basins show that the OHC increase over 2001–2010 is more than during 1994–2000 and a higher proportion of heating below the upper mixed layer contributed to the slowdown of global warming over 2001–2010. The OHC trends in the North Atlantic show distinct differences between the MOC increasing period (1993–2004) and the decreasing period (2005–2010), and also between two MOC increasing periods (1993–2004 and 2011–2020), which are consistent among datasets. These results do not support previous studies suggesting that the MOC has changed from transporting surface heat northwards, warming Europe and North America, to storing heat in the deeper Atlantic, buffering surface warming for the planet as a whole48.
Methods
Data
The monthly data from four global state-of-the-art ocean reanalyses provided by CMEMS, including the ECMWF ORAS557 which is an upgrade of ORAP531, the Mercator Ocean’s ocean analysis system GLORYS2V458, UK Met Office GloSea5 (Global Seasonal forecast system version 5)59 based on the FOAM (Forecast Ocean Assimilation Model) Ocean Analysis60 and CMCC (Centro Euro-Mediterraneo sui Cambiamenti Climatici) C-GLORS (CMCC Global Ocean Reanalysis System)61, and one objective analysis from IAP are used in this study. These datasets are shorted as ORAS5, GLORYS, FOAM, CGLORS and IAP, respectively. The four ocean reanalyses are all based on the NEMO model on the ORCA025 grid62, with the eddy-permitting horizontal resolution of 0.25 ° × 0.25 ° and 75 vertical levels. All models are forced at the surface by ERA-Interim fluxes and all assimilate sea surface temperature (SST), sea level anomalies (SLA), sea ice concentrations (SIC) and in situ temperature and salinity profiles63. All data are post-processed to create the new product GREP (Global Reanalysis Ensemble Product) and the data from 1993 onward are publicly available from the website. The GREP members exhibit larger consistency (smaller spread) than their predecessors, suggesting the advancement with time of the reanalysis vintage64,65. The IAP dataset used spatial covariance from model simulations to help provide spatial interpolation and it has advantages in both its instrumental error reduction and its gap-filling method1,66.
OHC, OHCT and OMHT calculations
The ocean heat content in a grid box is calculated from the sea water potential temperature using the following equation
where A is the horizontal area of the grid box, ρ the density of sea water, \({C}_{p}\) the specific heat of sea water. \({T}^{{\prime} }\) is the sea water potential temperature anomaly relative to the reference period of 2006–2018. z1 and z2 are the lower and upper layer boundaries of the integration. Since the changes in density and specific heat of sea water are small, they are selected as constants with values of ρ = 1027 kg m−3 and \({C}_{p}\,\)= 3987 J kg−1 K−1, respectively. The OHC integrated in a ___domain is divided by the ___domain area to have the unit of Jm−2.
The oceanic meridional heat transport (OMHT) at a latitude \(\theta\) can be written as
where \(R\) is the radius of the Earth and φ the longitude. v is the northward component of the current velocity.
The OHC tendency (OHCT) is defined as the first derivative of OHC and can be calculated by the central difference:
where the i denotes a particular month, ti-1 and ti+1 denote the time one month before and after the month i.
Analysis
The variability of the global area mean OHCT will be compared with the net surface heat flux (FS) from the observation-based DEEPC (Diagnosing Earth’s Energy Pathways in the Climate system) product67 to check its magnitude and variability, since the ocean absorbs over 90% of the energy entering the Earth system. The DEEPC FS is estimated from the residual method using the TOA radiative fluxes, the mass corrected atmospheric energy transport of ERA5 (the fifth generation ECMWF ReAnalysis68) and the atmospheric energy tendency9,69,70,71,72. This estimated FS can ensure the conservation of the energy in the entire atmospheric column and is believed to be more accurate than other products54,72,73. The DEEPC dataset has been verified54,71,74 and used in various studies11,73,75,76,77,78,79,80 for comparison with other datasets, model evaluation and understanding climate change and variability. Please note the FS used in this study is the energy integration over the ocean surface and divided by the global surface area for comparison purpose. The MOC (meridional ocean circulation) in the North Atlantic is the northward flow of water volume integrated from the ocean surface to a depth where it reaches the maximum and the OMHT is integrated to the same depth. The OMHT will be compared with RAPID observations. The SST data used for anomaly (SSTA) calculations are from ERSST (Extended Reconstructed Sea Surface Temperature, version 5). Unless stated otherwise all anomalies are calculated relative to the reference period of 2006–2018. The brief descriptions of each dataset are listed in Table S1. The Mann–Kendall test is applied to check the significance of the trend at a significance level of 0.0181 and the significance of the correlation coefficient (r) is checked by applying the two tailed test using Pearson critical values at the level of 0.01.
Data availability
The DEEPC data are available at https://doi.org/10.17864/1947.000347, the RAPID data can be downloaded from https://rapid.ac.uk/rapidmoc/rapid_data/datadl.php and the four ocean reanalyses can be available from https://data.marine.copernicus.eu/product/GLOBAL_REANALYSIS_PHY_001_031/description. The IAP is from http://www.ocean.iap.ac.cn/pages/dataService/dataService.html?navAnchor=dataService. The ERSST v5 is from http://www1.ncdc.noaa.gov/pub/data/cmb/ersst/v5/netcdf.
References
Cheng, L. et al. Improved estimates of ocean heat content from 1960 to 2015. Sci. Adv. 3. https://doi.org/10.1126/sciadv.1601545 (2017).
Stocker, T. et al. Technical summary, in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds T. F. Stocker et al.). https://doi.org/10.1017/cbo9781107415324.010 (Cambridge Univ. Press, 2013).
Bindoff, N. L. et al. Changing Ocean, Marine Ecosystems, and Dependent Communities. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (eds H.-O. Pӧrtner, et al.) (Cambridge University Press, 2019).
von Schuckmann, K. et al. An imperative to monitor Earth’s energy imbalance. Nat. Clim. Change 6, 138–144 (2016).
von Schuckmann, K. et al. Heat stored in the Earth system: where does the energy go? Earth Syst. Sci. Data. https://doi.org/10.5194/essd-12-2013-2020 (2020).
von Schuckmann, K. et al. Heat stored in the Earth system 1960–2020: where does the energy go? Earth Syst. Sci. Data 15, 1675–1709 (2023).
Cuesta-Valero, F. J., García‐García, A., Beltrami, H., González-Rouco, J. F. & García-Bustamante, E. Long-term global ground heat flux and continental heat storage from geothermal data. Clim. Past. 17, 451–468 (2021).
Johnson, G. C., Lyman, J. M. & Loeb, N. G. Improving estimates of Earth’s energy imbalance. Nat. Clim. Change 6, 639–640 (2016).
Liu, C. et al. Variability in the global energy budget and transports 1985–2017. Clim. Dyn. 55, 3381–3396 (2020).
Otto, A. et al. Energy budget constraints on climate response. Nat. Geosci. 6, 415–416 (2013).
Cheng, L., Abraham, J. P., Hausfather, Z. & Trenberth, K. E. How fast are the oceans warming? Science 363, 128–129 (2019).
Jackson, L. C. et al. The mean state and variability of the North Atlantic circulation: a perspective from ocean reanalyses. J. Geophys. Res. Oceans 124, 9141–9170 (2019).
Mayer, M., Haimberger, L. & Balmaseda, M. A. On the energy exchange between tropical ocean basins related to ENSO. J. Clim. 27, 6393–6403 (2014).
Wu, Q., Zhang, X., Church, J. A. & Hu, J. ENSO-related global ocean heat content variations. J. Clim. 32, 45–68 (2018).
Liu, C. et al. Long-range prediction of the tropical cyclone frequency landfalling in China using thermocline temperature anomalies at different longitudes. Front. Earth Sci. 11, 1329702 (2023).
Sparks, N. & Toumi, R. Pacific subsurface ocean temperature as a long-range predictor of South China tropical cyclone landfall. Commun. Earth Environ. 1. https://doi.org/10.1038/s43247-020-00033-2 (2020).
Mayer, M. et al An improved estimate of the coupled arctic energy budget. J. Clim. https://doi.org/10.1175/JCLI-D-19-0233.1 (2019).
Donohoe, A., Marshall, J., Ferreira, D. & McGee, D. The relationship between ITCZ ___location and cross-equatorial atmospheric heat transport: from the seasonal cycle to the last glacial maximum. J. Clim. 26, 3597–3618 (2013).
Marshall, J., Donohoe, A., Ferreira, D. & McGee, D. The ocean’s role in setting the mean position of the Inter-tropical convergence zone. Clim. Dyn. 42, 1967–1979 (2013).
Schneider, T., Bischoff, T. & Haug, G. H. Migrations and dynamics of the intertropical convergence zone. Nature 513, 45–53 (2014).
Roemmich, D. H. et al. Unabated planetary warming and its ocean structure since 2006. Nat. Clim. Change 5, 240–245 (2015).
Riser, S. C. et al. Fifteen years of ocean observations with the global Argo array. Nat. Clim. Change 6, 145–153 (2016).
Good, S., Martin, M. J. & Rayner, N. A. EN4: quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J. Geophys. Res. 118, 6704–6716 (2013).
Hosoda, S., Ohira, T., Sato, K. & Suga, T. Improved description of global mixed-layer depth using Argo profiling floats. J. Oceanogr. 66, 773–787 (2010).
Roemmich, D. H. & Gilson, J. The 2004-2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program. Prog. Oceanogr. 82, 81–100 (2009).
Smith, D. M. & Murphy, J. M. An objective ocean temperature and salinity analysis using covariances from a global climate model. J. Geophys. Res. 112. https://doi.org/10.1029/2005JC003172 (2007).
Trenberth, K. E., Fasullo, J. T., Schuckmann, K. V. & Cheng, L. Insights into Earth’s energy imbalance from multiple sources. J. Clim. 29, 7495–7505 (2016).
Kato, S. et al. Surface irradiances consistent with CERES-Derived Top-of-atmosphere shortwave and longwave irradiances. J. Clim. 26, 2719–2740 (2013).
Loeb, N. G. et al. Observed changes in top-of-the-atmosphere radiation and upper-ocean heating consistent within uncertainty. Nat. Geosci. 5, 110–113 (2012).
Loeb, N. G. et al. Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Top-of-Atmosphere (TOA) Edition-4.0 Data Product. J. Clim. 31, 895–918 (2018).
Zuo, H., Balmaseda, M. A. & Mogensen, K. The new eddy-permitting ORAP5 ocean reanalysis: description, evaluation and uncertainties in climate signals. Clim. Dyn. 49, 791–811 (2017).
Liao, F. & Hoteit, I. A comparative study of the Argo-era ocean heat content among four different types of data sets. Earth’s Future 10, e2021EF002532 (2022).
Smeed D. et al. Atlantic meridional overturning circulation observed by the RAPID-MOCHA-WBTS (RAPID-Meridional Overturning Circulation and Heatflux Array-Western Boundary Time Series) array at 26N from 2004 to 2017. [Dataset]. British Oceanographic Data Centre - Natural Environment Research Council, UK. https://doi.org/10.5285/5acfd143-1104-7b58-e053-6c86abc0d94b (2017).
Lozier, M. S. et al. A sea change in our view of overturning in the subpolar North Atlantic. Science 363, 516–521 (2019).
McCarthy, G. D. et al. Measuring the Atlantic Meridional Overturning Circulation at 26 °N. Prog. Oceanogr. 130, 91–111 (2015).
Cheng, L. & Zhu, J. Benefits of CMIP5 multimodel ensemble in reconstructing historical ocean subsurface temperature variations. J. Clim. 29, 5393–5416 (2016).
Trenberth, K. E. & Zhang, Y. Observed interhemispheric meridional heat transports and the role of the indonesian throughflow in the pacific ocean. J. Clim. 32, 8523–8536 (2019).
Chambers, D. P. et al. Evaluation of the global mean sea level budget between 1993 and 2014. Surv. Geophys. 38, 309–327 (2016).
Roemmich, D. & Gilson, J. The global ocean imprint of ENSO. Geophys. Res. Lett. 38, L13606 (2011).
Johnson, G. C. & Birnbaum, A. N. As El Niño builds, Pacific Warm Pool expands, ocean gains more heat. Geophys. Res. Lett. 44, 438–445, https://doi.org/10.1002/2016GL071767 (2017).
Liu, W. & Xie, S. P. An ocean view of the global surface warming hiatus. Oceanography 31, 72–79 (2018).
Xie, S. et al. Indian ocean capacitor effect on Indo–Western Pacific climate during the summer following El Niño. J. Clim. 22, 730–747 (2009).
Wang, L., Yu, J. & Paek, H. Enhanced biennial variability in the Pacific due to Atlantic capacitor effect. Nat. Commun. 8. https://doi.org/10.1038/ncomms14887 (2017).
Easterling, D. R. & Wehner, M. F. Is the climate warming or cooling? Geophys. Res. Lett. 36. https://doi.org/10.1029/2009GL037810 (2009).
Foster, G. & Rahmstorf, S. Global temperature evolution 1979–2010. Environ. Res. Lett. 6. https://doi.org/10.1088/1748-9326/6/4/044022 (2011).
Nieves, V., Willis, J. K. & Patzert, W. C. Recent hiatus caused by decadal shift in Indo-Pacific heating. Science 349, 532–535 (2015).
Liu, W., Xie, S. P. & Lu, J. Tracking ocean heat uptake during the surface warming hiatus. Nat. Commun. 7, 10926 (2016).
Chen, X. & Tung, K. K. Global surface warming enhanced by weak Atlantic overturning circulation. Nature 559, 387–391 (2018).
Buckley, M. W. & Marshall, J. Observations, inferences, and mechanisms of the Atlantic Meridional Overturning Circulation: A review. Rev. Geophys. 54, 5–63 (2016).
Dong, S. et al. Synergy of in situ and satellite ocean observations in determining meridional heat transport in the atlantic ocean. J. Geophys. Res. Oceans 126. https://doi.org/10.1029/2020JC017073 (2021).
Rahmstorf, S. et al. Exceptional twentieth-century slowdown in Atlantic Ocean overturning circulation. Nat. Clim. Change 5, 475–480 (2015).
Lopez, H., Dong, S., Lee, S. & Goñi, G. Decadal Modulations of Interhemispheric Global Atmospheric Circulations and Monsoons by the South Atlantic Meridional Overturning Circulation. J. Clim. 29, 1831–1851 (2016).
Karspeck, A. R. et al. Comparison of the Atlantic meridional overturning circulation between 1960 and 2007 in six ocean reanalysis products. Clim. Dyn. 49, 957–982 (2017).
Liu, C. et al. Discrepancies in simulated ocean net surface heat fluxes over the North Atlantic. Adv. Atmos. Sci. 39, http://www.iapjournals.ac.cn/aas/en/article/doi/10.1007/s00376-022-1360-7 (2022).
Li, S. et al. Ocean heat uptake and interbasin redistribution driven by anthropogenic aerosols and greenhouse gases. Nat. Geosci. 16, 695–703 (2023).
Liu, Y., Attema, J. J., Moat, B. I. & Hazeleger, W. Synthesis and evaluation of historical meridional heat transport from midlatitudes towards the Arctic. Earth Syst. Dyn. https://doi.org/10.5194/esd-11-77-2020 (2020).
Zuo, H., Balmaseda, M. A., Tietsche, S., Mogensen, K. & Mayer, M. The ECMWF operational ensemble reanalysis–analysis system for ocean and sea ice: a description of the system and assessment. Ocean Sci. 15, 779–808 (2019).
Lellouche, J. M. et al. Evaluation of global monitoring and forecasting systems at Mercator Océan. Ocean Sci. 9, 57–81 (2013).
MacLachlan, C. et al. Global Seasonal forecast system version 5 (GloSea5): a high‐resolution seasonal forecast system. Q. J. R. Meteorol. Soc. 141. https://doi.org/10.1002/qj.2396 (2015).
Blockley, E. W. et al. Recent development of the Met Office operational ocean forecasting system: an overview and assessment of the new Global FOAM forecasts. Geosci. Model Dev. 7, 2613–2638 (2013).
Storto, A., Yang, C. & Masina, S. Sensitivity of global ocean heat content from reanalyses to the atmospheric reanalysis forcing: a comparative study. Geophys. Res. Lett. 43, 5261–5270 (2016).
Madec, G. & the NEMO team “NEMO ocean engine”. Note du Pole de modélisation de l’Institut Pierre-Simon Laplace (IPSL). https://doi.org/10.5281/zenodo.3248739 (2012).
Gounou, A., Drévillon, M. & Clavier, M. Product User Manual for Global Ocean Reanalysis Products GLOBAL-REANALYSIS-PHY-001-031. https://documentation.marine.copernicus.eu/PUM/CMEMS-GLO-PUM-001-031.pdf.
Storto, A. et al. The added value of the multi-system spread information for ocean heat content and steric sea level investigations in the CMEMS GREP ensemble reanalysis product. Clim. Dyn. 53, 287–312 (2018).
Copernicus Ocean State Report (2022) Copernicus Ocean State Report, issue 6. J. Oper. Oceanogr, 15, 1–220, https://doi.org/10.1080/1755876X.2022.2095169.
Pan, Y. et al. Annual cycle in upper ocean heat content and the global energy budget. J. Clim. 36, 5003–5026 (2023).
Liu, C. & Allan, R. Reconstructions of the radiation fluxes at the top of atmosphere and net surface energy flux: DEEP-C (Version 5.0) [Dataset]. University of Reading. https://doi.org/10.17864/1947.000347 (2022).
Hersbach, H. et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049 (2020).
Allan, R. P. et al. Changes in global net radiative imbalance 1985–2012. Geophys. Res. Lett. 41, 5588–5597 (2014).
Liu, C. et al. Combining satellite observations and reanalysis energy transports to estimate global net surface energy fluxes 1985–2012. J. Geophys. Res. Atmos. 120, 9374–9389 (2015).
Liu, C. et al. Evaluation of satellite and reanalysis‐based global net surface energy flux and uncertainty estimates. J. Geophys. Res. Atmos. 122, 6250–6272 (2017).
Mayer, J., Mayer, M. & Haimberger, L. Consistency and homogeneity of atmospheric energy, moisture, and mass budgets in ERA5. J. Clim. 34, 3955–3974 (2021).
Trenberth, K. E., Zhang, Y. X., Fasullo, J. T. & Cheng, L. J. Observation-based estimates of global and basin ocean meridional heat transport time series. J. Clim. 32, 4567–4583 (2019).
Mayer, J., Mayer, M., Haimberger, L. & Liu, C. Comparison of surface energy fluxes from global to local scale. J. Clim. https://doi.org/10.1175/JCLI-D-21-0598.1 (2022).
Bryden, H. L. et al. Reduction in ocean heat transport at 26 ° N since 2008 Cools the Eastern Subpolar Gyre of the North Atlantic Ocean. J. Clim. https://doi.org/10.1175/JCLI-D-19-0323.1 (2019).
Hyder, P. et al. Critical Southern Ocean climate model biases traced to atmospheric model cloud errors. Nat. Commun. 9, 3625 (2018).
Mayer, M., Fasullo, J. T., Trenberth, K. E. & Haimberger, L. ENSO driven energy budget perturbations in observations and CMIP models. Clim. Dyn. 47, 4009–4029 (2016).
Mayer, M., Alonso, Balmaseda, M. & Haimberger, L. Unprecedented 2015/2016 Indo-Pacific heat transfer speeds up tropical pacific heat recharge. Geophys. Res. Lett. 45, 3274–3284 (2018).
Valdivieso, M. et al. An assessment of air-sea heat fluxes from ocean and coupled reanalyses. Clim. Dyn. https://doi.org/10.1007/s00382-015-2843-3 (2015).
Williams, K. D. et al. The Met Office Global Coupled model 2.0 (GC2) configuration. Geosci. Model Dev. 8, 1509–1524 (2015).
Hipel, K. W. & McLeod, I. Time series modelling of water resources and environmental systems, (Elsevier). https://doi.org/10.1016/s0167-5648(08)x7026-1 (1994).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (42075036, 42275017, 72293604, 42130605); the LASG key open project (20230273) from the Institute of Atmospheric Physics, Chinese Academy of Sciences; Fujian Key Laboratory of Severe Weather (2021KFKT02); and the Postgraduate Education Innovation Project of Guangdong Ocean University (202144; 202253). Michael Mayer and Susanna Winkelbauer received funding from Austrian Science Fund (FWF) P33177 and the Copernicus Marine Service contract 21003-COP-GLORAN Lot 7. C.L. is also supported by University of Reading as a visiting fellow and X.L. is currently visiting the University of Reading. We also acknowledge the RAPID team and ocean reanalysis groups making their data available.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Liu, C., Jin, L., Cao, N. et al. Assessment of the global ocean heat content and North Atlantic heat transport over 1993–2020. npj Clim Atmos Sci 7, 314 (2024). https://doi.org/10.1038/s41612-024-00860-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-024-00860-6