Resolving the electronic ground state of La₃Ni₂O_7-δ films

Unconventional superconductors, such as copper-oxide and iron-based compounds, often show superconductivity alongside the destruction of long-range antiferromagnetic ordering when they reach a critical carrier concentration level through doping. As the doping levels increase, the superconducting state may coexist or compete with various electronically ordered phases¹. For example, cuprate superconductors may exhibit the development of spin and charge order, known as ‘stripe’^2,3,4, while several Fe-based superconductors demonstrate electronic nematic order, breaking discrete rotational symmetry near or within the superconducting phase^5,6,7. Understanding the relationship between superconductivity and various emergent electronic orders is crucial for uncovering the mystery of high-temperature superconductivity.

The discovery of the signature of superconductivity in La₃Ni₂O_7-δ under a pressure of 14 GPa with T_c ≈ 80 K has garnered considerable interest recently as a promising high-temperature superconductor derived from a transition metal outside copper-oxides or iron-chalcogenides⁸. Furthermore, these bilayer 327-type nickelates, unlike the infinite layer 112-type nickelates, have a completely different electronic configuration compared to cuprates, i.e. they are not engendered by a (half-filled) d⁹ Mott state but are potentially more complex ground states. However, the research landscape is intricating, with ongoing debates on whether superconductivity is bulk or filamentary^9,10,11,12, complicated by the reported intergrowth of different Ruddlesden-Popper (RP) phases^13,14,15,16. Despite the nuances of sample synthesis, substantial theoretical progress has been made in understanding the superconducting mechanism in pressurized La₃Ni₂O_7-δ^{17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39}. However, it is essential to note that the orbital configuration of Ni ions and the role of the oxygen ligands in La₃Ni₂O_7-δ remain elusive^40,41,42,43; it is unclear whether it resembles cuprates, which are charge-transfer insulators, or is more akin to infinite-layer nickelates, which are Mott-Hubbard insulators^{44,45,46,47,48,49}. Besides, the potential for electronic ordering, like long-range antiferromagnetic order, has not been fully resolved^{50,51,52,53,54,55,56,57}.

In the present work, we used X-ray absorption spectroscopy (XAS) at the O K absorption edge and resonant X-ray scattering (RXS) measurements at the Ni L₃ absorption edge to investigate the electronic ground state of single-crystalline La₃Ni₂O_7-δ films. In the electronic structure, we have identified in-plane and out-of-plane mobile carrier peaks linked to the Ni \({d}_{{{{{\rm{x}}}}^{2}-{{\rm{y}}}}^{2}}\) and \({d}_{{{{\rm{z}}}}^{2}}\) orbitals, along with substantial interlayer coupling facilitated by the inner apical oxygen. Moreover, we have established the presence of collinear antiferromagnetic spin ordering and anisotropic charge-like ordering with a matching periodicity. Notably, the two orders are interconnected yet display distinct temperature-dependent behaviors. These findings offer pivotal insights into the electronic structures of La₃Ni₂O_7-δ and aid in comprehending the underlying mechanism of electron pairings for superconductivity under pressurized conditions.

Detection of superlattice reflections

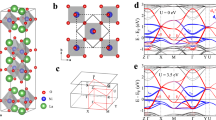
Figure 1a plots a schematic of the crystal structure of La₃Ni₂O₇. In Fig. 1b, we present the temperature-dependent resistivity measurements on two representative films of La₃Ni₂O_7-δ. These films were synthesized under different oxygen pressures, leading to oxygen variation. The resistivity versus temperature for Film 1 demonstrates insulating behavior. However, for Film 2, the resistivity decreases with decreasing temperature and exhibits an upturn around 80 K, indicating a transition to an insulator. This metal-to-insulator transition is likely due to disorder, given the negligible magnetoresistance across the transition temperature (see Supplementary Note 1, 2 for more details). Notably, the resistivity versus temperature for Film 2 resembles that of the bulk crystal, known for its superconductivity under pressure⁸. Since Film 1 was grown with a lower oxygen pressure than Film 2, we anticipate Film 1 to be less stoichiometric than Film 2 regarding oxygen content^{11,40,41,43,58,59,60,61}. The stark contrast in resistivity as a function of temperature between the two films aligns with the transport behavior observed in the bulk sample as oxygen content varies⁴¹. That could be crucial in understanding the electronic structure and origin of superconductivity of this material under pressure^8,9,10,11.

a Crystal structure of La₃Ni₂O₇ with lattice parameters a ≈ b = 3.789 Å and c = 20.313 Å. The green, blue, and red solid circles represent La, Ni, and O atoms, respectively. b The temperature-dependent resistivity for two typical films of La₃Ni₂O_7-δ; the dashed line represents the resistivity measurement of a La₃Ni₂O₇ single crystal in ref. ⁸ and is rescaled for clarity. c Reciprocal space map of the position of the resonant diffraction peaks in La₃Ni₂O₇. d A schematic of the RXS scattering geometry. k_in (k_out) represents the incoming (outgoing) photon wavevector with polarization σ and π; it determines the transferred momentum q = k_in − k_out. The cuboid illustrates a La₃Ni₂O_7-δ film sample (blue) grown on a LaAlO₃ substrate (gray). e Representative momentum scans across the wavevector (1/4, 1/4, 1.9) measured at T = 20 K and E = 852.2 eV with π polarized (red open circle) and σ polarized (blue open circle) incident photons. The solid lines fit the data using the Lorentz profiles and a linear background. The red and blue circles show the raw data from two typical scans in momentum space.

Full size image

Figure 1c,d illustrate the scattering geometry of the RXS experiments. We use a pseudo-cubic notation in defining the unit cell and use reciprocal lattice units (r. l. u.) for the reciprocal space (H, K, and L) components, which are given in units of (2π/a, 2π/b, 2π/c). At T = 20 K, the in-plane lattice constants are a ≈ b = 3.789 Å, and the out-of-plane lattice constant is c = 20.313 Å. We have observed superlattice reflections at (1/4, 1/4, 1.9) with photon energy tuned near the Ni L₃ absorption edge. This reflection exhibits strong photon polarization dependence, as shown in Fig.1e. It appears much stronger in π- than in σ- polarized incidence geometry, consistent with the recent report on bulk crystal La₃Ni₂O_7-δ⁵⁴. Such a photon polarization dependence suggests that the resonant reflection might be magnetic^54,62.

Linear dichroism of the pre-edge peak in O K-edge X-ray absorption spectroscopy

In Fig. 2a, we present the X-ray absorption spectra (XAS) for both films at the O K-edge and the corresponding X-ray linear dichroism (XLD) to uncover the orbital configurations of the Ni ions and the influence of oxygen ligands. According to the Zaanen-Sawatzky-Allen (ZSA) scheme, which classifies insulators into Mott-Hubbard and charge-transfer types, the role of ligands in determining the smallest energy gap of the charge excitations becomes evident⁶¹. The charge-transfer nature manifests as a pre-edge peak in the oxygen K-edge XAS⁶³. We observe clear pre-edge peaks in O K-edge XAS in both films around a photon energy of ~528 eV. They exhibit apparent polarization dependence: a sharp peak with in-plane polarization and two broad peaks with out-of-plane polarization. This indicates that the oxygen ligands significantly influence the electronic ground state of Ni cations. Notably, the XLD analysis of the difference of pre-edge peaks with different polarization enables us to deduce the Ni 3 d orbital configurations through p-d hybridization within the NiO₂ bilayers. As shown in Fig. 2a, the main peaks at ~528 eV with the in-plane polarization shows little sample dependence, consistent with \({d}_{{{{{\rm{x}}}}^{2}-{{\rm{y}}}}^{2}}-{p}_{x,y}\) Zhang-Rice singlet state in cuprate. Intriguingly, the two dips flanking the main peak with the out-of-plane polarization exhibit slight sample dependence, reflecting the strong hybridization of the inner apical O \({p}_{z}\) and the Ni \({d}_{{3{{{\rm{z}}}}^{2}-{{\rm{r}}}}^{2}}\) orbital, implying the formation of an out-of-plane \({d}_{{3{{{\rm{z}}}}^{2}-{{\rm{r}}}}^{2}}\) Zhang-Rice singlet state in bilayer nickelates. The energy difference of ~1.2 eV between the two dips is approximately two times that for the interlayer hopping of the \({d}_{{3{{{\rm{z}}}}^{2}-{{\rm{r}}}}^{2}}\) orbitals revealed from the density functional calculations^8,64,65. Thus, these two dips correspond to the \({d}_{{3{{{\rm{z}}}}^{2}-{{\rm{r}}}}^{2}}\) interlayer bonding and antibonding states, as illustrated in Fig. 2b (see Supplementary Note 3, 4 for more details). This contrasts with the recent angle-resolved photoemission spectroscopy (ARPES) measurements on a bulk crystal La₃Ni₂O_7-δ, where the correlation effects were proposed to push the bonding states derived from the \({d}_{{3{{{\rm{z}}}}^{2}-{{\rm{r}}}}^{2}}\) orbitals downward by about 50 meV below the Fermi level⁶⁵. Such discrepancy may arise from the variance in oxygen concentration and its impact on covalency (mainly through the apical oxygen) and/or the Fermi level position and the external pressure from substrates. As shown in Fig. 2a, the energy of the bonding states from the \({d}_{{3{{{\rm{z}}}}^{2}-{{\rm{r}}}}^{2}}\) orbitals appears to be more sensitive to the possible oxygen variation compared with the antibonding state from the \({d}_{{3{{{\rm{z}}}}^{2}-{{\rm{r}}}}^{2}}\) orbitals and the bands from the \({d}_{{{{{\rm{x}}}}^{2}-{{\rm{y}}}}^{2}}\)⁶⁶, consistent with observed prominent inner apical oxygen vacancy⁴³.

a The X-ray absorption spectra (XAS) and X-ray linear dichroism (XLD) near the O-K edge for Film 1 (red color) and Film 2 (blue color). The XAS are offset for clarity. I_ab and I_c represent in-plane and out-of-plane XAS intensity, respectively. The XLD signal is obtained by subtracting the in-plane and out-plane XAS intensity. The inset orbitals illustrate the origins of the peak and dip features. b Schematic density of states of La₃Ni₂O₇ and the corresponding bonding and antibonding orbitals. UHB and LHB represent the upper and lower Hubbard bands, respectively. c Energy profiles of the resonant reflection at (1/4, 1/4, 1.9) near the Ni-L₃ absorption edge with π- and σ-polarizations, and the peak intensity is maximized at E = 852.2 eV. Error bars are obtained from the Lorentzian fitting of RXS peaks. d Energy scans at constant wavevector on and off the Q_SP = (1/4, 1/4, 1.9) using different photon polarizations for two La₃Ni₂O_7-δ films. The solid (dashed) lines correspond to the π (σ) polarization. The curves are offset for clarity.

Full size image

Dependence of photon energy and temperature on superlattice reflections

We conducted momentum scans along high symmetry directions in momentum space for a comprehensive search of translational symmetry breaking signatures. This led us to the observation of a superlattice peak (SP) at the wavevector Q_SP = (1/4, 1/4, 1.9) in our La₃Ni₂O_7-δ films, as shown in Fig. 2c (see Supplementary Note 5 for L dependence of the scattering peak). To further understand the nature of this reflection, we performed momentum scans across the Q_SP with various photon energies. The results, depicted in Fig. 2c, demonstrate the resonant enhancement of the scattering signals, with a more pronounced increase in the scattered signal when using π-polarized incident photons, suggesting the magnetic nature of the reflection. In Fig. 2d, we present the energy scans with wavevector fixed at Q_SP, which reproduce the energy profiles in Fig. 2c. To provide a reference, we also repeated the energy scans slightly off this wavevector to characterize the scattering background under an identical geometry. The spectra taken slightly off the Q_SP exhibit much weaker signals (primarily resulting from fluorescence) than those measured at the wavevector, confirming the electronic nature of the reflection at Q_SP.

Figure 3a,b summarize the temperature dependence of the scattered intensity of the reflection at Q_SP with π- and σ-polarized incident photons, respectively. Figure 3a reveals a clear transition at T ≈ 160 K for both films. Figure 3c,d show the representative scans using π-polarized incident photons at various temperatures, confirming vanishing intensity above 160 K. This transition at T ≈ 160 K aligns with the earlier studies^{42,52,53,54,55}, suggesting the transition from magnetic ordering. However, surprisingly, the measurements with σ-polarized incident photons show different characteristics. The temperature dependence of the scattered signals takes an entirely different turn, exhibiting three characteristic temperatures near T ≈ 200 K, 160 K, and 110 K, respectively. The corresponding representative scans in Fig. 3e,f show the vanishing intensity near T ≈ 200 K. This unexpected behavior is a fascinating twist in our understanding. While the transition at T ≈ 160 K likely mirrors the same transition as revealed in the π channel, the transition at T ≈ 200 K suggests a different type of order with the same wavevector that already occurs about 40 K above the proposed magnetic order at T ≈ 160 K. Furthermore, the peak intensity starts decreasing at T ≈ 110 K as decreasing temperature, in sharp contrast to that measured in the π channel.

The diffraction peak intensity as a function of temperature taken with π (a) and σ (b) polarized incident light at 852.2 eV for the La₃Ni₂O_7-δ films. The dashed lines mark the transition temperature. c–f Representative momentum scans across the wavevector (1/4, 1/4, 1.9) for Film 1 and Film 2 measured with π (σ) polarization at various temperatures. The circle and triangle correspond to Film 1 and Film 2, respectively.

Full size image

Collinear antiferromagnetism and charge-like anisotropy

The discrepancy in the measurements of the scattering intensity versus temperature using the π- and σ- polarized incident photons indicates that the superlattice reflection at Q_SP may contain multiple components. Therefore, we conducted a symmetry-restricted tensorial examination of the azimuthal angle dependence of the scattered intensity to resolve the electronic texture underlying the superlattice reflection. The scattered intensity of the resonant reflection is given below^67,68,69,

where \({\varepsilon }_{{in}\left({out}\right)}\) represents the polarization of incoming (outgoing) photons, and \({{k}^{ \rightharpoonup }}_{{in}\left({out}\right)}\) stands for the wavevector of the incoming (outgoing) photons. \({{r}^{ \rightharpoonup }}_{j}\) and F_j stand for the position of the atom j and its scattering tensor, respectively. The polarization of the incident photons is resolved between the σ- and π-channel in the measurements, while outgoing photons are not polarization resolved. Therefore, we measured \({I}_{\pi \sigma }+{I}_{\pi \pi }\) when using π-polarized incoming photons, and \({I}_{\sigma \pi }+{I}_{\sigma \sigma }\) when using σ-polarized incoming photons.

We propose different ordered electronic motifs with an in-plane wavevector (1/4, 1/4) aligned with the wavevector revealed in the measurements. In Fig. 4a, we enforce the antiparallel alignment of next-nearest-neighboring spins while allowing the nearest-neighboring spins to align randomly except for being antiparallel; this comprises both collinear (double spin stripe) and non-collinear antiferromagnetism. In Fig. 4b, we propose a spin-charge stripe pattern that enforces the antiparallel alignment of next-nearest-neighboring spins with spinless charge domains; this would imply charge order with an in-plane wavevector (1/2, 1/2), double that of spin order. Figure 4c shows the measurements for the scattering intensity ratio π/σ as a function of the azimuthal angle. It turns out that the model of the spin-charge stripe cannot give a satisfactory fit to the measurements. The dashed curve represents the modeling of the spin-charge stripe with the magnetic moment pointing along the (1 -1 0) direction, as illustrated in Fig. 4b. This model substantially deviates from the measurements. We then explore a model with the spin textures as illustrated in Fig. 4a, and find both the non-collinear magnetic structures and double spin stripe yield a better agreement with the data, as indicated by the solid red curve from the fit to the data (see Supplementary Note 6 for further information). However, it still significantly deviates from the observed intensity ratios. Considering that the models of both collinear and complex magnetic spin textures cannot give a satisfactory fit to the data, we expect the likely presence of an anisotropic charge distribution that further lowers the symmetry on the spinless sublattices, as illustrated with green ellipses in Fig. 4b. A fit using the model that consists of both charge anisotropy and collinear antiferromagnetic spin order is given by the solid light blue curve in Fig. 4c, exhibiting a significantly improved agreement to the measurement, yielding the collinear antiferromagnetic spin ordering with spin moment primarily pointing along the (1 -1 0) orientation (see Supplementary Note 6 for details).

a, b A schematic of spin configuration illustrating the magnetic structure in real space. a shows spin configuration that can be both non-collinear antiferromagnetism (NCM) and collinear antiferromagnetism (CM). b shows spin-charge stripe configurations with charge anisotropy on the spinless sublattices (CM + charge anisotropy). The blue and red solid circles represent the spin and charge sublattices, respectively; brown arrows denote the spin momentum directions. The green shaded areas indicate the presence of charge anisotropy lowering the local symmetry on the spinless sublattices. c Azimuthal dependence of the integrated intensity of the reflection (1/4, 1/4, 1.9) at 20 K (where not shown, the error bars derived from the Lorentzian fitting of the RXS peaks are within the symbol size). The azimuthal angle ψ = 0 corresponds to a sample orientation where the (1 1 0) orientation lies within the scattering plane. The solid blue line represents the best fit for a model illustrated in (b) while the solid red line corresponds to the best fit illustrated in (a) corresponding to noncollinear spin configurations. The model of the spin-charge stripe without charge anisotropy does not seem to converge in the fit regardless of the initial parameters; the dashed line represents the simulation of the spin-charge stripe with the spin momentum direction fixed to the (1 -1 0) orientation. The inset in (c) shows a schematic of the scattering geometry of azimuthal angle-dependent measurements.

Full size image

The discovery of two components contributing to the resonant reflection at (1/4, 1/4) from the symmetry-restricted tensorial analysis naturally explains the remarkable differences in the scattering intensity measurements versus temperature when using σ- and π-polarized incident photons. In particular, the scattering tensor for the charge anisotropy contains only the diagonal components dominating the σ–σ channel. The scattering intensity versus temperature measured using the σ-polarized incoming light mainly reflects the presence of charge anisotropy that emerges around T ≈ 200 K, followed by the collinear spin ordering at T ≈ 160 K. Notably, the transition at T ≈ 160 K agrees with earlier studies using various experimental techniques^{42,52,53,54,55,57}. The anomaly at T ≈ 110 K occurs only in the σ channel indicating its charge origin. A possible explanation for this is that the arrangement of oxygen vacancies, if present, would dominate the charge channel and could compete with the charge-like anisotropy that occurs at 200 K, leading to the anomaly observed at 110 K.

In summary, we have revealed the electronic motif and the corresponding thermal dynamics in oxygen-varying films of La₃Ni₂O_7-δ using X-ray absorption spectroscopy and resonant X-ray scattering. We have uncovered the pivotal role of oxygen ligands, which hybridize with the Ni 3 d orbitals, forming the Zhang-Rice-like bands. However, unlike cuprates in which only the hybridization between O-2p and Cu 3\({d}_{{{{{\rm{x}}}}^{2}-{{\rm{y}}}}^{2}}\) dominates the lower energy physics, in our La₃Ni₂O_7-δ films, both the Ni \(3{d}_{{{{{\rm{x}}}}^{2}-{{\rm{y}}}}^{2}}\) and \({3d}_{{3{{{\rm{z}}}}^{2}-{{\rm{r}}}}^{2}}\) hybridize with the in-plane O-2p_x,y orbitals, and apical O-2p_z orbitals, as manifested by the pre-edge peak at the O K edge XAS, suggesting both the Ni-3\({d}_{{{{{\rm{x}}}}^{2}-{{\rm{y}}}}^{2}}\) and 3\({d}_{{3{{{\rm{z}}}}^{2}-{{\rm{r}}}}^{2}}\) play essential roles in the low-energy physics in La₃Ni₂O_7-δ^{8,17,19,20,21,31}.

The revelation of the possible spin ordering at (1/4, 1/4) at T ≈ 160 K in our film samples aligns with the recent studies on the bulk crystals⁵⁴. More subtly, our azimuthal angle measurements, along with the symmetry-restricted tensorial analysis, suggest the presence of an aspherical charge distribution at the sublattices of the spinless sites in the spin-charge model resulting in two components in the reflection at (1/4, 1/4). The ordering due to the charge anisotropy exhibits two characteristic temperatures at T ≈ 200 K and T ≈ 110 K. Note that our symmetry-restricted tensorial analysis cannot pinpoint the source accounting for the transition at T ≈ 200 K since any ordering of charge-like anisotropy would assume a similar format of a diagonal matric tensor. One possibility is that an ordered Jahn-Teller effect may exist on the spinless sublattices⁷⁰, leading to charge anisotropy. Another possibility is the presence of a magnetic quadrupole ordering on the spinless sites, which is compatible with our symmetry analysis (see Supplementary Note 6, 7 for further information).

Studying the electronic ground state of La₃Ni₂O_7-δ films with varying oxygen concentrations could have important implications for understanding the superconductivity discovered under pressurized conditions. In unconventional superconductors, various orderings, such as spin order, charge order, and spin-charge stripe, often appear to compete with superconductivity. Perturbations such as applying strain, pressure, or magnetic field can disrupt the balance between the superconducting phase and other competing orders. This scenario may also apply to La₃Ni₂O₇-_δ, where high pressure could suppress the spin-charge stripe while enhancing superconductivity. Notably, the resonant reflection at Q_SP in the film grown at lower oxygen pressure exhibits a much higher intensity than that in the film grown at higher oxygen pressure. The resistivity versus temperature in the high oxygenated film resembles that of the bulk samples which become superconducting under pressure. Variations in oxygen levels may have already suppressed the spin-charge ordering to some extent, thereby aiding pressure in eliminating it and enabling the full emergence of superconductivity.

Sample preparation

Thin films of the precursor phase La₃Ni₂O₇ with a thickness of ~30 nm were prepared using pulsed laser deposition (PLD) on (001)-oriented LaAlO₃ substrates with a 248-nm KrF excimer laser. The substrate was kept at 750 °C during growth under an oxygen partial pressure of 150 mTorr for Film 1 and 200 mTorr for Film 2, respectively. After deposition, the films were cooled to room temperature at 5 °C per min in the oxygen partial pressure of 100 Torr.

XAS and RXS measurements

The X-ray absorption spectroscopy (XAS) and resonant x-ray scattering (RXS) measurements at the Ni L-edge and O-K edge were performed at the REIXS (10ID-2) beamline of the Canadian Light Source (CLS). At these photon energy ranges, the beamline provides a photon flux of about 5 × 10¹¹ photons per second with energy resolution ΔE/E ~ 2 × 10⁻⁴. An in-vacuum 4-circle diffractometer hosts the endstation under an ultra-high vacuum (UHV) condition below 5 × 10⁻¹⁰mbar. The XAS spectra were collected in both total fluorescence yield (TFY) and total electron yield (TEY) modes at 20 K with linear vertical (σ) and horizontal (π) light polarizations. The XAS spectra are normalized to the incident photon flux. The RXS spectra are extracted after a Lorentzian fitting with a linear background.