Enhanced Weyl semimetal signature in Co₃Sn₂S₂ Kagome ferromagnet by chlorine doping

Weyl semimetals have been the subject of considerable research interest in the last decades due to the distinctive properties of the Weyl fermions^1,2,3. In the topological Weyl semimetals, pairs of Weyl points emerge when a specific symmetry, either inversion symmetry or time-reversal symmetry, is broken^1,4,5. The linear energy dispersion of the topological bands and the surface Fermi arcs can be observed by the angle-resolved photoemission spectroscopy (ARPES) and scanning tunneling microscopy (STM)^2,3,6,7,8. Meanwhile, Weyl semimetals are expected to exhibit exotic signatures such as non-zero Berry phase^9,10, chiral anomaly¹¹, large magnetoresistance¹², and anomalous Hall/Nernst effect (AHE/ANE)^{1,13,14,15,16}. To date, a large magnetoresistance (MR) is often observed in nonferromagnetic Weyl semimetals, which benefit from the linear dispersion of the topological bands and the electron-hole compensation^17,18. Although magnetic Weyl semimetals, such as Co₃Sn₂S₂, have been shown to exhibit a large AHE/ANE, the realization of high mobility and large MR remains experimentally challenging due to the ferromagnetic nature^13,14. Several reports have claimed an enhanced mobility in flaky Co₃Sn₂S₂ crystals grown by chemical vapor transport attributed to fewer defects. However, the enhancement in flux grown crystals has not yet been widely reported^19,20. The observed low mobility and small MR indicate that the role of Weyl fermions in the electrical transport properties is insufficient. This may be due to the large energy difference between the Weyl points and the actual Fermi energy.

To better illustrate the transport signature of the Weyl fermions in the Weyl semimetal Co₃Sn₂S₂, it is necessary to effectively shift the Fermi energy toward the Weyl points. As the first established magnetic Weyl semimetal, the Weyl points of Co₃Sn₂S₂ have been found to be approximately 60 meV above the Fermi energy by ARPES and STM^3,6. Various efforts have been made to shift the Fermi energy of Co₃Sn₂S₂ single crystals by extrinsic doping, such as doping iron/nickel on the Co site^21,22 or doping indium/antimony doping on the Sn site^23,24. Although an enhancement in the AHE is observed, it is contributed by extrinsic effects rather than the increase from the Weyl fermion contribution. Moreover, the MRs and the mobilities remain uninvestigated. It is noteworthy that previous reports about doped-Co₃Sn₂S₂ introduced a substitution in the Co-Sn Kagome layer^21,22,23,24, which often reduced the local moments leading to a decrease in the Curie temperature, and usually induced an increase in the longitudinal resistivity. Given the pivotal role of the Co-Sn Kagome layer in the magnetic structure and electronic band structure, it is of significant interest to achieve an effective shift of the Fermi energy shift by doping at the S sites while maintaining the integrity of the Kagome layer.

In this study, we have doped Cl at the S site in Co₃Sn₂S₂ by the self-flux method, which shifts the Fermi level toward the Weyl points without changing the magnetic structure (supplementary Fig. 1). The introduction of a nominal composition of 1% Cl into Co₃Sn₂S₂ results in an enhancement of the magnetoresistance from 17% up to 155% at 9 T, accompanied by a high electron mobility of 4000 cm²V⁻¹s⁻¹, which is twice higher than the previously reported value. This demonstrates a stronger Weyl semimetal signature compared to the pristine Co₃Sn₂S₂^13,19. Furthermore, an enhanced anomalous Hall conductivity (AHC) of 1680 Scm^-1 is observed around 40 K. These observations are corroborated ARPES and density function theory (DFT) calculations confirm a 15 meV shift of the Fermi energy toward the Weyl points. Our results emphasize the Weyl semimetal nature of Co₃Sn₂S₂, and bridge the gap between realistic materials and ideal physical models of Weyl semimetals.

Co₃Sn₂S₂ has a trigonal structure with \(R\bar{3}m\) space group. The structure consists of ferromagnetic Kagome Co₃Sn layers sandwiched between S layers, and further intercalated by a non-magnetic Sn layer, as shown in Fig. 1a. The Co-Sn Kagome layer determines the magnetic structure and electronic band structure of this compound, which is essential for the topological properties. In order to avoid causing a significant alteration to the Kagome layer, the doping of the S site with Cl (as illustrated in Fig. 1a with Cl highlighted in red) is employed in the present study. Moreover, since the ionic radii of Cl and S are similar, the change due to chemical stress in the Kagome layer is minimized. Consequently, the magnetic properties remain almost invariant after doping, which is shown in supplementary Fig. 1. We employed the power X-ray diffraction (XRD) to verify the phase purity. The XRD peaks and the refinement results are summarized in Fig. 1b. The peaks observed in the power XRD agree well with the previously reported data, meanwhile, no secondary phases are apparent. Following the refinement, the lattice parameters were determined to be a_doped = 5.3642 Å and c_doped = 13.1667 Å. Compared to the undoped result of a_original = 5.3689 Å and c_original = 13.176(2) Ź³, the decreased lattice parameters of the doped crystal indicate the effective doping of Cl at the S site, with a trace amount of smaller Cl^- ions replacing the larger S^2- ions in the lattice. More details of the XRD results can be found in Supplementary Data 1. The result of Laue diffraction further demonstrates the high crystal quality, as shown in Fig. 1c, d. A clear six-fold symmetry can be observed, and the experimental result is in good agreement with the simulation, indicating the high quality of the crystal.

a Crystal structure of Cl-doped Co₃Sn₂S₂. Upon doping with Cl, the Cl atom substitutes at the S site, and the change to the Co-Sn Kagome layer is minimal. b X-ray powder diffraction with Rietveld refinement. The fitted lattice constants are a = 5.3642 Å and c = 13.1667 Å, which are smaller than those of the intrinsic crystal due to doping. c and d Laue diffraction pattern on the (001) surface with simulation.

Full size image

The electrical transport properties for both the intrinsic and the doped crystals are summarized in Fig. 2. Figure 2a presents a comparison of the resistivities of the intrinsic and Cl-doped Co₃Sn₂S₂ crystals. Following doping, the temperature dependence of the resistivity remains similar to that of the intrinsic crystal, exhibiting a clear change in slope around the Curie temperature T_c of about 175 K. Above the T_c, the resistivities of the two crystals are nearly identical with a difference of less than 10%. However, below the Curie temperature in the ferromagnetic phase, the resistivity of the doped crystal drops at a much faster speed with a decreasing temperature. The absolute value of the Cl-doped crystal remains at a quarter of the intrinsic Co₃Sn₂S₂ at 2 K. The residual resistance ratio (RRR) therefore increases from 7 to 29 after doping, indicating a much higher mobility at low temperatures, which is often expected in topological semimetals. Figure 2b, c illustrate the MR and ordinary Hall resistivity (ρ_OHE) of the Cl-doped crystal at 2 K, with a comparison to the intrinsic Co₃Sn₂S₂. It is noteworthy that after doping, the MR increases from 17% in the undoped sample up to approximately155% for the doped crystals at 9 T, indicating a stronger compensation effect with the Fermi energy shifting towards the Weyl points. Similarly, the ordinary Hall effect (OHE), obtained by subtracting the anomalous part from the total Hall signal, also shows a stronger two-carrier signature, with a distinct negative slope at low field and a positive slope at higher field. The change in slope of the ordinary Hall curve indicates that the system is composed of high mobility low concentration electrons, which are responsible for the low field signal; and low mobility high concentration holes, which are responsible for the high field signal. The full Hall curves at 2 K are presented in supplementary Fig. 2. Furthermore, the MR result of the Cl-doped crystal in Fig. 2d at different temperatures up to 60 K is presented. At 60 K and 9 T, a 20% positive MR is observed, which is still large for ferromagnets. Above 60 K, the MR becomes small and negative as the field suppression of the magnetic scattering effect becomes dominant.

a Temperature-dependent resistivities of intrinsic and doped crystals from 2 K to 300 K. b Magnetoresistance (MR) of Cl-doped and undoped Co₃Sn₂S₂ at 2 K. A nine-fold increase is realized after doping, due to a stronger compensation effect. The raw curves at 2 K for both doped and undoped crystals are shown in Supplementary Fig. 2. c Ordinary Hall resistivities of intrinsic and doped crystals at 2 K. d MR of the Cl-doped crystal from 2 K to 60 K. The MR gradually disappears with an increasing temperature. Above 60 K, the MR becomes negligible. A two-carrier fitting is applied for the field dependent electrical conductivity acquired from the field-dependent resistivities with the resolved carrier concentrations and mobilities shown in e and f respectively. An electron concentration of 5 × 10¹⁹ cm⁻³ is resolved, along with a mobility of 4000 cm²V⁻¹s⁻¹ at 2 K in Cl-doped sample, exhibiting the effectiveness of Cl-doping. Assuming each Cl contribute 1 electron to the system, 0.46% of Cl are expected to be doped into the system.

Full size image

In Weyl semimetals, it is anticipated that both types of carriers should exhibit high mobilities because of their linear E-k dispersion. To date, observations of such high mobilities have been impeded, likely due to the considerable distance between the Fermi energy and the Weyl points, as well as the complex scattering effect in Co₃Sn₂S₂. The presence of the Kagome lattice is expected to result in the emergence of Dirac points and a low mobility flat band²⁵. It is proposed that the flat band in Co₃Sn₂S₂ is located close to the Fermi energy. The heavy d-band can result in a significant scattering effect on the electrons²⁶, which is commonly observed in ferromagnets. Consequently, a possible approach to enhance the mobility is to elevate the Fermi energy up toward the Weyl points, which can benefit more from the high-mobility Weyl bands and can effectively reduce the detrimental scattering from the heavy d-band. The mobilities and carrier concentrations are determined by fitting the field-dependent electrical conductivity with a classic two-carrier model²⁷:

where n_e and n_h are the electron and hole concentrations, respectively; μ_e and μ_h are the electron and hole mobilities. In our case it is found that fitting the longitudinal conductivity gives a more precise result compared to fitting the Hall conductivity, as shown in supplementary Fig. 3. The fitted carrier concentrations and mobilities from the intrinsic and doped crystals are shown in Fig. 2e, f. For the doped crystal, the electron concentration is resolved to be n_e = 0.5 × 10²⁰cm⁻³, with a high mobility of approximately 4000 cm²V⁻¹s⁻¹; the hole concentration, on the other hand, is n_h = 3.7 × 10²⁰cm⁻³, with a lower mobility of 1000 cm²V⁻¹s⁻¹ at 2 K. In contrast, the intrinsic crystal has a much lower electron concentration of n_e = 7.5 × 10¹⁸cm⁻³ compared to the doped crystal, almost an order of magnitude lower. Given that one Cl atom donates one excess electron to the system, the theoretical electron concentration induced by 1% Cl doping should be 9.1 × 10¹⁹cm⁻³. The actual doping concentration is then determined to be 0.46%, which suggests that the doping efficiency of no higher than 46%. The observed increase in electron concentration, coupled with the slight decrease in the lattice constants, provides compelling evidence that Cl is effectively doped at the S site. Moreover, using the DFT calculated electronic structure, the calculated theoretical carrier density is n_e= n_h = 1.7 × 10²⁰cm^-3 when the Fermi energy is located at the Weyl points^13,19. It is found that after doping the carrier density of electrons approaches the theoretical value, showing the effectiveness of Cl doping in achieving an ideal Weyl condition in Co₃Sn₂S₂. It is noteworthy that after doping the mobilities of both electrons and holes are approximately twice as high in the doped crystals as in the intrinsic Co₃Sn₂S₂. This observation provides additional evidence for an enhanced Weyl semimetal signature, given that high mobility carriers are expected in Weyl semimetals. At elevated temperatures, the mobilities of both crystals decrease due to phonon scattering. Above 60 K, when the MR becomes small and negative, the two-carrier model is no longer applicable due to the negative MR. The raw data of the electrical transport is summarized in Supplementary Data 2.

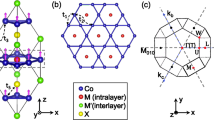
a Bulk Brillouin zone of Co₃Sn₂S₂ with high-symmetry points labeled. The Weyl points with opposite chirality are shown as red or blue dots. b Out-of-plane Fermi surface mapping within the k_x-k_z plane. The energy cut corresponds to the result shown in d. c ARPES intensity plots along Γ-K-M direction, acquired with hν = 120 eV with comparison to the DFT calculated band structure. d ARPES intensity plot and corresponding first-principles calculations through W1 Weyl point, acquired with hν = 115 eV.

Full size image

To confirm the extent of the shift of the Fermi energy, a systematic study of the electronic structure was conducted by ARPES, with the results being compared to those calculated by DFT. The predicted and confirmed Weyl nodes are labeled in Fig. 3a with the mirror planes shown in gray. In order to analyze the three-dimensional band dispersion, a k_z-dependent measurement was performed in k_x-k_z plane at k_y = 0, encompassing two Weyl nodes in the Brillouin zone (BZ). From the Fermi mapping shown in Fig. 3b, it can be observed that the ARPES intensity shows a pronounced k_z dependence, which is indicative of its bulk origination. The energy cut at the proposed Weyl point is of particular interest, which is labeled as cut 1. To validate the experimental results, the high-resolution spectra along the Γ-K-M direction can be compared to the first-principle calculations of the bulk bands. Figure 3c illustrates an overall concordance between the theoretical and experimental results in the Γ-K-M direction, when a 75% energy compression is applied to the calculations. A comparison between the theoretical and experimental results revealed a 15 meV energy shift in the Fermi energy relative to the intrinsic Co₃Sn₂S₂. To further investigate the band structure in the vicinity of the Weyl points, we obtained spectra through the W1 Weyl point depicted in Fig. 3d, from which a better k_z resolution was achieved. The experimental results align with the DFT calculations, confirming the effective shift in the Fermi energy.

Given that the shift in the Fermi energy and the observed stronger compensation behavior in the longitudinal transport measurement, it is of interest to investigate the variation in the AHE. Figure 4a, b show the field dependent anomalous Hall resistivities \({\rho }_{{yx}}^{A}\) of the undoped and Cl-doped crystals at various temperatures, respectively. The field dependence of the two crystals is identical, exhibiting a clear hysteresis loop near zero field. The field dependent \({\rho }_{{yx}}^{A}\) is consistent with the invariant magnetic structure obtained from the magnetic measurements (supplementary Fig. 1). The \({\rho }_{{yx}}^{A}\) magnitude for both crystals were extracted and replotted in Fig. 4c. The \({\rho }_{{yx}}^{A}\) of the chlorine doped crystal is considerably smaller than that of the intrinsic crystal at 2 K, but it increases more rapidly with temperature. Above 100 K, an even larger \({\rho }_{{yx}}^{A}\) is obtained from the Cl-doped crystal. Figure 4d compares the AHCs of both crystals below T_c. The AHC of the undoped crystal is consistent with the previous result, reaching approximately 1200 Scm⁻¹ at 2 K¹³. The AHC of the Cl-doped crystal is comparable to that of the intrinsic crystal at 2 K. As temperature increases, a notable enhancement in AHC is observed in the Cl-doped sample across the entire temperature range, reaching a maximum value of 1680 Scm⁻¹ at 40 K. This enhanced AHC can be attributed to the shift of the Fermi energy towards the Weyl points. Over a wide range of temperatures, the AHC of the doped crystals is greater than 1600 Scm⁻¹. This temperature dependent AHC is attributed to a mixed contribution from intrinsic and skew scattering contributions.

a Field dependent anomalous Hall resistivities \({\rho }_{{yx}}^{A}\) of intrinsic Co₃Sn₂S₂. b \({\rho }_{{yx}}^{A}\) of the Cl-doped Co₃Sn₂S₂. The two crystals have identical behavior with a clear hysteresis loop near zero field. c Temperature dependence of the \({\rho }_{{yx}}^{A}\) of both crystals. After doping, the \({\rho }_{{yx}}^{A}\) becomes significantly lower below 60 K. Above 100 K, the two crystals show comparable \({\rho }_{{yx}}^{A}\). d Temperature dependent anomalous Hall conductivities (AHCs) of both crystals. At 2 K, the two crystals exhibit comparable AHC as a consequence of a comparable nodal ring. The AHC of the doped crystal shows a rapid increase with temperature, reflecting a greater contribution from the Weyl points. e Fitting of the AHC σ_xy vs σ_xx². The intersection of the y-axis is taken to represent the intrinsic contribution. The separation of intrinsic and extrinsic contributions is illustrated in f. A negative skew scattering contribution has been resolved.

Full size image

It has been well-established that there are three mechanisms for the AHE: intrinsic, skew scattering, and side jump. This can be expressed as \({\sigma }_{{{\rm{total}}}}^{A}={\sigma }_{{\mathrm{int}}}+{\sigma }_{{{\rm{sk}}}}+{\sigma }_{{{\rm{sd}}}}\)⁹. In the high conductivity metals (σ_xx > 10⁶ Scm⁻¹), the skew scattering is typically the dominant mechanism; the intrinsic contributions dominate in the good metals, and the side jump is dominant in the bad metals (σ_xx < 10⁴ Scm⁻¹). In particular, the side jump contribution was proposed to be on the order of \(\frac{{e}^{2}}{h}({\varepsilon }_{{so}}/{E}_{F})\)²⁸, where e is the elemental charge, h is the Planck constant, \({\varepsilon }_{{so}}\) is the spin orbit coupling energy, and E_F is the Fermi energy. Due to the close atomic mass of Cl and S, the total spin-orbit coupling energy before and after doping is nearly identical. Consequently, any change in the side jump contribution can be attributed to the change in the Fermi energy E_F. According to the ARPES result, the change in the Fermi energy is from 60 meV to 45 meV, as a result, the side jump contribution should be comparable before and after doping. Conversely, since the doped Co₃Sn₂S₂ shows a fivefold reduction in resistivity compared to the intrinsic crystal at low temperatures, a stronger skew scattering effect can be expected as a result of the longer carrier lifetime after the Cl substitution. We first hypothesize that the side jump contribution is minor compared to the other two in the good metal regime. We then employ the well-established TYJ scaling to differentiate between the intrinsic and extrinsic contributions, as shown in Fig. 4e^29,30. By plotting the AHC against the squared longitudinal conductivity, the intercept on the y-axis can be regarded as the intrinsic contribution (the potential side jump contribution is discussed in supplementary Fig. 4. The fitted intrinsic contribution reaches the value of 1730 Scm⁻¹, which is shown as the purple curve in Fig. 4f. The fitting result allows us to separate the skew scattering from the total AHC. The separation reveals a negative contribution below 60 K. The largest skew scattering signal is approximately -500 Scm⁻¹ at 2 K, and it gradually vanishes with an increasing temperature until 60 K. The fitting details, as well as raw data of the AHE, are summarized in Supplementary Data 3. The fitted intrinsic AHC is 40% higher than the theoretical value of 1200 Scm⁻¹. A comparable outcome has been reported by Gao et al., showing a large enhancement in the anomalous Hall conductivity, in conjunction with a negative skew scattering contribution³¹. In their study it was asserted that their high-quality crystal is approaching the clean limit and exhibiting a more pronounced skew scattering and side jump contributions. Theoretically, when the crystals are in proximity to the clean limit, the skew scattering contribution is markedly amplified, whereas the side jump contribution is suppressed due to the reduction of scattering centers. Since the skew scattering effect introduces a negative contribution to the total AHE, and increase in intrinsic and side jump contributions is required to balance out this negative contribution. As previously discussed, the side jump contribution can be enhanced when the Fermi energy is shifted up. With regard to the intrinsic part, a tentative explanation is an enhanced contribution from the Weyl points, which is discussed in detail in supplementary Fig. 5. Though not fully proven, we believe that the shift in the Fermi energy, in addition to the better crystal quality, is necessary to explain the enhancement to the AHE.

Pristine and Cl-doped Co₃Sn₂S₂ single crystals are grown by a self-flux method, and the electrical transport properties are reported and compared to the intrinsic Co₃Sn₂S₂. A ninefold larger MR reaching the maximum value of 155%, along with a two times higher electron mobility over 4000 cm²V⁻¹s⁻¹ are observed in Cl doped Co₃Sn₂S₂ single crystal. Meanwhile, the Cl-doped crystal shows the stronger two-carrier effect in the ordinary Hall measurement and a significant enhancement in the anomalous Hall effect. After Cl doping, the smaller energy difference between the Fermi energy and the Weyl points brings a significant increase in the AHC, with a peak of 1680 Scm⁻¹ at 40 K, approximately 30% higher than the undoped crystal. ARPES and DFT calculation demonstrate that a nominal 1% doping of chlorine is found to be effective to shift the Fermi energy 15 meV up towards the Weyl points, making the chlorine doped Co₃Sn₂S₂ exhibit a stronger semimetal signature. We emphasize that more Weyl semimetal signatures of transport are likely to be revealed in Co₃Sn₂S₂ as long as alternative strategies are applied to further shift the Fermi level up.

Crystal growth

Intrinsic Co₃Sn₂S₂ single crystals have been grown with multiple techniques^13,19,20. In this study, in order to precisely control the stoichiometry and the doping level, the self-flux method similar to the previous reports is applied¹³. SnCl₂ is selected as the Cl dopant. Elemental Co, Sn, S and SnCl₂ compound are weighted by stoichiometry and loaded in a quartz ampoule. For the 1% Cl doped crystal, the actual molar ratio of the starting material is Co: Sn: S: SnCl₂ = 3:1.99:1.98:0.01, and the nominal composition is Co₃Sn₂S_1.98Cl_0.02. The ampoule is sealed under vacuum, loaded in a box furnace and heated up to 1100 °C at the rate of 100 °C per hour. The ampoule is kept at 1100 °C for one day and quickly cooled to 1000 °C. The ampoule is then cooled down to 800 °C over 100 h and afterwards, furnace cooled to room temperature. The acquired crystal is cut with a 25 μm wire saw to a parallelepiped bar for the later transport measurement.

Sample characterization

The single crystal quality and orientation of the cut crystal is determined by Laue X-ray diffraction. The phase purity is examined by Oxford energy-dispersive X-ray spectroscopy (Quantax, Bruker) X-ray powder diffraction of a powder ground from crystal cuttings. Rietveld refinement is then used to determine the lattice constants after doping.

Transport measurements

Longitudinal and Hall resistivities were measured in a Quantum Design Physical Property Measurement System (PPMS9) with the electrical transport option (ETO) by a standard four-probe method. The in-field electrical conductivity is taken as the inverse of the electrical resistivity due to the fact that the longitudinal resistivity is much larger than the Hall resistivity (\({\rho }_{{xx}} \sim \,20{\rho }_{{yx}}\) at 2 K) The in-field electrical conductivity is used to fit the carrier concentrations and mobilities.

ARPES

The ARPES experiments were carried out at the ULTRA end station at the SIS beamline of the Swiss Light Source with a Scienta Omicron DA30-L spectrometer. The single crystal samples were cleaved in-situ at 15 K with base pressure below 1 × 10⁻¹⁰ mbar. The data were collected using photon energies in the ultraviolet regions. The ARPES data were acquired with an overall energy resolution of 5 meV and angular resolution of 0.1°.

DFT calculations

The electronic band structures were calculated from density fluctional theory by the code of Vienna Ab-initio Simulation Package (VASP) with projector augmented wave method³². The exchange and correlation energies were considered in the generalized gradient approximation, following the Perdew-Burke-Ernzerhof parametrization scheme³³. We project Bloch wavefunctions into maximally localized Wannier functions (MLWFs) and the tight binding model Hamiltonian was constructed from the MLWFs³⁴. Based on the effective tight binding model Hamiltonian, we preformed the calculations for the AHC by the linear response Kubo formula approach in the clear limit¹⁰.