Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Unified deep learning framework for many-body quantum chemistry via Green’s functions

Nature Computational Science volume 5, pages 502–513 (2025)Cite this article

Subjects

A preprint version of the article is available at arXiv.

Abstract

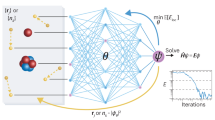
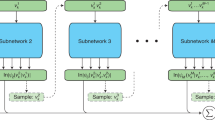
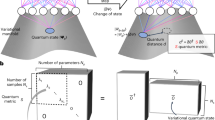
Quantum many-body methods provide a systematic route to computing electronic properties of molecules and materials, but high computational costs restrict their use in large-scale applications. Owing to the complexity in many-electron wavefunctions, machine learning models capable of capturing fundamental many-body physics remain limited. Here we present a deep learning framework targeting the many-body Green’s function, which unifies predictions of electronic properties in ground and excited states, while offering physical insights into many-electron correlation effects. By learning the many-body perturbation theory or coupled-cluster self-energy from mean-field features, our graph neural network achieves competitive performance in predicting one- and two-particle excitations and quantities derivable from a one-particle density matrix. We demonstrate its high data efficiency and good transferability across chemical species, system sizes, molecular conformations and correlation strengths in bond breaking, through multiple molecular and nanomaterial benchmarks. This work opens up opportunities for utilizing machine learning to solve many-electron problems.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Overview of the MBGF-Net workflow and architecture.
Fig. 2: MBGF-Net predictions of electronic properties of QM7 and QM9 molecules at the G0W0@PBE0 level.
Fig. 3: MBGF-Net predictions of excited-state properties of silicon nanoclusters at the G0W0@PBE0 level.
Fig. 4: MBGF-Net predictions of band gaps of azobenzene derivatives at the G0W0@PBE0 level.
Fig. 5: MBGF-Net predictions of orbital-specific many-body properties and downstream simulations in C–O single-bond breaking.

Similar content being viewed by others

Data availability

Source data are provided with this paper. The datasets used in this work are available via Zenodo at https://doi.org/10.5281/zenodo.15131927 (ref. 72).

Code availability

The code used in this work is available via Zenodo at https://doi.org/10.5281/zenodo.15175905 (ref. 73) and via GitHub at https://github.com/ZhuGroup-Yale/mlgf. Its implementation uses the fcDMFT code available at https://github.com/ZhuGroup-Yale/fcdmft and PySCF at https://github.com/pyscf/pyscf.

References

  1. Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133 (1965).

    Article  MathSciNet  Google Scholar 

  2. Cohen, A. J., Mori-Sánchez, P. & Yang, W. Challenges for density functional theory. Chem. Rev. 112, 289 (2012).

    Article  Google Scholar 

  3. Bartlett, R. J. & Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 79, 291 (2007).

    Article  Google Scholar 

  4. Hybertsen, M. S. & Louie, S. G. Electron correlation in semiconductors and insulators: band gaps and quasiparticle energies. Phys. Rev. B 34, 5390 (1986).

    Article  Google Scholar 

  5. Golze, D., Dvorak, M. & Rinke, P. The GW compendium: a practical guide to theoretical photoemission spectroscopy. Front. Chem. 7, 377 (2019).

    Article  Google Scholar 

  6. Keith, J. A. et al. Combining machine learning and computational chemistry for predictive insights into chemical systems. Chem. Rev. 121, 9816 (2021).

    Article  Google Scholar 

  7. Westermayr, J. & Marquetand, P. Machine learning for electronically excited states of molecules. Chem. Rev. 121, 9873 (2021).

    Article  Google Scholar 

  8. Deringer, V. L. et al. Gaussian process regression for materials and molecules. Chem. Rev. 121, 10073 (2021).

    Article  Google Scholar 

  9. von Lilienfeld, O. A., Müller, K. R. & Tkatchenko, A. Exploring chemical compound space with quantum-based machine learning. Nat. Rev. Chem. 4, 347–358 (2020).

    Article  Google Scholar 

  10. Behler, J. & Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98, 146401 (2007).

    Article  Google Scholar 

  11. Zhang, L., Han, J., Wang, H., Car, R. & Weinan, E. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics. Phys. Rev. Lett. 120, 143001 (2018).

    Article  Google Scholar 

  12. Schütt, K. T., Sauceda, H. E., Kindermans, P. J., Tkatchenko, A. & Müller, K. R. SchNet—a deep learning architecture for molecules and materials. J. Chem. Phys. 148, 241722 (2018).

    Article  Google Scholar 

  13. Smith, J. S. et al. Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning. Nat. Commun. 10, 2903 (2019).

    Article  Google Scholar 

  14. Qiao, Z., Welborn, M., Anandkumar, A., Manby, F. R. & Miller, T. F. OrbNet: deep learning for quantum chemistry using symmetry-adapted atomic-orbital features. J. Chem. Phys. 153, 124111 (2020).

    Article  Google Scholar 

  15. Schütt, K. T., Gastegger, M., Tkatchenko, A., Müller, K. R. & Maurer, R. J. Unifying machine learning and quantum chemistry with a deep neural network for molecular wavefunctions. Nat. Commun. 10, 5024 (2019).

    Article  Google Scholar 

  16. Westermayr, J. & Maurer, R. J. Physically inspired deep learning of molecular excitations and photoemission spectra. Chem. Sci. 12, 10755 (2021).

    Article  Google Scholar 

  17. Li, H. et al. Deep-learning density functional theory Hamiltonian for efficient ab initio electronic-structure calculation. Nat. Comput. Sci. 2, 367–377 (2022).

    Article  Google Scholar 

  18. Gong, X. et al. General framework for E(3)-equivariant neural network representation of density functional theory Hamiltonian. Nat. Commun. 14, 2848 (2023).

    Article  Google Scholar 

  19. Grisafi, A. et al. Transferable machine-learning model of the electron density. ACS Cent. Sci. 5, 57 (2019).

    Article  Google Scholar 

  20. Brockherde, F. et al. Bypassing the Kohn–Sham equations with machine learning. Nat. Commun. 8, 872 (2017).

    Article  Google Scholar 

  21. Li, C., Sharir, O., Yuan, S. & Chan, G. K.-L. Image super-resolution inspired electron density prediction. Preprint at http://arxiv.org/abs/2402.12335 (2024).

  22. Knøsgaard, N. R. & Thygesen, K. S. Representing individual electronic states for machine learning GW band structures of 2D materials. Nat. Commun. 13, 468 (2022).

    Article  Google Scholar 

  23. Hou, B., Wu, J. & Qiu, D. Y. Unsupervised representation learning of Kohn–Sham states and consequences for downstream predictions of many-body effects. Nat. Commun. 15, 9481 (2024).

    Article  Google Scholar 

  24. Shao, X., Paetow, L., Tuckerman, M. E. & Pavanello, M. Machine learning electronic structure methods based on the one-electron reduced density matrix. Nat. Commun. 14, 6281 (2023).

    Article  Google Scholar 

  25. Bai, Y., Vogt-Maranto, L., Tuckerman, M. E. & Glover, W. J. Machine learning the Hohenberg–Kohn map for molecular excited states. Nat. Commun. 13, 7044 (2022).

    Article  Google Scholar 

  26. Hedin, L. New method for calculating the one-particle Green’s function with application to the electron-gas problem. Phys. Rev. 139, A796–A823 (1965).

    Article  Google Scholar 

  27. Blase, X., Duchemin, I., Jacquemin, D. & Loos, P.-F. The Bethe–Salpeter equation formalism: from physics to chemistry. J. Phys. Chem. Lett. 11, 7371 (2020).

    Article  Google Scholar 

  28. Zhu, T. & Chan, G. K. L. All-electron Gaussian-based G0W0 for valence and core excitation energies of periodic systems. J. Chem. Theory Comput. 17, 741 (2021).

    Article  Google Scholar 

  29. Lei, J. & Zhu, T. Gaussian-based quasiparticle self-consistent GW for periodic systems. J. Chem. Phys. 157, 214114 (2022).

    Article  Google Scholar 

  30. Nooijen, M. & Snijders, J. G. Coupled cluster Green’s function method: working equations and applications. Int. J. Quantum Chem. 48, 15 (1993).

    Article  Google Scholar 

  31. Peng, B. & Kowalski, K. Green’s function coupled-cluster approach: simulating photoelectron spectra for realistic molecular systems. J. Chem. Theory Comput. 14, 4335 (2018).

    Article  Google Scholar 

  32. Zhu, T., Jiménez-Hoyos, C. A., McClain, J., Berkelbach, T. C. & Chan, G. K.-L. Coupled-cluster impurity solvers for dynamical mean-field theory. Phys. Rev. B 100, 115154 (2019).

    Article  Google Scholar 

  33. Laughon, K., Yu, J. M. & Zhu, T. Periodic coupled-cluster Green’s function for photoemission spectra of realistic solids. J. Phys. Chem. Lett. 13, 9122 (2022).

    Article  Google Scholar 

  34. Phillips, J. J. & Zgid, D. Communication: the description of strong correlation within self-consistent Green’s function second-order perturbation theory. J. Chem. Phys. 140, 241101 (2014).

    Article  Google Scholar 

  35. Hirata, S., Hermes, M. R., Simons, J. & Ortiz, J. V. General-order many-body Green’s function method. J. Chem. Theory Comput. 11, 1595 (2015).

    Article  Google Scholar 

  36. Banerjee, S. & Sokolov, A. Y. Algebraic diagrammatic construction theory for simulating charged excited states and photoelectron spectra. J. Chem. Theory Comput. 19, 3053 (2023).

    Article  Google Scholar 

  37. Ronca, E., Li, Z., Jimenez-Hoyos, C. A. & Chan, G. K. L. Time-step targeting time-dependent and dynamical density matrix renormalization group algorithms with ab initio Hamiltonians. J. Chem. Theory Comput. 13, 5560 (2017).

    Article  Google Scholar 

  38. Gull, E. et al. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 83, 349 (2011).

    Article  Google Scholar 

  39. Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865 (2006).

    Article  Google Scholar 

  40. Zhu, T., Cui, Z.-H. & Chan, G. K.-L. Efficient formulation of ab initio quantum embedding in periodic systems: dynamical mean-field theory. J. Chem. Theory Comput. 16, 141 (2020).

    Article  Google Scholar 

  41. Zhu, T. & Chan, G. K.-L. Ab initio full cell GW+DMFT for correlated materials. Phys. Rev. X 11, 021006 (2021).

    Google Scholar 

  42. Lan, T. N., Kananenka, A. A. & Zgid, D. Communication: towards ab initio self-energy embedding theory in quantum chemistry. J. Chem. Phys. 143, 241102 (2015).

    Article  Google Scholar 

  43. Venturella, C., Hillenbrand, C., Li, J. & Zhu, T. Machine learning many-body Green’s functions for molecular excitation spectra. J. Chem. Theory Comput. 20, 143 (2024).

    Article  Google Scholar 

  44. Arsenault, L. F., Lopez-Bezanilla, A., Von Lilienfeld, O. A. & Millis, A. J. Machine learning for many-body physics: the case of the Anderson impurity model. Phys. Rev. B 90, 155136 (2014).

    Article  Google Scholar 

  45. Dong, X., Gull, E. & Wang, L. Equivariant neural network for Green’s functions of molecules and materials. Phys. Rev. B 109, 075112 (2024).

    Article  Google Scholar 

  46. Batzner, S. et al. E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nat. Commun. 13, 2453 (2022).

    Article  Google Scholar 

  47. Reiser, P. et al. Graph neural networks for materials science and chemistry. Commun. Mater. 3, 93 (2022).

    Article  Google Scholar 

  48. Knizia, G. Intrinsic atomic orbitals: an unbiased bridge between quantum theory and chemical concepts. J. Chem. Theory Comput. 9, 4834 (2013).

    Article  Google Scholar 

  49. Qiao, Z. et al. Informing geometric deep learning with electronic interactions to accelerate quantum chemistry. Proc. Natl Acad. Sci. USA 119, e2205221119 (2022).

    Article  Google Scholar 

  50. Wilhelm, J., Seewald, P. & Golze, D. Low-scaling gw with benchmark accuracy and application to phosphorene nanosheets. J. Chem. Theory Comput. 17, 1662 (2021).

    Article  Google Scholar 

  51. Rupp, M., Tkatchenko, A., Müller, K. R. & Von Lilienfeld, O. A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108, 058301 (2012).

    Article  Google Scholar 

  52. Ramakrishnan, R., Dral, P. O., Rupp, M. & Von Lilienfeld, O. A. Quantum chemistry structures and properties of 134 kilo molecules. Sci. Data 1, 140022 (2014).

    Article  Google Scholar 

  53. Dunning, T. H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007 (1989).

    Article  Google Scholar 

  54. Woon, D. E. & Dunning, T. H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 98, 1358 (1993).

    Article  Google Scholar 

  55. Sun, Q. et al. Recent developments in the PySCF program package. J. Chem. Phys. 153, 024109 (2020).

    Article  Google Scholar 

  56. Adamo, C. & Barone, V. Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 110, 6158 (1999).

    Article  Google Scholar 

  57. Fediai, A., Reiser, P., Peña, J. E. O., Wenzel, W. & Friederich, P. Interpretable delta-learning of GW quasiparticle energies from GGA-DFT. Mach. Learn. Sci. Technol. 4, 035045 (2023).

    Article  Google Scholar 

  58. Zauchner, M. G., Horsfield, A. & Lischner, J. Accelerating GW calculations through machine-learned dielectric matrices. npj Comput. Mater. 9, 184 (2023).

    Article  Google Scholar 

  59. Gao, W., Tang, Z., Zhao, J. & Chelikowsky, J. R. Efficient full-frequency GW calculations using a Lanczos method. Phys. Rev. Lett. 132, 126402 (2024).

    Article  MathSciNet  Google Scholar 

  60. Kühne, T. D. et al. CP2K: an electronic structure and molecular dynamics software package—Quickstep: efficient and accurate electronic structure calculations. J. Chem. Phys. 152, 194103 (2020).

    Article  Google Scholar 

  61. Zhu, T., Peng, L., Zhai, H., Cui, Z.-H. & Chan, G. K.-L. Towards an exact electronic quantum many-body treatment of Kondo correlation in magnetic impurities. Preprint at http://arxiv.org/abs/2405.18709 (2024).

  62. Taube, A. G. & Bartlett, R. J. Frozen natural orbital coupled-cluster theory: forces and application to decomposition of nitroethane. J. Chem. Phys. 128, 164101 (2008).

    Article  Google Scholar 

  63. Li, J. & Zhu, T. Interacting-bath dynamical embedding for capturing non-local electron correlation in solids. Phys. Rev. Lett. 133, 216402 (2024).

    Article  Google Scholar 

  64. Cui, Z.-H., Zhu, T. & Chan, G. K.-L. Efficient implementation of ab initio quantum embedding in periodic systems: density matrix embedding theory. J. Chem. Theory Comput. 16, 119 (2019).

    Article  Google Scholar 

  65. Paszke, A. et al. Automatic differentiation in PyTorch. In Proc. 31st Conference on Neural Information Processing Systems (NIPS), Workshop on Automatic Differentiation (2017); https://openreview.net/pdf?id=BJJsrmfCZ

  66. Fey, M. & Lenssen, J. E. Fast graph representation learning with PyTorch Geometric. Preprint at https://arxiv.org/abs/1903.02428 (2019).

  67. Veličković, P. et al. Graph attention networks. In Proc. International Conference on Learning Representations (2018); https://openreview.net/forum?id=rJXMpikCZ

  68. Li, Y., Gu, C., Dullien, T., Vinyals, O. & Kohli, P. Graph matching networks for learning the similarity of graph structured objects. In Proc. 36th International Conference on Machine Learning, PMLR 97, 3835-3845 (2019); http://proceedings.mlr.press/v97/li19d.html

  69. Gastegger, M., Behler, J. & Marquetand, P. Machine learning molecular dynamics for the simulation of infrared spectra. Chem. Sci. 8, 6924 (2017).

    Article  Google Scholar 

  70. Krause, K. & Klopper, W. Implementation of the Bethe–Salpeter equation in the TURBOMOLE program. J. Comput. Chem. 38, 383 (2017).

    Article  Google Scholar 

  71. Hillenbrand, C., Li, J. & Zhu, T. Energy-specific Bethe–Salpeter equation implementation for efficient optical spectrum calculations. The Journal of Chemical Physics 162, 174117 (2025).

    Article  Google Scholar 

  72. Venturella, C., Li, J., Hillenbrand, C. & Zhu, T. Dataset for unified deep learning framework for many-body quantum chemistry via Green’s functions. Zenodo https://doi.org/10.5281/zenodo.15131927 (2025).

  73. Venturella, C., Li, J., Hillenbrand, C. & Zhu, T. Code for unified deep learning framework for many-body quantum chemistry via Green’s functions. Zenodo https://doi.org/10.5281/zenodo.15175905 (2025).

  74. Wolkin, M. V., Jorne, J., Fauchet, P. M., Allan, G. & Delerue, C. Electronic states and luminescence in porous silicon quantum dots: the role of oxygen. Phys. Rev. Lett. 82, 197 (1999).

    Article  Google Scholar 

Download references

Acknowledgements

The development of the MBGF-Net model was supported by the National Science Foundation under award number CHE-2337991 (C.V. and T.Z.) and the National Science Foundation Engines Development Award: Advancing Quantum Technologies (CT) under award number 2302908 (C.H.). The development of the Green’s function property analysis and the BSE code was supported by the Air Force Office of Scientific Research under award number FA9550-24-1-0096 (J. Li). C.V. acknowledges partial support from the Department of Defense through the National Defense Science and Engineering Graduate (NDSEG) Fellowship Program. J. Li acknowledges partial support from the Tony Massini Postdoctoral Fellowship in Data Science from Yale University. We thank the Yale Center for Research Computing for guidance and use of the research computing infrastructure.

Author information

Authors and Affiliations

  1. Department of Chemistry, Yale University, New Haven, CT, USA

    Christian Venturella, Jiachen Li, Christopher Hillenbrand, Ximena Leyva Peralta, Jessica Liu & Tianyu Zhu

Authors
  1. Christian Venturella
    View author publications

    Search author on:PubMed Google Scholar

  2. Jiachen Li
    View author publications

    Search author on:PubMed Google Scholar

  3. Christopher Hillenbrand
    View author publications

    Search author on:PubMed Google Scholar

  4. Ximena Leyva Peralta
    View author publications

    Search author on:PubMed Google Scholar

  5. Jessica Liu
    View author publications

    Search author on:PubMed Google Scholar

  6. Tianyu Zhu
    View author publications

    Search author on:PubMed Google Scholar

Contributions

C.V. and T.Z. designed the project and wrote the manuscript. C.V. developed the GNN model and code. C.V., J. Li and T.Z. developed the Green’s function postprocessing workflow. J. Li and C.H. developed the BSE code. C.V., C.H., X.L.P. and J. Liu performed Green’s function calculations and data analyses. T.Z. supervised the project. All authors contributed to the discussion of the results as well as the writing and editing of the manuscript.

Corresponding author

Correspondence to Tianyu Zhu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Computational Science thanks Yong Xu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Jie Pan, in collaboration with the Nature Computational Science team.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Sections 1–11, Figs. 1–14, Tables 1–4, Algorithm 1 and references.

Source data

Source Data Fig. 2

QM9 benchmark results.

Source Data Fig. 3

Nanocluster benchmark results.

Source Data Fig. 4

Azobenzene benchmark results.

Source Data Fig. 5

Bond-stretching benchmark results.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Venturella, C., Li, J., Hillenbrand, C. et al. Unified deep learning framework for many-body quantum chemistry via Green’s functions. Nat Comput Sci 5, 502–513 (2025). https://doi.org/10.1038/s43588-025-00810-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s43588-025-00810-z

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing