Introduction

Structural mechanics computation plays an important role in the field of civil and structure engineering, which is fundamental for the design and analysis of structures. In particular, with the emergence of Digital Twin (DT)1,2,3, it requires establishing a virtual digital model and implementing real-time simulation to accurately replicate physical structures. Therefore, the accurate and efficient computation of structural behavior is critical in the DT system4,5. Currently, Finite Element Method (FEM) is commonly used for structural computation, and several commercial FEM software options (e.g., ANSYS and ABAQUS) are available. However, there exit three main limitations associated with FEM, especially as a computational module in DT system6: (i) The repetitive process of establishing and computing FEM models hardly satisfies the real-time capability due to its cumbersome nature and time-consuming procedure; (ii) Integrating encapsulated FEM software into DT systems is challenging; (iii) The FEM approach cannot handle the infinite ___domain problems in which the boundary conditions or initial conditions may be unknown. In addition, FEM cannot solve the inverse problem, e.g., the inference of structure parameters from the structural response.

With the rise of artificial intelligence (AI) in recent years, especially the advancement of deep learning developed from neural network, AI technology has been broadly applied in the field of engineering structures7,8,9,10, such as damage identification11,12,13,14, model optimization15,16, and performance prediction17,18,19,20. Data-driven network models rely on large amounts of high-quality data and lack physical interpretability. Some studies currently explain the black box model by employing SHAP (SHapley Additive exPlanations) to quantify the contribution of each input feature to the output prediction21,22,23. However, physics-explaining machine learning still finds it difficult to directly learn physics prior knowledge. To address this issue, the physics-informed neural network (PINN) was proposed24,25,26, which has the capability to learn the prior knowledge of partial differential equations with or without labeled data. Moreover, PINN has the advantage of solving practical problems with unknown boundary conditions or initial conditions imposed on the boundary27. In addition, a well-trained PINN model with generalization capabilities can be regarded as a surrogate model, greatly enhancing computational efficiency and enabling real-time predictions. To this end, PINN has attracted increasing attention ever since it was first proposed28 and has been applied in various communities such as shape optimization29, thermochemical curing30, quantification of cracks31, metal additive manufacturing32, seismic response prediction33,34, nonlinear modeling35, structural design36, material defect identification37, subsurface flow problems38, engineering problems in heterogeneous domains39. In addition, there have been several extensions in computational science, including solving partial differential equations (PDEs) problems with optimized framework40,41,42,43,44,45,46, surrogate modeling47, multi-physics simulation framework48, fluid mechanics49,50,51,52,53, solid mechanics54,55,56,57, transfer learning58, computational elastic dynamic59. In general, the application of PINN could be divided into two categories: forward and inverse problems. The inverse problem aims to determine unknown physical parameters of a system from the known output by optimizing the prediction effect of data-driven neural networks through learning physical information. The forward problem is to implement PINN as a solver for PDEs without relying on labeled data, which can be regarded as an unsupervised learning approach by learning physical laws instead of labeled data. Previous studies related to the forward problem have mainly focused on optimizing the PINN framework according to the specific PDEs44.

Compared to the FEM approach that requires the generation of fine discrete meshes, PINNs directly model the continuous field, making them a meshless method. Moreover, PINNs demonstrate remarkable flexibility to solve problems by combining simulated data from FEM and relevant physical laws for training neural networks60. However, in the field of structural mechanics computation, the establishment of PINN for bending structures is still a challenging task due to the inherent complexity associated with solving higher-order PDEs. The governing equations for bending calculation of structures are characterized by fourth-order nonlinear PDEs featuring multiple orders of differential terms, which significantly decreases the accuracy of PINN when it comes to higher-order differentiation. More importantly, the presence of multi-order differential terms in PDEs can result in unstable convergence or even non-convergence due to the significant variations in the weights assigned to these differential terms42.

In this study, to address the above-mentioned challenge in computational structural mechanics, we propose a multi-level physics-informed neural network framework (herein termed as ml-PINN), enabling intelligent computation of bending structures governed by fourth-order nonlinear PDEs. Through comparison with FEM results, we validate the accuracy of ml-PINN for the solution of bending structures including the typical beam and shell structures. To our knowledge, this is the first application of PINN as a promising paradigm in computational structural mechanics. The proposed method provides a promising perspective for structure mechanics computation and holds potential as an intelligent computational module embedded into structural DT systems.

Results

Framework of ml-PINN

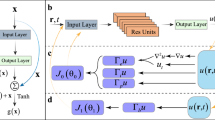
The classical PINN methodology for solving high-order PDEs involves utilizing the automatic differentiation technique to directly evaluate the high-order differential terms based on a single neural network (NN) (Fig. 1). Nevertheless, using a single NN for multi-order differentiations and multiple parameters can significantly increase the amount of computation, resulting in extended computation time and unstable convergence. (The relevant content is elaborated in the Supplementary information)

Fig. 1: Classical physics-informed neural network framework for solving high-order partial differential equations (PDEs).
figure 1

Lb() and Lp() represent the loss functions from boundary constraints and loss functions from the partial differential equation (PDE), respectively. LB/C and LPDE represent the loss of boundary condition and physical PDE. Here, ω represents the differentiated physical variable as well as the output of the single NN, and ω’, ω” and ω(n) are first-order derivative, second-order derivative, and n-order derivative. {W, b}i presents the model parameter of neural networks (NNs).

Full size image

To tackle this problem, we propose a multi-level physics-informed neural network (ml-PINN). Two strategies have been incorporated in the ml-PINN: (i) a aggregation model is established by combining multiple NNs, where the ensemble learning involves only first-order or second-order PDEs representing the geometrical, constitutive, and equilibrium relations of the structure. This effectively reduces the order of the original higher-order PDEs; (ii) The loss functions corresponding to each NN with lower-order PDEs are linked and combined into one loss function with similar weights for all variables. Additionally, the loss function for boundary constraints can be directly defined in each individual NN rather than through differential terms. These treatments enable successful solutions for structural bending calculation. The specific process is described below.

The ml-PINN model is established to predict the vertical displacements of bending structures, including the beam and shell structures. The beam structure can be regarded as a one-dimensional (1D) scenario, and the computation framework of ml-PINN for beam is correspondingly presented in Fig. 2. The beam is subjected to a uniform distributed load q (Fig. 2a), and the vertical displacement ω along with other important parameters including section angle θ, curvature κ, bending moment M, and shear force FQ can be simultaneously obtained by the ml-PINN model. The governing equation for the beam structure is a fourth-order differential equation relating q and ω, which can be transformed into five first-order equations. The five equations actually correspond to the three fundamental equations in structural mechanics: the geometric equation, stress-strain equation, and equilibrium equation with physical variables (i.e., θ, κ, M, and FQ) as transition parameters (see ‘Methods’ for details). Figure 2b illustrates how these physical variables are related during the transition from q to ω. Figure 2c presents the framework of ml-PINN to illustrate the computation process for beam structures. Firstly, three separate neural networks (NNs) are established to obtain the outputs of ω, κ, and M, which means that each parameter is trained independently within its own dedicated NN. This strategy facilitates the convergence of training owing to reducing the complexity of NN for each parameter. More details can be found in the ‘Discussion’ section. Secondly, the derivatives of the NN output are obtained by utilizing the automatic differentiation technique, including dω/dx, dθ/dx, dκ/dx, dFQ/dx. Lastly, the multiple NNs are connected by the loss functions to form a comprehensive loss function that includes both the loss functions from differential equations (Lp) and those from boundary constraints (Lb). During the iterative computation process, the updated parameters of multiple NNs are optimized to minimize the loss function until convergence is achieved.

Fig. 2: Multi-level physics-informed neural network (ml-PINN) for 1D beam.
figure 2

a Diagrammatic sketch of beam structure. b Physical relationship between the relevant variables that transforms the uniform load q into the vertical displacement ω by utilizing the three typical equations. M represents bending moment. EI is bending stiffness. The intermediate variables including shear force FQ, curvature κ, rotation angle θ, and displacement ω are outputted from each neural network. c Schematics of ml-PINN framework for beam structure. Lb() and Lp() represent the loss functions from boundary constraints and loss functions from PDE, respectively. Lp(ω’, θ), Lp(θ’, κ), Lp(M’, FQ) and Lp(FQ’, q) are loss functions corresponding to each differential equation. Lb(ω), Lb(θ) and Lb(M) are the loss functions from boundary constraints corresponding to the vertical displacement, section turning angle, and bending moment respectively. {W, b}i presents the model parameter of neural networks (NNs).

Full size image

For the two-dimensional (2D) scenario of shell structures, the computation framework of ml-PINN is presented in Fig. 3. Similar to beam structures, the approach to reduce the PDE order involves decomposing into the lower-order PDEs (i.e., the three typical equations). However, in shell structures, these decomposed equations are second-order differential terms such as the relationship between ωNN(x, y) and κNN(x, y) as well as the relationship between MNN(x, y) and q(x, y) (see Fig. 3b). Moreover, the framework for shell structure is more complicated due to the increase of dimension, the existence of second-order partial derivatives, and more boundary constraints (Fig. 3c). Hence, training the framework of shell structures requires more time-consuming iterations to achieve convergence.

Fig. 3: Multi-level physics-informed neural network (ml-PINN) for 2D shell.
figure 3

a Diagrammatic sketch of shell structures. b Physical relationship between the relevant variables that transform the uniform load q into the vertical displacement ω by utilizing the three typical equations. Mx and My represent the bending moment of shell structures in the x-direction and y-direction, respectively. Mxy denotes the torque in the z-direction. The vertical displacement is in the z-direction. For the direction, curvature (κx, κy, κxy) is similar to the bending moment (Mx, My, Mxy). The intermediate variables including shear force FQ, curvature κ and displacement ω are outputted from each neural network. c Schematics of ml-PINN framework for shell structures. Lb() and Lp() represent the loss functions from boundary constraints and loss functions from PDE, respectively. Lp(ω”, κ), Lp(κ, M) and Lp(M”, q) are the loss functions corresponding to PDEs. Lb(ω), Lb(ω’), and Lb(M) are the loss functions of boundary constraints from the vertical displacement, section turning angle, and bending moment, respectively.

Full size image

Computational results of bending structures

We first consider the computation of 1D beam structures under four different loading conditions, and the ml-PINN computed results of beam deformation are compared with the corresponding FEM results. As previously mentioned, the arbitrarily distributed points, termed as collocation points, are required to train the NN. A total of 25 randomly distributed collocation points along the beam structure are used for training (Fig. 4a). Regarding the influence of point number on the computational results, see the forthcoming sensitivity analysis.

Fig. 4: Computational results for 1D beam structure.
figure 4

a Randomly distributed training data for beam structures. b Verification for case 1 (simply supported beam). The boundary displacement ω constraint is given by ω | x/l=0,x/l=1 = 0. The vertical uniform load q is set to −1. c Verification for case 2 (double-clamped beam). The displacement ω and turning angle θ at the ends of the beam are imposed with ω | x/l=0,x/l=1 = 0 and θ | x/l=0,x/l=1 = 0. The vertical uniform load q is −1. d Verification for case 3. The turning angles θ at the beam ends are constrained, namely, θ | x/l=0,x/l=1 = 0, but the constraints of displacements ω are separately given by ω | x/l=0 = 0 and ω | x/l=1 = 1. e Verification for case 4. The constraints of displacements ω and turning angles θ are defined as ω | x/l=0,x/l=1 = 0 and θ | x/l=0 = 0 and θ | x/l=1 = 1, respectively.

Full size image

The loads exerted on the beam could be divided into external force (i.e., the uniform load q) and boundary constraints (i.e., the displacement ω and rotational angle θ imposed at the two ends of the beam). The specific conditions for different loading cases are listed in Table 1. Figure 4b–e exhibits the comparison of deformation results between ml-PINN and FEM under four different loading conditions. It shows that the vertical displacement computed by ml-PINN agrees quite well with that obtained from FEM. The profiles of beam deformation from both ml-PINN and FEM are almost overlapped (relative error <0.5%), indicating that the ml-PINN shares comparable accuracy with FEM in bending beam computation.

Table 1 The summary of loading conditions for beam structure
Full size table

We further applied the ml-PINN to solve the 2D shell. Table 2 lists the four cases corresponding to various loading conditions exerted on the shell. A total number of 1000 data points are randomly distributed within the interior zone, along with 50 data points at each boundary (S1–S4) (refer to Fig. 5a, b). The comparison indicates that the computed results by ml-PINN and FEM are very close (Fig. 5c–f). The error contours demonstrate that the deviation between ml-PINN and FEM in the corner region of the shell is more obvious than that at the interior region, especially for case 3 and case 4 (Fig. 5e, f). The primary reason is that more constraints imposed at the corners lead to the convergence of computation being more difficult in these regions. Nevertheless, the overall errors remain low, with relative errors below 2%, which means that the proposed ml-PINN model is capable of accurately solving the 2D structural mechanics problem, specifically the deformation of bending shells under various loading conditions.

Table 2 The summary of loading conditions for shell structure
Full size table
Fig. 5: Computational results for 2D shell structure.
figure 5

a Diagram of boundaries. ω and θ represent the displacement and rotation angle imposed on the boundaries, respectively. Note that the direction of θ is indicated as a blue arrow according to the right-handed screw rule, and the direction of ω is in the z-direction. b Distribution of collocation points. The random data points include points in the interior zone Ω and points on the boundaries S1 ~ S4. c Verification for case 1. Only the opposite pair of boundary displacements are constrained by ω | S∈S3, S4 = 0. Note that the three contour plots at the top row from left to right represent the proposed multi-level physics-informed neural network predictions (named PINN in the figure), Finite element method predictions (named FEM in the figure), and the relative error, respectively. The two plots at the bottom present the extracted results of deformation in x-directions and y-directions, respectively (as illustrated by the dotted line in the contour of FEM). d Verification for case 2. All surrounding boundary displacements are defined as ω | S∈S1, S2, S3, S4 = 0. e Verification for case 3. The displacement ω | S∈S1, S2, S3, S4 = 0 and section corner θ | S∈S1, S2, S3, S4 = 0 are imposed on all surrounding boundaries. f Verification for case 4. The displacement ω | S∈S1, S2, S3, S4 = 0 and section corner θ | S∈S1, S2, S3, S4 = 1 are defined, and the uniform load is given by q = −1.

Full size image

Sensitivity analysis of collocation points

For the ml-PINN computation, the number of collocation points is critical, affecting the resolution of the computational results. Hence, a sensitivity analysis of the collocation points is required. Figure 6 shows the comparison of ml-PINN predicted results using different numbers of collocation points (np). For the beam structure case, we tested 10, 25, 50, and 100 randomly distributed points. For the shell structure case, we used 10, 100, 500, and 1000 randomly distributed points in the interior area while keeping 50 data points fixed at each boundary of the shell structure.

Fig. 6: Comparison of multi-level physics-informed neural network prediction using a different number of collocation points.
figure 6

a Beam structure case with a different number of collocation points. The number of data points np at the interior zone is selected as 10, 25, 50, and 100. b Shell structure case with a different number of collocation points. np represents the number of data points at the interior zone, which is given by 100, 500, 1000, and 2000. nb denotes the number of data points at the boundaries.

Full size image

For the 1D beam (Fig. 6a), the computational error is relatively high (close to 3%) when rather sparse collocation points are used (np = 10), while the error is reduced to less than 1% as the number of collocation points increases (np > 25). Thus, to balance the computational precision and speed, the number of points np = 25 has been adopted. It is concluded that more collocation points are better than fewer collocation points. When there are fewer allocation points, there is not enough information in the data points to support a better prediction effect. As the number of allocation points reaches a certain value (np = 25 in beam element for the studied case), the prediction effect will be almost independent of the number of input data points. It is noted that the number of allocation points can be determined by sensitivity analysis in different applications.

For the 2D shell computation (Fig. 6b), Table 3 lists the quantitative comparison of loss residuals and relative errors corresponding to different numbers of collocation points. It is evident that a number of densely distributed points are required to improve the accuracy, and the error is reduced to approximately 2% when np = 1000. Thus, considering both the computational accuracy and efficiency, we used 1000 collocation points to compute the shell structure, as shown in Fig. 5.

Table 3 Loss residuals and errors of prediction using different number of collocation points
Full size table

Discussion

In summary, this study proposes a ml-PINN framework for structural mechanics computation with high-order PDEs, aiming to predict the response of bending beam and shell structures under different loading conditions. The PDEs of bending structures involve multiple physical parameters such as vertical displacement ω, section angles θ, and bending moment M. These parameters are correlated through differentiation terms (e.g., θ∝∂ω, κ∝∂2ω, and q∝∂4ω as described in the ‘Methods’ section), which are enforced by boundary constraints. Hence, multiple loss functions with different orders of magnitudes corresponding to each differential term exist in the classical PINN framework. The disparity in the magnitudes between these loss functions is substantial due to different orders of differentiation, which results in non-convergence or only local convergence. However, the proposed ml-PINN adopts multiple NNs for the output of each intermediate physical parameter, such as θ, κ, and M, to achieve both local and global convergence, meanwhile reducing the order of differential terms through the transition of the intermediate parameters (e.g., q∝∂FQ, FQ∝∂M, κ∝∂θ and θ∝∂ω in the beam as well as, q∝∂2M, κ∝∂θ and θ∝∂ω in shell). In other words, the advantage of the ml-PINN to solve the high-order PDEs lies in the underlying physical relationships, i.e., the three typical equations describing the correlation between these physical variables. It is evident that the proposed ml-PINN framework significantly enhances computational accuracy by reducing the error of beam and shell structures computation to 0.5% and 2%, respectively, surpassing that achieved by classical PINN, while simultaneously achieving four times faster computation time. This strategy of employing ml-PINN to reduce the order of PDEs can also be extended to address other solid mechanics issues characterized by similar governing PDE properties.

Currently, the primary disadvantage of ml-PINN lies in its time-consuming training process, which is a general problem yielded in PINN when solving the forward problem. However, once the ml-PINN is trained well, it can serve as a surrogate model to enable efficient end-to-end prediction. Overall, the aforementioned results and discussion indicate that the ml-PINN achieves comparable accuracy to FEM for solving bending structures. Moreover, unlike the FEM requiring repeated model establishment (e.g., mesh generation, parameters adjustment, and calibration) and computation for different conditions, the ml-PINN possesses generalization learning capabilities and has the potential to rapidly predict the results for different loading cases once the neural networks (NNs) are well-trained. Figure 7a shows the ml-PINN framework for generalization learning, where the physical variables related to loading conditions (u and q) are considered additional input parameters of the network. Figure 7b exhibits the direct prediction performance under different loading conditions, indicating that incorporating generalization into ml-PINN significantly improves computational efficiency while maintaining comparable accuracy with FEM computation.

Fig. 7: The multi-level physics-informed neural network (ml-PINN) for generalization computation.
figure 7

a Framework of ml-PINN for generalization learning by incorporating the physical variables related to loading conditions (u and q) as input parameters of the networks. u and q represent the displacement applied on the right boundary and the uniform load imposed on the entire region. b Direct prediction results of ml-PINN for bending beam cases under different loading conditions. FEM represents the result predicted by Finite Element Method, and Generalized PINN represents the result predicted by the proposed ml-PINN.

Full size image

Methods

Differential equations of beam structures

The governing equation describing the deformation of a bending beam is a fourth-order differential equation, given by

$$\frac{{d}^{4}\omega }{d{x}^{4}}=\frac{q(x)}{EI}$$
(1)

where q(x) represents the uniform load on the beam, EI denotes flexural stiffness, and ω represents vertical displacement. To reduce the order of Eq. (1), several intermediate variables are introduced, and Eq. (1) can be decomposed into five first-order differential equations:

$$q=-\frac{d{F}_{Q}}{dx}$$
(2a)
$${F}_{Q}=\frac{dM}{dx}$$
(2b)
$$M=-EI\kappa$$
(2c)
$$\kappa =-\frac{d\theta }{dx}$$
(2d)
$$\theta =\frac{d\omega }{dx}$$
(2e)

where θ and κ denote the section angle and curvature of the beam, respectively. M and FQ represent the bending moment and shear force. In structural mechanics, these equations are commonly referred to as equilibrium equation (Eqs. (2a) and (2b)), stress-strain equation (Eqs. (2c)), and geometric equation (Eqs. (2d) and (2e)).

There are two types of boundary constraints: (i) the vertical displacement \(\overline{\omega }\) and section angle \(\overline{\theta }\) are defined on the boundary st1 as,

$$\omega (x)=\overline{\omega }\cap \theta (x)=\overline{\theta },\, x\in {s}_{t1}$$
(3)

Specially, \(\overline{\omega }=0\) and \(\overline{\theta }=0\) means the endpoint consolidation; (ii) the vertical displacement \(\overline{\omega }\) and bending moment \(\overline{M}\) are imposed on the boundary st2 as,

$$\omega (x)=\overline{\omega }\cap M(x)=\overline{M},\, x\in {s}_{t2}$$
(4)

For a simply supported beam, the boundary condition is specified as \(\overline{\omega }=0\) and \(\overline{M}=0\).

Similar to the governing equations of beam structure described above, the governing PDEs for shell structures also incorporate the geometric equation, deformation equation, and equilibrium equation, as given by,

$${\kappa }_{x}=-\frac{{\partial }^{2}\omega }{\partial {x}^{2}}, {\kappa }_{xy}=-2\frac{{\partial }^{2}\omega }{\partial x\partial y}, {\kappa }_{y}=-\frac{{\partial }^{2}\omega }{\partial {y}^{2}}$$
(5)
$$M=\left[\begin{array}{c}{M}_{x}\\ {M}_{y}\\ {M}_{xy}\end{array}\right]=D\kappa =\frac{E{t}^{3}}{12(1-{\nu }^{2})}\left[\begin{array}{ccc}1 & \nu & 0\\ \nu & 1 & 0\\ 0 & 0 & (1-\nu )/2\end{array}\right]\left[\begin{array}{c}{\kappa }_{x}\\ {\kappa }_{y}\\ {\kappa }_{xy}\end{array}\right]$$
(6)
$$\frac{{\partial }^{2}{M}_{x}}{\partial {x}^{2}}+2\frac{{\partial }^{2}{M}_{xy}}{\partial x\partial y}+\frac{{\partial }^{2}{M}_{y}}{\partial {y}^{2}}+q(x,y)=0$$
(7)

where ω denotes the displacement in the z-direction; κx, κy, and κxy represent the curvature of shell structures in the x-direction, y-direction, and torsion rate in the z-direction respectively; Mx, My and Mxy denote the bending moment of shell structures in the x-direction, y-direction, and torque in the z-direction respectively; D, E, t, and ν denote the elastic relationship matrix, elastic modulus, shell thickness in the z-direction, and Poisson ratio of the material respectively; q(x, y) is the uniformly distributed load exerting on the shell, which is a known quantity.

Similarly, two types of boundary constraints are defined on the two boundaries St1 and St2, respectively, which are expressed as

$$\omega (x,y)=\overline{\omega }\cap \frac{\partial \omega }{\partial n}(x,y)=\overline{\theta },(x,\, y)\in {S}_{t1}$$
(8)
$$\omega (x,y)=\overline{\omega }\cap {M}_{n}(x,y)=\overline{{M}_{n}},(x,\, y)\in {S}_{t2}$$
(9)

where \(\overline{\omega }\), \(\overline{\theta }\) and \(\overline{M}\) represent vertical displacement, section angle and bending moment; n denotes normal direction of boundary.

Loss function of ml-PINN

The loss function of ml-PINN is defined as the residuals of PDEs and the boundary constraints. For the beam structure, the loss function of the PDE, Lp, is composed of residuals from geometric equation (Lp(ω‘, θ) and Lp(θ’, κ)) as well as equilibrium equation (Lp(M’, FQ) and Lp(FQ’, q)), as depicted below. Note that the loss function from the stress-strain equation is not established due to its simple linearity between κ and M.

$${L}_{p}(\omega ^{\prime},\theta )={\sum _{i=1}^{{n}_{p}}\left|\left|{\frac{d{\omega }_{NN}}{dx}}_{i}-{\theta }_{NN}{(x,y)}_{i}\right|\right|}_{2}^{2},x\in l$$
(10)
$${L}_{p}(\theta ^{\prime} ,\kappa )={\sum _{i=1}^{{n}_{p}}\left\Vert {\frac{d{\theta }_{NN}}{dx}}_{i}-{\kappa }_{NN}{(x)}_{i}\right\Vert }_{2}^{2},x\in l$$
(11)
$${L}_{p}(M^{\prime} ,{F}_{Q})={\sum _{i=1}^{{n}_{p}}\left\Vert {\frac{d{M}_{NN}}{dx}}_{i}-{F}_{QNN}{(x)}_{i}\right\Vert }_{2}^{2},x\in l$$
(12)
$${L}_{p}({{F}_{Q}}^{{\prime} },q)={\sum _{i=1}^{{n}_{p}}\left\Vert {\frac{d{F}_{QNN}}{dx}}_{i}-q{(x)}_{i}\right\Vert }_{2}^{2},x\in l$$
(13)

where np represents the number of collocation points in whole regions, l represents the interior zone within the computational ___domain of the beam structure, \(\sum ||\cdot |{|}_{2}^{2}\) is the quadratic norm, and \(\frac{d{\omega }_{NN}}{dx}\), \(\frac{d{\theta }_{NN}}{dx}\), \(\frac{d{M}_{NN}}{dx}\) and \(\frac{d{F}_{QNN}}{dx}\) correspond to the first-order derivatives of NNs output for ω, θ, M and FQ respectively.

The loss function of boundary constraints Lb comprises the loss functions for constrained vertical displacement Lb(ω), constrained section corner Lb(θ), and constrained bending moment Lb(M), namely,

$${L}_{b}(\omega )={\sum _{i=1}^{{n}_{b}}\left\Vert {\omega }_{NN}{(x)}_{i}-\overline{\omega {(x)}_{i}}\right\Vert }_{2}^{2},x\in {l}_{b}$$
(14)
$${L}_{b}(\theta )={\sum _{i=1}^{{n}_{b}}\left\Vert {\theta }_{NN}{(x)}_{i}-\overline{\theta {(x)}_{i}}\right\Vert }_{2}^{2},x\in {l}_{b}$$
(15)
$${L}_{b}(M)={\sum _{i=1}^{{n}_{b}}\left\Vert {M}_{NN}{(x)}_{i}-\overline{M{(x)}_{i}}\right\Vert }_{2}^{2},x\in {l}_{b}$$
(16)

where nb denotes the number of collocation points in the boundary regions. lb represents the boundary regions within the beam structure.\(\overline{\omega (x)}\), \(\overline{\theta (x)}\) and \(\overline{M(x)}\) represent the displacement, rotation angle, and bending moment at the boundary, respectively. The total loss function Ltotal of the beam structure is obtained by adding Lp and Lb together, namely,

$${L}_{total}= \left[{L}_{b}(\omega )+{L}_{b}(\theta )+{L}_{b}(M)\right]+\left[{L}_{p}(\omega ^{\prime} ,\theta )+{L}_{p}(\theta ^{\prime} ,\kappa ) +{L}_{p}(M^{\prime} ,{F}_{Q})\right] +{L}_{p}({{F}_{Q}}^{{\prime} },q)$$
(17)

Similarly, for the shell structures, the PDE loss function, Lp, consists of residuals from geometric equation Lp(ω“, κ), stress-strain equation Lp(κ, M), and equilibrium equation Lp(M”, q), which are written as

$${L}_{p}(\omega ^{\prime \prime},\kappa )= {\sum _{i=1}^{{n}_{p}}\left\Vert {\left[\frac{{\partial }^{2}{\omega }_{NN}}{\partial {x}^{2}},\frac{{\partial }^{2}{\omega }_{NN}}{\partial {y}^{2}},2\frac{{\partial }^{2}{\omega }_{NN}}{\partial x\partial y}\right]}_{i}^{T}-{\kappa }_{NN}{(x,y)}_{i}\right\Vert }_{2}^{2},\, (x,y)\in \Omega$$
(18)
$${L}_{p}(\kappa ,M)={\sum _{i=1}^{{n}_{p}}\left\Vert D{\kappa }_{NN}{(x,y)}_{i}-{M}_{NN}{(x,y)}_{i}\right\Vert }_{2}^{2},(x,y)\in \Omega$$
(19)
$${L}_{p}(M^{\prime \prime},q)={\sum _{i=1}^{{n}_{p}}\left\Vert {\left(\frac{{\partial }^{2}{M}_{NNx}}{\partial {x}^{2}}+2\frac{{\partial }^{2}{M}_{NNxy}}{\partial x\partial y}+\frac{{\partial }^{2}{M}_{NNy}}{\partial {y}^{2}}\right)}_{i}+q{(x,y)}_{i}\right\Vert }_{2}^{2},(x,y)\in \Omega$$
(20)

where Ω represents the interior zone of the computational ___domain within the shell structure; \(\frac{{\partial }^{2}{\omega }_{NN}}{\partial {x}^{2}}\), \(\frac{{\partial }^{2}{\omega }_{NN}}{\partial {y}^{2}}\) and \(\frac{{\partial }^{2}{\omega }_{NN}}{\partial x\partial y}\) represent the second-order partial derivative of the NN output of displacement ωNN(x, y); κNN(x, y) is the neural network (NN) output of curvature κ; \(\frac{{\partial }^{2}{M}_{NNx}}{\partial {x}^{2}}\), \(\frac{{\partial }^{2}{M}_{NNy}}{\partial {y}^{2}}\) and \(\frac{{\partial }^{2}{M}_{NNxy}}{\partial x\partial y}\) denote the second-order partial derivative of the NN output of bending moment MNN(x, y).

The loss functions of boundary constraints mainly include constrained vertical displacement Lb(ω), constrained section corner Lb(ω’), and constrained bending moment Lb(Mn), namely,

$${L}_{b}(\omega )={\sum _{i=1}^{{n}_{b}}\left\Vert \omega {(x,y)}_{i}-\overline{\omega {(x,y)}_{i}}\right\Vert }_{2}^{2},(x,y)\in {S}_{1},{S}_{2},{S}_{3},{S}_{4}$$
(21)
$${L}_{b}(\omega ^{\prime})={\sum _{i=1}^{{n}_{b}}\left\Vert \frac{\partial \omega {(x,y)}_{i}}{\partial n}-\overline{\theta {(x,y)}_{i}}\right\Vert }_{2}^{2},(x,y)\in {S}_{1},{S}_{2},{S}_{3},{S}_{4}$$
(22)
$${L}_{b}({M}_{n})={\sum _{i=1}^{{n}_{b}}\left\Vert {M}_{n}{(x,y)}_{i}-\overline{{M}_{n}{(x,y)}_{i}}\right\Vert }_{2}^{2},(x,y)\in {S}_{1},{S}_{2},{S}_{3},{S}_{4}$$
(23)

where S1, S2, S3, and S4 represent different boundary regions within the shell structure (Fig. 5a); \(\overline{\omega (x,y)}\), \(\overline{\theta (x,y)}\) and \(\overline{M(x,y)}\) represent the displacement, rotation angle, and bending moment at the boundaries.

Finally, the total loss function Ltotal of the shell structure is written as

$${L}_{total}=\left[{L}_{b}(\omega )+{L}_{b}(\omega ^{\prime})+{L}_{b}(M)\right]+\left[{L}_{p}(\omega ^{\prime \prime},\kappa )+{L}_{p}(\kappa ,M)+{L}_{p}(M^{\prime \prime},q)\right]$$
(24)

The NNs are automatically optimized to update the weights and biases of the network by minimizing the loss function, namely,

$${\{W,b\}}_{i}^{\ast }={{\mbox{arg}}}{\min }_{{\{W,b\}}_{i}}[Los{s}_{total}(\{W,b\})]$$
(25)

Model setting

All codes are optimized using the ADAM algorithm with a learning rate of 10−3. A total of four neural networks (NNs) were established to predict the output of ω, θ, M, and FQ in the 1D beam structure, namely ωNN, θNN, MNN, and FQNN. All four fully connected feedforward NNs with ml-PINN consist of an input layer with 1 node, 3 hidden layers with 10 nodes each, and an output layer with 1 node. For c-PINN, a single fully connected feedforward neural network (NN) was constructed with an input layer containing 1 node, 3 hidden layers comprising 20 nodes each, and an output layer with 1 node. The aim is to make c-PINN and ml-PINN possess the same capacity in terms of fully connected neural networks. Additionally and similarly, for the 2D shell structure with ml-PINN, three NNs were set up as ωNN, κNN(κx, κy, and κxy), MNN(Mx, My, and Mxy). The NN of ωNN consists of an input layer with 2 nodes, 3 hidden layers with 30 nodes, and an output layer with 1 node. Additionally, the NNs used in κNN and MNN were constructed with an input layer with 2 nodes, 3 hidden layers with 20 nodes, and an output layer with 3 nodes.