Can we develop a more targeted approach to mitigating seismic risk?

The high death tolls caused by large earthquakes in the past two decades (the Nepal earthquake in 2015, the Japan earthquake in 2011, the Haiti earthquake in 2010, and the Wenchuan earthquake in 2008, etc.) further indicate that earthquakes are among the most destructive natural hazards in the world^1,2,3. With rapid urbanization processes in moderate to large cities, the accumulation of population and wealth has greatly accelerated. Such a large-scale migratory influx requires the rapid construction of new dwellings and infrastructures within a short time, often while sacrificing quality and safety, which inevitably increases the physical vulnerability of exposed structures and thus poses potentially high seismic risk, especially when cities are located within a seismically active zone¹. The extensive collapse of buildings and the large number of fatalities caused by the recent 2023 Turkey-Syria earthquake further highlight the urgent need to utilize pre-disaster risk mitigation measures, which is critical for achieving the sustainable development goals set by the United Nations and the disaster risk reduction targets outlined in the Sendai Framework 2015–2023^4,5.

Since the 1960s⁶, probabilistic seismic hazard maps have been widely used in various countries and regions to regulate the seismic code of new buildings, but ways to systematically and effectively improve the seismic resilience of existing buildings have not been discussed in depth in the literature. Cost‒benefit analyses have shown that compared with the large cost of emergency response during post-earthquake management, the most effective way to achieve earthquake resilience is to be fully prepared prior to the arrival of an earthquake (e.g., by optimizing disaster risk reduction strategies, retrofitting fragile buildings and infrastructures, educating the public on reasonable earthquake response and execution, etc.)^7,8. However, at all levels of government, the available budgetary resources needed to utilize these risk mitigation measures are always limited, which is generally cited as the major obstacle in any disaster prevention policy⁹. In this context, the pre-identification of the “priority zone”, where the potential seismic damage will be most severe, is necessary since prioritizing seismic risk mitigation actions in these zones can help maximize the efficiency of limited budgets and minimize the loss of life and property in subsequent damaging earthquake events.

When the seismic threat to the target region is mainly from a single fault while information on the likelihood of future earthquakes on this fault is inadequate, to better identify the ___location of a regional high seismic risk zone, it is crucial to understand the severity of potential earthquake scenarios and their impacts on the social and economic systems, especially for low frequency/high consequence earthquake events providing the upper limit for contingency planning. Thus, assessment of seismic risk must be as accurate as possible given the available information and the associated uncertainties³. Seismic risk assessment is based on three layers of information: hazard, exposure, and vulnerability. Hazard refers to the spatial distribution of ground shaking generated by a potential earthquake; exposure includes the attributes of exposed elements to a potential earthquake in terms of value, ___location, and relative importance (e.g., building, critical facility, and infrastructure); and vulnerability describes the susceptibility of those exposed elements to being damaged in a future earthquake. Each information layer can be determined by using different methods and data inputs. Thus, uncertainties exist in every step of the seismic risk modelling chain. Holistic analyses of the effect of uncertainty on seismic risk in Cologne, Germany (an area with relatively low seismic hazard) showed that the greatest contribution to the total uncertainty in seismic risk was from the hazard part¹⁰. This conclusion is also supported by several other studies with similar focus^11,12,13. For high hazard areas, since the rupture patterns of large earthquakes are more complex, the variation in simulated ground motions is expected to have a large impact on the risk estimation as well, as revealed by studies conducted for Istanbul, Turkey and Thessaloniki, Greece^14,15. In contrast, when the spatial resolution of the exposure model was changed from 1 km × 1 km to 8 km × 8 km, the difference in the estimated seismic loss was less than 5%¹⁶. Additionally, studies in the field of earthquake engineering have indicated that the uncertainty in building response is more sensitive to changes in ground shaking than to changes in structural modelling^17,18,19,20. All these studies share the consensus that compared with the changes in exposure and building vulnerability, the variation in seismic hazards has the most notable impact on the final risk estimates. We are fully aware that there are other important uncertainties in risk modelling used for public policy actions, including quality of building inventory data, building collapse modelling, and casualty estimation, etc., but that examining them is not the focus of this paper.

Since for deterministic scenario earthquakes the uncertainty of the ground motion model controls the uncertainty of the risk model¹, precisely and accurately characterizing the ground motion caused by future earthquakes is the key to determining whether a reliable seismic risk model can be established. Similar to approaches used in other science and engineering research, studies involving predictions of earthquake ground shaking typically begin with empirical formulas, such as ground motion prediction equations (GMPEs), regressed from historical data and observed information²¹. GMPEs are easy to use and can be conveniently adapted to different tectonic environments. Most importantly, they are regressed from actual observations. However, although widely used, empirical GMPEs have shortcomings, such as the intrinsic ergodic assumption^22,23, insufficient consideration of spatial correlations^24,25,26 and relatively poor constraints in the near-source region of destructive earthquakes due to the sparsity and scarcity of recorded data^{14,15,27,28,29}. These GMPE shortcomings have limited the accuracy of seismic hazard and risk assessment for areas with densely distributed building portfolios and infrastructures^{25,26,30,31,32,33}.

With advances in high-performance computing and numerical modelling techniques in the past two decades³⁴, an alternative ground shaking simulation method, namely the physics-based simulation (PBS) method, has been rapidly developed^35,36 and is considered to be a next-generation tool for seismic hazard assessment¹⁴. Compared with the empirical GMPEs, the PBS method can directly simulate the physical processes of seismic rupture and wave propagation and incorporate the complexity in fault source structures and propagation media; additionally, it can adequately describe the spatial correlations among ground shaking measurements at multiple sites³⁷. Furthermore, the resolution of the spatial heterogeneity of ground motion simulated by using the PBS method is higher than that simulated based on GMPEs¹⁴. Moreover, having PBS-based ground motions can also supplement the earthquake scenarios without data, e.g., large earthquakes that weren’t recorded, or ground motion records in near-fault regions. Due to the advantages of the PBS method, it has recently been embedded in several seismic hazard assessment frameworks^29,38,39,40. However, despite being rapidly developed, the reliability of PBS-based ground motion simulations is strongly dependent on the robustness of model inputs (e.g., fault geometry, background stress and property of the rock media, and friction law) and different or even contrasting simulation results could be produced when the parameters associated with these inputs are changed³⁶, unless for regions with the advantage of having seismic monitoring networks that can collect or provide the input parameters required for PBS in a timely manner. Clearly, each ground shaking simulation method has advantages and disadvantages, as do the corresponding seismic risk assessment models. Efforts have been made to improve the assessment of seismic hazard by integrating the PBS-based predictions with those obtained from an empirical GMPE approach (e.g., the CyberShake Project of Southern California Earthquake Center)³⁸, by using PBS simulations to eliminate the ergodic assumption in newly developed GMPEs⁴¹, or by fostering interdisciplinary research on reducing future losses to extreme events (e.g., the M9 project in the Cascadia area)⁴². However, how to comprehensively combine the results of different seismic risk models into the identification of regional high seismic risk zones is a problem that still requires more in-depth exploration.

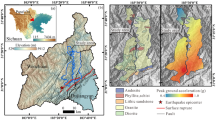
The focus of this paper is the proposal of a strategy that can delineate regional high seismic risk zones at fine resolutions and with high confidence. Considering the large impact on the risk estimation due to variation in seismic hazard, the key part of the high-risk zone delineation strategy is to compare the seismic risk calculated from two quite different ground shaking prediction methods. In particular, it is assumed that both exposure and vulnerability are reducible factors of risk, and their uncertainties can be decreased step by step when more information on the exposed elements is available. Therefore, the same exposure and vulnerability information will be combined with different hazard inputs to better reflect the impact on seismic risk due to the variation in seismic hazard. We demonstrate this regional high seismic risk zone delineation strategy by using the seismic hazard and loss estimation results for earthquake scenarios with a magnitude of Mw 7.5 for the Jiaocheng fault of the Shanxi Rift System, China; this magnitude represents the maximum magnitude of an earthquake that has occurred in this region according to historical seismicity and tectonic background. The earthquake scenarios considered are all associated with the Jiaocheng fault of the Shanxi Rift System, China (Fig. 1). This region is one of the most seismically active zones in China^43,44. The Jiaocheng fault is in the southwestern part of Taiyuan, which is the capital and largest city of Shanxi Province in northern China, and historically, this region has experienced many earthquakes (Fig. 1). Should new damaging earthquakes occur here, millions of people in Taiyuan and its neighbouring area would be seriously affected. Therefore, delineating the regional high seismic risk zone caused by earthquakes from the Jiaocheng fault is essential. We want to emphasize that for other cities located in active seismic zones and with dense populations and fixed assets, the strategy proposed in this paper can also be applied to delineate high seismic risk zones by considering the occurrence of low-frequency/high-consequence earthquakes at neighbouring seismic sources. Such information is crucial for local policy makers to determine how emergency response resources should be deployed and where pre-disaster risk mitigation actions should be prioritized to enhance response and recovery and decrease hazard exposure and vulnerability. Together with building more seismic-resistant structures, these measures are the best preparedness actions that we can take to minimize potential fatalities and financial losses and strengthen the resilience of society before the next destructive earthquake occurs.

a Topographic map. The blue and red arrows represent the directions and relative values of the maximum and minimum horizontal compressive stresses. The red line illustrates the surface trace of the nonplanar Jiaocheng Fault, which extends ∼110 km in the strike direction. The whole Jiaocheng Fault is categorized into three main segments (southern, middle, and northern) that have nearly planar geometries and are connected by corners located near Wenshui and Qingxu counties. The four black stars depict the epicentres of the four earthquake scenarios. The white circles are historical earthquakes that occurred in this region, and the three red solid circles have Ms≥7.0. b The 3D geometry of the Jiaocheng Fault. The white stars depict the epicentres of the four earthquake scenarios with a magnitude of ~Mw 7.5 (reproduced from Xin and Zhang³⁷).

Full size image

In this paper, we develop a series of seismic risk assessment models for earthquake scenarios at the Jiaocheng fault. Since the uncertainty in seismic hazards is considered to have the largest impact on seismic risk assessment and each of the current mainstream ground motion prediction methods (empirical GMPE and the PBS method) has its advantages and disadvantages, the ground shaking maps simulated by both methods for the four earthquake scenarios at the Jiaocheng fault (Fig. 1) will be used (Fig. 2) as the hazard inputs. The consistency of these ground shaking maps has been discussed in detail in our recent work³⁷. Then, by joining the rectified ground shaking maps (Figs. 3, 4) with the high-resolution residential building stock model (Fig. 5) and the vulnerability curves of representative building types (Figs. 6, 7) in the case study area, we will develop seismic risk models and evaluate their reliability by comparing modelled seismic losses (Fig. 8) with losses estimated from the empirical loss model (Fig. 9), which is specifically regressed from historical earthquake damage information for the study area. Finally, the verified seismic risk models will be comprehensively combined to demonstrate how to delineate the regional high seismic risk zone for the case study area (Fig. 10). Due to the content organization structure required by the journal, the Methods section is put at the end of this paper. However, for a better understanding of the workflow of this study, the readers are strongly recommended to read the technological details in the Methods section first before diving into the details in the Results and Discussion sections.

a–d The simulated PGA distribution maps for the four earthquake scenarios on the Jiaocheng Fault by using the curved grid finite-difference method (CG-DFM). The black pentacle in each panel represents the epicentre that initiates the rupture process of each scenario earthquake. e–i PGA maps generated by the empirical GMPEs of “BA08”⁴⁶, “CB08”⁴⁷, “BSSA14”⁴⁸ and “CB14”⁴⁹.

Full size image

a The site classes assigned by Li et al. ⁴⁴ for the Shanxi Rift System according to the definitions in Table 5. b Digitalized site classification map of the case study area.

Full size image

a–d The original PGA maps are those shown in Fig. 2a–d for the four earthquake scenarios on the Jiaocheng Fault by using the curved grid finite-difference method (CG-DFM). e–h The original PGA maps are those shown in Fig. 2e–h generated by the empirical GMPEs of “BA08”, “CB08”, “BSSA14” and “CB14”. Note that rectified PGAs are plotted only for the 28808 1 km × 1 km grids in Fig. 5 since they have available exposure information and will be further used for seismic risk calculation in Fig. 8.

Full size image

The distribution map of residential building replacement value in each 1 km × 1 km grid developed for the case study area.

Full size image

a The construction period distribution of surveyed individual buildings in the downtown area of Taiyuan city. b The ratio of surveyed buildings classified by construction periods and storey classes. c The ratio of surveyed buildings classified by construction periods and structure types. It is worth noting that the dividing threshold of each period (namely 1957, 1977, 1990 and 2001) corresponds to the issue year of the first, second, third, and fourth national seismic zonation map in China, which defines the seismic design code for new buildings built afterwards. d–f The median fragility curves derived by Xin et al. ⁵⁸ for brick-wood, mixed masonry, and steel-RC building types, respectively.

Full size image

a–c Digitalized second, third, and fourth probabilistic seismic hazard maps issued in 1977, 1990, and 2001 by the China Earthquake Administration for the case study area (PGA: peak ground acceleration). d–f The vulnerability curves used for brick-wood and other, mixed masonry, and steel-RC with different seismic design code levels.

Full size image

a–d The losses are calculated based on the rectified PGA maps in Fig. 4a–d using the PBS method. e–h The losses are calculated based on the rectified PGA maps in Fig. 4e–h using four empirical GMPEs (BA08, CB08, BSSA14, and CB14). Note the legend in Fig. 8 is the same as that in Fig. 5.

Full size image

The histograms in colour are based on seismic loss maps in Fig. 8a–h, while the histograms without fill colour are based on the empirical loss ratio function in Eq. (1) (Note: for BA08, CB08, BSSA14, and CB14, the maximum intensity is IX, while for PBS-based Scenarios 1-4, the maximum intensity is XI).

Full size image

a The distribution of the intersected top 10% loss grids (in green) by combining the PBS-based seismic loss maps in Fig. 8a–d. b The distribution of the intersected top 10% loss grids (in green) by combining the GMPE-based seismic loss maps in Fig. 8e–h. c The distribution of intersected grids (in blue) by combining the top 10% loss grids in each seismic loss distribution map in Fig. 8. Note: Intersected grids located on the boundary of two or three neighbouring counties/districts are counted repeatedly in the legend.

Full size image

After obtaining the three layers of information required for risk modelling, namely the predictions of ground motion in different scenario earthquakes, the asset estimations for residential buildings in potential earthquake-affected areas, and the assignment of vulnerability curves for different building types (see the Methods section for details), the seismic loss can be estimated instantly for each earthquake scenario by convolving the ground motion map with the exposure and vulnerability model. Notably, the simulated PGA values (Fig. 2) are presented at 200 m × 200 m resolution, while the exposure values (Fig. 5) are at 1 km ×1 km resolution. Therefore, before the calculation of seismic loss, the PGA values are first resampled to 1 km × 1 km resolution, then rectified by the soil amplification factors (Table 1). The rectified PBS-based and GMPE-based PGA distribution maps for 1 km × 1 km sites with exposed residential buildings are shown in Fig. 4. The final seismic loss distribution maps for the four earthquake scenarios with different nucleation positions in the Jiaocheng Fault with PGAs simulated by the PBS method in Zhang et al. ⁴⁵ and by the four empirical GMPEs of “BA08”⁴⁶, “CB08”⁴⁷, “BSSA14”⁴⁸ and “CB14”⁴⁹ are shown in Fig. 8a–d and Fig. 8e–h, respectively (see the selection criteria of these GMPEs in the Methods section). The legend used in these loss distribution maps is the same as that used for the exposure distribution map in Fig. 5.

From Fig. 8 it can be seen that in general, for regions far from the Jiaocheng fault, their seismic loss distribution pattern (namely the spatial locations of high and low loss grids) is quite different from the exposure distribution pattern (namely the locations of high and low exposure grids) in Fig. 5, while for regions close to the Jiaocheng fault, the locations of high seismic loss grids in Fig. 8 resemble those of the high exposure grids in Fig. 5. When calculated based on PBS-simulated PGAs, the overall seismic loss in panels (a–d) of Fig. 8 is 103.4 billion RMB, 103.3 billion RMB, 88.9 billion RMB, and 62.3 billion RMB, which accounts for 11.3%, 11.3%, 9.8%, and 6.8% of the total replacement value of residential buildings in the case study area (in total 911 billion RMB), respectively. Grids with losses higher than 100 million RMB are mainly centred around Taiyuan city due to its close distance to the Jiaocheng fault and high concentration of residential buildings. This characteristic does not change with the northeast shift of the epicentre of the earthquake scenario from panel (a) to panel (d) in Fig. 2. When calculated based on GMPE-simulated PGAs, the total seismic loss in panels (e)-(h) of Fig. 8 is 176.3 billion RMB, 160.1 billion RMB, 171.2 billion RMB, and 175.4 billion RMB, which correspondingly accounts for 19.4%, 17.6%, 18.8%, and 19.3% of the replacement value of all exposed residential buildings in the case study area. Compared with the PBS-based loss distribution maps, the seismic losses estimated from GMPE-based PGA maps are generally higher, although the spatial distribution pattern of grid losses in all the panels in Fig. 8 is similar.

To better demonstrate the difference among different loss distribution maps in Fig. 8, the rectified PGA maps (Fig. 4) are converted to seismic intensity by using the PGA-intensity conversion relation provided in the 2008 version of the China Seismic Intensity scale⁵⁰. The maximum intensity converted from rectified PGAs in Fig. 4a–d (PBS-based) and Fig. 4e–h (GMPE-based) is XI and IX, respectively. The distribution of residential building replacement value within each intensity range is given in Fig. 11a. Figure 11b summarizes the corresponding seismic loss within each intensity range, which reveals that the seismic losses of the PBS-based and GMPE-based hazard maps are mainly from intensities VIII and IX, respectively. This finding indicates that when the hazard map is simulated by using the PBS method, the largest seismic loss may not necessarily originate from the maximum intensity zone, while when the hazard map is generated by empirical GMPEs, the highest loss tends to cluster in the maximum intensity zone. It will be easier to understand this result when combing the exposure distribution in Fig. 11a. For PBS-based Scenario 1 ~ 3, there are many more buildings located in VIII than in IX, X and IX (the detailed building replacement values are listed in Table 2); while for GMPE-based BA08, BSSA14 and CB14, the largest portion of exposure is in IX. In this case, the cluster of exposure data plays an important role in determining the concentration of loss in which intensity range. Based on the exposure and loss values in each intensity range in Fig. 11a, b (values are listed in Table 2), we further calculate the corresponding loss ratio, as shown in Fig. 11c. The loss ratio for the same intensity range turns out to be similar, although the intensity zone in the four PBS-based and four GMPE-based PGA maps may cover different grids within the case study area. This consistency indicates that such intensity-loss ratio pairs could be used to rapidly predict the overall seismic loss after the occurrence of a damaging earthquake, as the loss ratio in each intensity is stable regardless of whether the intensity map is generated from the GMPE or from the PBS method.

a The replacement value, (b) the seismic loss, and (c) the ratio between the seismic loss and replacement value of exposed residential buildings within each intensity range (Note: for BA08, CB08, BSSA14, and CB14, the maximum intensity is IX, while for PBS-based Scenarios 1-4, the maximum intensity is XI).

Full size image

Delineation of the Regional High Seismic Risk Zone

It is specifically emphasized in the 2018-2022 strategic plan of the Federal Emergency Management Agency (FEMA) that the most successful way to achieve disaster resiliency is through preparedness⁷. In future earthquake disaster mitigation work, to reduce the potential number of casualties and economic losses more effectively, the top priority should be given to areas with high seismic risk considering the limited budgetary resources. Since the development of a seismic risk model is based on the modelling of seismic hazard, exposure, and vulnerability, uncertainty exists at every step of the seismic risk modelling chain. To determine those regional high seismic risk zones from such an uncertain process, the seismic risk modelling results from different earthquake scenarios and model inputs should be comprehensively combined.

Here, we propose a strategy to delineate the regional high seismic risk zone by combining the loss distribution maps in Fig. 8. Since the seismic losses in Fig. 8a–d and Fig. 8e–h are calculated from PGAs simulated using different methods, we try to combine the PBS-based and GMPE-based seismic loss distribution maps separately and check whether their intersected high loss grids are similar. First, we line up the grids in each panel of Fig. 8 (there are 28808 1 km×1 km grids within each loss distribution map) from highest to lowest according to the loss in each grid. Then for each loss distribution map, we select the top 10% of grids with the highest relative losses (in total, 2881 grids) and generate the intersected high-loss grids separately from Fig. 8a–d and Fig. 8e–h. As shown in Fig. 10a and Fig. 10b, their intersected high seismic loss grids have different spatial distribution characteristics. The former is in a quasi-linear shape with 2266 1 km×1 km grids, while the latter is in an ellipse shape with 2667 1 km×1 km grids (the corresponding loss values are summarized in Table 3). In addition, the summed seismic loss of grids in Fig. 10a ranges from 53 billion to 93 billion, which accounts for 86% ~ 90% of the overall seismic loss in the corresponding PBS-based seismic loss map in Fig. 8a–d, while the summed seismic loss of the intersected grids in Fig. 10b ranges from 146 billion to 164 billion and accounts for 92% ~ 93% of the overall seismic loss of the corresponding GMPE-based seismic loss map in Fig. 8e–h. Therefore, the difference in the distribution of intersected high-loss grids between PBS- and GMPE-based PGA maps does exist. Since both PBS- and GMPE-based PGA maps have corresponding advantages and disadvantages, a more appropriate practice is to further combine their intersected high-loss grids to obtain the final regional high seismic risk zone, as shown in Fig. 10c.

There are 2007 grids (see Table 3) remaining in Fig. 10c, which accounts for 7% of the total number of grids (28808) exposed to potential seismic hazards in the case study area. These final intersected grids account for 83% ~ 88% of the overall seismic loss in corresponding panel in Fig. 8. More importantly, their locations do not change with the variation in seismic hazard simulation methods or the shift in nucleation ___location of the scenario earthquakes. Therefore, the 1 km × 1 km grids in Fig. 10c are the regional high seismic risk zone delineated for the case study area with better confidence. With such information available, local policy makers can target their seismic risk mitigation measures in these grids, which is expected to be a more cost-effective approach. It is noteworthy that for practical reasons, earthquake risk mitigation programs may directly target at specific building types (i.e., unreinforced brick masonry or structures built several decades ago)⁵¹. For the scenario earthquakes considered in this paper, when we further categorize the economic losses in Fig. 8 by building types (brick-wood, steel-RC, mixed, other), as shown in Fig. 12a, it turns out that mixed masonry buildings (mainly refer to buildings with steams made of steel-concrete and the load-bearing walls made of brick-concrete) account for the largest share of overall seismic loss. Supposing all buildings are retrofitted to the high code level (in which case only the high code vulnerability curves shown in Fig. 7d–f are used for loss calculation), the corresponding losses after retrofitting and the decreased losses of each building type are shown in Fig. 12b and Fig. 12c, respectively. Figure 12b indicates that if all buildings are retrofitted to the high code level, for PBS-based scenarios the largest loss share is from the brick-wood buildings, while for GMPE-based scenarios, the largest loss share is still from the mixed masonry buildings. The largest decrease in seismic loss after retrofitting is from the mixed masonry buildings as well. However, these characteristics are gained when considering the overall loss of each building type in the case study area. When the loss distribution is checked in each 1 km × 1 km grid, the building type that dominates the loss may vary from grid to grid. This also indicates the necessity for mitigation programs at the local level to consider different types of buildings in different places. Specifically for those 2007 delineated high loss girds, such information needs to be investigated in detail before taking actions for engineering fortification.

a The distribution of seismic losses in Fig. 8 for each building type. b The losses calculated by assuming all buildings are retrofitted to the high code level, namely only the high code vulnerability curves shown in Fig. 7d–f are used for loss calculation. c The decreased loss after retrofitting.

Full size image

For local policy makers, seismic risk mitigation resources are usually allocated based on administrative units. Therefore, we further combine the administrative information with the number of intersected grids in Fig. 10c. These grids belong to 30 different counties and districts, as listed in Table 4. We suggest that the financial resources for seismic risk mitigation practice can be deployed based on the number of high seismic risk grids in the related county/district. However, it is worth emphasizing that the exposure model used in this paper only considers residential buildings. Before applying the delineated high-loss grids to the risk mitigation work for Taiyuan and its neighbouring area, the results in Fig. 10 and Table 4 should be modified by comprehensively considering the losses to both residential and non-residential buildings, as well as infrastructures^52,53,54. Specifically, there are 240 high loss grids in Taiyuan; for around 33 of them, there are detailed building investigation results, as shown in Fig. 6a. Therefore, it is worthwhile to have a closer look at the structure types that dominate the risk in these grids in a future follow-on study by considering several different risk indicators (i.e., economic losses of all types of buildings, human fatalities, the number of collapsed buildings, etc.).

To establish the best model to delineate regional high seismic risk zone, the ground motion distribution maps for four earthquake scenarios are simulated by using both the PBS and GMPE methods and rectified by considering the soil amplification effect. The exposure model of residential buildings in the case study area is revised by considering the actual construction prices of buildings in this region, and their vulnerability curves are separately determined by comprehensively considering attributes such as the construction year, seismic code level, structure type and story class. Finally, the estimated seismic losses of both ground motion models for four earthquake scenarios at the Jiaocheng Fault are combined to delineate the high seismic risk zone in this region, which accounts for only ~7% of the regional land area but ~85% of the overall potential seismic loss. It is noteworthy that using a lethality lens versus an economic loss lens is likely to change the specific local areas prioritized for mitigation investment, because highly lethal residential buildings (i.e., older pre-code buildings) may not be the same as high-economic-loss residential buildings (i.e., larger or newer buildings). Further, deaths are most often related to collapse, while a building can be a complete economic loss without collapse. For example, the buildings in the Christchurch central business district were completely damaged and had to be demolished after the 2011 earthquake, but they seldomly collapsed⁵⁵. This difference will be magnified once other building types (especially commercial) are considered. If seismic loss is considered the only criterion when assigning the limited budget resources, our findings indicate that the top priority should be given to those ~7% high loss grids when conducting seismic risk mitigation actions. However, since the earthquake scenarios considered in this paper are identified only as potential future scenarios to occur based on the available information, we have no corresponding recorded data to test the reasonability of the seismic loss estimation results. As an alternative, we turn to comparing our loss estimations with those calculated from the empirical loss function.

The empirical loss function used in this study is regressed from the intensity maps and damage information for historical earthquakes that occurred in the case study area and its neighbouring regions. These data were compiled in our previous work⁵⁶, in which a composite catalogue of damaging earthquakes that occurred in mainland China (hereafter referred to as MCCDE-CAT) during 1950–2019 was established. In MCCDE-CAT, data including (a) the macroseismic intensity maps of historical earthquakes, (b) the population exposed to each intensity zone of each damaging earthquake, and (c) the recorded losses of damaging earthquakes have been compiled systematically. Based on the information in MCCDE-CAT and the estimated fixed capital stock value exposed to each damaging earthquake, we further develop a set of empirical economic loss estimation models for five different subregions in Mainland China (including the Xinjiang region, the Qinghai-Tibet Plateau region, the Northeast region, the North China region, and the South China region)⁵⁷. The functional form of the empirical loss ratio function developed for North China (which covers the case study area in this paper) is given as follows:

where \(\beta ={3.469\times 10}^{-7}{and\; \theta }=6.192\). In Fig. 9, two different types of loss calculations within each intensity range are shown: the analytical losses are derived from the loss distribution maps shown in Fig. 8 (based on the rectified PGA maps in Fig. 4, the exposure model in Fig. 5, and the vulnerability curves in Fig. 7d–f); the empirical losses are calculated using the empirical loss ratio function (or empirical vulnerability function) in Eq. (1), the intensity map converted from PGA maps in Fig. 4, and the exposure data in Fig. 5. The comparison in Fig. 9 is based on the loss ratio since the sum of the exposure data at each intensity is the same for these two types of loss calculations. The detailed loss values in each intensity range are also listed in Table 2.

As shown in Fig. 9, for intensity ranges of VI and XI (note XI is only available for the PBS-based intensity map), the losses derived from Fig. 8 are close to those calculated from the empirical loss ratio function, while for intensity ranges of VII, VIII, IX, and X (note X is available only for the PBS-based intensity map), losses of the former are higher than those of the latter. The main reason lies in their difference in the way building vulnerability is considered. In Fig. 8, the differences in building structure types and seismic code design levels are considered by using the corresponding vulnerability curves in Fig. 7d–f. When using the empirical loss ratio function in Eq. (1) to calculate the loss, the vulnerability difference among buildings is ignored, and buildings within each grid are taken as a whole to calculate the overall seismic loss. More specifically, the vulnerability curves used in the analytical loss estimation is based on experimental fragility analysis data collected by Xin et al. ⁵⁸ for different types of buildings, while the loss ratio function in Eq. (1) is empirically regressed from the intensity maps and damage information of past earthquakes occurred in the case study area and its neighboring regions. Despite this difference, the overall seismic losses in the maps in Fig. 8 are approximately 1.32 ~ 1.50 times the corresponding losses calculated from the empirical loss ratio function (see Table 2 for detailed values). This narrow loss range can be regarded as a testimony of the reasonability of our estimated losses in Fig. 8. Then, the regional high seismic risk zone delineated from these loss maps can be prioritized for the implementation of targeted risk mitigation measures.

Understanding the scale and extent of potential risk is the first step to taking any effective seismic risk mitigation action. Different from the widely adopted PSHA (probabilistic seismic hazard assessment) map, which regulates the seismic design code of newly built buildings by considering the severity and frequency of all possible sources and magnitude ranges of future earthquakes, the strategy proposed here serves as a complement to the PSHA method² to secure the safety of people and their property in established buildings. Specifically, the strategy can be applied to cases in which the local governments want to strengthen the seismic resilience of existing buildings in their jurisdiction; notably, the delineated regional high seismic risk zones can be used to effectively allocate resources, and priority can be given to renovating or replacing fragile buildings. Compared with probabilistic risk modelling results, risk assessment based on earthquake scenarios can provide a clearer understanding of the consequences of possible earthquakes, which can better encourage proactive risk preparedness and mitigation investments⁷. The delineation strategy for regional high seismic risk zones proposed in this paper can be applied to other countries and regions for more targeted risk mitigation practice, especially for cities near seismically active faults.

The regional high seismic risk zone delineation strategy can have a variety of users for various departments, agencies, and community officials. For example, it can provide guidance for policymakers to identify where and why risk-sensitive land use planning interventions are necessary⁵⁹, emphasizing the need for proactive land use planning, zoning regulations, infrastructure improvements, and earthquake preparedness awareness to enhance community resilience⁶⁰. Knowing the severity of seismic risk that threatens a city and the ___location of the most seriously affected zone also helps local policy makers prioritize seismic retrofitting of critical structures/infrastructures or identify areas where emergency response plans need to be developed, which can help prevent and reduce seismic hazard exposure and vulnerability, increase response and recovery preparedness, and enhance the resilience of the local community to the largest extent before earthquakes occur. Emergency response teams may focus on the delineated high seismic risk zone to plan and perform emergency response exercises. Emergency planners can also comprehensively determine the temporary shelter requirements for different earthquake scenario events⁶¹. In addition, further investigation on the financial sustainability of seismic risk reduction programs can also be conducted focusing on specific building types that dominate the seismic loss⁶², thus to better plan mitigation measures and improve the level of preparedness in case of an earthquake, particularly in urban areas where human activities are concentrated⁶³. Only with continuous investment in these pre-disaster risk mitigation efforts can we truly protect life and property, reduce the increasing cost of earthquake disasters, and secure better sustainable development of society. We believe that the proposed strategy will add value to current knowledge for disaster risk management, providing a clearer reference for local risk managers to conduct risk mitigation actions.

The limitations of this study are multifaceted. First, although we employ two widely used methods (namely the physics-based method and the empirical GMPE method) to simulate ground shaking in earthquake scenarios, only the PGA values are used for building vulnerability assessments, and spectral accelerations with different periods are not considered. This is limited by the reliable frequency range of ground motions computed by the PBS method⁴⁵, which is relatively low (typically up to approximately 1.5 Hz) due to restrictions in computing capacity and the lack of a high-resolution medium velocity model. Second, the site amplification effect is only empirically rectified based on the site classification results of Li et al. ⁴⁴; currently, this is the best dataset we could find to perform such rectification for our case study area. Third, the replacement value of residential buildings is given at a 1 km × 1 km resolution and not estimated building by building. This is limited by the availability of investigation data for individual buildings for the whole case study area. Fourth, to demonstrate our strategy, the earthquake scenarios considered are only those with a magnitude of approximately Mw 7.5, and the exposure model only includes the residential buildings in the study area; thus, the delineated high seismic risk zone in this paper cannot be applied directly into seismic risk mitigation practice before being revised by considering more magnitude ranges and building types. Fifth, earthquake scenarios are assumed and have not yet occurred in the Jiaocheng Fault. Therefore, it is not possible to test the seismic loss estimations using observation records. Furthermore, we are also fully aware that complete risk assessment requires a holistic analysis of different types of losses, including social (fatalities and injuries) and financial losses (direct losses to all exposed fixed assets and indirect losses caused by business interruption, etc.). Here, we choose the financial losses of residential buildings to differentiate the seismic risk level. Other seismic risk indicators (e.g., collapsed buildings, human fatalities etc.) can also be explored in a similar way, but the calibration process of exposure and vulnerability information will be different^2,64, which might delineate different risk priority zone. However, an in-depth discussion on the use of different risk indicators is quite beyond the focus of this study. Additionally, the strategy proposed here only considers one fault. In regions threatened by multiple faults (such as areas near subduction zones facing both undersea and onshore faults or regions developed with multiple parallel faults), the number of scenarios considered should be increased to better include different rupture patterns on each of those faults. Further, the regional high seismic risk zone delineation strategy proposed in this paper is only the first step for actual seismic risk mitigation practice. More further studies (e.g., including evaluating the risk of building collapse and life loss) are needed to determine detailed measures and target safety levels for seismic intervention and timescales within which intervention must take place, which will be considered in our future work.

We emphasize that the focus of this paper is to propose a strategy that can identify a regional high seismic risk zone that is not specific to the simulation method of the hazard or the nucleation ___location of the earthquake. The final seismic losses also have reasonable consistency with empirical loss estimations. In addition, the seismic hazard, exposure, and vulnerability inputs used to derive the final losses have been calibrated and validated based on other hazard simulation methods³⁶, exposure datasets⁶⁵ and vulnerability curves⁵⁸. All these validation steps ensure the reasonability of our estimated losses and the accuracy of the delineated high seismic risk zone in the case study area. Therefore, the identified regional high seismic risk zone can be selected as the target of seismic risk mitigation efforts in Taiyuan and its neighbouring areas. In the future, to improve the accuracy of high seismic risk zone delineation, we will consider enlarging the frequency range of simulated ground motions by introducing artificial neural networks (ANNs) into our simulation⁶⁶, and enriching earthquake scenario analysis by considering wider magnitude ranges and more nucleation positions. Additionally, exposure and vulnerability analyses for non-residential buildings and infrastructures can be combined with the proposed approach. It is noteworthy that changes in data inputs (e.g., spatial resolution, unit construction price, building classification typology, average floor area per building type etc.) for exposure and vulnerability modelling will doubtlessly alter the loss estimation results. Therefore, in the future it is quite necessary to further explore the effect of changes in these factors on the modelled exposure, estimated loss and the final delineated regional high seismic risk zone. Currently, the first nationwide natural disaster risk investigation work is ongoing in China, and detailed structural information for individual buildings in many sample areas is being collected. If such data could be publicly accessible in the future, we could further refine the exposure model and conduct vulnerability analyses of individual buildings. These improvements would support more comprehensive and reliable delineation of regional high seismic risk zones in the future.

In this paper, we use the earthquake scenarios set on the Jiaocheng fault in the Shanxi Rift System, North China, to demonstrate the delineation strategy of the regional high seismic risk zone. The Jiaocheng Fault lies on the northwest of the Taiyuan basin and mainly strikes in the southwest‒northeast (SW‒NE) direction and approaches the city of Taiyuan from the west within a small distance (Fig. 1). The extent of the earthquake-affected area considered in this paper ranges from 110.8° N to 114.24° N longitude and from 35.8° E to 38.5° E latitude. GPS observations^67,68,69 indicate that the Taiyuan Basin is in a horizontal extensional environment. Therefore, the Jiaocheng Fault was set as a normal fault with a dip angle of 60°⁴⁵. The delineation of the regional high seismic risk zone is based on the combination of seismic loss distribution maps, which are calculated from ground shaking predictions, the replacement value of exposed buildings, and their corresponding vulnerability curves. In the following sections, we will separately introduce the generation process of these components.

Ground shaking simulated by the PBS method

To understand the seismic hazard caused by different earthquake scenarios on the Jiaocheng Fault, Zhang et al. ⁴⁵ studied the dynamic rupture and propagation process of four earthquake scenarios that nucleated at different locations but with the same hypocentre depth by using the PBS method (as represented by the black stars in Fig. 1). The magnitude of these four scenarios was set to ~Mw 7.5 according to the tectonic background and historical seismicity related research findings on the Jiaocheng Fault^44,70. The nucleation patches in these four scenarios were of the same size (with a radius of 2 km) and depth (8.66 km underground, as determined by trial-and-error test to achieve an ~Mw7.5 earthquake). Within the nucleation patch, a relatively high stress (0.1%) larger than the fault’s strength was imposed to initialize the dynamic modelling. As shown in Fig. 1, the hypocentres of the second and fourth scenarios were in two corners divided by Wenshui and Qingxu counties, respectively. These two corners acted as barriers, which affected the rupture of the fault. The Scenario 1 and 3 earthquakes were triggered by the hypocentres located in the southern and middle segments of the Jiaocheng Fault, respectively. These four nucleation locations are considered quite representative and allow for the observation of the major difference in ground motions among scenario earthquakes on the Jiaocheng Fault. The further change of nucleation ___location will not present obviously different ground motion distribution patterns from those of the four scenario earthquakes considered in this study. This is because the purely physics-based dynamic simulations in Zhang et al. ⁴⁵ are relatively stable and have the potential to reduce the ground motion variance at specific sites when compared with kinematic parameterization of the source, in which rupture velocity is specified without direct constraints from rupture dynamics⁷¹ and more simulations are required to better characterize the ground motion variation.

Zhang et al. ⁴⁵ generated peak ground accelerations (PGAs), peak ground velocities (PGVs) and spectral accelerations (SAs) in different periods by using the curved grid finite-difference method (CG-FDM), which was first proposed by Zhang et al. ⁷² to simulate seismic wave propagation in the presence of irregular topography and was further applied by Zhang et al. ⁷³ to model the dynamic rupture of irregular planes. The validity of the CG-FDM was demonstrated in the recent benchmark exercises of Harris et al. ³⁶, which were designed to test whether different dynamic earthquake rupture algorithms can produce the same results given the same set of model assumptions. The dynamic rupture and propagation processes of the four earthquake scenarios at the Jiaocheng Fault, the distribution of the final slip patterns, and the ground shaking characteristics in terms of PGV were discussed in detail by Zhang et al. ⁴⁵. In this paper, we use their simulated PGA results in Fig. 2a–d with a grid interval of 250 m as the hazard inputs to assess the seismic risk associated with these four earthquake scenarios.

Ground shaking simulated by empirical GMPEs

Since ground shakings predicted by empirical GMPEs remain popular in current seismic hazard and risk assessment practice, we generate GMPE-based ground shaking maps for the four earthquake scenarios at the Jiaocheng Fault. The GMPEs used in this paper were developed by Boore and Atkinson (abbreviated as “BA08”)⁴⁶, Campbell and Bozorgnia (abbreviated as “CB08”)⁴⁷, Boore et al. (abbreviated as “BSSA14”)⁴⁸, and Campbell and Bozorgnia (abbreviated as “CB14”)⁴⁹. BA08 and CB08 are chosen since they have been tested and are suitable for the probabilistic seismic hazard assessment for the Shanxi Rift System as described by ref. ⁴⁴, which covers our case study area. The compatibility of PGV values generated with the PBS method by Zhang et al. ⁴⁵ and based on the GMPEs of BA08 and CB08 were also verified in our prior work³⁷. BSSA14 and CB14 are the updated versions of BA08 and CB08, respectively; thus, they are also used to generate the empirical ground shaking maps and calculate the subsequent seismic risks. A local GMPE specifically developed for the Shanxi Rift System that covers our case study area by Wen et al. ⁷⁴ based on local intensity data of 19 Ms≥5.0 historical earthquakes was not used, since the ground motions predicted by this local GMPE have a significant deviation from other historical seismic data⁴⁴. Other empirical GMPEs regressed from more sufficient recordings and specifically developed for the fifth national seismic hazard map in China by Yu et al. ⁷⁵ are not chosen, since in these models the epicentral distance (R_epi) or hypocentral distance (R_hyp) is used, and the inherent assumption behind the use of R_epi or R_hyp is that the rupture source of an earthquake can be regarded as a point source. However, the earthquakes considered in this paper have a magnitude of ~Mw 7.5, and because of the complexity of the 3D geometry of the Jiaocheng Fault (Fig. 1b), the point source assumption is not appropriate³⁷.

The ground shaking maps generated with the four selected GMPEs are shown in Fig. 2e–h with the same grid interval of 250 m as that in Fig. 2a–d. In Fig. 2e and Fig. 2g, PGAs are calculated by considering only the magnitude scaling term and the distance function term in Eq. (1) of Boore and Atkinson for BA08 and BSSA14; in Fig. 2f, the magnitude term, the distance term and the style-of-faulting term in Eq. (1) of CB08 are considered, while the PGAs in Fig. 2h are calculated by considering more functional terms in Eq. (1) of CB14, such as the earthquake magnitude, geometric attenuation, style of faulting, hanging wall geometry, hypocentral depth, fault dip, and anelastic attenuation. All the PGA values in Fig. 2e–h are median predictions without considering the standard deviation term in the GMPEs. Additionally, a shift in the nucleation ___location of the earthquake scenarios at the Jiaocheng Fault will not change the final PGA distribution map predicted by using these four empirical GMPEs; therefore, in each panel of Fig. 2e–h, the PGA distribution map is the same for all four scenario earthquakes. In contrast, the PBS-based PGA map in Fig. 2a–d changes with the nucleation ___location, which results in improved spatial heterogeneity and a higher resolution of the ground motion distribution. The characteristics of and the differences between the PBS-based and GMPE-based PGA maps used in this paper are similar to those for PGV maps, which were analyzed in detail in our previous work³⁷. In general, the attenuation trends of PGAs with source-to-site distances simulated with the PBS method display better consistency with those predicted based on CB08 and CB14 than those predicted based on BA08 and BA14. However, the use of different GMPEs in generating the PGA map will not obviously change the relative difference in PGA values of grids within each map², thus the delineated regional high seismic risk zone will remain highly consistent.

Site effect rectification for simulated PGA distribution maps

Due to the lack of definite information on the plasticity of the Taiyuan basin and the local site conditions near the surface, Zhang et al. ⁴⁵ only considered the elastic response of the propagation media in their dynamic rupture simulation. Thus, the PGA predictions shown in Fig. 2a–d have not yet been rectified based on site conditions. Correspondingly, the site terms of the four empirical GMPEs are also not considered when generating the median PGA maps in Fig. 2e–h. However, it has been frequently shown for previous earthquakes that local site conditions can significantly amplify seismic ground motion^76,77,78. V_S30, the travel-time-averaged shear-wave velocity in the top 30 m of soil deposits, is typically used to represent the site conditions. The reference site conditions for BA08 and BSSA14 include V_S30 = 760 m/s, which is classified as a Type B/C condition according to the site classification of the National Earthquake Hazards Reduction Program (NEHRP)⁷⁹. For CB08 and CB14, the reference rock outcrop is characterized by V_S30 = 1070 m/s (namely NEHRP Type B). The minimum shear velocity in the 3D media considered in the dynamic simulations of Zhang et al. ⁴⁵ was V_s ≥ 1000 m/s.

Since detailed V_S30 information is not publicly available for our case study area, to perform site effect rectification for the simulated PGAs in Fig. 2, we use the site classes assigned by ref. ⁴⁴ for the Shanxi Rift System (which covers our study area) to differentiate the site amplification effects. Based on the shear-wave velocity profiles in boreholes at 3106 engineering sites, 31 strong motion stations and 65 seismic stations in Shanxi Province and its neighbouring area, Li et al. ⁴⁴ divided the whole Shanxi Rift System into five site classes according to the definitions (Table 5) in the fifth national Seismic Ground Motion Parameter Zonation Map issued in 2015 (GB 18306-2015)⁸⁰ for China. The site classification map used by Li et al. ⁴⁴ is digitalized in Fig. 3a, based on which we generate the continuous site distribution map for our case study area shown in Fig. 3b. According to the site class definitions in Table 5, the reference shear-wave velocity in the empirical GMPEs for BA08 and BSSA14, CB08 and CB14, and of Zhang et al. ⁴⁵ corresponds to site classes I1, I0, and I0, respectively. Following the site adjustment factors given in GB 18306-2015, the PBS-based and GMPE-based PGAs in Fig. 2 are rectified to the site classes in Fig. 3b by using the corresponding adjustment coefficients defined in Table 1. Notably, for certain regions in Fig. 3b (mainly in the southeast and northwest corners of the case study area), there is no available site classification information for reference; thus, we simply assume they are site class II (the base rock layer). The rectified PBS-based and GMPE-based PGA distribution maps for sites with exposed residential buildings are shown in Fig. 4.

The exposure model for residential buildings

By using the downscaling method, Xin et al. ⁶⁵ developed a publicly accessible residential building stock model (with 1 km × 1 km resolution) for three different levels (namely urban, township, and rural, as differentiated by population density) of 31 provincial administrative units in mainland China based on statistics from the 2010 population census of China and the population density profile released by the 2015 Global Human Settlement Layer project⁸¹. In this model, the floor areas and replacement values of 17 building subtypes (with different story classes and structure types; see Table 6) are given. However, for computational convenience, the unit construction price for each building subtype within each 1 km × 1 km grid was the same for the whole country in the study of Xin et al. ⁶⁵ (see their Table 7). We are fully aware that the construction prices of building stocks in China significantly vary across the country due to the variations in economic development level, geographic and climatic diversity, and standardization in building construction. Thus, in this paper, the replacement values of the 17 building subtypes of Xin et al. ⁶⁵ are modified specifically for Taiyuan and the neighboring area according to the construction prices issued by the Department of Housing and Urban-Rural Development of Shanxi Province (Table 6).

The distribution map of the modified residential building replacement value for Taiyuan and its neighbouring area, which reaches 911 billion RMB (in current price) in total, is shown in Fig. 5. We also analysed the building floor area data at each urbanity level for the case study area. The floor area ratios of buildings with different structure types and story classes are plotted in Fig. 13a, b, respectively. In each panel, the floor area ratio refers to the floor area percentage of corresponding building type in each urbanity level (rural, township, urban). In terms of structure type, brick-wood and other low construction quality buildings (e.g., bamboo structure, brick arc structure, cave structure, etc.) tend to be dominant in rural areas, while mixed masonry and steel-RC buildings are more common in township and urban areas. In terms of the storey class, it is obvious that most rural buildings are only 1 storey or 2-3 stories, while most high storey buildings are in urban areas.

a The floor area ratio distribution classified by structure type in urban/township/rural levels of the case study area (BRIWO, STLRC, MIXED, and OTHER refer to brick-wood, steel-reinforced concrete, mixed masonry and other building types, respectively). b The floor area ratio distribution classified by storey classes (1, 2–3, 4–6, 7–9, ≥ 10) in urban/township/rural levels of the case study area. c Comparison of the modelled floor area of residential buildings in Xin et al. ⁶⁵ with records in the 2010 census of China at the county level for the case study area.

Full size image

To further verify the general reliability of the residential building exposure model in Fig. 5, we compared the modelled floor area with census records at the county level, as shown in Fig. 13c. The R² value of these two sets of data reaches 0.97, which is quite high. It is also noteworthy that the modelled floor area is generally higher than that recorded in the census, since during the modelling process in Xin et al. ⁶⁵, they scaled the building-related census records from 2010 to 2015 by multiplying the population amplification ratio from 2010 to 2015 for each urbanity level, which is approximately 1.07, 1.16 and 1.19 for rural, township, and urban areas in Shanxi Province, respectively.

Vulnerability curves for different building types

Ideally, the vulnerability curves for different building types should be determined by considering the structure type, the number of stories, the built age, the seismic design code and the variation in seismic design code with time. The residential building stock model in Xin et al. ⁶⁵ has not provided sufficient information on structure characteristics, in which only the number of stories and structure type attributes are available, but other key attributes, such as the year the structure was built and its seismic design code, are missing. Therefore, in this paper, we devote more effort to investigating built year and seismic code information for residential buildings within the case study area. Experts from the China Earthquake Administration conducted a building-by-building survey in the downtown area of Taiyuan city, in which the address, construction year, structure type, footprint extent and floor area of individual buildings were recorded, as shown in Fig. 6a. It is noteworthy that these surveyed buildings take up around 33 1 km × 1 km grids in spatial extent and they are not used to construct the exposure model in Fig. 5. In this survey, 63712 buildings were investigated, but 10973 buildings were demolished during the investigation. Thus, we analyse the remaining 52739 buildings to determine the dominant construction period of buildings with different story classes and structure types.

In Fig. 6b, c, the investigated construction year information is regrouped into several periods, namely 1957–1976, 1977–1989, 1990–2000, and 2001–2014. These four periods are grouped according to the issue year of the first, second, third, fourth, and fifth national seismic zonation maps in China, which is 1957, 1977, 1990, 2001, and 2015, respectively. Each seismic zonation map regulates the seismic design code of new buildings built after its issue year until the appearance of an updated map. Based on the ratio of buildings (namely the percentage of all 52739 surveyed buildings) classified by the combination of construction period and story class/structure type in panel (b, c) of Fig. 6, we can approximately determine the dominant construction period for buildings with different combinations of story class and structure type. For example, the construction period for a 1-storey brick-wood building is most likely to be within the range of 1977-1989. As summarized in Table 7, the construction periods for the investigated buildings in the downtown area of Taiyuan are mainly in the ranges of 1977-1989, 1990-2000, and 2001–2014. To differentiate the vulnerability of buildings built in accordance with different versions of seismic design codes, we digitalized the second, third and fourth zonation maps issued in 1977, 1990 and 2001 by the China Earthquake Administration for our case study area, as shown in Fig. 7a–c. Combining the dominant construction period with seismic design code information, the vulnerability levels (precode, low-code, moderate-code, high-code) of different building types in the case study area can be determined (as listed in Table 8) according to the judgement criteria modified after Table 8 in Lin et al. ⁸².

The building vulnerability curve (which describes the relationship between the ground shaking indicator and loss ratio; loss ratio refers to the ratio between the structure repairment cost and structure replacement cost) is generated by combining the building fragility curve and the consequence function. A fragility curve describes the probability of a building being in different damage states when undergoing different ground shaking levels. Xin et al. ⁵⁸ performed a review of fragility curves for major building types in mainland China based on empirical post-earthquake survey data and analytical structural response experiment data, in which different ground shaking indicators (macro-seismic intensity for the former and PGA for the latter) were used. The median fragility curves derived for brick-wood, mixed masonry and steel-RC by Xin et al. ⁵⁸ based on analytical experimental data will be used in this paper, as plotted in Fig. 6d–f. Combining the building fragility curve with the corresponding consequence function, as listed in Table 9 for brick-wood⁸³ and in Table 10 for mixed masonry and steel-RC⁸⁴, the vulnerability curves for these building types with different seismic design code levels can be determined, as shown in Fig. 7d–f. For each building type, the vulnerability curves for three different seismic design code levels (pre/low-code, moderate-code, and high-code) are empirically assigned by using the upper, mean, and lower thresholds of the loss ratio given in the corresponding consequence function. For “other” building types (e.g., bamboo structure, brick arc structure, cave structure, etc.) in Table 7, there is no more detailed information on its exact building type; thus, we assume that storey classes 1 and 2-3 have the same vulnerability curves as the “brick-wood” building in Fig. 7d, while storey classes 4–6, 7–9, and ≥10 have the same vulnerability curves as the “mixed” masonry building in Fig. 7e. It is noteworthy that in locations where detailed building-by-building inventories are not available, researchers can still use the regional high seismic risk zone delineation strategy proposed in this study if they can generate reasonable estimates of exposure on a 1 km x 1 km grid (or a lower resolution) and have fragility or vulnerability functions for the main building types.