Broken symmetries associated with a Kagome chiral charge order

In the framework of Ginzburg–Landau theory, the phase transitions result from symmetry breaking of the ground state and associated order parameters¹. Therefore, scrutinizing the broken symmetries in the post-transition state is imperative for comprehending the mechanism driving the phase transition, particularly in systems where multiple interaction pathways are involved. For instance, charge density wave (CDW) like instabilities, where the electron density spontaneously undergoes periodic modulations, have been found to be widely present in high-temperature superconductors and strongly intertwined with the superconductivity^2,3,4. The microscopic structure of the intertwined charge orders in strongly correlated systems, including the symmetry and anisotropy, provides invaluable insight in the interactions between charge, lattice and spin degrees of freedom and therefore has been attracting significant research attention^5,6,7.

Recently, Kagome materials AV₃Sb₅ (A  =  K, Rb, Cs) have become a major focus of research endeavors, in which intertwined CDW and superconducting orders emerge at low temperatures^8,9,10. Below the CDW transition temperature (T_c = 79 K – 102 K), the vanadium atoms form a star-of-David pattern in the Kagome plane and the in-plane wave (Q) vectors connecting the van-Hove singularities at different M points, induce a strong electronic band reconstruction^11,12. Intriguingly, scanning tunneling microscopy (STM)¹³, muon spin relaxation¹⁴, optical Kerr¹⁵, and electrical transport measurements¹⁶ provided evidence for the spontaneous time-reversal symmetry breaking of the charge-ordered phase and the long-thought loop current state, although contradicting results were also reported^17,18,19. In parallel, scanning birefringence microscopy¹⁵ and STM¹⁷ studies revealed the broken six-fold rotation symmetry and the presence of nematicity in the charge order state, which are challenged by the recent thermodynamic measurements²⁰. The CDW was further demonstrated to be coexisting with superconductivity at lower temperatures²¹ and forms an electronic smectic state. However, despite intensive research, the exact symmetry of the highly unconventional charge-ordered states and the associated crystal structure is still under strong debate and remains elusive, partially due to the weak lattice distortion and the abundance of energy degenerate CDW configurations.

The circular photogalvanic effect (CPGE), which measures the change of second-order photocurrent response under light with opposite circular polarizations, have become a powerful tool for detecting broken symmetries^22,23 and Berry curvature distributions^24,25,26. The corresponding response tensor inherits the symmetry of the system, and the CPGE with long-wavelength probing light (such as mid to far infrared) can directly reveal the microscopic symmetry breaking of the wavefunctions of the low-energy states^22,27.

In this study, we leverage the nonlinear photogalvanic effect to thoroughly examine the symmetries of the enigmatic charge order in KV₃Sb₅. Notably, we observe the emergence of longitudinal CPGE upon the onset of the CDW order. The intrinsic CPGE directly exposes the broken mirror and inversion symmetries within the charge order. The absence of CPGE in the horizontal direction further imposes constraints on the rotational and point group symmetries of the charge order at low temperatures. Consequently, our study illuminates the symmetries of the unconventional CDW order in KV₃Sb₅ and lays the foundations for further understanding of the order parameter in charge-ordered phases.

We employed a mid-infrared (10.6 μm wavelength, ~120 meV photon energy) scanning photocurrent microscope to investigate the polarization-dependent photogalvanic response in KV₃Sb₅. The experimental setup is schematically illustrated in Fig. 1a, where the polarization of the mid-infrared laser beam is modulated using a quarter-wave plate prior to being directed perpendicularly to the sample surface. To measure the longitudinal (sample’s out-of-plane) photocurrent, we fabricated a sandwich structure consisting of graphite (as an electrode), KV₃Sb₅, and metal electrodes, as shown in Fig. 1b. The current generated across the top graphite electrode and the bottom metallic electrode was measured. The optical microscopy image of the device, including multiple electrodes, is presented in Fig. 1c.

a Overview of the mid-IR photocurrent microscope setup. b Schematic illustrating the device configuration for measuring the out-of-plane photocurrent (I_z). c Optical microscopy image of the device. The electrodes are labeled as A-E. d Spatial mapping of the I_z photocurrent, with the largest signal observed at the intersection between graphite and KV₃Sb₅. e Polarization dependence of I_z when the beam spot is positioned at the marked star in (d). The pump light polarization evolves from left-circular (LC) to horizontal (LH) to right-circular (RC) to horizontal (LH) and back to left-circular (LC) as the QWP angle changes from 45 to 225 degrees. f Decomposition of the photocurrent into four different channels, where A-D denote the fitting parameters in Eq. (1). The error bars are based on the combination of one standard deviation of the fitting parameters and the measurement uncertainties.

Full size image

We begin our investigation by measuring spatially resolved photocurrent at \(T=10\) K to identify the regions where the photocurrent is generated. The resulting map, depicted in Fig. 1d, reveals a prominent positive photocurrent source at the intersection region between graphite and KV₃Sb₅. Additionally, a small negative photocurrent appears at the interface between exposed KV₃Sb₅ and the bottom electrode. This uneven and bipolar distribution of photocurrent suggests the presence of out-of-plane photo-thermoelectric currents stemming from the variation in the Seebeck coefficient at the contacts^25,28. Such a distribution allows us to differentiate the contribution of CPGE from those associated with photo-thermoelectric currents in real space, as we will discuss further. Next, we focused the beam at the center of the positive photocurrent area (marked by the green star in Fig. 1d) and recorded the out-of-plane photocurrent (\({I}_{z}\)) as a function of the azimuthal angle of the quarter-wave plate. Remarkably, we find that the photocurrent generated under left-circular-polarized pump light is greater than that under right-circular-polarized light. This difference is the hallmark of the CPGE. To dissect the different components contributing to the photocurrent, we employed a fitting procedure using the following function²⁹:

where \(\phi\) represents the quarter-wave plate angle. The fitting results presented in Fig. 1f reveal the presence of both the CPGE (A term, exhibiting a periodicity of 180 degrees) and linear photogalvanic effect (LPGE) contributions (B and C terms, exhibiting a periodicity of 90 degrees). Additionally, a polarization-independent contribution from photo-thermoelectric currents is observed.

To elucidate the origins of the different photocurrent contributions, we investigated their temperature dependence. Figure 2a presents a series of polarization-dependent measurements acquired at the same ___location but at different temperatures. At low temperatures, and as discussed earlier, a distinct CPGE signal emerges, allowing us to define I_CPGE as half of the signal difference between left-circular-polarized and right-circular-polarized light. As the temperature increases, I_CPGE gradually becomes less prominent before sharply diminishing above \(T=100\) K. To quantitatively analyze the temperature dependence, we extracted the value of this nontrivial component at each temperature by fitting the data using Eq. (1). The results are summarized in Fig. 2b for the CPGE component and Fig. 2c for the LPGE component. We find that I_CPGE follows a power-law behavior below a critical temperature (T^*\(\simeq 95\pm 10\) K, close to the CDW transition temperature) and saturates at low temperatures with a magnitude of 3 nA. On the other hand, the helicity-independent component (\(\sqrt{{B}^{2}+{C}^{2}}\)) exhibits a gradual decrease with rising temperatures, likely due to the increasing resistivity of the system. This is consistent with the trend expected for the photo-thermoelectric effect and does not show any obvious anomaly near T^*30. The stark disparity in the temperature dependencies strongly supports a non-thermal origin for the CPGE (see also Supplementary Fig. 1). Instead, it suggests the emergence of an electronic order characterized by spontaneously broken symmetries, which accounts for the observed CPGE effect at lower temperatures.

a Polarization dependence of I_z at different temperatures. The curves are normalized and offset for better comparison. At 10 K, a nonzero circular photogalvanic effect (CPGE) component, I_CPGE, manifests as the half-difference between I_z acquired with left-circular and right-circular polarized light. At 120 K, the I_CPGE diminishes. b Temperature dependence of the I_CPGE. The blue dashed line represents the fitting result with the scaling function \(f\left(T\right)={({T}^{*}-T)}^{\alpha }\theta ({T}^{*}-T)\), where \(\theta\) denotes the unit step function and \(\alpha=\left(0.3\pm 0.1\right)\). c Temperature dependence of the linear photogalvanic effect (LPGE) component I_LPGE. It is worth noting that the I_CPGE nearly vanishes above \(T=100\) K, while the I_LPGE shows no distinguishable change across the charge density wave transition (T_CDW). T_CDW is extracted from measurements of the resistivity as a function of the temperature (see Supplementary Fig. 2) performed in a bulk KV₃Sb₅ crystal. The error bars in panels (b, c) are based on the combination of one standard deviation of the fitting parameters and the measurement uncertainties.

Full size image

Having observed the CPGE associated with the charge order, we investigate its underlying mechanisms. To this end, we conducted a series of experiments to explore its correlation with the laser power, cooling conditions, contact geometry, and spatial distribution. The linear power dependence of the CPGE, as demonstrated in Supplementary Fig. 6, is consistent with its characterization as a second-order effect; see additional discussion in Supplementary Note 4. We further cooled the device from \(T=120\) K to 20 K using either right-circular-polarized or left-circular-polarized light with an illumination power of 2.9 mW. Subsequently, we measured the polarization dependence of \({I}_{z}\) at the same ___location. The results are depicted in Fig. 3a, where the two curves exhibit close quantitative alignment. Importantly, \({I}_{z}\) shows no apparent dependence on the “induction process,” distinguishing itself from the previously observed chiral induction and gyrotropic charge density wave phase in 1T-TiSe₂²². Furthermore, we investigated the in-plane photocurrent at \(T=10\) K and found no detectable polarization dependence (Fig. 3b). This observation suggests that the CPGE predominantly manifests along the longitudinal direction when subjected to the normal incidence of light. Such direction sensitivity rules out extrinsic influences such as fabrication-related anomalies or variations in input power with the azimuthal angle of the quarter-wave plate rotation as potential sources of the observed CPGE. Lastly, we examined the spatial variability of the CPGE by analyzing the half-difference between the \({I}_{z}\) measured under right-circular-polarized and left-circular-polarized light as we scanned the beam across the device (Fig. 3c, d). Interestingly, the CPGE signal measured at \(T=10\) K is primarily localized in the region where the top graphite, KV₃Sb₅, and the bottom gold contact overlap, in contrast to the spatial mapping of \({I}_{z}\) (Fig. 1d). At \(T=120\) K, the CPGE signal becomes nearly undetectable across the entire sample. This distinct spatial distribution of the CPGE current further discredits the thermal effect as the underlying generation mechanism³¹. Collectively, these experiments shed light on the CPGE’s behavior and rule out potential extrinsic factors, providing compelling evidence for an intrinsic origin of the observed CPGE in the graphite-KV₃Sb₅ device.

a Polarization dependence of the normalized out-of-plane photocurrent measured on the same device which was cooled down with either right-circular (blue points) or left-circular polarized (orange points) light. b Out-of-plane (blue) and in-plane (red) photocurrent as a function of light polarization. The measurement was performed at \(T=10\) K. For the in-plane photocurrent measurement, all contacts except contacts C and B (as labeled in Fig. 1c) are grounded. c CPGE distribution measured as a function of the beam spot ___location at \(T=\,\)10 K. The major contribution of CPGE appears circular, consistent with prior reports of CPGE from other materials^22,31, and occurs at the overlap region between graphite, KV₃Sb₅, and the bottom contact (the blue dashed line). d CPGE distribution measured as a function of the beam spot ___location at \(T=\) 120 K.

Full size image

Having discussed our experimental observations, we turn to explore the plausible mechanisms and symmetry prerequisites underlying the intriguing longitudinal CPGE in KV₃Sb₅. As the spin-orbit coupling in KV₃Sb₅ is weak⁸ and long-range magnetic order is absent³², the spin photogalvanic effect is expected to be minimal in KV₃Sb₅. Therefore, the observed helicity-dependent photocurrent is mainly driven by the orbital excitations, which in turn inherit the global symmetry of the electronic structure.

The photocurrent contributed from a k-point in the momentum space is determined by the CPGE tensor \({\widetilde{\beta }}_{{ij}}\left({{\bf{k}}}\right)\), where i represents the current direction and j denotes the laser propagating direction. \({\widetilde{\beta }}_{{ij}}\left({{\bf{k}}}\right)\) is proportional to the product of the Fermi velocity \({v}_{i}\left({{\bf{k}}}\right)\) and the Berry curvature \({\varOmega }_{j}\left({{\bf{k}}}\right)\)³³. Initially, we focus on the impact of inversion symmetry on the CPGE. For a generic momentum point \({{\bf{k}}}\) and its partner \(-{{\bf{k}}}\) linked by inversion symmetry, the Fermi velocities will change the signs \({v}_{i}\left(-{{\bf{k}}}\right)={-v}_{i}\left({{\bf{k}}}\right)\), while the Berry curvatures remain unchanged \({\varOmega }_{j}\left(-{{\bf{k}}}\right)={\varOmega }_{j}\left({{\bf{k}}}\right)\). Consequently, the resulting photocurrents from each pair of inversion partner cancel each other out, with \({\widetilde{\beta }}_{{ij}}\left(-{{\bf{k}}}\right)={-\widetilde{\beta }}_{{ij}}\left({{\bf{k}}}\right)\) indicating that breaking inversion symmetry is essential for KV₃Sb₅ to exhibit a nonzero CPGE.

Next, we examine the influence of mirror planes M on the CPGE within KV₃Sb₅, starting with M_x, which transforms \({{\bf{k}}}=\) (k_x, k_y, k_z) into M_x\({{\bf{k}}}\,\)= (-k_x, k_y, k_z). This operation only alters the sign of k_x, leading to a sign change in the x-component of the velocity while leaving the others unaffected: \({v}_{x}\)(M_x\({{\bf{k}}}\)) \({=-v}_{x}\left({{\bf{k}}}\right)\), \({v}_{y}\)(M_x\({{\bf{k}}}\)) \({=v}_{y}\left({{\boldsymbol{k}}}\right),\) \({v}_{z}\)(M_x\({{\bf{k}}}\)) \({=v}_{z}\left({{\bf{k}}}\right)\)(Fig. 4b, left-top). On the other hand, Berry curvature, being a pseudovector, only maintains its components perpendicular to the mirror plane, resulting in \({\varOmega }_{x}\)(M_x\({{\bf{k}}}\)) = \({\varOmega }_{x}\left({{\bf{k}}}\right)\), \({\varOmega }_{y}\)(M_x\({{\bf{k}}}\)) = \({-\varOmega }_{y}\left({{\bf{k}}}\right)\), \({\varOmega }_{z}\)(M_x\({{\bf{k}}}\)) = \({-\varOmega }_{z}\left({{\bf{k}}}\right)\) (Fig. 4b, left-bottom). In scenarios where the laser propagates along the z-axis and the current is measured in the same direction, the presence of a mirror plane M_x results in a null net current, as \({\widetilde{\beta }}_{{zz}}\)(M_x\({{\bf{k}}}\)) = \({v}_{z}\)\(({{\bf{k}}}){{\boldsymbol{\times }}}\) [\({-\varOmega }_{z}\)(\({{\bf{k}}}\))] = \(-{\widetilde{\beta }}_{{zz}}\)(\({{\bf{k}}}\)). A similar rationale concludes that mirror plane M_y (or M_z) also eliminates \({\widetilde{\beta }}_{{zz}}\), as illustrated in Fig. 4b (right). Therefore, to observe the nonzero photocurrents reported in our study \({\widetilde{\beta }}_{{zz}}\), all mirror planes must be broken in the correlated phases of KV₃Sb₅.

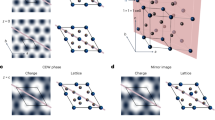
a Pristine phase of KV₃Sb₅, preserving inversion and mirror symmetries (M_x, M_y, and M_z). b Illustration of the effects of mirror symmetries on velocity \({v}_{i}\) and Berry curvature \({\varOmega }_{i}\). c Top and bottom patterns depicting structures with opposite chirality. The combination of two different chiral structures in a crystal yields an achiral structure with M_z mirror symmetry. d Calculated angle-resolved X-ray diffraction of high temperature (HT) and low temperature (LT) phase for TaTe₂. Significant differences in the peaks' intensities within the region encircled by the red-dashed box are observable, signaling the presence of strong structural deformations across the CDW phase transition in TaTe₂. e Calculated angle-resolved X-ray diffraction of the pristine phase and CDW phases of KV₃Sb₅.

Full size image

Taking all the above into consideration, we experimentally demonstrated that all the inversion and mirror symmetries are broken in KV₃Sb₅ at low temperatures. Subsequently, we turn to determining the potential point groups of chiral KV₃Sb₅. Our measurements, as illustrated in Fig. 3, revealed a polarization-dependent in-plane CPGE of zero, indicating that, \({\widetilde{\beta }}_{{xz}}\) and \({\widetilde{\beta }}_{{yz}}\) are both zero. This outcome stems from the rotational symmetries along the z-axis present in KV₃Sb_5. Specifically, any of the following rotational symmetries along the z-axis would nullify the in-plane CPGE: C_2z, S_2z, C_3z, S_3z, C_6z, and S_6z (see Supplementary Note 1 and Supplementary Fig. 3). Therefore, based on our measurements, we can infer that the possible point groups for the CDW phase of KV₃Sb₅ are C₂, D₂; C₃, D₃; C₆; D_6. Considering the evidence of a two-fold rotation charge distribution on the surface in previous studies^13,17, C₂ and D₂ are the most possible point groups. However, we cannot completely rule out the possibility that the bulk of chiral KV₃Sb₅ still preserves higher-fold screw rotations S_3z and or/and S_6z, which may not be detectable using surface-sensitive techniques.

We would like to further address the challenges of pinning down the structural chirality in KV₃Sb_5. Previous STM measurements observed a rotating surface charge distribution at low temperatures, suggesting a chiral charge order in KV₃Sb₅¹³. However, this rotating surface charge distribution only confirms the breaking of M_x and M_y. For instance, by applying the M_z operation, we can map a left-handed crystal into a right-handed crystal while the in-plane rotation direction remains the same (Fig. 4c). After the combination of the two opposite chiral crystals, the in-plane rotation remains unchanged, but the crystal is now an achiral structure with M_z. In other words, surface-sensitive experiments cannot fully rule out the existence of M_z. In another recent electronic magneto-chiral anisotropy measurement, the author also concluded that they can only confirm the breaking of M_x and M_y but not M_z¹⁶. In the current experiment, the long penetration depth of the 10 \(\mu m\) incident light (~20 nm) and the thickness of the device (~100 nm) ensures that the symmetry of the bulk crystal is probed, while the asymmetry induced by the interfaces is likely confined to a few layers at the interface and therefore is expected to be dominated by the bulk response. We note that the small atomic displacement in KV₃Sb₅ is the main reason challenging the experimental determination of the structure of KV₃Sb_5. Here, we compare KV₃Sb₅ with another CDW material TaTe₂³⁴. The average displacement is around 0.15 \(\mathring{\rm A}\) in TaTe₂, while the displacement in KV₃Sb₅ is only around 0.033 \(\mathring{\rm A}\). This difference can be visualized in our simulated X-ray diffraction (XRD) patterns. Detectable alterations can be observed between the high-temperature and low-temperature structures of TaTe₂ (Fig. 4d). In contrast, the XRD patterns of the two phases of KV₃Sb₅ are nearly identical (Fig. 4e). Our systematic photocurrent study thus provides strong constraints on the symmetries of the chiral charge order in KV₃Sb₅.

Our experimental observations of longitudinal CPGE in KV₃Sb₅ associated with its charge order provide direct evidence for broken inversion and mirror symmetries, indicating that the bulk CDW order is chiral, namely the electronic state is not superimposable on its mirror image. Although the atomic displacements in the charge-ordered state are small (Fig. 4d), the electron-phonon coupling may contribute to the symmetry breaking observed in KV₃Sb₅. Our phonon calculations for the pristine phase of KV₃Sb₅ reveal softened phonon modes along the path from M to L (Supplementary Fig. 7). This indicates that electron-phonon interactions could be a driving force behind the CDW phase transition in KV₃Sb₅, aligning with the findings from previous studies^35,36. Conversely, the detection of saddle points and quasi-nested electron and hole pockets on the Fermi surface points to inherent Fermi-surface instabilities¹¹. The high tunability of this intriguing CDW phase further underscores the potential role of electron-electron interactions, suggesting that they are also critical in the formation of the chiral CDW instability^13,16,37,38. Therefore, the CDW phase in AV₃Sb₅ (A = K, Rb, Cs) may result from a complex interplay between electron-phonon and electron-electron interactions. While this study provides a thorough investigation of the CPGE response in KV₃Sb₅, comparing it with other members of the metallic Kagome family, such as CsV₃Sb₅ and RbV₃Sb5, remains an important direction for future research. This is particularly relevant given the differences in chiral transport properties observed across the family³⁹. Furthermore, our approach utilizing non-linear photocurrent response can serve as a powerful tool for detecting subtle intrinsic symmetry breakings that lead to chiral electronic orders not only in other Kagome compounds but also in a broader range of quantum materials.

Single crystal synthesis

KV₃Sb₅ single crystals were grown by the flux method. K (99.95%), V (99.999%), and Sb (99.9999%) with the K/V/Sb=7: 3: 14 molar ratio were fully mixed. The mixture was then placed into an alumina crucible, sealed in a quartz tube with 10⁻³ Pa of Ar pressure, heated up to 1000 °C in 200 h, kept at 1000 °C for 12 h, and subsequently cooled to 200 °C over 230 h. After the stove had come down to room temperature, the flux was removed by putting the mixtures into deionized water. Finally, the high-quality single crystals of KV₃Sb₅ were harvested.

Device fabrication

We utilized a polydimethylsiloxane (PDMS) stamp-based mechanical exfoliation technique to fabricate KV₃Sb₅ devices. We patterned the electrical contacts onto the sample exfoliated onto the silicon substrates with a 280 nm layer of thermal oxide using electron beam lithography, followed by chemical development and metal deposition (5 nm Cr/35 nm Au). The fresh KV₃Sb₅ crystals were mechanically exfoliated from bulk single crystals on PDMS stamps. Prior to transferring them onto the SiO₂/Si substrates with pre-patterned Cr/Au electrodes, we visually inspected the crystals under optical microscopy to select samples with favorable geometries. Note that the KV₃Sb₅ flake was transferred on the top of the pre-patterned contacts labeled B-E in Fig. 1c. The in-plane photocurrent (vertical to the light incidence) of the KV₃Sb₅ device was measured between electrodes B-E. To measure the photocurrent perpendicular to the sample plane (along the incident light), a few-layer graphene (graphite) was introduced as a top contact to connect the electrode A and the KV₃Sb₅ flake. The entire sample fabrication process was conducted within a glovebox equipped with a gas purification system, maintaining an environment with low levels of oxygen and water vapor (<1 ppm).

Photocurrent measurements

The probing light for our experiments was generated from a CO₂ laser (Access Laser) and modulated using a mechanical chopper (Thorlabs) operating at a frequency of 167 Hz. To focus the laser onto the sample, we employed a ZnSe lens with a focal length of 50 mm, resulting in a beamspot size of ~25 μm at full width at half maximum. The input power on the sample surface was maintained at 2.9 mW. To detect the current signal, we employed a current preamplifier (SR570) for initial amplification, followed by the measurements using a lock-in amplifier (SR830). This setup ensured accurate and sensitive current detection. The device under investigation was cooled down using a customized cryostat (Oxford MicroHires) specifically designed for our experimental requirements. To ensure the reliability and consistency of our measurements, we repeated the experiments on multiple devices and performed multiple measurements for each device to ensure the reproducibility of the results.

First-principles calculations based on X-ray diffraction

The structures of the pristine phase and 2 × 2 × 2 CDW phase of KV₃Sb₅ are based on previous experimental work⁸ and theoretical predictions⁴⁰, respectively. To minimize structural disparities between experimental data and theoretical calculations, we performed structural relaxations using identical parameters. Our ab-initio calculations were performed within the framework of density functional theory (DFT), employing the Vienna Ab initio Simulation Package (VASP) with the Perdew−Burke−Ernzerhof exchange−correlation functional^41,42,43. The structural file (.cif) is provided as a Supplementary Data file. The valence electrons for K, V, and Sb were treated as 4s¹, 3d³4s², and 5s²5p³, respectively. In our calculations, we used a kinetic energy cutoff of 520 eV and a k-spacing parameter of 0.2 to ensure energy convergence within 1 meV/atom. An energy threshold of 10⁻⁶ eV and a force threshold of 3 × 10⁻³eV/Å were applied. To account for van der Waals interactions, we included the zero-damping DFT-D3 method⁴⁴ in our calculations. The simulated angle-resolved X-ray diffraction (XRD) data for the pristine phase and 2 × 2 × 2 CDW phase in the KV₃Sb₅ system were generated with an X-ray wavelength of 0.1671 Å⁹. For the TaTe₂ system, both the high-temperature and low-temperature phase structures were experimentally determined and directly used for simulating X-ray diffraction data, with an X-ray wavelength of 0.1173 Å⁴⁵.