Abstract
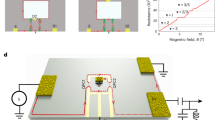
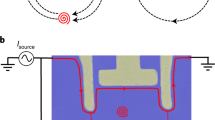
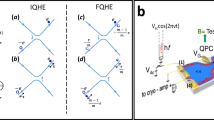
Fractional quantum statistics are the defining characteristic of anyons. Measuring the phase generated by an exchange of anyons is challenging, as standard interferometry set-ups—such as the Fabry–Pérot interferometer—suffer from charging effects that obscure the interference signal. Here we present the observation of anyonic interference and exchange phases in an optical-like Mach–Zehnder interferometer based on co-propagating interface modes. By avoiding backscattering and deleterious charging effects, this set-up enables pristine and robust Aharonov–Bohm interference without any phase slips. At various fractional filling factors, the observed flux periodicities agree with the fundamental fractionally charged excitations that correspond to Jain states and depend only on the bulk topological order. To probe the anyonic statistics, we used a small, charged top gate in the interferometer bulk to induce localized quasiparticles without modifying the Aharonov–Bohm phase. The added quasiparticles introduce periodic phase slips. The sign and magnitude of the observed phase slips align with the expected value at filling 1/3, but their direction shows systematic deviations at fillings 2/5 and 3/7. Control over added individual quasiparticles in this design is essential for measuring the coveted non-abelian statistics in the future.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
27,99 € / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
269,00 € per year
only 22,42 € per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided with this paper. These data are also publicly available via Zenodo at https://doi.org/10.5281/zenodo.15394075(ref. 42).
References
Halperin, B. I. Quantized Hall conductance, current-carrying edge states, and the existence of extended states in a two-dimensional disordered potential. Phys. Rev. B 25, 2185–2190 (1982).
de-Picciotto, R. et al. Direct observation of a fractional charge. Nature 389, 162–164 (1997).
Reznikov, M., de Picciotto, R., Griffiths, T. G., Heiblum, M. & Umansky, V. Observation of quasiparticles with one-fifth of an electron’s charge. Nature 399, 238–241 (1999).
Saminadayar, L., Glattli, D. C., Jin, Y. & Etienne, B. Observation of the e/3 fractionally charged Laughlin quasiparticle. Phys. Rev. Lett. 79, 2526–2529 (1997).
Wilczek, F. Magnetic-flux, angular-momentum, and statistics. Phys. Rev. Lett. 48, 1144–1146 (1982).
Arovas, D., Schrieffer, J. R. & Wilczek, F. Fractional statistics and the quantum Hall effect. Phys. Rev. Lett. 53, 722–723 (1984).
Halperin, B. I. Statistics of quasiparticles and the hierarchy of fractional quantized Hall states. Phys. Rev. Lett. 52, 1583–1586 (1984).
Leinaas, J. M. & Myrheim, J. in Fractional Statistics and Anyon Superconductivity (ed. Wilczek, F.) 132–156 (World Scientific, 1990).
Stern, A. Anyons and the quantum Hall effect – a pedagogical review. Ann. Phys. 323, 204–249 (2008).
Chamon, C. D. C., Freed, D. E., Kivelson, S. A., Sondhi, S. L. & Wen, X. G. Two point-contact interferometer for quantum Hall systems. Phys. Rev. B 55, 2331–2343 (1997).
Lee, J.-Y. M. et al. Partitioning of diluted anyons reveals their braiding statistics. Nature 617, 277–281 (2023).
Han, C., Park, J., Gefen, Y. & Sim, H. S. Topological vacuum bubbles by anyon braiding. Nat. Commun. 7, 11131 (2016).
Jeon, G. S., Graham, K. L. & Jain, J. K. Berry phases for composite fermions: effective magnetic field and fractional statistics. Phys. Rev. B 70, 125316 (2004).
Jain, J. K., Kivelson, S. A. & Thouless, D. J. Proposed measurement of an effective flux quantum in the fractional quantum Hall effect. Phys. Rev. Lett. 71, 3003–3006 (1993).
Ofek, N. et al. Role of interactions in an electronic Fabry–Perot interferometer operating in the quantum Hall effect regime. Proc. Natl Acad. Sci. USA 107, 5276–5281 (2010).
Zhang, Y. M. et al. Distinct signatures for Coulomb blockade and Aharonov-Bohm interference in electronic Fabry-Perot interferometers. Phys. Rev. B 79, 241304 (2009).
Schuster, R. et al. Phase measurement in a quantum dot via a double-slit interference experiment. Nature 385, 417–420 (1997).
Rosenow, B. & Simon, S. H. Telegraph noise and the Fabry-Perot quantum Hall interferometer. Phys. Rev. B 85, 201302 (2012).
Levkivskyi, I. P., Fröhlich, J. & Sukhorukov, E. V. Theory of fractional quantum Hall interferometers. Phys. Rev. B 86, 245105 (2012).
Ji, Y. et al. An electronic Mach–Zehnder interferometer. Nature 422, 415–418 (2003).
Neder, I., Heiblum, M., Levinson, Y., Mahalu, D. & Umansky, V. Unexpected behavior in a two-path electron interferometer. Phys. Rev. Lett. 96, 016804 (2006).
Neder, I. et al. Interference between two indistinguishable electrons from independent sources. Nature 448, 333–337 (2007).
Halperin, B. I., Stern, A., Neder, I. & Rosenow, B. Theory of the Fabry-Perot quantum Hall interferometer. Phys. Rev. B 83, 155440 (2011).
Nakamura, J. et al. Aharonov–Bohm interference of fractional quantum Hall edge modes. Nat. Phys. 15, 563–569 (2019).
Sivan, I. et al. Observation of interaction-induced modulations of a quantum Hall liquid’s area. Nat. Commun. 7, 12184 (2016).
Nakamura, J., Liang, S., Gardner, G. C. & Manfra, M. J. Direct observation of anyonic braiding statistics. Nat. Phys. 16, 931–936 (2020).
Kim, J. et al. Aharonov–Bohm interference and statistical phase-jump evolution in fractional quantum Hall states in bilayer graphene. Nat. Nanotechnol. 19, 1619–1626 (2024).
Samuelson, N. L. et al. Anyonic statistics and slow quasiparticle dynamics in a graphene fractional quantum Hall interferometer. Preprint at arxiv.org/abs/2403.19628 (2024).
Werkmeister, T. et al. Anyon braiding and telegraph noise in a graphene interferometer. Science 388, 730–735 (2025).
Byers, N. & Yang, C. N. Theoretical considerations concerning quantized magnetic flux in superconducting cylinders. Phys. Rev. Lett. 7, 46 (1961).
Kivelson, S. Semiclassical theory of localized many-anyon states. Phys. Rev. Lett. 65, 3369–3372 (1990).
Feldman, D. E., Gefen, Y., Kitaev, A., Law, K. T. & Stern, A. Shot noise in an anyonic Mach-Zehnder interferometer. Phys. Rev. B 76, 085333 (2007).
Law, K. T., Feldman, D. E. & Gefen, Y. Electronic Mach-Zehnder interferometer as a tool to probe fractional statistics. Phys. Rev. B 74, 045319 (2006).
Kundu, H. K., Biswas, S., Ofek, N., Umansky, V. & Heiblum, M. Anyonic interference and braiding phase in a Mach-Zehnder interferometer. Nat. Phys. 19, 515–521 (2023).
Giovannetti, V., Taddei, F., Frustaglia, D. & Fazio, R. Multichannel architecture for electronic quantum Hall interferometry. Phys. Rev. B 77, 155320 (2008).
Deviatov, E. V., Egorov, S. V., Biasiol, G. & Sorba, L. Quantum Hall Mach-Zehnder interferometer at fractional filling factors. Europhys. Lett. 100, 67009 (2012).
Batra, N., Wei, Z., Vishveshwara, S. & Feldman, D. E. Anyonic Mach-Zehnder interferometer on a single edge of a two-dimensional electron gas. Phys. Rev. B 108, L241302 (2023).
Biswas, S., Kundu, H. K., Umansky, V. & Heiblum, M. Electron pairing of interfering interface-based edge modes. Phys. Rev. Lett. 131, 096302 (2023).
Jeon, G. S., Graham, K. L. & Jain, J. K. Fractional statistics in the fractional quantum Hall effect. Phys. Rev. Lett. 91, 036801 (2003).
Su, W. P. Statistics of the fractionally charged excitations in the quantum Hall effect. Phys. Rev. B 34, 1031–1033 (1986).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Ghosh, B. Anyonic braiding in a chiral Mach-Zehnder interferometer. Zenodo https://doi.org/10.5281/zenodo.15394075 (2025).
Acknowledgements
M.H. thanks D. E. Feldman for fruitful discussions and M. Banerjee for her suggestions. B.G and M.L thanks A. K. Paul, H. K. Kundu and S. Biswas for the helpful comments that improved our device. B.G. and M.L. thank A. Gupta for help with the statistical phase analysis. D.F.M. acknowledges many illuminating conversations on quantum Hall interferometry with Y. Ronen. D.F.M. was supported by the Israel Science Foundation (grant no. 2572/21) and by the Deutsche Forschungsgemeinschaft within the CRC network TR 183 (project grant no. 277101999). M.H. acknowledges the support of the European Research Council under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 833078). M.L. thanks the Ariane de Rothschild Women Doctoral Program for their support.
Author information
Authors and Affiliations
Contributions
B.G. fabricated the devices. B.G. and M.L. performed the measurements and analysed the data with input from M.H. L.M. characterized the devices at the initial stage of the experiment. M.H. supervised the experimental design, execution and data analysis. D.F.M. worked on the theoretical aspects and data analysis. V.U. grew the GaAs heterostructures. All authors contributed to the writing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–12, Tables 1 and 2 and Discussion.
Source data
Source Data Figs. 1, 2, 3 and 4
Source Data Fig. 1 Raw data for Fig. 1d. Source Data Fig. 2 Raw data without background subtraction. Source Data Fig. 3 Raw data for each panel without background subtraction. Source Data Fig. 4 Raw data for each panel without background subtraction. Figure 4b,d were obtained from line cuts of Fig. 4a,c so source data are not provided.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ghosh, B., Labendik, M., Musina, L. et al. Anyonic braiding in a chiral Mach–Zehnder interferometer. Nat. Phys. (2025). https://doi.org/10.1038/s41567-025-02960-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41567-025-02960-3