Abstract
The coupling between electrons and phonons is one of the fundamental interactions in solids, underpinning a wide range of phenomena, such as resistivity, heat conductivity and superconductivity. However, direct measurements of this coupling for individual phonon modes remain a substantial challenge. In this work, we introduce a new technique for mapping phonon dispersions and electron–phonon coupling (EPC) in van der Waals (vdW) materials. By generalizing the quantum twisting microscope1 (QTM) to cryogenic temperatures, we demonstrate its capability to map not only electronic dispersions through elastic momentum-conserving tunnelling but also phononic dispersions through inelastic momentum-conserving tunnelling. Crucially, the inelastic tunnelling strength provides a direct and quantitative measure of the momentum and mode-resolved EPC. We use this technique to measure the phonon spectrum and EPC of twisted bilayer graphene (TBG) with twist angles larger than 6°. Notably, we find that, unlike standard acoustic phonons, whose coupling to electrons diminishes as their momentum tends to zero, TBG exhibits a low-energy mode whose coupling increases with decreasing twist angle. We show that this unusual coupling arises from the modulation of the interlayer tunnelling by a layer-antisymmetric ‘phason’ mode of the moiré system. The technique demonstrated here opens the way for examining a large variety of other neutral collective modes that couple to electronic tunnelling, including plasmons2, magnons3 and spinons4 in quantum materials.
Similar content being viewed by others
Main
EPC plays a key role in determining the thermal and electrical properties of quantum materials. In monolayer graphene, for instance, an exceptionally weak EPC5 results in ultrahigh electronic mobility, micrometre-scale ballistic transport6 and hydrodynamic behaviour7. By contrast, the nature of EPC in moiré systems is much less understood. Various theories have attributed superconductivity8 and ‘strange-metal’ behaviour9,10 in magic-angle twisted bilayer graphene (MATBG) to a strong coupling of electrons to optical11,12,13 or acoustic12,14,15,16,17,18 phonons. Specifically, as well as the phonons of the individual layers, twisted interfaces with quasiperiodic structures exhibit unique phononic modes involving an antisymmetric motion of atoms in the two layers. These modes, dubbed moiré phonons19,20,21 or phasons21,22,23,24, resemble acoustic modes and constitute a new set of low-energy excitations. Phason modes may induce strong electronic effects because the moiré pattern acts as an amplifier16—small shifts on the atomic scale lead to notable distortions of the moiré pattern—which, in turn, strongly couples to the moiré energy bands.
Existing techniques for examining phonon dispersions and EPC rely on inelastic scattering of photons (angle-resolved photoemission spectroscopy25,26, Raman27,28,29 and X-ray30,31), electrons (electron energy loss spectroscopy32,33), neutrons34 or helium atoms35, as well as on indirect measurement through the effect of EPC on electrical resistance36. Tunnelling across twistable graphitic interfaces37,38 revealed sharp conductivity peaks at commensurate angles of 21.8° and 32.8° superimposed on a continuous background attributed to momentum-resolved phonon absorption. These experiments were limited to room temperature, preventing the observation of phonon emission processes, key for examining their EPC. Quantitative extraction of EPC thus remains a challenge, especially for the low-energy acoustic modes in vdW devices, which are central to the physics at low temperatures.
In this work, we developed a cryogenic QTM and used it to directly map the phonon spectrum and mode-resolved EPC in TBG through inelastic momentum-resolved spectroscopy. Notably, we identify a low-energy mode whose coupling increases with decreasing twist angle, providing a clear signature of a layer-antisymmetric phason mode coupling directly and strongly to the interlayer tunnelling.
Measuring phonon dispersion with the cryogenic QTM
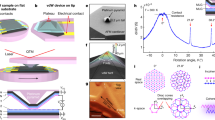
Our cryogenic QTM (Fig. 1a and Methods) consists of a custom-built cryogenic atomic force microscope (AFM) that allows forming a twistable two-dimensional interface between two vdW heterostructures, one on its tip and one on a flat substrate. The interface is created at low temperatures, gets self-cleaned in situ and remains in contact throughout the experiment.
a, Schematics of the cryogenic QTM (inset), allowing us to form a continuously twistable interface between two vdW materials at T = 4 K (main panel). We use an inelastic momentum-conserving electronic tunnelling process to emit and measure phonons at the interface with a well-defined momentum, continuously tunable by twisting (black arrow). b, The experiments in this figure are all performed in a twisted junction between two graphite flakes (several tens of nanometres thick), shown schematically. We apply a bias Vb across the junction and measure current, I, and conductance \(G=\frac{{\rm{d}}I}{{\rm{d}}{V}_{{\rm{b}}}}\). c, Measured G versus twist angle, θ, for Vb = 0 mV (black) and 50 mV (blue). d, Measured G versus Vb at θ = 30°, exhibiting discrete steps (arrows), indicative of a series of inelastic tunnelling processes. e, Two-dimensional measurement of G versus θ and Vb, showing that the steps in G appear at all twist angles and that their turn-on bias disperses smoothly with θ. f, The second derivative, \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\), obtained numerically from panel e, highlighting the steps in G that now appear as peaks. We see several peaks that disperse slowly with θ, exhibiting a mirror symmetry around θ = 30° and showing good symmetry between positive and negative bias. Also, we see sharply dispersing peaks near θ = 21.8° and 38.2°. The theoretically calculated phonon spectrum of graphite (dashed black lines; Methods section ‘Bulk-graphite phonon dispersion model’) shows excellent agreement with the slowly dispersing peaks. From the measurement, we can identify the acoustic (TA, ZA) and optical (LO, TO, ZO) phonon branches. The layer-antisymmetric ZA phonon is often also called ZO′. g, The Fermi surfaces in k-space of the top (blue) and bottom (red) graphite layers. h, The corresponding energy bands. At a finite twist angle, there is a momentum mismatch between these energy bands, and momentum-conserving electronic tunnelling between the layers can occur only by means of the emission of a phonon that provides the missing momentum, qph = 2KDsin(θ/2). This is an inelastic process that turns on when the bias voltage equals the phonon energy at this momentum, Vb = ωph(qph). By following the turn-on in the θ–Vb plane, we directly map the phonon dispersion line (orange). Symmetry around 30° in the experiment is explained by phonon emission processes starting from the K or K′ of one layer and ending at the same point in the other layer.
We begin our experiments with a twisted interface formed between two graphite layers, both several tens of nanometres thick (Fig. 1b). We set the bias across the interface, Vb, and measure the tunnelling current, I, and conductance, \(G=\frac{{\rm{d}}I}{{\rm{d}}{V}_{{\rm{b}}}}\), versus twist angle, θ. At zero bias, G exhibits a pronounced peak at commensurate angles θ = 21.8° and 38.2° (refs. 37,38) (Fig. 1c) resulting from elastic momentum-resolved tunnelling owing to overlapping Fermi surfaces on both sides of the interface1,39. At Vb = 50 mV (blue), G increases substantially across all twist angles. The bias dependence of G at θ = 30° shows that it increases in steps (Fig. 1d), signifying the onset of discrete inelastic tunnelling processes. Similar steps, observed in scanning tunnelling microscopy experiments of graphene40 and with fixed-angle tunnelling devices41,42,43, were attributed to inelastic electron tunnelling mediated by phonon emission.
Given that the QTM is a momentum-resolved tunnelling probe, it is natural to ask whether the observed inelastic processes are momentum-conserving by investigating their twist angle evolution. Figure 1e shows G measured versus θ and Vb, revealing again that G increases in steps with bias. This becomes even more apparent in the second derivative, \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\) (Fig. 1f), which exhibits sharp peaks at the turn-on biases of the steps. The measurement reveals a rich spectrum of low-energy peaks that slowly disperse with θ, exhibiting a mirror symmetry about θ = 30° and between positive and negative biases.
To understand these observations, we turn to momentum space (Fig. 1g). At large twist angle between the two graphite flakes, the momentum mismatch between their bands is too large to allow elastic momentum-conserving tunnelling. However, owing to the shallower dispersion of phonons, their emission in an inelastic tunnelling process across the interface may provide the missing momentum, qph = 2KDsin(θ/2) (Fig. 1h; KD is the Dirac point momentum). This process turns on when the bias is larger than the phonon energy at this momentum, eVb > ħωph(qph). Thus, the positions of the \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\) peaks in the θ–Vb plane directly trace the phonon spectrum. Indeed, overlaying the theoretically calculated spectrum for bulk graphite (dashed lines; Methods section ‘Bulk-graphite phonon dispersion model’) shows excellent agreement. Specifically, we identify various acoustic (TA, ZA) and optical (LO, TO, ZO) branches and follow their dispersion. However, because the graphite flakes have complex band structures, and their twisted interface has phonons both in the bulk of the graphite and at the interface, to better understand the underlying EPC mechanisms, it is instructive to switch to a simpler system.
EPC in TBG
We turn to the main system in this paper—TBG—in which EPC is believed to be of the most importance9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,26,29,44,45,46. We create a tunable TBG system by bringing a hexagonal boron nitride (hBN)-backed monolayer graphene, placed on a tip, into contact with another monolayer graphene on a bottom sample that incorporates a buried graphite gate (Fig. 2a). When in contact, the Dirac cones of the two graphene layers, now at the corners of a mini-Brillouin zone (mini-BZ), hybridize to yield the TBG energy bands (colour-coded in Fig. 2c by layer weight). For the twist angles in the current experiment, the hybridization is small and the bands remain largely similar to the original Dirac cones. For each θ, our experiment realizes a different TBG system and examines a specific zone-boundary phonon mode with a momentum \({q}_{{\rm{M}}}={2K}_{{\rm{D}}}\sin \left(\frac{\theta }{2}\right)\), connecting the two corners of the mini-BZ (Fig. 2b), as well as the back-folded phonon with \({\widetilde{q}}_{{\rm{M}}}={2K}_{{\rm{D}}}\sin \left(\frac{60-\theta }{2}\right)\). Figure 2d,e plots G and \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\) measured versus θ and Vb, showing how the energy of this zone-boundary phonon changes with the TBG twist angle. For comparison, the dashed lines show the energy of bulk graphite phonons at momenta qM (black) and \({\widetilde{q}}_{{\rm{M}}}\) (grey). Extended Data Fig. 3 shows the trajectory of qM in the phonon Brillouin zone (BZ).
a, A tunable TBG is formed by bringing into contact a monolayer graphene on the tip (blue) with a monolayer graphene on a flat sample (red), both backed by hBN and with a global graphite back gate. b, TBG’s mini-BZ, with Dirac points of the top and bottom layers at its corners (labelled KT and KB). The measured inelastic tunnelling processes involve an electron tunnelling between the layers while emitting a mini-BZ phonon that provides the missing momentum (qM, orange). c, The corresponding TBG band structure along the KT–KB line, colour-coded by layer weight. d, Measured conductance, G, versus bias voltage, Vb, and twist angle, θ, exhibiting steps in G that disperse with θ. e, The second derivative, \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\), obtained numerically from panel d, overlaid with the theoretically calculated phonon spectrum of graphite (dashed lines, various modes labelled; Methods section ‘Bulk-graphite phonon dispersion model’). Phonon lines measured at q = qM are marked in black and phonon lines measured at \(q={\widetilde{q}}_{{\rm{M}}}\) (see text) are marked in grey. f, Zoom-ins on the TA phonon peaks in panel e, at positive and negative bias, but with a colour map that reveals the variation of \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\) peak amplitude with θ. g, In-layer EPC mechanism, originating from the phonon modifying the in-layer hopping amplitude, t|| (top illustration). EPC strength is proportional to the stretching of the bonds by a single phonon, namely, with ZPM amplitude (marked). In the limit q → 0, the ZPM stretching is distributed over many bonds and the EPC tends to zero. Moreover, because our experiments measure only electrons that tunnel between the layers, the in-layer EPC appears in them only as a second-order process—a virtual tunnelling between the layers (right brackets) followed by phonon emission (left square). h, Interlayer EPC mechanism: here an antisymmetric motion of atoms in the two layers (a phason of the moiré lattice) directly modifies the tunnelling amplitude t⟂ between them (top illustration). In this case, the maximal bond stretching is independent of qM and is equal to the full ZPM. Because the latter increases with decreasing qM, counter-intuitively, this EPC should intensify with decreasing qM. Moreover, because here the phonon couples directly to the interlayer tunnelling, this process appears in the first order in our experiment (box). i, The experiment examines phasons with momentum q = qM (illustrated).
A key feature of our momentum-resolved inelastic tunnelling technique is that it allows us to directly determine the mode-dependent and momentum-dependent EPC. As will be shown below, the height of the step in G, or equivalently the area under the peak in \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\), is directly proportional to the strength of the EPC. Notably, Fig. 2d,e shows that the EPC varies greatly between the different phonon branches. Around Vb ≈ 160 mV, we observe a pronounced step in G that corresponds to the intervalley K-point optical phonons (LO and TO). Indeed, strong EPC to optical phonons is expected in monolayer graphene47,48 and is believed to be notable in MATBG13,26. More puzzling behaviours are observed in the acoustic branches. First, although the peaks corresponding to the out-of-plane and transverse modes (ZA and TA) are evident, the longitudinal mode (LA) is conspicuously missing. Second is the twist-angle dependence of the peak height (highlighted in colour in a detailed view of the TA branches at positive and negative bias, Fig. 2f). Instead of decreasing with decreasing momentum, as typically anticipated for acoustic modes, the measured EPC actually increases.
To understand these unusual observations, we consider the relevant EPC mechanisms in TBG. The simplest EPC occurs within the layer (an ‘in-layer’ mechanism Fig. 2g; Methods section ‘Theory model for inelastic tunnelling through phonon emission and the two mechanisms of EPC’): a phonon modulates the in-layer hopping amplitudes, t∥, scattering the electron within the layer. However, because our measurement examines electrons tunnelling between the layers, this EPC appears in a second-order process: initially, an electron tunnels to a high-energy virtual state with the same momentum in the other layer, with amplitude \(\alpha =\frac{{t}_{\perp }}{\hbar {\nu }_{{\rm{f}}}{K}_{{\rm{D}}}\theta }\ll 1\), followed by phonon emission through in-layer EPC, or vice versa (Fig. 2g). In TBG, there exists another ‘interlayer’ mechanism that couples electrons to antisymmetric vibrations of the two layers (Fig. 2h), whose acoustic branch is the phason of the TBG19,20,21,22,23,24. These antisymmetric vibrations stretch the interlayer bonds and therefore modify the tunnelling amplitudes between the layers, t⟂ (Fig. 2h). This leads to an interlayer EPC that already contributes in a first-order process (Methods section ‘Theory model for inelastic tunnelling through phonon emission and the two mechanisms of EPC’).
The unusual behaviour of the phason’s EPC becomes apparent in the limit of qM → 0. The strength of EPC is proportional to the stretching of the atomic bonds by a vibration whose amplitude is the zero-point motion (ZPM) of the phonon, \({\xi }_{{\rm{ZPM}}}=\sqrt{\hbar /2M{\omega }_{{\rm{M}}}}\) (ωM is the phonon frequency and M is the carbon atom mass). For in-plane bonds, the stretching by ξZPM is distributed over many bonds, N ≈ (qMa)−1 (Fig. 2g) and thus, in the limit qM → 0, the corresponding in-layer EPC tends to zero, as expected for an acoustic mode. Notably, when the layers vibrate antisymmetrically, the interlayer bond stretching is directly given by ξZPM, independent of qM (Fig. 2h). For a linearly dispersing phason \({\xi }_{{\rm{ZPM}}}\approx \frac{1}{\sqrt{{q}_{{\rm{M}}}}}\), this predicts that its interlayer EPC should increase as \(\frac{1}{\sqrt{{q}_{{\rm{M}}}}}\) in the limit qM → 0.
To study this quantitatively, we determine all key experimental parameters in situ. The inelastic conductance step is directly related to the interlayer, ginterlayer, and in-layer, gin-layer, EPCs through (Methods sections ‘Theory model for inelastic tunnelling through phonon emission and the two mechanisms of EPC’ and ‘Extracting EPC from the measured inelastic conductance steps’):
in which \(\beta ={N}_{{\rm{f}}}{N}_{{\rm{b}}}\frac{{2\pi e}^{2}}{\hbar }\frac{{a}^{2}\sqrt{3}}{2}\), Nf = 4 is the flavour degeneracy (spin/valley), Nb = 3 is the number of Bragg scattering processes, Nlayer = 2 is the number of layers, a = 0.246 nm is the lattice constant of graphene and α is as defined above. The experiment-specific parameters in equation (1) are the tip contact area (Atip) and the density of states (DOS) of the bottom and top layers (νB and νT), all of which we can tune and measure in situ.
To determine the dependence on tip contact area, we use unique QTM capabilities to both modify and image the tip area in situ. The imaging is achieved by spatially scanning the tip along fixed atomic defects (on an adjacent area with defects in a WSe2 layer; see Methods section ‘Imaging the tip contact area in situ and determining the pressure in the experiment’). The measured current in such a spatial scan (Fig. 3b,c) reveals several replicas of the tip shape, each produced when the tip overlaps a single atomic defect. Imaging after using mechanical manipulation to change the tip size shows a tip area that is enhanced approximately twofold (Fig. 3b, tip 1). Figure 3a shows the G versus Vb traces measured for the two tip areas, featuring conductance steps resulting from the ZA and TA phonon modes. When plotting G normalized by the measured area, the curves collapse on each other (Fig. 3a inset), demonstrating that we capture the area dependence quantitatively.
a, Tip area dependence of the inelastic tunnelling steps: measured G versus Vb for TBG with θ = 16.8° and Vbg = 4 V for two tip contact areas, Atip. The height of the inelastic steps corresponding to the ZA and TA phonon modes are marked (ΔGZA, ΔGTA). Inset, same traces but normalized by the measured Atip. b,c, To image the tip area in situ, we scan it along fixed atomic defects located in a WSe2 layer placed on top of the bottom graphene on the side of the main experiment. The panels show the imaged current in a spatial scan, exhibiting several copies of the tip shape, each produced by a different single defect. Scale bars, 100 nm. d, DOS dependence of the inelastic tunnelling steps: measured G versus Vb and Vbg for TBG with θ = 16.8°. The gate voltage modifies the carrier density in the two layers and, consequently, their DOS. Dashed lines are the charge neutrality of the top (blue) and bottom (red) graphene layers, calculated from an electrostatic model of the junction (Methods section ‘Electrostatic model for the QTM junction’). Inelastic tunnelling steps in G are visible as horizontal lines (corresponding phonon modes are marked). e, The second derivative, \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\), obtained numerically from panel d, exhibiting horizontal lines that correspond to the various phonon modes. We also see superimposed Fabry–Pérot oscillations owing to the finite size of the tip. f, Measured linecuts of G versus Vb taken from panel d at Vbg = 2 V and 8 V (vertical dashed lines in panel d). g, Amplitude of the conductance step of the TA mode, ΔGTA versus Vbg extracted from panel d (θ = 16.8°) and from two similar measurements in Extended Data Fig. 9 carried out at θ = 9.4° and 22.7°. Dashed lines plot the theoretical model that predicts a linear dependence of ΔGTA on Vbg, agreeing closely with the experiment. Notably, the overall ΔGTA amplitude (and therefore the corresponding EPC) increases with decreasing θ.
To investigate the dependence on the DOS, we plot G and \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\) measured versus back-gate voltage, Vbg, and Vb (Fig. 3d,e) exhibiting steps in G. Visibly, the steps amplitude scale linearly with Vbg (Fig. 3f,g, details in caption). An electrostatic model (Methods section ‘Electrostatic model for the QTM junction’) shows that, to a good approximation, both nB and nT vary linearly with Vbg and thus the product of their Dirac DOS follows \({\nu }_{{\rm{T}}}{\nu }_{{\rm{B}}}\approx \sqrt{| {n}_{{\rm{T}}}| | {n}_{{\rm{B}}}| }\), which aligns well with the observed linear dependence (Fig. 3g) and the flipping of its slope on carrier polarity change (Methods section ‘Further data from different samples and QTM tips’). Combining data from other twist angles (Methods section ‘Further data: G as a function of Vb and Vbg measured at two more twist angles, θ = 22.7° and 9.4°’), Fig. 3g highlights the distinct behaviour: ΔGTA increases with decreasing θ, showing that the coupling to the TA mode becomes stronger as qM decreases.
We can now determine the EPC from our experiments. For the optical phonons, we extract the inelastic conductance step near Vb = 160 mV from Fig. 2d (intervalley, K-point optical phonons), divide by 2 to obtain the average of the LO and TO modes (dominated by the TO mode; Methods section ‘Theory model for inelastic tunnelling through phonon emission and the two mechanisms of EPC’), normalize by the measured prefactors in equation (1) and plot the resulting quantity, ΔGoptical/2βνTνBAtip, versus θ in the inset of Fig. 4a (dots). This is compared with the theoretically predicted in-layer (α2Nlayer|gin-layer|2) and interlayer (|ginterlayer|2) contributions, calculated49 using existing models (Methods section ‘Theory model for inelastic tunnelling through phonon emission and the two mechanisms of EPC’). The theory reveals that, for optical phonons, the interlayer EPC is negligible and thus we can directly extract the average optical coupling \({g}_{{\rm{optical}}}=\sqrt{({g}_{{\rm{TO}}}^{2}+{g}_{{\rm{LO}}}^{2})/2}\) by identifying the measurement with the in-layer term. Plotted as a function of θ (main panel), we see that goptical is weakly dependent on θ and amounts to 300–350 meV, approximately two times larger than that determined by angle-resolved photoemission spectroscopy25,26 and in good agreement with Raman27,47.
a, Inset, measured inelastic conductance step, versus θ, corresponding to the intervalley (near the K point in the phonon BZ) optical modes (TO and LO), normalized following equation (1) using the measured tip area and DOS (we divided the measured step by 2 to obtain the average contribution of the TO and LO modes). Solid lines are theoretically calculated in-layer (green) and interlayer (yellow) contributions. Visibly, for optical phonons, the dominant EPC mechanism is the in-layer one (Methods section ‘Theory model for inelastic tunnelling through phonon emission and the two mechanisms of EPC’). Main, the intervalley average optical modes EPC, \({g}_{{\rm{optical}}}=\sqrt{({g}_{{\rm{TO}}}^{2}+{g}_{{\rm{LO}}}^{2})/2}\), determined from the measurements in the inset. Error bars are obtained from differences between measurements at positive and negative bias and all other experimental uncertainties. b, Intervalley TO phonon energy as a function of θ extracted from Fig. 2e. c, Inset, measured inelastic conductance step, versus θ, corresponding to the acoustic TA mode, normalized following equation (1) using the measured tip area and DOS. Solid lines are the theoretically calculated in-layer (green) and interlayer (yellow) contributions. In contrast to optical phonons, the EPC of the acoustic phonons is dominated by the interlayer coupling mechanism, which is the layer-antisymmetric phason mode. Main panel, the electron–phason coupling, gphason, determined from the measurements in the inset. Error bars are obtained from differences between measurements at positive and negative bias and all other experimental uncertainties. d, TA mode energy as a function of θ extracted from Fig. 2e.
Figure 4c analyses the EPC of the gauge (TA) acoustic phonon, comparing its measured and normalized conductance step (ΔGTA/βνTνBAtip, plotted versus θ in the inset (dots)) with theoretically calculated in-layer and interlayer terms (lines). Notably, the in-layer coupling contributes negligibly (Methods section ‘Theory model for inelastic tunnelling through phonon emission and the two mechanisms of EPC’) and the interlayer coupling, which exists only for a layer-antisymmetric mode (phason mode) is dominant. Identifying the measured ΔGTA with this mechanism provides the gauge phason EPC, gphason, plotted versus θ in the main panel. Notably, we see that gphason increases with decreasing twist angle as \(\frac{1}{\sqrt{{q}_{{\rm{M}}}}}\) (dashed line). The importance of this coupling becomes evident when it is compared with the measured mode energy, \({\hbar \omega }_{{q}_{{\rm{M}}}}\), which diminishes linearly with qM (Fig. 4d). We note that the theory also explains the absence of the LA mode in our experiment (Methods section ‘Theory model for inelastic tunnelling through phonon emission and the two mechanisms of EPC’), resulting from an orthogonality between its momentum and polarization.
We can estimate the dimensionless coupling, \(\lambda =\frac{2{\theta }^{2}}{W}\frac{{g}_{{q}_{{\rm{M}}}}^{2}}{\hbar {\omega }_{{q}_{{\rm{M}}}}}\), from the EPC we measure at qM (\({g}_{{q}_{{\rm{M}}}}\)) by assuming that gq follows \(\sqrt{q}\) for acoustic phonons (independent of q for optical phonons) and integrating it over the mini-BZ (Methods section ‘Implications for superconductivity in TBG’; W is the flat-band width). Our inelastic tunnelling measurements extend down to θ = 6° (limited by ohmic conductance background at smaller angles), but if we crudely extrapolate our results to lower angles, assuming that the observed dependence of the phason EPC on qM persists to the magic angle, we get that λgauge_phason = 1.1/W (meV). We note that, close to the magic angle, several assumptions of our model break down owing to strong renormalization of the energy bands, atomic reconstruction and phonon–phonon interactions (more details in ref. 49 and Methods section ‘Implications for superconductivity in TBG’). Also, our measurements show that each optical mode contributes λoptical = 0.45/W (meV). Recalling that there are four intervalley-coupling optical modes (LO/TO, top/bottom layers), we see that the phason and optical modes have comparable and possibly important contributions to superconducting pairing. Optical phonons, on the other hand, have too high energy to contribute to the observed linear-in-T resistivity (strange-metal) behaviour, and here the coupling to the phason is the main source of scattering24.
In summary, using the first realization of a cryogenic QTM, we demonstrate a new technique for measuring phonon dispersions as well as mode-resolved and momentum-resolved EPC in vdW materials. Our findings reveal that the phason coupling is at least as important to the physics of TBG as the coupling to optical phonons and that both couple rather strongly to the electronic degrees of freedom. More generally, the method demonstrated here should be applicable to a broad class of vdW materials as well as to mapping the dispersions and couplings of other collective modes, including plasmons2, magnons3 or spinons4, making it a powerful new tool for studying collective behaviour in quantum materials.
Methods
Cryogenic (T = 4 K) QTM
The cryogenic QTM consists of two nanopositioner towers facing each other. One tower is equipped with three translational degrees of freedom (XYZ) and carries a flat sample. The opposing tower holds an AFM cantilever and has a rotational degree of freedom (θ), as well as two lateral degrees of freedom for positioning the AFM tip at the centre of rotation. The entire assembly is cooled down in vacuum to liquid helium temperatures. In the experiment, we bring into contact a vdW heterostructure on the tip with a flat vdW heterostructure on the bottom sample, creating a two-dimensional interface, typically several hundred nanometres across in both directions. vdW attraction between the two heterostructures self-cleans the contact area, leading to a pristine interface. The tip and sample remain in continuous contact throughout the experiment, including during any twisting or scanning operation. Self-sensing AFM cantilevers equipped with piezoresistive elements are used for monitoring and maintaining a constant force, ensuring that the area of the contact interface remains constant during the scans. The QTM junctions in this paper do not have a tunnelling barrier separating the two conducting sides (apart from Fig. 3b,c, in which we used defects in the WSe2 barrier to image the tip shape). This means that the resistance of the tunnel junction, especially at low twist angles or at high bias, can be comparable with or lower than the resistance of the contacts or of the bulk of the two-dimensional layers leading from the contact to the junction. We obtain this contact resistance from measurement close to 0° twist angle and then directly calculate how much bias decreases on the contact resistance and how much is decreasing on the junction, Vb, which is the variable we use throughout the paper (Methods section ‘Removing contact resistance in the two-probe measurement’).
Fabrication of the vdW-devices-on-tip
The fabrication of the vdW-devices-on-tip follows the procedure we described previously1. In brief, we use tipless AFM cantilevers that have a thin metallic line reaching its end, which we use for electrically connecting to the active vdW layer. We make a custom tip using focused-ion-beam-deposited platinum pyramid, with base dimensions of 2 × 2 μm and a height of 1–2 μm. The vdW layers are transferred onto the pyramid using the polymer membrane transfer technique.
Conductance measurements
Voltages are applied using a custom-built digital-to-analogue converter consisting of a.c. + d.c. sources. Current is measured using a FEMTO amplifier, followed by an NI sampler. We use a Zurich Instruments lock-in amplifier (MFLI) for force feedback of the piezoresistive AFM cantilevers.
High-resolution elastic momentum-resolved tunnelling near the commensurate angle of 21.8° and the upper bound it puts on strain in the tip and sample
In Extended Data Fig. 1, we show high-resolution momentum-resolved imaging experiments conducted near the commensurate angle of 21.8°. These cryogenic experiments, performed during the same cooldown and using the same sample and tip as in the experiments in the main text, reveal an exceptionally sharp momentum-resolved map that aligns well with theoretical predictions. Below we explain how this measurement allows us to put a tight upper bound on the strain of the graphene layers on the tip and flat sample and show that the strains are very small, less than 0.1%.
Our experiment involves a TBG interface that is formed in situ, by bringing into contact a graphene layer on a tip and one on a flat substrate. It is instructive to ask whether this interface has substantial strains, owing to a strain present in one or both participating layers. Although monolayer graphene typically exhibits minimal strain when placed on a flat hBN substrate, we may imagine that placing graphene on the rough topography of the tip could introduce substantial strain, particularly near its apex.
To estimate the strain, we use elastic momentum-conserving tunnelling experiments. In such experiments, performed in a QTM geometry, we map the electronic energy bands by rotating two samples relative to each other and measuring the tunnelling current as a function of the rotation angle and bias1. Because current flows between the layers only when their states match in both momentum and energy, a two-dimensional θ–Vb scan effectively maps the energy bands of the system. For these experiments, we typically use a thin insulating barrier between the two layers, ensuring that the experiment remains in the tunnelling regime and allowing for the application of a well-defined bias across the junction. However, in this study, the two graphene layers are in direct contact, with no barrier material in between. Notably, when the experiment is conducted around a twist angle of 21.8°, we still observe elastic momentum-resolved current and the experiment is operating in the tunnelling regime even without a barrier. To understand this, we recall that, although at a twist angle of 21.8° the Fermi surfaces of the two graphene layers do not overlap in the first BZ, they do overlap in the third extended BZ1,37,39, as shown in Extended Data Fig. 2. Namely, the momentum-resolved tunnelling is performed between very high, in-plane momentum components of the wavefunction, which correspondingly decay much more rapidly in the z direction. As a result, despite the direct contact between the layers, the experiment operates in the tunnelling regime.
Extended Data Fig. 1a–c shows the measured tunnelling current and its derivatives versus twist angle and bias. The dashed lines in these panels correspond to theoretically calculated crossing conditions between the Fermi surface in each layer and the empty energy bands in the other layer, as illustrated in Extended Data Fig. 1d. The agreement between the measurement and theory is notable, given the fact that the theory is performed without free parameters (we used the capacitance values measured independently in the main text).
Even a tiny strain in the sample or in the tip would make the measurement look completely different—without strain, the BZ of graphene is a perfect hexagon with its six Dirac cones exactly 60° apart from each other. With strain, this perfect hexagon deforms and the Dirac points are no longer equidistant in angle. For example, 1% strain will make the angle between adjacent Dirac points vary between 59.5° and 60.5°. Remembering that our experiment examines momentum-conserving tunnelling collected simultaneously from all six Dirac points in the tip matching their corresponding six Dirac points of the bottom sample, it is clear that, if the layers are strained, we will see several copies of the crossing conditions, displaced along the angle axis. Each copy will result from one of the six Dirac points crossing its corresponding Dirac point in the other layer. The same holds for the experiments performed near 21.8°, at which the six crossing Dirac points are at the corners of the third BZ (Extended Data Fig. 2). Indeed, occasionally, we obtain tips that have strains and then we can clearly resolve such multiple copies. The fact that in the measurement in Extended Data Fig. 1 we see only one copy means that all six Dirac points are crossing at approximately the same twist angle. In fact, if we assume that the angular width of the lines in the measurement comes from smearing owing to several copies crossings, then we can put an upper bound on the strain in the tip and sample. In the measurement, we can identify lines whose full width at half maximum is approximately 0.05°, which puts an upper bound of 0.1% on the strain in our experiments.
Flat samples and QTM tips
Extended Data Fig. 4 shows the optical image of vdW devices used in the experiment. Extended Data Fig. 4a shows a monolayer graphene QTM tip. Extended Data Fig. 4b,c shows the graphite sample used in Fig. 1 and multilayer graphene (MLG)/hBN/graphite sample used in Figs. 2 and 3.
Symmetry of phonon modes in voltage bias
Extended Data Fig. 5 shows the mirrored I–V curve (in voltage bias) of the graphite–graphite tunnelling junction (as shown in Fig. 1d). The phonon peak positions appear at the same energy for both positive and negative voltage biases. However, there is an asymmetry in phonon peak intensity, which may arise from the complex, electron–hole asymmetric band structure of graphite.
Imaging the tip contact area in situ and determining the pressure in the experiment
The QTM geometry creates a clean two-dimensional interface between the QTM tip and the sample side. We can image this interface by scanning the tip laterally across a region of the sample that has a transition metal dichalcogenide (TMD) layer with atomic defects (three-monolayer-thick WSe2 in the current experiment, placed adjacent to the area in which the main experiment is performed). The defects provide an extra channel for the tunnelling current (Extended Data Fig. 6a). Thus, whenever the tip overlaps with a defect, we observe an increased current. As a result, in a measurement of the current as a function of lateral scanning (X and Y coordinates), each defect produces an image of the tip’s contact area. Extended Data Fig. 6b shows such imaging, in which we resolve several copies of the bulk and outline of the tip. Knowledge of the exact area of the tip is crucial for the quantitative analysis of the EPC strength. The left panel of Extended Data Fig. 6b shows the tip contact area of the hBN-backed monolayer graphene tip used in this work. The area of tip 1 is 37,602 nm2 and that of tip 2 is 18,106 nm2. We apply a d.c. bias close to the band edge (on the order of ±1 V for WSe2); in this energy window, many defects are active for tunnelling.
In the experiment, we use the built-in AFM in our cryogenic QTM to measure and maintain a constant force throughout the experiment. We generally apply small forces F ≈ 100 nN. Combined with the area of tip 1 mentioned above, this amounts to a pressure on the interface of P ≈ 2.5 MPa, which is much smaller than the vdW adhesion pressure, which is on the order of 1 GPa.
Theory model for inelastic tunnelling through phonon emission and the two mechanisms of EPC
The phonon-assisted inelastic tunnelling is modelled using Fermi’s golden rule:
in which we assume the interlayer tunnelling current δIinter is flowing from the tip (top layer) to the sample (bottom layer). δIinter results from the tunnelling of an electronic state |k, s⟩ in the top layer to another electronic state |p′, s′⟩ in the bottom layer, with the emission of a phonon mode r and momentum Q. s and s′ are the band index of graphene layers. Ek,s and ωr,Q are the corresponding electronic state energy and phonon mode energy. Nf = 4 accounts for the spin and valley degeneracy. fT(Ek,s) and fB(Ep′,s′) are the Fermi–Dirac distribution functions for the top and bottom layers. The chemical potential for the top and bottom layers and their relative energy shift are determined from the electrostatic model (Methods section ‘Electrostatic model for the QTM junction’). Here we denote Q for the phonons emitted in the top layer and Q′ for the phonons emitted in the bottom layer. For each layer, there are three possible Q vectors contributing to the tunnelling current in the leading order, which correspond to three Bragg scatterings within the first BZ.
The above formula is a general expression for phonon-assisted tunnelling and the matrix element ⟨k, s|Tin-el|p′, s′; r, Q⟩ contains two types of EPC49:
Hinter is the interlayer EPC, for which the phonon field affects the interlayer tunnelling amplitude t⟂ and gives rise to the coupling between the layers, as shown in Fig. 2h. The other two terms correspond to the in-layer mechanism shown in Fig. 2g. The microscopic expression includes: HT, accounting for the pure electronic interlayer tunnelling; G0, the Green’s function of the uncoupled layers accounting for the energy denominators of the virtual intermediate states; Hin-layer, the in-layer EPC originating from the changes of hopping amplitudes in the layer. The detailed derivation of the two types of EPC is shown in ref. 49. Here we give the final expressions of the interlayer EPC:
These two coupling matrices are for phonons emitted in the top and bottom layers, respectively. Inside the square brackets in equations (4) and (5), the first term describes in-plane phonons and the second term describes out-of-plane phonons (both ZA mode and ZO mode). α and β are sublattice indices and dz is the interlayer distance. ωr,Q and \({{\boldsymbol{\varepsilon }}}_{r,{\bf{Q}}}^{\alpha }\) are the phonon energy and polarization vector, respectively, for phonon mode r at momentum Q. M is the total mass in the unit cell. N is the number of unit cells. K (K′) and Gj=1,2 (\({{\bf{G}}}_{j=1,2}^{{\prime} }\)) are the Dirac point and reciprocal lattice vectors of top (bottom) layer, respectively. Gj=0 = 0 corresponds to the no Bragg scattering case. d is the shift vector between the two layers. qj is the vector connecting the Dirac points between the top and bottom layers, for which j = 0, 1, 2 accounts for three Bragg scatterings within the first BZ. They correspond to three emitted phonon vectors, as seen by the delta functions \({\delta }_{{\bf{Q}},{{\bf{q}}}_{j}}\) and \({\delta }_{{{\bf{Q}}}^{{\prime} },{{\bf{q}}}_{j}}\) in equations (4) and (5). Note that q0 = qM in our notation in the main text. The interlayer electronic tunnelling matrix \({T}_{j}^{\alpha \beta }\) is expressed as
in the sublattice space and \(\zeta =\frac{2\pi }{3}\). For the interlayer mechanism, the theory predicts: (1) the dominant twist angle dependence in equations (4) and (5) is coming from the ZPM factor \(\sqrt{\frac{\hbar }{2M{\omega }_{r,{\bf{Q}}}}}\), which results in an enhanced EPC as the twist angle decreases for the acoustic modes, whereas for optical modes, the coupling approximately remains constant. (2) There is a geometric factor between the K–Gj vector and phonon polarization vector, as seen by the term \(({{\bf{K}}}^{{\prime} }-{{\bf{G}}}_{j}^{{\prime} })\cdot {{\boldsymbol{\varepsilon }}}_{r,{\bf{Q}}}^{\alpha }\) in equation (4) and \(({\bf{K}}-{{\bf{G}}}_{j})\cdot {{\boldsymbol{\varepsilon }}}_{r,{{\bf{Q}}}^{{\prime} }}^{\beta }\) in equation (5). For the transverse mode, this dot product gives \(\cos \left(\frac{\theta }{2}\right)\) factor, in which θ is the twist angle, whereas for the longitudinal mode, it gives \(\sin \left(\frac{\theta }{2}\right)\) factor, which suppresses the EPC. This explains the missing LA mode in the experiment. In the experiment, the measured EPC is averaged over the Fermi surface of the top and bottom layers, and we define it as:
in which θk and θp′ are the polar angle of the electron momentum relative to the top and bottom layer Dirac point, respectively. Here we can change the phonon field basis of the top (Q) and bottom (Q′) layers into layer-symmetric and antisymmetric mode and account \(| {g}_{{\rm{inter}},r,{\bf{Q}}={{\bf{q}}}_{{\rm{M}}}}| \) as the EPC only for one phason mode, as the layer-symmetric mode does not couple to tunnelling electrons.
As for the second mechanism, the in-layer EPC is given by49:
in which β0 = ∂t∥/∂r∥ and \({\widehat{{\bf{e}}}}_{j}\) is the unit vector along the in-plane carbon–carbon bond direction. The in-layer contribution to the tunnelling current is given by \({T}_{\text{in-el}}^{\text{in-layer}}={H}_{{\rm{T}}}{G}_{0}{H}_{\text{in-layer}}+{H}_{\text{in-layer}}{G}_{0}{H}_{{\rm{T}}}\). After averaging over the Fermi surface, the matrix element is approximated by49:
in which the factor \(\alpha =\frac{{t}_{\perp }}{\hbar {\nu }_{{\rm{D}}}{{\bf{q}}}_{{\rm{M}}}}\) is from the virtual tunnelling process and \({| {g}_{\text{in-layer},r,{\bf{Q}}={{\bf{q}}}_{{\rm{M}}}}| }^{2}\) is the Fermi surface averaged in-layer EPC. As qM gets smaller, \({g}_{\text{in-layer},r,{\bf{Q}}={{\bf{q}}}_{{\rm{M}}}}\) for the acoustic mode tends to zero as \(\sqrt{{q}_{{\rm{M}}}}\), whereas the coupling to the optical mode remains constant. Compared with the phason mode, we have the extra Nlayer = 2 factor coming from phonons emitted in the top and bottom layers.
In the numerical calculations for the interlayer and in-layer EPC in Fig. 4, we use the following parameters50: t⟂ = 0.1 eV, νD = 106 m s−1, β0 = 4.22 eV Å−1. The phonon dispersion and polarization vectors are solved by diagonalizing the dynamic matrix of graphene51. The numerical calculations are shown in Extended Data Fig. 7, for Fermi surface averaged interlayer \(| {g}_{\text{interlayer},r,{{\bf{q}}}_{{\rm{M}}}}| \) and intralayer \(\alpha \sqrt{{N}_{{\rm{layer}}}}| {g}_{\text{in-layer},r,{{\bf{q}}}_{{\rm{M}}}}| \) contributions as a function of rotation angle. To simplify notation, we denote them as |ginter,r| and |gin-layer,r| in Extended Data Fig. 7. For the TA mode, the interlayer mechanism dominates over the in-layer mechanism. For the LA mode, the in-layer process is stronger than the interlayer one, owing to the geometric factor that suppresses the interlayer coupling. The overall coupling strength of the LA mode at the momentum qM that the QTM tip examines is weak compared with the TA mode. For TO and LO modes, we plot both the separate and averaged value in Extended Data Fig. 7c. The averaged contribution is dominated by in-layer coupling contributions, which become stronger as the twist angle decreases. The experiment measures the EPC to the TO and LO modes together, near the K point, along an arc in the momentum space. Along this trajectory, the TO and LO modes have an avoided crossing, as seen in Extended Data Fig. 7d. The corresponding bare in-layer EPC of TO and LO also differs, as shown in Extended Data Fig. 7e. Note that, near the K point, the TO phonon has larger bare EPC than the LO phonon. In Extended Data Fig. 7f, we further decompose the TO and LO contribution in terms of \({\alpha }^{2}{N}_{{\rm{layer}}}{| {g}_{\text{in-layer},r,{{\bf{q}}}_{{\rm{M}}}}| }^{2}\) and \({| {g}_{\text{interlayer},r,{{\bf{q}}}_{{\rm{M}}}}| }^{2}\) (r = TO, LO) and compare with the data: ΔGoptical/2βνTνBAtip from Fig. 4a. In the experiments, we cannot separate LO and TO phonon contributions, and the averaged value is consistent with the theory estimate, for which TO phonon has a stronger contribution. In short, both the interlayer and in-layer mechanism are, in general, the same order of magnitude. However, parametrically, the interlayer mechanism is much stronger for the acoustic TA mode, whereas the in-layer mechanism dominates for the optical modes.
Extracting EPC from the measured inelastic conductance steps
Equation (2) can be simplified (derivations are detailed in ref. 49). Here we show the result:
in which Ω is the tunnelling area of the twisted junction and, in our experiment, Ω = Atip, imaged directly by atomic defects (see Methods section ‘Imaging the tip contact area in situ and determining the pressure in the experiment’). νT and νB are the DOS of the top and bottom layers, respectively. θ(eVb − ωr,Q) is the step function, which onsets the conductance \(\frac{{\rm{d}}{I}_{{\rm{in-el}}}}{{\rm{d}}V}\) when the bias voltage reaches the phonon energy. We defined the angular averaged coupling:
in which N is the number of unit cells in the junction. Inserting into equation (10), we have:
in which \({A}_{0}=\frac{{a}^{2}\sqrt{3}}{2}\) is the unit-cell area and νT and νB are the DOS on the top and bottom layers, respectively. Because the phonon wave vector Q is related by the C3 symmetry (as seen by \({\delta }_{{\bf{Q}},{{\bf{q}}}_{j}}\) factor in equations (4) and (5)), we have the conductance step owing to the emission on a phonon mode r as:
in which \(\beta =\frac{{2\pi e}^{2}}{\hbar }{N}_{{\rm{f}}}{N}_{{\rm{b}}}\,{A}_{0}\), such that Nb = 3 accounts for the Bragg scatterings and Nf = 4 accounts for the flavour degeneracy (spin/valley). Given the two types of microscopic EPC, \({| {g}_{\text{in-el},r,{{\bf{q}}}_{{\rm{M}}}}| }^{2}\) includes:
For the in-layer mechanism, Nlayer = 2 because phonons in both layers contribute. For the interlayer mechanism, only the layer-antisymmetric phason mode contributes. For extracting the in-layer coupling in Fig. 4, we use the parameters t⟂ = 0.1 eV and νD = 106 m s−1 for estimating the value of the α factor.
Electrostatic model for the QTM junction
The QTM junction is modelled by a three-capacitor model1. A graphene layer on the tip side and a graphene layer on the sample side are separated by a vacuum gap. The third layer is the graphite back gate, separated by a hBN spacer on the bottom sample side. We have the following electrostatic equations:
in which Vb is the voltage bias applied between the two graphene layers and Vbg is the back-gate voltage with respect to the bottom graphene layer. nB (nT) and μB (μT) are the carrier density and chemical potential, respectively, of the bottom (top) layer graphene. Cg is the geometric capacitance per unit area between two graphene layers and Cbg is that between the back-gate and the bottom graphene layer. We use the values Cg = 11 μF cm−2 and Cbg = 38.6 nF cm−2 to fit the data. From the electrostatic model, we plot the charge-neutral Dirac point lines (dashed red and blue lines) in Fig. 3d,e and Extended Data Figs. 9 and 11.
Bulk-graphite phonon dispersion model
In the main text, the phonon dispersion of graphite is modelled using a dynamic matrix through the force constant approaches. For the in-layer force constants, we use the parameters from ref. 51 (GGA calculation, column 3 in table 3 in that reference), which includes the fourth nearest-neighbour coupling that fits to DFT calculations. To obtain the bulk-graphite phonon spectrum, we further include the interlayer mechanical coupling in the dynamic matrix, as detailed in ref. 52. We include only the nearest-neighbour out-of-plane radial and tangential coupling, denoted by \(\widehat{{\phi }_{{\rm{r}}}}\) and \(\widehat{{\phi }_{{\rm{t}}}}\), and rescale these two parameters together to match the ZA phonon gap measured in experiments, giving the values \(\widehat{{\phi }_{{\rm{r}}}}=\mathrm{3,296}\,{\rm{dyn}}\,{{\rm{cm}}}^{-1}\) and \(\widehat{{\phi }_{{\rm{t}}}}=-\mathrm{7,121}\,{\rm{dyn}}\,{{\rm{cm}}}^{-1}\). For other phonon modes, introducing these interlayer coupling parameters generates an energy splitting of less than 0.5 meV. In Extended Data Fig. 8, we compare the spectrum obtained from ref. 52 (Extended Data Fig. 8b) to the model described above (Extended Data Fig. 8a) and we can see that the latter fits the experiments much better.
Further data: G as a function of V b and V bg measured at two more twist angles, θ = 22.7° and 9.4°
In Fig. 3, we show the junction conductance as a function of Vb and Vbg at twist angle θ = 16.8°. Extended Data Fig. 9 shows the same map at two more angles, θ = 22.7° and 9.4°. These figures show similar features as in Fig. 3d,e: horizontal lines owing to inelastic phonon emission processes and conductance dips tracing the neutrality points of the top and bottom graphene layers. The dashed blue and red lines correspond to the neutrality points calculated using the electrostatic model for the QTM junction.
Further data from different samples and QTM tips
Here we show further measurements performed with different bottom graphene samples and QTM tips to those shown in the main text. Our scanning set-up allows us to create the twisted interface at different locations along the bottom graphene, which are separated by several micrometres. Because the tip contact area is only several hundreds of nanometres, measuring at such spatially separated positions effectively means that we have switched to a completely different bottom sample. Also, within the QTM set-up, we have the capability to modify in situ the tip shape. One example is shown in Fig. 3b, in which the area of the tip is changed by approximately a factor of two (tips 1 and 2). Because the area added to the tip is substantial and can potentially have different strains, edges and so on, the measurements with these two tips effectively amount to experiments performed with different tips. In Fig. 2, we show the phonon spectrum measured using tip 1. Extended Data Fig. 10a,b shows further inelastic phonon spectroscopy data obtained using tip 2, which was also measured in a different sample ___location, overlaid with the theoretical phonon dispersion of bulk graphite. This scan was performed only down to 10°, because, at this angle, the tip caught some dirt. Performing the same analysis as in Fig. 4, we extract the electron–phason and electron–optical couplings and compare them with the data in Fig. 4 over the angular range that they overlap. Extended Data Fig. 10c shows this comparison for the extracted intervalley optical TO/LO EPC and Extended Data Fig. 10d shows the comparison for the electron–phason coupling. We can see that there is a good agreement both in terms of the magnitudes of the coupling as well as on their twist angle dependence.
Extended Data Fig. 11 shows further measurements performed with a completely different tip and sample in a different cooldown. Extended Data Fig. 11a,b shows the graphene–graphene junction conductance G and d2I/dV2 and as a function of Vb and Vbg at twist angles θ = 30° and 20°. We can clearly resolve in both scans horizontal lines that correspond to inelastic processes with the different phonon modes. We also see that the step in conductance changes gradually with back-gate voltage. Performing a similar analysis as in the main text (Fig. 3g) and plotting the height of the conductance steps for the TA and ZA modes as a function of gate voltage (Extended Data Fig. 11c), we clearly resolve the predicted linear dependence. Moreover, unlike the sample in the main text, which could not be measured at large negative back-gate voltage owing to a gate leak, in the sample below, we also explored the hole side and we can clearly see how that, also there, the dependence is linear with a slope with inverted sign (dashed lines in Extended Data Fig. 11c are the model calculations).
Removing contact resistance in the two-probe measurement
In the experiments, we apply a voltage Vapplied between the contacts connected to the vdW-devices-on-tip and to the flat sample side and record the current I flowing through the twistable junction and its derivative, \(\widetilde{G}=\frac{{\rm{d}}I}{{\rm{d}}{V}_{{\rm{applied}}}}\). However, as these are two-terminal measurements, there will be a contact resistance Rc leading to/from the twistable junction area. Therefore, the voltage bias Vb falling on the junction will be smaller than Vapplied. The difference between Vapplied and Vb becomes notable when the junction resistance is low (either at high applied voltage or at low twist angles). To remove this effect, we rotate to zero twist angle (for which the resistance of the junction is the lowest) and record the resistance Rc (about 50 kΩ for the monolayer graphene–monolayer graphene experiment (Figs. 2–4) and about 4 kΩ for the graphite–graphite experiment (Fig. 1)). For each measurement, we remove the corresponding Rc to obtain:
Limitations at small twist angles
In the experiments, the QTM is capable of controlling the twist angle of TBG continuously down to 0°. However, the measurements show that phonon emissions steps in G start to disappear when the twist angle is less than 6° and, at low bias, we measure substantial junction conductance. There are several possible reasons for this. (1) The tail of elastic tunnelling processes becomes more and more dominant and overwhelms the inelastic phonon emission processes. (2) At smaller angles near the magic angle, the two layers become strongly hybridized such that Fermi’s golden rule approximation, which is used to interpret our measurements, breaks down, as electrons can tunnel back and forth several times across the junction coherently (Fermi’s golden rule assumes just a single pass). (3) Processes involving the absorption of thermal phonons can be notable at low angles and may dominate the phonon emission processes of interest to us. The energy of a phonon at q = qM becomes smaller with decreasing twist angle. For θ = 6°, it is already ωph ≈ 10 meV. For lower twist angles, it will be even smaller. Because the same EPC element is relevant for both the emission and absorption of phonons, absorption of thermally activated phonons at T = 4 K may well be responsible for the large conductive background at low angles44. (4) Contact resistance: at lower angles, the EPC gets stronger as shown in the main text and junction conductance becomes better. The tail of the onset of phonon emission already leads to a junction resistance that can be much smaller than the contact resistance. We can account for some of this effect with our theoretical model, but if the junction resistance becomes negligibly small, then it becomes impossible to resolve its behaviour.
The EPC for the ZA (ZO′) phonon mode
In the main text, we show the extracted EPC for the TO/LO and layer-antisymmetric TA phason mode. Here we show the ZA mode (the layer-antisymmetric ZA phonon is often also called ZO′) (Extended Data Fig. 12). This mode shows a gapped dispersion in the measurement. In the angle range we measure, ZA mode phonon energy decreases as the twist angle becomes smaller. The crossing between the ZA and TA modes is around θ = 6°. The theory discussions of the ZA mode are given in ref. 49, which shows that, similar to the TA mode, the ZA mode is dominated by the interlayer mechanism. Its coupling strength increases with decreasing angle at approximately \(\frac{1}{\sqrt{{\omega }_{{\rm{ZA}}}}}\), as seen by equations (4) and (5). Extended Data Fig. 12b shows the extracted gZA as a function of θ, which shows the coupling strength of around 25 meV at θ = 6°. At θ = 8°, at which this mode overlaps with the TA mode in bias, we divided the total conductance step according to the ratio of the conductance steps measured at larger angle. This assumption most likely overestimates the ZA mode coupling and underestimates the TA mode coupling at θ = 8°.
Implications for superconductivity in TBG
Given the EPC we measure, we can estimate the coupling constant λ in the Bardeen–Cooper–Schrieffer (BCS) theory. The attractive electron–electron interaction from EPC is given by:
in which gq,r is the EPC for phonon mode r and momentum q. Aunit is the unit-cell area. Our experiments measure the EPC at qM (\({g}_{{q}_{{\rm{M}}}}\)). For the acoustic phonons and phasons, we assume the q dependence of the EPC in the phonon mini-BZ to follow \(\sqrt{q}\). Because for these modes ωq ≈ q, we get that their Ueff,r(q) is independent of momentum. For optical phonons, we assume that the EPC is independent of q. Because for these modes ωq is independent of q, we get that, also for them, Ueff,r(q) is independent of momentum. We can thus readily integrate equation (18) over the phonon mini-BZ to obtain a Ueff,r that depends only on \({g}_{{q}_{{\rm{M}}}}\), measured in our experiments. Consequently, the coupling constant λ is given by:
We approximate the DOS \({\nu }_{0}=\frac{1}{W{A}_{{\rm{moire}}}}\), in which W is the bandwidth and Amoire is the moiré cell area. We then get:
For the phason mode, we measured the \({g}_{{q}_{{\rm{M}}}}\) and \({\omega }_{{q}_{{\rm{M}}}}\) at θ = 6°. Assuming the \(\frac{1}{\sqrt{{q}_{{\rm{M}}}}}\) dependence of \({g}_{{q}_{{\rm{M}}}}\) that we measured extends to θ = 1.1°, we get:
For the optical modes, we get:
Here we further discuss the limitations of the perturbative theory approach and possible breakdowns when extending it to the magic-angle regime:
-
a.
Hybridization of the energy bands at small angles owing to the strong interlayer coupling: this strong coupling will cause the lowest-order perturbative expansion of the interlayer coupling, resulting from the phonon field, to break down.
-
b.
Gapping of the TA layer-antisymmetric mode owing to interlayer mechanical coupling: in our theory, we assume that the interlayer symmetric and layer-antisymmetric phonons have the same energy. We may expect, however, that, at small twist angles, the layer-antisymmetric mode will be gapped as a result of mechanical coupling between the two layers. Such a mechanical gap was measured for the layer-antisymmetric mode in Bernal bilayer graphene using Raman28 and already they turned out be rather small, approximately 4 meV. We note that, in TBG, we expect the mechanical gapping of the TA mode to be much smaller—this gapping is directly related to the mechanical friction between the layers. In a bilayer, this friction is high because of the perfect commensuration between the layers. However, once the two layers are twisted, their friction reduces substantially as a result of superlubrication. Superlubrication should be relevant at angles already as small as the magic angle.
-
c.
Relaxation near the magic angle: lattice reconstruction effects are substantial below 2°. For twist angles near or above the first magic angle of TBG, linear response theory53,54 provides an adequate description of the relaxation effects, as confirmed by more accurate computational methods55,56. The applicability of linear response theory indicates that the displacements associated with relaxation do not greatly affect the phonon frequencies. In terms of the EPC, reconstruction will effectively increase the areas of AB stacking and decrease those of AA stacking. This will effectively decrease the tunnelling between the layers. Because the phason EPC is dominated by the interlayer coupling, namely the modulation of the tunnelling elements between the layers, scaling down this tunnelling is expected to scale down the EPC in proportion.
-
d.
Phonon–phonon interactions. As shown in ref. 23, the phason mode can be damped at low energies owing to the moiré superlattice disorder. This is very important for understanding phenomena such as the strange-metal behaviour, as studied in that paper, but as long as this does not reach the strong coupling phonon–phonon limit, this will not influence the EPC estimated by our model.
Possible future experiments for measuring neutral collective modes with the QTM
The inelastic momentum-resolved scanning technique demonstrated here should be applicable to a wide range of vdW materials, including both carbon-based systems and TMDs. Beyond phonons, this method could potentially measure other neutral collective modes as well. Two fundamental requirements make these measurements particularly straightforward:
-
1.
Materials with small Fermi pockets, preferably away from the Γ point.
-
2.
The Fermi velocity is larger than the velocity of the collective mode.
Requirement 1 is well met by many carbon-based materials, for which the band structure is derived from small Dirac points. More importantly, this condition is also satisfied by the broader class of TMD materials, for which small Fermi surfaces are typically found at the K or Q points in the BZ for both electron and hole carriers.
For requirement 2, the phonon sound velocity is much smaller than the Fermi velocity in all realistic materials within these families, including both carbon-based materials and TMDs. Other neutral collective modes, such as magnons and spinons, are also expected to have much lower velocities than electrons.
Even when these conditions are not met (for example, for plasmons, which travel faster than electrons), the technique can still provide valuable insights. In such cases, however, a more thorough analysis would be required to separate the electronic contributions from those of the collective modes.
Another important point is that the experiment can be performed in two different configurations. The first is when the ‘launching’ and ‘absorbing’ layers for the collective modes are in contact, as in the current experiment. In this configuration, we can examine the collective modes of each individual layer or that of the combined twisted interface. The second configuration involves placing an insulating material, whose collective modes are to be studied, between the ‘launching’ and ‘absorbing’ layers. In fact, momentum-conserving tunnelling experiments performed in devices with a fixed twist angle have already successfully detected the phonons of a hBN barrier between the layers41,42,43. Two examples of proposed experiments consider the possibility of studying spinons in quantum spin liquids4 and magnons in magnetic moiré heterostructures3.
Data availability
The data shown in this paper are provided with the paper. Further data that support the plots and other analysis in this work are available from the corresponding author on request.
References
Inbar, A. et al. The quantum twisting microscope. Nature 614, 682–687 (2023).
Koppens, F. H. L., Chang, D. E. & García de Abajo, F. J. Graphene plasmonics: a platform for strong light–matter interactions. Nano Lett. 11, 3370–3377 (2011).
Pichler, F., Kadow, W., Kuhlenkamp, C. & Knap, M. Probing magnetism in moiré heterostructures with quantum twisting microscopes. Phys. Rev. B 110, 045116 (2024).
Peri, V., Ilani, S., Lee, P. A. & Refael, G. Probing quantum spin liquids with a quantum twisting microscope. Phys. Rev. B 109, 035127 (2024).
Hwang, E. H. & Sarma, S. D. Acoustic phonon scattering limited carrier mobility in two-dimensional extrinsic graphene. Phys. Rev. B 77, 115449 (2007).
Mayorov, A. S. et al. Micrometer-scale ballistic transport in encapsulated graphene at room temperature. Nano Lett. 11, 2396–2399 (2011).
Polini, M. & Geim, A. K. Viscous electron fluids. Phys. Today 73, 28–34 (2020).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Cao, Y. et al. Strange metal in magic-angle graphene with near Planckian dissipation. Phys. Rev. Lett. 124, 076801 (2020).
Polshyn, H. et al. Large linear-in-temperature resistivity in twisted bilayer graphene. Nat. Phys. 15, 1011–1016 (2019).
Wu, F., MacDonald, A. H. & Martin, I. Theory of phonon-mediated superconductivity in twisted bilayer graphene. Phys. Rev. Lett. 121, 257001 (2018).
Choi, Y. W. & Choi, H. J. Strong electron-phonon coupling, electron-hole asymmetry, and nonadiabaticity in magic-angle twisted bilayer graphene. Phys. Rev. B 98, 241412 (2018).
Liu, C.-X., Chen, Y., Yazdani, A. & Bernevig, B. A. Electron–K-phonon interaction in twisted bilayer graphene. Phys. Rev. B 110, 045133 (2024).
Yudhistira, I. et al. Gauge-phonon dominated resistivity in twisted bilayer graphene near magic angle. Phys. Rev. B 99, 140302 (2019).
Wu, F., Hwang, E. & Sarma, S. D. Phonon-induced giant linear-in-T resistivity in magic angle twisted bilayer graphene: ordinary strangeness and exotic superconductivity. Phys. Rev. B 99, 165112 (2019).
Lian, B., Wang, Z. & Bernevig, B. A. Twisted bilayer graphene: a phonon-driven superconductor. Phys. Rev. Lett. 122, 257002 (2019).
Sharma, G. et al. Carrier transport theory for twisted bilayer graphene in the metallic regime. Nat. Commun. 12, 5737 (2021).
Lewandowski, C., Chowdhury, D. & Ruhman, J. Pairing in magic-angle twisted bilayer graphene: role of phonon and plasmon umklapp. Phys. Rev. B 103, 235401 (2021).
Koshino, M. & Son, Y.-W. Moiré phonons in twisted bilayer graphene. Phys. Rev. B 100, 075416 (2019).
Liu, X., Peng, R., Sun, Z. & Liu, J. Moiré phonons in magic-angle twisted bilayer graphene. Nano Lett. 22, 7791–7797 (2022).
Gao, Q. & Khalaf, E. Symmetry origin of lattice vibration modes in twisted multilayer graphene: phasons versus moiré phonons. Phys. Rev. B 106, 075420 (2022).
Ochoa, H. Moiré-pattern fluctuations and electron-phason coupling in twisted bilayer graphene. Phys. Rev. B 100, 155426 (2019).
Ochoa, H. & Fernandes, R. M. Degradation of phonons in disordered moiré superlattices. Phys. Rev. Lett. 128, 065901 (2022).
Ochoa, H. & Fernandes, R. M. Extended linear-in-T resistivity due to electron-phason scattering in moiré superlattices. Phys. Rev. B 108, 075168 (2023).
Na, M. X. et al. Direct determination of mode-projected electron-phonon coupling in the time ___domain. Science 366, 1231–1236 (2019).
Chen, C. et al. Strong electron–phonon coupling in magic-angle twisted bilayer graphene. Nature 636, 342–347 (2024).
Ferrari, A. C. Raman spectroscopy of graphene and graphite: disorder, electron–phonon coupling, doping and nonadiabatic effects. Solid State Commun. 143, 47–57 (2007).
Tan, P. H. et al. The shear mode of multilayer graphene. Nat. Mater. 11, 294–300 (2012).
Eliel, G. S. N. et al. Intralayer and interlayer electron–phonon interactions in twisted graphene heterostructures. Nat. Commun. 9, 1221 (2018).
Maultzsch, J., Reich, S., Thomsen, C., Requardt, H. & Ordejón, P. Phonon dispersion in graphite. Phys. Rev. Lett. 92, 075501 (2004).
Mohr, M. et al. Phonon dispersion of graphite by inelastic x-ray scattering. Phys. Rev. B 76, 035439 (2007).
Tanaka, S., Mukai, K. & Yoshinobu, J. Direct observation of the electron-phonon coupling between empty states in graphite via high-resolution electron energy-loss spectroscopy. Phys. Rev. B 95, 165408 (2017).
Senga, R. et al. Position and momentum mapping of vibrations in graphene nanostructures. Nature 573, 247–250 (2019).
Yildirim, T. et al. Giant anharmonicity and nonlinear electron-phonon coupling in MgB2: a combined first-principles calculation and neutron scattering study. Phys. Rev. Lett. 87, 037001 (2001).
Holst, B. et al. Material properties particularly suited to be measured with helium scattering: selected examples from 2D materials, van der Waals heterostructures, glassy materials, catalytic substrates, topological insulators and superconducting radio frequency materials. Phys. Chem. Chem. Phys. 23, 7653–7672 (2021).
Efetov, D. K. & Kim, P. Controlling electron-phonon interactions in graphene at ultrahigh carrier densities. Phys. Rev. Lett. 105, 256805 (2010).
Koren, E. et al. Coherent commensurate electronic states at the interface between misoriented graphene layers. Nat. Nanotechnol. 11, 752–757 (2016).
Chari, T., Ribeiro-Palau, R., Dean, C. R. & Shepard, K. Resistivity of rotated graphite–graphene contacts. Nano Lett. 16, 4477–4482 (2016).
Bistritzer, R. & MacDonald, A. H. Transport between twisted graphene layers. Phys. Rev. B 81, 245412 (2010).
Zhang, Y. et al. Giant phonon-induced conductance in scanning tunnelling spectroscopy of gate-tunable graphene. Nat. Phys. 4, 627–630 (2008).
Jung, S. et al. Vibrational properties of h-BN and h-BN-graphene heterostructures probed by inelastic electron tunneling spectroscopy. Sci. Rep. 5, 16642 (2015).
Vdovin, E. E. et al. Phonon-assisted resonant tunneling of electrons in graphene–boron nitride transistors. Phys. Rev. Lett. 116, 186603 (2016).
Chandni, U., Watanabe, K., Taniguchi, T. & Eisenstein, J. P. Signatures of phonon and defect-assisted tunneling in planar metal–hexagonal boron nitride–graphene junctions. Nano Lett. 16, 7982–7987 (2016).
Perebeinos, V., Tersoff, J. & Avouris, Ph. Phonon-mediated interlayer conductance in twisted graphene bilayers. Phys. Rev. Lett. 109, 236604 (2012).
Sarma, S. D. & Wu, F. Electron–phonon and electron–electron interaction effects in twisted bilayer graphene. Ann. Phys. 417, 168193 (2020).
Kwan, Y. H. et al. Electron-phonon coupling and competing Kekulé orders in twisted bilayer graphene. Phys. Rev. B 110, 085160 (2024).
Piscanec, S., Lazzeri, M., Mauri, F., Ferrari, A. C. & Robertson, J. Kohn anomalies and electron-phonon interactions in graphite. Phys. Rev. Lett. 93, 185503 (2004).
Neto, A. H. C. & Guinea, F. Electron-phonon coupling and Raman spectroscopy in graphene. Phys. Rev. B 75, 045404 (2007).
Xiao, J. et al. Theory of phonon spectroscopy with the quantum twisting microscope. Phys. Rev. B 110, 205407 (2024).
Ando, T. Anomaly of optical phonon in monolayer graphene. J. Phys. Soc. Jpn. 75, 124701 (2006).
Wirtz, L. & Rubio, A. The phonon dispersion of graphite revisited. Solid State Commun. 131, 141–152 (2004).
Al-Jishi, R. & Dresselhaus, G. Lattice-dynamical model for graphite. Phys. Rev. B 26, 4514–4522 (1982).
Ceferino, A. & Guinea, F. Pseudomagnetic fields in fully relaxed twisted bilayer and trilayer graphene. 2D Mater. 11, 035015 (2024).
Ezzi, M. M. A., Pallewela, G. N., Beule, C. D., Mele, E. J. & Adam, S. Analytical model for atomic relaxation in twisted moiré materials. Phys. Rev. Lett. 133, 266201 (2024).
Koshino, M. & Nam, N. N. T. Effective continuum model for relaxed twisted bilayer graphene and moiré electron-phonon interaction. Phys. Rev. B 101, 195425 (2020).
Kang, J. & Vafek, O. Pseudomagnetic fields, particle-hole asymmetry, and microscopic effective continuum Hamiltonians of twisted bilayer graphene. Phys. Rev. B 107, 075408 (2023).
Acknowledgements
We thank A. Jorio, E. Kaxiras, F. Mauri, S. Reich and J. Ruhman for fruitful discussions. This work was supported by the Leona M. and Harry B. Helmsley Charitable Trust grant, the Rosa and Emilio Segre Research Award, the ERC AdG grant (QTM, no. 101097125), the Deutsche Forschungsgemeinschaft (DFG) financed project number 277101999 – CRC 183 (project C02) and the BSF grant (2020260). A.I. was supported by the Azrieli Fellows Program. E.B. was supported by the European Research Council (ERC) under grant HQMAT (grant agreement no. 817799) and CRC 183 of the DFG (project C02). L.G. acknowledges the support by NSF grant no. DMR-2410182 and by the Office of Naval Research (ONR) under award no. N00014-22-1-2764. F.G. acknowledges support from the Severo Ochoa Programme for Centres of Excellence in R&D (CEX2020-001039-S/AEI/10.13039/501100011033, Ministerio de Ciencia e Innovacion, Spain) from the grant (MAD2D-CM)-MRR MATERIALES AVANZADOS-IMDEA-NC, NOVMOMAT, grant PID2022-142162NB-I00 financed by MCIN/AEI/ 10.13039/501100011033 and by ‘ERDF A way of making Europe’. F.v.O. acknowledges the support by the DFG through CRC 183 (project C02 and a Mercator Fellowship) and a joint ANR-DFG project (TWISTGRAPH).
Author information
Authors and Affiliations
Contributions
J.B., J.X., A.I. and S.I. designed the experiment. J.B., J.X. and A.I. built the cryogenic QTM microscope, fabricated the devices and performed the experiments. J.B., J.X., A.I. and S.I. analysed the data. J.X., E.B., L.G., F.G. and F.v.O. wrote the theoretical models. K.W. and T.T. supplied the hBN crystals. J.B., J.X., A.I. and S.I. wrote the manuscript, with input from the other authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 High-resolution momentum-resolved elastic tunnelling near the commensurate angle of 21.8°.
a, Measured conductance (G) as a function of twist angle (θ) and bias voltage (Vb), with a finite carrier density in both graphene layers induced by a back-gate voltage of Vbg = 4 V. b, The second derivative, \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\), obtained numerically from panel a. c, The derivative of conductance with respect to twist angle, \(\frac{{\rm{d}}G}{{\rm{d}}\theta }\), obtained numerically from panel a. The measured conductance clearly reveals a distinct ‘double X’ structure, within which the conductance is enhanced. This structure exhibits a mirror symmetry around θ = 21.8° and an approximate mirror symmetry with respect to bias. The boundaries of this structure are even more pronounced in the \(\frac{{\rm{d}}G}{{\rm{d}}\theta }\) plot, in which they appear as narrow red and blue lines. Superimposed on these features are nearly horizontal conductance steps, which are more prominent in the second derivative \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}_{{\rm{b}}}^{2}}\) plot, in which they manifest as horizontal lines. These lines correspond to inelastic, momentum-conserving phonon emission processes, as described in detail in the main text. The extra ‘double X’ structure around θ = 21.8° arises from elastic momentum-conserving tunnelling between overlapping Fermi surfaces at the corners of the third BZ (see illustration in Extended Data Fig. 2). These Fermi surfaces are associated with high-momentum components of the in-plane wavefunctions, which decay more rapidly in the z direction, explaining why the experiment operates in the tunnelling regime despite the two layers being in contact. The dashed black lines in all panels represent theoretically calculated conditions for which the Fermi surface of one layer touches the unoccupied energy bands of the other layer, marking the onset of momentum-conserving tunnelling. The various conditions are illustrated in panel d and their calculated trajectories in the θ–Vb plane show excellent agreement with the experimental data. Notably, this agreement is achieved with no free parameters (the geometric capacitance used in these calculations was determined by fitting the phonon spectrum measurements in the main text). As explained in the corresponding Methods section, this correspondence puts a tight upper bound on the strains of the graphene layers in the tip and on the flat substrate, to be smaller than 0.1%.
Extended Data Fig. 2 Overlap of Fermi surfaces in the extended BZ scheme for a twist angle close to 21.8°.
Schematic of the extended electronic momentum space for the top graphene (blue hexagons) and bottom graphene (red hexagons), when the twist between the layers is approximately 21.8°. Visibly, the Fermi surfaces of the top and bottom graphene layers (blue and red circles) at the corners of the first BZ do not overlap. However, at the corner of the third extended BZ, the Fermi surfaces overlap (top inset), leading to the elastic momentum-resolved structure observed in Extended Data Fig. 1.
Extended Data Fig. 3 The cut in the phonon BZ investigated in our experiments.
a, In the electronic momentum space, we show the first BZ of the top (blue) and bottom (red) graphene layers at a generic twist angle. The inelastic tunnelling processes examined in our experiments involve electrons scattering between the small Fermi surface of the top bottom layer, around the KB point (blue circle), to the Fermi surface of the top layer around the KT point (red circle), while emitting a phonon with momentum \({q}_{{\rm{M}}}={2K}_{{\rm{D}}}\sin \left(\frac{\theta }{2}\right)\). Electrons can also tunnel from the other valley at K′B of the bottom layer to the valley at the KT point in the top layer and emit a phonon with momentum \({\widetilde{q}}_{{\rm{M}}}={2K}_{{\rm{D}}}\sin \left(\frac{60-\theta }{2}\right)\). b, In the phononic momentum space, qM cuts through the phononic BZ along a specific arc that goes from the Γ point to the K point (orange). For \({\widetilde{q}}_{{\rm{M}}}\), the trajectory is reversed.
Extended Data Fig. 4 vdW-devices-on-tip and QTM flat side devices.
a, Optical image of a monolayer graphene QTM tip. b, Optical image of a graphite sample used for the graphite versus graphite measurement shown in Fig. 1. c, Optical image of the MLG/hBN/graphite sample used for MLG versus MLG experiments shown in Figs. 2 and 3. This sample also has a region with 3L-WSe2 for tip contact area imaging (see Extended Data Fig. 6).
Extended Data Fig. 5 Mirrored I–V curve in voltage bias.
a,b, Mirrored G and \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}^{2}}\) curves from Fig. 1d. Phonon peak positions appear at the same energy, whereas peak intensity is asymmetric.
Extended Data Fig. 6 Imaging the tip touching area.
a, Schematic of the QTM tip scanning spatially over atomic defects in WSe2. The tunnelling current increases when the tip overlaps the defect, generating an image of the shape and area of the tip. b, Real-space images of the graphene tips (tip contact area is shaded in blue). d.c. bias during scanning was −1 V for tip 1 and −1.2 V for tip 2.
Extended Data Fig. 7 Calculated EPC for the theoretical model in Methods section ‘Theory model for inelastic tunnelling through phonon emission and the two mechanisms of EPC’.
a–c, EPC contributions from the in-layer (red) and interlayer (blue) mechanisms for the TA, LA and TO/LO modes as a function of the twist angle. In c, the contribution from the TO and LO modes are further decomposed. In the experiment, the individual contribution of the TO and LO modes cannot be distinguished. However, in this plot, both modes contribute, with the TO mode having the dominant effect. d,e, The phonon dispersion and bare in-layer EPC for the TO and LO modes near the K point. f, Comparison of the extracted conductance step, ΔGoptical/2βνTνBAtip, with the theory estimates \({(\alpha \sqrt{{N}_{{\rm{layer}}}}| {g}_{{\rm{in-layer}},r,{q}_{{\rm{M}}}}| )}^{2}\) and \({| {g}_{{\rm{interlayer}},r,{q}_{{\rm{M}}}}| }^{2}\) for both TO and LO modes. The legend notations for TO, LO and interlayer/in-layer mechanisms follow those in panel c.
Extended Data Fig. 8 Bulk-graphite phonon dispersion model.
a, The phonon dispersions (dashed lines) obtained from the model in ref. 51 augmented by adding interlayer mechanical coupling (detailed in this section). The calculation is overlaid on the measured graphite–graphite phonon spectrum shown in Fig. 1f. b, Phonon dispersions obtained from the model in ref. 52, overlaid with the measured graphite–graphite phonon spectrum shown in Fig. 1f. In the main text, we use the first model, as it fits the measurements more accurately.
Extended Data Fig. 9 Conductance as a function of Vb and Vbg at two other angles.
G versus Vb and Vbg for TBG at θ = 22.7° (a) and at θ = 9.4° (b).
Extended Data Fig. 10 Measured phonon spectrum and EPC in TBG using tip 2.
a, Measured conductance, G, versus bias voltage, Vb, and twist angle, θ, exhibiting steps in G that disperse with θ. b, The second derivative, \(\frac{{{\rm{d}}}^{2}I}{{\rm{d}}{V}^{2}}\),obtained numerically from panel a, overlaid with the theoretically calculated phonon spectrum of graphite. c, The intervalley optical modes (TO and LO) EPC, \({g}_{{\rm{optical}}}=\sqrt{({g}_{{\rm{TO}}}^{2}+{g}_{{\rm{LO}}}^{2})/2}\), determined from this measurement (tip 2, cyan) compared with data in the main text (tip 1, blue). Error bars are obtained from differences between measurements at positive and negative bias and all other experimental uncertainties. d, The electron–phason coupling, gphason, determined from this measurement (tip 2, cyan) compared with data in the main text (tip 1, blue). Error bars are obtained from differences between measurements at positive and negative bias and all other experimental uncertainties.
Extended Data Fig. 11 Conductance as a function of Vb and Vbg at two angles for a different tip and sample.
G versus Vb and Vbg for TBG at θ = 30° (a) and at θ = 20° (b). c, Amplitude of the conductance step of the ZA and TA modes, ΔG versus Vbg, extracted from a and b, respectively. Dashed lines plot the theoretical model that predicts a linear dependence of ΔG versus Vbg.
Extended Data Fig. 12 EPC for the ZA (ZO′) mode.
a, Extracted EPC of the ZA (ZO′) mode from Fig. 2d. b, Extracted phonon dispersion of the ZA (ZO′) mode from the same figure.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Birkbeck, J., Xiao, J., Inbar, A. et al. Quantum twisting microscopy of phonons in twisted bilayer graphene. Nature 641, 345–351 (2025). https://doi.org/10.1038/s41586-025-08881-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-025-08881-8
This article is cited by
-
Interplay between light and heavy electron bands in magic-angle twisted bilayer graphene
Nature Physics (2025)