Abstract
Leaf springs are designed to bear loads as well as shocks in automotive vehicles. Two leaves of glass fiber-reinforced composites (GFRCs) of various shapes sandwiched between steel plates were analyzed for application in a minitruck. Computer-aided engineering analysis was performed for five different types of GFRC material leaf springs: flat leaf, flat and parabolic leaf, both parabolic leaf, both parabolic leaf springs with aluminium alloy bushes at the eye-end and spring steel multi-leaf springs. A silencer pad was used in the parabolic leaf spring to reduce delamination and vibration at contact points of the mating leaf. The various shapes and combinations of leaves provided varying parameters, namely, the deformation, maximum equivalent strain, maximum equivalent stress and fatigue life. The CAE results showed that compared with the other combinations, the flat leaf and parabolic leaf combinations provided the maximum equivalent strain, maximum equivalent stress and fatigue life.
Similar content being viewed by others
Introduction
The main function of leaf spring is to act as structural member as well as shock absorbing device in a vehicle. All flat or all parabolic leaf spring leaf springs are assembled in the laminated leaf in a vehicle. However, the combination of both flat and parabolic leaf in a laminated leaf spring is rare. This paper mainly focuses on the combination of flat and parabolic leaf springs in laminated leaf spring in light commercial vehicle. The silencer pad also absorbs all vibrations and reduces wear and tear between the two-mating leaf. The inclusion of steel plates on a composite leaf spring, increases modulus of elasticity, tensile strength, transmit equal stresses on composite leaf spring and protect them from mechanical damage. CAE analysis has been done to compare various combination of different types of leaf spring.
Gebremeskel’s1 study showed that a composite leaf spring made of epoxy/e-glass under static load conditions helps to reduce weight and provides more strength and flexibility as compared to the conventional leaf spring design used in lightweight vehicles. Kader et al.2 experimentally described the properties of a hybrid spring product of 95% epoxy and a 5% hybrid composite of carbon and glass fibers. The results showed improved hardness, impact and flexural strength using hybrid reinforcement. Kumar and Vijayarangan3 reported that, compared with steel leaf springs, composite leaf springs experience less stress than does existing steel springs. It was additionally concluded that the fatigue lifetime of the composite was comparable to that of a standard steel spring. Patunkar and Dolas4 presented the modeling and analysis of the composite mono leaf spring (GFRP) using the Pro-E (Wildfire) 5.0 and ANSYS 23 10.0 packages and compared the results for the estimation and comparison of various parameters. Bhanage and Padmanabhan5 performed a simulation study on the fatigue performance of a glass fiber/epoxy composite spring with a finite component technique and proved the reliability of the simulation study, thereby saving time, material, and production costs for product realization. Jolaiy et al.6 used a numerical technique to analyze composite leaf springs with an elastic core. There was an increase in the strain energy capability of the composite leaf spring. Hou et al.7 studied the evolution of eye ends for heavy axle loads. Various methods have been suggested for improving the static proofing load and fatigue load using FEM analysis.
Nayak et al.8 replaced laminated steel springs with composite materialled spring to obtain better efficiency in light vehicles. The composite-laminated spring showed better damping properties and reduced noise in an electric vehicle. Maneesh Babu and Prasanthi9 carried out experimental testing of leaf spring material by hybrid composite materials with natural fiber for electric vehicles. It was shown that as compared to a traditional steel spring with equivalent design criteria, the composite leaf spring is both lighter and more cost-effective.
Pertuz et al.10 carried out the alternative bending fatigue behavior of a polymeric matrix composite material reinforced with continuous Kevlar fiber. Manjunath et al.11 carried out analysis of steel and different composite leaf spring using ANSYS V10. The results were compared, and they were in good agreement with each other. Ashok et al.12 carried out investigation about design and analysis of composite leaf spring made of glass fiber reinforced polymer (GFRP). Stiffness and weight saving of multi composite leaf spring was estimated and compared with steel leaf springs.
Several researchers have found that the weight of glass fiber-reinforced composite parabolic leaf springs is less than that of multi-semielliptical steel flat-shaped leaf springs. Furthermore, friction is produced by the relative motion of the mating leaf in a semielliptical flat steel leaf spring and can be reduced by using a parabolic spring. Many researchers worked on improving the mechanical properties of composite mono leaf springs and compared the results with steel leaf spring. However, work related to the combination of flat leaf springs and parabolic leaf springs in a laminated leaf spring, is rare. In this paper, new type of leaf spring comprising various shapes and combinations of GRFC leaf springs with steel plates are analyzed for improving various mechanical properties in leaf spring suspension system in light commercial vehicle.
Design parameters of leaf spring
Multi-leaf spring steel design
The leaf spring design of a multi-steel leaf spring is shown in Fig. 1. The various properties of the 65Si7 spring steel are shown in Table 1.
Properties of the GFRC and silencer pad materials
Polyurethane is a thermosetting plastic-type material. This material shock absorption and wear and tear reduction tendency is very high; therefore, it is used in leaf springs as a silencer pad component. The different properties of the polyurethan are shown in Table 2.
Epoxy/S-glass UD orthotropic, polyurethane, aluminium alloy and structural steel material used for the analysis of different types of leaf spring. Orthotropic model used for composite material.
The mechanical properties of S-glass fiber-reinforced GFRC material: epoxy LY556- 50% + Hardener HY953 10% + S glass fiber 40% are shown in Table 3.
Design parameters of GFRC leaf springs
For the GFRC leaf spring, the Silencer pad design parameters are shown in Table 4, and other parameters of the leaf spring for design are shown in Table 5.
Camber radius calculations for GFRC types leaf spring13
Total Length of leaf spring 2L = 1050 mm.
Length (L) = 525 mm.
Camber (C) = 93.45.
48.06 [(2 × R) – 48.06] = \({270}^{2}\)
Camber Radius R = 1521.44 mm.
Four types of leaf springs were designed with CATIA software, and the different parameters of the leaf springs used for design are shown in Table 5.
Leaf spring assembly
The colors of the various materials in the assembly are shown in Table 6.
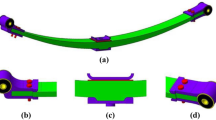
The assemblies of various parts of the leaf spring material are shown in Fig. 2. The green color represents the epoxy/s-glass material, the purple color represents the aluminium alloy material, the blue color represents the polyurethane material and the dark green material represents the structural steel material. In the present paper, various parameters, such as the maximum equivalent strain, maximum equivalent stress, strain energy, fatigue life and weight loss, are discussed for four different geometries: both leaf shapes of the leaf spring are flat, a combination of flat and parabolic leaf springs (1st leaf flat and 2nd leaf parabolic), and both a parabolic leaf shape of the leaf spring with or without an aluminium alloy eye-end bush.
Direct contact between flat and parabolic leaf is through silencer pad. The silencer pad helps to reduce interleaf friction, wear and tear and absorb vibrations. Flat leaf spring contact with parabolic leaf is shown in Fig. 3.
Pads are making bonded contact with their lower surface to 2nd leaf upper surface. Upper surface of pads is touching with 1st leaf lower surface. Bonded contact is between lower surface of top steel plate with upper surface 1st leaf, lower surface of silencer pad with upper surface of 2nd leaf and lower surface of 2nd leaf with upper surface of bottom steel plate. No separation contacts between lower surface 1st leaf with upper surface of silencer pad. Table 7 provides a list of different colour for various material parts.
Analytical method
Load estimation for the GFRC material leaf spring
Another name for a mini truck is a micro truck. It is a medium commercial vehicle used for transporting loads. The load calculation on the rear leaf spring is calculated as follows:
The gross weight of the vehicle was 1510 kg.
Payload = 710 kg.
Total weight = 2220 kg.
Take the factor of safety = 1.4
Load = 30,489.48 N.
A 40% load is applied on the front wheels, and a 60% load is applied on the rear wheels.
40% of 30489.48 N = 0.40 × 30489.48 N = 12195.792 N.
60% of 30489.48 = 0.60 × 30489.48 N = 18293.688 N (this load on both rear wheels).
Load on each rear wheel = \(\frac{18293.688N}{2}\) = 9146.8 N.
Analytical calculation of GFRC material of laminated leaf spring
No. of Leaf = 2.
S-glass yield stress = 1759 MPa.
Load = 9150 N.
FOS = 1.4 mm.
Length 2 L = 1050 mm = 1.053 m.
Length L = 525 mm = 0.525 m.
Bending stress (\({\sigma }_{b})\)= \(\frac{{s}_{y}}{FOS}\) = 1759* \({10}^{6}\)/1.4 = 1256.4 N/metre square.
Width = 60 mm = 0.06 m.
The thickness (t) is 13.86 mm. 14 mm thickness was selected for each leaf in the present study. Analytical Calculation for deflection and stiffness are as follows (Vinkel et al.2017):
CAE Design for different types of leaf spring
During the deformation convergence study, it was found that with 10% allowable changes, the deformation percentage change is in Table 8. Force convergence, moment convergence, displacement convergence, and rotation convergence have been done with the help of program control.
It may be noted from the table that the deformation convergence percentage is higher in case of GFRC flat with parabolic leaf, GFRC both parabolic leaf and GFRC both parabolic leaf with aluminium alloy bush, because of increase of number of components in laminated leaf spring.
Meshing
The meshing process discretizes geometry into elements and nodes. It has been observed that the combination of flat and parabolic leaf springs has different numbers of nodes and different numbers of elements at a 10 mm body size. The number of nodes and the number of elements were specified on the leaf spring before applying the boundary condition.
Element type in ANSYS analysis is solid 187 and solid 186 with the degree of freedom—UX, UY, UZ. Contact regions for different types of leaf springs are given in Table 9:
Boundary conditions applied for static modeling
Both types of leaf springs under flat conditions were modeled, and loading was applied for the initial conditions. The total load of 9150 N is divided on two eye-ends of the master leaf. The fixed support is considered on the nut and bolt. The CAE boundary conditions are shown in Fig. 4.
Boundary conditions weight analysis of different leaf springs with ANSYS 23 software
Weight reduction is the main concern in the case of leaf spring when the weight of the leaf spring is reduced,as is the weight of the vehicle.A decrease in the weight of the vehicle reduces the power consumption of the engine. Therefore, different types of leaf springs were analyzed via ANSYS 23 software. The different weight analysis results are shown in Table 10.
Analysis of structural steel multi-leaf springs with ANSYS 23 software
Different parameters, such as deflection, maximum equivalent strain, maximum equivalent stress and strain energy, of both flat leaf springs were analyzed via ANSYS 23 software at 9150 N (Fig. 5).
Analysis of the flat GFRC leaf spring with ANSYS 23 software
Different parameters, such as deflection, maximum equivalent strain, maximum equivalent stress and strain energy, of both flat leaf springs were analyzed via ANSYS 23 software at 9150 N (Fig. 6).
Analysis of flats with parabolic GFRC leaf springs with ANSYS 23 software
Different parameters, such as deflection, maximum equivalent strain, maximum equivalent stress and strain energy, of the flat surface with a parabolic leaf spring were analyzed via ANSYS 23 software at 9150 N (Fig. 7).
Analysis of both parabolic GFRC leaf springs with ANSYS 23 software
Different parameters, such as deflection, maximum equivalent strain, maximum equivalent stress and strain energy, of both parabolic leaf springs were analyzed via ANSYS 23 software at 9150 N (Fig. 8).
Analysis of both parabolic GFRCs leaf springs with an aluminium alloy bush with ANSYS 23 software
Different parameters, such as deflection, maximum equivalent strain, maximum equivalent stress and strain energy, of both parabolic leaf springs with aluminium alloy bushes were analyzed via ANSYS 23 software at 9150 N (Fig. 9).
Analysis of fatigue life on ANSYS 23 software
Fatigue analysis was done with fully reversed load at constant amplitude. Fatigue data come from applied boundary conditions and the S–N curve of structural steel13. Fatigue analysis through FEA helps to determine the real-life simulation conditions under which the approximate fatigue life of the model can be calculated and the reliability of the model as per the input and loading conditions can be predicted. For fatigue analysis, there are three basic elements: Material Selection, Input Parameters and Definition of Geometry (Fig. 10).
Results & discussion
A combination of flat and parabolic leaf spring analyses of the GFRC leaf spring was performed to improve the strength and fatigue life in combination with other geometric parameters. The various parameters of the CAE analysis results including average fatigue life are shown in Table 10. It is observed that factor of safety is highest with GFRC 1st flat leaf and 2nd parabolic leaf spring in laminated leaf spring (Table 11).
The combination of flat and parabolic GFRC leaf springs has a significant effect on various design parameters, such as fatigue strength, equivalent stress and equivalent strain, due to the combined effect of the constant thickness of the flat leaf and the varying thickness of the parabolic leaf (Figs. 11, 12, 13, 14, 15, 16, and 17).
The design parameters of spring steel multi leaf springs, such as fatigue strength, equivalent stress, fatigue life and strain energy, are lower than those of the combination of flat and parabolic leaf springs (1st leaf flat and 2nd leaf parabolic), while the weight of the GFRC leaf spring is lower. The combination of flat and parabolic leaf spring GFRC (1st leaf flat and 2nd leaf parabolic) can sustain greater stress, absorb more strain energy and sustain more fatigue cycles. The other cases of GFRC leaf spring at Sr. Nos. 2,4, and 5 improved several design parameters compared to those of the multi-leaf spring but not the GFRC leaf spring at Sr. No. 3 reported the greatest improvement in various design parameters (Table 10).
There was a greater change in the maximum equivalent strain, maximum equivalent stress and fatigue life of the 1st flat leaf and 2nd parabolic leaf springs than in the other three types of leaf springs. There were greater deformation changes in the case of both parabolic leaf springs than in the other types of leaf springs. Furthermore, compared with those of both the flat leaf spring and the flat and parabolic combination, the weight of both the parabolic leaf spring and the flat and parabolic combination leaf spring combinations was lower.
The combination of both the 1st flat and 2nd parabolic GFRC leaf springs results in more fatigue life cycles than does the other three methods. This is due to the higher maximum stress and higher maximum strain capacity than those of the other materials. Additionally, the deformation is greater than that in the case when both leaves are flat. As expected, the combination of both the 1st flat and 2nd parabolic GFRC leaf springs may provide better strength and fatigue life than the combination of various geometries of leaf springs.
Verification of the results
There is no exact work available for verification, as the work is novel. However, this approach was compared with somewhat matching work. Tadesse and Fatoba14 performed theoretical and finite element analysis (FEA) of coated composite leaf springs for heavy-duty truck application and reported similar results for heavy vehicles with a higher maximum equivalent stress of 518.29 MPa in a parabolic composite leaf spring. The stress and deformation were compared with those of Tridedi Achyut and Bhoraniya15, who reported that the maximum equivalent stress was 587.3 MPa and the deflection was 64.5 mm for the 65Si7 spring steel leaf spring used in similar mini-truck leaf springs.
However, in the present work, two leaves of GFRC leaf springs of various geometries were used, and the maximum equivalent stress was 529.34 MPa, while the deflection was40.879 mm for a combination of flat and parabolic composite leaf springs. The results for some parameters available in the literature do not differ much and are verified.
Conclusion
In the present paper, various parameters, such as the maximum equivalent strain, maximum equivalent stress, strain energy, fatigue life and weight loss, are discussed for four different geometries: both leaf shapes of the leaf spring are flat, a combination of flat and parabolic leaf springs (1st leaf flat and 2nd leaf parabolic), and both a parabolic leaf shape of the leaf spring with or without an aluminium alloy eye-end bush. The strength and fatigue life improvements were analyzed as follows:
-
(I).
The maximum equivalent strain and maximum equivalent stress in the case of a combination of flat and parabolic leaf springs (1st leaf flat and 2nd leaf parabolic) are higher than those in the case of the combination of GFRC leaf springs either the both flat type or both parabolic leaves.
-
(II).
The design parameters of spring steel multi-leaf springs, such as fatigue strength, equivalent stress, fatigue life and strain energy, are lower than those of a combination of flat and parabolic leaf springs (1st leaf flat and 2nd leaf parabolic), while the weight of the GFRC leaf spring is lower. The combination of flat and parabolic leaf spring GFRC (1st leaf flat and 2nd leaf parabolic) can sustain greater stress, absorb more strain energy and sustain more fatigue cycles.
-
(III).
The combination of both the 1st flat and 2nd parabolic GFRC leaf springs resulted in more fatigue life cycles than did the other three methods. This is due to the higher maximum stress and higher maximum strain capacity than those of the other materials. Additionally, the deformation is greater than that in the case when both leaves are flat.
-
(IV).
In the present study, the weight reduction in response to both GFRC parabolic leaf springs was greater than that in response to all the other combinations of various geometries of leaf springs. A parabolic shape provides a reduction in weight because the leaf is thick at the center and thin at the ends.
-
(V).
Deformation is least common when both leaves of the leaf spring are flat. It is greater with the combination of flat and parabolic leaf spring GFRC (1st leaf flat and 2nd leaf parabolic). However, the highest value was obtained for both the parabolic leaf of the leaf spring with and without the aluminium alloy eye-end bush. This is because the parabolic leaf provides better damping.
-
(VI).
The strain energy, in the case of the combination of flat and parabolic leaf spring GFRC (1st leaf flat and 2nd leaf parabolic) is higher than both parabolic leaf spring. However, the strain energy is higher in the case of both GFRC flat leaf springs as compared with that in the case of the combination of flat and parabolic leaf spring GFRC (1st leaf flat and 2nd leaf parabolic) because both GFRC flat leaf spring thicknesses do not fluctuate between the center and eye-end.
-
(VII).
It is observed that factor of safety is highest with GFRC 1st flat leaf and 2nd parabolic leaf spring in laminated leaf spring. The combination of both the 1st flat and 2nd parabolic GFRC leaf springs may provide better strength and fatigue life than other combinations of various other geometries of leaf springs.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
References
Gebremeskel, S. A. Design, simulation, and prototyping of single composite leaf springs for lightweight vehicles. Glob. J. Res. Eng. Mech. Mech. Eng. 12(7), 2–10 (2012).
Kader, E. E., Adwan, R. & Zedan, L. Y. Fabrication of hybrid composite materials leaf spring. J. Mech. Eng. Res. Dev. 44(2), 132–140 (2021).
Kumar, M. S. & Vijayarangan, S. Analytical and experimental studies on fatigue life prediction of steel and composite multileaf springs for light passenger vehicles using life data analysis. Mater. Sci. 13(2), 41–146 (2007).
Patunkar, M. M. & Dolas, D. R. Modeling and analysis of composite leaf spring under the static load condition by using FEA. Int. J. Mech. Ind. Eng. 1(1), 1–4 (2011).
Bhanage, A. & Padmanabhan, K. Design for fatigue and simulation of glass fiber/epoxy composite automobile leaf spring. ARPN J. Eng. Appl. Sci. 9(3), 196–203 (2003).
Jolaiy, S., Yousefi, A., Mashhadi, M. M., Amoozgar, M. & Bodaghi, M. Dynamic behaviors of composite leaf springs with viscoelastic cores. Mech. Based Des. Struct. Mach. 51, 1–23 (2021).
Hou, J. P., Cherruault, J. Y., Nairne, I., Jeronimidis, G. & Mayer, R. M. Evolution of the eye-end design of a composite leaf spring for heavy axle loads. Compos. Struct. 78(3), 351–358 (2007).
Nayak, S., Sadarang, J., Panigrahi, I., Nayak, R. K. & Maurya, M. Optimization of composite leaf spring for reduced weight and improved noise, vibration, and harshness in an electric vehicle. Noise Vib. Worldwide 51(7–9), 127–138 (2020).
Maneesh Babu, V. & Prasanthi, G. Modelling, analysis, fabrication and experimental testing of leaf spring material by hybrid composite materials with natural fiber for electric vehicle. J. Adv. Zool. 45(1), 70–85 (2023).
Pertuz-Comas, A. D. et al. Flexural fatigue in a polymer matrix composite material reinforced with continuous Kevlar fibers fabricated by additive manufacturing. Polymers 14, 3586. https://doi.org/10.3390/polym14173586 (2022).
Manjunath, H. N., Manjunath, K. & Rangaswamy, T. Static analysis and fatigue life prediction of composite leaf spring for a light commercial vehicle. Int. J. Eng. Res. 3(7), 422–425 (2014).
Ashok, D., Mallikarjun, M. V., Mamilla, V. R. Design and structural analysis of composite multi-leaf spring. Int. J. Emerg. Trends Eng. Dev. 5(2), 30–37 (2007).
Arora, V., Bhushan, G. & Aggarwal, M. L. Enhancement of fatigue life of multi leaf spring by parameter optimization using RSM. J. Braz. Soc. Mech. Sci. Eng. 39(4), 1333–1349 (2017).
Tadesse, B.A. & Fatoba, O. Theoretical and finite element analysis (FEA) of coated composite leaf spring for heavy-duty truck application. Mater. Today Proc. 62(1) 4283–4290 (2022).
Tridedi Achyut, V., Bhoraniya, R. M. Static and dynamic analysis of automobile leaf spring. Int. J. Sci. Technol. Eng. 1(11), 151–156 (2015).
Author information
Authors and Affiliations
Contributions
SA (corresponding author): conceptualization; methodology; software; supervision; validation; visualization; writing—original draft; writing—review & editing. KK: software; visualization. MLA: conceptualization; resources; data curation; investigation; writing—review & editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Aggarwal, S., Kumar, K. & Aggarwal, M.L. Analysis of glass fiber-reinforced composite leaf springs in a light commercial vehicle. Sci Rep 14, 20126 (2024). https://doi.org/10.1038/s41598-024-67616-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-67616-3