Introduction

The ongoing digital transformation has significantly deepened the integration between public services and information technologies1. Within this context, public guidance interfaces-digital platforms enabling service access in urban environments-exhibit distinct interaction characteristics compared to personal devices like smartphones or vehicle dashboards. These systems follow an intermittent usage pattern: while daily engagement remains limited, users demand immediate task completion during critical service encounters2.This operational paradigm creates three essential design requirements for public guidance interfaces deployed in healthcare facilities, transportation hubs, and cultural institutions (1) Visual salience to attract attention in crowded environments. (2) Zero-learning-curve operation for first-time users. (3) Time-constrained task efficiency for urgent service needs. Unlike high-frequency interfaces requiring habitual usage patterns, public guidance systems must achieve immediate usability without prior training while maintaining aesthetic appeal. This dual requirement of visual attractiveness and instant operational clarity defines their unique design challenges in public service scenarios.

Current public guidance interfaces suffer from three persistent design flaws: inadequate navigation cues, inefficient service delivery, and excessive operational complexity, collectively leading to suboptimal user experiences3. These shortcomings become particularly acute in healthcare settings where urgent service demands prevail4. As critical healthcare infrastructure, medical guidance desks must fulfill two essential functions: (1) providing immediate wayfinding solutions and (2) enabling rapid service acquisition for patients under time-sensitive conditions. Current research identifies critical challenges in healthcare interface design. Suboptimal guidance systems have been shown to induce user confusion and frustration5, particularly detrimental in emergency care environments where overcrowding and prolonged wait times exacerbate patient dissatisfaction6. The complexity of patient journeys—spanning registration, triage, treatment, and discharge—creates cumulative interaction barriers that challenge service quality maintenance7. Meanwhile, bedside clinical decision support (CDS) systems demonstrate the operational advantages of minimizing physician reliance on spatially distant desktop interfaces8. These findings collectively underscore the pressing need for interface designs that balance visual salience with operational immediacy in healthcare navigation systems.

This investigation establishes a dual-criteria evaluation framework for hospital guidance interfaces, systematically incorporating both aesthetic perception (spatial composition principles) and visual cognition patterns (information processing mechanisms). The proposed methodology generates actionable design guidelines to optimize medical navigation systems through enhanced interface intuitiveness and user-centric information architecture. These improvements directly target two operational objectives: (1) accelerating users’ task completion efficiency and (2) reducing dependency on staff-assisted navigation services.

Literature review

Visual interface design

Visual design quality evaluation operates through three interconnected dimensions: aesthetic perception, functional efficiency, and symbolic representation, each grounded in distinct theoretical foundations9. The aesthetic dimension traces its conceptual origin to Alexander Baumgarten’s 1750 treatise Aesthetica, which formalized aesthetics as the scientific study of sensory cognition (Greek: aisthētikos), positing aesthetics as the optimal realization of perceptual awareness10. This theoretical framework explains how interface aesthetics govern user perception dynamics, as evidenced by Sulikowski et al.‘s eye-tracking studies revealing aesthetic features’ influence on visual attention allocation11.

Functional evaluation employs interaction laws like Fitts’ Law12 - a mathematical model quantifying target acquisition time as a function of element size and movement distance - to assess interface operational efficiency. Meanwhile, the symbolic dimension incorporates cultural semantics and identity communication mechanisms, with Lee et al.13 and Lidwell et al.14 developing universal design principles for interface application scenarios through cognitive psychology theories and empirical case syntheses.

Aesthetics and functionality, as critical aspects of visual design for infrequently used interfaces, have garnered extensive academic attention. Research has primarily focused on aesthetic perception, aesthetic measurement, and human cognitive characteristics, yielding notable advancements. However, existing studies often fail to integrate these dimensions, potentially leading to discrepancies between interface design quality and actual user needs. On the one hand, aesthetics significantly influence visual design in unconventional public-oriented service interfaces. Visually appealing interfaces enhance user engagement. Scholars have explored user experience and usability by investigating intrinsic properties of design elements, including icons15, layouts16, and typography17. Research also addresses subjective dimensions like visual complexity18, utility19, and attractiveness20. Birkhoff (1933) proposed a seminal mathematical formula for macro-aesthetics: M = O/C, defining aesthetic measure as the order-complexity ratio21. Ngo et al. developed computational aesthetic models to quantify layout characteristics in interface design22.

On the other hand, visual perception serves as the primary channel for information perception in human interactions with infrequently used interfaces23. Integrating human cognitive features into interface design ensures alignment with user mental models, which is critical for effective interaction. Researchers have evaluated interface design through visual cognition theories. For instance, Zhi et al.24 analyzed layout types in train cockpit interfaces using eye-tracking experiments to assess visual cognitive load, search efficiency, and attention distribution. Similarly, Martinez et al.25 examined cockpit dashboard interfaces by analyzing pilots’ gaze patterns and visual cognition via eye-tracking metrics, focusing on gaze trajectories, fixation distribution, and frequency to minimize operational errors.

In summary, significant progress has been made in interface design evaluation, yet existing research predominantly focuses on frequently used interfaces, with limited attention to infrequently used systems such as medical guidance interfaces. Current studies often examine layout aesthetics or visual cognition in isolation, neglecting their combined influence, which risks incomplete assessments of design quality. Notably, quantitative investigations into the mapping relationships between interface layout aesthetics and visual cognitive features remain scarce.

Grey correlation analysis

The evaluation of public service guidance interface layouts can be conceptualized as a “grey system,” where aesthetic metrics and visual cognitive physiological measurements represent “white systems,” while their coupling relationships form an unknown “black system.” Grey theory excels in addressing uncertainties with partial information availability. Grey relational analysis, a core component of grey system theory, evaluates relational degrees based on geometric similarities of data sequence curves26. Existing models include the grey entropy correlation model27, grey B-type relational model28, and new grey absolute relational model29.

However, traditional grey correlation methods are limited to positive correlations and fail to capture negative relationships. To resolve this, Wu et al.30 proposed a grey convex correlation model that measures sequence convexity via vertical distances. Pan et al.31introduced the grey H-convex relational degree using span and arch height principles to quantify negative correlations through horizontal convexity. Recent advancements extend these methods to three-dimensional panel data, exemplified by Dang et al.‘s32 grey vector relational model based on 3D geometric features, addressing comparability in multi-dimensional data analysis.

While existing models have advanced significantly, they retain notable limitations. For instance, the assessment of sequence curve similarity often overlooks indicator weighting or relies on oversimplified or ambiguous weighting methods, introducing deviations from actual outcomes.

Weighting method

Existing studies divide weight determination methods into two categories: subjective and objective.

(1) Subjective methods rely on expert knowledge and experience to assign criterion weights. For example, Liu et al.33 applied the Analytic Hierarchy Process (AHP) to calculate weights for interface evaluation criteria, proposing a human-machine interface reliability evaluation framework. Vrtagić et al.34 employed the Step-wise Weight Assessment Ratio Analysis (SWARA) to assess weight coefficients for enhancing traffic route safety. Gul et al.35 (2022) utilized the Bayesian Best-Worst Method (BBWM) to prioritize criteria for assessing safety risks in specific environments.

(2) Objective methods employ mathematical techniques based on inter-criteria relationships within raw data, eliminating human subjectivity. Examples include the entropy weight method, Criteria Importance Through Intercriteria Correlation (CRITIC), and M-CRITIC-RP. Chen et al.36 integrated entropy weighting to evaluate product conceptual design. Sharkasi et al.37applied M-CRITIC-RP to compute multi-criteria weights, combined with a gravity model to analyze product export potential. Neither approach fully captures all criteria information. Thus, hybrid methods—such as least squares38and game theory-based approaches39—combine subjective and objective weighting to achieve balanced results.

BBWM

The Best-Worst Method (BWM), initially proposed by Rezaei et al., deviates from pairwise comparisons by focusing on identifying the most and least important criteria and evaluating their priority relative to others40. However, BWM is limited to individual decision-maker judgments. To address this, Mohammadi et al.41 developed the Bayesian Best-Worst Method (BBWM), which treats criteria as probabilistic events, with weights represented as occurrence probabilities. BBWM processes BWM inputs via multinomial distributions and calculates criterion weights using Dirichlet distributions. By constructing a Bayesian framework, BBWM derives optimal weights reflecting collective preferences across multiple decision-makers.

M-CRITIC-RP

The Criteria Importance Through Intercriteria Correlation (CRITIC) method faces two key limitations: (1) Its data normalization process requires categorizing criteria into strictly positive or negative attributes, leading to distortions when criteria do not strictly fit these categories. (2) Its reliance on Pearson correlation coefficients restricts weight calculation to linear relationships, ignoring nonlinear interdependencies.

To resolve these issues, Sharkasi et al.42 proposed the M-CRITIC-RP method, which employs fuzzy logic theory and Hamming distance to optimize normalization and mitigate rigid positive/negative attribute categorization. Additionally, distance correlation coefficients replace Pearson correlations to construct weighting matrices, enabling detection of both linear and nonlinear relationships.

Motivation

Existing research reveals limited exploration of evaluation methods for infrequently used interfaces, sparse integration of interface layout aesthetics with visual cognition, and minimal investigation into their interrelationships. Consequently, the proposed method demonstrates significant application potential in addressing these gaps.

In a previous study, we developed a grey H-convex relational model for the virtual museum interface using the Improving Criteria Importance through Inter-Criteria Correlation (ICRITIC) methodology43, which did not take into account subjective criterion weights. This work advances this framework through key method innovation: using BBWM and M-Critical-RP methods to determine the subjective and objective weights of indicators, and introducing game theory model to realize the dynamic balance between subjective and objective weights, thus improving the applicability of the model in the medical guidance interface.

To enhance the accuracy of mapping interface layout aesthetics to visual cognition, we introduced a weight determination step. BBWM and M-CRITIC-RP were selected due to their superiority over alternative weighting methods. Additionally, the grey H-convex relational model outperforms conventional grey models in handling nonlinear relationships, as demonstrated in subsequent comparative analyses.

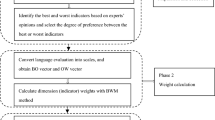
Research framework

The framework is structured as follows (Fig. 1). First, an evaluation criteria system for human-machine interface layouts is established through emotional imagery analysis and literature review, followed by metric data generation. Next, comprehensive criterion weights are computed using BBWM (subjective weights), M-CRITIC-RP (objective weights), and a game-theoretic equilibrium model to unify both weight types. Weighted normalization is then applied to standardize input data for the grey H-convex relational model, which quantifies correlations between layout aesthetics and visual cognition.

Fig. 1
figure 1

Research framework.

Full size image

Methods

Evaluation criteria

The evaluation criteria system for human-machine interface layouts comprises two components: interface layout aesthetics criteria and visual cognition evaluation criteria. Firstly, this study adopted a three-phase stratified validation protocol involving expert, professional, and non-professional groups with distinct roles. (1) Expert panel: To validate the evaluation system, comprising 4 human-computer interaction design professors and 2 chief information officers from tertiary hospitals. (2) Aligned with Nielsen’s parallel design theory44, consisting of trained designers (with interaction design expertise and medical interface project experience) for precise decomposition of layout aesthetic. (3) Non-professional group (n = 15): Representing end-users. A minimum sample size (n = 12) was determined via G-Power 3 (α = 0.05, β= 0.2, effect size = 0.4). Inclusion criteria: at least 2 visits to tertiary hospitals in the past 6 months45. Secondly, 26 smart medical console interface prototypes were designed following interface design principles. The professional group conducted emotional imagery analysis on the prototypes, which were then evaluated and refined by the non-professional group. This process yielded 16 distinct imagery descriptors through preliminary screening based on semantic divergence. The non-professional group subsequently assessed the prototypes using a 7-point Likert scale. Structural validity of the questionnaire was confirmed via Exploratory Factor Analysis (EFA) (KMO = 0.82, Bartlett’s sphericity test p < 0.001), with five factors accounting for 91.3% cumulative variance. Reliability testing using Cronbach’s alpha demonstrated strong internal consistency (α = 0.87; all factor-specific α > 0.7). Five layout aesthetic criteria were ultimately selected: Balance, Density, Simplicity, Order, and Uniformity.

On the other hand, existing research indicates that interface element layout significantly influences users’ visual cognitive performance46. Five validated eye-tracking metrics linked to interface layout aesthetics include gaze duration47, gaze count48, mean pupil diameter49, saccadic frequency50, and fixation time percentage51. These metrics were selected as evaluation criteria for public service-oriented interface design. The human-machine interface layout evaluation framework is depicted in Fig. 2.

Fig. 2
figure 2

Evaluation criteria system of human-machine interface layout.

Full size image

Evaluation model

Model frame

The model framework is divided into three parts, as shown in Fig. 3.

(1) Collecting data. On one hand, aesthetic evaluation values were obtained based on formulas. On the other hand, user visual cognitive characteristics were derived from eye-tracking experiments. Let the interface layout aesthetics evaluation criteria be \(\left\{ {C_{1}^{a},C_{2}^{a},C_{3}^{a} \cdots ,C_{n}^{a}} \right\}\), the eye movement criteria is \(\left\{ {C_{1}^{e},C_{2}^{e},C_{3}^{e} \cdots ,C_{n}^{e}} \right\}\).

(2) Weight distribution. The BBWM method determines subjective weights, while the M-CRITIC-RP method calculates objective weights. Finally, using the principles of game theory, the standard combination weights were determined.

(3) Construct an improved grey H-convex correlation model. Establish a weighted standardized indicator data sequence as input for the model. Using the grey H-convex correlation method, quantitatively evaluate the correlation between eye movement indicators and layout aesthetics indicators.

Fig. 3
figure 3

Model framework.

Full size image

Data collection

(1) Layout aesthetics value.

Building on the shape superiority effect in cognitive processing psychology, interface layout elements were functionally zoned and abstracted into black rectangles to achieve precise positioning52. A coordinate system was established to compute layout aesthetic metrics (Fig. 4), with four parameters defining spatial positioning: the horizontal coordinate x, the vertical coordinate y, the total width b and the total height h of the rectangle. Overall layout dimensions: b×h = 400 × 300 mm. Among them, along the interface from left to right is the x-positive direction, and from top to bottom scanning is the y-positive direction. According to aesthetic calculation formula proposed by Ngo et al.22, calculate the evaluation results of aesthetics indicators.

Fig. 4
figure 4

Coordinate system for interface layout aesthetics calculation. Origin (0,0) at top-left corner with x-axis positive to the right, y-axis positive downward. Interface elements are abstracted as black rectangles parameterized by position (\({x_{ij}}\),\({y_{ij}}\)) and dimensions (\({b_{ij}}\),\({h_{ij}}\)).

Full size image
  1. 1)

    Balance \(C_{1}^{a}\)

The degree of balance indicates the symmetry of the elements in the interface layout in three directions: vertical, horizontal and diagonal. It is calculated by the formula22.

  1. 2)

    Intensity \(C_{2}^{a}\)

Intensity represents the tightness or looseness of the elements in the interface. An optimal interface intensity is achieved at 50%22.

  1. 3)

    Simplicity \(C_{3}^{a}\)

Simplicity refers to the degree of element arrangement and integration in an interface layout to reduce users’ cognitive load in perceiving layout configurations22.

  1. 4)

    Order \(C_{4}^{a}\)

The human eye has reading habits from top to bottom, from left to right, from large objects. The interface layout according to this visual law can effectively guide the order of human attention22.

  1. 5)

    Uniformity \(C_{5}^{a}\)

Uniformity emphasizes the visual coherence of interface layout elements. It is usually calculated as the aspect ratio of the interface layout elements to the interface frame22.

(2) Visual Cognition Measurement.

Eye-tracking technology enables the acquisition of physiological data on visual cognition by observing interface element layouts and capturing variations in user gaze trajectories. The sample size of 42 participants was determined via a priori power analysis using G-Power 3.1, which indicated a minimum requirement of 38 subjects to detect a medium effect size (f²=0.25) with 95% power for multiple regression analysis involving five predictors at α= 0.05. This exceeds the recommended threshold in interface eye-tracking studies53. Participants underwent rigorous screening including: 1)Questionnaire-based exclusion of prior eye-tracking experience. 2) Gender-balanced recruitment (21 males/21 females). 3) Age stratification (24–55 years) ensured representation of key medical kiosk user demographics, with screening intentionally excluding individuals under 24 (infrequent users) and over 55. All participants had normal or corrected-to-normal vision in both eyes and were free from color vision deficiencies.

The subjects were seated in a fixed position, with the eye distance to the front of the monitor maintained at 60.2 ± 3.1 cm (mean ± SD) through postural adjustments. The experimental equipment was a Tobii X2-30 eye-tracker with a sampling frequency of 30 Hz, coupled with a 21.5-inch Hewlett-Packard desktop monitor, featuring a screen resolution of 1920 × 1080 PX. The experimental program was written and run with the help of ErgoLAB, designed for the acquisition of experimental data. The experiment utilized flicker-free LEDs (5500 K ± 5% color temperature) with stable illumination of 250 ± 10 lx (calibrated by Testo 540 light meter) to ensure environmental consistency for pupillometry. All participants underwent a 9-point eye tracker calibration procedure, achieving a mean error of < 0.5°, thereby guaranteeing measurement accuracy.

Criteria weights

(1) Subjective weighting.

The subjective weights are calculated based on BBWM.

Step.1 Identification of a collection of evaluation criteria \(C=\left\{ {{C_1},{C_2}, \cdots ,{C_n}} \right\}\).

Step.2 Experts based on industry information, actual investigation and subjective experience from the interface layout evaluation system \(C=\left\{ {{C_1},{C_2}, \cdots ,{C_n}} \right\}\) initially determine the best \({C_B}\) and worst \({C_W}\)criteria as reference and comparison object.

Step.3 Constructing comparison guidelines. Experts compare \({C_B}\) with other interface layout evaluation indicators in pairs to obtain a matrix:\({A_B}=\left\{ {{a_B}_{1},{a_B}_{2}, \cdots ,{a_{Bn}}} \right\}\). Among them, \({a_{Bj}}\)represents the ratio of the importance of \({C_B}\) to other interface layout evaluation indicators, expressed as integers ranging from 1 to 9, and \({a_{BB}}\)= 1. Similarly, by comparing other interface layout evaluation indicators with \({C_W}\) in pairs, a matrix is obtained: \({A_W}=\left\{ {{a_{1 W}},{a_{2 W}}, \cdots ,{a_{nW}}} \right\}\).Among them, \({a_{iW}}\) represents the ratio of the importance of other interface layout evaluation indicators to \({C_W}\), expressed as integers ranging from 1 to 9, with \({a_{WW}}\)= 1.

Step.4 Introduce polynomial distribution and Dirichlet distribution as the probability distribution assumptions for the input and output of BBWM model.

Step.5 Transform the weight judgment problem of interface layout evaluation indicators into a probability statistical problem of approximating the posterior distribution of the best weight vector, and calculate the best weight vector \({w^{agg}}\) for group decision-making.

Considering the joint influence of \({A_B}\) and \({A_W}\) the optimal weight vector for evaluating the layout of public guidance service interfaces in expert group decision-making is calculated based on a Bayesian hierarchical model. Setting with \({k^{{\text{th}}}}\) experts, \(k=1, \cdots ,K\), determines the best and worst comparison matrices \(A_{W}^{k}\) and \(A_{B}^{k}\)based on the interface layout evaluation criteria \({C_1}, \cdots ,{C_n}\), the set of best and worst-case comparison matrices for the k experts is \(A_{B}^{{1:K}}\) and \(A_{W}^{{1:K}}\). Let \({w^{agg}}\) denote the optimal weight vector for expert group decision-making, calculated based on the optimal weight vector \({w^k}\)\(\left( {k=1, \cdots ,K} \right)\) for each expert. Before calculating the \({w^{agg}}\), the joint probability distribution of the evaluation random variables for the public guidance service interface should be represented based on the given parameters. \(A_{B}^{{1:K}}\) and \(A_{W}^{{1:K}}\) are given, while \({w^{agg}}\) and \(w_{{}}^{{1:K}}\)are the quantities that need to be solved. Therefore, the joint probability distribution of \({w^{agg}}\) can be expressed as:

$$P\left( {{w^{agg}},{w^{1:K}}\left| {A_{B}^{{1:K}},A_{W}^{{1:K}}} \right.} \right)$$
(1)

In the Bayesian hierarchical model, \(w_{{}}^{{1:K}}\) is both the variable to be solved and the parameter to solve \({w^{agg}}\). According to the chain rule, Eq. (1) is represented as:

$$\begin{gathered} P\left( {{w^{agg}},{w^{1:K}}\left| {A_{B}^{{1:K}},A_{W}^{{1:K}}} \right.} \right) \hfill \\ \propto P\left( {A_{B}^{{1:K}},A_{W}^{{1:K}}\left| {{w^{agg}},{w^{1:K}}} \right.} \right)P\left( {{w^{agg}},{w^{1:K}}} \right) \hfill \\ =P\left( {{w^{agg}}} \right)\coprod\limits_{{k=1}}^{K} {P\left( {A_{W}^{k}{{\left| w \right.}^k}} \right)} P\left( {A_{B}^{k}\left| {{w^k}} \right.} \right)P\left( {{w^k}\left| {{w^{agg}}} \right.} \right). \hfill \\ \end{gathered}$$
(2)

Where \(P\left( {{w^{agg}},{w^{1:K}}\left| {A_{B}^{{1:K}},A_{W}^{{1:K}}} \right.} \right)\) represents the posterior distribution of \({w^{agg}}\),\(P\left( {{{\text{w}}^{agg}}} \right)\) represents the prior distribution of \({w^{agg}}\),\(P\left( {A_{W}^{k}{{\left| w \right.}^k}} \right)\)and\(P\left( {A_{B}^{k}{{\left| w \right.}^k}} \right)\)represents the polynomial distribution assumption of \(A_{W}^{k}\) and \(A_{B}^{k}\),\(P\left( {{w^k}\left| {{w^{agg}}} \right.} \right)\) represents the prior distribution of \({w^k}\).

The process of solving the posterior distribution of \({w^{agg}}\) and \({w^k}\) involves high-dimensional integration, which is difficult to calculate. Therefore, using the Markov chain Monte Carlo method in Gibbs sampling environment, fitting the posterior distributions of \({w^{agg}}\) and \({w^k}\), and finally taking the sample mean of the \({w^{agg}}\) posterior distribution as the optimal weight result.

(2) Objective weighting.

The M-CRITIC-RP method calculates the objective weights of interface layout evaluation criteria.

(1) Define the decision matrix R. With m interface programs and n criteria, there are,

$$R{\text{=}}{\left( {{r_{ij}}} \right)_{m \times n}}; i=1, \cdots ,m; j=1, \cdots ,n$$
(3)

Where \({r_{ij}}\) represents the elements of the decision matrix for the j criteria in the i interface program.

(2) The clear values of the decision matrix elements \({r_{ij}} \in \left[ {{A_j}} \right.,\left. {{B_j}} \right]\) are transformed into the fuzzy form \(\left[ {r_{{ij}}^{L}} \right.,\left. {r_{{ij}}^{U}} \right]\).

(3) Specify the fuzzy reference point RP for each standard \({c_j}\). The fuzzy RP points are \(\left[ {{a_{ij}},{b_{ij}}} \right] \subseteq \left[ {{A_j}} \right.,\left. {{B_j}} \right]\), where \({a_{ij}}={{\sum\nolimits_{{i=1}}^{m} {r_{{ij}}^{L}} } \mathord{\left/ {\vphantom {{\sum\nolimits_{{i=1}}^{m} {r_{{ij}}^{L}} } m}} \right. \kern-0pt} m}\);\({b_{ij}}={{\sum\nolimits_{{i=1}}^{m} {r_{{ij}}^{U}} } \mathord{\left/ {\vphantom {{\sum\nolimits_{{i=1}}^{m} {r_{{ij}}^{U}} } m}} \right. \kern-0pt} m}\) is the mean of\(r_{{ij}}^{L}\) and \(r_{{ij}}^{U}\), fuzzy element \(r_{{ij}}^{L}={r_{ij}} - {h_i},r_{{ij}}^{U}={r_{ij}}+{h_i}\),\({h_i}\) is some positive decimal, for all i and j: \(0<{r_{ij}}+{h_i}<1\), \(0<{r_{ij}} - {h_i}<1\).Besides, \({A_j}={\hbox{min} _i}r_{{ij^{\prime}}}^{L},{B_j}={\hbox{max} _i}r_{{ij^{\prime}}}^{U}\)。

(4) The decision matrix is normalized and the calculation is expressed as follows

$${N_{RP}}\left( {\left[ {r_{{ij}}^{L},r_{{ij}}^{U}} \right]} \right)=\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {1,}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{} \end{array}} \\ {1 - \frac{{\left| {r_{{ij}}^{L} - {a_j}} \right|+\left| {r_{{ij}}^{U} - {b_j}} \right|}}{{2\left( {{B_j} - {A_j}} \right)}}} \end{array}} \right.,\begin{array}{*{20}{c}} {\left[ {r_{{ij}}^{L},r_{{ij}}^{U}} \right] \subseteq \left[ {{a_j},{b_j}} \right]\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{}&{} \end{array}}&{}&{} \end{array}} \\ {\left[ {r_{{ij}}^{L},r_{{ij}}^{U}} \right] \not\subset \left[ {{a_j},{b_j}} \right],\left[ {r_{{ij}}^{L},r_{{ij}}^{U}} \right] \subseteq \left[ {{A_j},{B_j}} \right]} \end{array}$$
(4)

(5) Calculate the standard deviation \({S_j}\) of the j interface evaluation criteria.

$${S_j}{\text{=}}\sqrt {\frac{{{{\left( {\sum\nolimits_{{i=1}}^{m} {{x_{ij}} - {{\bar {x}}_j}} } \right)}^2}}}{{m - 1}}}$$
(5)

(6) Calculation of distance correlation coefficients \(dCor\left( {{c_j},{c_{j^{\prime}}}} \right)\).

$$dCor\left( {{c_j},{c_{j^{\prime}}}} \right)=\frac{{dCov\left( {{c_j},{c_{j^{\prime}}}} \right)}}{{sqrt\left( {dVar\left( {{c_j}} \right)dVar\left( {{c_{j^{\prime}}}} \right)} \right)}}$$
(6)

Where \(dCov\left( {{c_j},{c_{j^{\prime}}}} \right)\) denotes the distance covariance of \({c_j}\) and \({c_{j^{\prime}}}\),\(dVar\left( {{c_j}} \right)\)=\(dCov\left( {{c_j},{c_j}} \right)\)denotes the distance variance of \({c_j}\),\(dVar\left( {{c_{j^{\prime}}}} \right)\)=\(dCov\left( {{c_{j^{\prime}}},{c_{j^{\prime}}}} \right)\)denotes the distance variance of\({c_{j^{\prime}}}\).

(7) Calculation of the amount of information \({E_j}\).

$${E_j}={S_j}\sum\nolimits_{{j=1}}^{n} {\left( {1 - dCor\left( {{c_j},{c_{j^{\prime}}}} \right)} \right)}$$
(7)

(8) Calculation of the weighting factor \({w_j}\).

$${w_j}=\frac{{{E_j}}}{{\sum\limits_{{j=1}}^{n} {{E_j}} }}\begin{array}{*{20}{c}} {}&{j=1,2, \cdots ,n} \end{array}$$
(8)

(3) Combined weights.

By applying game theory principles, this study adopts the attainment of Nash equilibrium54 as the optimization goal for harmonizing subjective and objective weights. The objective is to identify an equilibrium point that minimizes deviations between the integrated weights and the original base weights, thereby deriving optimal composite weights.

Step.1 There are E different weighting methods to assign weights \({W_z}=\left\{ {{\omega _z}_{1},{\omega _z}_{2}, \cdots ,{\omega _{zn}}} \right\}\left( {z=1,2, \cdots ,L} \right)\), where \({\omega _{zj}}\)denotes the weight of interface layout criteria j under weighting method z, This paper \(L=2\). Let \(\alpha =\left\{ {{\alpha _1},{\alpha _2}} \right\}\) be a linear combination of coefficients, then:

$$W={\alpha _1}\omega _{1}^{T}+{\alpha _2}\omega _{2}^{T}\left( {{\alpha _{1,2}}>0,{\alpha _1}+{\alpha _2}=1} \right)$$
(9)

Step.2 Introducing the idea of game-theoretic aggregation model, the optimal weights W are obtained with the objective of minimizing the deviation between W and \({W_k}\). The objective function is:

$$\hbox{min} {\left\| {\sum\limits_{{l=1}}^{2} {{\alpha _l}\omega _{l}^{T} - {\omega _z}} } \right\|_2}\left( {z=1,2} \right)$$
(10)

According to the differential characteristics of the matrix, the optimal first-order derivative conditional equation of Eq. (10) is as follows:

$$\left[ {\begin{array}{*{20}{c}} {{\omega _1} \cdot \omega _{1}^{T}} \\ {{\omega _2} \cdot \omega _{1}^{T}} \end{array}} \right.\left. {\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {{\omega _1} \cdot \omega _{2}^{T}} \\ {{\omega _2} \cdot \omega _{2}^{T}} \end{array}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{\alpha _1}} \\ {{\alpha _2}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {{\omega _1} \cdot \omega _{1}^{T}} \\ {{\omega _2} \cdot \omega _{2}^{T}} \end{array}} \right]$$
(11)

Step.3 Normalizing the optimized combination coefficients \(\alpha =\left\{ {{\alpha _1},{\alpha _2}} \right\}\).

$$\alpha _{z}^{ * }=\frac{{\left| {{\alpha _z}} \right|}}{{\sum\limits_{{z=1}}^{2} {\left| {{\alpha _z}} \right|} }}$$
(12)

Step.4 Calculate the combined weights W.

$$W=\alpha _{1}^{ * }\omega _{1}^{T}+\alpha _{2}^{ * }\omega _{2}^{T}$$
(13)

Improved grey H-convex correlation model

The grey H-convex relational model applies principles of span and arch height from bridge engineering to characterize the horizontal convexity of polyline curves31. Crucially, it distinguishes both positive and negative correlations between data sequences.

Definition 1

As shown in Fig. 5, for a fold line \(DEF\), the line segment \(DF\) denotes the span.

Definition 2

As shown in Fig. 5, for a broken line \(DEF\), the vertical line \(HE\) between the vertex E and the span \(DF\) represents the height of the arch.

Fig. 5
figure 5

Schematic of H-convex correlation with bridge-inspired span-arch principles. Coordinate system: X-axis (Span), Y-axis (Arch height). The figure presents a schematic representation of four folds with different spans and arch heights.

Full size image

Definition 3

As shown in Fig. 6, for any concave-convex folding line \(DEF\),arch height \(HE\), spans \(DF\), Then the ratio \(\frac{{HE}}{{DF}}\) of the arch height \(HE\) to the span \(DF\) is the H-convexity of the fold \(DEF\), expressed as \({d_{H - convex}}=\frac{{HE}}{{DF}}\).

Fig. 6
figure 6

Schematic calculation of H-convexity. Figure 6-(a), Fig. 6-(b) shows the two cases of H-convexity calculation respectively. The X-axis represents the data series span and the Y-axis represents the H-convexity. Solid line folds show the change in convexity for three consecutive data (k, k + 1, k + 2).

Full size image

As shown in Fig. 6, based on \(x(k)\),\(x(k+1)\),\(x(k+2)\) in the interface evaluation criteria series X plotting the fold \(DEF\), spans\(DF=\sqrt {{{\left( {k+2 - k} \right)}^2}+{{\left[ {x\left( {k+2} \right) - x(k)} \right]}^2}} =\sqrt {4+{{\left[ {x\left( {k+2} \right) - x(k)} \right]}^2}}\), for ease of calculation, the value of \(GE\) is used instead of the arch height\(HE\),\(GE=x(k+1) - \frac{{x(k){\text{+}}x(k+2)}}{2}\), then the H-convexity of the sequence X at \(t=k+1\) is recorded as \({\hat {d}_H}(X,k+1)\),

$${\hat {d}_H}(X,k+1)=\frac{{x(k+1) - \frac{{x(k)+x(k+2)}}{2}}}{{\sqrt {4+{{\left[ {x(k+2) - x(k)} \right]}^2}} }}$$
(14)

Definition 4

Let the interface layout evaluation criteria M, and the interface N, \(x_{m}^{n}\) is the value of interface layout evaluation for the n \(\left( {n=1,2, \cdots ,N} \right)\) interface of criteria m, Set \({\omega _i}\) as the comprehensive weight of the i-th index. The weighted normalized data series form m criteria is then expressed as,\({X_a}={\omega _a}\left( {x_{a}^{1},x_{a}^{2}, \cdots ,x_{a}^{N}} \right),\)\({X_b}={\omega _b}\left( {x_{b}^{1},x_{b}^{2}, \cdots ,x_{b}^{N}} \right), \cdots ,\)\({X_M}={\omega _M}\left( {x_{M}^{1},x_{M}^{2}, \cdots ,x_{M}^{N}} \right)\). Then the grey H-convexity coefficients of \({X_a}\) and \({X_m}\) at \(t=k\)is,

$${\hat {\gamma }_{H\left( {{X_a},{X_m}} \right)}}\left( k \right)={\text{sgn}}\left( {{{\hat {d}}_H}\left( {{X_a},k} \right),{{\hat {d}}_H}\left( {{X_m},k} \right)} \right)\frac{1}{{1+\left| {\left| {{{\hat {d}}_H}\left( {{X_a},k} \right)} \right| - \left| {{{\hat {d}}_H}\left( {{X_m},k} \right)} \right|} \right|}}$$
(15)

For weighted normalized data series \({X_a}={\omega _a}\left( {x_{a}^{1},x_{a}^{2}, \cdots ,x_{a}^{N}} \right),\)\({X_b}={\omega _b}\left( {x_{b}^{1},x_{b}^{2}, \cdots ,x_{b}^{N}} \right), \cdots ,\)\({X_M}={\omega _M}\left( {x_{M}^{1},x_{M}^{2}, \cdots ,x_{M}^{N}} \right)\), The grey H-convex correlation between sequences \({X_a}\) and \({X_m}\) is denoted by \({\hat {R}_H}\left( {{X_a},{X_m}} \right)\), abbreviated as \({\hat {R}_H}\left( {a,m} \right)\), then,

$${\hat {R}_H}\left( {a,m} \right)=\frac{1}{{n - 2}}\sum\limits_{{k=2}}^{{n - 1}} {{{\hat {\gamma }}_{H\left( {{X_a},{X_m}} \right)}}} \left( k \right)$$
(16)

Application

The primary function of the guide desk is to provide convenient, accurate and friendly medical guidance and services to patients. The system provides personalized guidance processes based on each patient’s condition and treatment plan, including registration, diagnosis and treatment, examination, and guidance.

Samples

Using clustering analysis, 10 interface samples exhibiting high layout heterogeneity were ultimately screened. Figure 7 illustrates one schematic of the interactive interface. Key functions include: intelligent display of patients’ basic identity information, digital presentation of hospital department functionalities and information, and—most critically—generating personalized intelligent consultation guidance plans based on physicians’ prescriptions.

Fig. 7
figure 7

Interface design sample of intelligent medical guidance desk. (Fig. 7. was obtained from Xijing Hospital, Xi’an, China. In addition, considering the privacy of users, the personal information displayed in the case is computer-generated virtual data.).

Full size image

Figure 8 illustrates the schematic process of abstracting real interfaces into rectangular layouts. The original interface (Fig. 8-a) is simplified into a minimum bounding rectangle encompassing all internal elements, producing the rectangular layout interface shown in Fig. 8b.

Fig. 8
figure 8

The abstract representation diagram of the real interface.

Full size image

Abstract all real interfaces into rectangular samples schemes, as shown in Fig. 9.

Fig. 9
figure 9

Abstract rectangular sample schemes.

Full size image

Data source

Aesthetic evaluation values for layout samples were calculated using formulas, while visual cognitive characteristics were measured through eye-tracking experiments. To address potential mismatches between abstract rectangular layouts (Fig. 9) and real interface functionalities, experimental samples were redesigned as shown in Fig. 10. The optimized samples feature a layered design: underlaid with real interfaces and overlaid with semi-transparent abstract rectangular layouts. This hybrid approach ensures participants could intuitively assess rectangular layouts while retaining contextual awareness of the underlying real interfaces during evaluations.

Fig. 10
figure 10

Transparent abstract rectangular stimulus image schematic diagram.

Full size image

A Latin square design was implemented to counteract order effects, with 20 interface samples randomly divided into 10 pairs (1 abstract semi-transparent image and 1 corresponding real interface image). The experimental phases included: (1) 800 ms central fixation. (2) 5-second free-viewing phase (Fig. 10). (3) Task-oriented phase (locating the radiology icon in the Fig. 7). (4) 800 ms central fixation. All images underwent grayscale conversion (Fig. 11) to minimize color interference.

Fig. 11
figure 11

The process of eye movement experiment.

Full size image

Figure 12. shows two experimental scenes in which subjects viewed a transparent abstract rectangular stimulus image and a real interface stimulus image.

Fig. 12
figure 12

Experimental scene.

Full size image

Let \({N_i}\)be the i-th intelligent medical guide interface layout scheme, the final initial evaluation data of interface layout aesthetics and visual cognitive are shown in Table 1.

Table 1 The evaluation results of interface layout aesthetics and visual cognitive.
Full size table

Results and analysis

To Calculate the correlation degree between visual cognitive features and layout aesthetics, a sequence of system characteristic behaviors in terms of gaze duration, gaze count, mean pupil diameter, gaze shift frequency and gaze time percentage for the \({N_{\text{1}}}\)–\({N_{{\text{10}}}}\), denoted by\(Y=\left( {{Y_1},{Y_2},{Y_3},{Y_4},{Y_5}} \right)\). Balance, intensity, simplicity, orderliness and uniformity as comparison sequences, denoted by \(X=\left( {{X_1},{X_2},{X_3},{X_4},{X_5}} \right)\). First, the data in Table 1 were pre-standardized. Next, comprehensive criterion weights were calculated using Eqs. (1)–(13), with results presented in Table 2. Weighted normalized data outcomes are summarized in Table 3.

Table 2 Combination weights of criteria.
Full size table
Table 3 Standardized weighted evaluation results.
Full size table

Calculate the correlation value between visual cognition and layout aesthetics according to Eqs. (14)-(16), the statistical results are shown in Fig. 13.

(1) Correlation between average pupil diameter and layout aesthetics.

Pearson correlation analysis (data normality confirmed by Shapiro-Wilk test, p > 0.05) revealed a negative correlation trend between average pupil diameter and layout aesthetics metrics: (\({\hat {R}_H}\left( {3,1} \right)\)= −0.7404, p < 0.001), (\({\hat {R}_H}\left( {3,2} \right)\)= −0.7380, p < 0.001), (\({\hat {R}_H}\left( {3,3} \right)\)= −0.3706, p < 0.001), (\({\hat {R}_H}\left( {3,4} \right)\)= −0.9845, p < 0.001), (\({\hat {R}_H}\left( {3,5} \right)\)= −0.4910, p < 0.001). That is, average pupil diameter exhibited the strongest correlation with Orderliness, followed by Balance and Density, with weaker correlations to Unity and Simplicity. The high correlation between Orderliness and average pupil diameter suggests that the logical hierarchy of interface element layouts significantly impacts users’ cognitive load. Interface designers should prioritize information hierarchy and guidance cues to reduce cognitive demands and enhance search efficiency. Additionally, Balance demonstrated notable correlation with pupil dynamics, indicating users inherently seek symmetry in horizontal and vertical element distribution. Imbalanced layouts may disrupt visual cognition. Furthermore, Density significantly influenced pupil diameter, implying that excessive elements increase cognitive load.

Fig. 13
figure 13

correlation value(left)and positive and negative correlation(right).

Full size image

(2) The correlation between gaze duration and layout aesthetics.

Pearson correlation analysis (data normality confirmed by Shapiro-Wilk test, p > 0.05) revealed a negative correlation trend between gaze duration and layout aesthetics metrics: (\({\hat {R}_H}\left( {{\text{1}},1} \right)\)= −0.6981, p < 0.001), (\({\hat {R}_H}\left( {{\text{1}},2} \right)\)= −0.6895, p < 0.001), (\({\hat {R}_H}\left( {{\text{1}},3} \right)\)= −0.3379, p < 0.001),(\({\hat {R}_H}\left( {{\text{1}},4} \right)\)= −0.9384, p < 0.001), (\({\hat {R}_H}\left( {{\text{1}},5} \right)\)= −0.4424, p < 0.001). It is based on the size of the correlation ordering:\({\hat {R}_H}\left( {1,{\text{4}}} \right)\)\(>{\hat {R}_H}\left( {1,{\text{1}}} \right)\)\(>{\hat {R}_H}\left( {1,{\text{2}}} \right)\)\(>{\hat {R}_H}\left( {1,{\text{5}}} \right)\)\(>{\hat {R}_H}\left( {1,{\text{3}}} \right)\). Correlation analysis revealed that gaze duration exhibited the strongest correlation with Orderliness, followed by Balance and Density, while Uniformity and Simplicity showed the weakest associations.

(3) Correlation between gaze count and layout aesthetics.

Pearson correlation was used after confirming data normality (Shapiro-Wilk test, p > 0.05). The correlation results show a negative correlation. (\({\hat {R}_H}\left( {2,1} \right)\)= −0.5075, p < 0.001), (\({\hat {R}_H}\left( {2,2} \right)\)= −0.0275, p < 0.001), (\({\hat {R}_H}\left( {2,3} \right)\)= −0.3698, p < 0.001), (\({\hat {R}_H}\left( {2,4} \right)\)= −0.2567, p < 0.001), (\({\hat {R}_H}\left( {2,5} \right)\)= −0.2583, p < 0.001). That is, correlation analysis indicates that Balance and Simplicity exhibit the strongest associations with gaze count, followed by Uniformity and Orderliness, while Density shows the weakest correlation. The highest correlation between gaze count and Balance confirms users’ heightened sensitivity to interfaces with strong stability and symmetrical equilibrium. Concurrently, the role of Simplicity should not be underestimated: reducing design complexity and variability while maintaining effective information communication is critical for ensuring intuitive usability.

(4) Correlation between gaze shifts frequency and layout aesthetics.

Pearson correlation was used after confirming data normality (Shapiro-Wilk test, p > 0.05). The correlation results: (\({\hat {R}_H}\left( {4,1} \right)\)= 0.7427, p < 0.001), (\({\hat {R}_H}\left( {{\text{4}},2} \right)\)= 0.7408, p < 0.001), (\({\hat {R}_H}\left( {{\text{4}},3} \right)\)= 0.6119, p < 0.001), (\({\hat {R}_H}\left( {{\text{4}},4} \right)\)= 0.9800, p < 0.001), (\({\hat {R}_H}\left( {{\text{4}},5} \right)\)= 0.4906, p < 0.001). The frequency of gaze shifts demonstrated the strongest correlation with Orderliness, followed by Balance, Density, and Simplicity, while Uniformity exhibited the weakest association.

(5) Correlation between gaze time percentage and layout aesthetics.

Pearson correlation was used after confirming data normality (Shapiro-Wilk test, p > 0.05).The correlation is obtained by calculating: (\({\hat {R}_H}\left( {5,1} \right)\)= 0.7429, p < 0.001), (\({\hat {R}_H}\left( {5,2} \right)\)= 0.7443, p < 0.001), (\({\hat {R}_H}\left( {5,3} \right)\)= 0.3717, p < 0.001), (\({\hat {R}_H}\left( {5,4} \right)\)= 0.9773, p < 0.001), (\({\hat {R}_H}\left( {5,5} \right)\)= 0.4922, p < 0.001). That is, gaze time percentage correlates most strongly with Orderliness, followed by Density and Balance, while Uniformity and Simplicity show the weakest associations.

Discussion

Model validity and performance

(1) Model validity.

To validate the effectiveness of the proposed model, the same data preprocessing methods were employed. Using the average pupil diameter and interface balance as exemplar metrics, we compared the performance of the original grey correlation, new grey absolute correlation, original grey H-convex model and Random Forest across four evaluation criteria: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), correlation, and statistical significance, with aggregated results presented in Table 4.

The proposed comprehensive evaluation framework was systematically compared and demonstrated significant advantages across multiple key performance metrics, as detailed in Table 4. Compared with the random forest model55, Grey H-convex correlation31, the improvement of the accuracy of this model comes from the collaborative architecture: the game theory integration of BBWM and M-Critical-RP optimizes the allocation of subjective and objective weights, while the curvature correction term in the H-convex model significantly improves the non-monotonic relationship modeling. Regarding error stability, the proposed model achieved a leading Root Mean Square Error (RMSE) of 0.237, indicating 37.8% lower error fluctuation than conventional grey relational models (RMSE = 0.381), confirming its robustness against outliers. Crucially, correlation analysis revealed a strong negative correlation (− 0.7404, p< 0.001) in the proposed model, aligning with the observed phenomenon of “enhanced interface symmetry leading to systematic pupil diameter reduction” in eye-tracking experiments. In contrast, the new grey absolute correlation model22yielded a weaker negative correlation (− 0.3283). However, the traditional grey relational model26 produced a counterintuitive positive correlation (0.6377), exposing its theoretical limitations in handling inverse relationships. Statistical validation via Friedman test (χ²=23.17, p < 0.001) and Nemenyi post-hoc analysis (critical difference CD = 1.24) confirmed fundamental performance differences across all benchmarks at α = 0.05 significance.

Table 4 Comparison of model results.
Full size table

Furthermore, based on the evaluation results from Table 1, line graphs were plotted with interface samples as the X-axis and eye movement and layout aesthetics evaluations as the Y-axis, as illustrated in Fig. 14. Figures 14(a)–14(d) demonstrate that trends in layout aesthetics and visual cognition align closely with the model’s computational outputs.

Fig. 14
figure 14

Visual cognitive features vs. layout aesthetics trend line chart.

Full size image

(2) Model performance.

To validate the model’s performance, BBWM-CRITIC, BWM-CRITIC, and AHP-CRITIC were integrated with the grey H-convex relational model for comparative analysis. The comparative methods were implemented using identical input datasets and standardization protocols, following the same standardized preprocessing procedures as our model. Subjective methods (AHP, BWM) employed the identical expert panel for pairwise indicator comparisons, while objective methods (Entropy, CRITIC) were directly computed from raw data. Additionally, all comparative methods adopted classical implementations without parameter-specific adjustments.The calculation process is as follows: (1) Sample and Data Collection. Data collection involved acquiring layout aesthetic and eye-tracking cognitive data from 50 medical guidance interface prototypes. (2) Calculation of correlation degree. After calculating the comprehensive weight of indicators, the grey H- convex correlation model is used to calculate the correlation degree between \({X_i}\) and ideal sequence \({X_0}\). (3) Accuracy conversion. Through Receiver Operating Characteristic (ROC) curve analysis, it is determined that when the correlation degree \({\hat {R}_H}\)≥ 0.85, it is an effective scheme. The calculation method of accuracy is:

$$Accuracy=\frac{{N\left( {{{\hat {R}}_H} \geqslant 0.85} \right)}}{{{N_{total}}}} \times 100\%$$
(17)

(4) Cross-validation. Divide 50 samples into 5 groups, 10 in each group, and get the overall average accuracy.

Accuracy results across models are illustrated in Fig. 15. The grey H-convex relational model based on the BBWM-M-CRITIC-RP method achieved an overall average accuracy of 88% (± 1.8% SD), followed by BBWM-CRITIC with accuracy above 0.8, while other methods averaged around 0.6. The results indicate that using the BBWM-CRITIC method may increase errors, likely attributable to limitations in CRITIC’s normalization process and linear correlation-based weighting. As sample sizes grow, the accuracy of the AHP-CRITIC method declines below 0.6. This degradation stems from the escalating complexity of pairwise comparisons among criteria, which challenges experts’ ability to maintain consistent and precise judgments.

Fig. 15
figure 15

Comparison of model accuracy.

Full size image

We also evaluated the computation time of the four models. As shown in Fig. 16, under identical sample sizes, the execution time increases with the number of indicators. The BBWM-M-CRITIC-RP method enhances decision-making accuracy but requires the longest computation time due to its complex computational procedures and formulas. In contrast, AHP-CRITIC and BWM-CRITIC involve simpler processes, achieving computation times within 5 min.

Fig. 16
figure 16

Comparison of model computation time.

Full size image

Correlation between layout aesthetics and visual cognition

This study reveals the systematic coupling mechanisms between layout aesthetics and visual cognition in medical guidance interfaces through multidimensional correlation analysis. From the perspective of visual information processing theory, the negative correlation between balance and gaze duration (r= −0.6981) reflects the profound influence of Gestalt’s “law of Prägnanz”56 (Ma et al., 2024)—symmetrical spatial distribution of interface elements accelerates the formation of holistic perceptual schemas, thereby reducing cognitive resource consumption in local detail scanning. Additionally, strong negative correlations between density/order and gaze duration (r = −0.6895, r = −0.9384) provide new theoretical support for attention allocation strategies in visual interface design.

The significant correlation between density and pupil dilation changes (r= −0.7380) confirms the “information density threshold effect” in cognitive load theory, where marked pupil expansion indicates cognitive overload compensation, demonstrating isomorphism with the critical inflection phenomenon in interface complexity-efficiency curves57. Furthermore, the marked correlations between balance/orderliness and pupil changes (r = −0.7404, r = −0.9845) establish novel evaluation criteria for applying cognitive load theory to interface design.

The positive reinforcement relationship between order and gaze shift frequency (r= 0.9800) elucidates the guiding efficacy of visual hierarchy planning on ocular patterns, aligning with the “visual hierarchy gradient theory” regarding information layering and scanpath matching58 (Gomez et al., 2021). The linear correlation between uniformity and gaze time percentage (r= 0.4922) confirms that visual coherence optimizes attentional resource allocation by reducing Gestalt closure costs59. These findings deepen the mechanistic understanding of aesthetic-cognitive mapping and provide a theoretical foundation for adaptive interface design in smart medical systems through dynamic feedback modeling between layout parameters and cognitive metrics.

Limitations

1) One notable aspect is the complexity of the weight acquisition method, which, to a certain extent, leads to a slight increase in calculation time. Efforts will be directed towards streamlining and simplifying the weight assignment steps in order to mitigate this issue.

2) Interface layout is an important factor affecting cognitive efficiency, but it is also influenced by other factors. For example, the influence of interface style, color, technology and other factors. Future endeavors will center on further addressing the limitations in this research.

3) This study focuses solely on five eye movement metrics, while other metrics (such as gaze path length and gaze hotspot distribution60,61) may also influence interface layout aesthetics. Future research could further explore the potential of additional metrics.

4) While layout aesthetics and visual cognition demonstrate unique advantages for infrequently used medical interfaces, it is noteworthy that other dimensions (e.g., environmental dynamics, cultural symbolism, technological inclusivity) may also influence interface design, constituting a critical research agenda for future investigations.

Conclusion

This article studies the evaluation method of public guidance service interface design based on human aesthetic needs and cognitive characteristics, achieving the evaluation of interface layout aesthetics and measurement of user visual cognitive characteristics, and solving the quantification problem of the mapping relationship between the two. Taking the personal guidance interface of the intelligent medical guidance desk as an example, providing a new method attempt for the evaluation of infrequent contact interfaces.

1) In the theoretical ___domain of visual display design, this study integrates mathematical modeling and eye-tracking physiological experiments. By employing a more objective quantitative methodology, it elucidates the coupling relationship between interface layouts and human visual cognition. Building upon this foundation, we propose a scientific evaluation method that incorporates users’ visual cognitive characteristics, thereby providing methodological references for visual display design. Specifically, we have discovered several interesting phenomena. For public guidance service interfaces, the order has the most significant impact on user visual cognition, with the highest correlation, next is the balance. Density is the most important indicator affecting the fixation count. The impact of uniformity and simplicity on visual cognition is not significant.

2) An improved grey H-convex correlation model was proposed. This study introduces the BBWM and M-CRITIC-RP methods and proposes an improved grey H-convex correlation model to quantify the mapping relationship between user visual cognition and layout aesthetics. By comparing the effectiveness and performance of several existing models, the accuracy of this paper is higher than 88%, which is superior to existing methods.