Introduction

Urban flooding is a highly detrimental natural phenomenon that significantly impacts nearby communities and infrastructure. It induces morphological alterations by the transportation of silt and soil1, leading to the destruction of agricultural land and substantial economic repercussions2,3,4. In recent years, there has been an increase in the frequency of urban floods and flash floods caused by intense precipitation, rapid snowmelt, or the failure of dams. This trend may be attributed to the effects of climate change5. The worldwide risk of flooding has seen a notable rise of over 40% over the last two decades. This escalation is anticipated to persist due to global climate change and urbanization. Notably, the most substantial increases in flood risk are observed in the United States, Asia, and Europe, as shown by sources6,7. Between 1995 and 2023, an estimated 109 million individuals around the globe were impacted by flooding, resulting in an annual economic loss of roughly USD 75 billion. According to scholarly sources, Iran is one of the regions in Asia highly susceptible to urban floods8. In recent years, including in 2017 and in April and December 2019, Iran had severe flash floods that resulted in significant economic repercussions due to the destruction of agricultural land, bridges, tunnels, highways and loss of human lives.

To mitigate the impact of floods, it is necessary to optimize the arrangement of watershed management strategies such as wet ponds, detention dams, and early flood warning systems9. The FSM has emerged as a significant technology now extensively used for this objective10,11,12,13. While high precipitation is the primary factor contributing to flood occurrences in Iran, it is essential to note that river basins’ hydrological and geomorphological attributes may also influence flood characteristics. Consequently, various basins may display distinct flood responses to a given intensity of rainfall event14. Various methodologies have been used in the field of the FSM, including statistical analysis15, geographical information system (GIS) approaches, decision tree, multi-criteria decision model13,16, hydrological and hydrodynamic models, and ANN models.

The ANN technique has been widely utilized in various hydrological applications, such as river flow forecasting , rainfall-runoff modeling17, water quality modeling18, prediction of suspended sediment load in rivers19, determination of aquifer parameters20, prediction of salinity in water resources21, and natural hazard modeling22. The ANNs have shown considerable efficacy in prediction and are regarded as a non-parametric approach. Nevertheless, it should be noted that ANNs are considered black-box models. The optimization process of ANNs requires several iterations to determine the optimal weights for each input and the appropriate number of hidden layers. This iterative approach may be time-consuming, as previous studies show23.

The purpose of this study is to enhance the accuracy and efficiency of FSM through the innovative application of nature-inspired optimization algorithms combined with ANNs. Traditional flood prediction models, including statistical and physical methods, often face limitations in handling large, complex datasets or in adapting to changing environmental conditions. This research addresses these gaps by introducing evolutionary algorithms such as the BHA, FSA, HBO, and MVO, which simulate natural evolutionary processes to iteratively improve prediction accuracy.

There are several optimization algorithms, such as the BHA, FSA, HBO, and MVO. The BHA known for its efficiency in handling complex, nonlinear optimization problems. BHA mimics the behavior of black holes in space to find optimal solutions and is particularly effective in global optimization tasks with large search spaces. FSA is a newer approach that focuses on improved convergence in multi-dimensional search spaces. FSA has been shown to offer better balance between exploration and exploitation, which is crucial for dynamic flood prediction models. HBO is an efficient optimization algorithm that focuses on minimizing computational costs while maintaining a high accuracy rate. HBO’s ability to process large datasets quickly makes it ideal for real-time flood prediction applications. MVO algorithm is based on the idea of multiple universes searching for the best solution, which promotes a higher degree of solution diversity and has been shown to outperform other optimization techniques in multi-objective optimization problems.

Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) are indeed popular choices for optimization, especially in machine learning and predictive modeling24. However, both have well-known limitations. The GA tends to struggle with premature convergence, especially in highly complex, multi-modal landscapes, which can lead to suboptimal solutions. While efficient, PSO may not always strike the right balance between exploration (searching for new solutions) and exploitation (refining existing solutions), especially in dynamic problems like flood prediction where conditions can change rapidly. BHA, FSA, HBO, and MVO have been selected based on prior studies that demonstrated their superior performance in tasks similar to flood prediction (such as geospatial data modeling or environmental optimization). Benchmarking these algorithms against GA or PSO in preliminary experiments could show they provide better results in terms of prediction accuracy, convergence speed, or handling complex, multi-dimensional data.

The Multi-Layer perceptron (MLP) model is a supervised classifier and simulator that utilizes back-propagation. On the other hand, the SOM and FART models include both unsupervised and supervised clustering and classifier capabilities. These algorithms have been extensively used for land use/cover categorization; however, their application in the FSM context seems limited based on our current understanding. Hence, a consensus and standardized principles for implementing FSM have yet to be universally established. Supervised learning algorithms can generate the FSM as either a complicated classification, which involves categorizing instances into two distinct groups, namely flood and non-flood, or as a soft classification, which assigns a probability value between 0 (indicating no likelihood of flooding) and 1 (representing a 100% likelihood of flooding) to indicate the chance of flooding. In the process of classification, the whole territory is regarded as a flood-prone area, regardless of whether there is a likelihood of flooding in the area (e.g., at higher altitudes where floods are improbable). The likelihood map generated ranges from 0 to 1 and is divided into flood and non-flood. It does not take into account the non-flood region. Please refer to the following sources for further information:25,26,27.

Hence, the primary aim of this work was to evaluate the integration of the algorithms mentioned above to enhance the FSM accuracy. The evaluation of the model’s performance was conducted by using metrics such as MAE, MSE, and receiver ROC analysis, which includes the calculation of the area under the curve (AUC). Ultimately, FAM’s most optimal modeling strategy was determined based on its success and prediction rates. The findings of this research may serve as a valuable reference for using ANN algorithms in generating flood susceptibility maps, hence enhancing the efficacy of planning procedures.

The novelty and originality of this work lies in the integration of multiple optimization techniques to refine ANN-based models for flood susceptibility prediction, something not commonly explored in flood management studies. The Unlike previous research that focuses on single optimization approaches, this study evaluates four different algorithms, offering a more comprehensive and adaptable solution. While algorithms like GA and PSO are commonly used, BHA, FSA, HBO, and MVO are chosen for their superior performance in optimizing multi-dimensional, complex, and dynamic problems. These algorithms have been shown to converge more effectively in high-dimensional spaces, offering better exploration and exploitation capabilities than traditional approaches. Additionally, by testing the model on real-world flood data from the Fars region in Iran, this work not only contributes to advancing computational techniques in flood risk assessment but also provides practical insights for urban planners, policymakers, and disaster management agencies in addressing flood hazards more effectively. The most important question is: can the integration of evolutionary algorithms with artificial neural networks significantly improve the accuracy of flood susceptibility mapping and offer optimized flood management strategies compared to conventional methods? By answering this question, this study contributes to the development of more accurate, adaptive, and efficient models for urban flood risk management, offering valuable insights for real-time decision-making in flood preparedness and emergency response.

Description of study area

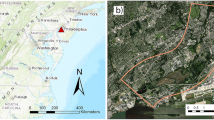
Fars Province in Iran exhibits a complex interplay of geological and hydrological features (Fig. 1), shaped by tectonic activities, diverse topography, and climatic conditions. The western part of Fars Province is dominated by the Zagros Mountain range, a significant geological feature resulting from the collision of the Arabian and Eurasian tectonic plates28. The Zagros Mountains showcase complex folding, faulting, and uplifted rock formations. It experiences ongoing tectonic activity, leading to the formation of intricate geological structures such as anticlines and synclines. The geological complexity is a result of the collision and convergence of tectonic plates. The region contains diverse sedimentary rock formations, including limestone, shale, and sandstone. These formations provide insights into the geological history and past environmental conditions of Fars Province29. While not as prevalent as the Zagros Mountains, there are areas in Fars Province that have experienced volcanic activity. Volcanic rocks and features, such as lava flows and volcanic cones, contribute to the geological diversity. Sedimentary rocks in the selected study area may contain fossilized remains, offering valuable information about past marine and terrestrial life. Fossil deposits contribute to understanding the region’s Paleo environmental history. Certain areas in Fars Province, especially where limestone is abundant, exhibit karst landscapes. Karst features, including sinkholes, caves, and underground drainage systems, influence both geological and hydrological aspects. As hydrological description of the study area it is traversed by several rivers, with the Kor River being one of the major watercourses. The topography, influenced by the Zagros Mountains, contributes to the formation of river systems with distinct drainage patterns. The region has significant groundwater resources stored in aquifers. Groundwater is a crucial source for irrigation and domestic use, particularly in areas where surface water may be limited. The presence of karst landscapes affects hydrogeology, influencing the movement and storage of groundwater. Karst regions may feature underground caves and conduits that impact water flow. The topography, with mountainous terrain and steep slopes, can contribute to flash flooding during intense rainfall events. Rapid runoff from the mountains can lead to sudden increases in river flows downstream. On the other hand, changes in climate patterns can impact both geological and hydrological processes30,31,32. Adapting to climate change is crucial for sustainable water resource management.

Fig. 1
figure 1

Geographical ___location of the study area in Fars Province (a) and Iran country (b).

Full size image

Established database

Previous research and expert opinions highlight eight key factors influencing flood risk. Employing ArcGIS 10.2, slope layers were generated from the Digital Elevation Model (DEM) layer. DEM data is included to capture the topographic variations of the region, which play a significant role in flood behavior by influencing water flow and accumulation. DEM data has been widely used in flood studies to model terrain and simulate hydrological processes33. The NDVI layer, derived from Landsat satellite images captured by the Landsat 8 ETM sensor on July 12th, 2021, was produced using ArcGIS 10.2 software downloaded from the USGS website (https://www.usgs.gov). Also, bands 4, and 5 were used to create this layer. Similarly, based on the information available in the geographic database, a geological map with a scale of 1:25,000 was extracted for the study area. This map was used to produce a lithological layer; a layer that includes the lithological characteristics and various geological compositions of the area and plays an important role in the hydrological behavior and flood zoning. Also, in order to investigate the effect of active geological structures, spatial data related to the existing faults in the area were processed in a GIS environment. Using spatial analysis tools, a distance-to-fault map was produced; in this step, the distance of each point from the study area to the nearest fault was calculated and a continuous layer was prepared for spatial analysis. Precipitation layers were generated using the IDW model, leveraging long-term average yearly precipitation data from rain gauge stations in Fars Province. In this study, a database comprising 326 observed flood points (228 for training and 98 for testing) was compiled from documented flood events in Fars Province. The dataset underwent preprocessing steps, including validation, outlier removal, and normalization to ensure consistency across spatial layers. These points were then randomly divided into training and testing subsets to support robust model development and evaluation. These factors are selected based on expert opinions and previous studies34 that have established their significance in flood risk assessment. The contributing factors include: (a) rainfall, (b) elevation, (c) NDVI, (d) slope, (e) aspect, (f) geology, (g) land use, and (h) distance to rivers. Elevation influences the flow and accumulation of water, with higher elevations generally being less prone to flooding. Rainfall is a direct driver of flooding, with heavy rainfall events being one of the leading causes of floods. Slope affects water runoff; steeper slopes often lead to faster water flow, increasing the risk of flooding in certain areas. NDVI provides insights into vegetation cover, which influences water infiltration and runoff, helping to reduce flood risks. Aspect describes the orientation of terrain slopes, which can affect water flow patterns. Geology impacts soil permeability, which in turn affects water absorption rates and flood risk. Land use categorizes areas based on human development, which can increase impervious surfaces, exacerbating flood risks. River data reflects the characteristics of rivers and their potential to overflow, directly influencing flood susceptibility. Information on the onset of floods in Fars province was integrated into the datasets by combining data from multiple layers (Figs. 2, 3, 4 and 5). Criteria for flood categorization and variables impacting these categories were identified. ArcGIS 10.2, SPSS 20, and MATLAB software were employed for model implementation and effectiveness evaluation.

Fig. 2
figure 2

(Source: By authors, 2023).

The potential of the geographical environment of Fars province against floods

Full size image
Fig. 3
figure 3figure 3figure 3figure 3

Layers created based on the desired factors for analysis.

Full size image
Fig. 4
figure 4

Input variables’ histogram.

Full size image
Fig. 5
figure 5

Input and output variables’ Andrew’s plot.

Full size image

Methodology

In this study, the dataset was divided into 70% for training and 30% for testing, a commonly used ratio in flood susceptibility mapping and machine learning applications. This split ensures a sufficient amount of data for model learning while preserving an independent dataset for evaluation. A larger training set (70%) ensures that the model learns effectively from a substantial portion of the data, capturing complex relationships among flood-conditioning factors. The 30% test set provides an independent dataset to evaluate model performance and prevent overfitting. To ensure that the model does not overfit the training data, evaluation metrics such as MSE, MAE, and AUC were used to validate the model’s performance on the test set. These metrics provide insights into the model’s predictive accuracy, error distribution, and classification performance. MSE measures the average squared difference between actual and predicted values. It emphasizes larger errors more due to squaring, making it sensitive to outliers. A lower MSE indicates a better-fitting model.

$$MSE=\frac{1}{n}\sum_{i=1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}$$
(1)

where \({y}_{i}\) actual observed value, \({\widehat{y}}_{i}\) is predicted value, and n is the total number of observations.

MAE calculates the average absolute differences between observed and predicted values. Unlike MSE, it treats all errors equally, making it less sensitive to large errors.

$$MAE=\frac{1}{n}\sum_{i=1}^{n}\left|{y}_{i}-{\widehat{y}}_{i}\right|$$
(2)

AUC measures the classifier’s ability to differentiate between flood-prone and non-flood-prone areas. The Receiver Operating Characteristic (ROC) curve plots the True Positive Rate (TPR) against the False Positive Rate (FPR) at different threshold values, and AUC represents the area under this curve.

$$AUC={\int }_{0}^{1}TPR(FPR)d(FPR)$$
(3)

where:

$$TPR=\frac{TP}{TP+FN}$$
(4)
$$FPR=\frac{FP}{FP+TN}$$
(5)

TP, FP, TN, FN are True Positives, False Positives, True Negatives, and False Negatives. A higher AUC (closer to 1) indicates better classification performance, while a value near 0.5 suggests random classification.

Training a MLP with nature-inspired optimization algorithms for flood assessment involves using an optimization algorithm to adjust the weights and biases of the neural network to improve its performance in predicting flood-related outcomes. Nature-inspired optimization algorithms are optimization techniques that draw inspiration from natural phenomena or processes to find optimal solutions. The general steps are illustrated here.

  • Identify the specific flood assessment problem you want the MLP to address. This could include predicting river discharge, flood risk, or other relevant parameters based on input features.

  • Collect and preprocess the dataset for training and testing the MLP. The dataset should include historical data on relevant variables such as rainfall, river levels, land use, and any other factors influencing floods.

  • Define the architecture of the MLP, including the number of layers, neurons in each layer, and activation functions. The input layer should correspond to the features in your dataset, and the output layer should represent the flood-related output.

  • Choose a nature-inspired optimization algorithm for training the MLP. In the case of current study, four specific hybrid methods, namely the BHA, FSA, HBO, and MVO, were employed.

  • Define a fitness function that quantifies how well the MLP performs on the flood assessment task. This function evaluates the model’s predictions against the actual outcomes in the training dataset.

  • Initialize the weights and biases of the MLP randomly or using a predefined strategy.

  • Implement the optimization algorithm’s iteration loop to update the weights and biases of the MLP. The optimization algorithm evaluates the fitness of the MLP based on the defined fitness function.

  • Set convergence criteria to determine when to stop the training process. This could include reaching a certain number of iterations or achieving a satisfactory level of performance.

  • Evaluate the trained MLP on a separate testing dataset to assess its generalization performance. Validate the model’s effectiveness in predicting flood-related outcomes.

  • Fine-tune hyperparameters, such as learning rates or swarm sizes, to optimize the performance of the trained MLP.

Once satisfied with the MLP’s performance, deploy the model for flood assessment tasks. Note that the success of this approach depends on the choice of the optimization algorithm, the quality and representativeness of the dataset, and the appropriateness of the MLP architecture. Data records with more than 20% missing values were removed to maintain reliability. For continuous variables such as rainfall, elevation, and slope, missing values were imputed using the mean or median of surrounding data points. For spatial data, including NDVI, rainfall, and river data, missing values were estimated using inverse distance weighting (IDW) and kriging interpolation to maintain spatial consistency. Continuous numerical variables (e.g., rainfall, slope) were normalized using min–max scaling to ensure uniformity across features. Categorical variables (e.g., land use, geology) were encoded using one-hot encoding to be compatible with machine learning models. Discrepancies between data sources (e.g., mismatched rainfall values between meteorological stations and satellite data) were resolved by cross-referencing official records and historical flood reports.

As stated, in current study, multiple solutions were used to generate flood susceptibility maps, including a comprehensive set of eight distinct influencing parameters. After selecting the MLP technique, we evaluated all eight contributing elements to determine their impact on flood occurrence. In this study, we used four distinct supervised machine learning methodologies, namely the BHA, FSA, HBO, and MVO, to perform network categorization inside the framework of FSM. The research used a technique consisting of three interconnected steps. The first phase included gathering and processing the dataset, which impacted the study. The subsequent phase included modeling techniques, whereby elements of significance were tested using sensitivity analysis. The classification process used BHA-MLP, FSA-MLP, HBO-MLP, and MVO-MLP methods. During the third stage of the study, the model’s outputs were classified into two distinct categories, namely flood and non-flood, using the classification outcomes. Subsequently, the results were subjected to calibration and validation processes to determine the success and projection rates, respectively.

Multi-layer perceptron (MLP)

Using a multi-layer perceptron, consisting of three or more layers, enables the effective isolation of nonlinear data. This is particularly useful in analyzing the intricate link between flood observation data and the many influencing elements contributing to its occurrence. The present approach involves transmitting input layer signals via nodes to the subsequent layer in a unidirectional pathway35. The signal undergoes adjustments as it traverses through various nodes, determined by the allotted weight associated with each connection36. The receiving node, connected to the preceding layer, combines the weighted signals from all nodes. The weight assigned to a node is computed using the formula presented by Nourani, Pradhan35.

$${net}_{j}=\sum {\omega }_{ji}{o}_{i}$$
(6)

where \({\omega }_{ji}\) represents the weights between node i and node j, and oi is the output from node i. The output from a given node j is then computed from:

$${o}_{j}=f({net}_{j})$$
(7)

The function f represents either a nonlinear sigmoid or linear function that processes the weighted total of the inputs before transmitting the signal to the subsequent layer.

Moreover, the signal is responsible for constituting the network’s output once it reaches the output layer. In the context of traditional complex classification, when pixels are exclusively assigned to a single class, the output of a single node is assigned a value of 1. In contrast, the other nodes in the output layer are assigned a value of zero. As mentioned, the network is presented with a training pattern, and the signals are propagated forward for the MLP. The network output is then compared to the intended output, which consists of a set of training data associated with recognized classes, and the resulting error is determined. Subsequently, the mistake mentioned above is transmitted backward through the neural network, and the weights of the connections, initially assigned randomly, are adjusted according to the generalized delta rule, which governs the modification process.

$$\Delta {\omega }_{ji}\left(n+1\right)=\eta \left({\delta }_{j}{o}_{i}\right)+\alpha \Delta {\omega }_{ji}\left(n\right)$$
(8)

In the above equation, η represents the learning rate parameter, \({\delta }_{j}\) denotes an index that quantifies the rate of change in the error, and α represents the momentum parameter. The process of transmitting signals in a forward direction and propagating the mistake in a backward direction is repeatedly performed until the network’s error is decreased or reaches an acceptable value. Furthermore, the neural network can acquire knowledge via the iterative adjustment of its adaptive weights. In the current investigation, the weights obtained from training the ANN were used to determine the contribution and relevance of each of the eight components. These weights were then used to generate the study region’s FSM, as seen in Fig. 6.

Fig. 6
figure 6

An MLP structure for the current article.

Full size image

Black hole algorithm (BHA)

The Black Hole Algorithm is a metaheuristic algorithm that operates on a population level, drawing inspiration from the gravitational pull of black holes and introduced by Hatamlou37. The starting locations of the candidate solutions, represented as stars, are randomly assigned within the search space \({\overrightarrow{x}}_{i}\in {\mathbb{R}}^{n}\text{with }i=1, 2, \dots , m,\) where n denotes the number of design variables, and m represents the number of stars. The objective function value is computed for all stars in the population, and the star with the highest objective function value is chosen as the black hole.

The motion of stars towards a black hole is attributed to the gravitational pull exerted by the black hole, which can absorb surrounding matter. Consequently, the ___location of each star is updated in the following manner:

$${\overrightarrow{x}}_{i}^{(t+1)}={\overrightarrow{x}}_{i}^{t}+\sigma \left({\overrightarrow{x}}^{*}-{\overrightarrow{x}}_{i}^{t}\right)$$
(9)

Let \({\overrightarrow{x}}_{i}^{t}\) represent the positional coordinates of the i-th star at iteration t. Similarly, let \({\overrightarrow{x}}^{*}\) denote the positional coordinates of the black hole inside the search space. Additionally, let \(\sigma \sim U\left(\text{0,1}\right)\) be a random variable following a uniform distribution between 0 and 1. Observing that the value of σ varies for each star and iteration is essential.

A spherically-shaped border referred to as the “event horizon” surrounds the black hole. Any star that crosses this barrier will be gravitationally captured by the black hole, leading to the generation of a new star inside the search region to begin a fresh exploration. The calculation of the radius, denoted as r, for the event horizon of the BHA is determined using the following mathematical formulation:

$$r=\frac{{f}^{*}}{\sum_{i=1}^{m}{f}_{i}}$$
(10)

The symbols \({f}^{*}\) and \({f}_{i}\) represent the objective function values of the black hole and the i-th star, respectively. When the separation between a star and a black hole is less than the radius r, the star undergoes gravitational collapse, forming a new star. The subsequent cycle occurs after the relocation of all celestial bodies. In broad terms, the concept of the BHA aims to preserve population variety while forming new black holes and mitigating the risk of stars being stuck in local optima. This technique ultimately contributes to both local exploitation and worldwide exploratory searches.

Furthermore, a binary vector is used as a solution representation when selecting a particular feature. In this vector, a value of 1 indicates that a feature will be chosen to form the new dataset, while 0 signifies that the feature will not be included. To facilitate the creation of the binary vector, Eq. (12) was used, which effectively constrains the newly generated solutions to only binary values.

$$S\left({x}_{ij}^{t}\right)=\frac{1}{1+{e}^{-{x}_{ij}^{t}}}$$
(11)
$$x_{ij}^{t} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\;S\left( {x_{ij}^{t} } \right) > \gamma } \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(12)

The variable γ follows a uniform distribution between 0 and 1. The notation \({x}_{ij}^{t}\) represents the j-th decision variable of the i-th star at iteration t.

Future search algorithm (FSA)

The heuristic search algorithm starts with a randomly selected population and iteratively refines it based on optimal solutions from the initial selection. Since the optimal population may be far from the starting point, multiple iterations are required for the FSA to reach the global optimum. With each repetition, FSA effectively updates and improves the population. Within each FSA, a local best population exists for different variables, while the global optima are determined throughout iterations. FSA updates the population based on the highest-quality neighboring population, with the remaining individuals adjusting only according to the global best optimum.

The random initialization may be generated using Eq. (13), where S represents the solution, k represents the current solution, d represents the dimension of the search space or the number of nations, and \({L}_{b}\) and \({U}_{b}\) represent the lower and upper bounds of the variables in the optimization problem.

$$S\left(k,:\right)={L}_{b}+\left({U}_{b}-{L}_{b}\right)\cdot *rand\left(1,d\right)$$
(13)

The objective function of each initial population is defined as a local solution (LS), and the best of all is defined as a global solution (GS). The FSA uses both LS and GS to find the optimal solution. The exploitation feature of the FSA is modeled using Eq. (14) by using the best-influenced person or LS of each country.

$${S\left(k,:\right)}_{L}=\left(LS\left(k,:\right)-S\left(k,:\right)\right)*rand()$$
(14)

The next step is to characterize the exploration feature of the FSA, which uses the global influencer person or GS, as given in Eq. (15).

$${S\left(k,:\right)}_{G}=\left(GS-S\left(k,:\right)\right)*rand()$$
(15)

By examining individuals impacted by local and global factors on a worldwide scale, each person has the potential to alter their approach to life or existing variables. This phenomenon is represented by Eq. (16), which incorporates the solutions influenced by both local and global factors.

$$S\left(k,:\right)=S\left(k,:\right)+{S\left(k,:\right)}_{L}+{S\left(k,:\right)}_{G}$$
(16)

At this stage, the FSA updates the GS and LS and is used to modify the initial population using Eq. (17), and this is the primary characteristic of the FSA to define its exploration ability compared to other HSA.

$$S\left(k,:\right)=GS+\left(GS-LS\left(k,:\right)\right)*rand()$$
(17)

The procedure mentioned above is iteratively executed until the convergence requirement is met. This is achieved by calculating the values of LS and GS using Eqs. (14) and (15), respectively. Subsequently, a new solution is determined using Eq. (17), and the values of LS, GS, and the starting population from Eq. (13) are updated using Eq. (17),38.

Multiverse optimizer (MVO)

The concept of MVO draws its primary inspiration from the multiverse theory within the field of physics 39. The fundamental constituents of the multiverse hypothesis include a black hole, a wormhole, and a white hole. Like other evolutionary algorithms, the optimization process begins by generating an initial population of solutions and aims to enhance these solutions over a predetermined number of iterations. Consistent with these theoretical frameworks, it is possible to conceptualize each solution of the optimization issue as a distinct universe, whereby each item inside this universe represents a single variable about a particular problem.

The universes are categorized according to their respective inflation rates within each iteration. Afterward, the roulette wheel selection process chooses one universe as the white hole. The approach is shown in Eq. (18).

$$U=\left[\begin{array}{c}{x}_{1}^{1}\\ {x}_{2}^{1}\\ \begin{array}{c}\vdots \\ {x}_{n}^{1}\end{array}\end{array}\begin{array}{c}{x}_{1}^{2}\\ {x}_{2}^{2}\\ \begin{array}{c}\vdots \\ {x}_{n}^{2}\end{array}\end{array}\begin{array}{c}\dots \\ \dots \\ \begin{array}{c}\ddots \\ \dots \end{array}\end{array}\begin{array}{c}{x}_{1}^{d}\\ {x}_{2}^{d}\\ \begin{array}{c}\vdots \\ {x}_{n}^{d}\end{array}\end{array}\right]$$
(18)

where U represents the population matrix of size n × d containing the set of universes, d signifies the objects’ number (i.e., decision variables) and n signifies the universe’s number (i.e., candidate solutions). Typically, the object j in solution i is randomly generated as follows:

$${x}_{i}^{j}={lb}_{j}+rand()\%\left(\left({ub}_{j}-{lb}_{j}\right)+1\right) \forall i\in \left(\text{1,2},\dots ,n\right)\Lambda \forall \in \left(\text{1,2},\dots ,n\right)$$
(19)

where [\({lb}_{j}\), \({ub}_{j}\)] denotes the discrete lower, as well as upper bound limits of object j, and rand() denotes a function, which generates a discrete random distribution number in the range (1, 2, . . . , MAX_INT), MAX_INT, where MAX_INT is the maximum integer number that the computer can generate.

In each iteration, each decision variable i in the solution j (i.e., \({x}_{i}^{j}\)) (i.e., the solution has the black hole) is assigned by value using two options, including a) the value is selected from its historical solutions like \({x}_{i}^{j}\in \left({x}_{i}^{1}, {x}_{i}^{2},\dots ,{x}_{i}^{j-1}\right)\) using the roulette wheel selection, and b) the value remains unchanged. This is formulated as shown in Eq. (20).

$${x}_{i}^{j}=\left\{\begin{array}{c}{x}_{m}^{j} {rand}_{1}<Norm\left({U}_{i}\right)\\ {x}_{i}^{j} {rand}_{1}\ge Norm\left({U}_{i}\right)\end{array}\right.$$
(20)

In this context, the notation \({x}_{i}^{j}\) represents the jth variable of the ith universe, where \({U}_{i}\) signifies the ith universe. The term Norm(\({U}_{i}\)) refers to the normalized inflation rate of the ith world. Additionally, rand1 represents a random integer drawn from the interval [0,1]. Lastly, \({x}_{m}^{j}\) means the jth variable of the mth universe, chosen using a roulette wheel selection method. To explore the potential impact of wormholes on the pace of inflation and the diversity of universes, let us consider the hypothetical scenario where the existence of wormholes is acknowledged inside the universe, and the most optimized world produced so far is taken into account. This mechanism is stated in the following manner:

$$x_{i}^{j} = \left\{ {\begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}c} {x_{j} + TDR \times \left( {\left( {ub_{j} - lb_{j} } \right) \times r_{4} + lb_{j} } \right)\quad \quad r_{3} < 0.5} \\ {x_{j} - TDR \times \left( {\left( {ub_{j} - lb_{j} } \right) \times r_{4} + lb_{j} } \right)\quad \quad r_{3} \ge 0.5} \\ \end{array} ~~~~~~r_{2} < WEP} \right.} \hfill \\ {x_{i}^{j} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad r_{2} \ge WEP} \hfill \\ \end{array} } \right.$$
(21)

The variable \({x}_{j}\) represents the jth universe variable that has been created up to this point. The symbol \({lb}_{j}\) denotes the minimum limit of the jth parameter, while ubj denotes the maximum limit of the jth parameter. The term \({x}_{i}^{j}\) refers to the jth parameter of the ith universe. Additionally, \({r}_{2}\), \({r}_{3}\), and \({r}_{4}\) represent random integers selected from the interval [0, 1]. Based on this formulation, it can be inferred that the presence of a wormhole (WEP) and the pace at which it allows for travel (TDR) are significant coefficients. The coefficients may be expressed using the following formula:

$$WEP=min+{c}_{i}\times \left(\frac{max-min}{{m}_{i}}\right)$$
(22)
$$TDR=1-\frac{{{c}_{i}}^{1/p}}{{{m}_{i}}^{1/p}}$$
(23)

where min and max represent constant pre-defined values, \({c}_{i}\) denotes current iteration, \({m}_{i}\) is the maximum iterations’ number, and p is the exploitation accuracy with iterations. When p is more significant, the exploitation will be faster and more precise.

Heap based optimizer (HBO)

The HBO draws inspiration from the social behavior shown by human beings40. One kind of interpersonal engagement among individuals may be seen inside organizational settings when individuals are organized into teams and structured hierarchically to accomplish a designated objective. This phenomenon is often called the corporate rank hierarchy (CRH). The CRH (Corticotropin-Releasing Hormone) is shown in Fig. 7a. The HBO algorithm exhibits a unique approach by using the CRH methodology. Figure 7b illustrates an instance of a ternary (3-ary) min-heap. The HBO algorithm included three distinct categories of employee actions. There are three sorts of interactions that may be seen within an organizational context: (1) the relationship between subordinates and their immediate superiors, (2) the interaction among colleagues or co-workers, and (3) the individual’s self-contribution.

Fig. 7
figure 7

Partial examples of corporate rank hierarchy (a) and 3-ary min-heap (b).

Full size image

The mapping of the heap concept is divided into several steps:

Modeling the corporate rank hierarchy

The technique of CRH modeling using a heap data structure is shown in Fig. 8. In this representation, \({x}_{i}\) represents the ith search agent inside the population. The curvature seen in the objective space delineates the form of the hypothetical objective function, while the search agents are positioned on the fitness landscape based on their preferences.

Fig. 8
figure 8

An illustration of the modeling of the CRH with min-heap.

Full size image

Mathematically modeling the collaboration with the boss

In a centralized organizational framework, the enforcement of rules and policies emanates from higher hierarchical levels, with subordinates being obligated to adhere to the directives of their immediate superiors. The mathematical representation of this phenomenon involves the updating of the agent’s ___location for each search in the following manner:

$${x}_{i}^{k}\left(t+1\right)={B}^{k}+\gamma {\lambda }^{k}\left|{B}^{k}-{x}_{i}^{k}\left(t\right)\right|$$
(24)
$$\gamma = \left| {2 - \frac{{\left( {t \bmod \frac{T}{C}} \right)}}{\frac{T}{4C}}} \right|$$
(25)
$${\lambda }^{k}=\left(2r-1\right)$$
(26)

where t is the current iteration, k is the kth component of a vector, B denotes the parent node, r is a random number from the range [0, 1], T is the maximum number of iterations, and C represents a user-defined parameter.

Mathematically modeling the interaction between colleagues

Colleagues cooperate and perform official tasks. It is assumed in a heap that the nodes at the same level are colleagues and each search agent \({x}_{i}\) updates its ___location based on its randomly selected colleague \({S}_{r}\) as follows:

$${x}_{i}^{k}\left(t+1\right)=\left\{\begin{array}{c}{s}_{r}^{k}+\gamma {\lambda }^{k}\left|{s}_{r}^{k}-{x}_{i}^{k}\left(t\right)\right|, f\left({S}_{r}\right)<f\left({x}_{i}\left(t\right)\right)\\ {x}_{r}^{k}+\gamma {\lambda }^{k}\left|{s}_{r}^{k}-{x}_{i}^{k}\left(t\right)\right|, f\left({S}_{r}\right)\ge f\left({x}_{i}\left(t\right)\right)\end{array}\right.$$
(27)

Self-contribution of an employee to accomplish a task

In this phase, the self-contribution of a worker is mapped as follows:

$${x}_{i}^{k}\left(t+1\right)={x}_{i}^{k}\left(t\right)$$
(28)

The following part explains how exploration can be controlled with this equation.

Putting all together

The primary objective of the roulette wheel is to attain an equilibrium of potential outcomes. The roulette wheel is partitioned into three distinct sections, namely \({p}_{1}\), \({p}_{2}\), and \({p}_{3}\). The value of \({p}_{1}\) is a determinant of population displacement, and it may be computed using the following equation:

$${p}_{1}=\frac{t}{T}$$
(29)

The selection of \({p}_{2}\) is computed from the following equation:

$${p}_{2}={p}_{1}-\frac{1-{p}_{1}}{2}$$
(30)

Finally, the selection of \({p}_{3}\) is calculated as follows:

$${p}_{3}={p}_{2}-\frac{1-{p}_{1}}{2}=1$$
(31)

Accordingly, a general position-updating mechanism of the HBO algorithm is mathematically represented as follows:

$$x_{i}^{k} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {x_{i}^{k} \left( t \right),~~p \le p_{1} } \hfill \\ {B^{k} + \gamma \lambda ^{k} \left| {B^{k} - x_{i}^{k} \left( t \right)} \right|,~~~p > p_{1} ~and~p \le p_{2} } \hfill \\ {\begin{array}{*{20}c} {s_{r}^{k} + \gamma \lambda ^{k} \left| {s_{r}^{k} - x_{i}^{k} \left( t \right)} \right|,~~~p > p_{2} ~and~p \le p_{3} ~and~f\left( {S_{r} } \right) < f\left( {x_{i} \left( t \right)} \right)} \\ {x_{r}^{k} + \gamma \lambda ^{k} \left| {s_{r}^{k} - x_{i}^{k} \left( t \right)} \right|,~~~p > p_{2} ~and~p \le p_{3} ~and~f\left( {S_{r} } \right) \ge f\left( {x_{i} \left( t \right)} \right)} \\ \end{array} } \hfill \\ \end{array} } \right.$$
(32)

where p is a random number in the range (0, 1).

Results and discussion

The present study used the MATLAB program to evaluate and simulate network designs. Several networks are developed with combinations of particular layers and neuronal features to select the most appropriate architecture. Table 2 evaluates the performance of typical ANN models concerning their correctness while considering differences in the number of layers and neurons. One of the designs built regularly yields an outstanding optimum network, as shown by the Root Mean Square Error (RMSE) and R-squared (R2) metrics. This design utilizes a feed-forward back-propagation approach with six hidden layers containing a transit function and six neurons. This information is presented in Table 1. The optimization results obtained in the first phase provide the foundation for further optimization methodologies. As a result, the results of these networks are used in later sections. Additionally, Fig. 10 depicts the variation in RMSE values concerning the number of neurons in each hidden layer. The sensitivity analysis of variations in the number of neurons used for flood susceptibility mapping prediction is shown in Table 1.

Table 1 The sensitivity evaluation for the changes in the neurons’ number used to predict the susceptibility mapping of floods.
Full size table

To ensure reproducibility and transparency in model training, it is essential to present the key hyperparameters used in each of the applied models. These hyperparameters—such as the number of hidden layers and neurons in the MLP, learning rate, number of iterations, population/swarm sizes, mutation rates, and convergence criteria—directly influence model performance and convergence behavior. In the present study, the optimization algorithms (BHA, FSA, MVO, HBO) were integrated with MLP by tuning specific parameters unique to each algorithm. For instance, the population size, number of generations, and exploration–exploitation balance parameters varied among the models to achieve the best possible AUC. A detailed table summarizing these hyperparameter settings is included to provide clarity on how each model was configured (Table 2).

Table 2 Hyperparameter settings for the applied hybrid models (MLP + optimization algorithms).
Full size table

The hyperparameter values, such as population sizes and iteration count, were selected based on iterative trial-and-error testing and benchmarking performance metrics (primarily AUC). Activation functions were chosen for their ability to model non-linear patterns in spatial flood data. The learning rate was fixed at 0.01 for all models to maintain stability during optimization. Specific algorithm-related parameters (e.g., wormhole existence in MVO or search radius in BHA) were configured based on literature defaults and adjusted slightly for performance improvement during preliminary runs.

The first stage of optimization results will provide the basis for further optimization processes, with the results of these networks being used in the following phases. Structures with MSE can provide predictions of higher accuracy. The suggested model in regression or classification solutions can provide improved estimate outcomes. Figure 9 illustrates the relationship between the MSE and the number of iterations the suggested artificial neural network-multilayer perceptron (ANN-MLP) structures achieve. These structures are used to forecast flood susceptibility mapping. The study incorporates several hybrid structures, including BHA-MLP, FSA-MLP, MVO-MLP, and HBO-MLP. Based on the provided data, it is evident that the BHA, FSA, MVO, and HBO algorithms have successfully identified the best solution at iteration numbers 400, 400, 300, and 350 correspondingly.

Fig. 9
figure 9

The best-fit model for the (a) BHAMLP, (b) FSAMLP, (c) MVOMLP, and (d) HBOMLP.

Full size image

Error analysis

In the succeeding phase, the outcomes are evaluated by comparing the actual data and the estimated values generated by the proposed hybrid structures. When attempting to ascertain the most optimal hybrid designs, a commonly used methodology involves utilizing ROC curves, often referred to as ROC curves. The presented graphs illustrate the variations in the diagnostic performance of a binary classifier system when the discrimination threshold is adjusted. An example situation would include achieving a maximum AUC value of 1, whereas an AUC value of 0 would indicate the absence of any association. There is no association between the projected and actual values since the observed correlation coefficient is 0. The AUC is a metric that quantifies the performance of a classifier in distinguishing between distinct categories by summarizing the ROC curves. Enhancing the area under the AUC improves the model’s capacity to differentiate between positive and negative classes. In relation to this matter, Figs. 10, 11, 12 and 13 display the ROC curves for the hybrid BHA-MLP and FSA-MLP models and the MVO-MLP and HBO-MLP models presented in this research.

Fig. 10
figure 10

Accuracy results of training dataset for different proposed BHAMLP structure.

Full size image
Fig. 11
figure 11

Accuracy results of training dataset for different proposed FSAMLP structure.

Full size image
Fig. 12
figure 12

Accuracy results of training dataset for different proposed MVOMLP structure.

Full size image
Fig. 13
figure 13

Accuracy results of training dataset for different proposed HBOMLP structure.

Full size image

Based on the outcomes of the iteration phase, the most optimal prediction modeling, as determined by the recommended models, was identified for population sizes of 400, 400, 300, and 350, respectively. The above outcome is derived from 20,000 modeling iterations, with the assessment of MSE indices. However, we use the AUC in the second evaluation phase to find the best-fit mode structures. In the BHA-MLP training databases (Table 3 & Fig. 10), the estimated AUC accuracy indices for population size in training databases equal to 50, 100, 200, 300, 400, 500, 150, 250, 350, and 450 were 0.9626, 0.9679, 0.9660, 0.9701, 0.9721, 0.9715, 0.9710, 0.9702, 0.9698 and 0.9687, respectively. Similarly, for the FSA-MLP training databases, the AUC for the 50, 100, 200, 300, 400, 500, 150, 250, 350, and 450 swarm sizes were obtained 0.9522, 0.9644, 0.9636, 0.9660, 0.9669, 0.9640, 0.9667, 0.9676, 0.9641 and 0.9650, respectively.

Table 3 Network results based on AUC statistical indices for various proposed BHAMLP swarm size.
Full size table

Concerning training and testing predictive modeling results, the best-fit hybrid model to predict the flood susceptibility mapping (e.g., how successful the model could predict the flood susceptibility) has a swarm size equal to 400, respectively. This also shows that the obtained results from phase one are very close to those obtained from phase two. In the case of MVO-MLP, the training and testing AUC were found (0.9829, 0.9867, 0.9870, 0.9914, 0.9873, 0.9874, 0.9829, 0.9877, 0.9849 and 0.9898) and (0.9653, 0.9653, 0.9746, 0.9679, 0.9645, 0.9696, 0.9674, 0.9366, 0.9615 and 0.9531) for the same swarm size conditions, showing the best fit MVO-MLP model is when we used the population size equal to 300 (Tables 4, 5), (Figs. 11, 12). In case of HBO-MLP, the training and testing AUC were found (0.9624, 0.9644, 0.9496, 0.9640, 0.9677, 09,641, 0.9640, 0.9593, 0.9651 and 0.9694) and (0.9607, 0.9619, 0.9636, 0.9573, 0.9531, 0.9632, 0.9463, 0.9497, 0.9649 and 0.9615) for the same swarm size conditions, showing the best fit for HBO-MLP model is when we used the population size equal to 350 (Tables 4, 5, 6), (Fig. 13).

Table 4 Network results based on AUC statistical indices for various proposed FSAMLP swarm size.
Full size table
Table 5 Network results based on AUC statistical indices for various proposed MVOMLP swarm size.
Full size table
Table 6 Network results based on AUC statistical indices for various proposed HBOMLP swarm size.
Full size table

While the AUC values for all four hybrid models (BHA-MLP, FSA-MLP, MVO-MLP, and HBO-MLP) demonstrate strong classification ability, further analysis is necessary to explain the differences in their performance. The MVO-MLP model achieved the highest AUC (0.9914 in training), indicating excellent discriminatory power in identifying flood-prone areas during training. This can be attributed to MVO’s strong balance between exploration and exploitation, achieved through its simulation of white holes, black holes, and wormholes. These mechanisms allow MVO to escape local optima and better fine-tune the MLP’s parameters. However, its validation AUC (0.9679) slightly declined, possibly due to slight overfitting or reduced generalization on unseen data.

The FSA-MLP showed an impressive validation AUC of 0.9797, the highest among all models for validation performance. This suggests that FSA effectively generalizes to new data. FSA benefits from its iterative refinement and memory-based selection, which may have contributed to more stable performance across datasets.

BHA-MLP also showed robust results, with AUCs of 0.9721 (training) and 0.978 (validation). The BHA’s strong global search mechanism and its strategy of pulling weaker solutions toward the best candidate help it maintain competitive accuracy and stability.

In contrast, the HBO-MLP achieved the lowest AUCs (0.9651 training, 0.9649 validation). While still within acceptable performance, this suggests that HBO may have limited capacity in global search or may converge prematurely, especially when dealing with high-dimensional data like that used in flood susceptibility mapping (Figs. 14, 15, 16 and 17).

Fig. 14
figure 14

The error and frequency of MAE for the best fit BHAMLP proposed model.

Full size image
Fig. 15
figure 15

The error and frequency of MAE for the best fit FSAMLP proposed model.

Full size image
Fig. 16
figure 16

The error and frequency of MAE for the best fit MVOMLP proposed model.

Full size image
Fig. 17
figure 17

The error and frequency of MAE for the best fit HBOMLP proposed model.

Full size image

Discussion

This study utilized four optimization algorithms for neural networks to generate a flood map, considering eight key criteria related to flooding. A dataset was created and split into a 70–30 ratio for training the neural networks. Flood susceptibility maps were produced using the most effective algorithms and classified into five Likert scales ranging from “very low” to “very high” sensitivity. The findings indicated that significant portions of the western, northwestern, and central regions were classified as high-risk areas (see Fig. 18).

Fig. 18
figure 18figure 18figure 18figure 18

The complete flood susceptibility mapping (FSM) utilizing optimized algorithms.

Full size image

Although the models performed well overall, some misclassifications were observed in areas with complex topographical or land-use transitions, such as urban–rural interfaces or mixed agricultural zones. These errors may be attributed to limited resolution of certain input datasets (e.g., DEM, land use), or omitted conditioning factors like drainage density or soil moisture, which could have improved spatial accuracy.

Interestingly, the MVO-MLP model, despite having the highest training AUC (0.9914), exhibited a lower validation AUC (0.9679) compared to FSA and BHA, suggesting possible overfitting or sensitivity to training data. This aligns with findings from Rezaei, Amiraslani41, who reported that some metaheuristic models tend to over-adapt to training sets without adequate generalization in flood mapping tasks.

Compared to studies using traditional machine learning models in Iran—such as Random Forest, Logistic Regression, or Support Vector Machines—the current hybrid models showed comparable or superior predictive power. For example, Tehrani, Bito42 reported RF models achieving AUC values around 0.93–0.95 for FSM in similar Iranian regions. The hybrid models in this study, particularly FSA-MLP and BHA-MLP, outperformed these values with AUCs nearing 0.978–0.9797.

Moreover, in global studies like Linh, Pandey43 and Panahi, Rahmati44, the integration of AI and evolutionary algorithms has shown increasing potential for enhancing flood prediction accuracy. Our results confirm these trends and further highlight the potential of tailored hybrid approaches in regional flood assessments.

The findings carry significant implications for land-use planning, conservation, and climate change adaptation strategies in Fars Province. High-susceptibility zones identified through the FSMs can guide urban expansion away from flood-prone areas and inform zoning regulations. Furthermore, reforestation or watershed restoration programs can be prioritized in regions identified as highly sensitive.

Given the increasing frequency and severity of floods due to climate variability, incorporating the presented FSM models into climate resilience planning could improve long-term infrastructure sustainability and reduce socioeconomic impacts. The hybrid models provide spatially explicit insights that support adaptive land management and disaster preparedness policies.

One of the key practical applications of FSM is its integration with early warning systems, emergency evacuation planning, and infrastructure design. The outputs of the hybrid models can be embedded into GIS-based decision support systems for real-time monitoring and response. Municipal authorities and environmental planners can use these insights to establish buffer zones, design flood mitigation structures, and allocate resources efficiently during crises.

The findings of this study offer significant applications and implications for water resources management, particularly in regions vulnerable to frequent flooding. By integrating advanced artificial intelligence techniques with evolutionary optimization algorithms, the developed flood susceptibility model provides a reliable tool for predicting high-risk flood zones with enhanced spatial accuracy. Water resource managers can utilize these predictive maps to prioritize investment in flood mitigation infrastructure such as levees, drainage systems, and reservoirs in the most vulnerable areas. Furthermore, the model enables real-time monitoring and early warning systems, improving preparedness and reducing the potential for loss of life and property. The data-driven approach also supports strategic planning of water storage and allocation, ensuring that water supply systems are resilient to flood events. In the context of integrated water resources management (IWRM), the model facilitates more informed decision-making by incorporating climatic, topographic, and hydrological factors into a unified predictive framework. Lastly, the outcomes of this research can guide the development of sustainable land use policies, promote climate adaptation strategies, and strengthen disaster risk reduction efforts, contributing to the long-term resilience of communities and ecosystems.

Study limitations and future research directions

This study has several limitations. First, uncertainty analysis and data bias assessment were not explicitly performed, which limits the confidence bounds of the susceptibility maps. Second, no comparison with deep learning models (e.g., CNNs, RNNs) or traditional hydrological models (e.g., HEC-HMS) was conducted, which could offer broader benchmarking. Third, the absence of feature importance analysis and multicollinearity testing may limit the interpretability of the chosen parameters.

Future research should include:

  • A comparison with a wider range of machine learning and physical models.

  • Integration of additional environmental variables (e.g., soil moisture, drainage density).

  • Application of ensemble modeling and uncertainty quantification techniques.

  • Testing the transferability of the models to other flood-prone regions.

Conclusions

Flooding is an inherently destructive natural occurrence resulting in annual fatalities and substantial property damage throughout various regions worldwide. Efficient FSM has emerged as a prominent strategy in flood risk management, aiming to mitigate the potential risks of this natural phenomenon. This research aimed to evaluate the efficacy of several methodologies (BHA, FSA, HBO, and MVO) in conjunction with ANN for FSM in the Fars region of Iran. The mapping process was conducted by considering eight influential parameters and using a dataset of 326 instances of observed floods within the basin for training and testing purposes. The ROC approach was used to determine the AUC, success rate, and prediction rate to evaluate the model’s performance.

A result of this study, the hybrid models offer a viable alternative for data-scarce regions. Testing these approaches across different climatic and geographical settings would help assess their transferability and robustness. As an effective flood mapping system could also be developed, utilizing optimized ANN as the primary method for assessing flood susceptibility. Although the ANN exhibits a reasonable level of accuracy in forecasting the absence of floods, it is essential to note that some regions without flood events may nevertheless possess inherent instability, hence increasing the probability of future flood occurrences. While it is preferable to address this issue, acquiring further data from forthcoming floods within the research region is essential to accomplish this objective. Future work should address these challenges by integrating higher-resolution environmental datasets and applying uncertainty analysis.

The flood susceptibility model developed in this study has significant implications for urban planning and policy-making. From a practical standpoint, the findings can support decision-makers in developing flood mitigation strategies. The susceptibility maps can assist urban planners in guiding infrastructure development away from high-risk zones, while also informing conservation efforts in vulnerable areas. Incorporating these models into local disaster management systems could enhance preparedness and response strategies.