Abstract
Gear-bearing drive systems often exhibit manufacturing and installation errors, which can significantly affect system performance, and longevity, and increase the probability of failures. This paper focuses on the reliability analysis of gear-bearing drive systems with uncertainties in system parameters such as gear backlash and bearing clearance, caused by gear and bearing manufacturing and installation errors. First, a dynamic model of the gear-bearing drive system, incorporating coupled dynamic meshing parameters, is established. Then, the deterministic dynamic model of the system is combined with the Chebyshev interval analysis method to develop a reliability analysis model for the gear-bearing drive system with uncertain parameters. The study analyzes the variations in system natural frequencies and vibration responses due to gear quality and initial gear and bearing clearances at different deviation rates. The results indicate that at the same rotational speed and deviation rate, the initial bearing clearance has a more significant impact on the system’s dynamic characteristics compared to the initial gear clearance. At different rotational speeds and the same deviation rate, system reliability decreases with increasing average initial interference of the bearing at low speeds. At high speeds, a large bearing clearance deviation may cause abnormal fluctuations in system vibration. This method provides a prioritization of parameter control for the structural optimization and design of gear-bearing systems.
Similar content being viewed by others
Introduction
The power systems of aircraft1,2,3, vehicles4, wind turbines5, and ships6 are all complex rotating mechanical systems that involve numerous uncertain internal and external factors. With the increasing performance demands on rotating machinery, there are higher requirements for the manufacturing precision and assembly clearances of transmission components such as gears and bearings7.
The dynamic analysis of gear-bearing transmission systems inherently involves internal parameter uncertainties arising from limitations in manufacturing precision and unavoidable assembly errors. These uncertainties, particularly those associated with gear backlash and bearing clearance, directly govern system performance and operational reliability. Consequently, investigating the dynamic characteristics of such systems under uncertain gear backlash and bearing clearance conditions holds critical importance for understanding nonlinear vibration mechanisms, predicting failure modes, and optimizing tolerance design to mitigate performance degradation.
At present, a substantial body of research has been conducted by numerous scholars on the uncertainty issues in gear transmission systems. According to the employed methodologies, the models can generally be categorized into three types: probabilistic models, fuzzy models, and interval models. Among them, probabilistic models, which are based on probability theory and statistics, are widely applied in cases involving material parameter fluctuations and random vibrations due to their well-established theoretical framework and clear probabilistic interpretation8,9,10. Yu11 employed a PC-Kriging adaptive algorithm to analyze the reliability of thermo-structural-dynamic coupled systems, addressing the high-temperature failure issues in aero-engine gear-rotor systems. Hajnayeb et al.12 proposed the use of power spectral density and frequency response functions to study the effects of various random manufacturing errors on the vibration response of bearings. Feng et al.13 adopted an extended interval stochastic method to analyze the interval natural frequencies of systems with mixed uncertain parameters. Onur Can Kalay14 et al. proposed a one-dimensional convolutional neural network (1-D CNN) model for gear systems with cracks and tooth asymmetry. Probabilistic models have also been widely used to investigate uncertainties in wind turbine gear systems15,16,17,18. However, stochastic models typically require a large amount of experimental data for support. Fuzzy models19, based on fuzzy mathematical analysis, are another type of uncertainty quantification method. They offer advantages such as not relying on probability distributions and exhibiting strong flexibility. Jing20 employed a genetic fuzzy immune PID algorithm to tune immune parameters for controlling system responses. Zhao21 applied a fuzzy comprehensive evaluation method to determine the optimal combination of processing parameters for non-circular gears. Gu22 developed an integrated gear fault diagnosis model by combining a Hidden Markov Model (HMM) with a fuzzy evaluation model. However, fuzzy models are generally not well-suited for systems involving multiple uncertain parameters. Both probabilistic and fuzzy models tend to have high computational complexity. In scenarios where data are scarce23 or rapid evaluation of transmission system robustness is required24, interval models are more suitable.
Interval models, which are characterized by low information requirements, high computational efficiency, and strong robustness assurance, have been widely applied by researchers in the uncertainty analysis of gear systems. Wu25 was the first to combine interval analysis with multibody dynamics, proposing an interval algorithm based on Chebyshev polynomial function approximation. Due to its rapid convergence and compatibility with various dynamic models, this interval method has since been applied by scholars to efficiently evaluate uncertainty in dynamic engineering problems. Subsequently, Wei26,27,28 was the first to introduce the Chebyshev interval analysis method into gear dynamics, demonstrating its feasibility through both numerical simulations and experimental validation. The study revealed that even small variations in certain uncertain parameters within a limited range can lead to significant uncertainty in system responses. Hu29 proposed a multi-degree-of-freedom nonlinear dynamic model of a spur gear system with misalignment uncertainty, based on Chebyshev polynomial function approximation. Zhao30 combined interval and stochastic analysis to develop a hybrid interval uncertainty structural dynamic analysis method. Guerine, A31 introduced a method based on polynomial chaos projection to evaluate the uncertainty in the dynamic response of gear systems. Guo32 proposed a method based on polynomial chaos expansion (PCE) to analyze the uncertainty in gear manufacturing errors. Beyaoui, M33 developed a computational approach to assess the robustness of wind turbine gearbox system responses while considering uncertainties in wind direction and blade pitch angle. Wu34 used PCE to model the uncertainties in mesh stiffness, bearing stiffness, and damping parameters of a double-helical gear–bearing system. Wei et al.35 studied the dynamic response of gear transmission systems with uncertainties in mass, mesh stiffness, and support stiffness using an interval analysis method based on Chebyshev inclusion functions. Yuhang Hu et al.29 also adopted the Chebyshev inclusion function approach to analyze misalignment uncertainties in multi-degree-of-freedom gear systems. Chao-Fu36 combined PCE with polynomial surrogate analysis (PSA) to address hybrid aleatory and epistemic uncertainties in transmission systems. Bel-Mabrouk37 proposed a polynomial chaos-based approach to study aerodynamic parameter uncertainties in bevel gear systems. Najib38 investigated the effect of static transmission error uncertainty, caused by gear manufacturing deviations, on the dynamic response of gear systems. In summary, previous studies have mainly focused on the application of interval analysis methods to parameter uncertainties in gear systems. However, the uncertainty associated with gear backlash and bearing clearance in gear–bearing transmission systems has not yet been adequately addressed.
The objective of this study is to propose a reliability analysis method for gear–bearing transmission systems considering gear manufacturing and installation errors. By integrating the Chebyshev interval analysis method with a gear transmission system dynamic model that incorporates coupled dynamic meshing parameters, the interval estimation of the inherent characteristics and vibration responses of a gear–bearing transmission system is investigated under uncertainties in gear mass, initial gear backlash, and initial bearing clearance. The proposed method is applicable for evaluating the dynamic behavior of gear transmission systems when uncertainties in gear backlash and bearing clearance are present.
The motivation of this paper is to propose a reliability analysis method for gear-bearing transmission systems that accounts for gear manufacturing and installation errors. By integrating the Chebyshev interval analysis method with a dynamic model of the gear transmission system that incorporates coupled dynamic meshing parameters, the paper achieves interval estimation of the inherent characteristics and vibration responses of the gear-bearing transmission system under uncertainties in gear quality, initial gear clearance, and initial bearing clearance. This method is suitable for evaluating the interval variations in dynamic characteristics of gear transmission systems when the ranges of certain uncertain parameters are known.
The remainder of this paper is organized as follows. In the second section, a dynamic model of the gear-bearing drive system has been established, considering dynamic meshing parameters. Then, in the third section, a modeling method for gear-bearing drive systems based on the Chebyshev interval analysis method has been developed, and the relevant formulas have been derived. In the fourth section, the uncertainty of the system’s natural frequencies under uncertain mass parameters has been calculated and analyzed. Finally, in the fifth section, the variation ranges of gear meshing parameters, gear backlash, and bearing clearance have been analyzed under different initial gear and bearing clearances.
Dynamic modeling of gear-bearing systems
In practical engineering, factors such as manufacturing precision and assembly errors lead to uncertainties in the initial gear backlash, gear mass, and initial bearing clearance within gear-bearing drive systems. However, these parameters are constrained within specific ranges according to design guidelines. Due to the presence of numerous nonlinear factors in the system, even slight variations in parameters can have a significant impact on the system. Therefore, these uncertainties are essential considerations in the dynamic modeling of gear-bearing drive systems. To more clearly analyze the dynamic characteristics of gear-bearing drive systems, this paper introduces a reliability analysis modeling method for gear-bearing drive systems based on the Chebyshev interval analysis method.
First, a dynamic model with deterministic parameters is established for the gear-bearing transmission system, focusing on the coupled relative positions of gears, dynamic gear backlash, and dynamic bearing clearance. It is assumed that the gear system moves only within a plane, and all gears are treated as rigid discs39. Changes in the relative positions of the gears affect the meshing force.
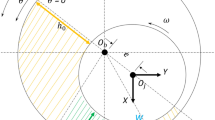
The variation in the geometric positional relationship of the gear-bearing transmission system at adjacent moments is shown in Fig. 1. At the previous moment, the mass centers are denoted as \({G_1}\)and \({G_2}\), and the geometric centers of the system are denoted as \({O_1}\) and \({O_2}\). At the subsequent moment, the geometric centers change to \(C_{1} \left( {x_{p} ,y_{p} } \right)\)\(C_{1} \left( {x_{p} ,y_{p} } \right)\) and \(C_{2} \left( {x_{g} ,y_{g} } \right)\). At this point, the relative position of the gears changes, resulting in alterations in the center distance \(L\), deflection angle \(\beta\), and engagement angle \(\alpha\).
where \({L_0}\) represents the original center distance, \({r_b}\) represents the base circle radius, and \({r_a}\) represents the addendum circle radius. Subscripts \(p\) and \(g\) denote the driving and driven gears, respectively.
Each gear can be represented by three generalized coordinates, \(x\), \(y\) and \({\theta _z}\). Considering factors such as gravity and torque, the equations of motion for the gear-bearing system are established and expressed as Eq. (4).
The mass matrix is expressed as\({M^s}\).
where \({m_p}\), \({J_p}\), \({m_g}\), and \({J_g}\) represent the masses and moments of inertia of the input and output gears, respectively. The damping matrix \({C^s}\)is denoted as Eq. (6).
The terms \(F_{b}^{s}\), \({F_{Tg}}\), \({F_w}\), and \({F_m}\) on the right-hand side of Eq. (4) are expressed as Eq. (7) through (10), respectively.
Among them, the gear meshing force on the tooth surface can be expressed by Eq. (11). Ball bearings are used to support the gear system and are simplified into a bearing model with time-varying clearance. The specific expression is given in Eq. (12).
In Eq. (11), \(k_{m}^{d}\) represents the time-varying meshing stiffness of the gear, calculated using the potential energy method40,41 during coupled gear vibration. The calculation method of gear meshing stiffness based on dynamic meshing parameters can be derived from Eq. (1) to (3) in combination with the potential energy method. The damping ratio \(c_{m}^{d}\), dynamic transmission error \({\delta _d}\), and half tooth side clearance \(b\left( t \right)\) are represented by Equations (13) through (15), respectively. Where \({\xi _{\text{m}}}\) is the damping coefficient, \({J_p}\) and \({J_g}\) represent the moments of inertia of the driving and driven gears, respectively, \({e_a}\) denotes the static transmission error magnitude, \({\omega _p}\) is the angular velocity of the driving gear, and \({b_0}\) is the initial half tooth side clearance. In Eq. (12), \({K_{bear}}\)is the Hertz contact stiffness of each ball. \(H\left( \cdot \right)\)serves as the criterion for deter-mining the contact between each ball and the bearing. \(H\left( x \right)=1\left( {x \geqslant 0} \right)\)indicates that the kth roller is engaged with the raceway, and \(H\left( x \right)=0\left( {x<0} \right)\) indicates that the kth roller is disengaged from the raceway. \({\delta _0}\) represents the initial bearing clearance, and \({N_{\text{b}}}\) denotes the number of rolling elements.
Reliability analysis model of the gear-bearing transmission system
For cognitive uncertainties such as manufacturing and installation defects, conducting extensive experiments42 or statistical analysis is both time-consuming and labor-intensive. This paper employs the Chebyshev interval analysis method, which is computationally convenient and applicable to various dynamic models43. These uncertainties can be described using vectors\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{\kappa } = (\kappa _{1} ,\kappa _{2} ,\kappa _{3} , \ldots ,\kappa _{m} )\).
The objective function of the gear system can be represented using Chebyshev polynomial fitting.
Here, \(\psi\) represents the rearranged Chebyshev polynomial coefficient matrix, \(Q\) is the matrix constructed from the values of interpolation points corresponding to n uncertain parameters, and \({p_i}\) contains the function values at the interpolation points.
where,
Since Eq. (19) has explicit upper and lower bounds, the boundaries of Equation can be approximately equivalent to Eqs. (24) and (25).
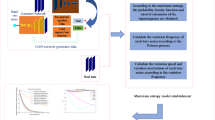
To systematically evaluate the reliability of gear-bearing transmission systems under manufacturing and installation uncertainties, this section proposes a hybrid analytical framework integrating deterministic dynamic modeling with Chebyshev interval analysis. The methodology shown in Fig. 2 follows a rigorous four-phase workflow:
(1) Deterministic System Characterization.
A dynamic model of the gear-bearing transmission system is established, as detailed in Sect. 2, incorporating critical deterministic parameters such as the geometric configurations of gear pairs and bearings, material properties, and operational load conditions.
(2) Uncertainty Quantification.
Key stochastic parameters are identified through manufacturing tolerance analysis, including variations in gear mass, ranges of initial gear backlash, and tolerance intervals of initial bearing clearance. Each parameter is quantified with its respective variation ___domain.
(3) Chebyshev Surrogate Modeling.
Interval analysis is conducted by evaluating the system’s dynamic response using the Chebyshev interval method. This approach enables the numerical determination of bounds for system characteristics, such as natural frequency intervals, vibration response envelopes, and critical dynamic thresholds.
(4) Reliability analysis.
The reliability of the system is assessed by evaluating the extent to which different uncertain parameters influence its dynamic behavior. This analysis identifies priority control parameters that necessitate stringent tolerance management during manufacturing and installation processes, such as backlash-sensitive gear components, mass-critical gear elements, and clearance-dependent bearing assemblies.
The gear-bearing transmission system can be simplified into a schematic of a single-stage gear transmission system, as shown in Fig. 3. Assuming fluctuating input and output torques for the gears, the single-stage gear system is equivalent to rigid disks connected by a time-varying stiffness spring and a time-varying damper. Both the driving and driven gears are considered as lumped mass elements. The specific model parameters of the system are listed in Table 1.
Analysis of system natural frequencies with parameter uncertainty
This section focuses on the impact of mass uncertainty caused by gear manufacturing errors on the natural frequencies of the system. It is assumed that the center of mass is the geometric center of the gear. For the gear-bearing transmission system with parameters listed in Table 1, the first five natural frequencies of the system with deterministic parameters are calculated and presented in Table 2.
Figure 4 shows the fluctuation curves of the first, third, and fifth-order natural frequencies of the system with respect to the deviation rate when the driving gear mass parameter is considered uncertain. It also depicts the fluctuation curves of their upper and lower bounds with respect to the deviation rate. From Figs. 4 (a), (c), and (e), it can be observed that these natural frequencies exhibit a positive correlation with the deviation rate of the uncertain parameter. Figures 4 (b), (d), and (f) reveal that, under the same deviation coefficient, the fifth-order natural frequency \({f_5}\) is most sensitive to the variation of the parameter, followed by the third-order natural frequency \({f_3}\). Additionally, the fluctuation of the upper and lower bounds of the fifth-order natural frequency is highly symmetric.
Analysis of system vibration response under parameter uncertainty
It is well known that controlling gear clearance and bearing clearance during the design, manufacturing, and installation of gears is crucial to ensure the stability and reliability of the gear-bearing transmission system during operation. Assuming the bearing clearance is based on the clearance between the rolling balls and the bearing outer ring, where the clearance is zero when they are in contact, and ignoring the deformation of the bearing; the variation in gear clearance is described by changes in the half-tooth side clearance. This section investigates the impact of clearance uncertainty on system response by varying the initial bearing clearance and initial gear clearance.
Analysis of system vibration response with uncertainty in initial gear clearance
In this subsection, to investigate the impact of the deviation rate of gear clearance on the reliability of the gear-bearing transmission system, it is assumed that the driving gear speed and initial gear clearance are given as \(r=1000{\text{ }}rad/min\) and \({b_0}=50\mu m\), respectively. The deviation rates are categorized into seven groups, with the maximum upper and lower limits being 20%. The time-varying states of meshing parameters such as center distance, pressure angle, and deflection angle, as well as the interval ranges of the meshing parameters, are shown on the left and right sides of Fig. 5. The time-varying states of gear clearance and bearing clearance, along with their interval ranges with deviation rates, are shown on the left and right sides of Fig. 6, respectively.
From the meshing parameter variation curves and interval fluctuation ranges shown in Fig. 5, it can be observed that: when the initial gear clearance varies from 0 to 20%, the changes in meshing parameters such as center distance, pressure angle, and deflection angle are relatively small. However, their average fluctuation amplitudes are within the upper and lower boundary ranges.
From the curves of gear and bearing clearances over time and their average value ranges shown in Fig. 6, the following observations can be made: In Figure (a), it is evident that the gear clearance exhibits noticeable variations with different initial gear clearances. Figure (c) describes the change in clearance between a particular rolling ball and the bearing outer ring, showing that the bearing clearance gradually increases from zero to its maximum value and then decreases back to zero. This reflects the rolling ball moving away from and then approaching the bearing outer ring until they make contact, with the entire process exhibiting fluctuating behavior. Figures (b) and (d) illustrate that the impact on gear clearance is significant and increases linearly.
Analysis of system vibration response with uncertainty in initial bearing clearance
In this subsection, to investigate the impact of the deviation rate of the bearing initial clearance on the reliability of the gear-bearing transmission system, it is assumed that the midpoint value of the bearing initial clearance is 30 µm. Two cases of driving gear speeds are considered: 1000 rad/min and 4000 rad/min. Seven sets of variations are made, with the upper and lower deviation rates having a maximum limit of 20%. The time-varying states of the gear-bearing system parameters such as center distance, pressure angle, and deflection angle, as well as the interval ranges of the meshing parameters, are shown in the left and right sides of Fig. 7. The time-varying states of the gear clearance and bearing clearance and their interval ranges with the deviation rates are shown in the left and right sides of Fig. 8, respectively.
From the curves and interval fluctuation ranges of meshing parameters shown in Fig. 7, it can be observed that: as the initial gear clearance varies from 0 to 20%, the changes in meshing parameters such as center distance, pressure angle, and deflection angle are relatively large. Additionally, the average value fluctuation ranges show a linear increase.
From Fig. 8, the time-varying curves and average value ranges of gear and bearing clearances reveal the following: In Figure (a), it is evident that the gear clearance shows noticeable changes with different initial gear clearances. Figure (c) describes the variation in the clearance between a ball and the bearing outer ring, showing that the bearing clearance increases from zero to a maximum and then decreases back to zero, indicating the ball moving progressively away from and then towards the bearing outer ring until contact is made, with the entire process exhibiting fluctuations. Figures (b) and (d) illustrate that the bearing clearance increases from 71 µm to 76 µm and the gear clearance increases from 83.5 µm to 84.5 µm, with the bearing clearance showing a more significant increase.
In Figs. 9 and 10, the variation in the time-varying states and average values of gear meshing parameters, as well as gear and bearing clearances, are illustrated for a gear rotational speed of 4000 rad/min, showing how they change with different deviation rates.
From the variation curves and range of fluctuations of the meshing parameters shown in Fig. 9, it can be observed that when the gear initial clearance varies within the range of 0–15%, the trends of parameters such as center distance, pressure angle, and deflection angle are similar. However, there are significant differences when the deviation rate reaches 20%. The average values of these parameters all show a linear increase. Compared to gear clearance, the impact of bearing initial clearance on the system is more pronounced under the same deviation rate conditions.
From Fig. 10, the time-varying curves and average value ranges of gear clearance and bearing clearance clearly show that: In Figures (a) and (c), it is evident that both gear clearance and bearing clearance exhibit significant changes with different deviation rates. The trend of bearing clearance remains consistent with previous observations. Figures (b) and (d) illustrate that bearing clearance increases from 71.2 µm to 76.1 µm and gear clearance increases from 83.9 µm to 84.9 µm, both showing a linear increase. Compared to the trends observed at 1000 rad/min, there are notable changes in the fluctuation trends of gear meshing parameters and gear clearance, with both gear and bearing clearances showing increased average values.
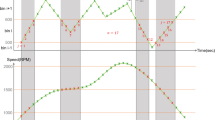
To validate the effectiveness and practicality of the proposed method, we performed a comparative analysis using the model parameters and results reported in References39. Figure 11(a) compares the displacement of the driving wheel obtained from our dynamic model with that from the literature. Figure 11(b) shows the theoretical response alongside the literature results for gear backlash varying within 50 μm ± 20%, and Fig. 11(c) presents a close-up of the region highlighted in Fig. 11(b). As shown in Fig. 11, our computed results closely match those reported in the literature. Moreover, the uncertainty analysis indicates that variations in gear backlash have a minimal effect on system behavior, and all literature values fall within our calculated interval bounds.
Conclusions
This paper has proposed a reliability analysis model for gear–bearing transmission systems based on Chebyshev interval analysis methods, aiming to reveal the impact characteristics of manufacturing and installation errors on the dynamic properties of gear systems. First, the dynamic model of the uncertain gear–bearing system has been formulated as a differential equation with uncertain parameters. Next, Chebyshev interval analysis has been incorporated, and numerical integration methods have been used to solve for the target function values. The effects of uncertain gear mass, initial gear backlash, and initial bearing clearance on system reliability have been studied. The main conclusions are as follows:
-
1.
When the mass of the driving wheel is an uncertain parameter, the fifth-order natural frequency is most sensitive to fluctuations under the same deviation rate, and the upper and lower bounds of the fifth-order natural frequency exhibit highly symmetrical fluctuation patterns.
-
2.
Under identical rotational speeds and deviation ratios, the initial bearing clearance demonstrates greater influence on the vibrational characteristics of the proposed gear–bearing transmission system compared to the initial gear backlash.
-
3.
Significant variations emerge in the temporal response patterns of the system under identical bearing initial clearance deviation ratios at different rotational speeds. At specified low-speed conditions, dynamic reliability decreases with increasing initial mean clearance deviations. However, nonlinear interactions arising from clearance-dependent contact transitions (engagement/disengagement states) induce anomalous vibration oscillations at high-speed operations with excessive bearing initial clearance deviation ratios.
This systematic approach bridges theoretical modeling with practical engineering applications. The results of this analysis can be used to optimize the design and maintenance of gear–bearing systems by considering uncertainties such as gear manufacturing errors and bearing clearance. In practice, the findings can guide engineers in determining optimal tolerance allocations, improving the reliability of gear–bearing systems, and minimizing the risk of performance degradation or failure under uncertain operational conditions. By integrating this model into the design phase, manufacturers can ensure better performance and longevity of gear systems, particularly in applications where precision and reliability are critical, such as in automotive, aerospace, and industrial machinery.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Tang, W., Chen, Y. & Zuo, M. J. Health index development for a planetary gearbox. Procedia Manuf. 49, 155–159 (2020).
Lu, F., Gao, T., Huang, J. & Qiu, X. Nonlinear Kalman filters for aircraft engine gas path health Estimation with measurement uncertainty. Aerosp. Sci. Technol. 76, 126–140 (2018).
Pan, M., Xu, Y., Gu, B., Huang, J. & Chen, Y. H. Fuzzy-Set theoretic control design for aircraft engine Hardware-in-the-Loop testing: mismatched uncertainty and optimality. IEEE Trans. Ind. Electron. 69, 7223–7233 (2022).
Zhou, B., Zi, B. & Qian, S. Dynamics-based nonsingular interval model and luffing angular response field analysis of the DACS with narrowly bounded uncertainty. Nonlinear Dyn. 90, 2599–2626 (2017).
Tabatabaeipour, S. M., Odgaard, P. F., Bak, T. & Stoustrup, J. Fault detection of wind turbines with uncertain parameters: A Set-Membership approach. Energies 5, 2424–2448 (2012).
Robertson, A., Bachynski, E. E., Gueydon, S., Wendt, F. & Schuenemann, P. Total experimental uncertainty in hydrodynamic testing of a semisubmersible wind turbine, considering numerical propagation of systematic uncertainty. Ocean. Eng. 195, 106605 (2020).
Hou, L. et al. Inter-shaft bearing fault diagnosis based on aero-engine system: A benchmarking dataset study. J. Dyn. Monit. Diagn. 2, 228–242 (2023).
Bernard, P. & Fleury, G. Stochastic newmark scheme. Probab. Eng. Eng. Mech. 17, 45–61 (2002).
Bernard, P. Stochastic averaging: Some methods and applications, in: N.S. Namachchivaya, Y.K. Lin (Eds.), IUTAM SYMPOSIUM ON NONLINEAR STOCHASTIC DYNAMICS, Springer, Dordrecht, : pp. 29–41. (2003).
Weinan, E., Han, J. & Jentzen, A. Algorithms for solving high dimensional pdes: from nonlinear Monte Carlo to machine learning. Nonlinearity 35, 278–310 (2022).
Yu, Z., Sun, Z., Zhang, S. & Wang, J. The coupled Thermal-Structural resonance reliability sensitivity analysis of Gear-Rotor system with random parameters. Sustainability 15, 255 (2023).
Hajnayeb, A. & Sun, Q. Study of gear pair vibration caused by random manufacturing errors. Arch. Appl. Mech. 92, 1451–1463 (2022).
Feng, J., Wu, D., Gao, W. & Li, G. Hybrid uncertain natural frequency analysis for structures with random and interval fields. Comput. Meth Appl. Mech. Eng. 328, 365–389 (2018).
Kalay, O. C., Karpat, E., Dirik, A. E. & Karpat, F. A One-Dimensional convolutional neural Network-Based method for diagnosis of tooth root cracks in asymmetric spur gear pairs. Machines 11, 413 (2023).
Yüce, C. et al. Prognostics and health management of wind energy infrastructure systems. ASCE‑ASME J. Risk Uncertain. Eng. Syst. B 8, 020801 (2022).
Guo, Q. & Ganapathysubramanian, B. Incorporating a stochastic data-driven inflow model for uncertainty quantification of wind turbine performance. Wind Energy. 20, 1551–1567 (2017).
Campobasso, M. S., Minisci, E. & Caboni, M. Aerodynamic design optimization of wind turbine rotors under geometric uncertainty. Wind Energy. 19, 51–65 (2016).
Shittu, A. A., Mehmanparast, A., Amirafshari, P., Hart, P. & Kolios, A. Sensitivity analysis of design parameters for reliability assessment of offshore wind turbine jacket support structures. Int. J. Nav Archit. Ocean. Eng. 14, 100441 (2022).
Tong, S., Wang, T. & Li, Y. Fuzzy adaptive actuator failure compensation control of uncertain stochastic nonlinear systems with unmodeled dynamics. IEEE Trans. Fuzzy Syst. 22, 563–574 (2014).
Jing, Z. Application of genetic fuzzy immune PID algorithm in cruise control for commercial vehicles. AIP Adv. 10, 095001 (2020).
Zhao, J. et al. Multi-objective optimization of Non-circular gear through orthogonal array and fuzzy comprehensive evaluation method in WEDM, Arab. J. Sci. Eng. 48, 11973–11988 (2023).
Gu, Y. K., Xu, B., Huang, H. & Qiu, G. Q. A fuzzy performance evaluation model for a gearbox system using hidden Markov model. IEEE Access. 8, 30400–30409 (2020).
Lombardi, M. & Haftka, R. T. Anti-optimization technique for structural design under load uncertainties. Computers Meth Appl. Mech. Eng. 157, 19–31 (1998).
Elishakoff, I., Haftka, R. & Fang, J. Structural design under bounded Uncertainty - Optimization with Anti-Optimization. Computers Struct. 53, 1401–1405 (1994).
Wu, J., Zhang, Y., Chen, L. & Luo, Z. A Chebyshev interval method for nonlinear dynamic systems under uncertainty. Appl. Math. Model. 37, 4578–4591 (2013).
Wei, S., Chu, F. L., Ding, H. & Chen, L. Q. Dynamic analysis of uncertain spur gear systems. Mech. Syst. Signal. Proc. 150, 107280 (2021).
Wei, S., Zhao, J., Han, Q. & Chu, F. Dynamic response analysis on torsional vibrations of wind turbine geared transmission system with uncertainty. Renew. Energy. 78, 60–67 (2015).
Wei, S., Chen, Y., Ding, H. & Chen, L. An improved interval model updating method via adaptive kriging models. Appl. Math. Mech. -Engl Ed. 45, 497–514 (2024).
Hu, Y. H., Du, Q. G. & Xie, S. H. Nonlinear dynamic modeling and analysis of spur gears considering uncertain interval shaft misalignment with multiple degrees of freedom. Mech. Syst. Signal Process. 193, 110261 (2023).
Yanlin, Z. Dynamic response analysis of structure with hybrid random and interval uncertainties, (2020).
Guerine, A., El Hami, A., Walha, L., Fakhfakh, T. & Haddar, M. Dynamic response of a spur gear system with uncertain parameters. J. Theor. Appl. Mech. 54, 1039–1049 (2016).
Guo, F., Li, C., Su, J. & Liu, C. Study on dynamic uncertainty and sensitivity of gear system considering the influence of machining accuracy. Appl. Sci. -Basel. 13, 8011 (2023).
Beyaoui, M. et al. Dynamic behaviour of a wind turbine gear system with uncertainties. C R Mec. 344, 375–387 (2016).
Wu, L. et al. Dynamic modeling and vibration analysis of herringbone gear system with uncertain parameters. Arch. Appl. Mech. 94, 221–237 (2024).
Wei, S., Chu, F. L., Ding, H. & Chen, L. Q. Dynamic analysis of uncertain spur gear systems. Mech. Syst. Signal Process. 150, 107280 (2021).
Fu, C. et al. Dynamic analysis of geared transmission system for wind turbines with mixed aleatory and epistemic uncertainties. Appl. Math. Mech. -Engl Ed. 43, 275–294 (2022).
Bel Mabrouk, I., El Hami, A., Walha, L., Zghal, B. & Haddar, M. Dynamic response analysis of vertical Axis wind turbine geared transmission system with uncertainty. Eng. Struct. 139, 170–179 (2017).
Najib, R., Neufond, J., Franco, F., Petrone, G. & De Rosa, S. Assessing the impact of manufacturing uncertainties on the static and dynamic response of spur gear pairs. Mech. Based Des. Struct. Mech. 52, 6973–7003 (2023).
Yi, Y., Huang, K., Xiong, Y. & Sang, M. Nonlinear dynamic modelling and analysis for a spur gear system with time-varying pressure angle and gear backlash. Mech. Syst. Signal Process. 132, 18–34 (2019).
Ma, H., Pang, X., Feng, R., Song, R. & Wen, B. Fault features analysis of cracked gear considering the effects of the extended tooth contact. Eng. Fail. Anal. 48, 105–120 (2015).
Dai, H., Long, X., Chen, F. & Xun, C. An improved analytical model for gear mesh stiffness calculation. Mech. Mach. Theory. 159, 104262 (2021).
Han, Y., Chen, X., Xiao, J., Gu, J. X. & Xu, M. An Improved Coupled Dynamic Modeling for Exploring Gearbox Vibrations Considering Local Defects, JDMD (2023).
Fu, C., Yang, Y., Lu, K. & Gu, F. Nonlinear vibration analysis of a rotor system with parallel and angular misalignments under uncertainty via a legendre collocation approach. Int. J. Mech. Mater. Des. 16, 557–568 (2020).
Acknowledgements
The authors are very grateful for the financial support from the National Natural Science Foundation of China (Grant Nos.12422213, 12372008), the National Key R&D Program of China (Grant No. 2023YFE0125900), the Natural Science Foundation of Heilongjiang Province (Grant No. YQ2022A008).
Author information
Authors and Affiliations
Contributions
The authors’ contributions are as follows: Jinzhou Song was in charge of the whole analyses and wrote the manuscript; Lei Hou assisted with sample analyses and revised the manuscript; Yifan Wang, Tao Zhang and Zhibin Zhang assisted with simulation analyses; Minghe Zhang, Yifan Jiang, Yi Chen and Rongzhou Lin participated in writing comments and editing. Yushu Chen revised the final manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Song, J., Wang, Y., Hou, L. et al. Reliability analysis of gear-bearing drive systems considering gear manufacturing and installation errors. Sci Rep 15, 23301 (2025). https://doi.org/10.1038/s41598-025-06446-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-06446-3