Introduction

The Pareto type II (PII) model is the most well-known of the five models that make up the Pareto family. In business, actuarial science, physical sciences, biological sciences, economics, engineering, income and wealth inequality research, theory of queuing, and size of cities data sets, the PII model, also known as the Lomax; see Lomax1, is a heavy-tail probability density. For more statistical papers that used the Lomax distribution, see Alsuhabi et al.2, Almetwally et al.3, Sapkota et al.4, Atchadé et al.5, Ahmad et al.6, Haj Ahmad et al.7, and Zaidi et al.8. The standard PII model, however, is regarded as a limiting model of residual lifetimes at great age and is part of the family of “monotonically decreasing” hazard/failure rate function (HRF) (see9 and10). In this work, however, we will present a new version whose HRF is part of the “upside down,” “monotonically decreasing” and “increasing-constant” families. The PII distribution was used by Harris11 and Atkinson and Harrison12 to describe and model wealth and income data. The PII distribution was utilised by Corbellini et al.13 to model the company size data. Sabry and Almetwally14 discussed estimation of the exponential Pareto distribution under ranked and double ranked set sampling designs. See Hassan Al-Ghamdi15 for real data applications in reliability testing and relaibility experiments. In addition to being seen as a hybrid of the standard gamma and exponential distributions, the PII model is a unique model form of the well-known Pearson type VI distribution. A heavy-tailed alternative model to the standard exponential, standard Weibull, and standard gamma distributions is proposed for the PII distribution, per16. Mustafa et al.17 discussed order statistics of inverse Pareto distribution. For additional information regarding the connection between the PII model, see Tadikamalla18, Almetwally et al.3, Durbey19, Korkmaz et al.20 and Minkah et al.21. If a random variable (rv) X has the following cumulative function (PDF) and the PII distribution with one parameter, \(\mathbf {\xi }_{3}\):

$$\begin{aligned} G_{\mathbf {\xi }_{3}}\left( x\right) =1-\left( 1+x\right) ^{-\mathbf {\xi } _{3}^{-1}}|x>0, \end{aligned}$$
(1)

where \(\mathbf {\xi }_{3}>0\) is the shape parameters, respectively. The primary goal of this work is to use the Poisson Topp-Leone (PTL) family, as established by Merovci et al. (2020), to give a flexible extension of the PII distribution. The PTL-G family’s CDF can be expressed as follows:

$$\begin{aligned} F_{\mathbf {\xi }_{1},\mathbf {\xi }_{2},\underline{\mathbf {\omega }}}\left( x\right) =\frac{1}{\Upsilon \left( \mathbf {\xi }_{1}\right) }\left( 1-\exp \left\{ -\frac{G_{\underline{\mathbf {\omega }}}\left( x\right) ^{\mathbf {\xi }_{2}}}{\mathbf {\xi }_{1}}\left[ 2-G_{\underline{\mathbf {\omega }}}\left( x\right) \right] ^{\mathbf {\xi }_{2}}\right\} \right) |x\in \mathbb {R}, \end{aligned}$$
(2)

where \(\mathbf {\xi }_{1}>0,\mathbf {\xi }_{2}>0\) and \(\Upsilon \left( \mathbf { \xi }_{1}\right) =1-\exp \left( -\mathbf {\xi }_{1}^{-1}\right)\), the vector \(\underline{\mathbf {\omega }}\) refers to the parameters vector of the base-line model. The CDF of the novel PII model can then be derived as

$$\begin{aligned} F_{\underline{\textbf{V}}}\left( x\right) =\frac{1}{\Upsilon \left( \mathbf { \xi }_{1}\right) }\left( 1-\exp \left\{ -\mathbf {\xi }_{1}^{-1}\left[ 1-\left( 1+x\right) ^{-2\mathbf {\xi }_{3}^{-1}}\right] ^{\mathbf {\xi } _{2}}\right\} \right) |x>0, \end{aligned}$$
(3)

The corresponding probability density function (PDF) of (3) can be written as

$$\begin{aligned} f_{\underline{\textbf{V}}}\left( x\right) =2\frac{\mathbf {\xi }_{1}^{-1} \mathbf {\xi }_{2}\mathbf {\xi }_{3}^{-1}}{\Upsilon \left( \mathbf {\xi } _{1}\right) }\frac{\left( 1+x\right) ^{-2\mathbf {\xi }_{3}^{-1}-1}\left[ 1-\left( 1+x\right) ^{-2\mathbf {\xi }_{3}^{-1}}\right] ^{\mathbf {\xi }_{2}-1} }{\exp \left\{ \mathbf {\xi }_{1}^{-1}\left[ 1-\left( 1+x\right) ^{-2\mathbf { \xi }_{3}^{-1}}\right] ^{\mathbf {\xi }_{2}}\right\} }|x>0. \end{aligned}$$
(4)

As \(x\rightarrow 0\), we have

$$\begin{aligned} f_{\underline{\textbf{V}}}\left( x\right) \approx 2\frac{\mathbf {\xi } _{1}^{-1}\mathbf {\xi }_{2}\mathbf {\xi }_{3}^{-1}}{\Upsilon \left( \mathbf { \xi }_{1}\right) }\left( 2\mathbf {\xi }_{3}^{-1}\right) ^{\mathbf {\xi } _{2}-1}x^{\mathbf {\xi }_{2}-1}. \end{aligned}$$

As \(x\rightarrow \infty\), we have

$$\begin{aligned} f_{\underline{\textbf{V}}}\left( x\right) \approx 2\frac{\mathbf {\xi } _{1}^{-1}\mathbf {\xi }_{2}\mathbf {\xi }_{3}^{-1}}{\Upsilon \left( \mathbf { \xi }_{1}\right) }\frac{\left( 1+x\right) ^{-2\mathbf {\xi }_{3}^{-1}-1}}{ \exp \left( \mathbf {\xi }_{1}^{-1}\right) }. \end{aligned}$$

The tail behavior of \(f_{\underline{\textbf{V}}}\left( x\right)\) for large x is dominated by

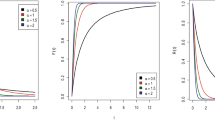
$$\begin{aligned} f_{\underline{\textbf{V}}}\left( x\right) \sim \frac{C}{\left( 1+x\right) ^{2 \mathbf {\xi }_{3}^{-1}+1}}, \end{aligned}$$

where \(C=2\frac{\mathbf {\xi }_{1}^{-1}\mathbf {\xi }_{2}\mathbf {\xi }_{3}^{-1} }{\exp \left( \mathbf {\xi }_{1}^{-1}\right) \Upsilon \left( \mathbf {\xi } _{1}\right) }\)is a constant. This indicates that the tail of the PDF decays polynomially with an exponent of \(2\mathbf {\xi }_{3}^{-1}+1\) as \(x\rightarrow \infty\). Hereafter, we will refer to the new model in (3) and (4) with the compound Pareto type II (CPII) model. Other PII extensions can be founded in Gupta et al.22, Lemonte and Cordeiro23, Cordeiro et al.24, Tahir et al.25, Alshanbari et al.26, Elbiely and Yousof27, Goual and Yousof28, Chesneau and Yousof29, Yadav et al.30, Hamed et al.31, Ibrahim and Yousof (2020), Abd El-Raheem et al.32, Haj Ahmad and Almetwally33, and Salem et al.34. The flexibility of the new PDF and its matching HRF are shown in Figures 1 and 2. where the HRF of the CPII can be “upside down,” “monotonically decreasing,” and “increasing-constant,” and the CPII density can be “right skewed with unimodal shape,” “right skewed with no peak,” and “left skewed with no peak”. The CPII model effectively captures asymmetric hazard rates in real life data with bimodal, nearly symmetric distributions. It can model a variety of skewness and kurtosis shapes, including U-skewness and various forms of mesokurtic, leptokurtic, and platykurtic distributions. This flexibility makes it suitable for a wide range of physical, social, and actuarial phenomena.

The CPII model proved its wide applicability in modeling the real-physical data sets against many well-known PII extensions. In modeling the times of failure of the aircraft windshields, the CPII model is statistically compared with many well-known PII versions. In statistical modeling of the times of service of the aircraft windshields, the CPII model is compared with many well-known PII extensions. Figure 1 gives some plots of the new PDF. It is clear from this figure that the new density function has a long tail on the right, and it may have one peak or no peak, and the tail may be down or up, and all of these properties qualify the distribution to deal with diverse data. Figure 2 gives some plots of the new HRF. Based on Figure 2, the HRF can be upside down, decreasing and increasing.

The importance and flexibility of the proposed reliability Peaks Above a Random Threshold Value at Risk (PORT-VAR) model are highlighted through its application to two distinct real data sets, demonstrating its robustness and adaptability in assessing extreme failure events and service times. For aircraft windscreen companies, PORT-VAR analysis is indispensable as it offers a rigorous and detailed examination of the product’s performance under rare but critical stress conditions. This analytical approach meticulously identifies the frequency and magnitude of failures that surpass predetermined VAR thresholds, allowing companies to gauge the upper limits of their windscreen products’ reliability under extreme circumstances. PORT-VAR analysis helps companies understand the upper bounds of product performance, guiding improvements in durability and safety. It enables optimization of design parameters to withstand high-stress conditions and informs material choices based on extreme performance data. Additionally, it supports the development of proactive maintenance strategies, preventing unexpected failures and extending the service life of windscreen products. Recently, Abiad et al.35 introduced a novel approach to reliability analysis by incorporating diverse copula structures into a new Fisk probability model. This advancement allows for a more flexible dependence structure between variables, improving the accuracy of reliability assessments in engineering and applied sciences. Ali et al.36 provided an in-depth exploration of statistical outliers, discussing their identification, impact on data interpretation, and potential methods for handling anomalies in many topics especially in risk analysis. Their work is crucial for ensuring robust statistical inference in various fields, including finance, healthcare, and quality control. Alizadeh et al.37 developed a new weighted Lindley distribution tailored for modeling extreme insurance claims. By refining the probability distribution to better fit heavy-tailed data, their model enhances risk assessment and decision-making in the insurance industry. Das et al.38 introduced a novel application of the Laplace distribution to analyze economic peaks and Value-at-Risk (VaR) in house price fluctuations. Their study provides a fresh perspective on risk modeling in real estate markets, offering insights for financial analysts and policymakers.

In the paper, we applied this comprehensive reliability PORT-VAR analysis to relaibility data sets, illustrating the model’s flexibility in adapting to various conditions and its effectiveness in delivering actionable insights. This approach not only reinforces the importance of the PORT-VAR model in ensuring the safety and longevity of aircraft windscreens but also underscores its role in guiding engineering decisions, enhancing product reliability, and supporting strategic maintenance planning. Through detailed analysis and application, the paper demonstrates how PORT-VAR can be leveraged to address critical challenges in windscreen reliability and contribute to the advancement of safety and performance standards in the aerospace industry. In this context, the mean-of-order-P (\(\hbox {MOO}^{P}\)) analysis under the mean squared error (MSE) and biases is presented due to \(P=5\). Moreover, a graphical assessment is presented for the \(\hbox {MOO}^{P}\), MSE and biases values.

Fig. 1
figure 1

Some plots of the new PDF.

Full size image
Fig. 2
figure 2

Some plots of the new HRF.

Full size image

Main characteristics

Useful expansions

Thanks to Merovci et al. (2020), the CPII model’s PDF in (3) can be expressed as follows

$$\begin{aligned} f_{\underline{\textbf{V}}}\left( x\right) =\overset{\infty }{\underset{\tau _{1},\tau _{2}=0}{\sum }}\left[ c_{\tau _{1},\tau _{2}}^{\left[ 1\right] } h_{\mathbf {\xi }_{2}^{*}}(x)-c_{\tau _{1},\tau _{2}}^{\left[ 2 \right] } h_{1+\mathbf {\xi }_{2}^{*}}(x)\right] , \end{aligned}$$
(5)

where \(h_{\gamma }(x)=\gamma G_{\underline{\mathbf {\omega }}}\left( x\right) ^{\gamma -1}g_{\underline{\mathbf {\omega }}}\left( x\right)\) refers to the exponentiated-PII (EPII) density,

$$\begin{aligned} c_{\tau _{1},\tau _{2}}^{\left[ 1\right] }=\left( \frac{1}{2}\right) ^{\tau _{2}-\mathbf {\xi }_{2}\left( \tau _{1}+1\right) }\frac{\mathbf {\xi } _{1}^{-\left( \tau _{1}+1\right) }\mathbf {\xi }_{2}\left( -1\right) ^{\tau _{1}+\tau _{2}}}{\tau _{1}!\Upsilon \left( \mathbf {\xi }_{1}\right) \mathbf { \xi }_{2}^{*}}\left( {\begin{array}{c}\mathbf {\xi }_{2}\left( \tau _{1}+1\right) -1\\ \tau _{2}\end{array}}\right) , \end{aligned}$$

and

$$\begin{aligned} c_{\tau _{1},\tau _{2}}^{\left[ 2\right] }=\left( \frac{1}{2}\right) ^{\tau _{2}-\mathbf {\xi }_{2}\left( \tau _{1}+1\right) }\frac{\mathbf {\xi } _{1}^{-\left( \tau _{1}+1\right) }\mathbf {\xi }_{2}\left( -1\right) ^{\tau _{1}+\tau _{2}}}{\tau _{1}!\Upsilon \left( \mathbf {\xi }_{1}\right) \left( 1+ \mathbf {\xi }_{2}^{*}\right) }\left( {\begin{array}{c}\mathbf {\xi }_{2}\left( \tau _{1}+1\right) -1\\ \tau _{2}\end{array}}\right) . \end{aligned}$$

Equation (5) allows for the expression of the density of X as a representation of EPII densities. Another way to rephrase the CDF of the CPII is as follows

$$\begin{aligned} F_{\underline{\textbf{V}}}\left( x\right) =\overset{\infty }{\underset{\tau _{1},\tau _{2}=0}{\sum }}\left[ c_{\tau _{1},\tau _{2}}^{\left[ 1\right] } H_{\mathbf {\xi }_{2}^{*}}(x)-c_{\tau _{1},\tau _{2}}^{\left[ 2 \right] } H_{1+\mathbf {\xi }_{2}^{*}}(x)\right] , \end{aligned}$$
(6)

where \(\mathbf {\xi }_{2}^{*}=\mathbf {\xi }_{2}\left( \tau _{1}+1\right) +\tau _{2}\) and \(H_{\mathbf {\xi }_{2}^{*}}(x)\) refers to the CDF of the EPII model.

Ordinary moment

The \(r^{\text {th}}\) ordinary moment of X is given by \(\mu _{r,X}^{\prime }= \mathbb {E}(X^{r})=\,\int _{-\infty }^{\infty }\,x^{r}\,f_{\underline{\textbf{V }}}\left( x\right) dx.\)Then we obtain

$$\begin{aligned} \mu _{r,X}^{\prime }=\overset{\infty }{\underset{\tau _{1},\tau _{2}=0}{\sum }}\left[ c_{\tau _{1},\tau _{2}}^{\left[ 1\right] } \mathbb {E}(Z_{ \mathbf {\xi }_{2}^{*}}^{r})-c_{\tau _{1},\tau _{2}}^{\left[ 2\right] } \mathbb {E}(Z_{1+\mathbf {\xi }_{2}^{*}}^{r})\right] . \end{aligned}$$
(7)

Henceforth, \(Z_{\left( \mathbf {\xi }_{2}^{*}\right) }\) denotes the EPII distribution with power parameter \(\mathbf {\xi }_{2}^{*}>0\).

$$\begin{aligned} \mu _{r,X}^{\prime }=\overset{\infty }{\underset{\tau _{1},\tau _{2}=0}{\sum }}\sum _{\tau _{3}=0}^{r}\left[ \begin{array}{c} c_{\tau _{1},\tau _{2}}^{\left[ 1\right] } \mathbf {\delta }_{\tau _{3}}^{\left( \mathbf {\xi }_{2}^{*},r\right) }B\left( \mathbf {\xi } _{2}^{*},1+\left( \tau _{3}-r\right) \mathbf {\xi }_{3}\right) \\ -c_{\tau _{1},\tau _{2}}^{\left[ 2\right] } \mathbf {\delta }_{\tau _{3}}^{\left( 1+\mathbf {\xi }_{2}^{*},r\right) }B\left( 1+\mathbf {\xi } _{2}^{*},1+\left( \tau _{3}-r\right) \mathbf {\xi }_{3}\right) \end{array} \right] |_{\left( \mathbf {\xi }_{3}^{-1}>r\right) }. \end{aligned}$$

where

$$\begin{aligned} \mathbf {\delta }_{\tau _{3}}^{\left( a,r\right) }=a\left( -1\right) ^{\tau _{3}}\left( {\begin{array}{c}r\\ \tau _{3}\end{array}}\right) , \end{aligned}$$

and

$$\begin{aligned} B(\nu _{1},\nu _{2})=\int _{0}^{1}\mathfrak {\hslash }^{\nu _{1}-1}\left( 1-\mathfrak {\hslash }\right) ^{\nu _{2}-1}d\mathfrak {\hslash }. \end{aligned}$$

Incomplete moments

The \(\mathfrak {\hslash }^{\text {th}}\) incomplete moment, say \(\mathcal {I}_{ \mathfrak {\hslash },x}\left( t\right)\), of X can be expressed from (9) as \(\mathcal {I}_{\mathfrak {\hslash },x}\left( t\right) =\int _{-\infty }^{t}x^{ \mathfrak {\hslash }}f_{\underline{\textbf{V}}}\left( x\right) dx.\)Then

$$\begin{aligned} \mathcal {I}_{\mathfrak {\hslash },x}\left( t\right) =\overset{\infty }{ \underset{\tau _{1},\tau _{2}=0}{\sum }}\sum _{\tau _{3}=0}^{\mathfrak { \hslash }}\left[ \begin{array}{c} c_{\tau _{1},\tau _{2}}^{\left[ 1\right] }\mathbf {\delta }_{\tau _{3}}^{\left( \mathbf {\xi }_{2}^{*},\mathfrak {\hslash }\right) } B_{t}\left( \mathbf {\xi }_{2}^{*},1+\left( \tau _{3}-\mathfrak {\hslash } \right) \mathbf {\xi }_{3}\right) \\ -c_{\tau _{1},\tau _{2}}^{\left[ 2\right] } \mathbf {\delta }_{\tau _{3}}^{\left( 1+\mathbf {\xi }_{2}^{*},\mathfrak {\hslash }\right) } B_{t}\left( 1+\mathbf {\xi }_{2}^{*},1+\left( \tau _{3}-\mathfrak { \hslash }\right) \mathbf {\xi }_{3}\right) \end{array} \right] |_{\left( \mathbf {\xi }_{3}^{-1}>\mathfrak {\hslash }\right) }, \end{aligned}$$
(8)

where \(B_{a_{3}}(a_{1},a_{2})=\int _{0}^{a_{3}}\mathfrak {w} ^{a_{1}-1}\left( 1-\mathfrak {w}\right) ^{a_{2}-1}d\mathfrak {w}.\)

Mean deviations

The mean deviations about the mean \([d_{x,\mu _{1}^{\prime }}=\mathbb {E} (|x-\mu _{1}^{\prime }|)]\) and about the median \(\left[ m_{x,M}=\mathbb {E} \left( \left| x-M\right| \right) \right]\) of X are given by \(d_{x,\mu _{1}^{\prime }}=2\mu _{1,x}^{^{\prime }}F(\mu _{1,x}^{\prime })-2 \mathcal {I}_{1,x}(\mu _{1,x}^{\prime })\) and \(m_{x,M}=\mu _{1,x}^{\prime }-2 \mathcal {I}_{1,x}\left( M\right)\), respectively, where \(\mu _{1,x}^{\prime }=\mathbb {E}\left( x\right)\), \(M=Med(x)=Q\left( \frac{1}{2}\right)\) is the median and \(\mathcal {I}_{1,x}\left( t\right)\) is the first incomplete moment given by (8) with \(\mathfrak {\hslash }=1\). Ageneral equation for \(\mathcal {I}_{1,x}\left( t\right)\) can be derived from (8) as

$$\begin{aligned} \mathcal {I}_{1,x}\left( t\right) =\overset{\infty }{\underset{\tau _{1},\tau _{2}=0}{\sum }}\sum _{\tau _{3}=0}^{1}\left[ \begin{array}{c} c_{\tau _{1},\tau _{2}}^{\left[ 1\right] }\mathbf {\delta }_{\tau _{3}}^{\left( \mathbf {\xi }_{2}^{*},1\right) } B_{t}\left( \mathbf {\xi }_{2}^{*},1+\frac{\tau _{3}-1}{\mathbf {\xi }_{3}^{-1}}\right) \\ -c_{\tau _{1},\tau _{2}}^{\left[ 2\right] } \mathbf {\delta }_{\tau _{3}}^{\left( 1+\mathbf {\xi }_{2}^{*},1\right) } B_{t}\left( 1+ \mathbf {\xi }_{2}^{*},1+\frac{\tau _{3}-1}{\mathbf {\xi }_{3}^{-1}}\right) \end{array} \right] |_{\left( \mathbf {\xi }_{3}^{-1}>1\right) }, \end{aligned}$$

Moment generating function

The moment generating function (MGF) can be derived from equation (5) as

$$\begin{aligned} M_{X}\left( t\right) =\overset{\infty }{\underset{\tau _{1},\tau _{2},r=0}{ \sum }}\sum _{\tau _{3}=0}^{r}\frac{t^{r}}{r!}\left[ \begin{array}{c} c_{\tau _{1},\tau _{2}}^{\left[ 1\right] } \mathbf {\delta }_{\tau _{3}}^{\left( \mathbf {\xi }_{2}^{*},r\right) }B\left( \mathbf {\xi } _{2}^{*},1+\left( \tau _{3}-r\right) \mathbf {\xi }_{3}\right) \\ -c_{\tau _{1},\tau _{2}}^{\left[ 2\right] } \mathbf {\delta }_{\tau _{3}}^{\left( 1+\mathbf {\xi }_{2}^{*},r\right) }B\left( 1+\mathbf {\xi } _{2}^{*},1+\left( \tau _{3}-r\right) \mathbf {\xi }_{3}\right) \end{array} \right] |_{\left( \mathbf {\xi }_{3}^{-1}>r\right) }, \end{aligned}$$

Numerical and graphical analysis

By analyzing the \(\mu _{1}^{\prime }\), \(\mu _{2}\), skewness \(\left( \textbf{S }_{X}\right)\), kurtosis \(\left( \textbf{K}_{X}\right)\) and dispersion index \(\left( \textbf{D}_{X}\right)\) numerically in Table 1, it is noted that, the \(\textbf{S}_{X}\) can be \(>0\). The spread for the \(\textbf{K}_{X}\) is ranging from 9.4557 to 4088911. The \(\textbf{D}_{X}\) can be in \(\left( 0,1\right)\) and also \(>1\) so the CPII model may be used as an “under-dispersed” and “over-dispersed” model. Three-dimensional skewness charts are shown in Figure 3. Three-dimensional kurtosis graphs are shown in Figure 4. Drawing from Figure 3, the CPII model’s skewness can assume several beneficial shapes. According to Figure 4, the CPII model’s kurtosis can take on a variety of useful shapes.

Table 1 \(\mu _{1}^{\prime }\), \(\mu _{2}\), \(\textbf{S} _{X},\)\(\textbf{K}_{X}\) and \(\textbf{D}_{X}\) of the CPII model.
Full size table
Fig. 3
figure 3

Three-dimensional skewness plot.

Full size image
Fig. 4
figure 4

Three dimensional kurtosis plot.

Full size image

Probability weighted moments

The \((\mathfrak {\hslash },r)^{th}\) probability weighted moments (PWM) of X following the CPII model, say \(\rho _{\mathfrak {\hslash },r}\), is formally defined by

$$\begin{aligned} \rho _{\mathfrak {\hslash },r}=\mathbb {E}\left\{ x^{\mathfrak {\hslash }}\,F_{ \underline{\textbf{V}}}\left( x\right) ^{r}\right\} =\int \nolimits _{-\infty }^{\infty }x^{\mathfrak {\hslash }}\,F_{\underline{\textbf{V}}}\left( x\right) ^{r}\,f_{\underline{\textbf{V}}}\left( x\right) \,dx. \end{aligned}$$

Using (5) and (6), we have

$$\begin{aligned} f_{\underline{\textbf{V}}}\left( x\right) \,F_{\underline{\textbf{V}} }(x)^{r}=\sum _{\tau _{1},\tau _{2}=0}^{\infty }\left[ \mathbf {\nu }_{\tau _{1},\tau _{2}}^{\left[ 1\right] } h_{\mathbf {\xi }_{2}^{*}}(x)- \mathbf {\nu }_{\tau _{1},\tau _{2}}^{\left[ 2\right] } h_{1+\mathbf { \xi }_{2}^{*}}(x)\right] , \end{aligned}$$

where

$$\begin{aligned} \mathbf {\nu }_{\tau _{1},\tau _{2}}^{\left[ 1\right] }=\sum _{\tau _{2}=0}^{\infty }\left( \frac{1}{2}\right) ^{\tau _{2}-\mathbf {\xi } _{2}\left( \tau _{1}+1\right) }\frac{\mathbf {\xi }_{2}\mathbf {\xi } _{1}^{\tau _{1}+1}\left( 1+\tau _{2}\right) ^{\tau _{1}}\left( -1\right) ^{\tau _{1}+\tau _{2}+\tau _{2}}}{\tau _{1}!\mathbf {\xi }_{2}^{*}\left[ \Upsilon \left( \mathbf {\xi }_{1}\right) \right] ^{1+r}}\left( {\begin{array}{c}r\\ \tau _{2}\end{array}}\right) \left( {\begin{array}{c}\mathbf {\xi }_{2}\left( \tau _{1}+1\right) -1\\ \tau _{2}\end{array}}\right) \end{aligned}$$

and

$$\begin{aligned} \mathbf {\nu }_{\tau _{1},\tau _{2}}^{\left[ 2\right] }=\sum _{\tau _{2}=0}^{\infty }\left( \frac{1}{2}\right) ^{\tau _{2}-\mathbf {\xi } _{2}\left( \tau _{1}+1\right) }\frac{\mathbf {\xi }_{2}\mathbf {\xi } _{1}^{\tau _{1}+1}\left( 1+\tau _{2}\right) ^{\tau _{1}}\left( -1\right) ^{\tau _{1}+\tau _{2}+\tau _{2}}}{\tau _{1}!\left[ 1+\mathbf {\xi }_{2}^{*}\right] \left[ \Upsilon \left( \mathbf {\xi }_{1}\right) \right] ^{1+r}} \left( {\begin{array}{c}r\\ \tau _{2}\end{array}}\right) \left( {\begin{array}{c}\mathbf {\xi }_{2}\left( \tau _{1}+1\right) -1\\ \tau _{2}\end{array}}\right) . \end{aligned}$$

Then, the \((\mathfrak {\hslash },r)^{th}\) PWM can then be written as

$$\begin{aligned} \rho _{\mathfrak {\hslash },r}=\sum _{\tau _{1},\tau _{2}=0}^{\infty }\sum _{\tau _{3}=0}^{\mathfrak {\hslash }}\left[ \begin{array}{c} \mathbf {\nu }_{\tau _{1},\tau _{2}}^{\left[ 1\right] } \mathbf {\delta }_{\tau _{3}}^{\left( \mathbf {\xi }_{2}^{*},\mathfrak {\hslash }\right) }B\left( \mathbf {\xi }_{2}^{*},1+\left( \tau _{3}-\mathfrak {\hslash } \right) \mathbf {\xi }_{3}\right) \\ -\mathbf {\nu }_{\tau _{1},\tau _{2}}^{\left[ 2\right] } \mathbf { \delta }_{\tau _{3}}^{\left( 1+\mathbf {\xi }_{2}^{*},\mathfrak {\hslash } \right) }B\left( 1+\mathbf {\xi }_{2}^{*},1+\left( \tau _{3}-\mathfrak { \hslash }\right) \mathbf {\xi }_{3}\right) \end{array} \right] |_{\left( \mathbf {\xi }_{3}^{-1}>\mathfrak {\hslash }\right) }\,\,. \end{aligned}$$

Residual and reversed moment

The \(\mathfrak {n}^{\text {th}}\) moment of the residual life of X is given by

$$\begin{aligned} m_{\mathfrak {n},x}(t)=\frac{1}{1-F_{\underline{\textbf{V}}}(t)}\overset{ \infty }{\underset{\tau _{1},\tau _{2}=0}{\sum }}\sum _{r=0}^{\mathfrak {n} }\sum _{\tau _{3}=0}^{\mathfrak {n}}c_{r}^{\left[ 1\right] }\left\{ \begin{array}{c} c_{\tau _{1},\tau _{2}}^{\left[ 1\right] } \mathbf {\delta }_{\tau _{3}}^{\left( \mathbf {\xi }_{2}^{*},\mathfrak {n}\right) }\left[ \begin{array}{c} B\left( \mathbf {\xi }_{2}^{*},1+\left( \tau _{3}-\mathfrak {n}\right) \mathbf {\xi }_{3}\right) \\ -B_{t}\left( \mathbf {\xi }_{2}^{*},1+\left( \tau _{3}-\mathfrak {n} \right) \mathbf {\xi }_{3}\right) \end{array} \right] \\ -c_{\tau _{1},\tau _{2}}^{\left[ 2\right] }\mathbf {\delta }_{\tau _{3}}^{\left( 1+\mathbf {\xi }_{2}^{*},\mathfrak {n}\right) }\left[ \begin{array}{c} B\left( 1+\mathbf {\xi }_{2}^{*},1+\left( \tau _{3}-\mathfrak {n}\right) \mathbf {\xi }_{3}\right) \\ -B_{t}\left( 1+\mathbf {\xi }_{2}^{*},1+\left( \tau _{3}-\mathfrak {n} \right) \mathbf {\xi }_{3}\right) \end{array} \right] \end{array} \right\} |_{\left( \mathbf {\xi }_{3}^{-1}>\mathfrak {n}\right) }, \end{aligned}$$

where \(c_{r}^{\left[ 1\right] }=\left( {\begin{array}{c}\mathfrak {n}\\ r\end{array}}\right) \left( -t\right) ^{ \mathfrak {n}-r}.\) The \(\mathfrak {n}^{\text {th}}\) moment of the reversed residual life of X becomes

$$\begin{aligned} M_{\mathfrak {n},x}(t)=\frac{1}{F_{\underline{\textbf{V}}}(t)}\overset{\infty }{\underset{\tau _{1},\tau _{2}=0}{\sum }}\sum _{r=0}^{\mathfrak {n} }\sum _{\tau _{3}=0}^{\mathfrak {n}}c_{r}^{\left[ 2\right] }\left[ \begin{array}{c} c_{\tau _{1},\tau _{2}}^{\left[ 1\right] } \mathbf {\delta }_{\tau _{3}}^{\left( \mathbf {\xi }_{2}^{*},\mathfrak {n}\right) }B_{t}\left( \mathbf {\xi }_{2}^{*},1+\left( \tau _{3}-\mathfrak {n}\right) \mathbf {\xi }_{3}\right) \\ -c_{\tau _{1},\tau _{2}}^{\left[ 2\right] }\mathbf {\delta }_{\tau _{3}}^{\left( 1+\mathbf {\xi }_{2}^{*},\mathfrak {n}\right) } B_{t}\left( 1+\mathbf {\xi }_{2}^{*},1+\left( \tau _{3}-\mathfrak {n} \right) \mathbf {\xi }_{3}\right) \end{array} \right] |_{\left( \mathbf {\xi }_{3}^{-1}>\mathfrak {n}\right) }, \end{aligned}$$

where \(c_{r}^{\left[ 2\right] }=\left( -1\right) ^{r}\left( {\begin{array}{c}\mathfrak {n}\\ r\end{array}}\right) t^{\mathfrak {n}-r}.\)

Simulation study

The purpose of this section is to evaluate the maximum likelihood (ML) method’s performance. The implementation of MLE has been widely discussed and applied in various domains. For example, see Rytgaard et al.39, Xu et al.40 and Yan et al.41. In general, evaluation of any estimation method’s performance can be done by numerical, graphical, or both methods. We can conduct the simulation experiments to evaluate the finite sample behaviour of the maximum likelihood estimations (MLEs) graphically and with the use of biases and mean squared errors (MSEs). Essentially, the hihjt biases of MLEs can be corrected by using the resampling bootstrapping method. The bootstrapping percentile approach can also be used to produce the estimations using intervals. The suggested version may also be subjected to likelihood ratio tests. The assessment was based on \(N=\)1000 replication for all \(n|_{\left( n=10,20,\ldots ,1500\right) }.\) The following algorithm is considered:

  1. 1.

    Generate N=1000 samples of size \(n|_{\left( n=50,100,\ldots ,500\right) }\) from the CPII distribution using (4);

    $$\begin{aligned} x_{u}=\left( \left\{ 1-\left[ -\mathbf {\xi }_{1}\ln \left( 1-u\left[ \Upsilon \left( \mathbf {\xi }_{1}\right) \right] \right) \right] ^{\frac{1}{ \mathbf {\xi }_{2}}}\right\} ^{-\frac{1}{2\mathbf {\xi }_{3}^{-1}}}-1\right) . \end{aligned}$$
  2. 2.

    Compute the MLEs for the N=1000,

  3. 3.

    Compute the standard errors (SEs) of the MLEs for the N=1000 samples.

  4. 4.

    Compute the biases and mean squared errors (MSEs) given for \(\underline{\textbf{V}}=\mathbf {\xi }_{1},\mathbf {\xi }_{2},\mathbf {\xi }_{3}\). We repeated these steps for \(\mathfrak {n}|_{\left( \mathfrak {n} =10,20,\ldots ,1500\right) }\) with \(\mathbf {\xi }_{1}=1,2,..,1000,\mathbf { \xi }_{2}=1,2,..,1000\) and \(\mathbf {\xi }_{3}=1,2,..,1000\), so computing biases\(\left( \text {Bias}_{\underline{\textbf{V}}}(\mathfrak {n})\right)\), MSEs \(\left( MSE_{h}(\mathfrak {n})\right)\) for \(\underline{\textbf{V}}= \mathbf {\xi }_{1},\mathbf {\xi }_{2},\mathbf {\xi }_{3}\)and \(\mathfrak {n} |_{\left( \mathfrak {n}=10,20,\ldots ,1500\right) }\) where

    $$\begin{aligned} Bias_{\underline{\textbf{V}}}(\mathfrak {n})|_{\left( \underline{\textbf{V}}= \mathbf {\xi }_{1},\mathbf {\xi }_{2},\mathbf {\xi }_{3}\right) }=\frac{1}{1500} \sum _{\mathfrak {n}=1}^{1500}\left( \widehat{\underline{\textbf{V}}}_{ \mathfrak {n}}-\underline{\textbf{V}}\right) , \end{aligned}$$

    and

    $$\begin{aligned} MSE_{\underline{\textbf{V}}}(\mathfrak {n})|_{\left( \underline{\textbf{V}}= \mathbf {\xi }_{1},\mathbf {\xi }_{2},\mathbf {\xi }_{3}\right) }=\frac{1}{1500} \sum _{\mathfrak {n}=1}^{1500}\left( \widehat{\underline{\textbf{V}}}_{ \mathfrak {n}}-\underline{\textbf{V}}\right) ^{2}. \end{aligned}$$

Figure 5, Figure 6 and Figure 7 give the biases (left panels) and MSEs (right panels) for the parameters \(\mathbf {\xi }_{1},\mathbf {\xi }_{2},\mathbf {\xi }_{3}\) andrespectively. The left panels from Figure 5, Figure 6 and Figure 7 show how the three biases vary with respect to \(\mathfrak {n}|_{\left( \mathfrak {n}=10,20,\ldots ,1500\right) }\). The right panels from Figure 5, Figure 6 and Figure 7 show show how the three MSEs vary with respect to \(\mathfrak {n}|_{\left( \mathfrak {n}=10,20,\ldots ,1500\right) }\). In Figure 6, the red broken line indicates that the biases are zero. As n goes to \(\infty\), the biases for each parameter are often negative, as seen in Figure 5, Figure 6 and Figure 7 (left panels). The right panels of Figure 5, Figure 6 and Figure 7 show that as n approaches \(\infty\), the MSEs for every parameter approach zero. The ML approach is highly advised for estimating the unknown model parameters based on Figure 5, Figure 6 and Figure 7.

Fig. 5
figure 5

biases and MSE for \(\mathbf {\xi }_{1}\).

Full size image
Fig. 6
figure 6

biases and MSE for \(\mathbf {\xi }_{2}.\).

Full size image
Fig. 7
figure 7

biases and MSE for \(\mathbf {\xi }_{3}\).

Full size image

Applications

Two real-life examples are given in this section to highlight the significance and adaptability of the CPII paradigm. The standard PII model, exponentiated PII (EPII), four-paramete Kumaraswamy PII (KmPII), four-paramete Macdonald PII (McPII), four-paramete Beta PII (BPII), three-parameter gamma PII (GaPII), three-parameter transmuted the three-parameter Topp-Leone PII (TTLPII), Reduced TTLPII (RTTLPII), three-parameter odd log-logistic PII (OLLPII), reduced OLLPII (ROLLPII), two-parameterreduced Burr-Hatke PII (RBHPII), three-parameter special generalised mixture PII (SGMPII), and three-parameter proportional reversed hazard rate PII (PRHRPII) are compared to the fits of the CPII.

The first dataset, which is provided by Murthy et al.42, shows the instances when the aircraft windscreen failed (84 observations). The second piece of data is the 63 aircraft windscreens’ service times, which are likewise provided by Murthy et al.42. The real-lifed data sets43 and Goual et al.44 have to offer are very helpful as well. Presented here are the kernel density estimations (KDEs) to investigate the initial density shape for the two real datasets in a nonparametric manner (see Figures 8 (top left) and 9 (top left). “Bimodal and positive skewed” is how the nonparametric KDE for the first dataset is displayed in Figure 8 (top left). Nonparametric KDE is likewise “bimodal and positive skewed” for the second dataset, as Figure 9 (top left) illustrates. The box-plot is shown in Figures 8 (bottom left) and 9 (bottom left) to help identify the extremes. We can see from Figures 8 (bottom left) and 9 (bottom left) that neither of the two real-life data sets contained any extreme values.

Furthermore, a variety of graphical methods will be examined, including the skewness-kurtosis plot (also known as the Cullen and Frey plot) for examining the initial fit to various theoretical distributions, including the logistic, uniform, normal, exponential, beta, and Weibull models. Plotting is used to apply bootstrapping with greater accuracy. A summary of a distribution’s characteristics is provided by the Cullen and Frey plot, which compares distributions in the space of squared skewness and kurtosis. The Cullen and Frey plot for the aeroplane windscreen data failure times is shown in Figure 10. The Cullen and Frey plot for the second data set is shown in Figure 11. The fitting PDF (upper left panel) and estimated HRF (upper right panel) are displayed in Figure 12. The fitted PDF (top left panel) and estimated HRF (top right panel) are displayed in Figure 13. The aircraft windscreen data’s failure times are fitted by the CPII model using Figure 12. The aeroplane windscreen data’s times of service are fitted by the CPII model based on Figure 13.

The competitive versions are compared using the Bayesian information criterion (BIC), Akaike IC (AIC), Hannan-Quinn IC (HQIC), and Consistent AIC (CAIC) goodness-of-fit statistic tests. Tables 3 and 4 present the findings for the times of failure data (initial data set). Regarding the times of service data (the second data set), Tables 5 and 6 present the findings. The MLEs and standard errors (SEs) for the failure data timings are listed in Table 3. The MLEs and matching SEs for the times of service data are listed in Table 5. The goodness-of-fits and \(-\hat{\ell }\) statistics for the times of failure data are listed in Table 4. The goodness-of-fits and \(-\hat{\ell }\) statistics for the times of service data are listed in Table 6. Tables 4 and 6 show that, out of all the fitted models, the CPII model has the lowest values for the CAIC=167.4124, AIC=v, BIC=174.4048, and HQIC=170.0439 values. Therefore, based on the CAIC=185.6753, AIC=185.2686, BIC=191.698, and HQIC=187.7973 criterion, the CPII model might be deemed the best model. Table 2 provides the summary statistics for the times of failure and times of service respectively.

Table 2 Summary statistics.
Full size table
Table 3 Estimation results for times of failure data.
Full size table
Table 4 Statistics for times of failure data.
Full size table
Table 5 Estimation results for times of service data.
Full size table
Table 6 Statistics for the times of service data.
Full size table
Fig. 8
figure 8

KDE and box plots for data set I.

Full size image
Fig. 9
figure 9

KDE and box plots for data set II.

Full size image
Fig. 10
figure 10

Cullen and Frey plot for times of failure data.

Full size image
Fig. 11
figure 11

Cullen and Frey plot for times of service data.

Full size image
Fig. 12
figure 12

FPDF and FHRF plots for failure data.

Full size image
Fig. 13
figure 13

FPDF and FHRF plots for service data.

Full size image

Reliability PORT-VAR analysis and assessment

As highlighted in the research conducted by Aljadani et al.45, Alizadeh et al.46, and Yousof et al.47, varying the Mean of Order-P (MOO\(^{P}\)) allows for a more comprehensive analysis. This approach is frequently applied to multiple values of P (\(P\in I^{+}=1,2,3,..\).) to assess how different moments affect the dataset. Such multi-order analysis is particularly important in the field of finance, where understanding both central trends and extreme risks is essential for making informed decisions (see also Shehata et al.48 and Yousof et al.49). The \(\hbox {MOO}^{P}\) is mathematically defined as

$$\begin{aligned} \text {MOO}^{P}=\left( \frac{1}{n}\overset{n}{\underset{i=1}{\sum }} x_{i}^{P}\right) ^{\frac{1}{P}}, \end{aligned}$$

In this equation, \(x_{i}\) denotes the individual data points, nn represents the total number of data points, and P indicates the order. For \(P=1\), the \(\hbox {MOO}^{P}\) simplifies to the arithmetic mean. When \(P=2\), it yields the quadratic mean, also known as the root mean square, which emphasizes larger values in the dataset. For \(P=0\), the \(\hbox {MOO}^{P}\) results in the geometric mean, though this is not strictly defined within the \(\hbox {MOO}^{P}\) framework and is applicable only when all \(x_{i}\)\(>0\). As the value of P increases, the \(\hbox {MOO}^{P}\) becomes increasingly sensitive to extreme values. For instance, the quadratic mean (with \(P=2\)) assigns greater weight to larger observations compared to the arithmetic mean. This characteristic makes the \(\hbox {MOO}^{P}\) a valuable tool for capturing the impact of outliers and understanding the distribution of reliability data more effectively. By utilizing varying orders of P, analysts can gain deeper insights into the behavior of datasets, particularly in contexts where extremes play a crucial role in risk assessment and decision-making processes. The field of risk analysis, particularly under insurance, reliability and claim-size data, has seen significant advancements through the introduction of novel statistical models. These models address complexities in real-world data, including asymmetry, bimodality, and heavy-tailed distributions. Shrahili et al.50 introduced an asymmetric density function for analyzing risk claim-size data, particularly in the context of bimodal distributions. This model addresses the challenge of bimodal data patterns, which often occur in insurance and financial datasets. In the context of bimodal and symmetric data modeling, Yousof et al.51 presented a novel model for quantitative risk assessment. Yousof et al.52 introduced the reciprocal Weibull extension, which provides a robust framework for modeling extreme values in insurance datasets. Similarly, Ibrahim et al.53 proposed the compound reciprocal Rayleigh model, a model designed for left-skewed insurance data. Yousof et al.54 explored the use of the bimodal heavy-tailed Burr XII model in insurance risk analysis. In another study, Alizadeh et al.55 introduced a novel XGamma extension for risk analysis under reinsurance data. Loubna et al.56 introduced the quasi-xgamma frailty model, which addresses the heterogeneity problem in emergency care data. In a related study, Teghri et al.57 proposed a two-parameter Lindley-frailty model. The integration of novel probability models (continuous and discrete) into economic and actuarial risk analysis is further demonstrated by Elbatal et al.58 Afify et al.59, Teamah et al.60, and Yousof et al.61. Furthermore, Alizadeh et al.46 extended the Gompertz model, focusing on extreme stress data. The authors employed this model in assessing risk under extreme conditions, which is essential for industries exposed to high-risk environments, such as insurance and finance. The study’s use of statistical threshold risk analysis highlights its practical relevance in risk-sensitive industries.

Aircraft windscreen safety, dependability, and cost-effectiveness depend on the analysis and assessment of reliability PORT-VAR. These studies assist control hazards, facilitate maintenance scheduling, guarantee adherence to safety regulations, and offer insightful information on how components behave in harsh environments. Companies can improve the safety and dependability of crucial aviation components by concentrating on extreme values and the dangers that go along with them. Due to Aljadani et al.45 and Yousof et al.47, the goal of PORT-VAR analysis is to comprehend the behaviour of data points that surpass a given threshold. This may entail examining impact forces or stress levels that exceed typical operating circumstances in the case of aircraft windscreens.

A PORT-VAR method study of extreme failures is shown in Table 7. A PORT-VAR method study of times of service is shown in Table 8. The purpose of this analysis is to determine the frequency and magnitude of failure values exceeding specific VaR thresholds. This kind of examination is essential to comprehending the dependability of parts in harsh environments, like aeroplane windscreens. The minimum (Min.) and maximum (Max.) value among the peaks exceeding the threshold are given 1\(^{st}\) Quartile (1\(^{st}\) Qu.), the median, the mean and 3\(^{rd}\) Quartile (3\(^{rd}\) Qu.) of peaks are calculated. The VAR-threshold under CL=50%, 60%, 70%, 75%, 80%, 85%, 90%, 95% and 99% presented. the N. of peaks above VAR-threshold are calculated. As a defults, we considered \(P=5\) and therefore we calculated MOO \(^{5}\).

Moreover, we presented Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 for \(\hbox {MOO}^{P}\) analysis. Figure 14 shows the hisograms and the peaks above VAR-threshold for CL=50%, 60%, 70%, 75%, 80%, 85%, 90%, 95% and 99% respectively for the extreme failures. Figure 15 illustrates the hisograms and the peaks above VAR-threshold for CL=50%, 60%, 70%, 75%, 80%, 85%, 90%, 95% and 99% respectively for the extreme times of service. Figure 16 presents a graphical description for the assessment of the \(\hbox {MOO}^{P}\) analysis for the extreme failures. Figure 17 provides a graphical description for the MOO\(^{P}\) values, MSE and biases for the extreme failures. Figure 18 gives a graphical description for the assessment of the \(\hbox {MOO}^{P}\) analysis for the extreme times of service. Figure 19 shows a graphical description for the \(\hbox {MOO}^{P}\) values, mean squared error and biases for the extreme times of service.

The evaluation of extreme failures is the main topic of Table 7. It describes how many peaks are above certain VaR thresholds, which range from 50% to 99%, and gives an overview of these peaks with the lowest, maximum, median, first quartile, mean, and third quartile values. Understanding the distribution and frequency of failure events at different risk categories is made easier by this study. Based on Table 7, we note that:

  1. 1.

    The VAR-threshold=2.35 |CL=50%. Then the VAR-threshold decreased to reach 0.26 |CL=59%. As the confidence level rises, the VAR-threshold values gradually drop. As we go from higher to lower confidence levels, this graph illustrates how criteria to identify extreme values become more stringent. Higher thresholds concentrate on the more uncommon and severe failures, while lower thresholds capture more frequent and less severe extreme readings. These thresholds can be analysed to determine the risk and reliability of severe events, which is important information for performance and safety assessments in areas such as aircraft windscreen reliability.

  2. 2.

    The nubmer of peaks above VAR-threshold is 42 for VAR-threshold=2.35 at CL=50. Then, it inceased to 83 for VAR-threshold=0.26 at CL=99%. As the threshold gets smaller, there are more peaks over the VAR-threshold, which indicates that a wider range of extreme values are being captured.

This analysis is extended to severe service times in Table 8. Similar summary information are provided, and it assesses the frequency with which service times surpass designated VaR criteria. Determining the dependability of windscreens over extended periods of use and in adverse environments requires this evaluation. Based on Table 8, it is seen thatL

  1. 1.

    The VAR-threshold is 2.06 at 50% confidence level, and there are 31 peaks (or extreme service times) above it. Because of its relatively high threshold, the more significant but less common extreme service times are captured. The thirty-one peaks show a modest degree of extreme values, indicating that although some service periods are lengthy, they are not the longest. However, the criterion is 0.10 at the 99% confidence level, and 62 peaks are over this value. Nearly all data points fall below the incredibly low criterion of 0.10, leading to the classification of 62 peaks as severe. This emphasises how frequently and to what extent exceptional service times occur, showing that nearly all observations at this level are considered extreme.

  2. 2.

    The findings show that the number of peaks (extreme service times) rises when the VAR-threshold falls. Since more data points are captured as extreme values at a lower threshold, this tendency is expected. The number of severe service times increases significantly as the criterion becomes less restrictive, as seen by the increase from 31 peaks at the 50% CL to 62 peaks at the 99% CL. This data is essential for determining the frequency and severity of extreme service times that may have an impact on performance and safety, as well as the component’s reliability and risk.

Table 7 PORT-VAR analysis and assessment for extreme failures.
Full size table
Table 8 PORT-VAR analysis and assessment for extreme times of service.
Full size table

Generally, a considerable number of peaks over certain Value-at-Risk (VaR) thresholds for extreme failures are shown in the data. As the VAR-threshold drops, more peaks appear, indicating that extreme failure occurrences occur more frequently at lower threshold values. There is also a significant frequency of peaks exceeding the VaR standards during excessive periods of service. Similar to Table 7, the frequency of peaks increases as the threshold drops, but the overall service time values fluctuate noticeably, indicating the variability of extreme service circumstances.

There are fewer peaks at higher VaR thresholds (such as 50% and 60%), which suggests that there are fewer extreme failure events at these levels. Lower criteria, such as 95% and 99%, on the other hand, exhibit more peaks, indicating that dramatic failures occur more frequently. Comparable patterns are seen, where lower thresholds denote a greater frequency of severe service times and higher thresholds suggest fewer peaks. When compared to other thresholds, the excessive service times at the 99% VAR-threshold are comparatively shorter, but they happen more frequently. As the bar for classifying an event as extreme decreases, both tables show that extreme events (failures or service times) become more common. This implies that, under some situations, there is a considerable risk of extreme occurrences for the windscreens of aircraft. The fact that both tables’ maximum values are noticeably high suggests that extreme events occasionally have the potential to be extremely severe. This highlights the necessity of sound design and quality control procedures.

Several suggestions can be made to enhance the product’s dependability and safety based on the PORT-VAR study for extreme failures of aircraft windscreens. The study results, which display the summary statistics for extreme service periods and the number of peaks above different VaR criteria, offer important information about how frequently and to what extent the windscreens are subjected to harsh conditions. These observations can be connected to engineering and reliability procedures in the following ways:

  1. 1.

    The examination reveals a broad range of peaks exceeding VaR thresholds, and as the threshold drops, the number of excessive service times rises. This suggests that extreme values are not uncommon, especially when thresholds are smaller. Adopt stricter testing procedures that more accurately replicate harsh environments. This could involve testing windscreens in a wider range of climatic circumstances (such as strong winds and harsh temperatures) to better understand performance limits, as well as subjecting them to accelerated conditions to replicate long-term usage and discover vulnerabilities.

  2. 2.

    Improved maintenance procedures can be required if there are a lot of severe service times. Create and put into action thorough maintenance procedures. Plan to get windscreens inspected more frequently, particularly if they are in use for longer than usual. Make use of predictive analytics to project future failures by analysing past performance data.

Analogously, for extreme times of service data, we have the following recommendations:

  1. 1.

    Improve the testing procedures to guarantee that the windscreens can tolerate harsh circumstances. Make sure the windscreens are capable of withstanding harsh and extended circumstances by simulating them using accelerated testing techniques. Conduct tests that surpass the existing operational and environmental parameters in order to detect any vulnerabilities.

  2. 2.

    Frequent extreme service times indicate that the current maintenance practices might need to be adjusted. Establishing a program for routine maintenance and inspections is advised, particularly for parts that have been in use for extended periods of time. Predictive analytics can be used to identify possible problems and take action before they become serious.

Fig. 14
figure 14

Hisograms and the peaks above VaR-threshold for the extreme failures.

Full size image
Fig. 15
figure 15

Hisograms and the peaks above VaR-threshold for the extreme times of services.

Full size image
Fig. 16
figure 16

Graphical description for the assessment of the MOOP analysis for the extreme failures.

Full size image
Fig. 17
figure 17

Graphical description for the MOOP values, mean squared error (MSE) and biases for the extreme failures.

Full size image
Fig. 18
figure 18

of the MOOP analysis for the extreme times of service.

Full size image
Fig. 19
figure 19

Graphical description.

Full size image

Conclusions

This work deduces and examines the compound PII distribution (CPII), a novel three-parameter lifespan distribution. Three possible densities for the CPII’s density function are “left skewed with no peak,” “right skewed with unimodal shape,” and “right skewed with no peak.” Three possible failure rate functions for the CPII are “increasing-constant,” “upside down,” and monotonically declining. It is possible to express the new CPII density as a straightforward combination of the exponentiated PII densities. It is observed that the skewness can be more than zero through numerical analysis of the skewness, kurtosis, and dispersion index. The kurtosis ranges in spread from 9.4557 to 4088911. The CPII model can be employed as a “under-dispersed” or “over-dispersed” model depending on whether the dispersion index is in the range of (0, 1) or greater. The three-dimensional U skewness form, the three-dimensional decreasing skewness shape, and the three-dimensional growing skewness shape are only a few of the many useful shapes that the skewness of the new density might take. The three-dimensional U kurtosis form, the three-dimensional falling kurtosis shape, and the three-dimensional growing kurtosis shape are only a few of the many interesting shapes that the new model’s kurtosis can take. Due to these features, the new model may describe and model a wide range of observable physical, social, geophysical, and actuarial events. The unknown CPII parameters are estimated using the highest likelihood technique. The finite sample behaviour of the estimate approach is evaluated using simulation trials, which are graphically represented and quantified by “biases” and “mean squared errors”. It can be observed that as n approaches \(\infty\), all parameter biases tend to be negative and fall to zero, and all parameter MSEs also decline to zero. Among the several well-known PII extensions, the new model deserves to be selected as the best model.

For manufacturers of aviation windscreens, the dependability Peaks Above a Random Threshold Value at Risk (PORT-VAR) analysis is essential because it offers a thorough evaluation of extreme failure occurrences and service times, both of which are vital for guaranteeing the durability and safety of their products. Through this study, organisations may determine the frequency and severity of failures that surpass particular Value-at-Risk thresholds. This information helps them to understand the limits of their products’ performance under stress, optimise their designs for increased durability, and create proactive maintenance plans. This understanding is crucial for reducing hazards, enhancing dependability, and upholding strict adherence to aviation safety regulations. Ensuring the dependability and safety of vital parts, like aeroplane windscreens, is crucial for the aviation sector. The overall safety and operational effectiveness of aircraft are directly impacted by these components’ performance in harsh environments, both in terms of failure rates and service times. Advanced analytical tools are used to evaluate and comprehend the behaviour of these components in such settings. The results of the PORT-VAR analysis for severe service times and failures, as shown in this paper. By comparing different Value-at-Risk (VaR) thresholds to the frequency and features of extreme events, these tables offer a thorough evaluation of the dependability of aeroplane windscreens.