Introduction

Concrete, as a material widely used in construction and infrastructure engineering, has its mechanical properties and durability directly affecting the safety and service life of projects. In practical applications, concrete often faces challenges posed by high-temperature environments, such as extreme conditions like fires and heat waves1,2. These high-temperature conditions can lead to significant degradation of concrete’s mechanical properties, thereby impacting its structural stability and safety. Therefore, studying the degradation mechanisms of concrete mechanical properties and dynamic response characteristics under high-temperature conditions, as well as improving the fire resistance of concrete and extending its service life, holds significant theoretical and practical importance3,4,5,6..

The mechanical properties and durability of concrete after high temperatures are influenced by various factors7,8,9,10,11. Kodur12 proposed the relationship between the thermal parameters of high-strength silicate and carbonate concrete and temperature, indicating that the type of cementing materials and aggregates has a significant impact on the thermal parameters. Yan Ruizhen conducted a study on the physical and mechanical properties of C40 high-performance concrete after exposure to high temperatures, using differential scanning calorimetry (DSC) and related mechanical experiments. The experimental results indicate that temperature has a significant impact on the mechanical properties of concrete. At temperatures close to 100 °C and 400 °C, the DSC curve shows notable endothermic peaks, and after heat treatment at 400 °C, obvious cracks appear on the surface of the specimens. Scott et al.13 investigated the effects of high temperatures on the strength and elastic modulus of high-performance concrete components, finding that the normal elastic modulus exhibited a continuous decline with temperature, without a recovery phase. Noumowe et al.14 studied the differences in heat transfer, pore structure, and thermal stability between ordinary concrete and high-strength concrete, concluding that the dense pore structure of high-strength concrete slows down the dissipation of steam, making it prone to explosive spalling between 250 and 300 °C. In addition, the dynamic load impacts often faced by residential buildings and underground projects can also affect the mechanical properties of concrete15,16,17,18,19,20, yet there is a lack of research on the mechanical properties of concrete under dynamic loads in high-temperature environments.

In response to these factors, researchers have explored various methods to enhance the comprehensive performance of concrete at high temperatures, such as optimizing the cement ratio, selecting appropriate types of aggregates and cementitious materials, and introducing fiber materials. Rice husk ash is commonly added to cementitious materials to improve the high-temperature resistance of concrete; however, most previous studies have focused on static mechanical tests, lacking research on dynamic tests. Among various fiber materials, steel fibers and polypropylene fibers have garnered significant attention due to their high-temperature resistance. Initially, beginners only incorporate one type of fiber into the concrete. Shihad et al.21 demonstrated that a polypropylene fiber volume fraction of 0.5% could significantly improve the residual compressive strength of concrete after high temperatures. However, the effect of polypropylene fibers on enhancing the residual compressive strength and elastic modulus of concrete is relatively limited22. To address this shortcoming, the addition of steel fibers has been shown to effectively improve the residual mechanical properties of concrete. Studies have indicated that the incorporation of steel fibers significantly enhances the ductility and toughness of concrete, especially under high-temperature conditions. Düğenci et al.23 found that although the compressive strength, elastic modulus, and toughness of steel fiber-reinforced concrete decrease at high temperatures, concrete containing 1.0% steel fibers exhibits the least loss in compressive strength under such conditions. Zhou et al.24 also confirmed that at 500 °C, the mechanical properties of steel fiber-reinforced concrete, particularly its flexural toughness, are superior to those of conventional concrete. Other types of fiber-reinforced concrete have also been studied in high-temperature conditions. Ashkezari and Razmara25 found that ultra-high-performance fiber-reinforced concrete (UHPFRC) exhibits better fire resistance than conventional concrete at high temperatures, with residual compressive strength initially increasing and then decreasing. Alaskar et al.26 suggested that basalt fibers can effectively fill micro-cracks within concrete, significantly enhancing the residual strength of fiber-reinforced concrete under high-temperature conditions. Agra et al.27 discovered that higher steel fiber content effectively reduces the rate of decline in compressive strength and elastic modulus of concrete at high temperatures, while significantly mitigating the degradation of post-crack tensile performance.Although single types of fiber reinforcement can improve the mechanical properties of concrete under high-temperature conditions to some extent, their respective limitations still exist28,29,30,31. Therefore, it is necessary to combine the advantages of multiple fibers to further enhance the performance of concrete after exposure to high temperatures32,33. However, existing research primarily focuses on the reinforcement effects of single fibers, with relatively few studies on the performance of hybrid fiber-reinforced concrete (HFRC) under high-temperature conditions.

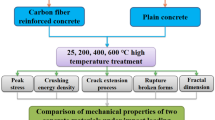
In this paper, rice husk ash, polypropylene fiber and steel fiber were innovatively incorporated into ordinary concrete to improve the fire resistance of ordinary concrete, and the mechanical properties and microscopic characteristics under static and dynamic tests were studied. The research contents include exploring the effects of rice husk ash, polypropylene fiber and steel fiber content on the properties of HFRC through orthogonal experiments, and providing theoretical support for optimizing composite design. The split Hopkinson pressure bar (SHPB) test technique was used to compare the dynamic properties of HFRC and ordinary concrete at different temperatures, and the influence path of temperature and strain rate on the dynamic properties of HFRC was revealed. The microstructure of the treated specimens was analyzed by scanning electron microscopy (SEM), and the micro-damage mechanism of HFRC performance degradation at high temperature was deeply understood. This study not only provides a scientific basis for enhancing the disaster resistance of concrete structures in fire environment, but also provides a theoretical basis for the practical application of hybrid fiber reinforced concrete in engineering.

Test materials and methods

Raw materials

Cement: The experiment utilized Conch brand P·O 42.5 ordinary Portland cement produced in Huainan, Anhui Province.

Rice Husk Ash: As an admixture, rice husk ash from the Hubei Huadian Xiangyang Power Plant was selected. Its appearance is shown in Fig. 1, and its main chemical components are listed in Table 1.

Fig. 1
figure 1

Rice husk ash.

Full size image
Table 1 Rice husk ash composition table.
Full size table

Coarse Aggregate: Locally produced crushed stone from Huainan, Anhui Province was used. To reduce void ratio and ensure material density, the crushed stone underwent washing, drying, and sieving to select continuous graded aggregates with particle sizes ranging from 5 to 20 mm.

Fine Aggregate: Natural river sand from the Huai River in Huainan, Anhui Province was used. To fill the voids between particles, medium sand with a fineness modulus of 2.65 was selected using sieve analysis.

Steel Fiber: Cold-drawn hooked-end steel fibers produced by Hebei Panjin (Hengshui) Building Materials Co., Ltd. were used. These fibers are bundled, as shown in Fig. 2(a), and their main physical properties are listed in Table 2.

Fig. 2
figure 2

Fiber.

Full size image
Table 2 Physical properties of steel fibers.
Full size table

Polypropylene Fiber: The polypropylene fibers used in this study were produced by Hebei Hengshui Shengying Metal Products Co., Ltd. These fibers are white, semi-transparent, and have a bundled monofilament structure (refer to Fig. 2(b)). Their main physical properties are listed in Table 3.

Table 3 Physical properties of polypropylene fiber.
Full size table

Water reducing agent: The HPWR-type standard high-performance water reducing agent produced by Shanxi Qinfeng Building Materials Factory was selected.

Mixture design

In this study, an orthogonal experimental design method was used for analysis34. The influencing factors considered were A (mass fraction of rice husk ash, MR), B (volume fraction of polypropylene fiber, VP), and C (volume fraction of steel fiber, VS). Each factor was set at three levels, forming a three-factor, three-level orthogonal experiment. Referring to the L9 (33) orthogonal array, the factors and levels are shown in Table 4, and the 10 groups of High-Performance Fiber Reinforced Concrete (HFRC) mix proportions are listed in Table 5.

Table 4 Factors-levels.
Full size table
Table 5 Orthogonal test mix ratio(kg/m3).
Full size table

According to the Standard for Test Method of Mechanical Properties on Ordinary Concrete (GB/50081-2002), cement, rice husk ash, coarse aggregate, and fine aggregate were sequentially placed into a mixer for blending. Fibers were then gradually added in multiple batches, mixing for 3 min. Water was subsequently added, and the mixture was wet-mixed for an additional 4 min. The mixture was then placed into pre-lubricated 100 mm × 100 mm × 100 mm cubic molds, compacted on a vibrating table to ensure proper consolidation, and the surface was leveled using a trowel. Afterward, the vibration was halted.

The concrete specimens were covered with plastic wrap and left to cure for 24 h before demolding. Following demolding, the specimens were subjected to standard curing for 28 days. A total of 60 cubic specimens, divided into 10 groups with different mix ratios, were prepared.

The tests for cubic compressive strength and cubic splitting tensile strength were conducted strictly in accordance with the GB/50,081–2002 standard. The loading rate for the cubic compressive strength test was set to 3 mm/min, while the loading rate for the cubic splitting tensile strength test was 1 mm/min. The specific process is illustrated in Fig. 3. Based on the experimental results, the optimal mix design for hybrid fiber reinforced concrete was obtained.

Fig. 3
figure 3

Sample preparation and test flow chart.

Full size image

Dynamic mechanical test design

The optimal mix ratio specimens obtained from the orthogonal experiment were selected, along with OC mix ratio specimens as the control group. To ensure uniformity within the concrete specimens, cylindrical molds with dimensions of Φ74mm × 37 mm and an aspect ratio of 0.5 were used. For each temperature gradient, 12 specimens were prepared for each of the two mix ratios, resulting in a total of 120 specimens. After curing, the specimens were taken out and dried in an oven, as shown in Fig. 4. The drying temperature was set at 60 °C for 24 h to prevent explosive spalling due to excessive moisture during high-temperature tests and to eliminate the effect of moisture content on the experiments.

Fig. 4
figure 4

Electric blast drying box.

Full size image

Subsequently, the specimens were subjected to high-temperature treatment using a muffle furnace, as illustrated in Fig. 5. The muffle furnace temperatures were set at 200 °C, 400 °C, 600 °C, and 800 °C, with a heating rate of 5 °C/min. Once the target temperature was reached, the temperature was maintained for 3 h to ensure uniform temperature distribution inside and outside the specimens. After the heating period, the power was turned off, and the furnace was allowed to cool down to 100 °C. The furnace lid was then opened to cool the specimens to room temperature before removal35.

Fig. 5
figure 5

Muffle furnace.

Full size image

Dynamic compression tests were conducted on the OC and HFRC specimens after high-temperature treatment. To simulate real engineering conditions, the OC and HFRC specimens were subjected to four levels of loading (0.3 MPa, 0.4 MPa, 0.5 MPa, and 0.6 MPa) at different temperatures . Each pressure level was tested three times in parallel, and the best results were selected to minimize experimental errors.

The dynamic compression tests were conducted at the Impact Dynamics Laboratory of the School of Civil Engineering and Architecture at Anhui University of Science and Technology. The tests employed a Φ74mm Split Hopkinson Pressure Bar (SHPB) apparatus. We have made efforts to optimize the surface smoothness of the contact surfaces between the samples and the pressure bars during the experiment, and we have employed lubricants or other techniques to reduce the influence of frictional forces. The pressure bars were made of steel with a density of 8.1 g/cm3 and an elastic modulus of 200 GPa. A schematic diagram of the testing apparatus is shown in Fig. 6.

Fig. 6
figure 6

SHPB loading device.

Full size image

Static experimental results analysis

Statistical analysis of static experimental results

Each group of samples was tested for slump, and the slump values were all within 25–75 mm, which complies with the standards in the Standard for Test Method of Mechanical Properties on Ordinary Concrete (GB/50081-2002). The compressive and tensile strength tests of the specimens after 28 days of curing are shown in Fig. 7, with the experimental results summarized in Table 6. As shown in Table 6, the 28-day compressive and tensile strengths of the specimens in Group 8 (A3B2C1) reached the highest values. This group had a rice husk ash mass fraction of 12%, a polypropylene fiber volume fraction of 0.1%, and a steel fiber volume fraction of 0.5%.

Fig. 7
figure 7

Strength test.

Full size image
Table 6 Test result.
Full size table

To investigate the influence of factors A, B, and C on the strength of the specimens, statistical analysis software SPSS was used for range analysis and analysis of variance (ANOVA). The results are presented in Tables 7 and 8.

Table 7 Range analysis.
Full size table
Table 8 Variance analysis.
Full size table

Analysis of compressive strength of cubes

As shown in Table 7, SF (steel fiber) has the greatest impact on the compressive strength of cubes, with a range (R) of 4.37 MPa; RHA (rice husk ash) follows, with an R value of 3.70 MPa; and PPF (polypropylene fiber) has the least impact, with a range of 2.61 MPa.

Figure 8 illustrates the influence of various factors on compressive strength. As the content of polypropylene fibers (PPF) increases from 0.05 to 0.1%, the compressive strength of the specimens rises by 0.3%. However, when the PPF content is further increased to 0.15%, the compressive strength experiences a significant decrease of 7.5%. Similarly, when the silica fume (SF) content is raised from 0.5 to 1%, the compressive strength of the specimens declines by 12.6%, and an additional increase to 1.5% results in a further reduction of 7.4%. This behavior can be attributed to the mixed incorporation of SF and PPF. At certain volumetric fractions, the fibers tend to overlap, cross, and entangle with one another, which disrupts the uniform dispersion of the hybrid fibers within the matrix. Consequently, this decreases the contact surface area between the fibers and the matrix, weakening the bonding effect and leading to a negative hybrid effect.

Fig. 8
figure 8

Effect of various factors on compressive strength.

Full size image

As the content of RHA increases from 6 to 9%, the compressive strength of the specimens decreases by 6.8%. However, when the RHA content is further raised to 12%, the compressive strength increases by 4.5%, indicating an overall upward trend. This behavior can be attributed to the ability of rice husk ash to significantly enhance the workability of concrete. Suman et al.36 mentioned that the increase in compressive strength may be attributed to the formation of C-S-H due to the reaction of reactive silica obtained from rice husk ash with cement silicates. The additional formation of C-S-H provides a pore-filling effect, reducing porosity and increasing the ITZ value, which leads to enhancement. The reduction in compressive strength of concrete with excessive RSA may be due to the decrease in the content of aluminum oxide and calcium oxide in the concrete.

According to Table 8, steel fiber, rice husk ash, and polypropylene fiber significantly affect compressive strength. Among these, steel fiber and rice husk ash are highly significant factors, while polypropylene fiber is a significant factor. The order of their influence on concrete compressive strength is: steel fiber volumetric fraction (C) > rice husk ash mass fraction (A) > polypropylene fiber volumetric fraction (B), which is consistent with the range analysis results.

From the perspective of compressive strength, the optimal combination is A3B2C1 (12% rice husk ash, 0.1% polypropylene fiber, 0.5% steel fiber), which increases the compressive strength by 10.41% compared to plain concrete.

Analysis of splitting tensile strength of cubes

As shown in Table 7, within the range of experimental factor levels, the order of influence on the 28-day splitting tensile strength of concrete specimens is C (steel fiber volumetric fraction) > B (polypropylene fiber volumetric fraction) > A (rice husk ash mass fraction). Figure 9 shows the influence of various factors on splitting tensile strength: With the increase of RHA, the splitting tensile strength increases, reaching a maximum increase of 15% compared to plain concrete; the splitting tensile strength is highest at an SF volumetric fraction of 0.5%, increasing by 23% compared to plain concrete, but decreases as SF continues to increase; as PPF increases, the splitting tensile strength first increases and then decreases, with a 23% increase when PPF increases from 0.05 to 0.1%, but an 11.05% decrease when PPF increases from 0.1 to 0.15%. This indicates that an appropriate amount of fibers can enhance concrete strength, but excessive fibers can cause agglomeration and uneven dispersion, reducing concrete workability and mechanical properties.

Fig. 9
figure 9

Effect of various factors on splitting tensile strength.

Full size image

The variance analysis in Table 8 shows that SF, PPF, and RHA all affect splitting tensile strength, with SF having the greatest impact, and PPF and RHA having similar levels of influence. These results are consistent with the range analysis. For splitting tensile strength, the optimal combination is A3B2C1 (A mass fraction of 12% rice husk ash, along with volumetric fractions of 0.1% polypropylene fiber and 0.5% steel fiber.), which increases the splitting tensile strength by 50.22% compared to plain concrete.

Analysis of tensile to compressive strength ratio

As shown in Table 6, the tensile to compressive strength ratio is highest for A3B2C1, at 0.179, which is a 42% increase compared to plain concrete. This indicates that the three factors significantly influence the tensile to compressive strength ratio of the specimens, and the ductility and crack resistance of hybrid fiber concrete are improved compared to plain concrete. According to Table 7, the order of influence of the three factors on the tensile to compressive strength ratio is B > A > C. Furthermore, variance analysis in Table 7 shows that RHA, PPF, and SF are all significant influencing factors, with PPF having the greatest impact on the tensile to compressive strength ratio, while SF and RHA have similar levels of influence. The variance analysis results are consistent with the range analysis results.

A3B2C1, or 12% rice husk ash mass fraction, 0.1% polypropylene fiber volumetric fraction, and 0.5% steel fiber volumetric fraction, is found to be the ideal combination of factor levels when taking into account the experimental conditions, factor levels, and strength performance.

Dynamic test results and analysis

Mass loss

After high-temperature treatment, the moisture content of the concrete specimen decreases, and its internal structure changes, resulting in a loss of mass of the concrete specimen. The formula for calculating the mass loss rate is as follows:

$$\Delta M_{T} = \frac{{M - M_{T} }}{M} \times 100\%$$
(1)

In In the formula, \(M\) represents the mass of the concrete specimen after drying at room temperature, and \(M_{T}\) represents the mass of the concrete specimen after treatment at \(T\)°C.

As the temperature continues to rise, the mass loss rate of OC and HFRC increases. After treatment at temperatures of 20 °C, 200 °C, 400 °C, 600 °C, and 800 °C, the mass loss rates for OC are 0%, 3.26%, 4.66%, 5.28%, and 16.04%, respectively, while the mass loss rates for HFRC are 0%, 4.12%, 5.97%, 7.43%, and 16.35%, respectively. Notably, the mass loss rates at 200 °C and 800 °C differ significantly from the previous temperatures. This is because at 200 °C, the free water inside the concrete specimen evaporates while the bound water in the cementitious materials is released. Additionally, the temperature reaches the melting point of polypropylene fibers, leading to rapid mass loss due to the loss of moisture and the melting of the fibers, which causes changes in the internal structure of the concrete specimen. At 800 °C, the C-S–H gel produced during the hydration of cement decomposes, resulting in a decrease in the integrity of the concrete specimen.

Dynamic mechanical test results

In the event of a fire in residential buildings and underground engineering, the complex and diverse engineering environment often leads to accompanying explosions37,38. Thus, it is crucial to investigate the mechanical characteristics and damage progression of concrete materials when dynamic loads and high temperatures are combined. In order to replicate the scenario of an explosion impact during a fire, dynamic mechanical performance tests were performed on ordinary concrete (OC) and high-performance fiber-reinforced concrete (HFRC) under various impact pressures following high-temperature treatment. The test results are shown in Tables 9 and 10. By analyzing the strength, toughness, and failure characteristics of HFRC, the dynamic damage mechanism of HFRC is revealed, providing a scientific basis for the evaluation of concrete structures after high-temperature fire environments and theoretical support for the practical application of HFRC in engineering.

Table 9 Dynamic test results of OC at different temperatures.
Full size table
Table 10 Dynamic test results of HFRC at different temperatures.
Full size table

Comparing the dynamic test results of OC and HFRC in Tables 9 and 10 allows for a better analysis of the dynamic mechanical properties of HFRC. This section will study the dynamic mechanical properties of HFRC based on Tables 9 and 10, focusing on the failure characteristics, stress–strain relationships, dynamic compressive strength, dynamic increase factor, and peak toughness of OC and HFRC specimens at different temperatures.

By comparing the dynamic test results of OC and HFRC, it becomes evident that HFRC generally exhibits superior dynamic mechanical properties, especially in terms of higher peak stress and dynamic increase factors. This indicates that HFRC has better resistance to dynamic loads and improved toughness, making it a more suitable material for applications in environments where both high temperatures and dynamic impacts are expected.

Failure characteristics

The impact failure morphologies of OC and HFRC under different temperature conditions are presented in Tables 11 and 12, respectively.

Table 11 Impact failure morphology of OC at different temperatures.
Full size table
Table 12 Impact failure morphology of HFRC at different temperatures.
Full size table

As can be seen from Tables 11 and 12, under the same temperature conditions, the strain rate significantly increases with the increase in impact pressure, resulting in a higher degree of fragmentation for both OC and HFRC. However, the degree of fragmentation in HFRC is noticeably less than that in OC. When the impact pressure reaches 0.6 MPa, some fragments of the specimens even exhibit pulverization. These phenomena indicate that both OC and HFRC exhibit a certain strain rate effect. As the temperature increases, under the same impact pressure and similar strain rate conditions, the degree of fragmentation of the specimens significantly increases, with more fragments and smaller fragment sizes. This indicates that both OC and HFRC have a temperature softening effect.

It is noteworthy that when the temperature is below 600°C, the failure morphology of HFRC is more intact compared to OC. Particularly within the temperature range of 20–200°C, HFRC exhibits good integrity, which can be attributed to both the strong bonding between the steel fibers and the matrix, as well as the bridging effect of polypropylene fibers. In other words, the incorporation of fibers can effectively alter the failure mode of HFRC under dynamic loading. However, at a temperature of 800°C, the integrity of HFRC deteriorates significantly, indicating that the beneficial effects of the fibers are limited at this elevated temperature39.

Unlike the failure characteristics of specimens under static tests, under dynamic loading, the specimens do not exhibit a single or a few main cracks but undergo cracking and expansion at multiple points. At high strain rates, the energy input into the specimens per unit time increases, and the primary cracks do not have enough time to absorb and expand, being instead absorbed by microscopic cracks in the interface transition zone and inherent pores of the specimens, leading to multi-point cracking. This is consistent with the failure morphologies of the specimens shown in Tables 11 and 12. The higher the temperature, the greater the internal damage of the specimens, the more microscopic cracks, and the more evident the fragmentation of the specimens, which is also in line with the aforementioned analytical results40.

Stress–strain curves

The dynamic stress–strain curves of OC and HFRC under different temperature conditions are shown in Figs. 10 and 11, respectively. The shapes of these curves are similar to those at room temperature. Under approximately similar strain rate loading conditions, as the temperature increases, the peak stress of OC decreases sharply, while the peak stress of HFRC slightly increases at 200°C and then shows a downward trend. At the same temperature, with an increase in loading strain rate, the peak stress of both OC and HFRC increases, indicating a significant strain rate enhancement effect.

Fig. 10
figure 10

Dynamic stress–strain curve of OC.

Full size image
Fig. 11
figure 11

Dynamic stress–strain curve of HFRC.

Full size image

The deformation behavior of concrete can be represented by the critical strain (the strain corresponding to the peak stress). Figure 12 shows that the critical strain of OC and HFRC increases with temperature, indicating that the temperature softening effect leads to greater overall deformation of the concrete specimens. Additionally, an increase in strain rate also causes an increase in the critical strain of the specimens. It is noteworthy that Table 10 and Fig. 12(b) show that when the temperature rises from 600°C to 800°C, the increments in the critical strain of HFRC at different strain rates are 1.04%, 1.37%, 7.84%, and 7.51%, respectively, which are lower than the increments at 600°C. This may be due to the degradation of fiber performance at high temperatures and the reduced bonding strength between fibers and the concrete matrix, weakening the fibers’ influence on the critical strain.

Fig. 12
figure 12

Critical strain of OC and HFRC.

Full size image

Furthermore, a comparison between Figs. 10 and 11 reveals that the descending segment of the stress–strain curve for OC is steeper. In contrast, with the reduction in peak stress and the increase in critical strain, the descending segment of the dynamic stress–strain curve for HFRC is flatter. Figure 11 indicates that HFRC exhibits a distinct plateau yield period after reaching the peak stress, primarily due to the toughening performance of the steel fibers.

Dynamic compressive strength

The relationship between the dynamic compressive strength of OC and HFRC and strain rates at different temperatures is shown in Fig. 13. The findings show that the dynamic compressive strengths of both OC and HFRC considerably increase at different temperatures as the loading strain rate increases. The dynamic compressive strength of OC at various temperatures increases by 24.93%, 31.81%, 29.76%, 22.66%, and 23.88%, respectively, when the loading strain rate is increased from 40 to 100 s⁻1. This indicates an initial increase followed by a decrease. The increment falls as the temperature increases from 200 to 400 °C, suggesting that the strain rate enhancement effect is lessened by the temperature softening effect. On the other hand, HFRC exhibits a continuous increasing trend with dynamic compressive strength increasing by 16.22%, 16.72%, 17.15%, 18.25%, and 19.48% at various temperatures. The test results demonstrate that the dynamic compressive strength of concrete specimens under high-temperature environments is jointly determined by the temperature effect and the strain rate enhancement effect. The 3D dynamic compressive strengths of OC and HFRC at different temperatures and loading strain rates are shown in Fig. 14.

Fig. 13
figure 13

Relationship between dynamic compressive strength and strain rate of OC and HFRC.

Full size image
Fig. 14
figure 14

Three-dimensional diagram of dynamic compressive strength scatter of OC and HFRC.

Full size image

A linear regression fitting was performed on the relationship between the dynamic compressive strength and loading strain rate for OC and HFRC, with the results shown in Fig. 13. It was found that there is a linear relationship between the two. The specific functional relationships between the dynamic compressive strength and strain rate for OC and HFRC at different temperatures are shown in Table 12, with correlation coefficients R2 all greater than 0.92, indicating a good fitting effect.

Table 13 and Fig. 13 illustrate that the coefficients in the fitting function relationships for OC and HFRC exhibit a trend of initially increasing and then decreasing with rising temperature. A fitting analysis of the relationship between the coefficients and temperature is performed, as shown in Fig. 15. From Fig. 15, it can be observed that the relationship between the fitting function coefficients of OC and HFRC and temperature follows a cubic function, with correlation coefficients R2 greater than 0.91. The relationship between the coefficients and temperature follows an exponential function, with correlation coefficients greater than 0.97, indicating a good fit.

Table 13 Fitting function relationship between dynamic compressive strength and strain rate of OC and HFRC at different temperatures41,42.
Full size table
Fig. 15
figure 15

The fitting relationship of a and b.

Full size image

By substituting the obtained coefficients and the fitted functional relationships into the linear relationship equations between the dynamic compressive strength of OC and HFRC and the loading strain rate, we can obtain:

$$\sigma_{OC} = \left( {0.{19 + 3}{\text{.10}} \times {10}^{{ - 4}} T - 8.12 \times {10}^{{ - 7}} T^{2} + 3.04 \times {10}^{{ - 10}} T^{3} } \right)\dot{\varepsilon } - 2.24e^{{\frac{T}{346.08}}} + 40.18$$
(2)
$$\sigma_{HFRC} = \left( {0.{13 + 9}{\text{.51}} \times {10}^{{ - 4}} T - 2.83 \times {10}^{{ - 6}} T^{2} + 2.02 \times {10}^{{ - 9}} T^{3} } \right)\dot{\varepsilon } - 3.71e^{{\frac{T}{401.78}}} + 54.65$$
(3)

Based on the above calculations, we obtained the dynamic compressive strength of OC and HFRC under different temperatures and loading strain rates. The specific data are shown in Tables 14 and 15, where the calculated results are compared with the experimental results. Upon comparison, it is found that the absolute errors between the calculated and experimental results for the dynamic compressive strength of OC and HFRC do not exceed 6%.

Table 14 Comparison of dynamic actual strength and calculated strength of OC.
Full size table
Table 15 Comparison of dynamic actual strength and calculated strength of HFRC.
Full size table

Although the results calculated from the fitting functions are very close to the experimental data, the complexity of the functional relationships makes them impractical for actual engineering applications. Therefore, a Poly2D fitting analysis was conducted directly using temperature and loading strain rate as influencing factors for the dynamic compressive strength of OC and HFRC. The fitting results are shown in Fig. 16.

Fig. 16
figure 16

Fitting relationship of dynamic compressive strength between OC and HFRC43,44.

Full size image

The obtained functional relationship equations for the dynamic compressive strength of OC and HFRC through fitting are as follows:

$$\sigma_{OC} = 32.717 + 0.288\dot{\varepsilon } + 0.032 - 3.686 \times 10^{ - 4} \dot{\varepsilon }^{2} - 7.18 \times 10^{ - 5} T^{2} - 1.592 \times 10^{ - 4} \dot{\varepsilon }T$$
(4)
$$\sigma_{HFRC} = 40.473 + 0.462\dot{\varepsilon } + 0.014T - 0.002\dot{\varepsilon }^{2} - 5.554 \times 10^{ - 5} T^{2} - 5.131 \times 10^{ - 4} \dot{\varepsilon }T$$
(5)

As can be seen from Fig. 16, the fitting indicates an approximate consistency with the experimental data, with correlation coefficients R2 of 0.984 and 0.978, respectively, indicating a good fit. Compared to the previously mentioned fitting relationships for OC and HFRC, the fitting results are similarly effective. However, the functional expressions are simplified, making them more convenient for practical engineering applications.

Dynamic increase factor

To evaluate the strain rate enhancement effect of OC and HFRC at different temperatures, the Dynamic Increase Factor (DIF), defined as the ratio of dynamic strength to static strength, is introduced. The DIF values are calculated based on the following formula, with results shown in Tables 9 and 10.

$$DIF = \frac{{f_{d} }}{{f_{c} }}$$
(6)

fd represents the dynamic compressive strength. fc represents the static compressive strength.

The DIF of OC and HFRC is illustrated in Fig. 17. As the loading strain rate increases, the DIF for both OC and HFRC increases, confirming that the dynamic strength performance of concrete specimens exhibits a strain rate enhancement effect under high-temperature conditions. As the temperature rises for OC, the DIF first falls and then rises. The DIF reaches its minimum at 200 °C under four approximate strain rate loadings, with values of 1.13, 1.29, 1.36, and 1.49, respectively. The DIF for HFRC typically exhibits a comparable pattern, with the lowest values at 400 °C being 1.32, 1.40, 1.48, and 1.54.

Fig. 17
figure 17

DIF change trend of OC and HFRC under different temperature conditions.

Full size image

At a temperature of 200 °C, the Dynamic Increase Factor (DIF) of HFRC shows an improvement compared to its DIF at room temperature. As the temperature rises to 800 °C, the DIFs of both OC and HFRC reach their maximum values, consistent with the trends and failure modes observed in the previous two sections regarding dynamic strength. By comparing Fig. 17(a) and (b), it can be observed that the DIF of HFRC is consistently greater than that of OC, indicating that HFRC is more sensitive to the strain rate enhancement effect.

Due to the concurrent effects of temperature softening and strain rate enhancement, the dynamic behavior of concrete specimens cannot be conclusively determined. Consequently, it is not feasible to directly ascertain the influence of temperature and loading strain rate on the dynamic increase factor (DIF) from Fig. 16. To tackle this issue, we first fitted the DIF with the strain rate using the DIF calculation formula for plain concrete at room temperature, as outlined in the CEB-FIP code. The formula is as follows:

$$DIF = \frac{{f_{d} }}{{f_{c} }} = \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right)^{0.014} ,} & {\dot{\varepsilon } \le 30s^{ - 1} } \\ {0.012\left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right)^{0.014} ,} & {\dot{\varepsilon } > 30s^{ - 1} } \\ \end{array} } \right.$$
(7)

\(\dot{\varepsilon }\) represents the dynamic loading strain rate. \(\dot{\varepsilon }_{0}\) represents the static loading strain rate, which in this study is taken as 5 × 10-4 s-1.

From Eq. (7), it can be observed that there exists a transitional strain rate, which divides the strain rate into two segments. The strain rates used in the experiments of this study fall within the second segment of this formula. Therefore, this study improves the second segment of the CEB-FIP code formula for data fitting. The modified formula is as follows:

$$DIF = \frac{{f_{d} }}{{f_{c} }} = \alpha \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right)^{\beta }$$
(8)

In this formula, \(\alpha ,\;\beta\) are parameters of the Dynamic Increase Factor (DIF), obtained through fitting.

The relationship between DIF and strain rate fitted according to Eq. (8) is shown in Fig. 18, with the fitted relationship detailed in Table 16. From Fig. 18 and Table 16, it can be seen that the correlation coefficients R2 are all above 0.9, indicating a good fit.

Fig. 18
figure 18

DIF fitting curve of OC and HFRC at different temperatures15,45.

Full size image
Table 16 DIF fitting relationship between OC and HFRC at different temperatures.
Full size table

Based on the fitted parameter values \(\alpha\) and \(\beta\) in Table 16, the trend of \(\alpha\) and \(\beta\) at different temperatures is illustrated in Fig. 19.

Fig. 19
figure 19

Changing trend of \(\alpha\) and \(\beta\) of OC and HFRC under different temperature conditions.

Full size image

As can be observed from Fig. 18, with the increase in temperature, the values of parameters \(\alpha\) and \(\beta\) are dispersed, and their trends alternate between increases and decreases without a clear pattern. Upon performing a fitting analysis, it was found that the changes in parameters \(\alpha\) and \(\beta\) exhibit a cubic function trend. The fitting correlation coefficients are all above 0.9. The resulting calculation relationships for \(\alpha\) and \(\beta\) are as follows:

$$\alpha_{{{\text{OC}}}} = 0.08 - 4.053 \times {10}^{{ - 4}} T{ + 1}{\text{.067}} \times {10}^{{ - 6}} T^{2} - 7.228 \times {10}^{{ - 10}} T^{3}$$
(9)
$$\alpha_{{{\text{HFRC}}}} = 0.237 - 0.001T{ + 3}{\text{.754}} \times {10}^{{ - 6}} T^{2} - 2.878 \times {10}^{{ - 9}} T^{3}$$
(10)
$$\beta_{{{\text{OC}}}} = 0.238 + 6.458 \times {10}^{{ - 4}} T{ - 1}{\text{.751}} \times {10}^{{ - 6}} T^{2} + 1.223 \times {10}^{{ - 9}} T^{3}$$
(11)
$$\beta_{{{\text{HFRC}}}} = 0.148 + 8.305 \times {10}^{{ - 4}} T{ - 2}{\text{.425}} \times {10}^{{ - 6}} T^{2} + 1.894 \times {10}^{{ - 9}} T^{3}$$
(12)

Similar to the situation discussed above, substituting the calculation formulas for parameters \(\alpha\) and \(\beta\) into Eq. (8) results in very complex DIF calculation formulas for both OC and HFRC. Analysis of the results from Li’s research suggests that this complexity is likely due to the combined effects of fiber reinforcement and temperature softening mechanisms, which jointly influence the \(\alpha\) and \(\beta\) parameters, making their relationship convoluted and impractical for engineering applications. Therefore, this study adopts the approximate linear relationship between DIF and the logarithm of the strain rate established by Tedesco. By combining this with the formula provided in the CEB-FIP code, it is modified into the following form:

$$DIF = \frac{{f_{d} }}{{f_{c} }} = k\;\log \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right) + b$$
(13)

According to the modified calculation formula, the experimental data from Tables 9 and 10 were processed, treating the strain rate \(\log \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right)\) as x. Using the nonlinear surface Plane model and polynomial fitting analysis, the fitting results are shown in Fig. 20.

Fig. 20
figure 20

DIF fitting of improved OC and HFRC.

Full size image

From the figure, it can be observed that most of the experimental data points are located near the fitted surface, with the correlation coefficients R2 of the fitting relationship functions being around 0.9, indicating a good fit. The resulting fitted relationship equations for the DIF of OC and HFRC are as follows:

$$DIF_{OC} = 0.85\log \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right) + 1.47 \times 10^{ - 4} T - 3.04$$
(14)
$$DIF_{HFRC} = 0.68\log \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right) + 1.6 \times 10^{ - 9} T^{3} - 1.6 \times 10^{ - 6} T^{2} + 3.81 \times 10^{ - 4} T - 2.01$$
(15)

The results of the DIF for OC and HFRC calculated using Eq. (14) and (15) are compared with the experimental DIF results from Tables 9 and 10, as shown in Tables 17 and 18. The comparison results indicate that the relative errors do not exceed 7%, demonstrating that the fitting equations can accurately predict the DIF. This provides a scientific basis for engineering applications.

Table 17 DIF comparison results of OC.
Full size table
Table 18 DIF comparison results of HFRC.
Full size table

Peak toughness

The energy absorption capacity of concrete can be used as an indicator to measure the toughness of concrete specimens, referred to as peak toughness. The value of peak toughness is defined as the area under the stress–strain curve up to the peak stress, as illustrated in Fig. 21. The specific calculation formula is as follows:

$$W = \int\limits_{0}^{{\varepsilon_{{\text{P}}} }} {\sigma {\text{d}}\varepsilon }$$
(16)
Fig. 21
figure 21

Schematic diagram of peak toughness calculation.

Full size image

Based on Eq. (16), the peak toughness of OC and HFRC at different temperatures is obtained, as shown in Fig. 22. From Fig. 22, it can be observed that under different environmental temperatures, the peak toughness of both OC and HFRC increases with the increase in loading strain rate. This is because an increase in loading strain rate results in higher peak stress and critical strain. While the critical strain consistently rises with increasing temperature, the peak strength experiences a significant decline. This leads to a trend in which the peak toughness of both OC and HFRC initially increases and then decreases. Therefore, the variation in peak toughness with temperature is influenced by the combined effects of peak stress and critical strain.

Fig. 22
figure 22

Peak toughness of OC and HFRC at different temperatures.

Full size image

Comparing Fig. 22(a) and (b), it is evident that the peak toughness of HFRC is always greater than that of OC, further indicating that the addition of fibers can inhibit crack development and enhance the energy absorption capacity of concrete specimens. When the temperature rises from 600 to 800 °C, the decrease in peak toughness for HFRC is not significantly different from that of OC, suggesting that the bonding ability of fibers to the specimen matrix in HFRC diminishes in high-temperature environments, rendering the fiber reinforcement effect almost ineffective.

Microstructural analysis of HFRC

The macroscopic mechanical properties of HFRC after exposure to high temperatures are critical indicators for fire prevention design and post-fire structural assessment. The internal microstructure of concrete plays a significant role in influencing the mechanical and physical properties of the concrete matrix. To further investigate the damage mechanisms of HFRC subjected to varying temperatures and to understand the reasons behind the deterioration of its macroscopic mechanical properties, a scanning electron microscope (SEM) was employed to analyze the microstructure of both OC and HFRC after exposure to different temperature treatments. By comparing the microstructural differences between OC and HFRC under these varying conditions, we were able to identify the microscopic mechanisms and damage evolution patterns associated with the decline in HFRC’s macroscopic mechanical properties. The testing instrument is shown in Fig. 23.

Fig. 23
figure 23

Hitachis-3400n scanning electron microscope.

Full size image

To facilitate the comparison of the microstructural differences between OC and HFRC treated at different temperatures, the magnification levels were chosen to be 500x, 1000x, and 2000x. The micro-morphology of OC and HFRC under different temperature treatments is shown in Fig. 24 and 25.

Fig. 24
figure 24

Micro-morphology of OC at different temperatures.

Full size image
Fig. 25
figure 25

Micro-morphology of HFRC at different temperatures.

Full size image

200°C Treatment: After heat treatment at 200°C, the microstructure of both OC and HFRC exhibits a dense C-S-H gel network. Figure 25(a) shows the connection region between fibers and the cement matrix, where particulate matter is attached to both the fiber surface and the matrix surface. Rice husk ash acts as a catalyst promoting the reaction with cement hydrates during high-temperature curing, with some unreacted rice husk ash remaining in particulate form. This enhances the homogeneity of the HFRC structure, thereby improving its mechanical properties.

400°C Treatment: Fig. 24(b) and 25(b) reveal the microstructure of OC and HFRC at 400°C. The formation of pores is partly attributed to the melting of polypropylene fibers, resembling coral reefs, suggesting a transformation from the spiky spherical structures formed at 200°C. The loss of moisture and the dehydration of C-S–H gel lead to minor structural changes, slightly affecting the mechanical properties of the specimens. Additionally, the appearance of small pores near the fibers indicates the thermal expansion coefficient differences between the matrix and fibers.

600°C and 800°C Treatments: Fig. 24(c), (d) and 25(c), (d) show the microstructural changes of OC and HFRC at 600°C and 800°C. At 600°C, the dehydration of C-S–H gel along with the decomposition of internal crystalline water leads to a significant increase in pores and particulate matter. When the temperature reaches 800°C, the microstructural degradation becomes more pronounced, with the disappearance of coral reef-like structures and the emergence of irregular clump-like structures. The reduction of gel and hydration products, along with the increase in pores and cracks, results in a significant decline in the macroscopic mechanical properties of the specimens.

Conclusions

This study systematically reveals the degradation patterns of the mechanical properties of hybrid fiber-reinforced concrete (HFRC) under high-temperature conditions. It elucidates the dynamic response characteristics and the microstructural evolution mechanisms of HFRC. These findings not only provide a scientific basis for enhancing the disaster resistance of concrete structures in fire environments but also offer theoretical support for the application of HFRC in engineering practices. The main conclusions are as follows:

The incorporation of rice husk ash, polypropylene fibers, and steel fibers significantly enhances the mechanical properties of high-performance fiber-reinforced concrete (HFRC). The optimal mix ratio is 12% rice husk ash, 0.1% polypropylene fiber, and 0.5% steel fiber, resulting in a 10.41% increase in compressive strength and a 50.22% increase in tensile strength compared to ordinary concrete, with a 42% improvement in the tensile-compressive strength ratio.

HFRC exhibits superior dynamic mechanical properties compared to ordinary concrete under high-temperature conditions. The dynamic compressive strength, dynamic increase factor, and peak toughness of HFRC remain at high levels across different strain rates and temperature gradients. However, at 800 °C, there is a significant decline in dynamic performance, indicating that the reinforcing effects of the fibers diminish at elevated temperatures. The interaction between temperature and strain rate has a considerable impact on the mechanical properties of the material.

As the temperature increases, the decomposition of hydration products (such as C-S–H gel) in HFRC leads to an increase in porosity and crack formation, resulting in a looser microstructure. This degradation is a primary factor contributing to the decline in mechanical properties at high temperatures. Between 300 and 600 °C, the fibers help maintain the integrity of the microstructure, mitigating the adverse effects of hydration product decomposition.

The interaction between temperature and the presence of hybrid fibers plays a crucial role in the mechanical behavior of HFRC under high-temperature conditions. The reinforcing effects provided by the fibers enhance the overall performance of HFRC at moderate temperatures, while these benefits diminish at extreme high temperatures.