Introduction

Mudded interlayer usually refers to thin layers of muddy rock formations in a rock mass due to constructed interlayer staggered and long-term physical and chemical action of groundwate1. This kind of interlayer structure is loose and the intergranular connection is weak. After significant weathering or structural variation, it becomes a completely argillized weak layer, resulting in shear sliding failure of the slope along the weak layer. Therefore, the shear properties and deformation characteristics of this type of structural surface are often the key factors controlling the safety and stability of laminated slopes2,3,4,5.

Established studies have shown that mudded interlayer has significant engineering geological properties due to their complex genesis, high content of clay particles, fractured structure, low strength and high compressibility6,7. The mechanical properties are also affected by several factors, including the formation conditions of the interlayer itself, the loading situation, the water content and the mineral composition. Ma et al. explored the effect of water content and normal stress in remodeling samples on the shear strength of weak interlayers8, Qin et al. explored the decay behaviour of the dynamic damping ratio of the muddy interlayer under small to medium strains and used a modified model to describe its relationship with dynamic strain, confining pressure, water content and clay content, revealing the influence of different factors on the dynamic damping ratio9, Xu et al. measured the real strength parameters of the weak interlayer on the sliding surface of Jiuding Mountain, and found that the failure of the weak interlayer began at the contact between the clay filler and the limestone boundary, rather than the clay material itself10, In order to explore the influence of clay content on the shear behavior of muddy interlayer slip zone soil, Miao et al. carried out direct shear creep test and ring shear test with different clay content, and discussed the influence of clay content on this kind of slope11, Tan et al. analyzed the material composition and mineral structure of the weak interlayer in the dam foundation of Datengxia Hydropower Station, and deeply discussed the shear strength characteristics of the weak interlayer; Based on the regression analysis method12, Hu et al.have shown that the interaction between groundwater and weak interlayer is the main factor leading to the failure of tunnel surrounding rock13, Han et al. systematically investigated the genesis, structure, mineralogical composition, physical properties, and shear strength of the interlayer weak structure of Baihetan Hydropower Station14, Luo et al. prepared weak interlayers with different filling degrees and water contents, and analyzed the variation of shear strength under different normal stresses through direct shear tests. It was found that the peak shear strength increased first and then decreased with the change of water content, and decreased first and then stabilized15, Chen et al.‘s research shows that fine-grained interlayers have a controlling effect on the safety and stability of tailings dams16. According to the above related studies, the mechanical properties of the weak muddy interlayer are significantly related to the influencing factors such as water content status, material composition and mineral structure.

Similarly, the mechanical behaviour of weakly muddy interlayers is closely related to their loading conditions and their state of formation.Yan et al. examined the dynamic behaviour of mudded interlayers under the influence of cyclic dynamic loading. The results indicated that the strength parameters of mudded interlayers exhibited a significant decline in response to repeated dynamic loading17, Zhang et al. carried out the rheological test of muddy interlayers under the combined action of static shear and discontinuous dynamic shear. It was found that when the static shear stress was close to the shear strength, the intermittent dynamic disturbance would significantly affect the deformation of muddy interlayers18, Guo et al. investigated the creep property and long-term strength of clay-type muddy interlayers under different normal stresses19, Tan et al.carried out in-situ direct shear tests on muddy interlayers in high-speed slopes, and established interlayer models considering thickness and shape to study the shear behavior and failure mechanism of muddy interlayers20, Zhang et al.studied the mechanical characteristics of weak interlayers under different confining pressures and dip angles, and believed that the shear characteristics of weak interlayers are of great significance to the stability of landslides21.

In summary, most of the existing researches focus on factors such as water content, material composition, mineral structure, loading and formation conditions of the weak muddy interlayer. There are relatively few researches on the shear characteristics of clay-mud type muddy interlayers with dry density and water content, which limits the in-depth understanding of their stability assessment and risk management. Therefore, this study focuses on the shear properties of clay-type muddy interlayers, analyses the effects of dry density and moisture content on the Shear stress-shear strain curve and strength parameters of clay-type muddy interlayers by conducting indoor rapid shear tests, and explores the shear damage characteristics of clay-type muddy interlayers. On the one hand, the research results can supplement the gap of the shear characteristics of clay-type muddy interlayer in this field, and on the other hand, they can provide important theoretical references for the disaster prevention and mitigation of this kind of slope.

Test materials and methods

Test materials

Sampling ___location and basic physical properties

The test samples were taken from the high slope of a waste incineration power plant in Yuxi, Yunnan, China, and the geographical ___location is shown in Fig. 1. According to the field sampling, three types of mudded interlayer were obtained, which were classified into Red mudded interlayer (RMI), Yellow mudded interlayer (YMI) and Mixed mudded interlayer (MMI) according to the colour, as shown in Fig. 2. The basic physical properties are shown in Table 1.

Fig. 1
figure 1

Geographical ___location of the study area.

Full size image
Fig. 2
figure 2

Field sampling situation.

Full size image
Table 1 Basic physical properties of muddy intercalations.
Full size table

Particle size and composition

To obtain samples with different initial particle size distributions, three kinds of mudded interlayers were dried and screened into five groups with particle size ranges of 2 mm < d, 1 mm < d < 2 mm, 0.5 mm < d < 1 mm, 0.25 mm < d < 0.5 mm, 0.075 mm < d < 0.25 mm. The sample screening results are shown in Fig. 3, and the grading curve is shown in Fig. 4. It can be seen that the content of clay (d < 0.005 mm) in RMI, YMI, and MMI was 75.389%, 49.93%, and 78.034%, respectively, with an average of 67.78%, and the content of gravel (2 mm < d) was very low, 0.078%, 12.91%, and 0.985%, respectively, with an average of 4.66%. According to the existing research results12, it shows that the clay content of the mudded interlayer in the study area is very high, which belongs to the clay-type mudded interlayer, and the degree of mudding of the sample is high.

Fig. 3
figure 3

Sample screening results.

Full size image
Fig. 4
figure 4

Particle gradation curve of the muddy interlayer.

Full size image

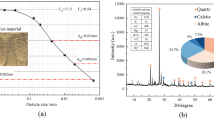
Due to the small number of samples collected on site and the similar basic physical properties of different types of interlayers, the pre-test samples were mixed with the three kinds of mudded interlayer, and the particles above 2.0 mm were removed. After the laboratory test, the liquid limit of the clay-type mudded interlayer is 61.4%, the plastic limit is 21.4%, and the plastic index is 40. The clay mineral composition of the mixed sample is measured, as shown in Fig. 5, it can be seen that the content of dolomite in the mixed muddy interlayer is 40%~45%, the content of illite is 30%~35%, the content of kaolinite is 10%~15%, the content of quartz is 1%~5%, the content of anatase is 1%~5%, and the content of hematite is 1%~5%. It can be seen that the mineral composition of the clay-type muddy interlayer is mainly dolomite, which is susceptible to promoting interlayer interactions after water action, and eventually leads to muddying.

Fig. 5
figure 5

XRD pattern of mudded interlayer after mixing treatment.

Full size image

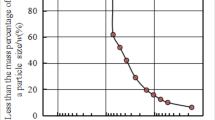
Figure 6 is the grain size distribution curve of the muddy interlayer after mixing treatment. It can be seen that the content of clay grains (d < 0.005 mm) is more than 60%, which belongs to the clay-type mud interlayer. Compared with other soils, these special soils have highly viscous and plastic characteristics as well as low permeability, which indicates that the sedimentation characteristics of clay-type muddy interlayers have a significant effect on the stability of slope engineering. The analysis shows that the non-uniformity coefficient (Cu) of the sample is 7.1, and the curvature coefficient (Cc) is 1.1, indicating that it has a wide particle size distribution and good gradation characteristics.

Fig. 6
figure 6

Particle size distribution curve of mudded interlayer after mixing treatment.

Full size image

Improvement of test instrument and data processing methods

Improvement of test instrument

In the direct shear test, the test instrument has the following problems: on the one hand, there is a rigid connection between the upper shear box and the force measuring ring. During the shear process, the expansion of the sample will lead to the upward movement of the upper shear box, and the force measuring ring will inevitably give the upper shear box. The downward friction force, which cannot be measured in the test, causes the vertical pressure on the sample to be larger than the actual applied vertical pressure, and the shear strength is larger22; on the other hand, the direct shear apparatus can not completely control the drainage of the sample, only through the fast shear or slow shear to achieve the purpose of undrained or completely drained. Slow shear can achieve the purpose of complete drainage, but fast shear is not necessarily able to achieve the purpose of complete drainage23.

Based on the shortcomings of the above test instruments, this test device changes the rigid contact between the upper shear box and the force measuring ring to the ball contact, and smears vaseline on the contact surface to minimize the vertical friction between the upper shear box and the force measuring ring. A polyester film with a thickness of 0.1 mm and the same diameter as the impervious plate is placed between the impervious plate and the top and bottom surfaces of the sample to minimize drainage. The improved strain-controlled direct shear device is shown in Fig. 7.

Fig. 7
figure 7

Indoor direct shear test instrument. (a) Side view; (b)Top view; (c)Ball contact between the upper shear box and the force measuring ring; (d)The relative position of the polyester film to the sample.

Full size image

Improvement of data processing method

There are the following problems in the direct shear data processing: on the one hand, it is considered that the area of the shear surface is constant, and the shear stress is only related to the reading of the force measuring ring, but in fact the area of the shear surface is gradually reduced; on the other hand, it is considered that the vertical compressive stress on the shear plane of the specimen is constant, but the vertical compressive stress on the shear plane of the specimen is continuously changing due to the decrease of the area of the shear plane and the eccentricity of the vertical load of the specimen. Given the problems existing in the above data processing, this study improves and corrects the calculation methods of shear surface area and vertical stress:

Improvement of the calculation method for shear surface area

Referring to the research results24, the stress mode of the specimen in the shear process is analyzed firstly. As shown in Fig. 8, the upper shear specimen is the analysis object, σv is the uniform compressive stress on the top surface of the specimen, σH is the uniform compressive stress applied to the right side of the upper shear specimen by the ring cutter, σ1 is the uniform compressive stress applied to the non-effective shear surface A1 by the lower shear box, σ2 is the uniform compressive stress applied to the effective shear surface A2 by the lower shear specimen, τ1 is the uniform shear stress applied to the non-effective shear surface A1 by the lower shear box, and τ’ is the uniform shear stress applied to the effective shear surface A2 by the lower shear specimen. The Q point is the geometric center of the effective shear area A2.

As shown in Fig. 8a, the radius of the circle is r, and the calculation formula of the effective shear area A2 of the sample is :

$${A_2}=4\int_{{\frac{S}{2}}}^{r} {\sqrt {{r^2} - {x^2}} dx} =4\int_{{r\cos \alpha }}^{r} {\sqrt {{r^2} - {x^2}} dx}$$
(1)

Where: S is shear displacement; r is the radius of the sample; α is the central angle in Fig. 8.

Fig. 8
figure 8

Force analysis of the specimen during the direct shear process.

Full size image

As\(x=r\sin t\), \(- \frac{\pi }{2}<t<\frac{\pi }{2}\), so \(t=\arcsin \frac{x}{r}\)

$$\cos t=\sqrt {1 - {{\sin }^2}t} =\sqrt {1 - {{\left( {\frac{x}{r}} \right)}^2}} =\frac{{\sqrt {{r^2} - {x^2}} }}{r}$$
(2)
$$\int {\sqrt {{r^2} - {x^2}} } dx=\frac{{{r^2}}}{2}\arcsin \frac{x}{r}+\frac{x}{2}\sqrt {{r^2} - {x^2}} +C$$
(3)

Therefore:

$$\begin{gathered} 4\int_{{r\cos \alpha }}^{r} {\sqrt {{r^2} - {x^2}} } dx=4\left[ {\frac{{{r^2}}}{2}\arcsin \frac{x}{r}+\frac{x}{2}\sqrt {{r^2} - {x^2}} } \right]_{{r\cos \alpha }}^{r} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=4\left( {\frac{{\pi {r^2}}}{4} - \frac{{{r_2}}}{2}\arcsin (\cos \alpha ) - \frac{{r\cos \alpha }}{2}\sqrt {{r^2} - {r^2}{{\cos }^2}\alpha } } \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\pi {r^2} - 2{r^2}\arcsin \left( {\frac{s}{{2r}}} \right) - \frac{{{r^2}}}{4}\sin 2\alpha \times 4 \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\pi {r^2} - 2{r^2}\arcsin \left( {\frac{s}{{2r}}} \right) - {r^2}\sin 2\alpha \hfill \\ \end{gathered}$$
(4)

As \(\sin \left( {\frac{\pi }{2} - y} \right)=\cos y\), let\(y=\arccos x\)

So \(\sin \left( {\frac{\pi }{2} - \arccos x} \right)=\cos \left( {\arccos x} \right)\)

As \(\sin \left( {\arcsin x} \right)=x\), \(\cos \left( {\arccos x} \right)=x\)

So \(\sin \left( {\frac{\pi }{2} - \arccos x} \right)=\sin \left( {\arcsin x} \right)\), \(\frac{\pi }{2} - \arccos x=\arcsin x\)

$$\begin{gathered} \pi {r^2} - 2{r^2}\arcsin \left( {\frac{s}{{2r}}} \right) - {r^2}\sin 2\alpha =\pi {r^2} - 2{r^2}\left( {\frac{\pi }{2}{\text{-}}\arccos \left( {\frac{s}{{2r}}} \right)} \right) - {r^2}\sin 2\alpha \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=2{r^2}\arccos \left( {\frac{s}{{2r}}} \right) - {r^2}\sin 2\alpha \hfill \\ \end{gathered}$$
(5)

\(\alpha =\arccos \left( {\frac{s}{{2r}}} \right)\)

$${A_2}=2{r^2}\alpha - {r^2}\sin 2\alpha$$
(6)

In the process of direct shear test, the following basic assumptions are made: (1) The shear surface is connected and straight; (2) The compressive stress applied by the pressure plate and the impervious plate is evenly distributed; (3) Before the test, the contact surfaces of the upper and lower shear boxes are coated with vaseline, so the friction force of the upper shear specimen A1 on the top surface of the lower shear box can be ignored, that is, τ1 can not be considered; (4) The vertical compressive stress on the shear plane is evenly distributed.

According to the force balance in the X direction of the upper shear specimen, it can be obtained :

$${F_S}{\text{=}}CR{\text{=}}\int\limits_{{{A_L}}} {{\sigma _H}dydz} =\int\limits_{{{A_2}}} {\tau ^{\prime}dxdy} =\frac{{\tau ^{\prime}{A_2}}}{{10}}$$
(7)

Therefore\(\tau ^{\prime}=\frac{{CR}}{{{A_2}}} \times 10\), combined with the shear stress formula \(\tau =\frac{{CR}}{{{A_0}}} \times 10\) of the shear surface in the test procedure, it can be obtained :

$$\tau ^{\prime}=\frac{{CR}}{{{A_0}}} \times 10 \times \frac{{{A_0}}}{{{A_2}}}=\tau \times \frac{{{A_0}}}{{{A_2}}}=\tau \times \beta$$
(8)

Where:\(\beta =\frac{{{A_0}}}{{{A_2}}}\), which is the shear stress correction coefficient.

Figure 9 shows the shear stress correction coefficient of the shear displacement within 0.8 cm, and the shear stress correction coefficient is greater than 1. It is shown that the corrected shear stress on the shear surface is larger than the shear stress treated by the test specification method.

Fig. 9
figure 9

Relationship between shear stress correction factor and shear displacement.

Full size image
Improvement of the calculation method for vertical stress

For the Y-axis moment balance MYQ = 0 over the Q point, it can be obtained:

$${M_{{\sigma _1}}}={M_{{\sigma _{\text{V}}}}}+{M_{{\tau _1}}}+{M_{\tau ^{\prime}}}{\text{+}}{M_{{\sigma _2}}}{\text{+}}{M_{{\sigma _{\text{H}}}}}$$
(9)

As \({M_{{\tau _1}}}=0\), \({M_{{\sigma _2}}}=0\), \({M_{{\sigma _H}}}=0\)

So

$${M_{{\sigma _1}}}={M_{{\sigma _{\text{V}}}}}+{M_{\tau ^{\prime}}}$$
(10)
$$\begin{gathered} {M_{{\sigma _1}}}{\text{=}}2\int_{{{\text{-}}r}}^{{{s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0pt} 2}}} {{\sigma _1}\left( {\frac{s}{2} - x} \right)} \sqrt {{r^2} - {x^2}} dx - 2\int_{{{s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0pt} 2}}}^{r} {{\sigma _1}\left( {x - \frac{s}{2}} \right)} \sqrt {{r^2} - {x^2}} dx \hfill \\ \;\;\;\;\;\;\;\;{\text{-}}2\int_{{{s \mathord{\left/ {\vphantom {s {2 - x}}} \right. \kern-0pt} {2 - x}}}}^{{{s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0pt} 2}}} {{\sigma _1}\left( {\frac{s}{2} - x} \right)} \sqrt {{r^2} - {{(x - s)}^2}} dx+2\int_{{{s \mathord{\left/ {\vphantom {s 2}} \right. \kern-0pt} 2}}}^{r} {{\sigma _1}\left( {x - \frac{s}{2}} \right)} \sqrt {{r^2} - {{(x - s)}^2}} dx \hfill \\ \;\;\;\;\;\;{\text{=}}\frac{{s{\text{\varvec{\pi}}}{r^2}{\sigma _1}}}{2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \hfill \\ \end{gathered}$$
(11)
$${M_{{\sigma _V}}}=\frac{{{A_0}s{\sigma _V}}}{2}$$
(12)
$${M_{\tau ^{\prime}}}=\frac{{\tau ^{\prime}{A_2}I}}{2}$$
(13)

Where: I is the height of the upper shear specimen. According to the initial height of the upper shear and the vertical deformation of the specimen during the test, if the specimen shrinks, I takes the initial height of the upper shear specimen minus the vertical deformation of the specimen. If the specimen has dilatancy, it is considered that the dilatancy only occurs on the shear surface, then I takes the height of the specimen before dilatancy.

The simultaneous formula (10)~(13) can be solved as follows :

$$s{\pi} {r^2}{\sigma _1}={A_0}s{\sigma _V}+\tau ^{\prime}{A_2}I$$
(14)

From the balance of the force in the Y direction, it can be obtained:

$${\sigma _1}{A_1}+{\sigma _2}{A_2}={\sigma _V}{A_0}$$
(15)
$${A_1}+{A_2}={A_0}$$
(16)

The simultaneous solution of formulas (6), (14)~(16) can be obtained:

$$\sigma ^{\prime}{\text{=}}{\sigma _2}{\text{=}}{\sigma _{\text{V}}}{\text{-}}\frac{{\tau ^{\prime}I}}{{s{\text{\varvec{\pi}}}}}({\text{\varvec{\pi}-}}2\alpha {\text{+}}\sin 2\alpha )$$
(17)

This can be obtained by bringing Eq. (8) into Eq. (17):

$$\begin{gathered} \sigma ^{\prime}{\text{=}}{\sigma _2}{\text{=}}{\sigma _{\text{V}}}{\text{-}}\frac{{\tau ^{\prime}I({\text{\varvec{\pi}-}}2\alpha {\text{+}}\sin 2\alpha )\;}}{{s{\text{\varvec{\pi}}}}} \hfill \\ \;\;\;\;\;\;\;\;\;={\sigma _{\text{V}}}{\text{-}}\frac{{10CR}}{{{A_0}}} \times \frac{{{A_0}}}{{{A_2}}} \times \frac{{I({\text{\varvec{\pi}-}}2\alpha {\text{+}}\sin 2\alpha )\;\;}}{{s{\text{\varvec{\pi}}}}} \hfill \\ \;\;\;\;\;\;\;\;\;={\sigma _{\text{V}}}{\text{-}}\frac{{10CR}}{{{A_0}}} \times \frac{{{\text{\varvec{\pi}}}{r^2}}}{{{r^2}(2\alpha - \sin 2\alpha )}} \times \frac{{I({\text{\varvec{\pi}-}}2\alpha {\text{+}}\sin 2\alpha )\;\;}}{{s{\text{\varvec{\pi}}}}} \hfill \\ \;\;\;\;\;\;\;\;\;={\sigma _{\text{V}}}{\text{-}}\frac{{10CR}}{{{A_0}}} \times \frac{{I({\text{\varvec{\pi}-}}2\alpha {\text{+}}\sin 2\alpha )}}{{s(2\alpha - \sin 2\alpha )}}\;\; \hfill \\ \end{gathered}$$
(18)

As.

\(\begin{gathered} 1 - \frac{{{A_0}}}{{A{}_{2}}}=1 - \frac{{{\text{\varvec{\pi}}}{r^2}}}{{{r^2}(2\alpha - \sin 2\alpha )}} \hfill \\ \;\;\;\;\;\;\;\;\;\;=1 - \frac{{\text{\varvec{\pi}}}}{{2\alpha - \sin 2\alpha }} \hfill \\ \;\;\;\;\;\;\;\;\;\;=\frac{{2\alpha - \sin 2\alpha - {\text{\varvec{\pi}}}}}{{2\alpha - \sin 2\alpha }} \hfill \\ \;\;\;\;\;\;\;\;\;\;= - \frac{{{\text{\varvec{\pi}-}}2\alpha +\sin 2\alpha }}{{2\alpha - \sin 2\alpha }} \hfill \\ \end{gathered}\)

So

$$\sigma ^{\prime}={\sigma _2}={\sigma _V}+\frac{{10CR}}{{{A_0}}} \times \frac{I}{S}\left( {1 - \frac{{{A_0}}}{{{A_2}}}} \right)$$
(19)

Let \({\beta _0}=\frac{{I\left( {1 - \beta } \right)}}{s}\), Which is the correction coefficient of normal stress, then

$$\sigma ^{\prime}={\sigma _2}={\sigma _V}+\frac{{10CR}}{{{A_0}}} \times {\beta _0}={\sigma _V}+\tau \times {\beta _0}$$
(20)

Figure 10 shows the relationship between the normal stress correction coefficient and the shear displacement and the height of the upper shear specimen. It can be seen that the normal stress correction coefficient is negative, which indicates that the normal stress of the shear plane after correction is smaller than that of the test specification method.

Fig. 10
figure 10

The relationship between the normal stress correction coefficient and the shear displacement and the height of the upper shear specimen.

Full size image

In summary, according to the relationship curve of shear displacement, modified shear stress, and modified normal stress, as shown in Fig. 11a, the shear strength τf is determined by referring to the method in Fig. 11b, and then the normal stress σ’ at shear failure is determined. Based on more than 4 groups of τf-σ’ scatter plots, the shear strength indexes are determined by referring to the method of Fig. 11c: c, φ.

Fig. 11
figure 11

Relationship between shear displacement and modified stress and determination method of shear strength index. (a) The relationship between shear displacement and modified shear stress, modified normal stress; (b) Determination method of shear strength; (c) Relationship between shear strength and vertical compressive stress.

Full size image

Test procedures

In this experiment, direct shear tests under seven different dry densities (1.5,1.55,1.6,1.7,1.8,1.9,2.0 g/cm3) and seven different moisture contents (18,20,23,25,28,30,32%) were carried out on the muddy interlayer. The vertical loads applied in the test are 50,100,150,200,300,400 kPa respectively. After a series of pre-tests, the test scheme is shown in Table 2, a total of 20 groups of test schemes.

Table 2 Direct shear test scheme.
Full size table

The specific test steps are as follows: (1)The mudded interlayer after mixing and screening is naturally dried; (2)Based on the test scheme, according to the requirements of dry density and moisture content of the sample, a certain amount of natural air-dried mudded interlayers were calculated and weighed in a small iron plate, while stirring the sample, a certain amount of water is sprayed with a spray pot, and fully stirred (Fig. 12a); (3)The samples were packed in fresh-keeping bags, sealed and placed in a water basin for 24 h (Fig. 12b), in order to ensure the balance of water diffusion; (4) Weigh a certain amount of wet samples, adopt self-made device to press the samples into the ring knife of the straight shear test in three layers, and rough the top surface of each layer (Fig. 12c); (5)Five parallel samples were prepared for each group of tests, sealed with a preservative film, and then the samples were placed in a constant temperature and humidity standard curing box for 7 days(Fig. 12d); (6)The samples were taken out for indoor direct shear test.

Fig. 12
figure 12

Indoor direct shear test. (a) Fully stir the sample; (b) The sample was stuffed in water for 24 h; (c) Rough treatment of the layered interface; (d) Constant temperature and humidity curing for 7 days.

Full size image

Test results and analysis

Shear stress-shear displacement curve

Shear stress-shear displacement relationship under different dry density conditions

Taking the moisture content ω = 20% as an example, Fig. 13 is the shear stress-shear displacement curve under different dry density conditions. It can be found that under the action of the first gradient normal pressure (black curve), as shown in Fig. 13a, the sample with a dry density of 1.6 g/cm3 shows a higher initial shear stiffness, and the peak shear stress quickly reaches 76.52 kPa, and then the increase of shear stress tends to be stable. As shown in Fig. 13b,c, the peak shear stress of the specimens with dry density of 1.7 and 1.8 g/cm3 reached 78.63 kPa and 90.86 kPa, respectively, indicating that with the increase of dry density, the specimens can maintain higher shear stress after experiencing greater displacement, showing better toughness and plasticity. When the dry density of the sample increases to 1.9 g/cm3 (Fig. 13d), the peak shear stress of the sample is 119.38 kPa, which is quite close to the peak stress of the sample with dry density of 2.0 g/cm3, indicating that the higher dry density has less effect on shear stress at lower normal stress levels. At the second gradient normal pressure (red curve), the peak shear stress of the sample with a dry density of 1.6 g/cm3 increased to 95.20 kPa, while the peak shear stress of the samples with a dry density of 1.7 and 1.8 g/cm3 reached 104.79 kPa and 98.07 kPa, respectively. These results show that the increase of dry density leads to the enhancement of mutual occlusion and locking between particles in the soil, which helps the material to maintain greater shear stress. Under the third and fourth gradient normal pressure (blue curve and pink curve), the peak shear stress of the samples with dry density of 1.6,1.7 and 1.8 g/cm3 reached 116.47,100.96 and 113.45 kPa and 117.66,137.37 and 109.49 kPa, respectively. The analysis shows that the samples with higher dry density have better toughness and plasticity, especially under the fourth gradient normal pressure, the sample with dry density of 1.7 g/cm3 shows the best ability to resist deformation. Under the condition of high normal pressure, the sample with a dry density of 1.9 g/cm3 has a significantly higher downward trend after reaching the peak than the sample with a dry density of 2.0 g/cm3. This significant difference may indicate that in addition to the influence factors of vertical stress, higher dry density helps the material to maintain its structural integrity, thus showing better toughness and shear strength. It is found that the samples with dry density of 2.0 g/cm3 have higher stiffness in the initial stage of shearing.

In summary, the shear stress response of the sample is significantly affected by the dry density and the vertical stress. With the increase of dry density, the samples show higher shear stress levels, better toughness and plasticity under the action of the normal direction of each grade, especially at high stress levels.

Fig. 13
figure 13

The shear stress-shear displacement curves of samples with 20% moisture content under different dry density conditions. (a)ρd = 1.6 g/cm3;(b)ρd = 1.7 g/cm3; (c)ρd = 1.8 g/cm3;(d)ρd = 1.9 g/cm3;(e)ρd = 2.0 g/cm3.

Full size image

Shear stress-shear displacement relationship under different moisture content conditions

Taking the dry density of 1.7 g/cm3 as an example, Fig. 14 is the shear stress-shear displacement curve under different moisture content conditions. When the dry density and normal stress are constant, the shear stress required for the specimen to achieve the same shear displacement gradually decreases with the increase of moisture content. When the moisture content increases from 20 to 28%, under the fourth gradient normal pressure condition, the peak shear stress decreases from 137.37 kPa to 41.03 kPa, and the attenuation degree exceeds 70%, which indicates that the clay-type muddy interlayer specimen has a marked water-softening effect, and the shear characteristics decrease significantly with the increase of moisture content. It can be seen that as the normal pressure increases, the shear stress of the muddy interlayer gradually increases. When the moisture content is 20% (Fig. 14a), the curves show obvious strain-softening characteristics, and the shear stress of the sample gradually decreases after reaching the peak. When the moisture content is 23% (Fig. 14b), the curves of the samples are all strain softening in the tests with normal pressures of 178.680 kPa, 277.925 kPa, and 376.053 kPa, but the curves show strain hardening characteristics at 82.111 kPa. When the moisture content is 25% (Fig. 14c), the curve of the sample is strain softening type in the test of normal pressure of 286.656 kPa and 385.461 kPa, but the softening effect is not obvious. The curve of the sample shows strain-hardening type characteristics at 86.468 kPa and 185.897 kPa, and finally remains stable in the hardening stage. When the moisture content is 28% (Fig. 14d), the shear stress-shear displacement curves of the samples under different normal pressure states show a slight strain-softening effect.

In summary, under the condition of low moisture content (ω = 20%), the shear stress-shear displacement of the muddy interlayer samples showed obvious strain-softening phenomenon. At medium moisture content (ω = 23%, ω = 25%), the shear stress-shear displacement curve of the sample shows hardening characteristics under low normal stress. With the increase of normal pressure level, the curve transits from softening type to hardening type. Under the condition of high moisture content (ω = 28%), the curves show a slight strain-softening phenomenon.

Fig. 14
figure 14

Shear stress-shear displacement curves of specimens with dry density of 1.7 g/cm3 under different moisture content conditions. (a) ω = 20%;(b) ω = 23%;(c)ω = 25%;(d)ω = 28%.

Full size image

Analysis of shear strength parameters of mudded interlayer

Angle of internal friction

The relationship between the internal friction angle and the dry density of the muddy interlayer sample is shown in Fig. 15.When the moisture content is 18%, the internal friction angle gradually decreases with the increase of the dry density, but it rebounds when the dry density reaches 1.9 g/cm3. When the moisture content is 20%, the internal friction angle first decreases with the increase of dry density, then increases, and maintains the change of small buoyancy. When the moisture content is in the state of 23–28%, with the increase of dry density, it shows the characteristics of fluctuation change, but the change is not large. When the moisture content is 30% or 32%, the internal friction angle of the sample is at a low level. It shows that the response characteristics of internal friction angle and dry density under different water content conditions are more complex and unstable. These complex changes may be related to the type of soil, particle size, particle shape, sample preparation method, and test conditions.

In general, the increase of moisture content usually reduces the internal friction angle, because the lubrication effect of water reduces the contact point between particles, resulting in the weakening of mutual occlusion and interlocking between soil particles. Under the condition of low moisture content (ω = 18% and ω = 20%), the internal friction angle decreases with the increase of dry density. With the increase of moisture content, the water content of the test reaches medium conditions (ω = 23%,ω = 25%, and ω = 28%), and the curve shows a fluctuating change, but the overall change is not large, indicating that the dry density has little effect on the internal friction angle under this condition. When the moisture content of the sample reaches ω = 30% and ω = 32%, the internal friction angle is reduced to the lowest.

Fig. 15
figure 15

Relationship between dry density and angle of internal friction of muddy interlayer.

Full size image

Cohesion

The relationship between cohesion and dry density of muddy interlayer samples is shown in Fig. 16. When the moisture content is 18%, the cohesion does not change much with the increase of dry density, and remains at a high level as a whole. When the moisture content is 20%, the cohesion increases linearly with the dry density. When the moisture content is 23%, the cohesion increases first and then decreases with the increase of dry density, and then rebounds at higher dry density, and the overall change is not large. When the moisture content is 25%, the cohesion increases first and then decreases with the dry density. When the moisture content is 28%, the cohesion tends to be stable. For the moisture content of 30% and 32%, the cohesion shows a lower level.

In summary, when the moisture content is low (ω = 18% and ω = 20%), the cohesion increases with the increase of dry density. This is because less water makes the attraction between soil particles more significant, resulting in higher cohesion. At medium moisture content (ω = 23% and ω = 25% ), the relationship between cohesion and dry density is more complex, and it fluctuates dynamically with the increase of dry density, which indicates that there is an optimal dry density range, in which the cohesion of soil is maximized. At high moisture content (ω = 28%~ω = 32%), the dry density response effect is not obvious, and the cohesion is usually low and not changed much. This may be because too much water forms a continuous water film between particles, which reduces the direct contact and attraction between soil particles, thus reducing the cohesion.

Fig. 16
figure 16

Relationship between dry density and cohesion of muddy interlayer.

Full size image

Conclusion

In this paper, the effects of dry density and moisture content on the shear characteristics of clayey mud-type muddy interlayers are investigated, and the main conclusions are as follows:

(1) The shear stress of the muddy interlayer increases with dry density, while it is the opposite with moisture content. The shear stress-shear displacement at 20% moisture content shows a obvious strain softening phenomenon; at 23% and 25% moisture content, hardening characteristics are shown at low normal stress levels, while the curve transitions from softening to hardening at high stress levels; at 28% moisture content, the curves all show a slight strain softening phenomenon.

(2) At low moisture content, the internal friction angle decreases with the increase of dry density, and shows fluctuating change with dry density at medium moisture content, and dry density has little effect on the internal friction angle at high moisture content; due to the lubrication effect of water, the internal friction angle shows a decreasing trend with the increase of moisture content.

(3) At low moisture content, the cohesive force increases with the increase of dry density; and shows dynamic fluctuation with the increase of dry density at medium moisture content; and the effect of dry density response is not obvious at high moisture content. Under different dry density conditions, the weakening of water leads to a gradual decrease in the cementation between soil particles and the water film bonding force, and the disintegration of the soil agglomerate structure, and the cohesive force generally decreases with the increase of water content.

(4) Dry density and moisture content directly affect the pore structure of soil and the interaction between particles. Low moisture content and high dry density have a strengthening effect on the shear characteristics of clay-type muddy interlayers.