Introduction

The advancement of drone technology and high-definition imaging has facilitated the increasing use of aerial surveying in digital city projects. Rotorcraft UAVs, known for their agility and adaptability1,2,3,4,5, employ visual sensors to achieve real-time spatial awareness in unfamiliar surroundings. This capability not only overcomes obstacles in motion planning but also facilitates instantaneous data transmission to ground stations, ensuring the promptness and precision of information. However, urban settings pose various challenges for rotorcraft UAV path planning due to diverse city layouts, dense building clusters, and unpredictable factors, resulting in a rich yet intricate 3D environment6. These challenges, combined with limited battery life, complicate aerial survey missions4,6,7. Consequently, the optimization of flight paths that balance safety and efficiency has become a key research focus. This entails addressing spatial navigation complexity and the trade-off between energy usage and task completion to develop collision-free trajectories that enhance safety and operational efficiency within UAV motion constraints8,9,10.

UAV path planning algorithms are commonly classified into traditional, sampling-based, and bio-inspired categories11,12,13. Traditional methods such as A*14, artificial potential field15, and Dijkstra are popular for finding the shortest path but encounter challenges in 3D planning due to computational complexity and dynamic constraints. Sampling-based techniques, such as Probabilistic Roadmap (PRM)16and Rapidly-exploring Random Tree (RRT)17, are effective in navigating high-dimensional spaces with efficient exploration but may produce suboptimal routes. Although traditional approaches are known for their reliability, they often fall short of achieving global optimality and are associated with high computational demands and low success rates in intricate environments, thereby limiting their practical utility.

Traditional path planning algorithms have limitations in determining optimal routes. To address challenges such as high-dimensional search spaces, multi-constraint conditions, and dynamic environments in UAV path planning, researchers have proposed heuristic metaheuristic algorithms inspired by natural phenomena. Examples include Ant Colony Optimization (ACO)18, Particle Swarm Optimization (PSO)19, Grey Wolf Optimizer (GWO)20, Whale Optimization Algorithm (WOA)21, Jellyfish Search Algorithm(JS)22, Coati Optimization Algorithm(COA)23, etc. Despite their flexibility and effectiveness, these algorithms often suffer from premature convergence to local optima. Recent enhancements have focused on algorithm-specific optimizations. For instance, Wu et al.24 integrated PSO’s global search capabilities with ACO’s local search strengths for robotic motion planning, albeit with suboptimal dynamic adaptability. Phung et al.25 introduced Spherical Vector-based PSO (SPSO) for UAV path planning in multi-threat environments, but its performance under ideal conditions requires improvement. Yin et al.26 enhanced WOA through quasi-oppositional learning and improved search mechanisms, although energy consumption considerations were overlooked. Pehlivanoglu et al.27 combined ACO, Voronoi diagrams, and clustering with GA initialization, neglecting actual terrain characteristics. Huang et al.28 optimized BAT using nonlinear functions but introduced subjective limitations. Liu et al.29 developed IDBA with variable neighborhood operators to prevent local optima, while Lin et al30. enhanced ABC initialization using chaotic mapping and Pareto principles, albeit in static environments.

The Dung Beetle Optimizer (DBO) is a metaheuristic algorithm inspired by dung beetle behaviors such as ball-rolling, dancing, foraging, stealing, and reproduction, introduced by Xue et al. in 202231. Despite exhibiting robust global and local search capabilities, DBO encounters challenges in balancing exploration–exploitation trade-offs and achieving rapid convergence in high-dimensional spaces, often resulting in local optima. Recent enhancements have been proposed to address these limitations. Chen et al.32 integrated exponentially decreasing inertia weights for faster convergence and Cauchy mutation to preserve diversity. Lyu et al.33 improved initialization through chaotic mapping, replaced ball-rolling with global exploration strategies, and utilized adaptive t-distribution to balance exploration–exploitation, albeit with limited real-world validation. Shen et al.34 utilized Beta distribution to escape local optima and Levy flights for boundary handling, though comprehensive environmental testing was lacking. Zhang et al.35amalgamated chaotic mapping with Levy flights to enhance search quality and introduced dynamic weights during theft phases. Zhang et.al. proposed EDBOA for drone path planning based on biomimetic social behaviors36. While these advancements demonstrate enhanced performance in static benchmark tests, challenges persist in dynamic, complex real-world scenarios.

While demonstrating enhanced optimization efficiency and accelerated convergence in existing studies, the DBO fundamentally suffers from critical operational constraints: its inadequate population diversity preservation mechanisms induce premature convergence tendencies, particularly evident in multimodal optimization landscapes where compromised global search efficacy frequently results in local optima entrapment. Furthermore, the algorithm’s static balance regulation between exploration and exploitation phases intensifies parameter sensitivity, severely degrading performance scalability when handling high-dimensional nonlinear problems characterized by complex solution spaces and dynamic fitness landscapes. To enhance the search performance of the DBO algorithm in three-dimensional complex environments, this paper proposes a multi-strategy integrated DBO algorithm with the following main contributions:

  1. (1)

    Considering the flight parameters and environmental constraints of drones, we propose a new fitness-weighted function that comprehensively evaluates flight path length, safety, altitude changes, and posture changes, ensuring that the final solution is practically optimal.

  2. (2)

    We propose a Multi-strategy DBO algorithm(MSDBO). The algorithm employs chaos-driven population initialization to enhance diversity, designs a dynamic balance mechanism to coordinate OOA-enhanced global search with simulated annealing-based local refinement, and achieves multi-stage self-adaptive optimization.

  3. (3)

    We rigorously evaluate the exploration and exploitation capabilities of the MSDBO algorithm using 21 benchmark functions and the CEC2021 test functions. These assessments clearly demonstrate the algorithm’s proficiency in effectively navigating and utilizing the solution space.

  4. (4)

    We designed a complex scenario to compare the MSDBO algorithm with seven other intelligent algorithms, evaluating their initialization effectiveness and optimization performance.

Problem description

Scenario building

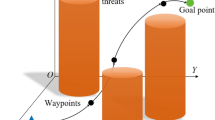
During aerial photography missions in complex urban environments, UAVs must navigate through dense structures while maintaining stable flight postures and optimal camera angles to capture building features. Operational constraints like limited battery life and obstacle avoidance, further complicate path planning, requiring balanced optimization of route costs, search time, and computational complexity. The objectives of this article and the specific urban environment are illustrated in Fig. 1.

Fig. 1
figure 1

The environment model of Building. (a) Flight Path Planning Task. This study aims to identify feasible flight paths under these urban constraints. (b) Approximate Model. Tall, irregularly shaped buildings are simplified into geometric primitives (e.g., cuboids, cylinders) for environmental modeling.

Full size image

Fitness function

Flight distance cost

This paper focuses on UAV flight tasks for aerial photography and surveying. A shorter flight path effectively reduces energy consumption and extends UAV endurance, so the flight path is selected to minimize the path length. The UAV flight path \({X}_{i}\) is represented by a sequence of waypoints, which are defined as three-dimensional coordinates. Since the UAV navigates in three-dimensional space, each waypoint is denoted as \({W}_{ij}\left({x}_{ij},{y}_{ij},{z}_{ij}\right)\). The distance between two waypoints can be calculated using the Euclidean distance formula. The flight distance cost formula is expressed as follows:

$$D\left( {X_{i} } \right) = \sum\limits_{j = 1}^{n - 1} {\left\| {\overrightarrow {{W_{ij} W_{i,j + 1} }} } \right\|}$$
(1)

Flight altitude cost

During urban data acquisition, drones are constrained by minimum \({h}_{min}\) and maximum \({h}_{max}\) altitude limits to ensure optimal camera resolution and viewing angles for capturing terrain feature, as illustrated in Fig. 2. Let \({h}_{ij}\) denote the altitude of the waypoint \({W}_{ij}\) relative to the reference surface. A penalty value \({p}_{ij}\) is imposed when \({h}_{ij}\) exceeds \({h}_{max}\) or falls below \({h}_{min}\), with the altitude cost formulated as follows:

$${\text{H}}_{{{\text{ij}}}} { = }\left\{ {\begin{array}{*{20}c} {P_{h} (h_{ij} - h_{\max } )} & {(h_{ij}> h_{\max } )} \\ 0 & {(h_{\min } < h_{ij} < h_{\max } )} \\ {P_{h} (h_{\min } - h_{ij} )} & {(0 < h_{ij} < h_{\min } )} \\ \infty & {(h_{ij} < 0)} \\ \end{array} } \right.$$
(2)
$${\text{H}}\left( {X_{i} } \right) = \sum\limits_{j = 1}^{n} {H_{ij} }$$
(3)
Fig. 2
figure 2

Altitude cost explanation.

Full size image

Flight attitude cost

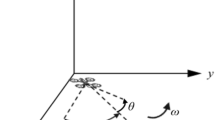
During flight operations, a drone’s key attitude control parameters include the horizontal rotation angle and the vertical pitch angle. These parameters enable obstacle avoidance through coordinated turns and facilitate vertical maneuvers for capturing architectural features at varying altitudes. Both angles must comply with the drone’s real-world angular constraints to ensure feasible flight path generation. As illustrated in Fig. 3, the principles of forming the horizontal angle and the vertical pitch angle are depicted.

Fig. 3
figure 3

Turning and climbing angle calculation. \(\overrightarrow {{W_{ij} W_{i,j + 1} }}\) and \(\overrightarrow {{W_{i,j + 1} W_{i,j + 2} }}\) represent consecutive flight segments in the planned route, with \(\overrightarrow {{W_{ij}{\prime} W_{i,j + 1}{\prime} }}\) and \(\overrightarrow {{W_{i,j + 1}{\prime} W_{i,j + 2}{\prime} }}\) denoting their projections on the XOY horizontal plane.

Full size image

These projections are calculated using the unit vector \(\overrightarrow{M}\) along the positive Z-axis direction, as follows:

$$\overrightarrow {{W_{ij}{\prime} W_{i,j + 1}{\prime} }} = \overrightarrow {M} \left( {\overrightarrow {{W_{ij} W_{i} ,_{j + 1} }} \times \overrightarrow {M} } \right)$$
(4)

From this, the formula for the horizontal turn angle \({\sigma }_{ij}\) is:

$$\sigma_{ij} = \arctan \left( {\frac{{\left\| {\overrightarrow {{W_{ij}{\prime} W_{i,j + 1}{\prime} }} \times \overrightarrow {{W_{ij + 1}{\prime} W_{i,j + 2}{\prime} }} } \right\|}}{{\overrightarrow {{W_{ij}{\prime} W_{i,j + 1}{\prime} }} \overrightarrow {{W_{ij + 1}{\prime} W_{i,j + 2}{\prime} }} }}} \right)$$
(5)

The climb and descent angles are the angles formed between the flight segment connecting two waypoints and its projection vector. From this, the vertical pitch angle \({\varphi }_{ij}\) can be derived as follows:

$$\varphi_{{\text{i,j + 1}}} = {\text{arctan}}\left( {\frac{{\left| {z_{i,j + 2} - z_{i,j + 1} } \right|}}{{\overrightarrow {{\left\| {W_{i,j + 1}{\prime} W_{i,j + 2}{\prime} } \right\|}} }}} \right)$$
(6)

In summary, set the penalty coefficients \({a}_{1}\) and \({a}_{2}\) for the horizontal turning angle and the vertical pitch angle of the UAV when they exceed the constraint conditions. The cost function, which establishes a connection with the flight attitude, is shown in Eq. (7):

$$P\left( {{\text{X}}_{{\text{i}}} } \right){\text{ = a}}_{1} \sum\limits_{j = 1}^{{{\text{n - }}2}} {\phi_{{{\text{ij}}}} } {\text{ + a}}_{2} \sum\limits_{{{\text{j = }}1}}^{{{\text{n - }}1}} {\left| {\varphi_{ij} - \varphi_{i,j - 1} } \right|}$$
(7)

Flight safety cost

In urban environments with dense and complex structures, drones require obstacle avoidance capabilities to maintain safe flight paths during aerial surveys. As illustrated in Fig. 4.

Fig. 4
figure 4

Determination of the threat cost. rectangular threat zones (expanded by a safety buffer \({d}_{i}\)) are defined around buildings. For the waypoint set \({d}_{k}\), if a path point enters zone \({d}_{k}\in \left({X}_{i}-{d}_{i},{X}_{i+1}-{d}_{i}\right)\) (extended boundary), penalty R applies; if within \({d}_{k}\in \left({X}_{i},{X}_{i+1}\right)\) (obstacle space), penalty \(\infty\) activates.

Full size image

The specific condition thresholds are defined in the following expressions:

$$\begin{array}{*{20}l} {S(X_{i} ) = \sum\limits_{j = 1}^{n - 1} {\sum\limits_{k = 1}^{K} {A_{k} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{W_{ij} W_{i,j + 1} }} )} } } \hfill \\ {A_{k} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{W_{ij} W_{i,j + 1} }} ) = \left\{ {\begin{array}{*{20}c} R & {if(X_{i} - d_{i} < d_{k} < X_{i + 1} + d_{i} )} \\ \infty & {if(X_{i} < d_{k} < X_{i + 1} )} \\ \end{array} } \right.} \hfill \\ \end{array}$$
(8)

where \(k\) is the set of building numbers.

Overall objective cost

Combine the five costs—flight distance, flight altitude constraint, flight attitude, flight safety, and flight energy consumption—using their respective weight coefficients \({b}_{i}\) The total cost is defined as follows:

$${\text{F}}({\text{X}}_{{\text{i}}} ){\text{ = b}}_{1} {\text{D}}({\text{X}}_{{\text{i}}} ){\text{ + b}}_{2} H({\text{X}}_{{\text{i}}} ){\text{ + b}}_{3} {\text{P}}({\text{X}}_{{\text{i}}} ){\text{ + b}}_{4} {\text{S}}({\text{X}}_{{\text{i}}} )$$
(9)

where the decision variable \({X}_{i}\) includes \({W}_{ij}\left({x}_{ij},{y}_{ij},{z}_{ij}\right)\) waypoints, ensuring that \({W}_{ij}\) always remains within the drone’s operational space.

Multi-strategy DBO algorithm

This section initiates with a systematic exposition of the fundamental principles underlying the original DBO. In response to the identified limitations inherent in the baseline algorithm. The section content proposes five strategic enhancements through a multi-mechanism integration approach. A comprehensive investigation is subsequently conducted, encompassing both procedural analysis of the Modified Multi-Strategy DBO (MSDBO) framework and rigorous computational complexity evaluation.

DBO

Ball-rolling dung beetle

Dung beetles exhibit two distinct navigation modes: obstacle-free and obstacle-avoidance. In unobstructed environments, they utilize celestial cues to maintain straight-line dung ball movement. Figure 5 demonstrates this obstacle-free navigation mechanism, showing a beetle aligning its rolling direction with solar positioning.

Fig. 5
figure 5

Dung beetle trajectory model.

Full size image

To simulate the rolling behavior, the dung beetle must maintain a consistent direction throughout the search area. It is assumed that the intensity of the light source influences the beetle’s rolling trajectory. As the beetle rolls, its position information is updated according to the following formula:

$${\text{X}}_{{\text{i}}}^{{{\text{t + }}1}} {\text{ = X}}_{{\text{i}}}^{{\text{t}}} {\text{ + k}}\alpha {\text{X}}_{{\text{i}}}^{{{\text{t - }}1}} { + }\left| {X_{i}^{t} - X_{w}^{t} } \right|\omega$$
(10)

where t denotes the current iteration number; \({X}_{i}^{t}\) represents the positional information of the i-th dung beetle during the t-th iteration; \(k\) is a constant termed the deflection coefficient, bounded within the interval (0,0.2]; \(\omega\) is a constant value defined over the range (0,1); signifies a natural coefficient that assumes values of either 1 or −1, where −1 indicates deviation from the original direction and 1 denotes no deflection; and \({X}_{w}^{t}\) corresponds to the current global worst position.

Dung beetles overcome rolling obstacles by performing rotational pauses atop their dung balls to reorient in challenging terrain. This adaptive navigation mechanism is mathematically modeled using tangent functions for directional adjustment. Figure 6 depicts the tangent function model and the beetles’ pattern of movement, confined to the [0,π] interval.

Fig. 6
figure 6

Tangent function and dancing model of dung beetles. (a) Tangent function in the rolling direction. (b) dancing model of dung beetles.

Full size image

Once the dung beetle successfully determines a new direction, it continues rolling the dung ball. At this point, the position update expression for the rolling beetle is as follows:

$${\text{X}}_{{\text{i}}}^{{{\text{t + }}1}} {\text{ = X}}_{{\text{i}}}^{{\text{t}}} {\text{ + tan}}\left( \theta \right)\left| {X_{i}^{t} - X_{i}^{t - 1} } \right|$$
(11)

the yaw angle \(\theta\) belongs to the interval [0, π]. In the equation, t represents the current iteration count, \({X}_{i}^{t}\) denotes the position information of the i-th dung beetle at the t-th iteration, and \(\left|{X}_{i}^{t}-{X}_{i}^{t-1}\right|\) is the absolute value of the difference between the position of the i-th dung beetle at the t-th iteration and its position at the previous (t−1)-th iteration.

Dung beetle reproduction

Selecting an appropriate oviposition site is crucial for dung beetles to provide a secure environment for their offspring. As illustrated in Fig. 7, the current local optimum position \({X}_{lbest}^{t}\) is represented by a large orange sphere, while the small black spheres surrounding \({X}_{lbest}^{t}\) denote the egg balls. Each dung ball contains a dung beetle egg A, and the red dots indicate the upper and lower boundaries.

Fig. 7
figure 7

Concept model of boundary selection strategy.

Full size image

When a female dung beetle identifies an oviposition area and proceeds with reproductive behavior, each female produces one larva per iteration. As the oviposition area is dynamically adjusted, the position of the larva during its development is also uncertain. The specific formula is as follows:

$${\text{B}}_{{\text{i}}}^{t + 1} = {\text{X}}_{{{\text{lbest}}}}^{{\text{t}}} + b_{1} \left( {{\text{B}}_{{\text{i}}}^{t} - lb*} \right) + b_{2} \left( {{\text{B}}_{{\text{i}}}^{t} - ub*} \right)$$
(12)

where \({X}_{lbest}^{t}\) represents the local optimal position of the current population, while \({B}_{i}^{t+1}\) denotes the positional information of the i-th egg ball at the t-th iteration. Here, b1 and b2 are two independent random D-dimensional vectors, and D signifies the dimensionality of the optimization problem. \({lb}^{*}\) and \({ub}^{*}\) represent the lower and upper bounds of the oviposition area, respectively.

Small dung beetle

The foraging behavior of dung beetles primarily originates from the larvae. The position update of the larva is as follows:

$${\text{X}}_{{\text{i}}}^{t + 1} = {\text{X}}_{{\text{i}}}^{{\text{t}}} + {\text{S}}_{1} \left( {{\text{X}}_{{\text{i}}}^{t} - lb^{{\text{g}}} } \right) + {\text{S}}_{2} \left( {{\text{X}}_{{\text{i}}}^{t} - ub^{{\text{g}}} } \right)$$
(13)

where \({X}_{gbest}^{t}\) represents the current global optimal position, where \({lb}^{g}\) and \({ub}^{g}\) denote the lower and upper bounds of the foraging area, respectively. S1 follows a normal distribution of random numbers, and S2 is a random vector between 0 and 1.

Thieving dung beetle

During the iteration process, considering that some dung beetles may steal dung balls from others, the position update for such beetles is as follows. From Eqs. (12) and (13), it can be observed that \({X}_{lbest}^{t}\) is the optimal source for food acquisition. Assuming \({X}_{lbest}^{t}\) is the primary ___location for food competition, the position update for the stealing beetles is as follows:

$${\text{X}}_{{\text{i}}}^{t + 1} = {\text{X}}_{{{\text{gbest}}}}^{{\text{t}}} + {\text{Wm}}\left( {\left| {{\text{X}}_{{\text{i}}}^{t} - {\text{X}}_{{{\text{gbest}}}}^{t} } \right| + \left| {{\text{X}}_{{\text{i}}}^{t} - {\text{X}}_{{{\text{lbest}}}}^{{\text{t}}} } \right|} \right)$$
(14)

where W is a constant, and m represents a random vector of size \(1\times D\), following a normal distribution.

Although the DBO exhibits strong optimization capabilities and fast convergence, it suffers from an imbalance between global exploration and local exploitation, often leading to local optima and weak global search ability. To enhance DBO’s performance, this study proposes five strategies to strengthen the algorithm.

MSDBO

Through an analysis of the operational mechanism of the original DBO, it becomes evident that although the algorithm demonstrates significant optimization efficiency and convergence speed compared to classical heuristic methods, it still suffers from fundamental limitations when addressing complex constrained optimization problems. The absence of a population diversity maintenance mechanism renders the algorithm prone to local optima entrapment, with its global search capability notably diminishing in multimodal optimization scenarios. Concurrently, the static exploration–exploitation balance strategy exacerbates parameter sensitivity, leading to severe performance degradation when handling high-dimensional nonlinear problems. As shown in Table 1, the academic community has proposed various improvement strategies to address these limitations.

Table 1 Summary of DBO Improvements.
Full size table

The objectives of the aforementioned improvements to the DBO are summarized in Table 1. The improvement strategies proposed in this study are developed based on the four aforementioned aspects, introducing five strategies—Piecewise chaotic map, Global exploration strategies, Sigmoid nonlinear convergence factor, dynamic weight coefficient, and improved local exploration strategy for simulated annealing algorithm—to enhance the performance of the original DBO.

Piecewise chaotic map

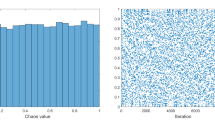
The original DBO employs random initialization to maximize global exploration, yet excessive stochasticity risks population clustering and diversity depletion, compromising optimization stability. This study introduces Piecewise chaotic mapping for structured population initialization, enhancing search space coverage and accelerating heuristic convergence through improved distribution uniformity. Figure 8 compares the distribution and histograms of Piecewise chaotic mapping and random initialization.

Fig. 8
figure 8

Initialization Testing. (a)-(b) The Distribution Chart. (c)-(d) The Histograms Chart.

Full size image

As a typical chaotic mapping function, Piecewise offers simplicity, strong ergodicity, and randomness. Its mathematical expression is as follows:

$${ = }\left\{ {\begin{array}{*{20}c} {\frac{{{\text{x}}_{{\text{i}}} }}{P}} & {0 \le {\text{x}}_{{\text{i}}} < P} \\ {\frac{{{\text{x}}_{{\text{i}}} - P}}{0.5 - P}} & {P \le {\text{x}}_{{\text{i}}} < 0.5} \\ {\frac{{1 - P - {\text{x}}_{{\text{i}}} }}{0.5 - P}} & {0.5 \le {\text{x}}_{{\text{i}}} < 1 - P} \\ {\frac{{1 - {\text{x}}_{{\text{i}}} }}{{\text{P}}}} & {1 - P \le {\text{x}}_{{\text{i}}} < 1} \\ \end{array} } \right.$$
(15)

Global exploration strategies

The DBO’s barrier-free rolling mode relies on decentralized parameters with limited agent coordination, risking local optima entrapment. To overcome this, we propose an adaptive directional adjustment strategy via stochastic dung ball detection, enhancing global exploration through optimized swarm interactions. The phase-specific update mechanism is formulated as:

$${\text{X}}_{{\text{i}}}^{t + 1} = {\text{X}}_{{\text{i}}}^{t} + {\text{Rand}}\left( {{\text{X}}_{{{\text{Fbest}}}}^{t} - {\text{I}}_{{\text{i}}}^{t} \times {\text{X}}_{{\text{i}}}^{t} } \right)$$
(16)

where \(rand\) is a random number in (0,1), \({I}_{i}^{t}\) is a random vector between 1 and 2, and \({X}_{Fbest}^{t}\) represents the best solution selected from the current position, i.e., the global optimal solution.

We hybridize DBO’s obstacle-present stage with Osprey Optimization’s global exploration through phase-specific integration. This stochastic enhancement enables simultaneous position updates via worst-case scenario referencing and probabilistic superior area sampling, effectively reducing premature convergence risks while expanding solution space exploration for improved global optimum identification.

Adaptive t-distributed perturbation strategy

This study integrates adaptive t-distribution mutations into dung beetle foraging dynamics, using iteration count as a self-tuning parameter to achieve phase-aware search optimization. The strategy progressively transitions from global exploration to local refinement through adaptive randomness regulation, accelerating convergence while maintaining solution quality. The position update mechanism operates as follows:

$$\left\{ {\begin{array}{*{20}c} {X_{i}^{t = 1} = X_{gbest}^{t} + t{(}C_{iter} {)} \times X_{gbest}^{t} } \\ {C_{iter} = {\text{exp}}\left( {\frac{{4t^{{2}} }}{T}} \right)} \\ \end{array} } \right.$$
(17)

where c is the adaptive t-distribution parameter, and is the random number generated by the adaptive t-distribution. T represents the maximum number of iterations.

Sigmoid nonlinear convergence factor and dynamic weight coefficient

The foraging and breeding phases of DBO are critical factors influencing route optimization. The original K variation affects the exploration between these phases, and as t increases, the algorithm transitions to local exploration. However, the actual search process is a highly complex nonlinear process, and fixed transition boundaries can reduce optimization performance. To balance global and local search, this study introduces a Sigmoid nonlinear convergence factor.

As shown in Fig. 9, this paper adopts the Sigmoid function as the convergence factor, replacing the original convergence factor in the traditional DBO. The Sigmoid function maintains a high degree of individual freedom in the early stages of the algorithm, enhancing global search capability. In the later stages, it rapidly reduces individual freedom, effectively improving the precision and efficiency of local search. expressed as follows:

$$\left\{ {\begin{array}{*{20}c} {K_{new} = \frac{w}{{1 + exp\left( \frac{10R}{T} \right)}}} \\ {R = t - \frac{T}{2}} \\ \end{array} } \right.$$
(18)
Fig. 9
figure 9

Comparison of convergence factors.

Full size image

As shown in Eq. (14), the thief beetle’s position is influenced by the global optimum, helping generate optimal solutions. However, if the optimal individual gets trapped in a local optimum, the algorithm’s efficiency decreases significantly. To balance global and local exploration, a dynamic weight coefficient is introduced in the position update formula during the theft phase, as follows:

$$\left\{ {\begin{array}{*{20}c} {{\text{k}}_{1} { = }1{ - }\frac{{{\text{t}}^{3} }}{{{\text{T}}^{3} }}} \\ {{\text{k}}_{2} { = }\frac{{{\text{t}}^{3} }}{{{\text{T}}^{3} }}} \\ \end{array} } \right.$$
(19)

In the early stages, k1 is large, encouraging beetles to explore near the optimal beetle, enhancing global search. Later, k2 gradually increases, helping beetles escape local optima. This strategy balances global exploration and local exploitation. The specific update formula is as follows:

$$X_{i}^{t + 1} = X_{gbest}^{t} + Wm\left( {k_{1} \left| {X_{i}^{t} - X_{gbest}^{t} } \right| + k_{2} \left| {X_{i}^{t} - X_{lbest}^{t} } \right|} \right)$$
(20)

Improved local exploration strategy for simulated annealing algorithm

In the proposed optimization algorithm, a local search mechanism is introduced to enhance search accuracy and convergence speed. By activating local search in later iterations and integrating it with simulated annealing, the algorithm’s local optimization capability is strengthened. New solutions are generated by adding small-scale Gaussian perturbations and then filtered using the simulated annealing mechanism. The update formula is as follows:

$$X_{new}^{t} = X_{i}^{t} + \alpha \times \beta \times Gaussian\left( {u,\sigma^{2} } \right)$$
(21)
$${\text{X}}_{{\text{i}}}^{{\text{t}}} { = }\left\{ {\begin{array}{*{20}c} {{\text{X}}_{{{\text{new}}}}^{t} } & {{\text{if X}}_{{{\text{new}}}}^{t} {\text{ < X}}_{{\text{i}}}^{t} } \\ {\exp ( - \frac{{{\text{X}}_{{{\text{new}}}}^{t} - {\text{X}}_{{\text{i}}}^{t} }}{{T_{{\text{w}}} }})} & {{\text{if X}}_{{{\text{new}}}}^{t} {\text{> X}}_{{\text{i}}}^{t} } \\ \end{array} } \right.$$
(22)

Equation (21), \(\alpha\) is a small constant, \(\beta\) is the perturbation scale factor, \(\mu\) is the mean, and \({\sigma }^{2}\) is the variance. Equation (22) represents the decision mechanism of the simulated annealing strategy, where \({T}_{i}\) is the temperature change parameter.

Algorithm analysis

Process analysis

In the MSDBO, a Piecewise chaotic map is used to obtain high-quality initial solutions. During the rolling phase, the global search strategy of the OOA replaces the original position update method, enhancing information sharing among populations, simplifying parameter selection, and improving global search performance. The Sigmoid convergence factor is used to replace the original convergence factor, allowing for extensive exploration in the early optimization stages to avoid local optima. In the later stages, the algorithm performs more detailed searches around better solutions to further improve solution quality. An adaptive t-distribution is introduced in the foraging phase to update the positions of foraging dung beetles, enhancing algorithm performance and robustness. The thieving beetles use a dynamic weight coefficient to adjust the importance of different search strategies or components dynamically, balancing exploration and exploitation. The algorithm also employs an improved simulated annealing strategy to enhance accuracy and exploration while avoiding local optima. The flow of the MSDBO algorithm is shown in Fig. 10.

Fig. 10
figure 10

Flow chart of MSDBO.

Full size image

The pseudo-code of MSDBO is shown in Algorithm 1.

figure a

Algorithm 1: The pseudo code of MSDBO

Computational complexity

Assessing MSDBO’s efficacy necessitates computational complexity analysis via big-O notation, determining feasibility in resource-constrained environments37. The computational complexity of MSDBO is impacted by several key variables, including the number of solutions (N), the maximum number of iterations (M), and the problem dimension (D). Specifically, the complexity of the initialization phase is O(N), reflecting a linear relationship with the number of solutions. The core function’s overall time complexity is O(T✻N✻D), taking into account the number of iterations (T), the number of solutions(N), and the problem dimension (D). The complexity for population initialization is O(N), and the core complexity of the original algorithm is O(T✻N✻D). Each individual in the chaos mapping process requires O(N) computations. The position update strategy in each iteration depends on the population size, search dimension, and the maximum number of iterations, leading to a complexity of O(T✻N✻D) for the dung beetle optimization process. Therefore, the total complexity of MSDBO is O(N) + O(T✻N✻D) + O(T✻N✻D) + O(T✻N✻D) + O(T✻N✻D) = O(T✻N✻D). Despite the additional steps involved, MSDBO significantly improves performance compared to the original DBO.

Results

This study systematically evaluates the performance of the MSDBO through 21 benchmark functions, the CEC2021 test suite, and a 3D drone route planning experiment. Algorithm evaluation and comparison largely depend on benchmark testing, as benchmark experiments are essential for selecting the optimal algorithm to address practical problems38. For the benchmark validation, we adopted the 21 classical test functions and the CEC2021 test functions published by the IEEE Congress on Evolutionary Computation39. These functions cover critical characteristics such as unimodal, multimodal, and fixed-dimensional properties, enabling rigorous analysis of the algorithm’s convergence precision and its ability to escape local optima. All experiments were conducted in the standardized testing environment provided by CEC, utilizing convergence trajectory analysis and quantitative metrics (e.g., success rate, computational efficiency) for multidimensional comparisons. Statistical significance was ensured through the Wilcoxon signed-rank test at a 95% confidence level40. Finally, the 3D drone route planning experiment validated the algorithm’s comprehensive performance in practical engineering metrics, including obstacle avoidance efficiency, trajectory smoothness. To ensure objectivity, fairness, and reliability, the simulation environment of this study runs on a Windows 11 64-bit operating system, with a CPU model of 12 th Gen Intel(R) Core(TM) i5-12400 F, a base frequency of 2.50 GHz, and equipped with 32 GB RAM. The algorithms were implemented on the MATLAB R 2024a platform.

Experimental design

In this chapter, the MSDBO is tested using 21 benchmark test functions and CEC2021 test functions to verify its robustness through statistical and convergence analysis. MSDBO is compared with six heuristic algorithms (DBO, WOA, GWO, PSO, AOA41, HHO42). Table 1 details the parameter settings for all algorithms. The parameters are set as population size N = 30, maximum iterations T = 500, and 30 independent runs.

The superiority of MSDBO is evaluated by comparing the Best (Best), Average, and standard deviation (Std) across the 21 benchmark functions. These metrics are chosen due to their distinct exploration and exploitation characteristics. Table 2 summarizes the parameter settings, which are based on recommendations from respective reference papers.

Table 2 Parameter variable settings.
Full size table

Benchmark test functions

To evaluate the performance of the MSDBO, a set of 21 benchmark test functions as shown in Table 3 is selected. Among these, F1-F7 are high-dimensional unimodal functions with a single global optimum, suitable for assessing the algorithm’s local exploration capability. Functions F8-F13 are high-dimensional multimodal functions, while F14-F21 are fixed-dimension multimodal benchmark functions with multiple local optima, designed to test the algorithm’s ability to escape local optima.

Table 3 Benchmark test functions.
Full size table

Tables 4 and Appendix A (Table A1, Table A2) present the mean and standard deviation results of all algorithms on the 21 benchmark functions, with comparisons at 30, 50, and 100 dimensions (F16-F21 have fixed dimensions). The algorithm with the lowest mean and standard deviation in each test is highlighted in bold, indicating superior performance. As shown in Table 4, MSDBO achieves the best results on most functions. Vertically, MSDBO ranks first in other function tests, converging to the theoretical optimum of 0 for F1, F3, F9, and F11, and achieving optimal fitness values with a standard deviation of 0 for F2, F4, and F10. For F8, F14, F15, and F17-F21, MSDBO attains optimal fitness values and outperforms others in standard deviation. Although MSDBO does not achieve the best values for F5, F6, F7, F12, F13, and F16, it demonstrates significant advantages over other algorithms. Dimension-wise comparisons (30, 50, and 100) show similar results with minimal changes in ranking. Overall, MSDBO exhibits a more competitive edge in solving both unimodal and multimodal functions.

Table 4 Experimental results (dim = 30).
Full size table

Figure 11 displays the rankings of all algorithms based on their average, best, and standard deviations. To enhance visualization clarity, we have categorized the rankings into five groups: Best Ranking, Second Ranking, Third Ranking, Worst Average Ranking, and other Ranking Cases. As clearly demonstrated in the Fig. 11, the MSDBO significantly outperforms other heuristic sub-algorithms in both optimization capability and algorithmic stability in most cases.

Fig. 11
figure 11

Comparison chart of rankings for 21 benchmark test functions. (a) Average comparison chart. (b) Best comparison chart. (c) Standard deviation comparison chart.

Full size image

Figure 12 demonstrates MSDBO’s dominance in 20/21 benchmark functions. The algorithm’s median nearly reaches the vertical axis zero in 20 functions, with box heights (15 th-25 th percentiles) significantly smaller than competitors. For F8, MSDBO achieves 1/5 the IQR of DBO, reflecting superior solution density. This method demonstrates significant outlier reduction compared to benchmark approaches. In F15, MSDBO generates only 1 outlier versus PSO’s 9, with lower maximum values, proving stronger robustness to initialization. The exception occurs in F5, where dense local optima around the global minimum trap MSDBO in suboptimal solutions in the trials due to parameter sensitivity, exacerbated by the function’s exponentially growing local optima with dimensionality. PSO results were excluded from F5-F7 and F12-F13 boxplots due to two-order magnitude fitness differences in these high-dimensional/multimodal problems, which would distort visualization clarity.

Fig. 12
figure 12

Comparative boxplots of seven optimization algorithms across 21 benchmark test functions (30 independent runs). Subfigures (a–u) correspond to functions F1-F21, respectively.

Full size image

Figures 13, 14, and 15, it is observed that MSDBO consistently converges to the global optimum with a 100% success rate for functions F1, F3, F9, F11, F16, F17, and F18. Its convergence accuracy and speed significantly outperform the other six algorithms, which fail to find the global optimum. For F2, F4, F8, F10, and F14, MSDBO distributes the population more uniformly across the solution space, increasing the number of individuals near the optimal solution. This enables the algorithm to quickly find the best solution during iterations, producing nearly linear convergence curves.

Fig. 13
figure 13

Convergence processes of different algorithms for a unimodal function. Subfigures (a–g) correspond to functions F1-F7, respectively.

Full size image
Fig. 14
figure 14

Convergence processes of different algorithms for a multimodal function. Subfigures (a–f) correspond to functions F8-F13, respectively.

Full size image
Fig. 15
figure 15

Convergence processes of different algorithms for a fixed-dimensional multimodal function. Subfigures (a–h) correspond to functionsF14–F21, respectively.

Full size image

In high-dimensional multimodal functions (F14-F21), MSDBO achieves higher optimization precision, demonstrating superior exploration capabilities. For fixed-dimension functions (F14, F16-F21), while all methods exhibit similar curves due to algorithmic complexity, MSDBO performs slightly better, converging rapidly in early iterations. Overall, MSDBO excels in convergence speed, accuracy, global search capability, and escaping local optima, outperforming other algorithms in exploration ability.

MSDBO demonstrated the fastest optimization process among 21 benchmark functions, effectively saving optimization time and quickly converging to the global optimum in later stages. This significantly reduces the risk of getting trapped in local optima, a common issue with other algorithms. In summary, the MSDBO consistently exhibits superior convergence speed and accuracy.

To further validate the effectiveness of MSDBO, the Wilcoxon rank-sum test was utilized to assess statistical significance. Each algorithm was independently executed 30 times, ensuring that the data volume was sufficient for robust statistical analysis. The p-values from the Wilcoxon rank-sum test, conducted at a 5% significance level, are provided. If a p-value is less than 0.05, the null hypothesis is rejected in favor of the alternative hypothesis43. In Table 5, the notation “ +/−/= ” represents the number of instances where MSDBO outperformed, underperformed, or matched the performance of other algorithms, with “NAN” indicating similar performance. The majority of the p-values were below 0.05, suggesting significant differences in performance. Thus, MSDBO exhibits superior convergence capabilities.

Table 5 Wilcoxon rank sum test results.
Full size table

Performance on CEC2021 suite

To further evaluate MSDBO’s performance, the challenging CEC 2021 test functions was used to test seven metaheuristic algorithms. For detailed function specifications, please refer to Table A3 in Appendix A. The population size was set to 30, maximum iterations to 500, and dimensions to 20. Each algorithm was independently run 30 times to ensure fairness. The Wilcoxon signed-rank test was conducted, with “gm” representing the difference between the number of “ + ” and “-” signs.

Table 6 presents the experimental results. MSDBO ranked first in CEC-1, CEC-5, CEC-9, and CEC-10. For CEC-2, CEC-3, CEC-4, and CEC-8, MSDBO achieved the best average results. In CEC-6 and CEC-7, MSDBO’s performance was second only to AOA. The “gm” score indicates significant differences between MSDBO and other algorithms in most cases. Overall, the CEC 2021 results demonstrate MSDBO’s effectiveness and applicability to engineering problems.

Table 6 CEC 2021 test function results.
Full size table

As illustrated in Fig. 16, the experimental ranking results comprehensively evaluate the optimization algorithms based on three criteria: mean, best, and standard deviation. The analysis demonstrates that MSDBO exhibits significant advantages over the original DBO algorithm across most test functions, achieving higher convergence accuracy, faster iteration speed, and lower standard deviations. Notably, MSDBO consistently ranks first in all test cases, particularly outperforming other heuristic algorithms in addressing multimodal and hybrid function problems. These results validate the innovative improvements in MSDBO’s exploration–exploitation balancing mechanism, which enhances its global optimization capability and stability.

Fig. 16
figure 16

Comparison chart of rankings for CEC 2021 test functions. (a) Average comparison chart. (b) Best comparison chart. (c) Standard deviation comparison chart.

Full size image

Convergence analysis serves as a critical method for evaluating the local exploitation and global exploration capabilities of algorithms, with its core value lying in the quantitative characterization of dynamic optimization processes. The convergence curve comparison illustrated in Fig. 17 reveals a noteworthy phenomenon: despite occasional curve interruptions observed in the MSDBO algorithm during continuous iterations (attributed to the discretized representation of average values under a logarithmic coordinate system), its overall convergence performance demonstrates notable superiority. Particularly in eight representative functions from the CEC test series—specifically CEC-1, CEC-2, CEC-3, CEC-5, and CEC-7 to CEC-10—the MSDBO algorithm exhibits significantly accelerated convergence characteristics compared to other heuristic algorithms.

Fig. 17
figure 17

Convergence processes of different algorithms for the CEC 2021 results. Subfigures (a–j) correspond to functions CEC-1– CEC10, respectively.

Full size image

Simulation experiments on UAV path planning

Scenario Setup

To further validate MSDBO’s capability and effectiveness in flight path planning, comparative experiments were conducted using MATLAB. The environment was a 1000 m × 1000 m × 30 m area with multiple known obstacles (coordinates and dimensions provided). The start and end points were [130,760,2] and [950,320,10], respectively. Seven representative heuristic algorithms (PSO, GWO, DBO, NGO44, WOA, AOA, HHO) were compared. For fairness, all algorithms used a population size of 30 and a maximum of 100 iterations, each run independently 30 times. Performance was evaluated using metrics: Best (Best), Average (Avge), standard deviation (Std), Time, Path, Threat (Trat), High (High), and Smoothness (Smh).

Effect of the cost function parameters

The objective function weighting scheme prioritizes component significance through systematic allocation. The route cost (incorporating flight distance and altitude parameters) receives the highest weighting as the critical determinant of endurance performance, ensuring maximal energy efficiency through geometrically optimized path planning. Meanwhile, attitude adjustment cost obtains secondary weighting priority due to its inherent kinematic necessity and nonlinear decay characteristics in global energy consumption impact. Experimental validation showed that after conducting the tests below, all tested optimization algorithms demonstrated precise obstacle avoidance capability, with the threat cost being assigned the lowest weighting priority. Following systematic parameter tuning via orthogonal experimental design and gradient-based optimization, the calibrated coefficients are formulated as: b₁ = 5, b₂ = 2, b₃ = 1, b₄ = 134,37,45.

Experimental results and performance analysis

Table 7 present the numerical results and performance of the eight heuristic algorithms. In Table 7, MSDBO achieves the best results in height cost, best, standard deviation, and mean. While its path cost is slightly inferior to DBO, it significantly outperforms other algorithms. MSDBO also performs well in runtime. Although PSO is the fastest, its optimization results are notably inferior to MSDBO. Overall, MSDBO demonstrates superior performance in this experiment.

Table 7 Comparison of the performance of the seven algorithms with tasks.
Full size table

As shown in Fig. 18, in this experimental study, the MSDBO algorithm demonstrates significant advantages: it ranks first across multiple evaluation metrics, achieving marked improvements in solution quality and algorithm stability compared to DBO. Notably, the integration of five strategies in MSDBO leads to an extended overall runtime relative to DBO. However, experimental data indicate that this moderate increase in computational cost effectively translates into enhanced algorithmic performance—MSDBO not only achieves superior global optimization results but also reduces the fluctuation range of experimental outcomes by 24% compared to the baseline algorithm. This robustly validates the effectiveness of the novel strategies in improving algorithmic robustness.

Fig. 18
figure 18

Algorithm comparison radar chart.

Full size image

The average convergence curves over 100 iterations are shown in Fig. 19. In all cases, MSDBO achieves the optimal solution compared to other algorithms. MSDBO, WOA, PSO, DBO, and HHO converge rapidly in the early stages, reaching near-optimal values by around 35 iterations. Comparison of final results reveals MSDBO has the highest solution accuracy, followed by DBO. Additionally, MSDBO converges to the optimal value very quickly at the start of iterations, showing significant performance improvement over the original DBO. This demonstrates that the proposed search strategy enhances both convergence speed and accuracy.

Fig. 19
figure 19

Avg. best vs. iteration for Map.

Full size image

In Fig. 20, PSO, AOA, and GWO exhibit redundant path segments, resulting in longer distances compared to MSDBO. HHO’s path lacks smoothness, reducing UAV endurance. DBO, WOA, NGO, and MSDBO show similar trajectory topologies, but MSDBO’s path is smoother with fewer turns. The results indicate that MSDBO, enhanced by multi-strategy improvements, maintains convergence speed while significantly improving global optimality and engineering applicability in path planning.

Fig. 20
figure 20

The UAV paths of all algorithms. Subfigures (a–q)3D perspective effect flight path. Subfigures (r–y) 2D perspective effect flight path.

Full size image

Discussion

In benchmark function tests, the MSDBO demonstrates superior convergence speed, accuracy, and stability compared to other heuristic algorithms. Within the three-dimensional UAV flight simulation environment designed in this study, it also exhibits optimal route planning capabilities. However, the MSDBO presents limitations: The integration of multiple strategies increases computational complexity, consuming additional time and storage resources. For instance, chaotic mapping initialization involves random number generation, which, though linear in complexity, marginally prolongs runtime. Meanwhile, the adaptive t-distribution mechanism requires extra computations to adjust mutation parameters, such as updating the degrees of freedom based on iteration counts or fitness values. These operations introduce a constant-factor time complexity increase proportional to the population size (e.g., scaling as O(k × N)), though the overall complexity remains linearly bounded. Simulation results corroborate that the MSDBO incurs a significantly extended runtime. Additionally, like most improved heuristic algorithms, MSDBO’s path planning for UAVs remains constrained by its architectural characteristics, necessitating reliance on global environmental information and precise execution mechanisms to generate feasible trajectories46.

This study achieves high-fidelity combat flight simulation via ​​integrated​​ 3D modeling and multi-cost constraint configuration. While replacing traditional cylindrical obstacles with convex polyhedrons enhances collision detection efficiency47, ​​the​​ current modeling approach overly simplifies geometries and fails to characterize dynamic motions, ​​thus inaccurately representing irregular urban architectures​​ and non-stationary intruder drones48. ​​Most existing studies assume static environments​​ while ignoring coupled interactions between time-varying factors (e.g., wind/rain) and UAV dynamics49. Sensor-induced hardware constraints—​​notably edge detection errors from low-resolution RGB cameras50,51​​—also degrade environmental perception. ​​Notably​​, integrating multi-state mission importance metrics52 (e.g., reliability models with sensor degradation and noise accumulation) into path optimization ​​enables​​ sustainable mechanisms ​​that​​ balance equipment health management and route safety.

This study focuses on performance optimization of heuristic algorithms for UAV route planning. While existing research has integrated multidimensional theoretical knowledge and engineering practical experience in the UAV ___domain, accurately quantifying the performance bottlenecks of metaheuristic algorithms in complex engineering scenarios remains critically important. Our work systematically demonstrates the optimization potential of heuristic algorithms in path planning, providing theoretical foundations for autonomous navigation in aerial photography, logistics delivery, and related fields, thereby advancing the technological evolution of intelligent unmanned systems.

Conclusion

This study proposes an MSDBO integrating multi-strategy enhancements to improve 3D path planning for UAVs in complex urban environments. Addressing limitations of the original algorithm in convergence precision and local optima entrapment, five innovative strategies are introduced: chaotic mapping initialization, adaptive t-distribution mutation, Sigmoid-based nonlinear convergence factor, dynamic weighting coefficients, and an improved simulated annealing mechanism. These collectively establish an optimization framework with dynamic balance between global exploration and local exploitation.

The proposed algorithm’s efficacy is systematically demonstrated through a three-phased validation framework: First, fundamental performance enhancements are quantitatively verified through Wilcoxon rank-sum tested benchmarking across 21 standard test functions. Second, adaptability to nonlinear multimodal challenges is rigorously validated through CEC2021 complex test suite evaluations. Third, practical superiority is evidenced in urban 3D path planning experiments, where the algorithm achieves a 7.4% reduction in path cost function, 10.56% improvement in altitude optimization efficiency, and 31% lower solution variability compared to existing approaches.

Future work will focus on applying the MSDBO to real-world UAV route planning and collaborative route planning for multiple UAVs in complex scenarios. Additionally, efforts will be made to reduce its runtime and extend its application to other complex optimization scenarios.