Introduction

Accurate weather forecasting with higher resolution plays a crucial role in modern society, especially for surface meteorological variables1. Research in numerical weather prediction (NWP) has advanced rapidly over the past decades2,3. Traditional NWP involves numerically solving the governing equations of fluid dynamics4,5, which is often computationally expensive and time-consuming6,7,8,9,10.

Recently, several artificial intelligence-based (AI-based) global weather forecasting models have been developed11,12,13,14,15,16,17,18,19,20, such as FourCastNet21, Pangu-Weather22, GraphCast23, FengWu24, FuXi25, ClimaX26, Aurora27, and AIFS28. Most of these models are trained using global ERA5 reanalysis data29 with a spatial resolution of 0.25° × 0.25°, matching the ECMWF Integrated Forecasting System30. AI-based models consume much fewer computational resources and run much faster than NWPs. Since ERA5 reanalysis data is generated by assimilating observations into NWP forecasts, it can correct some model errors related to NWP, such as those associated with the parameterization of physical processes31. Therefore, AI-based weather forecasting models trained on ERA5 reanalysis data could potentially be more skillful than traditional NWPs.

For weather forecasts with finer spatial resolution (such as 3 km) in domains ranging from several countries to a county or city, limited area models (LAMs) are developed. However, most work on LAMs is related to NWP, and studies on AI-based LAMs remain limited. The MetNet series32,33 is an attempt in this area, pre-trained using finer spatial resolution analysis data and focusing on precipitation, radar, satellite, and ground site observations. Building on the architecture of GraphCast, a graph-based neural model was developed34 to generate forecasts for the Nordic region by fully replacing the lateral boundary region with NWP data at the corresponding time.

Recently, AI-based models with high resolution in a region have been established by training on both fine resolution regional analysis data and coarse resolution global reanalysis data. For example, StormCast35 applied generative diffusion modeling trained with 3 km resolution analysis data from the High-Resolution Rapid Refresh (HRRR) and 0.25° resolution ERA5 data for high-resolution forecasts in Central America. A graph-based neural model with a global stretched grid was developed36, and trained using 2.5 km resolution resolution operational analyses from the MetCoOp Ensemble Prediction System data37 and ERA5 data for high-resolution forecasts in the Nordics. Recently, OMG-HD38 used observation data from the past 6 hours from meteorological stations and satellites to train an AI-based LAM for forecasting surface meteorological variables on a resolution of 0.05° × 0.05°. However, due to the lack of an imposed lateral boundary condition (LBC), only 12-h effective forecasts are available.

In this study, an AI-based LAM, called YingLong, is developed for forecasting surface meteorological variables, including surface temperature, pressure, humidity, and wind speed. These variables are highly sensitive to human life, alongside precipitation. Unlike previous work, YingLong is trained solely using 3 km resolution HRRR regional analysis data. Although global coarse resolution data are not used for training, they are required to supply the LBC. This study investigates YingLong with LBC imposed by Pangu-weather for forecasting surface meteorological variables.

YingLong is also applied to investigate issues related to LBCs of AI-based LAMs. As is well known, the ___domain of a LAM is divided into an inner area and a surrounding lateral boundary region. The meteorological conditions on the lateral boundary region are provided by coarse-resolution models, while the inner area is the focus of research and application. The coarse-resolution atmospheric information on the lateral boundary region is transmitted to the inner area through the forecast of the high-resolution LAM. Numerical LAMs require extensive processing of coarse resolution LBCs to accommodate differences in the model structure and parameterization schemes, ensuring that certain physical constraints are met. However, this may not be necessary for AI-based LAMs. As statistical models, AI-based LAMs have fewer physical restrictions on the model structure and initial values compared to numerical models. Furthermore, effectively transferring meteorological information from the lateral boundary region to the inner area is also a key objective of this paper.

Results

This section is dedicated to the construction of YingLong and its predictability with LBC imposed by Pangu-weather for the two selected limited areas in North America.

Construction of YingLong

YingLong is an AI-based limited area weather forecasting model with a 3 km spatial resolution and 24 weather variables (see Table 1). It is trained on hourly HRRR analysis data (denoted as HRRR.A), created by assimilating observations into WRF-ARW (Advanced Research WRF39) in the period 2015–2021, and validated and tested on HRRR.A in 2023 and 2022, respectively (see Methods “Datasets” for more details). Since the WRF-ARW forecasts are documented in HRRR dataset and used in data assimilation for HRRR.A, it is denoted as HRRR.F for convenience. To test YingLong’s sensitivity to topography, YingLong is constructed and evaluated on two domains: the east ___domain (ED), which is relatively flat, and the west ___domain (WD), which includes considerable mountain ranges (see Fig. 1). Both ED and WD are divided into an inner area (the area within the red dashed line) and a lateral boundary region (the region outside the red dashed line).

Fig. 1: The topography of ED and WD.
figure 1

The dots represent observation sites. In total, there are 205 sites, 78 in WD and 127 in ED.

Full size image
Table 1 The weather variables of YingLong include a total of 24 variables, consisting of 20 upper-air variables from 4 pressure levels (50 hPa, 500 hPa, 850 hPa, and 1000 hPa, following FourCastNet) and four surface variables
Full size table

The architecture of YingLong includes an embedding layer, a spatial mixing layer (comprising the Local branch and Global branch), and a linear decoder (see Fig. 2 and Methods “Architecture” for details). YingLong is trained using the procedure documented in Methods “Training”, with a smoothing boundary condition imposed (see Methods “Lateral boundary condition”). The procedure for YingLong’s rolling forecasting is documented in Methods “Rolling forecast” and briefly illustrated in Fig. 3. Two indicators, including root mean squared error (RMSE, Supplementary Eq. (S1) in Supplementary Note 1) and anomaly correlation coefficient (ACC, Supplementary Eq. (S2) in Supplementary Note 1), are used to evaluate the models. Specifically, a smaller RMSE or a larger ACC indicates a better performing model.

Fig. 2: The architecture of YingLong.
figure 2

The architecture of YingLong includes an embedding layer, a spatial mixing layer composed of the Local branch and Global branch, and a linear decoder. FFT and IFFT represent the fast Fourier transform and inverse fast Fourier transform, respectively. See Methods “Architecture” for details.

Full size image
Fig. 3: The framework of YingLong model.
figure 3

Rolling forecasts of YingLong on the region ED through the process in Methods “Rolling forecast”. The prediction of Yinglong on the ED \({\hat{X}}_{t+i\Delta t}\left({{{\rm{ED}}}}\right)\) is divided into \({\hat{X}}_{t+i\Delta t}\left({{{{\rm{ED}}}}}_{{{{\rm{in}}}}}\right)\) on the inner area and \({\hat{X}}_{t+i\Delta t}\left({{{{\rm{ED}}}}}_{{{{\rm{LB}}}}}\right)\) on the lateral boundary region. Then boundary smoothing (Eq. (3)) is applied to \({\hat{X}}_{t+i\Delta t}\left({{{{\rm{ED}}}}}_{{{{\rm{LB}}}}}\right)\) and \({\hat{Y}}_{t+i\Delta t}\left({{{{\rm{ED}}}}}_{{{{\rm{LB}}}}}\right)\) (the forecast of Pangu on \({{{{\rm{ED}}}}}_{{{{\rm{LB}}}}}\)) to form \({X}_{t}\left({{{{\rm{ED}}}}}_{{{{\rm{LB}}}}}\right)\). Finally, \({\hat{X}}_{t+i\Delta t}\left({{{{\rm{ED}}}}}_{{{{\rm{in}}}}}\right)\) and \({X}_{t}\left({{{{\rm{ED}}}}}_{{{{\rm{LB}}}}}\right)\) are merged for the initial value of YingLong prediction \({\hat{X}}_{t+\left(i+1\right)\Delta t}\left({{{\rm{ED}}}}\right)\).

Full size image

Forecasting skills of YingLong-Pangu

To construct a fully AI-based LAM with fine spatial resolution, the Pangu-weather medium-term forecasts are applied as the LBC of YingLong (denoted as YingLong-Pangu). To evaluate its forecasting skills more objectively, the in-situ observation data40 is used as the benchmark to calculate the RMSEs of the forecasts. In this study, the forecast for a station observation is defined as the model forecast at the 3 km grid point containing the observation site.

Figure 4 shows the RMSEs of 48-hour rolling forecasts for YingLong-Pangu and HRRR.F, starting at 00:00 UTC, for surface variables (U10, V10, T2M, MSLP) at the stations in the inner areas of ED and WD in 2022. The results indicate that the RMSEs of YingLong-Pangu (green lines) are generally smaller than those of HRRR.F (red lines) for U10 and V10. However, this is not the case for T2M and MSLP. For T2M in ED, the RMSEs of YingLong-Pangu and HRRR.F are comparable, while for T2M in WD and MSLP in both domains, the RMSEs of YingLong-Pangu are generally larger than those of HRRR.F.

Fig. 4: Forecast evaluations Yinglong models.
figure 4

RMSEs with in-situ observations as benchmark of HRRR.F (red lines), YingLong-HRRR.F24 (blue lines), and YingLong-Pangu (green lines) in ED and WD.

Full size image

To test the impact of the LBC provided by the Pangu-weather forecast on the performance of YingLong, the HRRR.F results with 24 km spatial resolution are applied as the LBC for YingLong (denoted as YingLong-HRRR.F24) which provides less information than HRRR.F. Figure 4 shows that the RMSEs of YingLong-HRRR.F24 (blue lines) are generally smaller than those of YingLong-Pangu for all surface variables. Moreover, the RMSEs of YingLong-HRRR.F24 are comparable to those of HRRR.F for T2M and MSLP in WD, and even smaller than those of HRRR.F for T2M in ED. These results indicate that the HRRR.F with 24 km spatial resolution provide a better LBC than the Pangu-weather forecasts. This suggests that the performance of YingLong can be further improved by providing better LBCs. The conclusions drawn from the RMSEs in Fig. 4 are consistent with those from the ACCs (Supplementary Fig. S4), and are further confirmed by the selected visualizations of YingLong-Pangu forecasts in Fig. 5a, b (also see Supplementary Figs. S6–S11 in Supplementary Note 6). Although surface specific humidity observations are available, it is not a variable included in YingLong (see Table 1). Therefore, there are no rolling forecasts for surface specific humidity observations. Finally, the statistical significance test among Yinglong-Pangu, YingLong-HRRR.F24, and HRRR.F (shown in Supplementary Table S1), indicates that the differences between Yinglong models with different LBCs and HRRR.F are statistically significant in most cases for forecasting variables, with p-values less than 0.01 in the negative t-statistic.

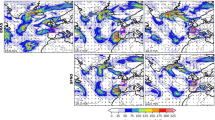
Fig. 5: Forecast visualization of wind speed forecast results of YingLong model.
figure 5

a Forecasts in ED with forecast initialization time at 2022-11-10 00:00 UTC, and lead time is 36 h (first row) and 48 h (second row). The three columns on the left hand side are HRRR.A, YingLong-HRRR.F24, and HRRR.F results at the corresponding forecast time. The two columns on the right hand side are the spatial distributions of MAE of YingLong-HRRR.F24 and HRRR.F using HRRR.A as benchmark. b Forecast visualization of wind speed forecast results in WD are initialized at 2022-02-17 00:00 UTC.

Full size image

To exam the seasonal variability of the predictability, the average values of the cumulative error of the daily 24-h forecast are shown in Supplementary Fig. S12. The figure reveals some interesting features. For example, for all three forecasts of wind speed, the error is general larger in spring (around day 100) and smaller in autumn (around day 200). The T2M (WD) forecast error of Yinglong-Pangu is larger than those of YingLong-HRRR.F24 and HRRR.F in summer (around day 180), indicating that the Pangu forecast is the major error source.

The skills of both YingLong-Pangu and YingLong-HRRR.F24 are higher than those of HRRR.F for predicting U10 and V10, while this is not always the case for predicting T2M and MSLP. The reason could be that U10 and V10 are hydrodynamic variables, while T2M and MSLP are thermodynamic variables that are more sensitive to regional surface conditions, which are not sufficiently discribed in AI-based models. Specifically, U10 and V10 relate to fluids in motion, which are dominated by pressure gradients. The AI-based YingLong is trained using the analysis states of pressure and wind speed at several geopotential heights (see Table 1). Since the analysis was generated by assimilating observations into HRRR.F, some model errors related to HRRR.F could be corrected by those observations. Therefore, U10 and V10 are likely better predicted by YingLong than by HRRR.F. On the other hand, T2M and MSLP are more closely related to surface radiative forcing. The radiative forcing data is not used for training YingLong but is a forcing variable for HRRR.F. Therefore, T2M and MSLP could be better predicted by HRRR.F than by YingLong. The RMSEs (and ACCs) of all forecasts in ED are smaller (larger) than those in WD. This could be due to the more complex terrain in WD compared to ED.

Accurately predicting wind speed is very important for wind power forecasting, scheduling, operation and maintenance41,42. The wind speed at wind turbine levels (i.e., 85 m) can be estimated from U10 and V10 using a power law, with the power parameter estimated using high-resolution analysis data or numerical LAM simulations43. Wind data at a 1-hour time scale is a crucial input for modeling the performance and impact of wind farms on many countries’ electricity systems43. Since YingLong can forecast hourly high-resolution wind surface speed more promptly and accurately than NWPs, it has the potential to be applied to the planning and operation of the wind power generation industry.

Discussions

Results “Forecasting skills of YingLong-Pangu” relates to the forecast skill of YingLong-Pangu, with in-situ observation data as the benchmark. This section addresses modeling issues for improving YingLong, such as the architecture, the LBCs, the homogeneity of training data, and the extremes simulated by YingLong.

The HRRR.A is used as the benchmark for the evaluation and testing of YingLong because it serves as the labels for training YingLong. If other data were used as a benchmark, it would be difficult to determine whether the improvement of a model is due to the model itself or because the model fits the benchmark better. Since the HRRR.A data is a fusion of HRRR.F and observations, HRRR.F with 24 km resolution are chosen as LBC, because they are likely to be more consistent with YingLong forecasts than other LBCs studied in this paper and provide no more information than HRRR.F. Therefore, the modeling issues are less affected by the choice of LBCs. Moreover, the smooth LBC scheme (see Eq. (3)) is imposed, and 207 km is selected as the width of the lateral boundary region. These choices are confirmed as good in the following.

To select a suitable deep neural network architecture, a comprehensive ablation experiment was conducted to compare different model architectures, including the adaptive Fourier neural operator (AFNO44, the main module of FourCastNet21), the SWIN transformer (the main module of Pangu-weather22,45), and the parallel architecture of AFNO and SWIN (introduced in Methods “Architecture”).

Intuitively, the parallel architecture of AFNO and SWIN can effectively extract multi-scale features of meteorological variables. Specifically, AFNO can extract global features of meteorological variables, while SWIN can extract local features. In the parallel architecture, the C channels of the neural network’s hidden tensor are divided, with the first α·C channels subjected to the SWIN transformer and the remaining (1-α)·C channels subjected to AFNO. The two calculation results are then concatenated together (see Method “Architecture” for details). This parallel architecture allows for the integration of global and local meteorological variable features, resulting in more accurate predictions. The hyperparameter α is estimated to be 0.25, as determined by the ablation test documented in Method “Training”.

YingLong can perform rolling forecasts for the entire area, including the internal area and the lateral boundary region, but only the forecast results in the internal area are the focus of this paper. As the forecast time increases, the analysis variables in the inner area are increasingly affected by the initial values outside the inner area. However, if the information of the variables outside the inner area is not included in the rolling forecast, meaning that YingLong only uses the variables inside the ___domain as the initial field, then the prediction cannot account for the inner area being affected by the initial conditions outside of the ___domain in the next step. This could cause the difference between the YingLong forecast and the benchmark to become larger with increasing iterations of the rolling forecasts, as demonstrated in Fig. 6 (black lines). To solve this problem, a lateral boundary region is established outside the inner area. This region contains meteorological information from outside the inner area within a forecast time step ∆t of the rolling forecast, so it can affect the next forecast at time t+∆t of meteorological variables in the inner area. The LBC can be provided by coarse-resolution global weather forecast models and can be transferred to the inner area through YingLong’s forecast on the lateral boundary region (see Methods “Lateral boundary condition”).

Fig. 6: The impact of different width of lateral boundary strategies on the forecast effect of inner region.
figure 6

RMSEs (HRRR.A as benchmark) of YingLong-HRRR.F24 forecast in the inner area with no LBC (black lines), lateral boundary with widths 24 km (green lines), 96 km (purple lines), 207 km (blue lines) and HRRR.F (red line).

Full size image

To obtain high-quality forecast results, it is necessary to ensure that the initial state of the lateral boundary at each step of the rolling forecast closely matches the actual atmospheric state. Directly using the coarse-resolution forecast on the lateral boundaries (coarse LBC, see Methods “Lateral boundary condition”) at each step of the rolling forecast may cause discontinuities at the junction between the lateral boundary region and the inner area, potentially affecting the forecast results. However, by employing the boundary smoothing strategy (see Methods “Lateral boundary condition”, Eq. (3)), the state of meteorological variables between the lateral boundary region and the inner area can be made more coherent, which could be beneficial for the rolling forecast.

Figure 7 shows the difference in RMSEs (taking the analysis data as the benchmark) when using or not using the boundary smoothing strategy, as well as how this difference changes with the spatial range. It can be seen from Fig. 7 that within the 0–30 km strip from the inner area boundary (the red dashed box in Fig. 1), there is a large difference between the boundary smoothing strategy and the direct replacement strategy. As the area under consideration gets closer to the regional center, such as a strip area 60–90 km from the inner area boundary, the difference between these two boundary strategies is reduced. Within a range greater than 120 km from the inner zone boundary, the difference is negligible. Therefore, different boundary strategies have an impact on AI-LAM forecasts, with a smaller impact closer to the ___domain center. In addition, the significance tests between YingLong with coarse and smooth LBC are also made (see Supplementary Section SI 1.2 of Supplementary Material and Supplementary Table S3 in Supplementary Note 3). The t-statistic is negative in the majority of cases from different variables from 12 to 48 h’ forecasting, indicating improvement of YingLong with smooth LBC over coarse LBC. The majority of p-values in the negative t-statistic are statistically significant at the 1% level for the strip within the 0–30 km, and at the 5% level for the strip within the 60–90 km.

Fig. 7: The impact of smooth and coarse lateral boundary strategies on the forecast effect at different ranges in the inner region.
figure 7

The RMSEs in this figure are calculated by choosing HRRR.A as benchmark. By selecting strip areas with distances of 0-30 km and 60–90 km from the inner region boundary, the performance of YingLong-HRRR.F24 with boundary smoothing (blue lines) and coarse (i.e. direct replacement, green lines) are compared.

Full size image

The width of the lateral boundary region is related to how much information from outside the inner area is introduced into the LAM at each step. A principle for selecting this width is that the analysis data in the inner area at time t+∆t should be related to the analysis in the lateral boundary region at time t, but not related to that outside the ___domain at time t. If the width of the lateral boundary region is too small, the forecast of the inner area at t+∆t will lack the necessary information from the lateral boundary region at time t, thus affecting the forecast accuracy for the inner area. Conversely, if the width is too large, some meteorological information in the lateral boundary region that has little to do with the rolling forecast could be introduced, resulting in wasted computational resources. The top speed of level 3 hurricanes in North America is 207 km per hour. Unless there is a level 4 or 5 hurricane, the variability outside of the ___domain has no influence on the inner area within one hour. To validate the 207 km width against other shorter widths, i.e., 24 km or 96 km, RMSEs of the YingLong-HRRR.F24 forecast in the inner area on smooth LBC with lateral boundary widths of 24 km, 96 km, and 207 km are shown in Fig. 6. The lateral boundary region with a width of 207 km corresponds to the smallest RMSEs. On the other hand, the RMSEs for the lateral boundary region with a width of 96 km are fairly close to those with a width of 207 km, indicating that 207 km is a reasonable choice.

Figure 6 shows that the skills of YingLong-HRRR.F24 are higher than those of HRRR.F for predicting HRRR analysis U10 and V10, while this is not always the case for predicting HRRR analysis T2M and MSLP. This is similar to the skills for predicting station observations (see Fig. 4). Moreover, the skills of YingLong-HRRR.F24 are higher than those of HRRR.F for predicting HRRR analysis S1000, especially in ED, suggesting that YingLong could be more skillful than HRRR.F in forecasting surface specific humidity. Similar conclusion is also supported by ACC results (see Supplementary Fig. S5).

YingLong is constructed on two domains shown in Fig. 1, both with 440 × 408 grid points in Lambert projection. The training dataset spans the period from 2015 to 2021 and includes HRRR outputs from four different versions of the system (v1–v4). The differences among these versions can be large46,47, including changes in physics schemes, data assimilation methods, and land-surface data. The HRRR datasets for 2022 and 2023, used for testing and validation respectively, are in version v4 only.

To verify the impact of version inhomogeneity, two experiments were performed. The first experiment tested the sensitivity of YingLong’s parameters to version inhomogeneity. YingLong was further fine-tuned on HRRR v4 data from 2021 to 2023 and tested on 2024 HRRR data. The RMSEs of the fine-tuned YingLong were very close to those of the original YingLong, indicating that the parameters of YingLong may be robust to version inhomogeneity in this study. The second experiment tested the reliability of only using HRRR v4 data for training. YingLong was trained on HRRR v4 data from 2021 to 2023 and tested on 2024 data. The RMSE of the test result was generally larger than that of YingLong trained using 7-year HRRR v1-v4 data (see Supplementary Fig. S2). This suggests that data length is more important than data homogeneity in this study. Therefore, training YingLong using 7-year HRRR v1-v4 data is a reasonable choice. The HRRR.A data is hourly, resulting in 7 × 365 × 24 records used for training YingLong, which is roughly comparable to the ERA5 records (40 × 365 × 4) used for training global AI models.

In this study, wind speed at 10 meters above the surface (\(\sqrt{U{10}^{2}+V{10}^{2}}\)) is selected for evaluating the predictability of extreme wind events for both YingLong and NWP. For WD, the threshold is set at 17.2 ms-1 (approximately the Beaufort wind gale scale48,49). Since gale-scale wind is rare for the ED, it is difficult to estimate the three metrics accurately. Therefore, the threshold is reduced to 10.8 ms−1 (about a strong breeze). The Probability of Detection (POD, Eq. (S4) in Supplementary Note 4) and False Alarm Ratio (FAR, Eq. (S5) in Supplementary Note 4) of the wind over the two domains are shown in Fig. 8. It shows that both POD and FAR for the YingLong forecast are lower than those of HRRR.F. These facts are consistent with those of global AI-based models50. Additionally, Symmetric Extremal Dependence Index (SEDI, which takes into account both the hit rate and the false alarm rate, providing a comprehensive assessment of the prediction accuracy for extreme events, see Eq. (S6) in Supplementary Note 4 for definition) of forecast for wind speed is also shown in Fig. 8. The SEDIs of the YingLong forecast in both domains are larger than those of HRRR.F overall.

Fig. 8: Comparisons of POD, FAR and SEDI for wind speed 10 m above surface between YingLong-HRRR.F24 and HRRR.F.
figure 8

From top to bottom, the extreme wind speed thresholds are 10.8 ms−1 for ED, and 17.2 ms−1 for WD, respectively. From left to right, the extreme event metrics are POD (higher is better), FAR (lower is better), and SEDI (higher is better). The blue and red lines represent the corresponding results of YingLong and HRRR.F, respectively.

Full size image

Methods

Datasets

The hourly analysis data of the HRRR dataset46,47,51 at 3-km resolution, covering the continental US and Alaska, is used for training and evaluating the YingLong model. The HRRR dataset also provides NWP at 3-km resolution, generated through the WRF-ARW (referred to as HRRR.F in this study). The hourly NWP starts from 00UTC and continues for 48 hours.

To test the forecast skill of YingLong-Pangu, the in-situ observation data from HadISD40 in 2022 are selected as benchmarks for calculating RMSEs and ACC. The in-situ observation data includes hourly T2M, U10, V10, and MSLP. This study uses a total of 205 observational sites, with 78 sites in WD and 127 sites in ED.

Architecture

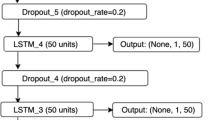
YingLong consists of three components shown in Fig. 2: an embedding layer, spatial mixing layers, and a linear decoder. The input data for the embedding layer are the 24 variables listed in Table 1 and one forcing elevation. They form a tensor with dimensions of 440 × 408 × 25. The embedding layer consists of patch embedding, position embedding and time embedding, to integrate both the spatial and temporal information into the latent tensor. Patch embedding partitions the input tensor into 2805 patches, each patch with a size 8 × 8 × 25. Then, through a convolution layer, each patch is encoded into a C dimensional vector, resulting in the entire input variables being encoded as a tensor of size 2805×C. Position embedding consists of 2805 learnable parameter vectors associated with each of those 2805 relative positions, enabling the model to learn the encoding for each relative position in the region. The dimension of the position embedding vectors is also set to C. Time embedding encodes the specific time information of input data, including year, month, day, and hour, in a vector of dimensions C. Summing up the output vectors from the patch embedding, the position embedding, and the time embedding, yields the output of the embedding layer of size 2805×C. In this study, C = 768.

The output of the embedding layer is reshaped into a 55 × 51×C tensor and delivered to the spatial mixing layer. The tensor is further split by a ratio α along the channel dimension. The tensor of size 55 × 51× (α∙C) is delivered to the Local branch, and the remaining tensor of size 55 × 51× ((1-α)∙C) is sent to the Global branch. The Local and Global branches operate independently and in parallel. The outputs from the two branches are concatenated along the channel dimension, and a new tensor with a dimension of 55 × 51×C is obtained. The Local branch contains Window Multi-head Self-Attention (W-MSA) to capture the features within the window, and Shift Window Multi-head Self-Attention (SW-MSA) blocks in the Swin Transformer45 to detect possible relationships among different windows by a shifting operation. For W-MSA, padding is performed so that the 55 × 51× (α∙C) tensor is transferred to 56 × 56× (α∙C) tensor. Then, it is divided by an 8 × 8 window to get 7 × 7 patches. For SW-MSA, the window is shifted by three patches at each time. After a few alternating steps of W-MSA and SW-MSA, the padding data is removed and a tensor of size 55 × 51 × (α·C) is returned. The Global branch mainly utilizes the Adaptive Fourier Neural Operator (AFNO) block44. A 2D fast Fourier transform is applied to the area of 55 × 51 along each (1-α)·C channel. In the Fourier frequency ___domain, feature mixing is carried out using a Multilayer Perceptions (MLP) consisting of two fully connected layers. Information from the frequency ___domain is transferred to the spatial ___domain by inverse fast Fourier transform. The outputs of the two branches are concatenated along the channel dimension, and a new tensor with a dimension of 55 × 51 × C is obtained.

An MLP consisting of two fully connected layers is applied to map the channel dimension from C to (8 × 8 × 24) for Linear Decoder. The tensor of size 55 × 51 × (8 × 8 × 24) is then reshaped back to 440 × 408 × 24 as the final output of YingLong as the forecast result at t + Δt with Δt = 1 h.

Training

The input for YingLong pretraining, denoted as Xt, is the HRRR analysis in 2015–2021 and the elevation. The output YingLong(Xt) is denoted by \({\hat{X}}_{t+\varDelta t}\), the analysis data \({X}_{t+\varDelta t}\) at the corresponding time is used as labels for supervised learning. The parameters of YingLong are updated by minimizing the loss function

$${{{{\mathscr{L}}}}}_{1}=\frac{1}{\left|{D}_{{batch}}\right|}{\sum}_{t\in {D}_{{batch}}}\frac{{{||}{\hat{X}}_{t+\varDelta t}-{X}_{t+\varDelta t}{||}}_{2}}{{{||}{X}_{t+\varDelta t}{||}}_{2}}$$
(1)

where the l2 norm of a vector \(X=\left({x}_{1},{x}_{2},\ldots ,{x}_{n}\right)\) is expressed as \({{{{\rm{||}}}}X{||}}_{2}=\sqrt{{x}_{1}^{2}+{x}_{2}^{2}+\ldots +{x}_{n}^{2}}\), \(t\in {D}_{{batch}}\) is the initial forecast time in a minibatch52 of forecasts in the training dataset. To achieve better predictability at longer forecast time, the pretrained parameters are fine-tuned by minimizing the loss function

$${{{{\mathscr{L}}}}}_{2}=\frac{1}{\left|{D}_{{batch}}\right|}{\sum}_{t\in {D}_{{batch}}}{\sum}_{i=1}^{T}\frac{{{||}{\hat{X}}_{t+i\varDelta t}-{X}_{t+i\varDelta t}{||}}_{2}}{{||}{X}_{t+i\varDelta t}{||}_{2}}\,$$
(2)

where \({\hat{X}}_{t+\left(i+1\right)\varDelta t}={{{\rm{YingLong}}}}\left({\hat{X}}_{t+i\varDelta t}\right)\) for \(i\ge 1\). In this paper, we set \(T=6\). The larger time step \(i\), the more error is induced to \({\hat{X}}_{t+i\varDelta t}\) from outside of the ___domain. Based on the trial, \(T > 6\) not only fails to improve YingLong’s long-range forecast skill, but also requires more computational resources.

The Adam optimizer52,53 is utilized to minimize the two loss functions. The model employs a cosine learning rate schedule for pre-training, starting at an initial learning rate of 0.005, iterated over 30 epochs. Following pre-training, the model is fine-tuned for 15 epochs using a cosine learning rate schedule with a lower learning rate of 0.0001. YingLong is trained on two A100 Graphical Processing Units, taking approximately 7 days. The trained YingLong takes about 0.5 s to generate a 48-h hourly forecast result on a single A100 Graphical Processing Unit.

In this study, the hyper parameter α is selected from 0 (AFNO), 0.25 (YingLong), 0.5, 0.75, and 1 (SWIN) by conducting ablative tests. For each α, the parameters of YingLong are estimated using HRRR.A in 2015-2021; then the RMSEs of the YingLong-HRRR.F24 forecast with HRRR.A as benchmark in the training period, the validation period 2023 and testing period 2022 are shown in Supplementary Fig. S1 in Supplementary Note 2, respectively. In ED RMSEs for α = 0.25 are overall smallest for all the periods. This is also the case in WD, but with less significance to the case of α = 0 (AFNO). The number of parameters of the AI-based models are listed in Table 2. It shows that the number of the parameters of YingLong (60.5 M) is less than that of SWIN (85.0 M), so YingLong is trained more economically than SWIN. For all of these reasons, α = 0.25 (YingLong) is selected. The statistical significance tests for ablation experiments of Yinglong are shown in Supplementary Table S2. The t-statistic is negative in the majority of cases from different variables from 12 to 48 h’ forecasting, indicating improvement of YingLong over SWIN and AFNO. The majority of p-values in the negative t-statistic are statistically significant at the 5% level for SWIN and the 1% level for AFNO. So YingLong (α = 0.25) is validated.

Table 2 Model parameter count for various hyperparameter α values
Full size table

Lateral boundary condition

To run a LAM requires an LBC \({\hat{Y}}_{t}\), which is normally obtained from AI-based global forecast or coarse resolution NWP, given by Pangu-weather or coarsen HRRR to 24 km (i.e. HRRR.F24) depending on the purpose for forecast or research application. Two LBC schemes, including a coarse LBC and a smooth LBC, are tested. For the coarse LBC scheme, a forecast at fine resolution grid n within the lateral boundary region (\({\hat{X}}_{t}\left(n\right)\)) is altered as \({\hat{Y}}_{t}\left(m\right)\), where m is each coarse resolution grid in the lateral boundary region that is nearest to the fine resolution grid n. For the smooth LBC scheme, it is further smoothed by the YingLong forecast \({\hat{X}}_{t}\left(n\right)\) based on the inverse distance weighting approach on the lateral boundary. Specifically, for any point n in the lateral boundary, there is a YingLong forecast result \({\hat{X}}_{t}\left(n\right)\), and the coarse-resolution NWP or AI-based global forecast result \({\hat{Y}}_{t}\left(m\right)\) at the point m closest to n in the coarse-resolution grid. When the distance from point n to the corresponding inner area, denoted as d(n), is less than the width of the lateral boundary region, which is 207 km in this paper, the result of boundary smoothing Xt (n) (See Fig. 3) can be expressed as

$${X}_{t}\left(n\right)=\left(1-d\left(n\right)/207\right){\hat{X}}_{t}\left(n\right)+d\left(n\right)/207{\hat{Y}}_{t}\left(m\right)$$
(3)

When d(n) is greater than the width of the lateral boundary (this is the case in the four corners of lateral boundary area), i.e., 207 km, \({X}_{t}\left(n\right)={\hat{Y}}_{t}\left(m\right)\). The closer the fine resolution grid n to the inner area, the more weight of YingLong forecast at the grid.

Rolling forecast

We take ED as an example to introduce the process of YingLong rolling forecast. Let \({X}_{t}\left({{{\rm{ED}}}}\right)\), \({X}_{t}\left({{{\rm{E}}}}{{{{\rm{D}}}}}_{{{{\rm{in}}}}}\right)\), \({X}_{t}\left({{{\rm{E}}}}{{{{\rm{D}}}}}_{{{{\rm{out}}}}}\right)\) and \({X}_{t}\left({{{\rm{E}}}}{{{{\rm{D}}}}}_{{{{\rm{LB}}}}}\right)\) represent states in entire, inner, outside and lateral boundary regions of ED at time t, respectively. Firstly, YingLong maps an initial state \({X}_{t}\left({{{\rm{ED}}}}\right)\) (the corresponding HRRR.A data) to the forecast state

$${\hat{X}}_{t+\Delta t}\left({{{\rm{ED}}}}\right)={{{\rm{YingLong}}}}\left({X}_{t}\left({{{\rm{ED}}}}\right)\right)$$
(4)

Then \({\hat{X}}_{t+\Delta t}\left({{{\rm{E}}}}{{{{\rm{D}}}}}_{{{{\rm{LB}}}}}\right)\) and a coarse resolution LBC \({\hat{Y}}_{t+\Delta t}\left({{{\rm{E}}}}{{{{\rm{D}}}}}_{{{{\rm{LB}}}}}\right)\) are smoothed by Eq. (3) to form the initial state \({X}_{t+\Delta t}\left({{{\rm{ED}}}}\right)\) for the next time step (see Fig. 3). It should be noted that during the validation and testing phases, the analysis data of the 24 meteorological variables listed in Table 1 at time t and the topography of the corresponding area are first concatenated to form a 440 × 408 × 25 tensor. This tensor is then used as the input for YingLong to obtain the forecast results of these 24 meteorological variables at time t + Δt, resulting in a 440 × 408 × 24 tensor. YingLong’s forecast results cover both the inner ___domain and the lateral boundary area. In the subsequent steps of the rolling forecast, YingLong’s forecast results in the lateral boundary area are smoothed with the corresponding coarse-resolution forecast results. The smoothed boundary results are then spliced with YingLong’s forecast results in the inner ___domain to form the initial field for YingLong’s next forecast. Therefore, it can be seen that these 24 meteorological variables are predicted simultaneously.