Introduction

Temporal modulations have recently emerged as a powerful tool for wave manipulations1,2,3,4 and hence stimulate growing interest in the electromagnetic community. As a typical operation in temporal modulations, when a system experiences a change of material properties abruptly in time and uniformly in space with its timescale comparable to the period of the electromagnetic wave, the so-called temporal interface (TI)5,6 is created. Unlike its spatial counterpart (i.e. spatial boundary), the system holds the translational symmetry at TI while the time-reversal symmetry is broken, thus providing intriguing opportunities for exploring novel scattering features in controlling waves7,8,9,10. If multiple TIs are aligned sequentially, a temporal multilayer structure can be built11, and a variety of promising applications are unveiled including temporal aiming12, antireflection temporal coating13, frequency conversion14, and temporal optical activity15. In analogy to continuous electromagnetic systems, one can introduce TI by abruptly varying the configuration of the lattice16,17,18,19,20 in discrete systems where the field can be expanded by a set of finite, discrete set of bound states or modes21. Fruitful implementations are also conceivable by using multiple TIs in these discrete systems, such as tunable temporal cloaking17, temporal beam encoder19 and temporal interference20. Therefore, cascade TIs offer a unique opportunity to explore new electromagnetic phenomena in discrete systems.

On the other hand, the Aharonov-Bohm (AB) interference shows a crucial verification of the physical consequences of gauge fields22,23, and hence is a long-standing important research subject in physics24. In particular, recently, there has been emerging interest in synthesizing non-Abelian gauge fields to explore novel phenomena25,26,27,28,29, and the resulting non-Abelian AB interference30,31,32,33, therefore, becomes an important example of non-Abelian effects that is important to topological quantum computing34. It is of fundamental interest to find a flexible way to construct non-Abelian AB interference and push such effect into higher-dimensional gauge-field cases. Obviously, the operation of TIs in electromagnetic systems holds the potential in accomplishing such a task, which demands the study.

In this paper, we tackle this problem by utilizing the concept of temporal multilayer structure by introducing cascade TIs in the discrete tight-binding model. We explore a temporal interference of degenerate states, and further develop it into an AB interference under a temporal non-Abelian gauge field using the construction with two types of TIs. Such a non-Abelian gauge field can be achieved by leveraging the temporal degenerate-state interference created by TI operations. Both SU(2) and SU(3) non-Abelian gauge fields are studied in theory and are verified by simulations, which can potentially be extended to a SU(N) one. Our work reveals that noncommutative operations can be performed in a temporal multilayer structure which further empowers wave manipulation by temporal engineering systems. Besides, the proposed method of non-Abelian AB interference holds unique features compared to previous works25,27,32,33 (see supplementary material Section I), which enables the extension to a higher dimensional gauge field, and, therefore, offers a way of studying high-dimensional non-Abelian gauge field-related physics in the time ___domain.

Results

Temporal multiplayer structure and two types of TIs

We first introduce the concept of the temporal multilayer structure and its usage in wave manipulations. A simple example is illustrated in Fig. 1a, where the system experiences two TIs during the evolution of wave pulse. Suppose the pulse having an initial eigenstate of the system (ω1, k) is injected at t = 0, where ωn represents the quasi-energy, n denotes the band index, and k represents the quasi-momentum. When the first TI occurs, the structure of the system changes, and the eigenstate varies into the new ones \(\{({\omega }_{n}^{{\prime} },k)\}\). Therefore, the input pulse projected into the new eigenstates while the momentum k still conserves as the system holds translational symmetry. One can expect that if there are multiple bands (n > 1), different projections of the pulse onto different bands experience evolutions with different group velocities, so the pulse can be divided into multiple parts which accumulate different phases during evolutions due to the difference in their quasi-energies. We now assume the second TI occurs, and the system changes back to the original one. Under this operation, instead of getting projected onto the original eigenstate (ω1, k), the pulse with eigenstates \(\{({\omega }_{n}^{{\prime} },k)\}\) is actually projected onto all the eigenstates {(ωn, k)}. Therefore, by judicious engineering the temporal multilayer structure, one can obtain the desired final state of the wave. Such temporal architecture exploits various degrees of freedom of the system offered by multiple and even different types of TIs, which enables advanced wave controls. Moreover, the system under multiple temporal operations can be discrete in model, which offers a versatile platform for a diverse family of TIs thanks to the flexibility in controlling lattice structures through on-site gain or loss35, coupling phases16, and strengths18, and more importantly provides possible experimental feasibility compared to its continuous counterparts17,19,20.

Fig. 1: Wave evolution in a temporal multilayer structure and two kinds of TIs.
figure 1

a Illustration of the concept of a temporal multilayer structure, where a wave evolves inside a discrete system experiencing two TIs at different times. Schematic operations of band-unfolding (and band-folding as the inverse operation) and band shifting. b, c Changes of the lattice structure by changing the ranges of couplings or coupling phase for realizing operations. d, e Changes of the states and band structures accordingly. Red (violet) lines are the bandstructures before (after) the TI. Green (yellow) dots denote the states before (after) the TI.

Full size image

Next, we introduce two simple temporal operations as two types of TIs, which are building blocks of the temporal multilayer structure in our study. The first one is the band-folding/band-unfolding operation (see Fig. 1b). Consider two lattice models which are described by Hamiltonians

$${H}_{1}=g{\sum}_{m}({e}^{-i\varphi }{a}_{m}^{{{\dagger}} }{a}_{m+1}+{e}^{i\varphi }{a}_{m+1}^{{{\dagger}} }{a}_{m}),$$
(1)
$${H}_{2}=g{\sum}_{m}({e}^{-i\varphi }{a}_{m}^{{{\dagger}} }{a}_{m+2}+{e}^{i\varphi }{a}_{m+2}^{{{\dagger}} }{a}_{m}).$$
(2)

where g is the coupling strength, am (\({a}_{m}^{{{\dagger}} }\)) is the annihilation (creation) operator at the m-th lattice site, and φ is the coupling phase. The lattice constants of H1 and H2 are l and 2l, respectively, i.e., H1 includes only the nearest-neighbor hoppings while H2 includes only the next-nearest-neighbor hoppings. In particular, the Hamiltonian H2 can be split into two individual sublattices which only contain the even number sites or odd number sites with lattice constant 2l,

$${H}_{2}=g{\sum}_{m\in 2n}({e}^{-i\varphi }{a}_{m}^{{{\dagger}} }{a}_{m+2}+{e}^{i\varphi }{a}_{m+2}^{{{\dagger}} }{a}_{m})+g{\sum}_{m\in 2n+1}({e}^{-i\varphi }{a}_{m}^{{{\dagger}} }{a}_{m+2}+{e}^{i\varphi }{a}_{m+2}^{{{\dagger}} }{a}_{m}),$$
(3)

where n is an integer, and therefore the system supports a twofold degenerate state for given ω and k, whose eigenstates can be written in the odd number site basis with (1, 0)T (i.e., odd-distributed mode) and even number site basis with (0, 1)T (i.e., even-distributed mode), respectively. The two Hamiltonians H2 and H1 can be interconverted by the operation of band-folding/band-unfolding by changing the range of all couplings between sites from {lr} to {lr/s}. Here, both {lr} and {lr/s} denote the coupling range. Particularly, lr (lr/s) represents the range of couplings between sites and their lr-th (lr/s-th) nearest neighbors, which is a positive integer. s is the scaling factor of band folding or unfolding. We take the band-unfolding operation shown in Fig. 1b as an example. Such operation transforms H2 to H1 by varying the next-nearest neighboring couplings to the nearest neighboring ones for all sites, corresponding to {lr} = {2} and s = 2. After the band-unfolding operation, the first Brillouin zone is expanded from [ − π/2l, π/2l] to [ − π/l, π/l], and an initial eigenstate (ω, k) (with k = k0 + rπ/l, where k0 ∈ [ − π/2l, π/2l] and r is an integer) marked by the green dots on the red band projects onto two different eigenstates (ω1,2, k1,2) (with k1 = k0 + 2rπ/l and k2 = k1 + π/l) shown as the yellow dots on the violet band with different group velocities in Fig. 1d. Such a phenomenon is the result from the change of the lattice constant in discrete systems. Due to the translational symmetry of the lattice in Eq. (3), the two initial eigenstates (ω, k1) and (ω, k2) are indistinguishable. However, when the lattice constant changes from 2l to l in the model, i.e., H2 is changed to H1, the two projected eigenstates are distinguishable as the first Brillouin zone is expanded. Therefore, after this type of TI, we can represent the wave state in a new basis, where (1, 0)T represents the k1 mode and (0, 1)T represents the k2 mode. If we assume the wave state before the TI as \({({I}_{{{{\rm{o}}}}},{I}_{{{{\rm{e}}}}})}^{T}\) in the odd/even-distributed mode basis and the wave state after the TI as \({({O}_{{k}_{1}},{O}_{{k}_{2}})}^{T}\) in the k1/k2 mode basis, the input-output relation of this band-unfolding operation can be written by

$$\left(\begin{array}{c}{O}_{{k}_{1}}\\ {O}_{{k}_{2}}\end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1&1\\ 1&-1\end{array}\right)\left(\begin{array}{c}{I}_{{{{\rm{o}}}}}\\ {I}_{{{{\rm{e}}}}}\end{array}\right),$$
(4)

whose derivation is given in Methods. Similarly, the band-folding operation as the inverse operation of the band-unfolding one, changes the short-range couplings to the long-range ones, i.e., H1 is changed to H2, which folds the first Brillouin zone, and hence the eigenstates (ω1,2, k1,2) project onto the twofold degenerate state, where the mathematical description is the inverse function of Eq. (4).

The second temporal operation is the band shifting, illustrated in Fig. 1c, corresponding to the operation that the TI occurs at t = t0 with the coupling phase changed from φ to \({\varphi }^{{\prime} }=\varphi+\Delta \varphi\) on the Hamiltonian H1. The bandstructure then becomes

$$\omega=2g\cos (k-{\varphi }^{{\prime} })=2g\cos (k-\varphi -\Delta \varphi ),$$
(5)

which is shifted by Δφ in the k-axis. Such band shifting is related to the change of the effective vector potential A introduced by φ, which is linked to φ with the expression36

$$\varphi=\int_{m}^{m+1}{{{\bf{A}}}}\cdot {{{\rm{d}}}}{{{\bf{l}}}},$$
(6)

where l is the vector along the direction form site m to site m + 1. At this TI, an initial wave state, for example, marked by the green dot on the red band, experiences a vertical transition to the final state marked by the yellow dot on the violet band as shown in Fig. 1e, with the conservation of the momentum k and the change of the group velocity. In particular, if Δφ = π, such transition corresponds to a time reversal operation16. Before we end this section, we note that such two types of TIs can be combined together so one can perform the band-folding/band-unfolding and band-shifting operations simultaneously.

Temporal non-Abelian AB interference in 2D gauge field

With the two types of TIs introduced in the previous section, we now construct a temporal multilayer structure with three TIs which are operated at t = 6, 30, 54 g−1, respectively (Fig. 2a). At the first TI, we apply the band-unfolding operation which changes the system’s Hamiltonian from H2 to H1 with φ = 0. The initial wave state (ω, k) marked by the green dots in Fig. 2a projects onto two wave states (ω1,2, k1,2) marked by the yellow dots with different group velocities, and hence the initial wave packet splits into two parts with different propagation directions as shown in Fig. 2b. At the second TI at t = 30 g−1, we shift the coupling phase φ from 0 to π corresponding to a time reversal operation which changes the signs of group velocities of the two wave packets to the opposite ones. Then two wave states (ω1, k1) and (ω2, k2) project onto two new wave states (−ω1, k1) and (−ω2, k2), respectively. At the same time, we add an additional phase θ (i.e., phase shift operation) onto the k1 mode (details are given in “Methods” section). Lastly, at the third TI when the two wave packets encounter, we apply the band-folding operation and shift the coupling phase φ from π back to 0 simultaneously (detailed boundary conditions in temporal operations used in simulations are given in Methods). The two wave states (−ω1, k1) and (−ω2, k2) both project onto the state (ω, k) with interference. However, there is the added phase difference θ in two temporal paths, the combined wave state at the third TI may not return to the initial one. Such a temporal interference process between two degenerate states (i.e., the odd-distributed and even-distributed modes) can be described by the input-output relation

$$\left(\begin{array}{c}{O}_{{{{\rm{o}}}}}\\ {O}_{{{{\rm{e}}}}}\end{array}\right)=\frac{1}{2}\left(\begin{array}{cc}1&1\\ 1&-1\end{array}\right)\left(\begin{array}{cc}{e}^{i\theta }&0\\ 0&1\end{array}\right)\left(\begin{array}{cc}1&1\\ 1&-1\end{array}\right)\left(\begin{array}{c}{I}_{{{{\rm{o}}}}}\\ {I}_{{{{\rm{e}}}}}\end{array}\right)={e}^{i\theta /2}\left(\begin{array}{cc}\cos (\theta /2)&i\sin (\theta /2)\\ i\sin (\theta /2)&\cos (\theta /2)\end{array}\right)\left(\begin{array}{c}{I}_{{{{\rm{o}}}}}\\ {I}_{{{{\rm{e}}}}}\end{array}\right),$$
(7)

where \({({O}_{{{{\rm{o}}}}},{O}_{{{{\rm{e}}}}})}^{T}\) denotes the output state in the odd/even-distributed mode basis. We give a specific example with the numerical simulation in Fig. 2b by preparing the initial wave as a pure odd-distributed mode \({({I}_{{{{\rm{o}}}}},{I}_{{{{\rm{e}}}}})}^{T}={(1,0)}^{T}\) and choose θ = 0.5π in the phase shift operation. The output wave can be predicted by Eq. (7), and the detailed evolution process is summarized in Fig. 2c, d where evolutions of odd number sites and even number sites are plotted separately. One can find the emergence of the even-distributed mode after the third TI (t > 54 g−1) in Fig. 2d which shares the same intensity as that of the odd-distributed mode. Therefore, we here show a temporal interference in a temporal multilayer structure that offers us the opportunity to explore non-Abelian physics29,37,38,39 which requires the transition between the internal degenerate states of a system.

Fig. 2: Temporal interference of degenerate state.
figure 2

a Lattice structures at different time intervals and changes of the band structure and states at different TIs, accordingly. Green (yellow) dots denote the states before (after) the TI. Blue arrows denote the change at the TI. b Evolution of the intensity distributions of the wave packet in the proposed temporal multilayer structure. The additional phase θ is taken as θ = 0.5π. c, d Evolutions of the intensity distribution only for odd number sites and even number sites, respectively. Arb. Units arbitrary units.

Full size image

Before we explore the signatures of the non-Abelian AB interference, let us briefly review the non-Abelian AB interference in a two-dimensional (2D) gauge field30,31,32,33. If we consider a particle with pseudospin under a gauge field \({{{\bf{{{{\mathcal{A}}}}}}}}\), which is described by

$${{{\bf{{{{\mathcal{A}}}}}}}}={A}_{x}{{{{\bf{e}}}}}_{x}+{A}_{z}{{{{\bf{e}}}}}_{z},$$
(8)

where ex and ez are the vectors along x and z direction in the parameter space, respectively. Suppose there are two paths with equal distance L along x and z direction for the particle to move from point A to point B as depicted in Fig. 3a.

Fig. 3: Temporal AB interference and Wilson loop calculation in a 2D gauge field.
figure 3

a Schematic of two paths for a particle moving from point A to point B under a gauge field \({{{\bf{{{{\mathcal{A}}}}}}}}\). b, c Evolutions of the state vector of a particle following the two paths under a non-Abelian gauge field in the Bloch sphere. The red (yellow) arrow denotes the initial state (final state). d Plot of the logarithm of S versus parameters of the applied gauge field ϕ and θ, which shows whether the corresponding gauge field is Abelian (blue lines at θ = 0, ±π or ϕ = 0, ±π) or non-Abelian. e Theoretical calculation and g numerical calculation results of the intensity contrast ρ between the two degenerate states after the interference versus initial intensity distribution α and phase difference β under the non-Abelian interference. f, h Theoretical calculation and numerical calculation results of ρ under the Abelian interference. i Theoretical calculation and j numerical simulation results of the Wilson loop ∣WCW∣, where ∣WCW∣ ≠ 2 is a necessary but insufficient condition for a non-Abelian gauge field. Black dash lines indicate the genuine non-Abelian cases.

Full size image

The initial state of the particle Ψi and the final state Ψf can be linked by an operation Uγ, which is written by38

$${U}_{\gamma }={{{\mathcal{P}}}}\left[\exp \left(i\int_{\gamma }{{{\bf{{{{\mathcal{A}}}}}}}}\cdot {{{\rm{d}}}}{{{\bf{l}}}}\right)\right],$$
(9)

where γ is a specific path and \({{{\mathcal{P}}}}\) denotes a path-ordered integral, indicating that Ψf may depend on which path the particle chooses. If the particle first travels along x direction and then z direction, the final state is given by \({\Psi }_{{{{\rm{f}}}}}=\exp \left(i{A}_{z}L\right)\exp \left(i{A}_{x}L\right){\Psi }_{{{{\rm{i}}}}}\). If the particle chooses the path first along z direction and then x direction, the final state is given by \({\Psi }_{{{{\rm{f}}}}}=\exp \left(i{A}_{x}L\right)\exp \left(i{A}_{z}L\right){\Psi }_{{{{\rm{i}}}}}\). If \({{{\bf{{{{\mathcal{A}}}}}}}}\) is a non-Abelian gauge field, Ax and Az do not commute and Ψf will be different depending on which path the particle takes. We make an illustration of the evolution of the particle for the two paths in the Bloch sphere as shown in Fig. 3b, c by taking AxL ∝ σx and AzL ∝ σz, where σx and σz are the Pauli matrices. The non-Abelian gauge field results in sequential rotations of the state vector around two different axes. One can find that although the system starts with the same initial state Ψi (red arrows in Fig. 3b, c), it ends in different final states Ψf (yellow arrows in Fig. 3b, c). The non-Abelian AB interference corresponds to the interference of these two different final states in such a non-Abelian gauge field.

Now we finally illustrated the way in constructing the non-Abelian AB interference occurs with the temporal multilayer structure in Fig. 2a and the resulting signatures for observing such temporal interference presented in Fig. 3e–j. We first show how to realize the two non-commutable operations in the temporal ___domain, which is the key to emulating non-Abelian AB interference. The temporal degenerate-state interference previously discussed in Fig. 2a can be represented as an operation \({U}_{\theta }={e}^{i\frac{\theta }{2}}{e}^{i\frac{\theta }{2}{\sigma }_{x}}\), which can be used to simulate the σx gauge field. To construct the relevant σz gauge field, we apply the phase shift operation on the even-distributed mode with the phase ϕ, which can be represented by the operation \({U}_{\phi }={e}^{i\frac{\phi }{2}}{e}^{-i\frac{\phi }{2}{\sigma }_{z}}\). With the two temporal operations on-hand, we show the temporal version of the non-Abelian AB interference under the gauge field in Fig. 3a. Firstly, we perform the Uθ operation and then the Uϕ operation at t = 57 g−1 to obtain a final state \({\Psi }_{{{{\rm{f}}}}}^{\theta \phi }={e}^{-i\frac{\phi }{2}{\sigma }_{z}}{e}^{i\frac{\theta }{2}{\sigma }_{x}}{\Psi }_{{{{\rm{i}}}}}\) with the global phase being neglected (details are shown in the supplementary material Section II), which corresponds to the state vector sequentially rotates around the x and z axis in Fig. 3b. Similarly, we can obtain a final state \({\Psi }_{{{{\rm{f}}}}}^{\phi \theta }={e}^{i\frac{\theta }{2}{\sigma }_{x}}{e}^{-i\frac{\phi }{2}{\sigma }_{z}}{\Psi }_{{{{\rm{i}}}}}\) by performing the Uϕ operation at t = 3 g−1 with a followed Uθ operation, which corresponds to the sequential rotation of state vector around the z and x axis in Fig. 3c. Such two sequential operations can be performed simultaneously so the resulting interference pattern \({\Psi }_{{{{\rm{inter}}}}}={\Psi }_{{{{\rm{f}}}}}^{\theta \phi }+{\Psi }_{{{{\rm{f}}}}}^{\phi \theta }={({\psi }_{1},{\psi }_{2})}^{T}\) can be reached. Constructing other forms of non-Abelian gauge field needs a cascade of the two operations described above. By engineering other kinds of TIs, one may possibly generate the desired non-Abelian gauge field independently.

We now study the choices of values of θ and ϕ that can synthesize a non-Abelian gauge field. The criterion of a genuine non-Abelian gauge field is the non-commutativity of two holonomies38. Here we choose a pair of time-reversal operations UCW and UCCW which start and end at point A in Fig. 3a defined as32

$${U}_{{{{\rm{CW}}}}}\equiv {{{\mathcal{P}}}}\left[\exp \left(i{\oint }_{{{{\rm{CW}}}}}{{{\bf{{{{\mathcal{A}}}}}}}}\cdot {{{\rm{d}}}}{{{\bf{l}}}}\right)\right]={e}^{i\frac{\phi }{2}{\sigma }_{z}}{e}^{-i\frac{\theta }{2}{\sigma }_{x}}{e}^{-i\frac{\phi }{2}{\sigma }_{z}}{e}^{i\frac{\theta }{2}{\sigma }_{x}},$$
(10)

and

$${U}_{{{{\rm{CCW}}}}}\equiv {{{\mathcal{P}}}}\left[\exp \left(i{\oint }_{{{{\rm{CCW}}}}}-{{{\bf{{{{\mathcal{A}}}}}}}}\cdot {{{\rm{d}}}}{{{\bf{l}}}}\right)\right]={e}^{i\frac{\theta }{2}{\sigma }_{x}}{e}^{-i\frac{\phi }{2}{\sigma }_{z}}{e}^{-i\frac{\theta }{2}{\sigma }_{x}}{e}^{i\frac{\phi }{2}{\sigma }_{z}},$$
(11)

respectively. We plot the logarithm of the summation \(S={\sum }_{a,b}| {[{U}_{{{{\rm{CW}}}}},{U}_{{{{\rm{CCW}}}}}]}_{ab}{| }^{2}\) as the phase diagram in Fig. 3d, where \({[{U}_{{{{\rm{CW}}}}},{U}_{{{{\rm{CCW}}}}}]}_{ab}\) is the element at the a-th row and the b-th column of the commutation [UCW, UCCW]. At ϕ = 0, ±π and θ = 0, ±π, one can see \(\left[{U}_{{{{\rm{CW}}}}},{U}_{{{{\rm{CCW}}}}}\right]=0\), indicating the Abelian case, while at other choices of ϕ and θ, \(\left[{U}_{{{{\rm{CW}}}}},{U}_{{{{\rm{CCW}}}}}\right]\, \ne \, 0\), corresponding to the non-Abelian case. The Abelian case with θ = 0 or ϕ = 0 can be easily understood, as the state vector only rotates around the x or z axis through the whole holonomy, and therefore the two operations UCW and UCCW are commutable, while the Abelian cases with θ = ± π or ϕ = ± π cases are special since the state vector rotates around both the x and z axis, but the two operations are still commutable.

The non-Abelian AB interferences are explored in Fig. 3e, g, with comparisons from their Abelian counterparts in Fig. 3f, h. In detail, we prepare the initial state by \({\Psi }_{{{{\rm{i}}}}}(\alpha,\beta )=(\cos \alpha /2,{e}^{i\beta }\sin \alpha /2)\) with parameters α, β ∈ [−π, π]. Here, α denotes the intensity distribution between the two degenerate states, and β denotes the phase difference between them. The intensity contrast is defined as

$$\rho=\log (| {\psi }_{1}{| }^{2}/| {\psi }_{2}{| }^{2}),$$
(12)

which are calculated both theoretically and numerically to present the interference pattern Ψinter. We plot theoretical results of a non-Abelian case in Fig. 3e with θ = 0.3π and ϕ = 0.4π, as well as an Abelian one in Fig. 3f with θ = π and ϕ = 0.4π, which are depicted as the yellow and green dots respectively in the phase diagram in Fig. 3d. The choice of these parameters supports a general case of an Abelian (non-Abelian) AB interference. For the non-Abelian case in Fig. 3e ρ varies with both the intensity distribution α and the phase difference β, indicating a mixture between the two degenerate states, and hence reflecting the non-Abelian nature of the gauge field. Moreover, we can see that poles emerge at specific choices of (α, β) = (0.25π, − 0.7π), ( − 0.25π, 0.3π), ( − 0.75π, − 0.7π) and (0.75π, 0.3π) where the even-distributed or odd-distributed modes of \({\Psi }_{{{{\rm{f}}}}}^{\theta \phi }\) and \({\Psi }_{{{{\rm{f}}}}}^{\phi \theta }\) take destructive interference. For the Abelian case, as θ = π which causes a switching rather than a mixture between the two degenerate states, the phase difference β of the initial state has no effect on the interference (Fig. 3e). As a result, the intensity contrast ρ only varies with the distribution α of the initial state. We also perform numerical simulations to verify our theoretical calculations (where detailed numerical procedure can be found in the supplementary material Section II) and plot numerical results in Fig. 3g, h, which are well consistent with the theoretical results in Fig. 3e, f.

Another criterion of the existence of a non-Abelian gauge field is the Wilson loop \(W={{{\rm{Tr}}}}({U}_{C})\)38, where UC is the Berry holonomy. For an N-dimensional loop operation UC, ∣W∣ = N points to the case of the Abelian gauge field. Here we calculate the theoretical result of the Wilson loop in the proposed temporal multilayer structure by taking \(| {W}_{{{{\rm{CW}}}}}|=| {{{\rm{Tr}}}}({U}_{{{{\rm{CW}}}}})|\) versus θ and ϕ and plot it in Fig. 3i. Compared with the phase diagram in Fig. 3d, one sees that the results of ∣WCW∣ = 2 in Fig. 3i and \(\left[{U}_{{{{\rm{CW}}}}},{U}_{{{{\rm{CCW}}}}}\right]=0\) in Fig. 3d are matched well at θ = 0 or ϕ = 0, while they are inconsistent in the vicinity of θ = ± π or ϕ = ± π. The reason is that ∣W∣ ≠ 2 is a necessary but insufficient condition for the presence of a non-Abelian gauge field38. We also perform the numerical simulation to extract ∣WCW∣ plotted in Fig. 3j, which also shows good agreement with the theoretical result in Fig. 3i.

Towards interference in higher-dimensional gauge field

It is of fundamental interest in exploring non-Abelian gauge fields in higher dimensions (N > 2). However, to do so, an N-fold degenerate state is required as the key ingredient, which is intrinsically challenging in previous atomic or photonic platforms27,32,40,41,42,43 due to the limitation of the degenerate modes in nature. One advantage of the proposed temporal multilayer structure is the capability for constructing an arbitrary N-fold degenerate state. Therefore, in this section, we showcase an example of the temporal non-Abelian AB interference in a three-dimensional gauge field, and point out the possibility in generalizing towards higher dimensions.

We here consider a third lattice Hamiltonian

$${H}_{3}=g{\sum}_{m}({e}^{-i\varphi }{a}_{m}^{{{\dagger}} }{a}_{m+3}+{e}^{i\varphi }{a}_{m+3}^{{{\dagger}} }{a}_{m}),$$
(13)

that supports the next-next-nearest neighbor couplings. The model of H3 can be splitted into three independent subsystems, which therefore the system supports a trifold degenerate state for given \({\omega }^{{\prime} }\) and \({k}^{{\prime} }\) with \({k}^{{\prime} }={k}_{0}^{{\prime} }+2r\pi /3l\), where \({k}_{0}^{{\prime} }\in [-\pi /3l,\pi /3l]\). The trifold degenerate eigenstates can be written into mode site basis with \(({\psi }_{1}^{{\prime} },{\psi }_{2}^{{\prime} },{\psi }_{3}^{{\prime} })={(1,0,0)}^{T},\, {(0,1,0)}^{T}\) and (0,0,1)T where \({\psi }_{i}^{{\prime} }\) represent the (3n + i)-th sites with n and i being integers. After performing a similar band-unfolding operation by converting H3 into H1, states project into three eigenstates with different momentum, denoted by \(({\omega }_{1}^{{\prime} },{k}_{1}^{{\prime} })\), \(({\omega }_{2}^{{\prime} },{k}_{2}^{{\prime} })\) and \(({\omega }_{3}^{{\prime} },{k}_{3}^{{\prime} })\) with \({k}_{1}^{{\prime} }={k}_{0}^{{\prime} }+2r\pi /l\), \({k}_{2}^{{\prime} }={k}_{1}^{{\prime} }+2\pi /3l\) and \({k}_{3}^{{\prime} }={k}_{1}^{{\prime} }+4\pi /3l\), respectively. The noncommutative operations \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\) and \({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }\) can be achieved by a similar manner as the twofold case, where

$${U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }=\frac{1}{3}\left(\begin{array}{ccc}1&1&1\\ 1&{e}^{i2\pi /3}&{e}^{-i2\pi /3}\\ 1&{e}^{-i2\pi /3}&{e}^{i2\pi /3}\end{array}\right)\left(\begin{array}{ccc}{e}^{i{\theta }_{1}}&0&0\\ 0&{e}^{i{\theta }_{2}}&0\\ 0&0&1\end{array}\right)\left(\begin{array}{ccc}1&1&1\\ 1&{e}^{-i2\pi /3}&{e}^{i2\pi /3}\\ 1&{e}^{i2\pi /3}&{e}^{-i2\pi /3}\end{array}\right)$$
(14)

is realized by a band-unfolding operation followed by a time reversal operation as well as phase shift operations θ1 and θ2 for modes \(({\omega }_{1}^{{\prime} },{k}_{1}^{{\prime} })\) and \(({\omega }_{2}^{{\prime} },{k}_{2}^{{\prime} })\) respectively, and finally a band-folding operation;

$${U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }=\left(\begin{array}{ccc}{e}^{i{\phi }_{1}}&0&0\\ 0&{e}^{i{\phi }_{2}}&0\\ 0&0&1\end{array}\right)$$
(15)

is realized by phase shifts ϕ1 and ϕ2 to \({\psi }_{1}^{{\prime} }\) and \({\psi }_{2}^{{\prime} }\) in H3. With these two operations, we can construct the same configuration of non-Abelian gauge field \({{{{\bf{{{{\mathcal{A}}}}}}}}}^{{\prime} }={A}_{x}^{{\prime} }{{{{\bf{e}}}}}_{x}+{A}_{z}^{{\prime} }{{{{\bf{e}}}}}_{z}\) as shown in Fig. 3a. \({A}_{x}^{{\prime} }\) and \({A}_{z}^{{\prime} }\) are linked with \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\) and \({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }\) by \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }=\exp (i{A}_{x}^{{\prime} }L)\) and \({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }=\exp (i{A}_{z}^{{\prime} }L)\). We then perform the non-commutativity of the two operations. The wave state \(\Psi ({\psi }_{1}^{{\prime} },{\psi }_{2}^{{\prime} },{\psi }_{3}^{{\prime} })\) can be parametrized by \(\Psi (\alpha,\beta,\xi,\chi )={({e}^{i\xi }\cos (\alpha )\sin (\beta ),{e}^{i\chi }\sin (\alpha )\sin (\beta ),\cos (\beta ))}^{T}\), where α, β ∈ [0, π/2] and ξ, χ ∈ [0, 2π]44. Here, α, β denotes the intensity distribution between the degenerate states, and ξ, χ denotes the phase differences between them. These four parameters thus span a four-dimensional parameter space, which can be represented by the direct product of two 2D surfaces, i.e., an octant (α, β) and a torus (ξ, χ) shown in Fig. 4a, b. Any pure state can be viewed as a point on the two surfaces respectively. We choose an initial state Ψi, and then successively implement operations \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\) and \({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }\) or \({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }\) and \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\). The trajectories of state vector in the parameter space are shown in Fig. 4a–d, where green (blue) arrow lines denote the action of \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\) (\({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }\)) to the state vector. One can find that \({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }\) has no effect on the octant (α, β) as it only changes the phase differences ξ and χ, while \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\) change the state vector in both the octant (α, β) and the torus (ξ, χ). Moreover, the two operations \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\) and \({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }\) show non-commutativity in Fig. 4a–d, implying that \({A}_{x}^{{\prime} }\) and \({A}_{z}^{{\prime} }\) are not commutable. In Fig. 4e–g, the results of \(\left[{U}_{{{{\rm{CW}}}}},{U}_{{{{\rm{CCW}}}}}\right]\) are shown. The red dots, lines and surface represent regions where \(\left[{U}_{{{{\rm{CW}}}}},{U}_{{{{\rm{CCW}}}}}\right]=0\) (i.e., an Abelian gauge field). Apart from the common Abelian cases being denoted by the red lines and surface where only one type operation is taken on Ψ actually (i.e., either ϕ1 and ϕ2 or θ1 and θ2 take 0), the special Abelian cases being denoted by red dots appear in Fig. 4e, g but not in Fig. 4f for the reason that \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\) is noncommutative with \({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }\) except for (ϕ1, ϕ2) = (0, 0). Therefore we can conclude that the condition for a special Abelian case is θ1, θ2, ϕ1, and ϕ2 take the value 0 or  ± π with (∣θ1∣ + ∣θ2∣)(∣ϕ1∣ + ∣ϕ2∣) ≠ 0. We also show the slices of \({S}^{{\prime} }={\sum }_{a,b}| {[{U}_{{{{\rm{CW}}}}},{U}_{{{{\rm{CCW}}}}}]}_{ab}|\) in Fig. 4e–g. One can find that the patterns of \({S}^{{\prime} }\) display a central symmetry at (ϕ1, ϕ2, θ1) = (0, 0, 0) in Fig. 4e, g, while the center of symmetry of the pattern in Fig. 4f seems to be shifted along θ1 direction.

Fig. 4: Extension to a three-dimensional gauge field.
figure 4

a, b Evolutions of the state vector in the parameter space with two sequential operations \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\) and \({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }\). c, d Evolutions of the state vector in the parameter space with two sequential operations \({U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }\) and \({U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\). Red (yellow) arrows denote the initial state Ψi (final state Ψf). e–g Theoretical calculation results of commutation of the two evolution operators \(\left[{U}_{{{{\rm{CW}}}}},{U}_{{{{\rm{CCW}}}}}\right]\) versus parameters of the applied gauge field θ1, ϕ1 and ϕ2 for e θ2 = 0, f θ2 = π/2, and g θ2 = π, respectively. The red dots, lines, and surface represent regions where \(\left[{U}_{{{{\rm{CW}}}}},{U}_{{{{\rm{CCW}}}}}\right]=0\) (i.e., an Abelian gauge field). The colormaps are the slices of \({S}^{{\prime} }\), where \({S}^{{\prime} }\ne \, 0\) represents the genuine non-Abelian cases.

Full size image

We then perform the AB interference under a trifold non-Abelian gauge field with θ1 = 0.3π, θ2 = 0.4π, ϕ1 = 0.7π, and ϕ2 = 1.2π to give an example of a general case of the consequence of such a high-dimensional non-Abelian gauge field. The theoretical results of intensity contrast ρ12 and ρ13 which are defined as \({\rho }_{ij}=\log (| {\psi }_{i}^{{\prime} }{| }^{2}/| {\psi }_{j}^{{\prime} }{| }^{2})\) with various initial state Ψi(α, β, ξ, χ) are shown in Fig. 5a–c and d–f, respectively. The interference patterns again vary with not only the intensity distribution α and β, but also the phase differences ξ and χ, which reflects the non-Abelian nature of the mixing between the degenerate states. Moreover, one finds that not only the strip-like patterns in Fig. 5d–f similar to the twofold case in Fig. 3e, but also more complex patterns in Fig. 5a–c are displayed. This may indicate that there are exotic phenomena lying on a higher dimensional gauge field. We also show the simulation results of ρij by numerically solving the temporal multilayer structure with a similar approach of the twofold case in Fig. 5g–l, which consists quite well with the theoretical ones. We further plot the theoretical and numerical results of the Wilson loop ∣WCW∣ in Fig. 6 with θ1, θ2, ϕ1, and ϕ2 varying, which gives good agreement between each other. Furthermore, one can find that the regions of ∣WCW∣ = 3 correspond to the common Abelian case by comparing Figs. 4e–g and 6. For example, the red region near θ1 = 0 in Fig. 6a always exists along ϕ1 direction, which corresponds to the red surface in Fig. 4e, but the red region near ϕ1 = 0 along θ1 direction only exists for ϕ2 = 0 in all three cases in Fig. 6 which correspond to the red lines in Fig. 4e–g. Furthermore, one can find that ∣WCW∣ ≠ 3 for the points of the special Abelian cases (see the corners of the figures). These again show the necessity but insufficiency of the Wilson loop criterion. We want to point out that the presented temporal multilayer structure can only simulate specific types of three-dimensional non-Abelian gauge fields because of the limited number of parameters. As the operation U ∈ SU(3) under an arbitrary three-dimensional non-Abelian gauge field is characterized by eight independent parameters45, while there are only four parameters in our model. However, an arbitrary operation U ∈ SU(3) may also be possibly achieved by sequential operations \({U}_{{\phi }_{1}^{{\prime} },{\phi }_{2}^{{\prime} }}^{{\prime} }{U}_{{\theta }_{1}^{{\prime} },{\theta }_{2}^{{\prime} }}^{{\prime} }{U}_{{\phi }_{1},{\phi }_{2}}^{{\prime} }{U}_{{\theta }_{1},{\theta }_{2}}^{{\prime} }\) where eight independent parameters are included (see the supplementary material Section III).

Fig. 5: Temporal non-Abelian AB interference in a three-dimensional gauge field.
figure 5

Theoretical calculation results of the intensity contrast a–c ρ12 and d–f ρ13 between the degenerate states after the non-Abelian interference versus parameters initial intensity distribution α, β and phase differences ξ for χ = 0, π/2, and π, respectively. Numerical simulation results of the intensity contrast g–i ρ12 and j–l ρ13 versus parameters α, β and ξ for χ = 0, π/2, and π, respectively.

Full size image
Fig. 6: Wilson loop calculation of a three-dimensional gauge field.
figure 6

a–c Theoretical calculation and d–f numerical simulation results of the Wilson loop ∣WCW∣ versus parameters of the applied gauge field θ1, θ2, ϕ1, and ϕ2 for θ2 = 0, π/2, and π, respectively. Here, ∣WCW∣ ≠ 3 is a necessary but insufficient condition for a non-Abelian gauge field.

Full size image

Before ending this section, we discuss the potential generalization to a higher-dimensional gauge field in our proposal. We introduce a model with the Hamiltonian

$${H}_{N}=g{\sum}_{m}({e}^{-i\varphi }{a}_{m}^{{{\dagger}} }{a}_{m+N}+{e}^{i\varphi }{a}_{m+N}^{{{\dagger}} }{a}_{m}).$$
(16)

We can again split HN into N independent subsystems, and therefore such a lattice model can support an N-fold degenerate state. Band unfolding/folding and phase shift operations may also be applied with the temporal multilayer structure. An N-dimensional non-Abelian gauge field can be constructed by a similar manner as the procedure similar to the twofold and trifold cases. The temporal multilayer structure cooperating with phase shift operations can generate rotations of the state vector around two non-parallel axes, which correspond to two noncommutative operations for the state and therefore realize two noncommutative gauge field components. Further AB interference under an N-dimensional non-Abelian gauge field may also be demonstrated.

Possible experimental implementations

We have shown the in-principle capability for the proposed temporal multilayer structure to create N-dimensional non-Abelian gauge fields in a space including the time dimension. Here in this section, we further discuss possible experimental implementations for achieving such a proposal, as well as the potential outputs in future experiments. Although our proposal desires several flexible operations in connecting discrete sites with required hopping phases, it can be potentially realized in various kinds of discrete physical systems, ranging from real space to synthetic dimension. In real space, waveguide arrays46,47 and coupled-resonator optical waveguides48 could be potential candidates for the proposed temporal multilayer structure. Spatial discrete photonic crystal models may also be possible as long as one can apply all desired operations at different times1,2,3,4,49,50. Recent developed synthetic dimensions in photonics51,52,53,54,55 such as time-bins17,20,35,56,57,58 and frequency lattice59,60,61,62,63,64,65 also provide a convenient way to fulfill these tasks. Here, as a pedagogical example, we take the toy model in the synthetic frequency dimension59,60,61,62,63,64,65, which leverages the discrete resonant frequency modes of light as the sites in synthetic space. With appropriate external modulations61,62,63,64,65, the connectivities between resonant modes can be designed, which provide desired operations and Hamiltonians. In the following, we take the twofold case as an example to explicitly illustrate the possible experimental implementation with the synthetic frequency dimension. As a side note, we also give a brief discussion on the possible implementations for other experimental platforms such as time bins, waveguide arrays, and coupled-resonator optical waveguides in the supplementary material Section IV.

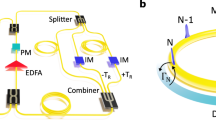
The scheme of our proposal is shown in Fig. 7a, where light circulates inside a ring resonator with zero group velocity dispersion, supporting resonant modes at frequencies ωp = ω0 + pΩ. Here ω0 is the reference frequency, Ω is the frequency spacing between two nearby modes, and p is an integer. The resonator is dynamically modulated by an electro-optic modulator (EOM) with the phase modulation \(\Gamma=\exp [i\kappa \cos (q\Omega t+{\varphi }_{{{{\rm{m}}}}})]\), where κ ≪ 1 is the modulation strength, qΩ is the modulation frequency (q is a positive integer) and φm is the modulation phase. The coupling strengths and phases between lattice sites may vary with the number of resonances in principle. However, such variation could be neglected for the case we considered from rigorous theoretical analysis in ref. 59 and from recent experiments59,61,62,63,64,65, so the translational symmetry of the synthetic frequency lattice can hold. Such a scheme constructs a synthetic lattice with the site spacing qΩ along the frequency axis of light59. In order to conduct a band-unfolding operation, i.e., turning the Hamiltonian H2 in Eq. (2) to H1 in Eq. (1), one can change the modulation frequency from 2Ω to Ω60,61. A time reversal operation can be realized by tuning the modulation phase from ϕm = 0 to ϕm = π. Moreover, a pair of wavelength demultiplexer (WDM) and wavelength multiplexer (WM) is used to separate even-distributed modes (even p) and odd-distributed modes (odd p) propagating into different paths (Fig. 7a)66 while in the upper path there exists a phase shifter 1 (PS1) providing a phase shift ϕ. In the modulated resonator supporting the synthetic frequency dimension, the circulating time inside the ring resonator gives the momentum that is reciprocal to the frequency59,60,61,62. Hence we place another phase shifter 2 (PS2) in the main path of the resonator, and if it is only turned on in the vicinity of the time corresponding to the momentum k1 for each roundtrip, a phase shift θ can then be added onto the k1 mode. By conducting these operations in a proper time sequence, one can construct the temporal non-Abelian gauge field following the procedure of the temporal multilayer structure described in the previous section.

Fig. 7: Schematic of the possible experimental implementation proposal for achieving the proposed temporal multilayer structure and simulations based on WE method.
figure 7

a A modulated ring resonator supports the synthetic frequency lattice model to realize the non-Abelian gauge field. b Scheme for measuring the non-Abelian AB interference using two such resonators. EOM electro-optic modulator, PS1(2) phase shifter 1(2), WM wavelength multiplexer, WDM wavelength demultiplexer, 50:50 50:50 coupler, PD photodetector. c, d Numerical calculation results based on WE method of the intensity contrast ρ between the two degenerate states after the interference versus initial intensity distribution α and phase difference β under the non-Abelian interference c without or d with GVD being included.

Full size image

To observe the resulting non-Abelian AB interference, we use two configurations of ring resonators in Fig. 7a to produce two wave states \({\Psi }_{{{{\rm{f}}}}}^{\theta \phi }\) and \({\Psi }_{{{{\rm{f}}}}}^{\phi \theta }\) respectively (see Fig. 7b). Such two wave states are interfered at a 50:50 coupler via external waveguides and get detected by the photodetector (PD). The key difference in the resulting intensity distributions from the output spectra at PD can therefore provide key potential experimental evidence between an Abelian AB interference and a non-Abelian one (see supplementary material Section V). For the Abelian case, the resulting intensity distribution is identical to the input field spectral distribution except for a shift of the envelope along the frequency axis, meaning that the phase difference β between the even-distributed and odd-distributed modes in the proposed system has no effect on the interference pattern. As a comparison, for the non-Abelian case, the resulting intensity distribution is different from the input one, with a clear interference pattern that varies with both α and β.

To further demonstrate the confirmation of the adequacy for experimental situations, we introduce the rigorous numerical approach based on wave-equation (WE) method (see details in the supplementary material Section VI), which has been successfully proven as very useful in predicting/verifying experimental observations59,61,62,63,64,65. In Fig. 7c, d, we show numerical calculation results of the intensity contrast ρ based on WE method without (Fig. 7c) or with (Fig. 7d) the group velocity dispersion (GVD) being included. One can find that both simulation results based on WE method show a good agreement with the one based on the tight-binding Hamiltonian in Fig. 3g. Therefore, we can conclude that the effect of frequency-dependent dispersion is negligible for the experimental proposal in our considerations. We also discuss the effects of the presence of losses or noises in the supplementary material Section VII, where we find that the interference patterns still preserve under losses and coupling temporal noises. To evaluate the effect of the intracavity loss and noise which broaden the spectral linewidth of the resonant modes, we summarized the experimental characteristics of recent experiments in synthetic frequency dimension62,63,67,68 and find that the resonant modes can still be well distinguished with the presence of intracavity loss and noise (see the supplementary material Section VII). As for noises in the input field, the results can still be valid for small perturbations, but they may no longer be maintained if the disorder of the input field becomes too strong, because it causes a severe broadening of the input wave packet in the frequency or reciprocal space and then the two wave packets cannot be well separated after the band unfolding operation. Therefore, a high preparation fidelity of the input wave packet is essential to the experimental demonstration of our proposal, which can be achieved with the current photonic technology63. Moreover, the TI could be smooth in experiments. We analyze how the sharpness of the TI influences the interference, and conclude that the required operation speed for the modulation frequency and phase change can be loosened in the supplementary material Section VIII. Lastly, one should also notice that the scattering feature at a TI is different between a Maxwell’s-equations-governed system and a Schrödinger-equation-governed system69,70. Such a difference should be taken into account for experimental realization in some platforms. All the simulation results in this work are performed without taking an analytical solution of the TIs.

Discussion

In summary, we showcase the construction of the temporal multilayer structure with multiple functional TIs to support simulations of the two-/three-dimensional non-Abelian gauge field in the time ___domain. Discrete systems are modeled so one can perform flexible band engineerings at different times. The degenerate states in bandstructures are taken so noncommutative operations for the combined state with the time evolution can be designed to realize the non-Abelian AB interference. As the unique advantage, the proposed method provides a simple strategy to construct a high-dimensional degenerate space, and the noncommutative operations to realize non-Abelian AB interference are relatively straightforward, which enables the extension to arbitrary dimensional interference, especially when the synthetic dimension is used. Such a proposal may be potentially implemented in various discrete physical systems with the recently developed technology, including real space46,47,48 and synthetic dimensions in photonics51,52,53,54,55 as well as in atoms55,70.

At last, we want to emphasize that the studied temporal multilayer structure in discrete systems here holds unique features which have not been pointed out in previous works to the best of our knowledge. In particular, for a discrete system, the lattice structure can be flexibly tuned with reconfigurable long-range couplings and coupling phases, so it provides key ingredients for the realization of the non-Abelian gauge field with higher dimensions. The resulting arbitrary non-Abelian AB interference in the time ___domain is fundamentally important for deepening our understanding of non-Abelian physics and wave field manipulation in real and synthetic space. Therefore, our work may trigger further research interests in the temporal periodic structure in discrete systems including both spatial boundaries and TIs. Furthermore, the scattering features of TI in discrete systems are still largely unexplored, so further studies could enrich the building blocks to build more temporal multilayer structures with different functionalities. Lastly, the combination of spatial and temporal degrees of freedom can also guide the multilayer structure into the spatiotemporal regime1,2,3,4,49.

Methods

Derivation of Eq. 4

The input-output relation of the band-unfolding operation can be written by

$$\left(\begin{array}{c}{O}_{{k}_{1}}\\ {O}_{{k}_{2}}\end{array}\right)=\left(\begin{array}{cc}{P}_{11}&{P}_{12}\\ {P}_{21}&{P}_{22}\end{array}\right)\left(\begin{array}{c}{I}_{{{{\rm{o}}}}}\\ {I}_{{{{\rm{e}}}}}\end{array}\right),$$
(17)

where \({({I}_{{{{\rm{o}}}}},{I}_{{{{\rm{e}}}}})}^{T}\) is the initial wave state, \({O}_{{k}_{1}},{O}_{{k}_{2}}\) is the final wave state, and \({P}_{ij}=\langle \tilde{{\psi }_{i}}(k)| {\psi }_{j}(k) \rangle\) with \(| \tilde{{\psi }_{i}}(k) \rangle\) (\(| {\psi }_{j}(k) \rangle\)) being the i-th (j-th) eigenstate of after (before) the band-folding operation. However, we can not directly obtain Pij since \(| \tilde{{\psi }_{i}}(k) \rangle\) and \(| {\psi }_{j}(k) \rangle\) are Bloch waves with different periods. Nevertheless, we can obtain the eigenstates of H1 and H2 with the same lattice constant 2l and then determine Pij accordingly. The eigenstates of H2 are (1, 0)T and (0, 1)T which are given in the main text. For H1, we can regard that the even number sites and odd number sites are different and the lattice constant is 2l, and then obtain the eigenstates (ω±, k) whose corresponding eigenvectors are \({(1/\sqrt{2},\pm 1/\sqrt{2})}^{T}\). One can find that (ω+, k) corresponds to (ω1, k1) and (ω−, k) corresponds to (ω2, k2), and therefore determines Pij.

Details of the temporal degenerate-state interference

Here, we give the details of the numerical simulation procedure for the temporal degenerate-state interference as shown in Fig. 2b. We set a Gaussian-shaped-like initial state \({c}_{m}(t=0)=\exp [-{(m-81)}^{2}/40]\cdot \exp (i{k}_{0}ml)\) with k0 = 0.25π/l for odd number m, where m = 1, 2, …, 201. Note that the Gaussian-shaped-like initial state in the m space corresponds to a Gaussian-shaped-like distribution \(\tilde{k}({k}_{0})\) centered at k0 in the momentum space. For t ∈ [0, 6 g−1] the Hamiltonian of the system is H2 with g = 0.002 and φ = 0. At t = 6 g−1, we switch the coupling from the next nearest neighbor one to the neatest neighboring one so that the Hamiltonian becomes H1 with φ = 0. The original state now projects into two new states with different momenta \(\tilde{k}({k}_{1})\) and \(\tilde{k}({k}_{2})\). To achieve a time reversal operation16, we switch φ from 0 to π at t = 30 g−1. Meanwhile, we give an additional phase θ to the \(\tilde{k}({k}_{1})\) component. Such an additional phase shift can be obtained by firstly performing the Fast Fourier transformation (FFT) on cm at the time t = 30 g−1 to obtain ck(n) where n = 1, 2, …, 201, then multiplying a phase factor eiθ for ck(n) at 0 < k < 3π/4l, and finally performing an inverse FFT to obtain the new \({c}_{m}^{{\prime} }(t=30{g}^{-1})\). We show the FFT ck from cm(t = 30 g−1) and corresponding phase shift θ(n) of different ck in Fig. 8. Lastly, we change both the coupling range and coupling phase so that the Hamiltonian returns back to H2 in the main text with φ = 0. In addition, the phase shift operation can be approximately applied by directly multiplying the phase factor eiθ to cm(t = 30 g−1) for 0 < m < 101 since the states \(\tilde{k}({k}_{1})\) and \(\tilde{k}({k}_{2})\) are separated in the m space (Fig. 2b). Such an operation may help to apply phase shift on one of the modes in the momentum space.

Fig. 8: Illustration of the phase shift operation in the momentum space.
figure 8

Blue line: ∣ck∣ at t = 30 g−1. Red line: additional phase θ(n) for different k components.

Full size image

Moreover, all the simulation results based on the TB method are performed by the rigorous numerical method. No analytical solution of the temporal interfaces is applied in the numerical simulation. The boundary condition of the Hamiltonian we use for band-folding operation is

$$H=\left\{\begin{array}{ll}{H}_{1}\quad &t\, \leqslant \, {t}_{0}\\ {H}_{2}\quad &t \, > \, {t}_{0}\end{array}\right.,$$
(18)

where t0 is the corresponding time of the temporal interface. The boundary condition for band-unfolding operation is similar. The boundary condition of the coupling phase for the time reversal operation is

$$\varphi=\left\{\begin{array}{ll}0\quad &t\, \leqslant \, {t}_{0}\\ \pi \quad &t \, > \, {t}_{0}\end{array}\right..$$
(19)

Although we show the sharp change has been used in simulations for Figs. 2 and 3, the influence of the sharpness of these temporal interfaces on the interference in simulations are discussed in the supplementary material Section VIII.