Introduction

Moiré superlattices in twisted van der Waals heterostructures have been found to host strongly correlated electrons, giving rise to exotic phenomena1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21 such as correlated insulators, superconductivity, ferromagnetism, (fractional) Chern insulators, and the counterintuitive isospin Pomeranchuk effect22,23,24. The Pomeranchuk effect is an entropy driven liquid-to-solid transition in 3He, in which the system symmetry is lowered with increasing temperature. By replacing the 3He atoms with flavor polarized electrons, one can observe its electronic analogy in twisted bilayer graphene (TBG)—isospin Pomeranchuk effect, where spin–valley unpolarized electrons at low temperature turn to be flavor polarized at high temperature. Correspondingly, the Fermi liquid grows into an isospin-ordered insulator upon heating. Among various theoretical models proposed for TBG, a consensus has been reached that spin/valley symmetry breaking will result in energy gaps at commensurate fillings, whereas there are occasional exceptions that the ground state has no gap but exhibits a Fermi liquid owing to the restored flavor symmetry. The counterintuitive temperature dependence of flavor polarization, and the inferred local magnetic moment as proposed in previous theories and experiments25,26,27,28, gain renowned interests about their role in shaping ground states of a flat band moiré system. However, experiments so far have been mainly focusing on filling factors v = ±1 in TBG, i.e., one electron/hole per moiré superlattice cell; even in twisted WSe2/MoTe2 bilayer29,30, the effect emerges only at v = −1. While signatures of the effect at v = −3 and 3.5 are available11,31, its existence at filling factors other than one remains to be confirmed. Whether this counterintuitive temperature dependence is a general property of isospin flavor polarization is important for constraining various theoretical models.

As a tunable quantum simulator of the Hubbard model32,33, rhombohedral trilayer graphene (r-TLG) moiré superlattices (formed by crystallographic alignment with hexagonal boron nitride (hBN)) exhibit various exotic properties such as Chern insulators, ferromagnetism and signatures of superconductivity34,35,36,37. The advantages of this system include the strong tunability of electronic correlation by displacement fields, and more importantly, the clear and complete characterization of its moiréless counterpart38,39. The high transparency of such a system is expected to be suitable for examining the consistency between theories and experiments.

Here we focus on the non-topological regime of a hole-doped r-TLG moiré superlattice and find that at v = −3 (i.e., three holes per moiré superlattice cell) a Fermi-liquid ground state turns into a correlated insulating peak upon either rising temperatures or applying parallel magnetic fields. Such a counterintuitive phenomenon resembles that in TBG, but takes place at a distinct filling factor. In addition, this behavior is observed at v = −1 and −2 when the displacement field is large enough to suppress the correlated insulators. At last, we discuss the potential theoretical models including isospin Pomeranchuk effect and Kondo lattice. The wide exploration of the counterintuitive temperature dependence in the phase diagram of various heterostructures may help establishing a theoretical model of isospin flavor dynamics in correlated electronic systems.

Results

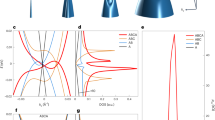
The van der Waals heterostructure is schematically shown in the inset of Fig. 1a, where the r-TLG is aligned with the top hBN to generate a moiré superlattice. Top and bottom gates (Vt and Vb) are used to independently control the displacement field D and carrier density n. Here we define n = (Db + Dt)/e, D = (Db-Dt)/2, with Db(t)= ε0εrVb(t)/db(t), εr as the relative dielectric constant of hBN, db(t) as the thickness of the bottom (top) hBN flake. For simplicity, a filling factor v = 4n/ns is used, where ns is the density required to fully fill the moiré band. As shown in Fig. 1a, the D-v phase diagram taken at 1.5 K displays resistance peaks at charge neutral point (CNP) at v = 0 and full filling point (FFP) of the moiré valence band at v = -4, and correlated peaks at fractional fillings v = -1, -2 (See the full phase diagram of Sample 1 in Supplementary Information (SI), Supplementary Note 1; Sample 2 in Supplementary Note 2 and Sample 3 in Supplementary Note 3).

Fig. 1: Flavor polarization in a r-TLG superlattice.
figure 1

a The D-v phase diagram at 1.5 K. Inset: Device schematic showing the direction of displacement fields from moiréless to moiré interfaces. b Normalized Hall carrier density νH = 4nH/ns at B = ± 1 T, versus v and D. Inset: definitions of three colored dashed lines for band gap (blue), VHS (yellow) and reset (red). See details in the main text. c Profiles of carrier density (right axis) and Hall resistance (left axis) along the white dot line in (b) where phase boundaries are denoted by colored bar. d–f Correspondence between symmetry breaking and phase boundaries is evidenced in the moiré conduction band (D = 0.5 V/nm). Here, symmetry breaking among spin and valley flavors is identified by the lifted degeneracy of Landau levels associated with correlated insulators (d, e). The degeneracy is one for v = 1 and two for v = 2. The phase boundaries (bandgap, VHS and reset) can also be found at low (1 T in the upper panel of (f) and high (3 T in the lower panel) magnetic fields. g At D = −0.45 V/nm, the resistance peak of v = −2 is found to increase with parallel B fields. h The energy gap at v = −2 shows a g factor of the order of 2 in B// fields. Error bars are estimated from the uncertainty in the range of the simply activated regime. Inset: Schematic of spin polarization induced gap at half filling in parallel fields.

Full size image

Symmetry-breaking phases

To gain more insight into the phase diagram, the corresponding mapping of the normalized Hall carrier density, νH = 4nH/ns, is presented in Fig. 1b, where nH = -[e(dRxy/dB)]−1 (with e being the electron charge and Rxy representing the Hall resistance, see more in Supplementary Note 1.6). In this mapping, blue and red colors denote for electron and hole carriers, respectively. There are three types of transitions40,41 (insets of Fig. 1b): The ‘gap’ means when the Fermi level crosses a gap, nH continuously crosses zero. The ‘reset’ denotes the behavior that nH drops suddenly to zero but it does not change sign, which has been found at integer filling factors in twisted bilayer graphene due to the Coulomb-induced phase transitions. The ‘VHS’ (abbreviated for Van Hove singularity) exhibits a divergent nH with a zero crossing, which is typically observed at saddle-points on the Fermi surface. Accordingly, three types of dashed lines divide the phase diagram into several regions. Taking the white section line as an example, we plot in Fig. 1c Hall resistance and carrier density to the left and right axes, respectively. At v = −4 and 0, there are typical band gaps isolating the narrow moiré band. During the electron filling of the moiré band, for −4<v < −2 electron density firstly increases linearly, then gradually resets to zero at v = −2. Subsequently, it increases again and resets at v = −1. In the region of −1<v < 0, the carrier type changes from electron to hole by crossing VHS. The carrier reset behavior within a flat band has been observed in twisted bilayer graphene, which is accompanied by spin and valley symmetry breaking42 evidenced by reduced degeneracies. However, in the hole band of r-TLG moiré superlattice quantum oscillation is found to be absent under moderate magnetic fields, prohibiting the confirmation of lifted degeneracy.

In contrast, for the conduction band we can readily observe correlated insulators and associated Landau levels (Fig. 1d, e). Obviously, the degeneracy close to v = 1 is one and that close to v = 2 is two. It’s interesting to see that the sequence of lifted degeneracies is exactly the same as that of r-TLG without moiré superlattice38, although the onset carrier densities of the reset may be different. At B = 1 T, no correlated insulator can be seen (Fig. 1d), and the carrier reset (Fig. 1f, upper panel) is not bound to integer filling; Only when B = 3 T (Fig. 1f, lower panel), the energy gaps can be observed at integer filling, in agreement with correlated insulators shown in Fig. 1d. To summarize, the degeneracy sequence in the conduction band is not changed by the moiré potential. We tentatively apply this argument to the valence band: it is spin–valley polarized for v = −1 and spin polarized for v = −2. The former postulation can be firmly established for D > 0 where a spin–valley polarized flavor with a nontrivial Chern number has been observed35. The latter is supported by strong magnetoresistance in in-plane magnetic field B// (Fig. 1g), for which the extracted g factor agrees with a spin polarized gap (Fig. 1h). In addition, spin–valley polarization at v = −1 is in line with the fact that the resistance peak changes little in B// fields but increases significantly in B⊥ fields (Supplementary Fig. 2). To this end, we assign the symmetry-breaking patterns, which is inherited from flavor polarization of a moiréless r-TLG38, to different regions of the phase diagram.

Suppression of the symmetry-breaking insulator at v = −3

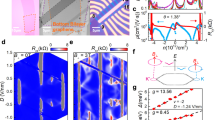
At low temperatures, the correlated insulator at v = −3 is missed (Fig. 1a). The absence is understandable because the state with a degeneracy of three is also lacking in its moiréless counterpart38. However, at high temperature (e.g., 20 K in Fig. 2a), a resistive peak emerges within −0.45 < D < −0.25 V/nm. Also, for v = −1 the D range for correlated insulators increases rather than decreases. To quantify the difference, we remove the smooth background (dashed curves in Fig. 2c) that originates from thermal broadening of adjacent resistive peaks and denote R* as the indicator that evaluates the influence of the emerging correlated gap (See Supplementary Note 1.4 for more discussion). Then the contours can be compared in Fig. 2d, where significant differences could be found at v = −3, and v = −1 at a large displacement field (D < −0.55 V/nm). Intriguingly, the recovery of resistive peaks is also found by applying strong in-plane magnetic fields (Fig. 2b). The duality between temperature and magnetic field suggests that the counterintuitive behavior may stem from magnetic interaction. In the following, we firstly examine the case of v = −3.

Fig. 2: Counterintuitive temperature dependence of resistive peaks.
figure 2

Phase diagrams at high temperatures (a) and strong in-plane magnetic fields (b). c To evaluate the magnitude and the range of correlated peaks, a smooth background (dashed lines) are removed for transfer curves at low temperature (red) and high temperature (black). d. Temperature induced difference of correlated resistance peaks (R* in c) at commensurate fillings v = −1, −2 and −3. The peaks seem to disappear at low temperature for v = −3 and −1. Overlaid are phase boundaries defined in Fig. 1b.

Full size image

Figure 3a shows the temperature dependence of resistance at D = −0.3 V/nm, where the resistance peak at v = −3 gradually decreases and vanishes at 1.5 K. The transfer curves at various temperatures are compared in Fig. 3b. Corresponding nH(v) is presented in Fig. 3c (See more details of the analysis in Supplementary Note 1.6). Below 15 K, the absolute value of nH increases monotonically, accompanied by an emergent dip at v = −3. The dip, ascribed to the incomplete carrier reset at v = −3, grows stronger at 7.5 K and then gradually diminishes at lower temperatures. This carrier reset should not be mixed with the one for v = −2. The latter starts to develop right after v = −3, and grows stronger towards lower temperature.

Fig. 3: Temperature and B field dependences at v = −3.
figure 3

a In the T-v diagram with D = −0.3 V/nm, the resistance peak at v = −3 gradually decreases and almost vanishes at 1.5 K. At v = −1, a similar decrease in resistance is observed but the peak remains significant at low temperature. In contrast, the peak at v = −2 grows stronger. b Line cut from a at various temperatures. Hall carrier density is plotted as a function of temperature (c) and in-plane magnetic field (d) at v = −3 and D = −0.3 V/nm. Carrier reset manifested as a dip is maximized at T = 7.5 K (c) or B// ~ 11.96 T (Btotal = 12 T). With increasing in-plane magnetic fields, the correlated peak at v = -3 emerges at low temperature (T = 1.5 K in e) or is significantly enhanced at higher temperature (T = 12.5 K in f). The peak position (black dot) is shifted gradually towards v = -3 in B// fields (e); whenever it was shifted to v = −3 by rising temperature, the position would be fixed, regardless of B// fields (f).

Full size image

The carrier reset at v = −3 also develops with growing (Fig. 3d). Compared to the weak temperature-driven dip, the field driven reset close to v = −3 is much stronger. With increasing B// fields, the reset shifts towards v = −3, consistent with the varying position of resistive peaks (Fig. 3e). The duality between temperature (Fig.3a) and B// field (Fig. 3e) can be further confirmed in Fig. 3f, in which at elevated temperature 12.5 K the B// field continues to strengthen the correlated peak (i.e., promoting the symmetry-breaking insulator).

Before discussing its mechanism, we need to firmly exclude another mechanism, i.e., a semimetal due to the small correlation gap. For a correlated semimetal, during cooling process the resistance peak first increases because of the growing gap size owing to increasing correlation, then decreases due to suppressed electron-phonon scattering. While the temperature dependence of resistance seems to be similar, its carrier density is expected to decrease monotonically during cooling down, in contrast to the growing Fermi surface in Fig. 3b.

Extension to more filling factors

The counterintuitive temperature dependent isospin flavor polarization is not limited to v = −3. As shown in Fig. 4a, the phenomenon also exists at v = −1 at D = −0.7 V/nm (see more in Supplementary Note 1.5). The B// dependence is also depicted in Fig. 4c. As expected, the resistive peak at v = −1 becomes more significant at higher temperature and in-plane magnetic field. Corresponding carrier reset shows similar dependence on temperature (Fig. 4b) and B// field (Fig. 4d). Note that the carrier reset and resistive peak still survive at 1.5 K, although severely suppressed. For a complete suppression, a much lower temperature and/or a higher D are needed (Fig. 4e, and Supplementary Fig. 18 and Supplementary Note 2).

Fig. 4: Similar behaviors at v = −1 and −2.
figure 4

a At sufficiently large D, e.g. −0.7 V/nm, both correlated peaks at v = −1 and −2 tend to diminish at low temperature, despite that a weak feature remains at 1.5 K. b Corresponding Hall carrier density at various temperatures. The carrier reset is maximized around 11 K for v = −1 and −2. c Correlated peaks are recovered by in-plane magnetic fields. d Corresponding Hall carrier density at various magnetic fields. The carrier reset at v = −1 cannot be correctly measured above 9 T due to the large gap at v = −2. However, the stronger reset with increasing fields can be identified. Note that the significant energy gap at high fields for v = −2 is probably due to that the gap is spin polarized. e All correlated peaks at v = −1, −2 and −3 are fully suppressed at ultralow temperatures. Inset: Expanded view below 2 K.

Full size image

For v = −2, the temperature dependence of resistive peaks and carrier reset are similar to that of v = −1. One should be cautious about the field dependence, since the intrinsic spin polarized gap at v = −2 may also give rise to similar behavior. Nevertheless, the overall similarity between these three filling factors probably suggests the same working mechanism.

Discussion

Proximity to boundaries of symmetry-breaking phases

The requirement for observing the counterintuitive effect can be probed by examining the similarities between r-TLG moiré superlattice and other systems. The most significant phenomenon takes place at v = −3 in r-TLG, whereas it happens at v = ±1 in TBG. Superficially, they are different filling factors. However, in r-TLG the carrier at v = −3 is of electron characteristics inferred from Hall effects (Fig. 1b), which is due to the proximity of VHS to CNP under a large displacement field. Consequently, the state at v = −3 stands for one electron per superlattice cell. This is actually similar to the case of TBG in which the Pomeranchuk effect occurs for one electron/hole per superlattice cell. More importantly, both of them stay between a phase with a full degeneracy (i.e., four around v = 0 and +/−4) and a phase with lifted degeneracy (i.e., two around v = +/−2). The reduction in degeneracy indicates spin–valley symmetry breaking at v = −2, resulting in a ferromagnetic order (with ordered magnetic moment), e.g., spin polarization in r-TLG moiré superlattice. This rule is also valid for the effect at v = −1 and −2 in r-TLG and v = −1 in MoTe2/WSe2, where a large D drives the metal-insulator transition and the counterintuitive phenomenon is observed on the metallic side. The insulating phase itself is of spin/valley symmetry breaking: although a long-range magnetic order may be not available29, abundant spatially localized magnetic moments are expected to exist. Note that, for the small D where the insulating phase also disappears, at present we cannot firmly exclude another mechanism, i.e., the weak correlation at a small D will lead to a normal metal. This is because the behavior of carrier reset cannot be reliably characterized by Hall effects due to the proximity to VHS (Fig. 1b). Overall, fluctuation of ordered phases resulted by tuning carrier density or displacement field may be the prerequisite for observing this phenomenon. Otherwise, when the interaction of local moment is strong, a ferromagnetic order may be preferred, resulting in a symmetry-breaking insulator.

Possible theoretical models

We now discuss possible mechanisms for the observed phenomena. One is the isospin Pomeranchuk effect22,23, in which local moment of flavor polarized electrons is developed from unpolarized Fermi liquid upon increasing temperature. In the r-TLG moiré superlattice, the growing feature of the carrier reset at v = −3 upon increasing temperature or B// fields is consistent with this scenario, but a direct evidence of entropy is required to substantiate this proposal. Another is the Kondo lattice model based on the topological heavy fermion model43,44, where the resistance grows significantly when the heavy Fermion liquid turns into a state with incoherent scatterings between itinerant electrons (c-electron) and localized electron (f-electron). It was developed specifically for twisted bilayer graphene45,46,47,48,49,50 that also exhibits the counterintuitive temperature dependence, and signatures of Kondo effect – zero-bias conduction peak in the tunneling spectra – has been found10,28,51,52. Nevertheless, for the r-TLG moiré superlattice, theoretically a concrete model is required to check whether the Kondo lattice model is appropriate in this crystallographically distinct system. On the experimental side, we need to further examine the signature of heavy Fermions (see Supplementary Note 1.3 for r-TLG), and search for the direct spectroscopic evidence in the future.

To conclude, we report transport evidences of counterintuitive temperature dependence of isospin flavor polarization in a rhombohedral trilayer graphene moiré superlattice. The observation at various filling factors and displacement fields enriches the exploration of this counterintuitive phenomenon in a quantum simulator of Hubbard model, shedding light on the controlled interplay between Coulomb and spin interactions of correlated electronic states in moiré superlattice systems.

Methods

Sample fabrication

Rhombohedral trilayer graphene flakes are mechanically exfoliated from natural graphite crystals, whose stacking order is identified by Raman spectroscopy. Standard dry transfer using polycarbonate film is used to sequentially pick up hexagonal boron nitride and graphene flakes on demand. After finishing the multilayer heterostructure, Raman mapping is conducted to confirm the rhombohedral stacking order. At last, e-beam lithography/evaporation and reactive ion etching are used to define a metallic top gate (Cr/Au 5/30 nm) and one-dimensional edge contact.

Electrical measurement

Most transport measurements (above 1 K) were carried out in a 4He cryostat with base temperature of 1.5 K and a superconducting magnet up to 14 T. Unless specified otherwise, the sample temperature was at base temperature. A standard four-probe method of constant current was performed. The AC current (10 nA) was supplied by Stanford Research Systems SR830 lock-in amplifiers with a ballast resistor at frequency of 17.777 Hz. The DC gate voltages were output by two Keithley 2400 Source Meters.

The ultralow temperature measurements (below 1 K) were carried out in a dilution refrigerator (Oxford Instrument Triton500) with a base temperature of 8.7 mK and a highest magnetic field of 12 T. Composite low-pass filters (LPF) are installed for every lead, each including a 3-meter long thermocoax between the 3 K stage and the mixing chamber stage, followed by a RC filter on the mixing chamber stage. The cutoff frequency is 400 MHz with an attenuation of −100 dB, minimizing the electron temperature. Lock-in amplifiers (NF5640) were used to measure the resistance, with an excitation ac current of 2 nA at frequency of 17.77 Hz. Bias current was supplied by a DC source meter (Keithley 2612B) for the differential resistance measurements.

The extraction and physical meaning of R*

The parameter R*, obtained by subtracting a smooth background from the transfer curve R(v), is used to identify the potential regions with counterintuitive temperature dependence of isospin flavor polarization. In some circumstances, the feature of a resistance peak R(v) has a non-monotonic evolution as a function of temperature, whereas the absolute value of the peak resistance decreases upon cooling the sample. The inconsistency obviously stems from the incomplete flavor polarization and the coexistence of carriers with distinct characteristics, which complicate the macroscopic electronic transport. To derive the key information on a qualitative level, the smooth background is removed to highlight the behavior of R*. In essence, R* represents the variation of resistance resulted from the emerging carrier localization, which simultaneously affects the carrier density and mobility. Consequently, R* remains a convolution of changes in carrier density and mobility. Nevertheless, it can be taken as a sensitive indicator to detect whether the state has an emerging gap at the Fermi surface. More concrete examples can be found in Supplementary Note 1.4.