Introduction

Transport electrification, a critical sector in a low-carbon energy transition1, has unprecedentedly reshaped the fossil fuel-based transport paradigm. Lithium-ion batteries are vital to this transition by providing affordable, durable, and safe energy supplies to electric vehicles (EVs)2,3. The total capacity of in-use and end-of-life EV batteries will surpass 32–62 terra-watts by 2050, considerably higher than the estimation in International Renewable Energy Agency and Storage Lab scenarios4. However, retired EV batteries are strongly regulated with a huge remaining capacity value under-exploited, typically over 80% of the rated capacity5,6. If not handled properly, it leads to economic burdens7 for manufacturers and users, as well as subsequent environmental and societal issues8, including resource wastage, supply chain risks, and carbon emissions9,10,11.

Promising strategies to address concerns regarding the intermittent surging of battery retirement are reuse6,12,13 and recycling14. In reuse, retired batteries are repurposed for applications such as grid-connected energy storage systems15, residential power supplies16, and low-speed vehicles. However, reuse requires preliminary pretreatments, including consistency screening17, capacity sorting18, and regrouping19,20 to meet application requirements21. Despite the initiation of pilot programs22,23,24, the absence of stringent standards for use scenarios and retirement pathways hamper the rational use of the residual capacity25. Recycling alternatively uses residual values of retired batteries by materials extraction or structural repair26,27, suitable for irreversibly degraded retired batteries. Compared with pyrometallurgy and hydrometallurgy28,29, direct recycling stands out for superior profitability, lower energy consumption, and reduced carbon emissions26,27,30. Leveraging lithium replenishment and post-processing of cathode materials, direct recycling achieves efficient material structure repair, and performance restoration31. However, the state of health (SOH) determines the required chemical reagent and anticipated lithium supplementation dosages in direct recycling strategy formulations32,33,34. Insufficient dosage can result in an incomplete repair, while excessive dosage can lead to the generation of residual alkali on the cathode surface, deteriorating the restoration performance27,35. Unfortunately, SOH retrieval requires invasive material characterization36,37 and lengthy capacity calibration tests, the non-invasive, rapid, and sustainable SOH acquisition remains an outstanding challenge.

To secure consistent SOH information, EV batteries are monitored, and operational data are recorded by cloud platforms38 and battery passports24. European Parliament adopted the Batteries Directive on June 14, 2023, to ensure that retired batteries could be reused, reconditioned, or recycled at the end of service life39. However, the required monitoring and recording procedure is merely accessible in the EV service phase, retired batteries are no longer connected to the in-vehicle monitoring unit. Thus, it is challenging to retrieve field-available SOH data. The lifetime data integrity remains a major challenge, calling for the SOH estimation only using field data, opposite to historical data or under controllable conditions30,40,41. One solution is to perform a capacity calibration test at the retired battery collection field, i.e., state of charge (SOC) conditioning, which is straightforward, however, it requires unaffordable test time and extra electricity costs. The hybrid pulse power characterization test is an alternative for SOH estimation by dynamic pulse injection, but the complete test sequence takes over 12 hours. Tao et al. utilized short pulses for SOH estimation of retired batteries, assuming that a SOC conditioning to 5% SOC was performed, which was barely compatible with random retirement SOC conditions41. Recent advances in sensory-based measurements include X-ray imaging42, electrochemical impedance43,44, optical fiber sensing45,46, acoustics sensing47,48, partial charging49,50, and pulse injection17,41. Sensing-based techniques are in the laboratory stage due to invasion, while pulse injection features untangling the battery degradation without physical damage, simultaneously faster than partial charging and electrochemical impedance-based methods17,51,52,53,54,55. However, pulse injection is a data-centric method that is only feasible under the ideal assumption that physically measured data encompasses retirement conditions of the model deployment phase, known as the common challenge of ___domain shift in the machine learning community. Despite advances in transfer learning and ___domain adaption methods56,57,58, challenges persist since the target ___domain to align still requires prior information upon deployment, and existing learning methods can hardly be updated for random retirement conditions59. An alternative is spanning data testing scale under unexplored retirement conditions to mitigate data scarcity and heterogeneity while it can lead to increased costs. Wang et al. proposed a temperature excavation method to interpolate reaction kinetic preferences at different intermediate states during a thermochemical process, allowing for the construction of extensive training databases at minimal thermochemistry experimental scale and cost as a data augmentation for machine learning model training60. Besides, generative learning also demonstrates the possibilities of estimating SOH with augmented data from partially cycled profiles, saving required physically tested data61,62. However, the data scarcity and heterogeneity in battery reuse and recycling context are even more complex due to a mixture of cathode material types, physical formats, capacity designs, and historical usages, restricting the potential integration of condition-specific knowledge of degradations into machine learning models. Thus, it is reasonable to consider the dependency relationship between retirement conditions and pulse voltage responses for data generation, inflicting no lengthy time series capacity calibration and extra physical experiments simultaneously, to boost SOH estimation performance.

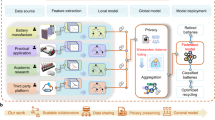
In this study, we perform retired battery pretreatment, i.e., SOH estimation, using the pulse voltage response data generated by an attentional variational autoencoder at a saved physical measurement time and cost. The high-level process of general pretreatment steps, generative model training, and practical model deployment steps are illustrated in Fig. 1. The research idea is to use generative learning to exploit already measured data for the pulse voltage responses exploration in continuous retirement conditions, i.e., SOC distribution in retired battery collection stage. Downstream SOH estimation is implemented without physically measured pulse response data, saving pretreatment electricity costs and carbon emissions otherwise required from conditioning SOC to the anticipated level. Compared with the ampere-hour integral method and the machine-learning pulse injection, generative learning underscores a faster generation speed and accurate estimation. With generated data, a simple regressor successfully estimates the SOH with low error under unseen or inaccessible SOC retirement conditions in the database, a challenging out-of-distribution (OOD) issue. The OOD issue is resolved by learning the inherited physical pattern between the SOC condition and voltage response induced by the rapid pulse. We demonstrate the generalizability of our method by verifying through 2700 physically measured samples, spanning 3 cathode material types, 3 physical formats, 4 capacity designs, and 4 historical usages (1 laboratory accelerated aging, 1 pure battery EV driving, and 2 hybrid EV driving). Generative learning suits interpolation and extrapolation by integrating prior knowledge of retirement conditions into latent space scaling of the model parameters, saving measurement time, electricity costs, and consequent carbon emissions while not compromising SOH estimation accuracy. A conservative global case study of battery retirement in 2030 highlights the significance of rapid and sustainable SOH estimation in pyrometallurgical, hydrometallurgical, and direct recycling circumstances. Through technical-economic analysis, generative learning-assisted SOH estimation could save $4.9 billion electricity costs and 35.8 billion kg CO2 emissions by 2030 worldwide. We discuss the model interpretability, recycling pretreatment implications, and broader aspects of future smart recycling pretreatment directions integrated with machine learning.

Fig. 1: Conceptualization of the state of health (SOH) estimation of retired batteries under random conditions, i.e., state of charge (SOC) distributions, using attentional variational autoencoder.
figure 1

a The retired battery pretreatment steps include SOC conditioning, physical measurements, machine learning for SOH diagnosis, and the second-life decision-making process before reuse or recycling. SOC conditioning refers to adjusting the SOC values of the retired batteries to desired levels using the traditional constant current constant voltage (CCCV) method. b The schematic of attentional variational autoencoder for pulse voltage response data generation. c The practical usage of the data generation model for SOH estimation requires no extra SOC conditioning. The trained machine learning model is supervised by the generated data and receives immediate pulse voltage responses when in the deployment phase. d The economic and environmental benefits and rapid generation speed of our generative learning methodology by saving SOC conditioning costs in the 2030 battery retirement scenario globally.

Full size image

Results

Dataset acquisition

Data scarcity and heterogeneity are major challenges in data-driven battery diagnosis and prognosis, especially for retired batteries. We collected 2700 samples from 270 physically retired batteries across wide SOC levels, i.e., from 5% to 50% with a 5% grain. In Fig. 2a, the dataset covers 3 prevailing cathode material types, including 119 physically collected NMC (nickel manganese cobalt oxide), 56 LFP (lithium iron phosphate), and 95 LMO (lithium manganese oxide) retired batteries, spanning 3 physical formats (cylindric, pouch, prismatic) and 4 historical usage patterns (1 laboratory accelerated test, 3 EV usages, including 1 purely electrified power-train mode and 2 hybrid power-train modes). We stress that the inclusion of highly heterogeneous testing samples makes our dataset the largest rapid pulse-based dataset for SOH estimation of retired batteries up to date, facilitating the model generalizability beyond the physically measured datasets.

Fig. 2: The dataset acquisition.
figure 2

a The Sankey plot for retired batteries distribution, comprises cathode material types, physical formats, capacity designs, and historical usages. b Pulse current and the subsequent voltage response of the retired batteries, where the features are extracted from the turning points, i.e., the points with zero second-order derivative of the voltage response curve. The 21 feature points, from U1 to U21, are extracted. The recording frequency for the raw data is 100 Hz. The rest time is 25 seconds between each pulse in C-rate. Note that the term C stands for charge (discharge) rate when a 1 h of charge (discharge) is performed. The ambient temperature is controlled at 25 \(^{\circ}{{{\rm{C}}}}\). c The state of health (SOH) distribution (Gaussian fit) of the 2.1 Ah and 21 Ah retired batteries for illustration, respectively. For SOH distribution of other battery types, one can refer to Supplementary Fig. 1. d The relationship between measured pulse voltage response and calibrated SOH from capacity calibration test, with varying state of charge (SOC) conditions. The first feature dimension, U1, is illustrated. e The interpolation and extrapolation data generation case illustration under different battery retirement SOC distributions. Detailed testing settings are in Supplementary Notes1 and 2, noting that the C-rate setting is identical across cathode material types. Source data are provided as a Source Data file.

Full size image

In contrast to regular constant current constant voltage (CCCV) testing, the pulse test inflicts no lengthy test time and extra damage to the retired batteries. Therefore, we use the CCCV results as the SOH benchmarking capacity values. Pulse test data are used as training data for the generative learning model. Even though the battery cathode material type varies, we perform a standardized and accessible feature engineering, ensuring compatibility in practical use. Figure 2b demonstrates the feature extraction after pulse current injection. The CCCV and pulse injection experimental settings can be found in Supplementary Note 1. For the first five injected pulses, the turning points, i.e., the points with zero second-order derivative of the voltage responses, are recorded as features, resulting in 21-dimensional features. Despite pulse time at a 5 s level, we also perform sensitivity measurement on pulse width with dual aims to verify pulse robustness and further shorten test time, ranging from 30 ms to 5 s.

We consider accelerated aging in laboratory tests (Supplementary Note 2) and real EV driving aging, though agnostic to the explicit driving profiles due to data privacy restrictions. In Fig. 2c, the SOH distribution of accelerated aging batteries (NMC, 2.1 Ah) and pure battery EV driving aging batteries (NMC, 21 Ah) are illustrated. Noting that SOH values are complementary in a wide SOH region, from 0.6 to 1, the collected data is representative of battery retirement scenarios, also with extreme early retirement cases. SOH distributions of other collected batteries (LMO, 10 Ah, and LFP 35 Ah) cover a wide SOH distribution, see Supplementary Fig. 1. The pulse tests are repeated in different SOC levels, ranging from 5% to 50%, to simulate the randomness of retirement batteries collection. The tested SOC region is under the assumption that retired batteries either exhibit low SOC or are subject to compulsory discharging for safe stationary warehouse storage requirements, thus the SOC upper limit is set at 50%. In Fig. 2d, the first dimension of the extracted features from accelerated aging batteries (NMC, 2.1 Ah) and EV driving aging batteries (NMC, 21 Ah) are illustrated. Despite differences in capacity designs and historical usages, the pulse voltage responses exhibit a consistent degradation pattern, and so do other retired batteries for other feature dimensions, see Supplementary Figs. 2–5. However, the SOC distribution of retired batteries is continuous, and thus it cannot be exhausted by physical measurements. Rather than spanning the data test scale, we use already-tested pulse voltage response data to generate more diversified data across SOC conditions. In Fig. 2e, two-generation scenarios, i.e., the interpolation and extrapolation, are illustrated, with unit conditioning savings, electricity savings, CO2 emissions reductions, and their calculation methods presented in Supplementary Tables. 1–3, respectively.

Pulse voltage response data generation

We first consider using the already-measured pulse voltage response data to reconstruct themselves, rather than directly generating new data samples. The reconstruction means that the measured data are first compressed into a latent variable space while maintaining a learned structure from original statistical distributions (Supplementary Fig. 6) and then decompressed to the original dimensions. In this study, the reconstruction is equivalent to supervising the encoder neural network model and decoder neural network model training phase, as illustrated in Fig. 1b. The core idea is to balance the exploitation of limited measured data and the exploration of extended data space using latent dependencies between retirement conditions and pulse voltage response data with cross-attention mechanisms, see “Methods”. Then measured data fused with conditional information are fed into the encoder neural network, obtaining latent variables containing retirement conditions. Compressed latent variables are decompressed by training a decoder neural network model and reconstructing the input data samples, also guided by the feed-forward retirement conditions. Another input of the decoder neural network is only random noise, subject to Gaussian assumption (Supplementary Fig. 7), inflicting no physical experimental measurement otherwise involved with additional test time, energy consumption, and even safety hazards.

Figure 3a shows the data reconstruction results of the first feature dimension U1 at selected SOC values (35% and 50%), with a mean absolute percentage error (MAPE) lower than 1%, indicating that the model learned the dependencies between pulse voltage response data and SOC conditions. Such dependencies are of generality in a wide SOH range, from 0.6 to 0.95. Regarding other feature dimensions, the data reconstruction results are still satisfactory, with a MAPE lower than 1%, see Fig. 3b. The reconstruction results for other types of retired batteries (NMC, 21 Ah, LMO, 10 Ah and LFP, 35 Ah) are presented in Supplementary Figs. 8–10, demonstrating the model generality and flexibility. It is noted that lower SOC regions exhibit comparatively higher reconstruction MAPE, though still lower than 1%, which can be rationalized by the sensitivity of the polarization response at low SOC regions. It is, therefore, recommended to perform pulse injections at a middle SOC region for reliable representation of battery degradation. However, as we highlight the random retirement conditions with different SOCs, pulse injection at fixed SOC needs extensive conditioning time and energy consumption, exacerbating a dilemma between pulse injection regions and unaffordable conditioning time and cost, see Supplementary Fig. 11.

Fig. 3: The model performance in terms of mean absolute percentage error (MAPE) and energy-environmental benefit.
figure 3

a The parity plot of the model training results (reconstruction), with feature U1 at the selected state of charge (SOC) condition (35% and 50%), is illustrated. b The heatmap of the model training performance for features U1 to U21. c SOC simulation of the retired batteries under random retirement scenarios, including interpolation and extrapolation cases. d The data generation performance under the random retirement scenarios, where error bars indicate the standard deviation (\({{{\rm{\sigma }}}}\)) computed across 21-dimensional features (n = 21 at each SOC in each case) and the height of the bar indicates its mean. e The electricity cost savings and CO2 emission reductions for different battery retirement scales using the different data generation case settings. Note that the battery retirement scale is logarithmic. All results are from NMC, 2.1 Ah batteries for illustration. Source data are provided as a Source Data file.

Full size image

With the proposed generative learning methodology, we stress that the already-measured data for training purposes is at the cost of extra physical tests, however, the generation is free of extra cost. In Fig. 3c, we validate eight data generation cases, including interpolation and extrapolation. In the interpolation cases (from Case0 to Case3), the lower and upper bounds of the SOC for training data are fixed at 5% and 50%, respectively. In comparison, the extrapolation cases (from Case4 to Case7) mean that the already-measured data are exclusive with unseen OOD data to generate, a challenging and open issue in machine learning communities. Here we use prior knowledge of retired batteries to scale the latent distribution in the encoder neural network, generalizing already-measured data to OOD conditions, see Methods. We note that Case4 and Case5 are toy examples since the training costs of these cases are higher than the cost savings of generating the same volume of data under unseen SOC conditions. However, we still use the toy cases to demonstrate the robustness of latent space scaling in more generalized battery retirement settings. In practical use, therefore, the users could customize the data generation strategy based on the trade-off between model training cost and data generation accuracy.

In Fig. 3d, the distance-based data generation performance under unseen retirement conditions is illustrated. It is noted that the as-trained generative learning model is used to generate more data samples, especially under, but not limited to, unseen retirement conditions. For instance, Case3 uses the physically tested pulse voltage response data at 5%, 25%, and 50% SOCs to generate data at 10, 15, 20, 30, 35, 40, and 45% SOCs. All interpolation cases exhibit a low MAPE error below 2%, even if the model is never trained with such data. From intuition, the extrapolative Case6 and Case7 are more promising in saving pretreatment costs since the used training data are time and cost-efficient to retrieve. We demonstrate that even in OOD cases, the generative learning strategy successfully guides the already-measured data to generalize for OOD data. Without latent space scaling, the data generation exhibits a clear increasing error when the physically measured training data is far away from the condition to generate, see Supplementary Fig. 12. This phenomenon has an attractive implication that one can exploit the measured data to explore the unseen data to retrieve the data of higher cost using customized generation strategies. Regarding the distribution-based data generation performance, the model achieves low Kullback-Leibler divergences across verification settings, suggesting that the model can automatically learn the distribution of already measured data to create diversified data instances, see Supplementary Figs. 13–16.

We evaluate the electricity and CO2 emission savings using different data generation cases. Figure 3e shows the electricity and CO2 emission savings in an ascending case order, and the color bar maps the according values. Except for Case4 and Case5, two toy examples, the extrapolation strategy can save up to 60,000 USD in electricity costs and 460,000 kilograms of CO2 emissions, assuming a 1000-ton battery retirement scale. This priority is achieved by generating expensive data, which needs SOC conditioning costs, from cost-efficient physically measured data. Inside the interpolation generation, we found that the model does not require stringent intermediate points to interpolate on, leading to a usage priority in Case 3, using 5, 25, and 50% SOC data. Despite different case difficulties, the data generation model is easy to train, converging in less than 50 iterations within a milliseconds level, see Supplementary Fig. 17. Once the generative model is properly trained, the users can generate unlimited data across wide retirement conditions, without any measurement costs, facilitating rapid, accurate and sustainable retired battery SOH estimation for reuse and recycling decision-making.

Retired battery SOH estimation with generated pulse voltage response features

We use the generated pulse voltage response features to estimate the SOH of retired batteries. In Fig. 4a, the SOH estimation performance under different battery retirement cases is illustrated, where shaded scatters and the void regions stand for the testing and training conditions of the generation model, respectively. Taking Case 3 as an example, physical pulse measurements are performed at 5, 25, and 50%, which are used to train the generation model. The as-trained model generates unseen data at 10, 15, 20, 30, 35, 40, and 45% SOCs, utilized as input data of a regressor to realize SOH estimation in these unseen SOC levels. Regardless of data scarcity, we demonstrate that the generated data successfully facilitates accurate SOH estimation with an average MAPE and standard deviation of 4.9% and 2.9% in both interpretative and extrapolative cases, respectively. However, the interpolative data generation leads to more accurate and stable estimations, compared with extrapolative generation. The average MAPE and standard deviation in interpolative cases are 4.4% and 2.5%, respectively; the average MAPE and standard deviation in extrapolative cases are 6.0% and 2.7%, respectively. This phenomenon can be rationalized by the challenges in OOD issues, however, which is calibrated thanks to the integration of prior knowledge into the latent space scaling, see “Methods”. SOH estimation results under selected SOC values are presented in Fig. 4b with parity plots, indicating a successful data generation across wide SOC conditions.

Fig. 4: State of health (SOH) estimation performance in terms of mean absolute percentage error (MAPE) for retired batteries using generated data.
figure 4

a SOH estimation performance under different cases, which are illustrated in Fig. 3c. b The parity plot of true and estimated SOH in Case3, i.e., estimating retired battery SOH at 10, 15, 20, 30, 35, 40, and 45% state of charge (SOC) using data generated from physically measured at 5, 25, and 50% SOC. c SOH estimation comparison between using the available data at tested conditions (gray-shaded region) and the generated data in Case 3. d SOH estimation performance comparison between using the available data at tested conditions (gray-shaded region) and the generated data in Case 7. e The time cost comparison of retrieving unseen data between pulse test at the required SOC level41 and the generative learning assisted data generation. All results are from NMC, 2.1 Ah batteries for illustration. Source data are provided as a Source Data file.

Full size image

Here, we compare the SOH estimation results with and without data generation, highlighting its necessity under highly random retirement conditions. In Fig. 4c, an interpretative case shows limited data access in some discrete SOC values, indicated by gray-shaded regions. Using these data, the regressor produces inaccurate estimations biased to the centroid of the available data distribution, with an average MAPE of 17.3% and a standard deviation of 7.3. In comparison, the generative learning-assisted SOH estimations show a rigorous increase. The average MAPE is 5.4% and a standard deviation of 2.7, indicated by stars in the plot. We observe an interesting overestimation and underestimation of SOH under higher and lower SOC regions, which can be interpreted by the zero mean and unit variance Gaussian distribution in its latent space (see “Methods”). Specifically, taking the underestimation as an example, generated pulse voltage responses conditioned on low SOC regions exhibit higher values, otherwise characterized by a more degraded battery with lower SOH, and vice versa for the overestimation63. The observation has an important implication that the data generation model can be tuned by manipulating the latent space for unseen but conditional data generation.

We consider an extreme, yet more preferred situation where the accessible data can be at low SOC regions. This situation has a clear physical meaning that data curation in these regions can minimize the SOC conditioning time. However, the data curation strategy brings more difficulties in accurate estimations, despite that the curation time and costs are saved. In Fig. 4d, we take accessible data at 5% and 10% SOC for an illustration. It clearly shows an asymptotically increased error when using the accessible data to make SOH estimations. The asymptotic effect can be interpreted as the shift from the accessible data distribution increases with SOC values, adhering to the observation in Fig. 2d. Such a challenge results in an average MAPE of 23.8% and a standard deviation of 7.3 when using data in low SOC regions. In comparison, the estimation performance is increased to a MAPE of 6.0% and a standard deviation of 2.9 using generated data. The estimation results for other retired batteries, with different cathode material types, physical formats, and historical usage patterns, are consistently improved, see Supplementary Fig. 18. Therefore, generative learning empowers rapid SOH pretreatment of retired batteries, by generating data in unseen SOC conditions at saved time requirements otherwise required by SOC conditioning41, thus advancing efficient and sustainable battery reuse and recycling in a data-driven manner.

Technical-economic-environmental evaluation

A technical-economic-environmental evaluation of SOH estimation, including the traditional CCCV capacity calibration test, pulse test-enabled machine learning method, and the proposed generative learning-assisted SOH estimation method, is performed. The boundary of technical-economic-environmental evaluation includes the entire process from the time when the retired batteries enter the pretreatment stage, selecting from recycling methods, and ends with the evaluation of economic and environmental impacts. Despite the differences in pyrometallurgy, hydrometallurgy, and direct recycling presented in Fig. 5a, retired battery pretreatment is a common step for determining the potential capital return of recycling. The pretreatment is linked to the electricity costs of charging and discharging retired batteries, while the recycling process is linked to material input, electricity costs, equipment depreciation, labor, disassembly, and sewage treatment.

Fig. 5: Economic-environmental analysis of constant current constant voltage (CCCV), pulse, and generation.
figure 5

a Comparison of pretreatment methods in pyrometallurgy (pyro-), hydrometallurgy (hydro-), and direct recycling. b CO2 emission assessment for both pretreatment and recycling using different pretreatment methods in pyro-, hydro-, and direct recycling under different states of health (SOH) and state of charge (SOC). c Comparative analysis of electricity cost against battery retirement scale using direct recycling at 80% SOH, with pulse electricity in the post-training phase excluded. d Overall cost analysis, excluding the material flow using different pretreatment methods, assuming a 1-ton retired battery scale at 80% SOH and 50% SOC, indicated by the gray shaded region in panel (c). e Pretreatment costs against the battery retirement scale, with pulse electricity in the post-training phase included, towards the 2030 battery retirement scenario, assuming 80% SOH and 50% SOC. f Detailed pretreatment cost in the 2030 battery retirement scenario. The pulse electricity in the model deployment phase is included. The noted values stand for the absolute cost of each method. Panel (a) was created using flaticon.com. Source data are provided as a Source Data file.

Full size image

The profit and carbon footprint per ton of retired batteries are functional units. We examine two prevalent cathode material types, i.e., NMC and LFP, to determine material investment and revenue, with detailed methodology present in Supplementary Note 3. We show the environmental benefits of pretreating retired NMC batteries in Fig. 5b–g, and the results for economic benefits are presented in Supplementary Fig. 19. The results for pretreating retired LFP batteries are shown in Supplementary Figs. 20, 21. Analysis of retired LMO batteries is not covered due to data shortage and uncertainties in recycling routines. In Fig. 5b, the pyrometallurgy exhibits the highest CO2 emissions, followed by the hydrometallurgy and direct recycling. CO2 emissions using CCCV in pyrometallurgy, hydrometallurgy, and direct recycling are 1104-, 729-, and 579 kilograms eq. per ton of retired NMC batteries, respectively, with 80% and 50% of the retirement SOH and SOC conditions assumed. We found that with our generative learning-assisted SOH estimation, CO2 emissions were reduced to 753-, 379-, and 228 kilograms eq. per ton of retired NMC batteries, respectively. Besides CO2 emissions, the electricity cost savings using the identical pretreatment are in Supplementary Figs. 19 and 20 for NMC and LFP retired batteries, respectively. Supplementary Figs. 22 and 23 show a clear trend that saved CO2 emission and cost increase with SOH, particularly favorable in facilitating fewer electricity and recycling investments. In the future, with the growth of renewable energy penetration, there will be a boosted decrease in evaluated carbon emission results. The increase in electricity prices will result in a rise in economic benefits.

In Fig. 5c, we clarify the impact of an efficient pretreatment by providing a comparative analysis of electricity costs against the battery retirement scale at 80% SOH, excluding the pulse injection electricity costs in the post-training phase. At the 1.07 tons retirement scale, generative learning costs are lower than that of pulse tests for retired batteries with 25% SOC, making it the second-best pretreatment method in terms of cost. At the 5.33 tons retirement scale, the costs of the generative learning are lower than that of pulse tests for retired batteries with a 5% SOC, establishing it as optimal. Moreover, the advantage of generative learning does not rely on a retirement scale of retired batteries when it goes beyond 5.33 tons, suitable for massive retirement battery processing. It is conservatively estimated that data collected from 1 ton of retired batteries (25,500 samples of 18650 batteries) are adequate to supervise the data generation model. However, our model only uses 10.6% of such a training data scale (2700 samples), indicating that the model training costs for data generation can still be further reduced to that is lower than \(5.7\times {10}^{-3}\) USD.

Direct recycling is selected for evaluation due to its cost-sensitive nature. We analyze the impact on overall cost proportions with electricity cost reductions. In Fig. 5d, the ring plot and stacked bar plot of pretreatment costs are illustrated to show the changes in electricity consumption for 1 ton of retired batteries with the relative and absolute value, excluding material flows, respectively. When the retirement condition is at 80% SOH and 50% SOC, the electricity consumption proportion using deliberate data generation decreases from 13.3% to 6.6% compared to the traditional CCCV capacity calibration test. The absolute electricity cost, inclusive of the pretreatment and recycling process, decreases from 80 to 36 USD per ton of retired batteries. The overall impact on direct recycling of retired LFP using generative-learning-assisted SOH estimation can be found in Supplementary Fig. 24. Considering a battery retirement scenario in 2030 globally, as illustrated in Fig. 5e, pretreatment electricity saving exponentially increases with retirement scales up to a \({10}^{9}\) USD level. In Fig. 5f, generative learning saves up to 4.9 billion USD in electricity costs and reduces 35.8 billion kilograms of CO2 emissions compared to traditional CCCV-based capacity calibration tests, see Supplementary Fig. 25. Regarding LFP batteries, a similar scale effect can be observed in electricity cost saving, and CO2 emission reduction under the 2030 scenario, see Supplementary Figs. 26−27. The cost saving and CO2 emission reduction do not solely stem from priorities of direct recycling but, more importantly, from saving exhaustive data curation at random retirement conditions using the proposed generative learning-assisted SOH estimation.

Discussion

We have elaborated on the success of using generative learning in generating high-fidelity pulse voltage response data of retired batteries while saving conditioning costs and time. The success is attributed to the generation model to learn the dependency between retirement conditions and pulse voltage responses, inclusive of heterogeneities in cathode material types, physical formats, capacity designs, and historical usages, see Supplementary Fig. 28. Diverging from the traditional SOC conditioning using capacity calibration tests, even the state-of-the-art pulse tests combined with machine learning at a specific SOC level41, the proposed data generation model underscores a balance between exploiting already measured data and exploring potential data space with random SOH and SOC retirement conditions. The proposed method inflicts no extra physical measurements, reducing secondary energy use and environmental burden in practical use. With a portion of the generated data, downstream SOH estimation tasks still perform consistently compared to the sufficient data situations, a useful implication for reducing computational cost and improving estimation accuracy in real-world cases, see Supplementary Figs. 29−32. Discussions on advancements of the proposed method, including model interpretability, battery recycling implication, and inspiration for machine learning integrated battery reuse and recycling pretreatment towards sustainability, can be found in Supplementary Discussions.

In conclusion, the proposed generative learning demonstrates consolidated promises in estimating the SOH of retired batteries rapidly, accurately, and sustainably. We present a generative learning model supervised by a few physically measured pulse voltage response data that can effectively generate new data across wide SOC and cathode material types, with a mean absolute percentage error of interpretative and extrapolative cases below 2%. With generated data, a regressor obtains a mean absolute percentage error below 6% for SOH estimation, including unseen SOC conditions. The results are verified through 3 prevailing cathode material types (NMC, LFP, and LMO), 3 physical formats (cylindric, pouch, and prismatic), 4 capacity designs (2.1, 10, 21, and 35 Ah), and 4 historical usages (1 laboratory accelerated aging and 3 different EV-driving aging patterns). We showcase the economic and environmental viability of the data generation in an upcoming battery retirement scenario of 2030 globally by saving 4.9 billion USD in electricity costs and reducing 35.8 billion kilograms of CO2 emissions. Generally, the proposed data generation method enables sustainable battery reuse and recycling decision-making64, especially for direct recycling, by devising appropriate use of lithium supplements and other chemical reagents, critically important to recycling costs and product qualities. Broadly, the generative learning method inspires the promises of exploiting already measured data to explore the unexhaustive data space, as opposed to separate physical measurements, alleviating the data scarcity and heterogeneity issues in critical estimation and predictive applications where data are time-consuming, expensive, and polluting to retrieve.

Methods

Cross-attention mechanism

Cross-attention in neural networks enables a model to focus on specific parts of one input, i.e., the query, based on the information in another input, i.e., the key and value. It is useful in scenarios where the relevance of certain features in one data stream depends on the additional information provided and has demonstrated successful applications in battery health diagnosis and prognosis65,66,67,68. In battery recycling pretreatment, retired batteries are under random retirement conditions, i.e., state of charge (SOC) distributions. From expert knowledge, the pulse voltage response exhibits considerable shift with SOC. Therefore, the cross-attention enables the exploration of conditional dependencies between pulse voltage responses and the SOC retirement conditions. The general formulation of the cross-attention mechanism is:

$${\mbox{Attention}}(Q,K,V)={{{\rm{softmax}}}}\left(\frac{Q{K}^{T}}{\sqrt{{d}_{k}}}\right)V$$
(1)

where, \(Q,K,V\) represent the query, key, and value sequence, respectively. \({d}_{k}\) is the scaling factor, typically the dimension value of the key \(K\). \(T\) is the transpose operator. The \({{{\rm{softmax}}}}\) function normalizes the input vector so that the sum of the probabilities is 1, making the calculated attention a valid probability distribution. In the cross-attention, the \({{{\rm{softmax}}}}\) is used to calculate the weights representing the importance of different elements in the input sequence. Given a vector \({{{\bf{v}}}}=[{v}_{1},{v}_{2},\bullet \bullet \bullet,{v}_{P}]\) of real numbers, the \({{{\rm{softmax}}}}\) function for the \(i\)-th element of this vector is given by:

$${{{{\rm{softmax}}}}({{{\bf{v}}}})}_{i}=\frac{{e}^{{v}_{i}}}{{\sum }_{p=1}^{P}{e}^{{v}_{p}}}$$
(2)

where the denominator is the sum of the exponentials of all elements \({v}_{i}\) in the vector \({{{\bf{v}}}}\), \(i=1,\ldots,P\). \(P\) is the number of elements in the vector \({{{\bf{v}}}}\).

Encoder neural network with cross-attention

The encoder network in the variational autoencoder is designed to compress input data into a latent space. It starts by taking the 21-dimensional battery voltage response feature matrix \({{{\bf{x}}}}\in {{\mathbb{R}}}^{N\times 21}\) as main input and retirement condition matrix \({{{\bf{cond}}}}=[{SOC},{SOH}]\in {{\mathbb{R}}}^{N\times 2}\) as input, where \(N\) is the sample size. The condition input is first transformed into an embedding \({{{\bf{C}}}}\), belonging to a larger latent space with 64 dimensions. The conditional embedding \({{{\bf{C}}}}\) is formulated as:

$${{{\bf{C}}}}={{{\rm{ReLU}}}}\left({{{{\bf{cond}}}}\cdot {{{\bf{W}}}}}_{{{{\bf{c}}}}}^{{{{\bf{T}}}}}+{{{{\bf{b}}}}}_{{{{\bf{c}}}}}\right)$$
(3)

where, \({{{{\bf{W}}}}}_{{{{\bf{c}}}}}\in {{\mathbb{R}}}^{64\times 2},{{{{\bf{b}}}}}_{{{{\bf{c}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 64}\) are the condition embedding neural network weighting matrix and bias matrix, respectively.

The main input matrix \({{{\bf{x}}}}\), representing pulse voltage response features, is also transformed into this 64-dimensional latent space \({{{\bf{H}}}}\):

$${{{\bf{H}}}}={{{\rm{ReLU}}}}\left({{{{\bf{x}}}}\cdot {{{\bf{W}}}}}_{{{{\bf{h}}}}}^{{{{\bf{T}}}}}+{{{{\bf{b}}}}}_{{{{\bf{h}}}}}\right)$$
(4)

where, \({{{{\bf{W}}}}}_{{{{\bf{h}}}}}\in {{\mathbb{R}}}^{64\times 21},{{{{\bf{b}}}}}_{{{{\bf{h}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 64}\) are the main input embedding neural network weighting matrix and bias matrix, respectively.

Both \({{{\bf{H}}}}\) and \({{{\bf{C}}}}\) are then integrated via a cross-attention, allowing the network to focus on the voltage response matrix \({{{\bf{x}}}}\) conditioned by the additional retirement condition information \({{{\boldsymbol{cond}}}}\):

$${\mbox{AttenEncoder}}={\mbox{Attention}}({{{\bf{H}}}},{{{\bf{C}}}},{{{\bf{C}}}})$$
(5)

where, \({{{\bf{H}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 64}\) and \({{{\bf{C}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 64}\) are embeddings of pulse voltage response data and retirement condition data, respectively. \({{{\bf{AttenEncoder}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 64}\) is the cross-attended output matrix from the voltage response embedding \({{{\bf{H}}}}\) and the retirement condition embedding \({{{\bf{C}}}}\).

\({{{{\bf{z}}}}}_{{{{\bf{mean}}}}}\) and \({{{{\bf{z}}}}}_{{{\log }}\_{{{\bf{var}}}}}\) constitute a Gaussian distribution for each \(L=2\) dimensional latent space:

$${{{{\bf{z}}}}}_{{{{\bf{mean}}}}}={\mbox{AttenEncoder}}{\cdot {{{\bf{W}}}}}_{{{{{\bf{z}}}}}_{{{{\bf{mean}}}}}}^{{{{\bf{T}}}}}+{{{{\bf{b}}}}}_{{{{{\bf{z}}}}}_{{{{\bf{mean}}}}}}$$
(6)
$${{{{\bf{z}}}}}_{{{\log }}{{{\rm{\_}}}}{{{\bf{var}}}}}={\mbox{AttenEncoder}}{\cdot {{{\bf{W}}}}}_{{{{{\bf{z}}}}}_{{{\log }}{{{\rm{\_}}}}{{{\bf{var}}}}}}^{{{{\bf{T}}}}}+{{{{\bf{b}}}}}_{{{{{\bf{z}}}}}_{{{\log }}{{{\rm{\_}}}}{{{\bf{var}}}}}}$$
(7)

where, the \({{{{\bf{z}}}}}_{{{{\bf{mean}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times {{{\rm{L}}}}}\), \({{{{\bf{z}}}}}_{{{\log }}\_{{{\bf{var}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times {{{\rm{L}}}}}\) are the mean and logarithm of the variance of the Gaussian distributions, respectively. \({{{{\bf{W}}}}}_{{{{{\bf{z}}}}}_{{{{\bf{mean}}}}}}\in {{\mathbb{R}}}^{{{{\rm{L}}}}\times 64}\), \({{{{\bf{b}}}}}_{{{{{\bf{z}}}}}_{{{{\bf{mean}}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times {{{\rm{L}}}}}\) are the trainable weighting matrix and bias matrix, respectively. \({{{{\bf{W}}}}}_{{{{{\bf{z}}}}}_{{{\log }}\_{{{\bf{var}}}}}}\in {{\mathbb{R}}}^{{{{\rm{L}}}}\times 64}\), \({{{{\bf{b}}}}}_{{{{{\bf{z}}}}}_{{{\log }}\_{{{\bf{var}}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times {{{\rm{L}}}}}\) are the neural network weighting matrix and bias matrix for the latent space variance embedding, respectively.

Latent space scaling informed by prior knowledge

Certain retirement conditions, e.g., extreme SOH and SOC can be under-represented in the battery recycling pretreatment due to data scarcity or measurement budget. Specifically, the retired batteries exhibit concentrated SOH and SOC, leading to poor estimation performance when confronted with out-of-distribution (OOD) batteries. Collected retired batteries are discharged lower than a certain voltage threshold due to the safety concerns of the warehouse storage requirement, resulting in an upper-limit SOC typically lower than 50%. Even if the explicit battery retirement conditions are still unknown, we can use this approximated prior knowledge to generate enough synthetic data to cover the actual retirement conditions. Given two data generation settings, namely, interpolation and extrapolation, we use different latent space scaling strategies. In the interpolation setting, the scaling matrix \({{{\bf{T}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times {{{\rm{N}}}}}\) is an identity matrix \({{{\bf{I}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times {{{\rm{N}}}}}\) assuming the encoder network and decoder network can learn inherited data structures without taking advantage of any prior knowledge. In the extrapolation setting, however, the assumption cannot be guaranteed due to the OOD issue, a general challenge of machine learning models. Here, we use the means of training and testing SOC distributions to define the scaling matrix, and prior knowledge of the battery retirement conditions, then the latent space is scaled as:

$${\hat{{{{\bf{z}}}}}}_{{{{\bf{mean}}}}}={{{{\bf{T}}}}}_{{{{\bf{mean}}}}}\cdot {{{{\bf{z}}}}}_{{{{\bf{mean}}}}}$$
(8)
$${\hat{{{{\bf{z}}}}}}_{{{\log }}{{{\rm{\_}}}}{{{\bf{var}}}}}={{{{\bf{T}}}}}_{{{\log }}{{{\rm{\_}}}}{{{\bf{var}}}}}\cdot {{{{\bf{z}}}}}_{{{\log }}{{{\rm{\_}}}}{{{\bf{var}}}}}$$
(9)

where, \({{{{\bf{T}}}}}_{{{{\bf{mean}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times {{{\rm{N}}}}}\) and \({{{{\bf{T}}}}}_{{{\log }}\_{{{\bf{var}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times {{{\rm{N}}}}}\) are the scaling matrices defined by the broadcasted mean, and variance ratio between the testing and training SOC distributions, respectively. We emphasize that the SOH distributions are irrelevant to such a scaling. This is because these identical SOH values could be seen as representing physically distinct batteries, i.e., they do not affect the scaling process. Thus, feeding the model with the same SOH values during training and reconstruction does not present an OOD problem. On the other hand, for the SOC dimension, our goal is to generate data under unseen SOC conditions, where physical tests cannot be exhausted.

Sampling in the scaled latent space

The sampling step in the VAE is a bridge between the deterministic output of the encoder neural network and the stochastic nature of the scaled latent space. It allows the model to capture the hidden structure of the input data, specifically the pulse voltage response \({{{\boldsymbol{x}}}}\) and \({{{\boldsymbol{cond}}}}\) to explore similar data points. The sampling procedure can be formulated as:

$${{{{\bf{z}}}}={{{\bf{z}}}}}_{{{{\bf{mean}}}}}{+{{{\rm{e}}}}}^{\frac{1}{2}\cdot {{{{\bf{z}}}}}_{{{\log }}{{{\rm{\_}}}}{{{\bf{var}}}}}}\cdot {{{\boldsymbol{\epsilon }}}}$$
(10)

where, \({{{\boldsymbol{\epsilon }}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times {{{\rm{L}}}}}\), is a Gaussian noise vector sampled from \({{{\boldsymbol{\epsilon }}}} \sim {{\boldsymbol{{{\mathscr{N}}}}}}({{{\bf{0}}}}{{,}}{{{\bf{I}}}})\). The exponential term \({{{{\rm{e}}}}}^{\frac{1}{2}\cdot {{{{\bf{z}}}}}_{{{\log }}\_{{{\bf{var}}}}}}\) turns the log variance vector into a positive variance vector. \({{{\bf{z}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times {{{\rm{L}}}}}\) is the sampled latent variable.

Decoder neural network with cross-attention

The Decoder Network transforms the sampled latent variable \({{{\boldsymbol{z}}}}\) back into the original dataspace, reconstructing the input data or generating new data attended on the original or unseen retirement conditions. The first step in the decoder is a dense layer that transforms \({{{\boldsymbol{z}}}}\) into an intermediate representation:

$${{{{\bf{H}}}}}^{{\prime} }={{{\rm{ReLU}}}}\left({{{{\bf{z}}}}\cdot {{{\bf{W}}}}}_{{{{\bf{d}}}}}^{{{{\bf{T}}}}}+{{{{\bf{b}}}}}_{{{{\bf{d}}}}}\right)$$
(11)

where, \({{{{\bf{W}}}}}_{{{{\bf{d}}}}}\in {{\mathbb{R}}}^{64\times {{{\rm{L}}}}}\), \({{{{\bf{b}}}}}_{{{{\bf{d}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 64}\) are the neural network weighting matrix and bias matrix for the latent variable decoding embedding, respectively. \({{{{\bf{H}}}}}^{{{{\prime} }}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 64}\) is the embedded latent variable.

\({{{{\bf{H}}}}}^{{{{\prime} }}}\) is then integrated via a cross-attention, allowing the network to focus on relevant aspects of the voltage response matrix \({{{\bf{x}}}}\) conditioned by the additional retirement condition embedding \({{{{\bf{C}}}}}^{{{{\prime} }}}\):

$$\,{\mbox{AttenDecodeder}}={\mbox{Attention}}({{{{\bf{H}}}}}^{{\prime} },{{{{\bf{C}}}}}^{{\prime} },{{{{\bf{C}}}}}^{{\prime} })$$
(12)

where, \({{{{\bf{H}}}}}^{{{{\prime} }}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 64}\) and \({{{{\bf{C}}}}}^{{{{\prime} }}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 64}\) are embedded latent variables and retirement condition embedding, respectively. \({{{\bf{AttenDecodeder}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 64}\) is the cross-attention output matrix from the embedded latent variable \({{{{\bf{H}}}}}^{{{{\prime} }}}\) and the retirement conditions embedding \({{{{\bf{C}}}}}^{{{{\prime} }}}\). When training, we let \({{{{\bf{C}}}}}^{{{{\prime} }}}{=}{{{\bf{C}}}}\), and the decoder reconstructs the input pulse response data. When generating new data, \({{{{\bf{C}}}}}^{{{{\prime} }}}\) are the SOH and SOC conditions of the new data to be generated. The reconstructed (generated) data \(\hat{{{{\bf{x}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 21}\) is calculated as:

$$\hat{{{{\bf{x}}}}}={{{\rm{\sigma }}}}\left({\mbox{AttenDecodeder}}{\cdot {{{\bf{W}}}}}_{{{{\bf{o}}}}}^{{{{\bf{T}}}}}+{{{{\bf{b}}}}}_{{{{\bf{o}}}}}\right)$$
(13)

where, \({{{{\bf{W}}}}}_{{{{\bf{o}}}}}\in {{\mathbb{R}}}^{21\times 64}\), \({{{{\bf{b}}}}}_{{{{\bf{o}}}}}\in {{\mathbb{R}}}^{{{{\rm{N}}}}\times 21}\) are the neural network weighting matrix and bias matrix for the output transformation, respectively. \(\sigma\) is the sigmoid activation function.

Loss functions

The loss function consists of two parts, i.e., the reconstruction loss and the Kullback-Leibler (KL) divergence loss. The reconstruction loss, i.e., the mean square error (MSE) loss \({{Loss}}_{{MSE}}\) between original and reconstructed (generated) data, is:

$${{{{\rm{Loss}}}}}_{{{{\rm{MSE}}}}}=\frac{1}{N}{\sum}_{i=1}^{N}{({{{{\bf{x}}}}}_{{{{\bf{i}}}}}{{{\boldsymbol{-}}}}{\hat{{{{\bf{x}}}}}}_{{{{\bf{i}}}}})}^{2}$$
(14)

where, \({{{{\bf{x}}}}}_{{{{\bf{i}}}}}\in {{\mathbb{R}}}^{1\times 21}\) and \({\hat{{{{\bf{x}}}}}}_{{{{\bf{i}}}}}\in {{\mathbb{R}}}^{1\times 21}\) are the original and reconstructed (generated) pulse voltage response data in each sample, respectively. \(N\) is the sample size.

KL divergence loss \({{Loss}}_{{KL}}\), i.e., the KL divergence between original and generated data, is:

$${{{{\rm{Loss}}}}}_{{{{\rm{KL}}}}}=-\frac{1}{2}{\sum}_{i=1}^{N}\left(1+{{{{{\bf{z}}}}}_{\log {\mbox{\_}}{{\mathrm{var}}}}}_{{{{\bf{i}}}}}-{{{{{\bf{z}}}}}_{{{\mathrm{mean}}}}^{2}}_{{{{\bf{i}}}}}-{{{{\rm{e}}}}}^{{{{{{\bf{z}}}}}_{\log {\mbox{\_}}{{\mathrm{var}}}}}_{{{{\bf{i}}}}}}\right)$$
(15)

The total loss is the linear combination of \({{Loss}}_{{MSE}}\) and \({{Loss}}_{{KL}}\):

$${{{\rm{Loss}}}}={{{{\rm{\omega }}}}}_{{{{\rm{xent}}}}}\cdot {{{{\rm{Loss}}}}}_{{{{\rm{MSE}}}}}+{{{{\rm{\omega }}}}}_{{{{\rm{KL}}}}}\cdot {{{{\rm{Loss}}}}}_{{{{\rm{KL}}}}}$$
(16)

where, \({{{{\rm{\omega }}}}}_{{{{\rm{xent}}}}}\) and \({{{{\rm{\omega }}}}}_{{{{\rm{KL}}}}}\) are set to 0.5 to achieve a balance between the generation accuracy and the diversity, respectively69. \(N\) is the sample size.

Random forest regressor

We adopt a random forest algorithm to perform SOH estimation due to the suitability of tabular data after feature engineering of the pulse voltage response curves, which can be formulated as:

$$\bar{{{{\bf{y}}}}}{=}\bar{h}({{{\bf{X}}}})=\frac{1}{K}{\sum}_{m=1}^{M}h\left({{{\bf{X}}}}{{;}}{{{{\boldsymbol{\vartheta }}}}}_{{{{\rm{m}}}}},{{{{\boldsymbol{\theta }}}}}_{{{{\rm{m}}}}}\right)$$
(17)

where \(\bar{{{{\bf{y}}}}}\) is the predicted SOH value vector. \(M\) is the tree number in the random forest. \({{{{\boldsymbol{\vartheta }}}}}_{{{{\rm{m}}}}}\) and \({{{{\boldsymbol{\theta }}}}}_{{{{\rm{m}}}}}\) are the hyperparameters, i.e., the minimum leaf size and the maximum depth of the \({{{\rm{k}}}}\) th tree in the random forest, respectively. The hyperparameters are set as equal across different cases, i.e., \({{{\rm{M}}}}=20\), \({{{{\boldsymbol{\vartheta }}}}}_{{{{\rm{m}}}}}=1\), and \({{{{\boldsymbol{\theta }}}}}_{{{{\rm{m}}}}}=64\), for a fair comparison. Implementations are in the Sklearn Package (version 1.3.1) in the Python 3.11.5 environment, with a random state at 0.

Evaluation metric

The mean absolute percentage error is defined as:

$${{{\rm{MAPE}}}} \% = 100 \% \times \frac{1}{N}{\sum}_{i=1}^{N}\left|\frac{{A}_{i}\,-\,{F}_{i}}{{A}_{i}}\right|$$
(18)

where, \({A}_{i}\) and \({F}_{i}\) are the actual and estimated values, respectively. \(N\) is the sample size.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.