Matrix plainification leads to high thermoelectric performance in plastic Cu2Se/SnSe composites

Ying, Pan; Jian, Qingyang; Gong, Yaru; Song, Tong; Yang, Yuxuan; Geng, Yang; Huang, Junquan; Sun, Rongxin; Chen, Chen; Shen, Tao; Li, Yanan; Dou, Wei; Liang, Congmin; Liu, Yuqi; Xiang, Deshang; Feng, Tao; Fei, Xiaoyu; Zhang, Yongsheng; Song, Kun; Zhang, Yang; Wu, Haijun; Tang, Guodong

doi:10.1038/s41467-025-58484-0

Download PDF

Article
Open access
Published: 07 April 2025

Matrix plainification leads to high thermoelectric performance in plastic Cu₂Se/SnSe composites

Nature Communications volume 16, Article number: 3305 (2025) Cite this article

4060 Accesses
2 Citations
Metrics details

Subjects

Abstract

Thermoelectric technology exhibits significant potential for power generation and electronic cooling. In this study, we report the achievement of exceptional thermoelectric performance and high plasticity in stable Cu₂Se/SnSe composites. A novel matrix plainification strategy was employed to eliminate lattice vacancies within the Cu₂Se matrix of the Cu₂Se/SnSe composites, resulting in a marked improvement in carrier mobility and power factor. The presence of quasi-coherent interfaces induces phonon scattering, reducing lattice thermal conductivity without compromising carrier mobility. Consequently, a high figure of merit (ZT) of 3.3 was attained in the Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se composite. Additionally, the presence of high-density nanotwins imparts remarkable plasticity to the composite, yielding a compressive strain of 12%. The secondary phase contributes to the stability of the composite by hindering the extensive migration of Cu ions through bonding interactions. Our findings present a novel strategy for enhancing the thermoelectric performance of composite semiconductors, with potential applicability to other thermoelectric systems.

Compositing effects for high thermoelectric performance of Cu₂Se-based materials

Article Open access 27 April 2023

Crystal symmetry modification enables high-ranged in-plane thermoelectric performance in n-type SnSe crystals

Article Open access 20 February 2025

Prediction of high thermoelectric performance in the low-dimensional metal halide Cs₃Cu₂I₅

Article Open access 14 April 2021

Introduction

Thermoelectric materials can directly convert waste heat into electricity and vice versa without moving parts, noise, and pollution based on charge carrier and phonon transport only^1,2. Development of highly efficient thermoelectric materials has become increasingly critical as the world seeks sustainable solutions to alleviate energy and environmental crisis^3,4. The thermoelectric energy conversion efficiency is primarily determined by the dimensionless figure of merit, ${ZT}=\sigma {S}^{2}T/{{\kappa }}_{{\mbox{tot}}}$^5,6,7, where σ, S, and T denote the electrical conductivity, the Seebeck coefficient and absolute temperature, respectively. κ_tot is the total thermal conductivity, which is the sum of the contribution from the lattice thermal conductivity (κ_lat) and the electronic thermal conductivity (κ_ele). The thermoelectric parameters σ, S, κ_ele are strongly coupled via carrier concentration, which is quite difficult to decouple. Therefore the electron and phonon transport are the limiting conditions for thermoelectric optimization^8,9. To date, several approaches have emerged to substantially enhance ZT values, which include maximizing power factor (PF = S²σ) through engineering carrier concentration^10,11,12, manipulating band structure^13,14,15 and modulating the phonon transport through nanostructuring^16,17,18,19, phase separation^20,21,22, and all-scale hierarchical architecturing^23,24,25.

Cu₂Se-based materials are of great potential due to their earth-abundant and nontoxic elements, high ZT value, and wide service temperature range²⁶. It undergoes a structural transition from low symmetry monoclinic phase (α-phase) to high symmetry cubic phase (β-phase) at around 400 K²⁷. The high temperature β-phase Cu₂Se is classified as a superionic conductor, exemplifying the “electron-crystal, phonon-liquid” concept²⁷. The high thermoelectric performance derives from its intrinsically low thermal conductivity and superior electrical transport properties due to highly mobile and diffusive Cu ions²⁸. The mobile and diffusive Cu ions cause strong phonon scattering, leading to low lattice thermal conductivity^27,29. Meanwhile, enhanced carrier concentration induced by mobile and diffusive Cu ions and formation of abundant conductive framework contribute to high electrical transport properties²⁷. However, stability and carrier mobility were seriously deteriorated by their superionic feature. The Cu ion migration leads to the deposition of Cu to the interface at the high temperature end of the material device under large external electric fields and gradients³⁰, which adversely affects the stability and damages its thermoelectric performance^31,32. High intrinsic carrier concentration coupled with low solubility limits of dopants prevents the hole concentration of Cu₂Se from being optimized to the optimal level^33,34, significantly constraining ZT optimization. Therefore, it is a great challenge for achieving a high ZT while improving the stability of Cu₂Se.

Ion confinement effect was demonstrated to inhibit the long-range migration of Cu ions and obtain highly stable Cu₂Se based material²⁶. Additionally, phase interface engineering has been shown to be an effective strategy to an ion-blocking interface to hinder Cu ion migration^26,35,36. Furthermore, the composite phase can serve as phonon scattering center, reducing the lattice thermal conductivity and partially decoupling electron-phonon transport^28,37. However, the introduction of secondary phases and interfaces in composite materials contribute strong carrier scattering, thereby leading to deterioration of carrier mobility³. Moreover, plenty of Cu vacancies exists in Cu₂Se due to the weak chemical bonds and low vacancy formation energy²⁷. The intrinsic Cu vacancies and mobile Cu ions significantly diminish carrier mobility at high temperatures. The reduction in carrier mobility leads to lower electrical conductivity and thus compromise the power factor³⁸. Synergistic approach of boosting carrier mobility while suppress the lattice thermal conductivity is the key point to achieve optimal thermoelectric performance. Inspired by the concept of “lattice planification” in the study of single-phase materials³⁹, we first proposed an innovative matrix planification strategy to fill matrix vacancy defects and boost carrier mobility in composite materials.

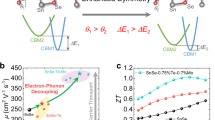
Here, considering that Sn_0.96Pb_0.01Zn_0.03Se have significantly enhanced thermoelectric performance than pure SnSe⁴⁰, we chose Sn_0.96Pb_0.01Zn_0.03Se as the additive to design Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se composites for maximizing thermoelectric performance. It successfully achieved ultrahigh thermoelectric performance in Cu₂Se by introducing SnSe based secondary phase. Sn atoms of Sn_0.96Pb_0.01Zn_0.03Se secondary phase effectively fill Cu vacancies of matrix Cu₂Se, plainification of the crystal lattice of Cu₂Se matrix and significantly enhance carrier mobility of composite (Fig. 1a, b). Furthermore, the large difference in work functions (Cu₂Se: 5.16 eV and Sn_0.96Pb_0.01Zn_0.03Se: 4.38 eV) effectively optimizes the carrier concentration (Supplementary Fig. 1) and enhances the Seebeck coefficient. The sharp increase in carrier mobility and the enhanced Seebeck coefficient leads to a marked increase of power factor. Meanwhile, the observed smooth and quasi-coherent interfaces cause strong phonon scattering, leading to substantial reduction in the lattice thermal conductivity without carrier mobility deterioration. These synergistic effects contribute to a record-high ZT value of 3.3 at 973 K in Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se composite, which is the highest value among utmost reported thermoelectric systems (Fig. 1c)^{41,42,43,44,45,46,47,48}. First-principles calculations found that the migrating Cu ions are effectively captured by the exposed Se atoms in SnSe, facilitating charge transfer between Cu and Se atoms. This effectively hinders the long-range migration of Cu ions and improves the stability of the Cu₂Se based material. These findings provide a comprehensive framework for designing high-performance, stable, and mechanically robust thermoelectric materials with superionic characteristics.

**Fig. 1: Matrix plainification in composite leads to high carrier mobility and ultrahigh ZT values.**

Results and discussions

Crystal structure and phase description

The XRD patterns of the synthesized Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se (x = 0, 1, 3, 5 and 10) are shown in Supplementary Fig. 2a. The Bragg diffraction peaks of the primary phase align well with the monoclinic α-Cu₂Se fingerprint peaks, except for the detection of the high-temperature β-Cu₂Se phase in the pristine Cu₂Se sample. Cu₂Se has two energetically similar structures under ambient condition: a monoclinic structure (α-Cu₂Se) at room temperature and a cubic structure (β-Cu₂Se) above 375 K (Supplementary Fig. 3)⁴⁹. The structural transition was evidenced by Differential Scanning Calorimeter (DSC) tests (Supplementary Fig. 4). According to the Cu-Se binary phase diagram, even a slight Cu deficiency can induce the β-Cu₂Se phase, which arises from Cu deposition during the preparation process. We can speculate that the addition of Sn_0.96Pb_0.01Zn_0.03Se during this process might hinder the migration and deposition of copper³⁶, thus preventing the appearance of the β-Cu₂Se phase. Due to the detection limits of X-ray characterization, secondary phases related to Sn_0.96Pb_0.01Zn_0.03Se are only observed at doping levels above 3%. Rietveld refinement of the X-ray diffraction data (Supplementary Fig. 5) provides precise crystallographic information, indicating minimal variation in lattice parameters (Supplementary Fig. 2b and Supplementary Table 3). X-ray photoelectron spectroscopy (XPS) was performed on the Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se sample to determine the valence states of elements. The peaks with binding energy of 932.8 eV, and 940.6 eV can be assigned to Cu⁺ (Supplementary Fig. 2c)⁵⁰. The peaks with binding energies of 486.6 eV and 495 eV can be attributed to Sn²⁺ (Supplementary Fig. 2d).

Electrical transport properties

Figure 2a presents the temperature dependence of electrical conductivity (σ) for Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se composites. Temperature-dependent σ demonstrates a degenerate semiconducting behavior, which primarily originates from intrinsic high Cu deficiency. The composites exhibit a noticeable reduction in σ as compared with the pristine Cu₂Se. The temperature-dependent carrier concentration (n) and mobility (μ) were measured and illustrated in Fig. 2b, c, respectively. It is found that the decrease of σ is attributed to a significantly reduced carrier concentration (n) after the introduction of Sn_0.96Pb_0.01Zn_0.03Se (Fig. 2b). This phenomenon can be explained by examining their work functions: Cu₂Se has a work function of 5.16 eV³⁶, while Sn_0.96Pb_0.01Zn_0.03Se has a work function of 4.38 eV (Supplementary Fig. 6). The large difference in work function would drive holes from Cu₂Se matrix to Sn_0.96Pb_0.01Zn_0.03Se secondary phase until their Fermi levels reach equilibrium (Supplementary Fig. 1), which ultimately leads to a reduction in carrier concentration. Hall mobility (μ) displays a negative correlation with carrier concentration (n) and decreases with increasing temperature (Fig. 2c). Notably, carrier mobility (μ) shows a remarkable enhancement as compared with pristine Cu₂Se in the whole investigated temperature range. At room temperature, the Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se sample achieves a remarkable carrier mobility of 33.7 cm²·V⁻¹·s⁻¹, which is about three times higher than that of pristine Cu₂Se (9.3 cm²·V⁻¹·s⁻¹). This value is significantly surpassing previously reported Cu₂Se-based composites (4.65-16.60 cm²·V⁻¹·s⁻¹)^{36,51,52,53,54,55} (Fig. 1b). At 973 K, the carrier mobility of the Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se sample reduces to 4.57 cm²·V⁻¹·s⁻¹, which is still more than four times bigger than that of the pristine Cu₂Se (1.32 cm²·V⁻¹·s⁻¹). The significantly enhanced carrier mobility facilitates electrical transport, leading to high power factor. To understand the mechanism of the large enhancement of carrier mobility in the composites, we performed a systematical analysis combining theoretical calculations and experimental characterization. First defect formation energy calculations using the density-function theory (DFT) was carried out to understand the defect behaviors in Cu₂Se (Supplementary Table 1 and Supplementary Fig. 7). Using the defect formation energies at the Cu- or Se-rich conditions, it will not change the conclusion.) It was found that the defect formation energy of Cu vacancy (V_Cu) is very low (–0.66 eV). The negative formation energy indicates the spontaneously forming Cu vacancies in the Cu₂Se matrix, which is consistent with the previously observed large amount of Cu vacancies in Cu₂Se^27,56. When Sn fills the Cu vacancy (the notation is Sn_Cu), its formation energy is low (0.73 eV) as well, suggesting that the defect can be highly formed in the Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se composites. Additionally, once the Sn_Cu defect binding with the neighboring V_Cu, it forms a complex defect (Sn_Cu+V_Cu) and its formation energy is as low as 0.07 eV, which is lower than that of Sn_Cu. Obviously, the formation of such complex defect further facilitates the Sn_Cu formation. This indicates that Sn can easily fill the Cu vacancies to plain lattice of matrix Cu₂Se in the composites. The high temperature during the SPS sintering process provides the thermodynamic and kinetic conditions for this migration of Sn atoms from the secondary phase to the Cu vacancy sites in the matrix lattice. This leads to large enhancement of carrier mobility, as evidenced by experimental results. Aberration-corrected STEM characterization provides compelling evidence that the high-density Cu vacancies in the pristine Cu₂Se matrix are filled by Sn atoms from the secondary phase (Sn_0.96Pb_0.01Zn_0.03Se) in the composite. Figures 3a–d depict atomic-resolution HAADF images of pristine Cu₂Se along two distinct zone axes, accompanied by fast Fourier transform (FFT) patterns and atomic configuration diagrams. These results precisely define the crystal structure of the room-temperature α-Cu₂Se phase. To reveal subtle distinctions in the atomic structure of the Cu₂Se matrix between pristine Cu₂Se and Cu₂Se/Sn_0.96Pb_0.01Zn_0.03Se composites, Figs. 3e–j present representative atomic-resolution HAADF images alongside quantitative analyses of individual atomic intensities. The calculation method is to divide the intensity α of Cu/Se sites by the average contrast β of the surrounding Se atoms to obtain the numerical value ϒ, and then obtain the figure using the ratio of α and the average value ϒ (ϒ_avg), in order to eliminate the effect of the sample thickness. Among them, blue and red points represent lighter/fewer and heavy/more atoms, respectively. Thus, the atomic columns that contain a large fraction of vacancies will show as blue contrast. These analyses provide precise determinations of atomic coordinates and intensity values. In pristine Cu₂Se, the Cu atoms exhibit weak intensities at various lattice sites, indicating the presence of Cu vacancies due to the intrinsic low vacancy formation energy of Cu₂Se (Fig. 3f1-f4). And Se atoms exhibit a uniform intensity distribution across all positions.

**Fig. 2: Transport properties of Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se composites.**

**Fig. 3: Vacancy characterization in pure Cu₂Se and Cu₂Se/Sn_0.96Pb_0.01Zn_0.03Se composites.**

The high density of Cu vacancies induces significant lattice distortions (Supplementary Figs. 8a–c), disrupting the regular lattice periodicity, intensifying carrier scattering, and severely impairing charge carrier mobility. Upon incorporating Sn_0.96Pb_0.01Zn_0.03Se, these Cu vacancies are effectively eliminated, as evidenced by the absence of low-intensity sites in the Cu₂Se matrix (Fig. 3g). Further magnified HAADF intensity images demonstrate that heterovalent cations with higher atomic mass have occupied the regions previously deficient in Cu (Fig. 3h1-j). Energy-dispersive X-ray spectroscopy (EDS) line scan confirms that these sites are predominantly occupied by Sn atoms originating from the Sn_0.96Pb_0.01Zn_0.03Se secondary phase (Supplementary Figs. 8d–f). The intensity statistics of individual Cu atomic columns and regional atomic planes in STEM images also confirm that the incorporation of Sn atoms from the secondary phase Sn_0.96Pb_0.01Zn_0.03Se into the Cu vacancies, leading to matrix plainification. Matrix plainification significantly boosts carrier mobility within the Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se composites through weaken carrier scattering.

The positive Seebeck coefficient (Fig. 2d) indicates the dominant p-type charge transport. Compared to pristine Cu₂Se, the composites samples exhibit enhanced Seebeck coefficients at entire temperature range due to reduced carrier concentration as indicated in Fig. 2c. At 973 K, the Seebeck coefficient increases from 168.3 μV·K^-1 for pristine Cu₂Se to 228 μV·K^-1 for Cu₂Se/3% wt. Sn_0.96Pb_0.01Zn_0.03Se. Enhanced carrier mobility and the optimized carrier concentration result in a substantial increase in power factor (PF) (Fig. 2e). The highest PF of 16.22 μW·cm^-1·K^-2 is achieved in Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se sample at 973 K. More comparisons of the PF of Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se sample with those of previously reported Cu₂Se-based thermoelectrics is presented in Supplementary Fig. 9. Significantly enhanced PF indicates that incorporation of Sn_0.96Pb_0.01Zn_0.03Se markedly optimizes electrical transport property of Cu₂Se matrix. The intrinsic electrical transport characteristics can be further evaluated by the weighted mobility (μ_w) provides a direct assessment of the intrinsic electrical transport characteristics (Fig. 2f)⁵⁷. As shown in Fig. 2f, the μ_w of our samples all displays the typical T^−1.5 dependence, indicating the metallic conducting behavior with dominant acoustic phonon scattering mechanism. The Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se sample possesses higher μ_w than other composites (x = 1, 3, and 10), reflecting its better electrical transport properties.

Thermal transport properties

Figure 2g illustrates the temperature-dependent total thermal conductivity (κ_tot) of Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se (x = 0, 1, 3, 5 and 10) composites. Introducing Sn_0.96Pb_0.01Zn_0.03Se significantly reduced the total thermal conductivity in the whole temperature range. In particular, the composite with 5 wt.% Sn_0.96Pb_0.01Zn_0.03Se exhibits lowest total thermal conductivities (κ_tot) among all investigated samples. To gain deeper insights into the exceptionally low thermal conductivity of the composites, we calculated the carrier thermal conductivity (κ_ele) (Supplementary Fig. 10a) using the Wiedemann–Franz relation κ_e = LσT, where Lorenz number (L) was calculated by a two-band model and acoustic phonon scattering (Supplementary Fig. 10b). The lattice thermal conductivity (κ_lat) was obtained by subtracting κ_ele from the total thermal conductivity (Fig. 2h). The reduction in κ_ele is primarily due to the regulation of carrier concentration and carrier mobility, optimizing electrical conductivity within a reasonable value. The κ_lat of Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se composites markedly decreases compared with that of pristine Cu₂Se. The sound velocities including both longitudinal and transverse sound velocities were measured for Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se composites (Supplementary Fig. 11). The calculated average sound velocity (v_a) and the phonon mean free path (l_ph) were illustrated in Fig. 2i. With increasing content of Sn_0.96Pb_0.01Zn_0.03Se, the average sound velocity gradually decreases, and correspondingly, the phonon mean free path decreases from 2.52 nm for pure Cu₂Se to 0.79 nm for the high-performance Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se sample. The reduction in sound velocity and phonon mean free path suggests that the incorporation of Sn_0.96Pb_0.01Zn_0.03Se induces phonon softening and enhances phonon scattering in Cu₂Se, thereby significantly reducing κ_lat.

Microstructural characterization

Scanning electron microscopy (SEM) image shows that numerous pores present in the composite (Supplementary Fig. 12), which originate from Se volatilization during sintering³⁵. Some bright domains disperse within the composite, as illustrated by the back scattered electron (BSE) image of the polished surface (Supplementary Fig. 13a). Lower magnification SEM image reveals the uniformity and dispersion of the Sn_0.96Pb_0.01Zn_0.03Se secondary phase within the Cu₂Se matrix (Supplementary Fig. 14). SEM-EDS elemental mapping (Supplementary Fig. 13b–d) confirms Sn enrichment at the domains, indicating the presence of Sn_0.96Pb_0.01Zn_0.03Se secondary phase. A line scan of the secondary phase region was also performed, and the increase in the Sn elemental intensity as well as the decrease in the Cu content prove the presence of the Sn_0.96Pb_0.01Zn_0.03Se secondary phase (Supplementary Fig. 15). Figure 4a displays a low-magnification HAADF image of the synthesized Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se composite. Micropores can be found in the sample, consistent with the SEM observation (Supplementary Fig. 12). Grains with different contrasts from the matrix were identified. STEM-EDS analysis confirmed the presence of submicron Sn_0.96Pb_0.01Zn_0.03Se grains embedded within the composite, indicating the existence of Sn_0.96Pb_0.01Zn_0.03Se (Fig. 4b). When the sample is oriented along the [10-1] zone axis of Sn_0.96Pb_0.01Zn_0.03Se (Fig. 4c, d), the atomic arrangement closely aligns with SnSe. Focused observations were carried out to investigate the interfaces between composite phase (Sn_0.96Pb_0.01Zn_0.03Se) and matrix (Cu₂Se), which reveal a prevalence of smooth, planar phase interfaces (Fig. 4e–h). These heterointerfaces exhibit atomic-scale flatness, contrasting with the commonly observed rough interfaces, and demonstrate quasi-coherence across different zone axes. Moreover, extensive nanotwins substructures were observed within both Cu₂Se and Sn_0.96Pb_0.01Zn_0.03Se grains of the synthesized composite (Fig. 4i, j). A noticeable presence of dislocations in the Cu₂Se matrix is also detected (Fig. 4k), which induce slight lattice strain (Fig. 4l). The smooth and quasi-coherent interfaces between the Sn_0.96Pb_0.01Zn_0.03Se and the Cu₂Se matrix, in contrast to traditional rough interfaces, is very beneficial for the migration of Sn ions from Sn_0.96Pb_0.01Zn_0.03Se to Cu₂Se due to the virtually nonexistent of defects and dislocations, thereby facilitating matrix plainification. Meanwhile, the smooth and quasi-coherent interfaces has minimal adverse effects on carrier transport, but cause strong phonon scattering, leading to substantial reduction of lattice thermal conductivity without carrier mobility deterioration. Statistical grain size distributions of the SnSe secondary phase derived from SEM images range from 794 nm to 4.4 μm (Supplementary Fig. 16), indicating that the SnSe secondary phase primarily facilitate the scattering of low-frequency phonons. A considerable presence of nanotwins and dislocations provide extra phonon scattering sources, which suppresses the propagation of mid- to high-frequency phonons in the Cu₂Se-SnSe composites. Ultimately, these factors lead to enhanced phonon scattering across wide range of frequencies. The strong phonon scattering was proved by the decline trend of sound velocity and phonon mean free.

Enhanced thermoelectric performance and mechanical properties

Incorporation of Sn_0.96Pb_0.01Zn_0.03Se secondary phase can efficiently enhance ZT of Cu₂Se thanks to the enhanced electrical transport properties and significantly reduced lattice thermal conductivity (Fig. 5a). A maximum ZT of 3.3 is achieved at 973 K in Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se composite, which surpasses utmost reported Cu₂Se thermoelectrics^{26,28,35,51,52,53,54,58} (Fig. 5b). This value presents the highest reported among any thermoelectric systems (Fig. 1c). Good experimental repeatability for this high ZT is achieved, which is evidenced by the reproducible results from the measurements on several samples independently prepared (Supplementary Fig. 17). Moreover, the composite material maintains its thermoelectric performance after heating-cooling cycles (Supplementary Fig. 18).

**Fig. 5: Dimensionless figure of merit ZT and mechanical properties of the Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se composites.**

Furthermore, the Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se sample exhibits better mechanical properties than pristine Cu₂Se (Fig. 5c, d). Vickers hardness and nanoindentation hardness are both improved over pristine Cu₂Se. Figure 5d illustrates the compressive strength profile of the Cu₂Se/x %wt. Sn_0.96Pb_0.01Zn_0.03Se. (x = 0, 5). The composite sample exhibits higher compressive strengths of 172.45 MPa, which is more than four times larger than that of pristine Cu₂Se (41.95 MPa). It is worth to note that the compressive strain increases from 3% for pristine Cu₂Se to 12% for Cu₂Se/5 %wt. Sn_0.96Pb_0.01Zn_0.03Se composite. Large plastic deformation is achieved in the composite, which is higher than the most of traditional thermoelectric semiconductors and ceramics (usually have compressive strain below 3%)^22,59,60,61, and closes to strain of the plastic semiconductor Ag₂Se.

This significantly enhanced plastic deformability is most likely associated with the observed high density of nanotwin boundaries in the introduced composite component (Fig. 4h, i), i.e., Sn_0.96Pb_0.01Zn_0.03Se. The nanotwin boundaries act as additional slip planes within the material, particularly in the densely twinned Sn_0.96Pb_0.01Zn_0.03Se, effectively increasing the number of active slip systems. Under applied stress, the twin boundaries facilitate slip, allowing for greater strain energy absorption. This structural modification consequently leads to a remarkable enhancement in plasticity, which is attributed to the material’s enhanced capacity to sustain greater plastic strain prior to fracture. In the composite, the presence of high-density nanotwins in Sn_0.96Pb_0.01Zn_0.03Se grains are also likely to play a pivotal role in enhancing dislocation mobility. These nanotwin boundaries act as efficient sites for dislocation nucleation and propagation, reducing the energy barrier for slip and providing a pathway for dislocation migration through the material. The increased dislocation mobility leads to a more pronounced plastic response under compressive stress, allowing the composite to deform more easily. Additionally, these dense nanotwins effectively refine the microstructural characteristic size of the material, resulting in a hardening effect. This hardening is typically accompanied by an enhanced ability of the material to withstand higher stresses without fracturing, thereby exhibiting greater compressive strain. Moreover, the high-density nanotwin boundaries in Sn_0.96Pb_0.01Zn_0.03Se grains are likely to facilitate stress relaxation in the heterointerfaces between Cu₂Se and Sn_0.96Pb_0.01Zn_0.03Se, creating efficient stress transfer zones. These zones help dissipate applied stress more uniformly throughout the composite, preventing localized strain accumulation and mitigating the risk of interfacial delamination or fracture. Collectively, the high-density nanotwins in Sn_0.96Pb_0.01Zn_0.03Se, combined with the reinforcing effect at these interfaces, empower the material to endure higher compressive stresses without localized fracture or slip, thus substantially enhancing the overall compressive strain of the composites. The significantly enhanced plasticity grants the material with large deformability, processibility, and machinability, which increases the impact resistance of thermoelectric components, thus significantly increasing their service life⁵⁹. The discovered composite with large plasticity has great potential in flexible thermoelectric technology. This work sheds light to advance highly effective thermoelectric materials.

Stability test

We conducted a detailed investigation into the stability of Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se composite. Thermogravimetric analysis (TGA) was performed to assess the thermal stability of the material (Supplementary Fig. 19), and the results indicated negligible weight loss over a wide temperature range, confirming that elemental volatilization is negligible. Further compositional analysis before and after thermoelectric property measurements at high temperature provided evidence for the enhanced stability of the composites. The pristine Cu₂Se sample exhibits pronounced Cu enrichment on its surface due to the intrinsic long-range migration of Cu ions after thermoelectric property measurements at high temperature (Supplementary Fig. 20a). Stoichiometric changes in pristine Cu₂Se after thermoelectric properties measurements were evidenced by SEM-EDS analysis. In contrast, much less Cu enrichment on the composite sample surface and at least less alterations in the composition are observed after thermoelectric properties measurements (Supplementary Fig. 20b), indicating its stability is enhanced. SEM investigation reveals that the microstructural integrity of the synthesized Cu₂Se/5 wt.%Sn_0.96Pb_0.01Zn_0.03Se composite material was effectively preserved after thermoelectric measurements (Supplementary Fig. 14). XRD analysis reveals that the pure sample undergoes stoichiometric changes due to Cu loss of the matrix, which facilitates the formation of β-Cu₂Se after thermoelectric properties measurements (Supplementary Fig. 21a), whilst the composite samples almost maintain consistent phase components after the testing process (Supplementary Fig. 21b). To evaluate the stability under real operational conditions, we subjected the sample to simultaneous current field and temperature gradient field (Fig. 6a, b). A pulsed current with a maximum current density of 25 A/cm² was applied (Fig. 6c), and the relative resistance of the sample was monitored for up to ∼333 min. As shown in Fig. 6e, the relative resistance of pristine Cu₂Se exhibits a steep increase with test time, indicating substantial Cu ions migration and subsequent accumulation at the interface, which significantly affects the resistance³¹. In contrast, the relative resistance of the composite containing x = 5 wt.% Sn_0.96Pb_0.01Zn_0.03Se exhibits less variations under the same conditions, suggesting that the addition of Sn_0.96Pb_0.01Zn_0.03Se effectively hinders the long-range migration of Cu ions and improves the stability of the Cu₂Se based material. After repeated tests, the thermoelectric properties of pristine Cu₂Se sample could not remain stable, and the electrical conductivity declines (Supplementary Fig. 22). We tested the thermoelectric properties of the material after annealing at 973 K for ∼333 min to further evaluate the long-term performance and stability of the sample at high temperature. As shown in Supplementary Fig. 23, the results show that the synthesized Cu₂Se/SnSe composites almost maintains electrical transport performance under high-temperature conditions. To further demonstrate the enhanced stability of Cu₂Se/SnSe composites, cyclic tests were conducted within the temperature range of 300 K-973 K. For Cu₂Se/SnSe, the electrical properties show negligible fluctuation after three cycles, as shown in Supplementary Fig. 24. This further indicates that the composites exhibit enhanced stability. First-principles calculations was conducted to delve deeper into the mechanism why Sn_0.96Pb_0.01Zn_0.03Se suppresses the migration of Cu ions in Cu₂Se. Charge density difference analysis reveals a strong interaction between Cu ions and Se atoms in SnSe upon Cu ions migrate at elevated temperatures (Fig. 6g). Specifically, the migrating Cu ions are effectively captured by the exposed Se atoms in SnSe, facilitating charge transfer between Cu and Se atoms. This interaction leads to bonding between Cu and Se atoms, which plays a crucial role in inhibiting the long-range migration of Cu ions in the Cu₂Se matrix. The secondary phase thus acts as a stabilizing agent, preventing the migration of Cu ions and thereby enhancing the stability of the composite material. The improved stability is essential for extending the service lifetime of thermoelectric materials.

In conclusion, we show that the mechanism for increased performance and stability is through Cu vacancies in matrix Cu₂Se being filled by Sn atoms of secondary phase, leading to matrix plainification. Moreover, a more optimized carrier concentration can be achieved through the large difference in different work functions between matrix Cu₂Se and the Sn_0.96Pb_0.01Zn_0.03Se secondary phase, contributing to enhanced Seebeck coefficient. The sharp increase of carrier mobility and Seebeck coefficient contribute to substantial increase in power factor. Strong phonon scattering is induced by a prevalence of smooth and quasi-coherent interfaces, which greatly reduces lattice thermal conductivity without carrier mobility deterioration. Ultimately, an unprecedented high ZT value of 3.3 is achieved at 973 K in Cu₂Se/5 wt.% Sn_0.96Pb_0.01Zn_0.03Se composite. Notably, high-density nanotwins in the composite significantly enhance plasticity (compressive strain of 12%). The high plasticity grants the material with large deformability, processibility, and machinability, which significantly increasing their service life and has great potential in flexible thermoelectrics. We simultaneously improve the stability of Cu₂Se due to inhibition the long-range migration of Cu ions by through bonding through introducing the Sn_0.96Pb_0.01Zn_0.03Se secondary phase. These findings pave the way for designing of high-performance, stable, and durable liquid-like thermoelectric materials.

Methods

Sample preparation

A series of polycrystalline Cu₂Se/Sn_0.96Pb_0.01Zn_0.03Se samples were synthesized in two steps by melting and hydrothermal methods. Stoichiometric high-purity raw elements Cu powders (shots, 99.999%, Alfa Aesar), Se powders (pieces, 99.999%, Alfa Aesar) were weighted in stoichiometric ratio and mix well by hand grinding for 30 min in a mortar. Then the mixture was vacuum sealed in quartz tubes. The sealed tubes were slowly raised to 1423 K within 10 h and held at this temperature for 12 h, followed by a cooling process for 50 h down to 923 K. Finally, after holding at 923 K for 7 days, the sealed tubes were naturally cooled to room temperature. The obtained ingot was ground by hand in a mortar for 1 h to obtain Cu₂Se powder. Sn_0.96Pb_0.01Zn_0.03Se powder was carried out through a hydrothermal method. SnCl₂‧2H₂O (99.99%, Aladdin), PbCl₂ (99.99%, Aladdin), ZnCl₂ powder (99.99%, Aladdin), Se powder (99.99%, Aladdin), and NaOH (98%, Aladdin) were used as raw materials to prepare SnSe powders and detailed methods were in our previously reported literature⁴⁰. The Cu₂Se and Sn_0.96Pb_0.01Zn_0.03Se powders were weighed in mass ratio and mixed in a mortar for half an hour. The mixture was then subjected to spark plasma sintering (SPS, Sumitomo SPS-2040) and sintered at 50 MPa and 923 K for 5 min.

Structural characterization

The crystal structure of synthesized Cu₂Se/x wt.% Sn_0.96Pb_0.01Zn_0.03Se composites was examined by powder X-ray diffraction (Bruker D8 Advance) with Cu Kα radiation and a scanning step size of 0.02°. The structural morphology of samples were characterized using a scanning electron microscope (SEM, FEI Quanta 250 FEG) equipped with energy-dispersive X-ray spectroscopy (EDS). The grain size of SnSe secondary phase was obtained by intercept method·from·200 grains in multiple SEM images. The Differential Scanning Calorimeter (DSC) was determined on DSC2500 under a N₂ flow during heating at a rate of 5 K/min. An X-ray photoelectron spectroscopy (XPS) instrument (Krayos AXIS Ultra DLD) was used to analysis the valence of element. The valences of element Cu and Sn were measured using X-ray photoelectron spectroscopy (XPS) on a Krayos AXIS Ultra DLD instrument. High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM), and EDS investigations were performed at an aberration-corrected scanning transmission electron microscopy (STEM, JEM-ARM300F2) with a 300 kV accelerating voltage.

Mechanical properties

Prior to the hardness test, the surface of the sample is first polished to a mirror finish. The Vickers hardness (H_V) was measured with a microhardness tester (KB 30 BVZ, Prüftechnik GmbH) under loads of 0.98 N. The microhardness images were measured using a nanoindenter (G200). Compressive strength was tested with a tensile/compressive system (SANS, UTM/CMT 5000).

Stability test

Stability tests were measured by our homemade TEG test system. In the testing process, the hot and cold end of a TEG are respectively controlled by the heating plate and water-cooling plate. An electronic load meter and a multi-channel temperature tester were utilized to measure the output power and temperatures, while the resistance of the TEG can be derived by utilizing the open-circuit voltage, the closed-loop voltage, and the current. The TEG under test consists of 17 pairs of P-type/N-type TE legs. P-type TE legs are prepared Cu₂Se/5 % Sn_0.96Pb_0.01Zn_0.03Se compositions and N-type TE legs are commercially available Bi₂Te₃-based TE material. All the TE legs are cut into a size of 1.5 × 1.5 mm² in cross-section and 4.0 mm in length. Thermogravimetric curves were measured by simultaneous thermal analysis (TGA/DSC3 + ) in an argon atmosphere.

Theoretical calculations

The formation energy was performed using the Fritz Haber Institute ab initio materials simulations (FHI-aims) with the all-electron numeric atomic-centered basis functions⁶². The basis set with the 2020 species defaults are used for atoms, and the generalized gradient approximation of Perdew, Burke, and Ernzerhof (GGA-PBE) is for the exchange-correlation functional⁶³. The defect formation energy (E_f) calculations using:

$${E}_{f}=E\left( defect \right)-E\left( perfect \right)+{\sum}_{i}{n}_{i}{{{\rm{\mu }}}}_{i}$$

(1)

where E(defect) and E(perfect) are the total energies of cells with and without defects, respectively. The integer n_i represents the number of type i atoms that have been added to (n_i > 0) or removed from (n_i < 0) the cell. μ_i is the chemical potential of added or removed atom i. Based on the experimental observed Cu₂Se/SnSe composite, we further consider the constrains in formation the Cu₂Se matrix either Cu or Se rich conditions. At such environment, we can achieve the chemical potential of each element by solving the following equations. At the Cu-rich condition,

$${\mu }_{{\rm{{Cu}}}}=E({{\rm{C}}}u)$$

$$2{{\mu }}_{Cu}+{{\mu }}_{Se}=E({{{\rm{Cu}}}}_{2}{{\rm{Se}}})$$

$${\mu }_{Sn}+{\mu }_{Se}=E({{\rm{SnSe}}})$$

where E(Cu), E(SnSe) and E(Cu₂Se) are the total energies of bulk Cu, SnSe and Cu₂Se compounds, respectively.

At the Se-rich condition,

$${\mu }_{Se}=E({{\rm{Se}}})$$

$$2{\mu }_{Cu}+{\mu }_{Se}=E({{{\rm{Cu}}}}_{2}{{\rm{Se}}})$$

$${\mu }_{Sn}+{\mu }_{Se}=E({{\rm{SnSe}}})$$

where E(Se) is the total energies of bulk Se.

The charge density difference was investigated based on the Cambridge sequential total energy package (CASTEP) code⁶⁴. GGA-PBE is used to describe the electronic exchange–correlation energy function.

Transport property measurement

Both the electrical and thermal transport properties of all samples were measured perpendicular to the pressing direction. Rectangular bulks (3 × 3 × 8 mm³) and disks (ϕ 6 mm × 1.2 mm) were cut from the SPS pellets for electrical and thermal transport measurements, respectively. The electrical conductivity (σ) and Seebeck coefficient (S) were measured on a commercial system (Ulvac-Riko ZEM-3). The thermal diffusion coefficient D was measured by Netzsch LFA-457 instrument under argon atmosphere. The specific heat (C_p) was taken from the ref. ³⁰. The density (ρ) (Supplementary Table 2) was measured through the Archimedes’ method. Then the total thermal conductivity was calculated based on the formula κ_tot = D C_p ρ. Carrier concentration (n) and carrier mobility (μ) were obtained using a Hall measurement instrument (HMS-3000). The uncertainty of the Seebeck coefficient, electrical conductivity, thermal diffusion, specific heat capacity, and density error involved in calculating ZT is close to 20%. The longitudinal sound velocity (v_l) and shear sound velocity (v_s) were measured via an advanced ultrasonic material characterization system (UMS-100, France).

The calculation of Lorenz number

The Lorenz number is obtained according to the two-band model and acoustic phonon scattering:

$$\delta {L}_{lh}={\left(\frac{{\kappa }_{B}}{e}\right)}^{2}\left[\frac{{{}^{2}F}_{-2}^{1}\left(\eta,\alpha \right)}{{{}^{0}F}_{-2}^{1}\left(\eta,\alpha \right)}-{\left(\frac{{{}^{2}F}_{-2}^{1}\left(\eta,\alpha \right)}{{{}^{0}F}_{-2}^{1}\left(\eta,\alpha \right)}\right)}^{2}\right]$$

(2)

and

$$\delta {L}_{lh}={\left(\frac{{\kappa }_{B}}{e}\right)}^{2}\left[\frac{{{}^{2}F}_{-2}^{1}\left(\eta -\varDelta \nu,0\right)}{{{}^{0}F}_{-2}^{1}\left(\eta -\varDelta \nu,0\right)}-{\left(\frac{{{}^{2}F}_{-2}^{1}\left(\eta -\varDelta \nu,0\right)}{{{}^{0}F}_{-2}^{1}\left(\eta -\varDelta \nu,0\right)}\right)}^{2}\right]$$

(3)

In the above equations, the integral ${{}^{n}F}_{l}^{m}$ is defined by

$${}^{n}F_{l}^{m}={\int }_{\!\!\!\!0}^{\infty }-\frac{\partial f}{\partial {{\rm{\varepsilon }}}}{{{\rm{\varepsilon }}}}^{n}{\left({{\rm{\varepsilon }}}+\partial {{{\rm{\varepsilon }}}}^{2}\right)}^{m}{\left[{\left(1+2\partial {{\rm{\varepsilon }}}\right)}^{2}+2\right]}^{\frac{1}{2}}d{{\rm{\varepsilon }}}$$

(4)

Where ${L}_{lh}$ and ${L}_{{hh}}$ are the $L$ of light-hole band and heavy-hole band, respectively, $\alpha$ is the nonparabolic parameter obtained by the formula $\alpha={k}_{B}T/{E}_{g}$, $\eta$ is the reduced chemical potential evaluated by $\eta={E}_{f}/{k}_{B}T$, and ${{}^{n}F}_{l}^{m}$ is the generalized Fermi function. We set $\alpha=0$ and replace $\eta$ with $\eta -\varDelta \nu$ in equation for the second valence band, where $\varDelta \nu=\varDelta E/{k}_{B}T$, $\varDelta E$ is the energy difference between the first and second valence band. The total $L$ can be calculated by the following equation:

$${L}_{{total}}=\frac{\left({\sigma }_{lh}{L}_{lh}+{\sigma }_{{hh}}{L}_{{hh}}\right)}{\left({\sigma }_{lh}+{\sigma }_{{hh}}\right)}$$

(5)

Weighted mobility calculation in detail

Weighted mobility (μ_w) can be calculated based on the availability of combined electrical conductivity and Seebeck coefficient according to the following equation:

$${\mu }_{W}=\frac{3{h}^{3}\sigma }{8\pi e{\left({2m}_{e}{k}_{B}T\right)}^{3/2}}\left[\frac{exp \left[\frac{\left|S\right|}{{k}_{B}/e}-2\right]}{1+exp \left[-5\frac{\left|S\right|}{{k}_{B}/e}-1\right]}+\frac{\frac{3}{{\pi }^{2}}\left[\frac{\left|S\right|}{{k}_{B}/e}\right]}{1+exp \left[5\frac{\left|S\right|}{{k}_{B}/e}-1\right]}\right]$$

(6)

where T is the absolute temperature, k_B is the Boltzmann constant, e is the electron charge, h is the Planck constant, and m_e is the electron mass, respectively.

Sound velocity calculation

The longitudinal sound velocity (v_l) and transverse sound velocity (v_t) were measured at room temperature via an advanced ultrasonic material characterization system (UMS-100, France). The average sound velocity (v_a), Poisson ratio (r) and phonon mean free path (l_ph) were calculated as follows,

$${v}_{a}={\left[\frac{1}{3}\left(\frac{1}{{v}_{l}^{3}}+\frac{1}{{v}_{t}^{3}}\right)\right]}^{-\frac{1}{3}}$$

(7)

$$r=\frac{1-2(vt/{{v}_{l}})^{2}}{2-2(vt/{{v}_{l}})^{2}}$$

(8)

$${l}_{ph}=\frac{3{\kappa }_{L}}{{C}_{p}\rho {v}_{a}}$$

(9)

Data availability

The authors declare that all data supporting the findings of this study are available within the article and its Supplementary Information files or from the corresponding author.

References

Bell, L. E. Cooling, Heating, Generating Power,and Recovering Waste Heat with Thermoelectric Systems. Science 321, 1457–1461 (2008).
Article ADS CAS PubMed MATH Google Scholar
He, J. et al. Advances in thermoelectric materials research: Looking back and moving forward. Science 357, 1369 (2017).
Article CAS MATH Google Scholar
Xiao, B. Y. et al. Seeking new, highly effective thermoelectrics. Science 367, 1196–1197 (2020).
Article ADS CAS PubMed MATH Google Scholar
Zhao, L. D. et al. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 508, 373–377 (2014).
Article ADS CAS PubMed MATH Google Scholar
Zhang, X. et al. Thermoelectric materials: Energy conversion between heat and electricity. J. Materiomics 1, 92–105 (2015).
Article MATH Google Scholar
Chang, C. et al. Anharmoncity and low thermal conductivity in thermoelectrics. Mater. Today Phys. 4, 50–57 (2018).
Article MATH Google Scholar
Case, E. D. Thermal Fatigue and Waste Heat Recovery via Thermoelectrics. J. Electron. Mater. 41, 1811–1819 (2012).
Article ADS CAS MATH Google Scholar
Snyder, G. J. et al. Complex thermoelectric materials. Nat. Mater. 7, 105–114 (2008).
Article ADS CAS PubMed MATH Google Scholar
Zhu, T. et al. Compromise and Synergy in High-Efficiency Thermoelectric Materials. Adv. Mater. 29, 1605884 (2017).
Article Google Scholar
Pei, Y. et al. Stabilizing the optimal carrier concentration for high thermoelectric efficiency. Adv. Mater. 23, 5674–5678 (2011).
Article CAS PubMed MATH Google Scholar
Liu, W.-D. et al. Kinetic condition driven phase and vacancy enhancing thermoelectric performance of low-cost and eco-friendly Cu_2−xS. J. Mater. Chem. C. 7, 5366–5373 (2019).
Article ADS CAS MATH Google Scholar
He, Y. et al. High thermoelectric performance in non-toxic earth-abundant copper sulfide. Adv. Mater. 26, 3974–3978 (2014).
Article CAS PubMed MATH Google Scholar
Zhao, L.-D. et al. The panoscopic approach to high performance thermoelectrics. Energy Environ. Sci. 7, 251–268 (2014).
Article CAS MATH Google Scholar
Zhou, C. et al. High-Performance n-Type PbSe-Cu₂Se Thermoelectrics through Conduction Band Engineering and Phonon Softening. J. Am. Chem. Soc. 140, 15535–15545 (2018).
Article CAS PubMed Google Scholar
Liu, Y. et al. Improved Solubility in Metavalently Bonded Solid Leads to Band Alignment, Ultralow Thermal Conductivity, and High Thermoelectric Performance in SnTe. Adv. Funct. Mater. 32, 2209980 (2022).
Article CAS Google Scholar
Deng, R. et al. High thermoelectric performance in Bi_0.46Sb_1.54Te₃ nanostructured with ZnTe. Energy Environ. Sci. 11, 1520–1535 (2018).
Article CAS MATH Google Scholar
Tan, G. et al. High thermoelectric performance of p-type SnTe via a synergistic band engineering and nanostructuring approach. J. Am. Chem. Soc. 136, 7006–7017 (2014).
Article CAS PubMed MATH Google Scholar
Zhang, Q. et al. Achieving Ultralow Lattice Thermal Conductivity and High Thermoelectric Performance in GeTe Alloys via Introducing Cu₂Te Nanocrystals and Resonant Level Doping. ACS Nano 15, 19345–19356 (2021).
Article CAS PubMed Google Scholar
Zhao, L. D. et al. High thermoelectric performance via hierarchical compositionally alloyed nanostructures. J. Am. Chem. Soc. 135, 7364–7370 (2013).
Article CAS PubMed Google Scholar
Wu, H. J. et al. Broad Temperature Plateau for Thermoelectric Figure of Merit ZT > 2 in Phase-Separated PbTe_0.7S_0.3. Nat. Commun. 5, 4515 (2014).
Article ADS CAS PubMed MATH Google Scholar
Tang, G. et al. Realizing High Figure of Merit in Phase-Separated Polycrystalline Sn_1–xPb_xSe. J. Am. Chem. Soc. 138, 13647–13654 (2016).
Article CAS PubMed MATH Google Scholar
Zhao, P. et al. Plasticity in single-crystalline Mg₃Bi₂ thermoelectric material. Nature 631, 777–782 (2024).
Article CAS PubMed MATH Google Scholar
Biswas, K. et al. High Performance Bulk Thermoelectrics with All-Scale Hierarchical Architectures. Nature 489, 414–418 (2012).
Article ADS CAS PubMed MATH Google Scholar
Zheng, Y. Y. et al. Extraordinary Thermoelectric Performance in MgAgSb Alloy with Ultralow Thermal Conductivity. Nano Energy 59, 311–320 (2019).
Article CAS MATH Google Scholar
Gong, Y. et al. Realizing the high thermoelectric performance of highly preferentially oriented SnSe based nanorods via band alignment. Energy Environ. Sci. 17, 1612–1623 (2024).
Article CAS MATH Google Scholar
Hu, H. et al. Highly stabilized and efficient thermoelectric copper selenide. Nat. Mater. 23, 527–534 (2024).
Article ADS CAS PubMed MATH Google Scholar
Zhang, Z. et al. Cu2Se-Based liquid-like thermoelectric materials: looking back and stepping forward. Energy Environ. Sci. 13, 3307–3329 (2020).
Article CAS MATH Google Scholar
Zhou, Z. et al. Compositing effects for high thermoelectric performance of Cu₂Se-based materials. Nat. Commun. 14, 2410 (2023).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Liu, W. D. et al. Promising and Eco-Friendly Cu₂X-Based Thermoelectric Materials: Progress and Applications. Adv. Mater. 32, e1905703 (2020).
Article PubMed Google Scholar
Qiu, P. et al. Suppression of atom motion and metal deposition in mixed ionic electronic conductors. Nat. Commun. 9, 2910 (2018).
Article ADS PubMed PubMed Central MATH Google Scholar
Qiu, P. et al. High-Efficiency and Stable Thermoelectric Module Based on Liquid-Like Materials. Joule 3, 1538–1548 (2019).
Article CAS MATH Google Scholar
Yan, Q. et al. High-performance thermoelectrics and challenges for practical devices. Nat. Mater. 21, 503–513 (2022).
Article ADS CAS PubMed MATH Google Scholar
Liu, H. et al. Copper ion liquid-like thermoelectrics. Nat. Mater. 11, 422–425 (2012).
Article ADS PubMed MATH Google Scholar
Liao, W.-W. et al. Realizing Bi-doped α-Cu₂Se as a promising near-room-temperature thermoelectric material. Chem. Eng. J. 371, 593–599 (2019).
Article CAS Google Scholar
Yu, J. et al. Interface‐Enhanced High‐Temperature Thermoelectricity in Cu_1.99Se/B₄C Composites with Synergistically Improved Mechanical Strength. Adv. Energy Mater. 14, 2303942 (2024).
Article CAS Google Scholar
Yang, D. et al. Blocking Ion Migration Stabilizes the High Thermoelectric Performance in Cu₂Se Composites. Adv. Mater. 32, e2003730 (2020).
Article PubMed Google Scholar
Song, C. et al. Employing multi-functional SnSe inclusions to boost the thermoelectric performance of the shear-exfoliated Bi₂Te_2.7Se_0.3. Acta Mater. 254, 119023 (2023).
Article CAS Google Scholar
Chang, C. et al. 3D charge and 2D phonon transports leading to high out-of-plane ZT in n-type SnSe crystals. Science 360, 778–782 (2018).
Article CAS PubMed MATH Google Scholar
Liu, D. et al. Lattice plainification advances highly effective SnSe crystalline thermoelectrics. Science 380, 841–846 (2023).
Article ADS CAS PubMed Google Scholar
Liu, J. et al. Achieving high thermoelectric performance with Pb and Zn codoped polycrystalline SnSe via phase separation and nanostructuring strategies. Nano Energy 53, 683–689 (2018).
Article CAS MATH Google Scholar
Fu, C. et al. Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials. Nat. Commun. 6, 8144 (2015).
Article ADS PubMed MATH Google Scholar
Ahmad, A. et al. Largely enhanced thermoelectric performance in p-type Bi2Te3-based materials through entropy engineering. Energy Environ. Sci. 17, 695–703 (2024).
Article CAS MATH Google Scholar
Shi, X. et al. Multiple-filled skutterudites: high thermoelectric figure of merit through separately optimizing electrical and thermal transports. J. Am. Chem. Soc. 133, 7837–7846 (2011).
Article CAS PubMed MATH Google Scholar
Li, F. et al. Rare three-valence-band convergence leading to ultrahigh thermoelectric performance in all-scale hierarchical cubic SnTe. Energy Environ. Sci. 17, 158–172 (2024).
Article MATH Google Scholar
Wang, L. et al. High-performance Mg(3)Sb(2)-based thermoelectrics with reduced structural disorder and microstructure evolution. Nat. Commun. 15, 6800 (2024).
Article CAS PubMed PubMed Central MATH Google Scholar
Zhu, Y. et al. Breaking the sodium solubility limit for extraordinary thermoelectric performance in p-type PbTe. Energy Environ. Sci. 15, 3958–3967 (2022).
Article CAS MATH Google Scholar
Jiang, B. et al. High figure-of-merit and power generation in high-entropy GeTe-based thermoelectrics. Science 377, 1–6 (2022).
Article MATH Google Scholar
Kim, T. et al. SnSe: The rise of the ultrahigh thermoelectric performance material. Bull. Korean Chem. Soci. 45, 186–199 (2024).
Article CAS MATH Google Scholar
Gulay, L. et al. Crystal structure of Cu₂Se. Chem. Met. Alloy. 4, 200–205 (2011).
Article MATH Google Scholar
Yu, J. et al. Thermoelectric properties of copper-deficient Cu_2-xSe (0.05 ≤ x ≤ 0.25) binary compounds. Ceram. Int. 43, 11142–11148 (2017).
Article CAS MATH Google Scholar
Olvera, A. A. et al. Partial indium solubility induces chemical stability and colossal thermoelectric figure of merit in Cu₂Se. Energy Environ. Sci. 10, 1668–1676 (2017).
Article CAS MATH Google Scholar
Li, M. et al. Ultra-high thermoelectric performance in graphene incorporated Cu2Se: Role of mismatching phonon modes. Nano Energy 53, 993–1002 (2018).
Article CAS MATH Google Scholar
Lei, J. et al. High thermoelectric performance in Cu₂Se superionic conductor with enhanced liquid-like behaviour by dispersing SiC. J. Mater. Chem. A 7, 7006–7014 (2019).
Article CAS MATH Google Scholar
Nunna, R. et al. Ultrahigh thermoelectric performance in Cu₂Se-based hybrid materials with highly dispersed molecular CNTs. Energy Environ. Sci. 10, 1928–1935 (2017).
Article CAS MATH Google Scholar
Yang, L. et al. Te-Doped Cu₂Se nanoplates with a high average thermoelectric figure of merit. J. Mater. Chem. A 4, 9213–9219 (2016).
Article CAS MATH Google Scholar
Zhao, K. et al. Enhanced Thermoelectric Performance through Tuning Bonding Energy in Cu₂Se_1–xS_x Liquid-like Materials. Chem. Mater. 29, 6367–6377 (2017).
Article CAS MATH Google Scholar
Snyder, G. J. et al. Weighted Mobility. Adv. Mater. 32, 2001537 (2020).
Article CAS Google Scholar
Hu, H. et al. Chemical bond engineering toward extraordinary power factor and service stability in thermoelectric copper selenide. Joule 8, 416–429 (2024).
Article CAS MATH Google Scholar
Chen, J. et al. Simultaneously enhanced strength and plasticity of Ag₂Se-based thermoelectric materials endowed by nano-twinned CuAgSe secondary phase. Acta Mater. 220, 117335 (2021).
Article CAS MATH Google Scholar
Qiu, J. et al. 3D Printing of highly textured bulk thermoelectric materials: mechanically robust BiSbTe alloys with superior performance. Energy Environ. Sci. 12, 3106–3117 (2019).
Article CAS MATH Google Scholar
Guo, F. et al. Ultrahigh Thermoelectric Performance in Environmentally Friendly SnTe Achieved through Stress‐Induced Lotus‐Seedpod‐Like Grain Boundaries. Adv. Funct. Mater. 31, 2101554 (2021).
Article ADS CAS Google Scholar
Blum, V. et al. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 180, 2175–2196 (2009).
Article ADS CAS MATH Google Scholar
Perdew, J. P. et al. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Article ADS CAS PubMed MATH Google Scholar
Segall, M. D. et al. First-principles simulation: ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 14, 2717 (2002).
Article ADS CAS MATH Google Scholar

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 52071182 to G.D.T., 52202049 to P.Y., 52472250 and 52172128 to H.J.W.), the National Key R&D Program of China (2021YFB3201100 to H.J.W.), “Qinglan Project” of the Young and Middle aged Academic Leader of Jiangsu Province (to G.D.T.), the Fundamental Research Funds for the Central Universities (No. 30921011107 to G.D.T., 30924010206 to P.Y.), the program of “Distinguished Expert of Taishan Scholar” (No. tstp20221124 to Y.S.Z.). The authors thank the Instrument Analysis Center of Xi’an Jiaotong University for the assistance of aberration-corrected STEM.

Author information

These authors contributed equally: Pan Ying, Qingyang Jian.

Authors and Affiliations

School of Materials Science and Engineering, Nanjing University of Science and Technology, Nanjing, 210094, China
Pan Ying, Qingyang Jian, Yaru Gong, Yang Geng, Yanan Li, Wei Dou, Congmin Liang, Yuqi Liu, Deshang Xiang, Tao Feng & Guodong Tang
State Key Laboratory for Mechanical Behavior of Materials, Xi’an Jiaotong University, Xi’an, China
Tong Song, Yuxuan Yang & Haijun Wu
Center for High Pressure Science (CHiPS), State Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao, 066004, China
Junquan Huang, Rongxin Sun, Chen Chen & Tao Shen
Advanced Research Institute of Multidisciplinary Sciences, Qufu Normal University, Qufu, Shandong Province, 273165, China
Xiaoyu Fei & Yongsheng Zhang
School of Mechanical and Power Engineering, Nanjing Tech University, Nanjing, 211816, China
Kun Song
Electronic Materials Research Laboratory (Key Lab of Education Ministry), School of Electronic and Information Engineering, and Instrumental Analysis Center, Xi’an Jiaotong University, Xi’an, 710049, China
Yang Zhang

Authors

Pan Ying
View author publications
Search author on:PubMed Google Scholar
Qingyang Jian
View author publications
Search author on:PubMed Google Scholar
Yaru Gong
View author publications
Search author on:PubMed Google Scholar
Tong Song
View author publications
Search author on:PubMed Google Scholar
Yuxuan Yang
View author publications
Search author on:PubMed Google Scholar
Yang Geng
View author publications
Search author on:PubMed Google Scholar
Junquan Huang
View author publications
Search author on:PubMed Google Scholar
Rongxin Sun
View author publications
Search author on:PubMed Google Scholar
Chen Chen
View author publications
Search author on:PubMed Google Scholar
Tao Shen
View author publications
Search author on:PubMed Google Scholar
Yanan Li
View author publications
Search author on:PubMed Google Scholar
Wei Dou
View author publications
Search author on:PubMed Google Scholar
Congmin Liang
View author publications
Search author on:PubMed Google Scholar
Yuqi Liu
View author publications
Search author on:PubMed Google Scholar
Deshang Xiang
View author publications
Search author on:PubMed Google Scholar
Tao Feng
View author publications
Search author on:PubMed Google Scholar
Xiaoyu Fei
View author publications
Search author on:PubMed Google Scholar
Yongsheng Zhang
View author publications
Search author on:PubMed Google Scholar
Kun Song
View author publications
Search author on:PubMed Google Scholar
Yang Zhang
View author publications
Search author on:PubMed Google Scholar
Haijun Wu
View author publications
Search author on:PubMed Google Scholar
Guodong Tang
View author publications
Search author on:PubMed Google Scholar

Contributions

G.D.T. conceived and supervised the project. G.D.T., P.Y., H.J.W. and Q.Y.J. designed and carried out the experiments, analyzed the results, and wrote the paper. Q.Y.J. and Y.R.G. carried out the XRD, XPS experiments and electrical property measurements. C.C. and T.Shen measured the thermal transport properties. T.Song, R.X.S., Y.X.Y., J.Q.H., Y.Z., and H.J.W. conducted the microstructural characterization. P.Y. X.Y.F., and Y.S.Z. carried out the DFT calculations. T.F. performed the mechanical property measurements. K.S. performed the TEG fabrication and measured the stability. Y.G. and Y.N.L. helped with some of the charts. W.D. and Y.Q.L. helpfully provides certain formulas for calculations. C.M.L. and D.S.X. helped sinter the samples. All authors analyzed the results and coedited the manuscript.

Corresponding authors

Correspondence to Haijun Wu or Guodong Tang.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Taras Parashchuk, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Transparent Peer Review file

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Ying, P., Jian, Q., Gong, Y. et al. Matrix plainification leads to high thermoelectric performance in plastic Cu₂Se/SnSe composites. Nat Commun 16, 3305 (2025). https://doi.org/10.1038/s41467-025-58484-0

Download citation

Received: 30 December 2024
Accepted: 21 March 2025
Published: 07 April 2025
DOI: https://doi.org/10.1038/s41467-025-58484-0

Subjects

Abstract

Similar content being viewed by others

Compositing effects for high thermoelectric performance of Cu2Se-based materials

Crystal symmetry modification enables high-ranged in-plane thermoelectric performance in n-type SnSe crystals

Prediction of high thermoelectric performance in the low-dimensional metal halide Cs3Cu2I5

Introduction

Results and discussions

Crystal structure and phase description

Electrical transport properties

Thermal transport properties

Microstructural characterization

Enhanced thermoelectric performance and mechanical properties

Stability test

Methods

Sample preparation

Structural characterization

Mechanical properties

Stability test

Theoretical calculations

Transport property measurement

The calculation of Lorenz number

Weighted mobility calculation in detail

Sound velocity calculation

Data availability

References

Acknowledgements

Author information

Authors and Affiliations

Contributions

Corresponding authors

Ethics declarations

Competing interests

Peer review

Peer review information

Additional information

Supplementary information

Supplementary Information

Transparent Peer Review file

Rights and permissions

About this article

Cite this article

Share this article

Search

Quick links

Compositing effects for high thermoelectric performance of Cu₂Se-based materials

Prediction of high thermoelectric performance in the low-dimensional metal halide Cs₃Cu₂I₅