Introduction

Parkinson’s disease (PD) is a complex neurodegenerative disease characterized by pronounced motor symptoms, including bradykinesia, rigidity, and tremor1,2, whose neural basis is believed to be abnormal neuronal activity in the cortico-basal ganglia-thalamic circuit (CBTC) induced by dopamine depletion3,4,5. Deep brain stimulation (DBS) targeted on the subthalamic nucleus (STN) has become a standard clinical regimen, effectively suppressing these motor symptoms6. However, the mechanism underlying the STN-DBS regulating the abnormal CBTC deserves to be further explored7. A large number of researchers strive to explore the DBS mechanism based on physiological and physical models8,9, however, there is often a lack of in-depth understanding for multi-scale dynamic mechanisms of DBS. Such model studies, which often disregard real individual patient data, make it difficult to obtain an accurate understanding of STN-DBS in PD patients. Especially, it is challenging to separate the specific neural expression that corresponds to different motor symptoms. Over the years, various forms of neurophysiological evidence demonstrate changes in brain activity across different spatiotemporal resolutions10,11, ranging from single neurons to local field potentials and brain-wide cortical network effects, are closely associated with the fluctuations of PD motor symptoms. Although these investigations have yielded significant findings, they have not yet been instrumental in the implementation of symptom-specific diagnostic and therapeutic strategies for PD.

High-frequency stimulation generates interference, disrupting the pathological firing patterns of neurons within the stimulated regions. However, the stimulation simultaneously affects the propagation of neural information along with the axons in both orthodromic and antidromic directions. Consequently, DBS may act through multiple mechanisms to disrupt abnormal neuronal oscillations in the CBTC at various network nodes12. In PD, abnormal neuronal oscillations have been observed in the STN, as well as in the internal (GPi) and external (GPe) segments of the globus pallidus. The oscillatory activity in the STN is believed to originate and intensify with cortical glutamatergic inputs to the STN and interconnections between STN and GPe, eventually transmitting to the GPi, thereby contributing to parkinsonian symptoms. The diverse frequencies of these oscillatory activities at multiple levels are thought to contribute to various motor symptoms13. High-frequency DBS targeting the STN operates on the fundamental principle of reducing the pathological excessive synchronization at the target site. To correct the imbalance in the GABA inhibitory pathway and the glutamate excitatory pathway within the CBTC in PD.

In recent years, numerous studies have attempted to reveal the neural basis underlying the motor symptoms in PD3,14. It has been found that the motor symptoms of PD are associated with dysfunction in various neural regions15. Dopamine depletion in the basal ganglia may directly cause motor impairment16. Our previous study discovered that excessive inhibitory impact of basal ganglia on the thalamus may be a neural mechanism underlying bradykinesia symptoms17. The depletion of dopaminergic cells in the nigrostriatal pathway results in a gradient of dopamine reduction in the striatum, inducing an imbalance between the excitatory and inhibitory pathways within the basal ganglia, which might be the pathological reason of the bradykinesia of PD patients18. Additionally, it is also shown that rigidity is associated with the neuronal firing frequency in the STN with PD19. Moreover, the improvement of bradykinesia by levodopa was associated with a decrease in connectivity of the STN-thalamic-cortical motor pathway20. Prior research has extensively examined the broad hypothesis that STN-DBS therapeutically modulates neural activities across disparate scales in PD7,21,22,23,24,25,26,27,28,29,30. With a particular emphasis on the motor circuitry, Fig. 1 delineates the neurochemical alterations within the motor pathways under various conditions, providing insights into the circuit-specific effects of STN-DBS31. This raises an interesting question: What is the essential mechanism underlying the DBS improving various PD motor symptoms? Are there different neural mechanisms for the effective alleviation of different symptoms? To answer these questions, we aim to construct multi-scale computational models to probe the alterations in neural activity within the CBTC for PD patients when DBS is applied.

Fig. 1: Various potential interpretations of the effect of STN-DBS.
figure 1

STN-DBS = Deep brain stimulation targeting the subthalamic nucleus; HC = healthy controls; GPe = globus pallidus externa; GPi = globus pallidus interna; Th = thalamus; STN = subthalamic nucleus.

Full size image

Functional MRI (fMRI) with high spatial resolution can accurately record the activity data of each nucleus and brain region in the CBTC32. This capability has advanced the development of physiological-physical models, which serve as a means to investigate and rehabilitate the brain state in patients, providing a framework for understanding the mechanisms underlying neural restoration. Moreover, several fMRI studies have shown that PD patients exhibit altered blood-oxygen-level dependent (BOLD) functional connectivity (FC) between different anatomical regions of a large-scale brain network33,34,35,36. Previous research has shown that mean FCs in areas such as the primary motor cortex, premotor cortex, and supplementary motor areas are attenuated in PD patients as compared to healthy controls (HCs)37. In addition, previous study found that STN-DBS restored relatively weak FC fluctuations in all motor areas back to levels closer to those of HCs38. The aforementioned studies analyzed the impact of DBS on FCs in PD patients, but the link between these macroscopic observations and microscopic mechanisms is lacking.

One way to connect the cell-level neuropathological hypothesis to neuroimaging data is by using bio-inspired multi-scale computational models39,40,41. Neuronal models greatly enrich the findings from the analysis of FC. The Izhikevich neuron model42, capable of producing more than twenty common neural spike and burst patterns, is one of the most frequently used neuronal models. Previously, we proposed a modified version of the CBTC network model based on the Izhikevich neuron model to investigate the closed-loop strategies of DBS43. Following the previous model, here, we incorporated the balloon model linking the neural synapses to the BOLD signal to achieve the connections between the neurodynamics and brain functions44.

In this study, we explored the related connectivity changes of microscopic CBTC in PD patients induced by DBS, using macroscopic fMRI data to reveal more realistic and physiologically meaningful effects of DBS. We fit the free coupling parameters in the neuron-balloon model by the BOLD data from 27 PD patients receiving STN-DBS, as well as 30 age-matched HCs. To match the real FC, we conducted a multi-step statistical analysis to examine the relationship between the 33 PD complex motor symptoms and the strength of the 10 synaptic connections within the CBTC. Our aim was to investigate the micro-regulatory mechanisms of DBS by only using the macroscopic data. It breaks through the limitations of previous research19,27 that solely relied on a single feature to simulate the PD state by proposing a multi-scale model. This multi-scale computational model provides a better understanding for the complex interactions within the motor pathway.

Methods

Cortico-basal ganglia-thalamic circuit network description

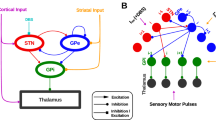
Brain function is a macroscopic reflection of circuit dynamics, and while the characteristics of DBS are known to influence brain function, the specifics of this influence remain to be elucidated. Thus, we assume all the synaptic coupling intensity are unknown while establishing the computational model of CBTC based on our previous work43. As shown in Fig. 2b, the connections between neurons were organized in a random pattern, with 100 neurons per nucleus. The neuronal membrane potential obey the first-order dynamics given by Izhikevich equations. The Izhikevich model facilitates the simulation of neural dynamics in brain areas including the basal ganglia and thalamus. It was introduced by Eugene M. Izhikevich in 200342 with the aim of capturing the dynamic properties of neurons in a relatively simple mathematical form. The Izhikevich model is particularly well-suited for simulating neuronal membrane potential and action potential firing. Employing this model could aid in uncovering the mechanisms behind PD and in devising effective stimulation approaches to rectify abnormal firing patterns.

Fig. 2: Overall design of DBS loop mechanisms elucidated via fMRI.
figure 2

a The dataset employed in this study. b The idea of fMRI-driven multi-scale model construction, from expressing the microscopic neuronal level synaptic activity by the CBTC model to the mesoscopic cluster scale, and then connecting the Balloon model to the macroscopic level aim to generate BOLD signal, demonstrating the calculation of BOLD signal using neural activity in a specific region. c The fitting effect of the fMRI-driven multi-scale model, showing that the trend of model simulation is basically consistent with real data. fMRI = functional MRI; PD = Parkinson’s disease; HC = healthy controls; DBS-OFF = patients with PD with the deep brain stimulation switched off; DBS-ON = patients with PD with the deep brain stimulation switched on; GPe = globus pallidus externa; GPi = globus pallidus interna; STN = subthalamic nucleus; Th = thalamus; PY = pyramidal neuron; IN = interneuron; Cor = cortex.

Full size image

In basal ganglia, each STN neuron receives inhibitory projections from two randomly selected GPe neurons, each GPe neuron receives excitatory projections from three randomly selected STN neurons, and recurrent inhibitory projections from two randomly selected GPe neurons. The GPi receives excitatory synaptic input from three randomly selected STN neurons, and inhibitory synaptic input from a randomly selected GPe neuron. In the cortex, each pyramidal (PY) neuron receives inhibitory projection from a randomly selected interneuron (IN), and each IN receives excitatory projections from four randomly selected PY neurons. Thalamus (Th) links these two critical brain regions. Each PY neuron receives excitatory stimuli from two randomly selected Th neurons, and each Th neuron received inhibitory synaptic input from eight randomly selected GPi neurons. Finally, STN closed the loop by receiving excitatory projections from two randomly selected PY neurons.

The Izhikevich model employs a set of nonlinear differential equations to describe the temporal evolution of the membrane potential and the recovery variable. These equations account for the active ionic channels and passive conductance of the membrane potential. The differential equations of Izhikevich model are given as follows:

$$d{v}_{M,i}/dt=0.04{v}_{M,i}^{2}+5{v}_{M,i}+140-{u}_{M,i}+\sum {I}_{M,i}^{syn}$$
(1)
$$d{u}_{M,i}/dt={a}_{M}({b}_{M}{v}_{M,i}-{u}_{M,i})$$
(2)

that are combined with the following discontinuous auxiliary after-spike resetting rule:

$${\rm{If}}\,{{\rm{v}}}_{m,i}\ge 30{\rm{mV}},\,then\left\{\begin{array}{c}{v}_{M,i}\leftarrow {c}_{M}\\ {u}_{M,i}\leftarrow {u}_{M,i}+{d}_{M}\end{array}\right.$$
(3)

In the formula, (\(M,i\)) represents the i-th neuron in the \(M\) nuclei, i = 1-100, and \(M\) belongs to the STN, GPe, GPi, Th, PY, and IN. v represents the membrane potential of the cell, and u is the recovery variable that provides negative feedback to the v. When the membrane potential v reaches 30 mV, the action potential is considered to be triggered, v and u will be reset according to Eq. (3). The dynamics of different nucleus M are characterized by an appropriate combination of four dimensionless model parameters, aM, bM, cM, and dM, which depend on the neuron type of the corresponding populations, with fixed parameters for each population shown in Table 1.

Table 1 Parameter values for the neuron models
Full size table

\(\sum {I}_{M,i}^{syn}\) represents the total synaptic current into the \(i\) th neuron in nuclei M from its pre-synaptic neurons at time t:

$$\sum {I}_{M,i}^{syn}=\sum _{J}\sum _{j}{g}_{J\to M}{r}_{J,j}(t)[{E}_{J}-{v}_{M,i}(t-{\tau}_{M})]$$
(4)

In the formula,\({g}_{J\to M}\) describes the strength of the synaptic connections from the pre-synaptic to post-synaptic neurons, which is the critical parameter need to be fit by an optimization procedure from BOLD signals. Additionally, \({E}_{J}\) denotes the reversal potential with \({E}_{J}\)=0 mV for excitatory synapses and \({E}_{J}\)= −80 mV for inhibitory synapses. Based on biological realization, we add synaptic delay \({\tau }_{M}\) in the model. The synapse variable \({r}_{J,j}\), as a fraction of the post-synaptically bound neurotransmitter, obeys first-order kinetics as follows:

$$d{r}_{J,j}/dt=\alpha (1-{r}_{J,j})/(1+\exp (-{v}_{J,j}))-\beta {r}_{J,j}$$
(5)

The neuro-computational model has been implemented using Matlab R2021a (The MathWorks Inc., Natick, MA, USA). To solve the differential equations of the model, the forward Euler method is used with a fixed integration step of 0.1 ms for the duration of 5000 ms.

BOLD signal computation

We use the Balloon model to reconstruct the BOLD signal from the synaptic dynamics revealed by CBTC model45,46. The principle of the Balloon model is to simulate the hemodynamics using the identification method of the nonlinear input-state-output system. Balloon model delineates the transformation of neuronal or synaptic activity into the observed response, equates to BOLD signal, denoted by y. Previous studies have shown that synaptic activity is a better predictor of BOLD signals, therefore, we used the Balloon model relied on the synaptic activity (S) to calculate BOLD signals47 (Fig. 2b).

The BOLD signal is considered a static nonlinear function of the volume (w) and deoxyhemoglobin (q), composed of a volume-weighted sum of extravascular and intravascular signals. In the R-th region (R belongs to STN, GPe, GPi, Th and Cortex), the generation of the BOLD signal is expressed by Eq. (6):

$$\begin{array}{c}{y}_{R}=g({q}_{R},{w}_{R})\\ ={V}_{0}({k}_{1}(1-{q}_{R})+{k}_{2}(1-{q}_{R}/{w}_{R})+{k}_{3}(1-{w}_{R}))\\ {k}_{1}=7{\rho }_{R}\\ {k}_{2}=2\\ {k}_{3}=2{\rho }_{R}-0.2\end{array}$$
(6)

The parameters value and description in Eq. (6) and Eq. (7) refer to the work by Friston et al. as shown in Table 2.

Table 2 Parameterization of the balloon model
Full size table

In the R-th region, synaptic activity, denoted as SR, leads to an enhancement of the vasodilation signal sR, which is subject to the influence of autoregulatory feedback mechanisms. The inflow, represented by fR, responds in proportion to this signal and is accompanied by variations in wR and the concentration of qR.

$$\begin{array}{c}{\bar{S}}_{R}={S}_{R}-{K}_{R}{S}_{R}-{\gamma }_{R}({f}_{R}-1)\\ {\bar{f}}_{R}={S}_{R}\\ {\tau }_{R}{\bar{w}}_{R}={f}_{R}-{w}_{R}^{1/\alpha }\\ {\tau }_{R}{\bar{q}}_{R}={f}_{R}E({f}_{R},{p}_{R})/{p}_{R}-{w}_{R}^{1/\alpha }{q}_{R}/{w}_{R}\end{array}$$
(7)

Synaptic activity at the level of individual neurons is represented by the synaptic variable \({r}_{J,j}\) in Izhikevich model. The calculation of the synaptic activity SR for a given region R is described by Eq. (8).

$${S}_{R}=\sum _{M\in R}\frac{1}{{N}_{M}}\mathop{\sum }\limits_{i}^{{N}_{M}}{r}_{M,i}+{\phi }_{R}$$
(8)

It is calculated as the sum of all mean synaptic activities of the neuron populations belonging to the region M∈R with population sizes NM. Only when R=cortex consisted of two neuronal population (M = PY & M = IN). Finally, in order to simulate the noise affecting the BOLD signal, the noise value \({\phi }_{R}\) (randomly selected from a uniform distribution between 0 and 0.05) is added to SR, and then put SR into the balloon model to generate the BOLD signal in the specified region.

Dataset

We collected fMRI data from 27 PD patients in the medication-off state (21 males, 6 females, age: 57.5 ± 18.5 years old), who underwent STN-DBS (both on and off state), along with 30 age-matched healthy control subjects (15 males, 15 females, age: 62 ± 11 years old) in Shanghai Ruijin Hospital. The scores of the Unified PD Rating Scale-Motor (UPDRS-III) were evaluated by the clinicians for all the PD patients. The detailed patients’ information and fMRI data preprocessing have been described in the previous work48.

Fitting procedure

For each subject, we processed the fMRI data with the DPABI49 (a MATLAB toolbox for Data Processing & Analysis for Brain Imaging) to obtain the FC between the nuclei (GPe\GPi\STN\Th\Cortex). Our model was independently fitted to each subject’s FC data, including 27 patients with DBS-ON and OFF conditions and 30 HCs.

Considering Bayesian Adaptive Direct Search (BADS) is a general model-fitting tool and a free MATLAB package, and is a novel, fast Bayesian optimization algorithm designed to solve difficult optimization problems, in particular related to fitting computational models. We used the BADS algorithm50 to fit all the free coupling parameters in the CBTC model to match the subjects’ FCs. For each subject, we performed 20 optimization iteration procedures using BADS (Fig. 2a), there the loss value is then calculated by Eqs. (9) and (10), and the ultimate goal of BADS fitting is to converge the loss value to the minimum.

$$D=F{C}_{M}-F{C}_{E}$$
(9)
$$loss={\left({\sum _{i,j}\left|{D}_{i,j}\right|}^{2}\right)}^{1/2}$$
(10)

The loss is the Frobenius norm of the difference (D) between model functional connectivity (FCM) and experimental data functional connectivity (FCE). For each subject, we finally obtained the stable-state values of the 10 synaptic coupling intensity parameters that made the lowest loss values during the optimization.

Statistical analysis

We used Spearman’s correlations to assess the correlation between synaptic coupling strength and motor symptom UPDRS-III scores, also between change in synaptic coupling strength and STN-DBS induced improvement in motor symptoms. Additionally, we conducted dependent-sample t-tests to assess differences between patients under DBS on and off. Statistical significance level was set at P < 0.05.

Ethics statement

The ethics committee of the Shanghai Ruijin Hospital approved all the study procedures (approval number: 2018017). All patients provided written informed consent following the Declaration of Helsinki.

Results

To focus on the spontaneous neural activity and FC patterns of the brain, and to investigate the interaction between different brain networks, we explore the synaptic coupling intensity changes related to CBTC in PD patients induced by DBS, using data-driven model to demonstrate more realistic and physiologically meaningful effects of DBS (Fig. 2a).

To verify our model, we compared the reconstructed FCs to the measured FCs from BOLD data in Fig. 2c. It can be seen that the FCs derived from our computational model were similar to those quantified of the real BOLD data for all the three data groups, which demonstrates that our model can reveal the micro-macro-dynamics of PD and DBS. Based on individual data, we totally obtained 54 patients’ models (27 patients with PD with the DBS switched on (DBS-ON) plus 27 patients with PD with the DBS switched off (DBS-OFF)) and 30 HCs’ models. The mean loss of all the 84 fitted FCs is M = 1.06 with a standard deviation of SD = 0.70. Specific model parameters and the physiological features captured by the model are detailed in the Supplementary Fig. 1 and Supplementary Tables 1 and 2.

Based on the model, the specific mechanism of different PD motor symptoms and the action ways of DBS are our concerns. For this goal, the motor symptoms of PD were first subdivided into 33 subtypes based on the UPDRS-III51 as shown in Fig. 3. To uncover the synaptic pathology underlying motor symptoms, the correlation between the intensity of synaptic connections in our model (including 54 Parkinson’s model: 27 for DBS-ON and 27 for DBS-OFF) and the corresponding 33 UPDRS-III scores was conducted (Step 1). The relationship between the changes in synaptic intensity and the rate of symptom improvement was then further revealed, so as to elucidate the circuit mechanisms responsible for the amelioration of specific symptoms (Step 2). Last, we assessed the impact of the DBS on the synaptic intensity, exploring whether such circuit-specific changes obtained from step 2 were contingent on the effects of DBS (Step 3). The results of these three steps were presented in Fig. 3. The overlap between the yellow and blue stars denote that STN-DBS had obvious regulatory effects on the improvement of rigidity and bradykinesia symptoms.

Fig. 3: Symptom-specific findings derived from the personalized model.
figure 3

DBS-OFF = patients with PD with the deep brain stimulation switched off; DBS-ON = patients with PD with the deep brain stimulation switched on; PD = Parkinson’s disease; g = synaptic connection strength between different encephalic region; GPe = globus pallidus externa; GPi = globus pallidus interna; STN = subthalamic nucleus; Th = thalamus; PY = pyramidal neuron; IN = interneuron.

Full size image

Symptom-specific firing rate changes induced by DBS

To further explore the therapeutical effect of DBS on these two typical motor symptoms, i.e., rigidity and bradykinesia, we screened and identified partial patients with the principle of improvement rate of the corresponding symptoms higher than 50% induced by DBS to perform the subsequent studies to dig out the various therapeutical mechanisms of DBS. The “improvement rate” refers to the percentage of alleviation in motor symptoms of patients with PD attributable to DBS. It is calculated using the formula: improvement rate = (DBS-OFF UPDRS-III score - DBS-ON UPDRS-III score)/DBS-OFF UPDRS-III score × 100%. Here, the UPDRS-III score is employed as the metric for assessing the severity of PD symptoms before and after the intervention with DBS. Given that higher scores on the scale reflect more severe symptoms, the score obtained in the DBS-OFF state is subtracted from that of the DBS-ON state to ensure that the calculated improvement rate is positive. This approach guarantees that the improvement rate reflects the reduction in symptom severity as a result of DBS therapy.

Figure 4 shows the symptom-specific firing rate changes of patients with rigidity and bradykinesia symptoms, illustrating the differences in firing rates of various nuclei under DBS OFF/ON conditions. For patients with rigidity, the firing rate of GPi (rate-GPi) significantly increased (p < 0.01) after DBS switch on, accompany by a slight increase on the firing rate of the thalamus (rate-Th), and a slight decrease on the firing rate of the internal nucleus (rate-IN) (Fig. 4b). In contrast, the rate-GPi exhibited a slight decrease, simultaneously inducing a slight decrease on rate-Th and raise on rate-IN. Besides, DBS caused a consistent increase on the rate of GPe and lessen on the rate of STN and PY for both rigidity and bradykinesia patients. These results indicate that the multi-scale model is an effective tool to visualize the micro-scale neuronal characteristics from macro-scale brain information so as to explore the neural basis of DBS.

Fig. 4: STN-DBS effects on rigidity and bradykinesia symptoms.
figure 4

a Patients with PD were divided into two groups with rigidity and bradykinesia improvement rate greater than 50%. The rigidity cohort comprises a total of 12 participants, while the bradykinesia cohort consists of 8 individuals. b Box plot of the firing rates for all individuals within the rigidity patient group. c Box plot of the firing rates for all individuals within the bradykinesia patient group. PD = Parkinson’s disease; DBS-OFF = patients with PD with the deep brain stimulation switched off; DBS-ON = patients with PD with the deep brain stimulation switched on; GPe = globus pallidus externa; GPi = globus pallidus interna; Th = thalamus; PY = pyramidal neuron; IN = interneuron.

Full size image

Symptom-specific push-pull effect of synaptic coupling strength

Before the exploration of the impact of DBS on synaptic connectivity, an interesting question is raised. Whether does DBS improve the specific symptom by restoring the pathological synaptic connectivity underlying this symptom? To answer this question, we first calculated the Spearman’s correlation between the 10 synaptic connectivity parameters within the CBTC model and the 33 subscores of UPDRS-III (Fig. 5a), where the scores can evaluate the severity of symptoms. The higher the score, the more severe the damage. We discovered that changes in pathway connectivity can “push” the CBTC to a pathological state to induce various motor symptoms of PD. Specifically, we observed abnormal enlargement of basal ganglia-thalamo-cortical connections (gGPi-Th, gTh-PY) leading to deterioration of rigidity symptoms, and abnormal elevated cortico-basal ganglia reciprocal coupling (gPY-STN) and decreased intra-regional self-coupling (gPY-IN, gIN-PY, gSTN-GPe, gSTN-GPi) triggering bradykinesia symptoms (Fig. 5a). The significant Spearman’s correlation results were also given in Supplementary Table 3. Also, Supplementary Fig. 3 illustrates the correlation between the synaptic coupling strengths and all 33 symptoms.

Fig. 5: Symptom-specific DBS mechanism analysis.
figure 5

a The spearman’s correlation between synaptic parameter values and PD symptom severity. b Significant correlation observed between changes in connection strength parameters and symptom improvement rates. c Results of the paired-samples t-test between DBS-ON and DBS-OFF. Different motor symptoms are represented by different colors, and coupling connections consistent with symptom colors indicate a significant correlation between them. PD = Parkinson’s disease; g = synaptic connection strength between different encephalic region; GPe = globus pallidus externa; GPi = globus pallidus interna; STN = subthalamic nucleus; Th = thalamus; PY = pyramidal neuron; IN = interneuron.

Full size image

In order to further identify the specific mechanisms behind symptom improvement, we analyzed the effects of STN-DBS on different symptoms. The Spearman’s correlation between the changes in 10 synaptic connection strengths (from DBS-OFF to DBS-ON state) and the improvement rate of individual symptoms were calculated. As shown in Fig. 5b, the improvement of rigidity symptoms was significantly correlated with the changes of gGPe-GPi, gTH-PY, and gSTN-GPi. The change in inhibitory connection strength between GPe and GPi was significantly and positively correlated with the improvement of the patient’s neck rigidity (p = 0.026*, r = 0.429). The weakening of the excitatory connection between Th and PY is closely correlated with Rigidity-RUE improvement. Additionally, the strengthening of the excitatory connection of STN output to the GPi exhibits a correlation to the rate of improvement for Rigidity-RLE. Figure 5b demonstrates that the improvements of rigidity symptoms depend on the pull effects of synaptic dynamics in the CBTC network induced by DBS, reflected by the enhancement of internal connections within the basal ganglia and by attenuated excitatory connections from Th to cortical. However, in terms of bradykinesia symptoms, there was a significant negative correlation between the change in inhibitory connectivity from GPe output to STN and the improvement of symptoms. These symptoms included right hand finger tapping, left hand movement, right hand pronation-supination movement, and global spontaneity of movement. The excitability effect of PY on STN showed a significant negative correlation with the improvement rate of left finger tapping (p = 0.048*). Bradykinesia symptoms were significantly “pulled” back into a normal state of affairs by weakening the hyperdirect pathway connections (Fig. 5b). Supplementary Table 4 displays the results indicating significant associations between parameter changes and the rate of symptom improvement in rigidity and bradykinesia symptoms. Correlation plots for all symptoms are shown in Supplementary Fig. 4.

Comparing Fig. 5a, b, we found that the synaptic connections that induce the symptoms do not match the parameters that improve the symptoms. This discrepancy is likely due to the clinical manifestation that PD patients are usually accompanied by the coexistence of multiple symptoms. Therefore, we grouped patients who showed a high rate (≥50%) of improvement in each individual symptom. We then conducted a paired sample t-test to compare the parameter values between the DBS-ON and DBS-OFF states, aiming to identify significant differences between the two groups. Following the second phase of our investigation, which revealed that DBS exerts a pulling effect on synaptic coupling strength to ameliorate motor symptoms, we now aim to elucidate the specific mechanisms by which DBS achieves this restorative pulling action. Figure 5c shows that improvements in rigidity symptoms were closely associated with changes in synaptic connectivity parameters for rigidity-neck and rigidity-LUE symptoms. After STN-DBS startup, the parameters of gGpe-GPi and gGPe-GPe amplified significantly in patients with a high improvement rate of neck rigidity (p = 0.035*, p = 0.019*), and gPY-STN diminished significantly in patients with a high improvement rate of rigidity-LUE (p = 0.046*). Notably, the improvement of bradykinesia symptoms was associated with a significant decrease in gPY-STN. Additionally, the improvement of left hand finger tapping and right hand movement were demonstrated correlated with a significant increase in gGPe-GPe. Significant results from paired sample t-tests are presented in Supplementary Table 5, and boxplots of the paired sample t-tests conducted for all symptoms are plotted in Supplementary Fig. 5.

By examining the intersection of significant findings in Supplementary Tables 4 and 5, we can gain a comprehensive understanding of the improvement mechanism and impact of STN-DBS on specific symptoms. By calculating the Spearman’s correlation between the synaptic connection strength parameter value and the patient score in the DBS switch state, Supplementary Table 3 shows that the parameter significantly and positively associated with the neck rigidity symptoms was gGPi-Th. Furthermore, the larger the parameter value, the more severe the rigidity symptoms (Fig. 5a). STN-DBS inhibited the discharge activity of GPi by enhancing the connection strength between GPe and GPi (Fig. 6b, c). This, in turn, the inhibition on Th from GPi might be the neural basis of DBS improving the neck rigidity (Fig. 6a, d).

Fig. 6: Results of the statistical analysis associated with neck rigidity and finger tapping-left hand symptoms.
figure 6

a−c The results of statistical analysis of Rigidity-Neck symptom correspond to those for Fig. 5a−c. d Conclusion on the loop mechanism of STN-DBS treatment on Rigidity-Neck. e−g The results of statistical analysis of Finger tapping-Left hand symptom correspond to those for Fig. 5a−c. h Conclusion on the loop mechanism of STN-DBS treatment on Finger tapping-Left hand. Dark blue lines denote light blue indicates the corresponding results for the first step, green lines represent the corresponding results for the respective symptom in the second step, and the corresponding significant group differences for the respective symptom in the third step. Square arrow lines represent the Glutamatergic projections, while round arrow lines represent the GABAergic projections. PD = Parkinson’s disease; DBS-OFF = patients with PD with the deep brain stimulation switched off; DBS-ON = patients with PD with the deep brain stimulation switched on; GPe = globus pallidus externa; GPi = globus pallidus interna; STN = subthalamic nucleus; Th = thalamus; PY = pyramidal neuron; IN = interneuron.

Full size image

Figure 6e−g presents the results of the statistical analysis associated with the finger tapping symptom in the left hand. Figure 6e reveals that the parameter significantly negatively associated with the left finger tapping symptoms was gIN-PY, and the smaller the parameter value, the more severe the left finger tapping symptoms (Supplementary Table 3). However, STN-DBS inhibited the firing activity of STN by weakening the connection from PY to STN (Supplementary Tables 4, 5, Fig. 6f). This resulted in a decrease in the firing rate of the STN, indirectly alleviating the inhibitory effect of GPi on Th, and the excitability effect between Th to cortex was subsequently enhanced, leading to an enhanced interaction between IN and PY. The slight increase in the parameter gIN-PY may be possible mechamism of DBS alleviating the tapping symptoms of the left finger. Here, a functionally important pathway of STN-DBS may involve the reverse activation of the motor cortex via retrograde cortical circuits (Fig. 6h). The electric field effect of STN-DBS activates the reverse cortical circuit through the axon side of the STN projection PY, inducing the decrease of gPY-STN.

Discussion

This study explored the circuit mechanisms specific to motor symptoms of STN-DBS, using a computational model that connects the microscopic, mesoscopic, and macroscopic neural levels. Initially, to reveal the coupling strength associated with the severity of each motor symptom, the correlation between the scores of UPDRS-III and the estimated coupling intensity within the CBTC are meticulously analyzed. Afterward, to investigate the relativity between coupling strength within the CBTC from fMRI data and symptoms recovery, further elucidation is provided regarding the correlation between the rate of symptom amelioration and the degree of coupling alteration. Finally, the study highlights the impact of DBS on inter-nuclei coupling within the CBTC by emphasizing the differences in coupling strength before and after DBS activation. It demonstrated that the CBTC network has a push-pull effect on synaptic dynamics induced respectively by dopamine loss and the impact of DBS. In the context of the CBTC network, synaptic coupling alterations that “push” the system towards pathological states are implicated in the emergence of the varied motor symptoms characteristic of PD. Conversely, the therapeutic intervention of DBS exerts a “pull” effect on synaptic coupling, restoring it to a normalized state and ameliorating specific motor symptoms.

We found that in the CBTC, the inhibitory projections from basal ganglia to thalamus and excitatory projections from thalamus to the cortex are obviously increased in patients with more severe rigidity symptoms. However, the excitatory connectivity from the cortex to the basal ganglia was unexpectedly strengthened. Also, the weakened interaction between cortical interneurons and pyramidal neurons was closely correlated with the severity of bradykinesia, while the internal coupling within the basal ganglia remained at the same level as other PD patients.

Furthermore, our study elucidates the mechanism by which STN-DBS relieves rigidity and bradykinesia symptoms via establishing a link between the improvement of motor symptoms and the variations in synaptic strength. STN-DBS attenuated the firing activity of GPi by enhancing the inhibitory connection between GPe and GPi. This further weakened the inhibitory impacts of GPi on thalamus, ultimately reversing the synaptic variations induced by rigidity. This may reveal the mechanism of STN-DBS in alleviating rigidity symptoms. Additionally, STN-DBS also inhibits the firing activity of STN by weakening the connection strength between PY and STN (gPY-STN). The weakening of the STN glutamatergic efferents would inhibit the activity of the structures receiving their projections. Additionally, weakening the output of basal ganglia would enhance the inhibitory projection from IN to PY (gIN-PY) along the CBTC. This compensation would help alleviate the bradykinesia symptom caused by diminished gIN-PY through reverse cortical activation. Increased coupling between pyramidal neurons and interneurons within the cortex is believed to contribute to the improvement of bradykinesia symptoms. Overall, STN-DBS improves brain function by normalizing the output of the basal ganglia, which in turn stimulates other structures to better compensate for underlying defects.

Also, to verify the confidence of the experimental results, we compared the DBS-OFF and HC data characteristics with previous popular studies and explained the conclusions accordingly shown in the supplementary information section. Previous research suggests that reduced DA in PD result in increased inhibition of the GPe, leading to disinhibition of the STN52,53 (Fig. 1). Hyperactive STN causes stronger stimulation of GPi. Active GPi leads to a strong inhibition of the thalamus, resulting in reduced excitatory input from the Th to the cortex. Suppressed thalamus and less responsive cortex are thought to cause motor retardation54,55. Our study found a 15.39% increase in the inhibitory output from GPi and a 21.49% decrease in the excitatory output from thalamus in PD compared to HC (Supplementary Fig. 2, Supplementary Tables 6 and 7). In the presence of STN-DBS, the inhibitory projections of GPi output to the thalamus were reduced by 24.97%. Additionally, the excitation projections from the thalamus to the cortex were restored to only a 0.3% reduction. These findings suggest that STN-DBS has a restorative effect on the neural loop. The findings on firing rates are also consistent with previous studies that the firing rates of the GPe and Th were lower in PD patients56. Our study confirms that the mean firing rate of each brain region in PD patients was lower than that of HC. A characteristic alteration of neural changes in PD patients is the increased connectivity between STN and the cortex, resulting in hyperactivation of the hyperdirect pathways57. Some studies have shown that the pathological synchrony of STN is associated with bradykinesia58. STN-DBS can normalize neural activity in thalamic and cortical motor areas, thereby modulating the striatal-thalamic-cortical pathway and STN-cortical pathway. This modulation subsequently leads to an improvement in bradykinesia symptoms. Our findings confirm that STN-DBS improves bradykinesia symptoms by reducing neural activity in the hyperdirect pathway. Also, the effects of STN-DBS inhibited the GPi to thalamic GABAergic projection59, resulting in enhanced thalamic activity and excitatory outflow. Consequently, this improvement in thalamic function led to a reduction in the severity of rigidity symptoms.

However, the current study still has several limitations: (1) Our model still has a way to go in replicating the complex details of biological processes. The current model still lacks physiological details, such as ion channel properties, FCs cannot perfectly reflect pathological details. Fortunately, it is sufficient for us to study the relationship between coupling connectivity and Parkinson’s pathology. The significance of our modeling is not only to reveal symptom-specific stimulation mechanisms but also to provide a testbed and research framework for the optimization of STN-DBS. In the future, we will explore the dynamic characteristics of the ionic channels and make further modifications to the model. Personalized models based on FC might be further improved by taking into account the volume of brain regions and the structural connectivity between them. (2) Due to the continuous interaction of all relevant structures during STN-DBS, accurately attributing stimulus effects to specific primary pathways is a crucial challenge in designing stimulus parameters. We applied the complex effect of positive and reverse activation to interpret the results. However, it is not clear if this explanation is universal. For instance, we are unsure how thalamic changes to cortical input, which occur as a result of the effects of STN-DBS on basal ganglia activity, interact with retrograde evoked activity. (3) DBS has the capability to interrupt the irregular neural impulses within the brain responsible for the tremors in the hands and arms, thereby reinstating natural balance. The precise mechanism involves the disruption of abnormal oscillatory patterns and the reestablishment of more normalized signal flow within the affected neural networks, leading to significant alleviation of tremor symptoms. Yet the mechanism of DBS for tremor has not been explained by this study. The reason for this may be the existence of different characteristics of basal ganglia coupling in PD patients characterized by tremor, which needs to be explored based on more detailed modeling. In our subsequent research, we will expand the model to include other brain regions related to the motor circuitry, such as the striatum. Furthermore, DBS may not solely ameliorate the motor symptoms of PD by “pulling” synaptic coupling back to normal levels. We need to explore the impact of other factors within the model on neural activity, as there are many underlying causes that remain to be uncovered and investigated.

Our study explores the mechanism of STN-DBS in improving various symptoms in PD patients with heterogeneous. In addition, the symptom-specific brain model we constructed can effectively simulate brain activity in patients with different motor symptoms. This research aims to facilitate the optimization of personalized DBS treatment regimens and explore the potential benefits of virtual DBS using our connected multi-level brain model. It will help to establish a corresponding virtual brain for PD individual with different symptoms in the future and explore the optimal adaptive stimulation parameters. Our model may provide an possible effective tool to real decipher the physiological characteristics of the fMRI information, establish a backward link of macro-to-microscopic dynamics, and elucidate an in-depth exploration of the potential push-pull network mechanisms through which DBS ameliorates motor symptoms. This push-pull concept provides a framework for understanding the dualistic mechanisms underlying the progression of PD and its alleviation through DBS, highlighting the dynamic interplay between pathological neural interactions and the restorative potential of neuromodulation.