A foundation model of transcription across human cell types

Transcriptional regulation constitutes a critical yet largely unresolved ___domain that underpins diverse biological processes, including those associated with human genetic diseases and cancers¹¹. Transcriptional changes are orchestrated by a conserved regulatory machinery, including transcription factors (TFs) that bind to regulatory sequences; coactivators, mediators, and core transcriptional factors; and RNA polymerase II (PolII)¹². Although different cell types may possess different subsets of regulatory regions, the biochemistry of protein–protein and protein–DNA interactions remains largely the same across cell types when epigenetic conditions are fixed. Clustering of known TF binding site motifs¹³ demonstrates significant homology in TF DNA-binding domains, further reducing the combinatorial variability of regulatory interactions. However, our understanding of transcription regulation is often limited to specific cell types, and it is not clear how the combinatorial interaction of different TFs determines the diversity of expression profiles observed across cell types. As an example, previous expression prediction methods such as Expecto¹⁴, Basenji2 (ref. ¹⁵) and Enformer⁴ are designed to make predictions on the training cell types after they have been fine-tuned, hindering the generalizability and utility of these models.

Recently, foundation models such as GPT-4 (ref. ¹⁶) and ESM-2 (ref. ¹⁷) have emerged as a transformative approach. With extensive pretraining on broad and diverse datasets, foundation models provide a generalized understanding of their training data, upon which specialized adaptations can be built to address specific tasks or challenges. For example, recent developments in single-cell foundation models such as Geneformer¹⁸, scGPT¹⁹ and scFoundation²⁰ have demonstrated how diverse transcriptome profiles can be encoded in one model, enabling various contextualized downstream tasks including cell type annotation and perturbation prediction. However, no foundation model of how transcription emerges from the chromatin landscape has yet been explored.

Here we introduce the general expression transformer (GET), an interpretable foundation model for transcriptional regulation. GET learns transcriptional regulatory syntax from chromatin accessibility data across 213 human fetal and adult cell types and accurately predicts gene expression in both seen and unseen cell types (Fig. 1a). In addition, GET offers zero-shot prediction of reporter assay readout, outperforms previous state-of-the-art models in identifying cis-regulatory elements, and identifies previously unknown and known upstream regulators of fetal haemoglobin. GET also provides rich cell-type-specific regulatory insights: using coregulation information predicted by GET, we pinpointed potential motif–motif interactions and constructed a structural interaction catalogue of human TFs and coactivators (Fig. 1b). Using this, we identified a lymphocyte-specific TF–TF interaction involving PAX5 and nuclear receptor family TFs and highlighted a possible disease-driving mechanism of a leukaemia-associated germline variant that affects the binding of the PAX5 disordered region to the nuclear receptor ___domain.

a, Schematic illustration of GET. The input of GET is a peak (accessible region) × TF (motif) matrix derived from a human single-cell (sc)ATAC-seq atlas, summarizing regulatory sequence information across a genomic locus of more than 2 Mbp. Through self-supervised random masked pretraining of the input data across more than 200 cell types, GET learns transcriptional regulatory syntax (p). GET is fine-tuned on paired scATAC-seq and RNA-seq data and learns to transform the regulatory syntax to gene expression, even in leave-out cell types (f⋅p). b, Schematic illustration of downstream applications of GET. CRE, cis-regulatory element. c, Benchmark of GET prediction performance on an unseen cell type (fetal astrocytes). Each point represents a gene. Colour represents normalized chromatin accessibility in the TSS. Gene activity is a score widely used in modern scATAC-seq analysis pipelines²⁵. Top correlated cell type is the training cell type whose observed gene expression has the strongest correlation with fetal astrocyte (in this case, fetal inhibitory neurons). Mean cell type is the mean observed gene expression across training cell types. Dashed line represents linear fits. Prediction is made for all accessible TSS in astrocytes and averaged to gene level. Schematics in a and b were created using BioRender (https://biorender.com).

Full size image

The design philosophy of GET is rooted in the transcription regulation mechanism. A local genomic region (approximately 2 Mbp) with promoters and regulatory elements can be characterized by how well these elements bind different TFs and how accessible they are in specific cell types. These features shape a chromatin environment (p(X)) that governs how PolII drives expression at each individual element, which can be approximated from RNA sequencing (RNA-seq) data. Using an embedding and attention architecture²¹ specifically designed for the regulatory elements, we performed self-supervised pretraining to allow GET to learn how the regions and features interact with each other across diverse cell types. Specifically, by randomly masking out regulatory elements, the model is trained to predict motif binding scores and optionally accessibility scores in the masked regions. Subsequently, PolII will read out the chromatin environment p(X) into an expression E. A fine-tuning stage with the same architecture but a different output head simulates this process (Fig. 1a and Extended Data Fig. 1). This two-stage design makes it possible to use chromatin accessibility data without paired expression measurement, greatly improving the diversity of regulation information in the training data. The pretraining of GET uses pseudobulk chromatin accessibility gathered from single-cell assay for transposase-accessible chromatin with sequencing (scATAC-seq) data across 213 human fetal and adult cell types^1,2,22. Of these, 153 cell types were coupled with expression data acquired through either a multiome protocol or separate single-cell RNA-seq experiments^23,24 (Methods: ‘ATAC-seq data processing’ and ‘RNA-seq data processing’) and used for fine-tuning and evaluation.

We first assessed GET’s ability to accurately predict gene expression in unseen cell types in a setting where one cell type is left out during the expression fine-tuning process. On left-out astrocytes and genes with accessible promoters, the Pearson correlation between GET’s predicted expression values and the observed expression reached 0.94 (R² = 0.88) (Fig. 1c), in line with experimental accuracy across different culture systems and biological replicates of human astrocytes³ (Pearson r = 0.92–0.99, Extended Data Fig. 2a). GET’s performance surpassed that of both transcription start site (TSS) accessibility (r = 0.47, R² = −0.23) and gene activity score²⁵ (r = 0.51, R² = −0.67), emphasizing the significance of DNA sequence specificity and distal context information in transcription regulation. Furthermore, GET outperformed top correlated cell type expression (r = 0.83, R² = 0.62) and mean expression across training cell types (r = 0.78, R² = 0.53; Fig. 1c). GET also accurately predicted expression log fold change between two cell types, even when one of them was unseen (Extended Data Fig. 2b). Across a wide range of fetal cell types evaluated, GET consistently outperformed genome-wide prediction using Enformer’s cap analysis of gene expression (CAGE) output tracks and the training cell type mean expression baseline (Extended Data Fig. 2c). We found that the pretraining stage was crucial for leave-out cell type prediction accuracy, as GET with only the fine-tuning stage suffered a significant performance drop (Pearson r = 0.6; Extended Data Fig. 2d). GET also outperformed simpler machine learning approaches in both the leave-out cell type and leave-out chromosome evaluation settings when trained using the same data and number of epochs (Extended Data Fig. 2e,f).

GET also showed generalizability to adult cell types when trained solely on fetal data, with an average R² of 0.53 across diverse adult cell types, surpassing the baseline (R² = 0.33) obtained using corresponding fetal cell types for prediction (Extended Data Fig. 3a). Furthermore, GET can be transferred to different sequencing platforms, including 10× multiome sequencing of lymph nodes (Extended Data Fig. 3b,c) and glioblastoma (GBM) tumour cells²⁶ (Extended Data Fig. 3d–f), as well as other experimental assays, including prediction of CAGE and chromatin accessibility (Extended Data Fig. 4). Detailed analyses are provided in the Supplementary Information (‘Generalizability study of GET’).

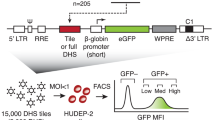
Given the versatility of GET across diverse platforms and measurements, we examined its capacity for zero-shot prediction of expression-driving regulatory elements in unseen cell types. Lentivirus-based massively parallel reporter assay (lentiMPRA) provides a robust mechanism to test the regulatory activity of numerous genetic sequences by integrating them into the genome, thereby circumventing the limitations inherent to episomal MPRAs and ensuring relevant biological readouts in hard-to-transfect cell lines⁵. This experimental assay was recently used to assess 226,243 sequences in the K562 cell line and enabled the creation of a comprehensive benchmark dataset for evaluation of whether the GET model could identify regulatory elements in a cell-type-specific context⁶ (Fig. 2a). In an in silico procedure akin to the lentiMPRA experiment, we used the GET model fine-tuned on bulk ENCODE K562 OmniATAC chromatin accessibility and expression data from NEAT-seq (sequencing of nuclear protein epitope abundance, chromatin accessibility and the transcriptome in single cells). Using the GET model, which had seen no lentiMPRA data, we inferred the activity of the mini promoter in the corresponding chromatin context and averaged over all insertions to obtain a mean readout indicative of the regulatory activity (Fig. 2a and Methods: ‘LentiMPRA zero-shot prediction’). Overall, the predicted readout distribution for different types of element matched expectation (Supplementary Information: ‘Overall distribution of GET-MPRA prediction’).

a, Schematic workflow of lentiMPRA experiments and in silico lentiMPRA using GET model fine-tuned on K562 multiome data. b, Benchmarking of GET lentiMPRA prediction against Enformer on a random subset of elements. The x axes show observed lentiMPRA readout (log₂(RNA/DNA)); y axes show predicted expression (log₁₀ transcripts per million (TPM)). repr., repressive; quies., quiescent. Schematic in a was created using BioRender (https://biorender.com).

Full size image

When benchmarking our model against Enformer, which was trained on 486 tracks of functional K562 genomics data including TF and histone modification chromatin immunoprecipitation followed by sequencing (ChIP–seq), CAGE and chromatin accessibility measurements, we found that our model made more accurate predictions and scaled better overall (Pearson’s r = 0.55, slope = 0.63 when combined with K562 accessibility signal, and Pearson’s r = 0.45, slope = 0.38 when using only the expression prediction model, versus Enformer’s Pearson’s r = 0.44, slope = 0.14; Fig. 2b and Extended Data Fig. 5a), and its predicted regulatory elements showed biologically meaningful enrichment in histone marks and TF binding sites (Extended Data Fig. 5b–d and Supplementary Information: ‘Enrichment analysis of GET-MPRA prediction’). Enformer showed better correlations in enhancer and repressed regions; this could be attributed to greater coverage of heterochromatin and vast numbers of functional K562 assays in its training data. GET also had significant advantages in terms of computational cost. For this comparison, subsampling to 2,000 elements was required to benchmark Enformer in 3 days, whereas using the same amount of computing time allowed GET to screen all 226,243 elements (Supplementary Information: ‘Computational cost comparison’).

Through model interpretation techniques (Methods: ‘Model interpretation’), we can efficiently derive region or motif contribution scores for genes with accessible promoters across cell types, producing results for virtually all genes in even less abundant cell types (approximately 1,000 cells). Focusing on fetal erythroblasts, we leveraged published genome base-editing data to investigate four known fetal haemoglobin-regulating loci⁷ (BCL11A, NFIX, KLF1 and HBG2; the first three of these are known to regulate fetal haemoglobin, and HBG2 encodes a fetal haemoglobin subunit; Fig. 3a).

a, Case study identifying cis-regulatory elements and regulators controlling a phenotype, fetal haemoglobin (HbF) level. b, GET identifies the GATA motif in an erythroid-specific enhancer that upregulates BCL11A, an HbF repressor. Top, guide RNA (gRNA) enrichment scores (HbFBase); higher scores indicate enrichment in a greater number of HbF cells, implying that these edits disturb a cis-regulatory element or regulator binding site that can upregulate BCL11A. Middle, scATAC-seq signal and peaks from fetal erythroblasts. Bottom, motif contribution score for BCL11A expression in the erythroid-specific enhancer. c, Genome tracks displaying inferred cis-regulatory elements for BCL11A and NFIX loci. Plots for HBG2 and MYB loci can be found in Supplementary Fig. 4c. From top to bottom, the tracks represent: HbFBase, showing the gRNA enrichment score from base-editing experiments; GET, showing the inferred region importance score; Enformer, showing the inferred region importance score; HyenaDNA, showing an in silico mutagenesis (ISM) result using the pretrained HyenaDNA language model; ABC Powerlaw, showing the activity-by-contact prediction using fetal erythroblast ATAC and K562 Hi-C powerlaw; ATAC-seq data from HUDEP-2, an erythroblast cell line; ATAC-seq data from fetal erythroblast cells, used in the training of GET; and HiChIP–seq data from HUDEP-2, demonstrating chromatin interactions. d, Benchmarking results comparing GET to other methods for predicting enhancer–promoter pairs, including analysis of distal (greater than 100 kb) interactions. Top, erythroblast fetal haemoglobin-regulating enhancer prediction. Bottom, K562 CRISPRi enhancer target prediction; the area under the precision–recall curve (AUPRC) is shown. Ablation of different GET prediction components (Jacobian, DNase, Powerlaw; Methods: ‘Enhancer–gene pair prediction’) is also shown in the plot. Data are presented as mean values with 95% confidence intervals across random bootstrapping (N = 1,000, 80% of the pairs). GWAS, genome-wide association study. Schematic in a was created using BioRender (https://biorender.com).

Full size image

Applying GET to fetal erythroblasts yielded insights into the regulation of fetal haemoglobin. We rediscovered the central role of the GATA TF, which, through its binding to an erythroid-specific enhancer, orchestrates the expression of BCL11A, a known modulator of haemoglobin regulation²⁷. GET also highlighted the role of the SOX family of TFs in this enhancer, which have previously been linked to fetal haemoglobin²⁸ but were not known to function through this specific enhancer (Fig. 3b).

Examining all four loci—BCL11A, NFIX, KLF1 and HBG2—we benchmarked GET against established models including Enformer⁴, HyenaDNA²⁹, DeepSEA³⁰ and Activity-by-Contact (ABC)^31,32. GET outperformed these counterparts, especially in detecting long-range enhancer–promoter interactions (Fig. 3c,d and Extended Data Fig. 6a–c). We also found that although enhancer chromatin accessibility was predictive of regulatory activity for proximal enhancer–promoter relationships, its precision diminished for long-range interactions. Alternative evaluations using different functional enhancer thresholds (top 10% or 25% of the experimental readout HbFBase) reaffirmed the precision of GET in this scenario (Fig. 3d, top). We also benchmarked the same task for the K562 cell line using a CRISPR interference (CRISPRi)-based benchmark dataset from ENCODE³³ and reached a similar conclusion (Fig. 3d, bottom, and Extended Data Fig. 6d).

GET can extract aggregated motif importance across cis-regulatory elements for specific genes. For HBG2, BCL11A and NFIX, the top motifs identified were consistent with their known transcriptional regulators or haematopoietic TFs (Extended Data Fig. 7a), including NFY and SOX motifs for HBG2 and KLF1 for BCL11A⁷. In addition, for NFIX, GET highlighted TAL1, a known GATA1 binding partner and haematopoietic factor³⁴ that has not been linked directly to NFIX regulation.

To determine downstream targets for specific regulators, we developed an in silico analysis, taking the GATA motif as a case study. Using the GET motif contribution matrix, we identified the top 10% of genes influenced by the GATA motif. Notably, consistent with the role of GATA1 in erythroid development, the ‘hemopoiesis’ biological process was enriched³⁵ (Fisher exact test, multiple hypothesis adjusted P = 7.6 × 10⁻⁴; Extended Data Fig. 7b and Methods: ‘Gene ontology enrichment of top target genes of a regulator’) within this gene set. Known erythroid-lineage TFs including KLF1, GATA1, TAL1 and IKZF1 were also predicted to be regulated by the GATA motif³⁶. Further analysis of motif importance across different cell types demonstrated a link between motif contribution and target gene expression, supported by a universal regulatory embedding (Supplementary Information: ‘Cross-cell-type motif contribution analysis’ and ‘Cross-cell-type embedding analysis’, Extended Data Fig. 7c–g).

Given the proficiency of GET in elucidating regulatory mechanisms across diverse cellular contexts, we next investigated whether it learned TF–TF functional interactions implicitly. Using a cell-type-agnostic gene-by-motif matrix (Methods: ‘Causal discovery of regulator interaction’), we considered the hypothesis that high correlation between motif columns might represent common genomic targets between different TFs. Indeed, TF pairs with correlation values in the top decile were more likely to participate in the same biological functions compared with those in the bottom decile (Extended Data Fig. 7h, Kolmogorov–Smirnov test, P = 6.78 × 10⁻⁸²). For example, MBD2 and MECP2, a high-correlation TF pair, both function as readers of DNA methylation^37,38.

Applying a causal discovery algorithm to the cell-type-agnostic gene-by-motif matrix led to the discovery of known and previously unknown motif–motif interactions (Fig. 4a, Methods: ‘Causal discovery of regulator interaction’; examples shown in Extended Data Fig. 7i, Supplementary Figs. 5 and 6, and Supplementary Information: ‘Analysis of the GET causal network’). To quantitatively assess the overlap with known physical interactions between TFs, we compared the GET motif–motif interaction network using two different approaches, GET Causal and GET Correlation, with the STRING v.11 database³⁹ (Methods: ‘Causal discovery of regulator interaction’). Our results showed a precision (true positive rate) of 5.6% for random chance. However, by selecting the top 1% (n = 793 pairs) of causal or correlation pairs from GET’s predictions, we achieved precisions of 25.2% and 15.9%, respectively (Fig. 4b), confirming the advantage of our causal-discovery-based model interpretation approach. As a comparison, a recent mass-spectrometry-based TF–TF interaction study⁴⁰ reported 30.4% precision with the top 1.25% (n = 990) pairs, whereas a colocalization score computed from HepG2 ChIP–seq for 677 TFs yielded a larger number of motif–motif interactions yet had slightly lower precision and macro F1 score than GET Causal. Furthermore, GET Causal outperformed two accessibility-aware motif colocalization baselines, computed either across cell types or in hepatocytes. This reflects the incompleteness of annotated TF–TF interactions and highlights the value of GET-predicted motif pairs for identifying new interactions.

a, Causal discovery using the GET motif contribution matrix identifies motif–motif interactions. Edge weights represent interaction effect size. Edge directions mark casual directions. Blue and red edge colours mark negative or positive estimated causal effect size by LiNGAM, respectively. Node colour indicates community detected on the full causal graph. In-community edges are marked by reduced saturation. b, Benchmark of concordance of inferred TF–TF interactions using different methods with physical interactions from the STRING database. The x axis shows different cutoffs for retained interactions by percentile of 79,242 total possible interactions; y axis shows the ratio of selected interactions that are also marked as interactions in STRING. The dashed line indicates the random selection background; the orange line indicates the results of selection using motif–motif contribution score correlation; the red line marks the mean of causal discovery results across five bootstraps; the shaded area indicates the standard error; and green and aqua lines show results from motif colocalization, computed as correlations between motif binding vectors in accessible regions across all cell types (green) or in hepatocytes (aqua). The star indicated a result from a recent mass-spectrometry-based TF–TF interaction atlas⁴⁰ (0.23 Macro F1 at 1.09% recall); and the round dot indicates the performance of a colocalization score computed from 677 HepG2 TF ChIP–seq (0.13 Macro F1 at 5.24% recall, Methods: ‘Causal discovery of regulator interaction’).

Full size image

Having obtained the network of causal motif interactions predicted by GET, we next built a structural catalogue of the human TF interactome using AlphaFold2 (ref. ⁴¹). We started by categorizing TF–TF interactions into several different catalogues: direct interactions, which included homodimers and intrafamily and interfamily heterodimers; and cofactor-mediated interactions, which encompassed both cooperative and competitive binding (Extended Data Fig. 8a). Starting with the most straightforward intrafamily interactions, we first acquired all dimeric structure predictions of more than 1,700 known human TFs and found that AlphaFold seemed to reliably capture known dimer structures and potentially could be used to detect intrafamily heterodimers (Methods: ‘AlphaFold benchmark on intrafamily binder prediction’, Extended Data Fig. 9a,b).

We then questioned whether the disordered region in the structure could fold upon binding to partners. On the basis of the causal-discovery-predicted TF–TF interactions, we sought to identify potential structural interactions using AlphaFold2. We first focused on two motif clusters with small numbers of member TFs, TFAP2/1 and ZFX, which were among the largest out-degree motifs in the GET causal network (Extended Data Fig. 7j). We segmented the TFAP2A and ZFX proteins into four distinct structured or disordered domains on the basis of the predicted local distance difference test (pLDDT) (Extended Data Fig. 8b) and predicted the multimer structure of all pairwise combinations of these segments. Remarkably, the originally unstructured ZFX intrinsically disordered region (IDR) (Extended Data Fig. 8c) folded into a well-defined multimeric structure when paired with TFAP2A structured domains; this was mainly driven by electrostatic interactions (Extended Data Fig. 8d). Molecular dynamics simulations (Methods: ‘Molecular dynamics simulation’) suggested that the monomer IDR had a more collapsed structure after 100 ns (Extended Data Fig. 8e) and fewer interchain hydrogen bonds (Extended Data Fig. 9c,d). Known motifs of the two TFs shared a common core (Extended Data Fig. 8f). In a coimmunoprecipitation experiment (Extended Data Fig. 8g), we were able to pull down ZFX using a TFAP2A antibody, whereas a negative control TF, SRF, showed no interaction with TFAP2A (Extended Data Fig. 9e, Methods: ‘TFAP2A coimmunoprecipitation’, and raw gel image in Supplementary Fig. 1).

In another example, the pair SNAI1 (Ebox/CACCTG) and RELA (NFKB/1) showed a strong predicted interaction effect size, but the absence of robust predicted structural interactions between the TFs led us to explore cofactor-mediated interactions (Extended Data Fig. 8a, bottom). Both of these TFs are known to physically interact with EP300 (ref. ³⁹), and the predicted structures indicated electrostatic interactions with the TAZ1 and TAZ2 domains of EP300 (Extended Data Fig. 8h–j). This is consistent with findings of previous studies on the electrostatic binding of the TF IDR to EP300 TAZ domains^42,43,44,45.

We expanded our analysis to include a broader range of TF interactions predicted by GET. We focused on the top 5% of predicted interactions in each cell type; this resulted in 1,718 TF pairs (or 24,737 pairs when considering individual protein segments). Using these data, we constructed a comprehensive structural catalogue of TF interactions (Methods: ‘Causal discovery of regulator interaction’). Further discussion and analysis of this catalogue can be found in the Supplementary Information: ‘Analysis of the GET causal network’ (Extended Data Fig. 9f–h).

To demonstrate the utility of information provided by the GET Catalog, we performed a case study on PAX5, a driver TF of B cell precursor acute lymphoblastic leukaemia (B-ALL)⁸. B-ALL is the most frequent paediatric malignancy, and somatic genetic alterations (deletions, translocations and mutations) in PAX5 occur in approximately 30% of sporadic cases⁹. Whereas most PAX5 somatic missense mutations affect the DNA-binding ___domain (V26G or P80R), G183S is a recurrent familial germline mutation that confers an elevated risk of developing B-ALL^8,9,10. Somatic mutation of G183 and frameshift in a nearby hotspot are also seen in patients with B-ALL⁴⁶. Although the pLDDT plot of PAX5 highlighted G183 and the octapeptide ___domain as a small peak in the entire IDR, its functional role has remained elusive (Fig. 5a).

a, pLDDT plot for PAX5, showing three mutational hotspots (V26G, P80R and G183S/A/V) and a frameshift hotspot⁴⁶. DBD, DNA-binding ___domain. b, B cell-specific motif interactions of PAX/2. PAX5 is the most highly expressed TF with a PAX/2 motif. The colour scheme follows that of Fig. 4a. c, AlphaFold3-predicted multimer structure of PAX5 IDR and NR2C2 NR ___domain showing contacts around G183 (B, back; f, front). The blue–yellow surface at the back represents hydrophilicity–hydrophobicity, respectively. Blue–red strands in the front show low–high prediction confidence. d, Detection of NCOR1, NRIP1, NR3C1 and NR2C2 PAX5-interacting proteins in streptavidin-enriched eluates (enrichment) from PAX5-WT, PAX5 G183S and RHOA WT-BioID-expressing B-ALL REH cell lines and in total protein lysates (1% input) using proximity labelling assays. Three independent experiments with similar results. A representative experiment is shown. GAPDH was used as a loading control in the same gel. Raw gel images are in Supplementary Fig. 2. e, Quantification of PAX5–NR2C2 interaction in the streptavidin immunoprecipitation shown in d. Data are presented as mean values with s.d. as well as total NR2C2-normalized values.

Full size image

To probe this, we first explored potential interaction pairs involving PAX5 (PAX/2 motif) in fetal B lymphocytes (CXCR5⁺). We identified interactions with several motifs, including E2F/2, RFX/1, MECP2, ZSCAN3 and NR/3 (Fig. 5b). Subsequent exhaustive segment interaction screening with AlphaFold Multimer revealed a new interaction between the nuclear receptor ___domain of NR/3 TFs and the octapeptide ___domain of PAX5; this was supported by AlphaFold3 (Fig. 5c). This interaction was further corroborated by both positive affinity purification mass spectrometry data for their paralogue PAX2-NR2C2 (ref. ⁴⁰) and a study using BioID proximity labelling followed by mass spectrometry in mouse pre-B cells⁴⁷. The binding interface of the PAX5 IDR and NR domains showed hydrophobicity and, surprisingly, contained the G183 residue as well as a series of serine residues linked by hydrogen bonds. Thus, the glycine-to-serine mutation could potentially affect PAX5 interaction with the NR ___domain.

To validate the interaction between PAX5 and NR/3-motif-containing proteins, we selected candidate NR/3 TFs by assigning priority to all TFs in the NR/3 motif family on the basis of their expression in 15 B-ALL PAX wild-type (PAX-WT) patient samples in a longitudinal study. We found the highest expressed NR/3 TFs to be NR4A1 and NR2C2, with NR2C2 showing less variable expression across patients. We performed proximity labelling assay using PAX5-WT and the PAX5 G183S mutant linked to a biotin ligase in the B-ALL REH cell line. Analysis of proteins biotinylated by their proximity to the PAX5-BioID fusions identified the nuclear corepressor NCOR1 (a previously described PAX5 interactor^48,49), NR2C2 (an NR/3-motif-containing nuclear corepressor) and NRIP1 (a nuclear-receptor-interacting protein). This experiment showed a clear interaction between PAX5 and NR2C2, consistent with a previous report^40,47, whereas NR4A1 showed no interaction with PAX5. NR3C1, a NR/20 motif TF that was predicted by GET to interact with NR/3 but not PAX/1, showed no interaction with PAX5. Notably, the presence of the G183S mutation resulted in an increased interaction between PAX5 and NR2C2 (Fig. 5d,e, Extended Data Fig. 10 and raw gel image in Supplementary Fig. 2).

To determine whether the PAX/2 and NR/3 motifs coregulated genes, we examined the top 10,000 promoters predicted to be most influenced by these motifs. Our analysis identified a set of 2,570 genes commonly regulated by both (Extended Data Fig. 11a); these included surface markers such as CD19 and CD79B, as well as known oncogenes that have been implicated in B-ALL, including MYC, CEBPD and LMO2, although these oncogenes were also predicted to be strongly repressed by IKZF1 (IKAROS tumour suppressor, with ZNF143 motif) and were not highly expressed. Enrichment analysis showed over-representation of genes involved in lymphocyte activation and genes affected by PAX5 perturbation during B cell differentiation (Extended Data Fig. 11b), consistent with previous work on the G183S mutation^{8,50,51,52,53,54,55}. On the other hand, the genes that were specifically regulated by PAX/2 or NR/3 were enriched in neuronal pathways and the cell cycle, respectively (Extended Data Fig. 11c,d).

To investigate the effects of the PAX5 G183S mutation on transcriptional programs of NR/3- and PAX5-regulated genes, we examined 141 sporadic childhood B-ALL samples, including four familial B-ALL samples with PAX5 G183S germline variants. We first selected only CDKN2A loss cases (n = 20) to match with familial cases (n = n, biallelic mutations, loss of PAX5-WT and CDKN2A). We further stratified the patients into two groups to perform two different comparisons: PAX5-WT (n = 10) versus PAX5 loss (n = 10) as a negative control; and PAX5 G183S (n = 4) versus PAX5 loss-of-function cases (for instance, PAX5 P80R, PAX5 loss, n = 12) to define the G183S-specific transcriptome signature. The analysis identified a specific transcriptional program associated with the G183S mutation (Extended Data Fig. 11e). To evaluate whether this specific transcriptional program was relevant to PAX5–NR interaction, we performed further gene set enrichment analysis and found enrichment in the PAX5-loss-associated differential expression genes (fold enrichment: 1.22, P = 1.5 × 10^–3, hypergeometric test with Benjamini–Hochberg correction) with predicted PAX5 targets and no significant enrichment in NR/3-regulated and PAX5 + NR/3-regulated genes, as expected. However, the PAX5-G183S-specific differential expression genes show significant enrichment in NR/3- and PAX5 + NR/3-regulated genes (fold enrichment: 1.41 and 1.35; P = 1.05 × 10⁻³⁰ and 1.57 × 10⁻¹⁸, respectively). Moreover, we found that this mutant specific differential expression gene set was also enriched among the genes activated in ProB cells (fold enrichment: 1.57, P = 2.2 × 10⁻³), including well-known functionally relevant genes such as CD19, EBF1, BACH2 and PML (Extended Data Fig. 11f).

In this study, we introduce GET, a state-of-the-art foundation model specifically engineered to decipher mechanisms governing transcriptional regulation across a wide range of human cell types. By integrating chromatin accessibility data and genomic sequence information, GET achieves a level of predictive precision comparable with experimental replicates in leave-out cell types. Furthermore, GET demonstrates exceptional adaptability across an array of sequencing platforms and assay types, as well as non-physiological cell types such as tumour cells. Through interpretation of the model, we identified long-range regulatory elements in fetal haemoglobin and their associated TFs. Collecting regulatory information from all 213 cell types and synergizing TF–TF interactions deduced through GET with protein structure predictions, we constructed the publicly accessible GET Catalog (https://huggingface.co/spaces/get-foundation/getdemo). Using the PAX5 gene as a case study, we illustrated the utility of the catalogue in identifying functional variants in disordered protein domains that were previously difficult to study.

Current limitations of GET include a reliance primarily on chromatin accessibility data, bounded resolution to distinguish between TF homologues that have very similar motifs, and training on only coarse-grained cell states and region-level sequence information. Future enhancements to GET could involve the incorporation of multiple layers of biological information, including but not limited to nucleotide-level regulator footprints^13,56,57, three-dimensional chromatin architecture^58,59, and regulator expression profiles or single-cell embeddings^18,19,20. Future iterations of GET could incorporate more diseased, perturbed or treated cell states and a broader range of assays, including those that directly measure TF binding, histone modifications and PolII activity, to provide a more holistic view of the regulatory landscape.

Multiplexed nucleotide-level perturbations or randomizations will be instrumental in calibrating GET for precise prediction of the functional impact of non-coding genetic variants. Determining the effects of non-coding variants in modulation of gene expression and disease susceptibility remains an important area of exploration. Integrating genomic variants into the GET framework will enable more accurate prediction of their impact on gene regulation, resulting in insights into the genetic basis of complex traits and diseases. In addition, the kinetics of gene regulation, reflecting the temporal changes in transcriptional activity in response to developmental cues or environmental stimuli, is another dimension of complexity that could be integrated into the model. As in our PAX5–NR2C2 example, other types of information such as TF expression in specific cell types or protein–protein interaction data could help to further narrow down specific TFs within motif–motif interaction networks predicted by GET. With our efficient fine-tuning framework, comparative interpretation analysis using pretrained and fine-tuned GET could be used to identify important regulatory regions or motifs driving cell state changes. Generative models built upon GET could be developed and used to design megabase-scale enhancer arrays and engineer cell-type-specific TFs or their interaction inhibitors for targeted therapeutic interventions. Collectively, GET represents a pioneering approach in cell-type-specific transcriptional modelling, with broad applicability in the identification of regulatory elements, upstream regulators and TF interactions.

ATAC-seq data processing

Pseudobulk

To determine the chromatin accessibility score for each region, we used the scATAC-seq count table and cell annotation table from each respective study. To aggregate single cells into ‘pseudobulk cell types’, we used the Louvain clustering results from each study. Log count per million (logCPM) was used for each pseudobulk. The annotations of each cluster were used to determine the biological cell type. Empirically, we set a threshold of more than 600 cell counts to ensure adequate sequencing depth for selected cell clusters. A comprehensive table of pseudobulk cell types used during the training process can be found in Supplementary Table 1.

In summary, we used ATAC-seq and expression data from refs. ^1,2,22. In total, the dataset encompassed 1.3 million single nuclei. The data were only presented in pseudobulked format. All cell types were primary cell types from normal tissue. No disease states were included in the pretraining dataset. We incorporated further datasets in downstream tasks such as K562 and zero-shot analysis in tumour cells.

Cell-type-specific accessible region identification

For identification of cell-type-specific accessible regions, the peak calling results from the original studies of each dataset were used to obtain a union set of peaks. Subsequently, to compile a list of accessible regions specific to each cell type, we filtered out peaks with no counts.

In the context of the human fetal and adult chromatin accessibility atlas, we used the peak set produced by Zhang et al.², incorporating the fetal chromatin accessibility atlas originally published by Domcke et al.¹. We also trained a version of the fetal-only GET model using the original peak calling and cell type annotation from Domcke et al.¹, resulting in comparable expression prediction and regulatory analysis performance. For the 10× multiome data, we used the provided peak fragment count matrix. For the K562 NEAT-seq and bulk chromatin accessibility data, a more permissive version of peaks was called using MACS2 (ref. ⁶⁰), and different logCPM cutoffs were applied to the resulting peak set to select accessible regions. This accessibility-based data augmentation enhances the diversity of input data and fine-tunes the GET model for data from a single cell type.

Accessibility features

In this study, the chromatin accessibility score for a specific genomic region was defined by the count of fragments located within that region for a given cell type pseudobulk. To enhance the generalizability of the model, these counts were further normalized through the logCPM procedure. Specifically, let t be the total fragment count in a pseudobulk, and let c_i be the fragment count in region i. Then, the accessibility score s_i can be computed as:

For most of the regulatory analysis, the binary ATAC version of the GET model was used to comprehensively evaluate the regulatory influences exerted by TFs. In both the training and inference phases of this specific model version, the accessibility scores were uniformly set to 1 if the region was identified as a chromatin accessibility peak. This equates to assuming binary chromatin accessibility states in the studied scenario.

Motif features

To calculate the motif binding score within a specific genomic region, the corresponding sequence was scanned against the hg38 reference genome, using 2,179 TF motif position weight matrices previously compiled by Vierstra et al.¹³ (accessible at https://www.vierstra.org/resources/motif_clustering). For the scanning process, the MOODS tool was used with default threshold⁶¹.

More specifically, to represent sequence information while mitigating feature redundancy, a specialized motif scoring process was implemented. Building on Vierstra’s research, we categorized these 2,179 motifs into 282 motif clusters, a classification determined by position weight matrix similarity. Using this established clustering definition, we eliminated redundant nucleotide-level motif matches, retaining only the match with the highest score within overlapping matches belonging to the same motif cluster. Subsequently, the scores of all non-overlapping motif matches within each motif cluster were summed, yielding one cumulative score for each of the 282 clusters. As a final step, motif binding scores for all regions within a given cell type were determined and subjected to min–max normalization across regions. This normalization facilitates model generalization and the training process, ensuring that each motif cluster’s score is processed in a standardized manner.

The annotation of the 213 cell types used in pretraining followed the original cell type classification provided in the fetal and adult accessibility atlases^1,2,22. This classification was achieved through clustering of ATAC-seq count profiles, with subsequent labelling on the basis of the expression of known marker genes. The comprehensive list of tissues and cell types, along with their annotations, can be found at the Human Cell Atlas (http://catlas.org/humanenhancer/#!/cellType). The original atlas included 222 fetal and adult cell types but was further filtered to remove cell types with low sequencing coverage (number of cells less than 600). This approach ensured that our model was trained across diverse cellular contexts while ensuring enough coverage in the chromatin accessibility pseudobulk tracks. The data were not further balanced or curated.

Input data

GET is designed to capture the interaction between different regions and regulators. To facilitate this, we needed each input sample to contain a certain number of consecutive accessible regions, mimicking the ‘receptive field’ of an RNA PolII. Through previous experiments, we found that the ideal equivalent genome coverage is around or more than 2 Mbp, a range in which most of the chromatin contact happens. As a result, on the basis of our current data prepossessing pipeline, we chose to use 200 input regions per training sample. We used non-overlapping sampling during the pretraining and a sliding window approach during fine-tuning. The stride of the sliding window was set to half the number of regions in one sample (that is, 100 peaks per step for samples with 200 peaks).

This number of regions per sample was selected to achieve a balance between computational efficiency and the need to encompass a representative sample of the regulatory landscape for each cell type. It is important to note that the actual genomic span covered by these 200 peaks could vary depending on several factors, including cell-type-specific variations in chromatin accessibility, the threshold applied during peak calling and the chromosomal distribution of the peaks. In the context of the uniformly processed datasets covering fetal and adult cell types, we have observed that 200 peaks typically correspond to a genomic range of approximately 2–4 Mbp. This estimation was derived from the understanding that the human genome, with its roughly 3 billion base pairs, yields about 150,000 accessible peaks when analysed comprehensively. Therefore, a subset of 200 peaks would, on average, represent a genomic span of 2–4 Mbp, given the distribution and density of peaks across different cell types. In the training of our main model, the borders were entirely dependent on the boundary of sampled peaks; no other priors were used. Sampling was performed independently in each chromosome starting from the beginning of the chromosomes.

RNA-seq data processing

Cell type matching

For experiments encompassing multiomics, the correspondence between accessibility and expression was inherently determined through cell barcodes. In pseudobulk cases, where accessibility and expression were assessed independently, cell type annotations were used to facilitate the mapping. Specifically, the fetal expression atlas from Cao et al.²³ was used for fetal cell types, whereas adult data were extracted from Tabula Sapiens²⁴. When several ATAC pseudobulk shared the same cell type annotation, identical expression labels were assigned. This compromise was necessitated by the current dearth of multiome sequencing data, a situation expected to change dramatically in the near future.

Expression values

To improve training stability, we log-transformed the expression values as log₁₀(TPM + 1). To overcome the problem of most scRNA-seq quantification being at gene level, not transcript level, we mapped the gene expression to accessible regions using the following approach: if a region overlapped with a gene’s TSS, the gene’s expression value was assigned to that region as a label; if a region overlapped with multiple genes’ TSS, the expression values of the corresponding genes were summed, and the sum was used as the label of that region; if a region did not overlap with any TSS, the corresponding expression label was set to 0. Further, if a promoter had very low accessibility (for instance, an accessibility CPM (aCPM) less than 0.05), we also set the corresponding expression value to 0. Finally, each regulatory element was assigned to an expression target value.

Expression values were allocated to each region within our input. Owing to the limitations of poly(A) scRNA-seq data, only aggregated mRNA levels could be captured, resulting in values that were not reflective of the nascent transcription rate more closely tied to regulatory events. Nonetheless, these values provided valuable cell-type-specific information. The process begins by intersecting the input region list with GENCODE v.40 transcript annotation to pinpoint promoters, followed by assignment of logCPM values to regions corresponding to these promoters. All remaining regions are assigned a value of 0. Although this does not perfectly represent all transcription events happening in a cell, we believe the zero label on the non-promoter region helps to deliver informative negative labels to the model.

Input target

In alignment with the 200 × 283 input matrix, the target input is a 200 × 2 matrix, symbolizing the transcription levels of the corresponding 200 regions across both positive and negative strands.

Model architecture

The GET architecture consists of three parts: (1) a regulatory element embedding layer (RegionEmb); (2) regulatory-element-wise attention layers (Encoder); and (3) a linear output layer as the expression prediction head, or, alternatively, other output heads. GET takes 200 regulatory elements, each with 282 motif binding scores and optionally one accessibility score as an input sample. As a result, the input is a 200 × 283 matrix. When we choose to not use the quantitative accessibility score, we set the values in the 283-th column to 1.

We feed the sample into the RegionEmb layer to generate the regulatory element embedding with a dimension of 768 for each peak. As we do not want to lose information in the input of the original regulatory element, we apply a linear layer to capture the general information in the different classes of TF binding sites. To learn the cis- and trans-interactions between regulatory elements and TFs, we apply 12 Encoder layers with a multihead attention (MHA) mechanism on the regulatory element embeddings.

Suppose N_h, d_v and d_k denote the number of heads, the depth of values and the depth of keys, respectively. The output from each head h is computed as

where \({W}_{q},{W}_{k}\in {{\mathbb{R}}}^{(n\times D)\times {d}_{{\rm{k}}}},{W}_{v}\in {{\mathbb{R}}}^{(n\times D)\times {d}_{{\rm{v}}}}\) are learnable linear transformations.

Then, we concatenate the output from each head h for the regulatory-element-wise attention block. The layer normalization (LN), feed-forward network (FFN) and residual connections are finally used to generate the output for each layer. Thus, the mechanism behind the regulatory-element-wise attention block can be summarized as:

where \({{\rm{z}}}_{l}^{{\prime} },{{\rm{z}}}_{l-1}\) denote the intermediate representation in the block \(l\), \({{\rm{z}}}_{l-1}\) denotes the output from the block \(l-1\), LN is the layer normalization and FFN is the feed-forward network. We apply two linear layers with a GELU activation layer in the feed-forward network layer.

The GET architecture is similar to the state-of-the-art model Enformer⁴. However, the following changes helped us to improve upon and exceed the performance of that model: GET uses the regulatory element embedding layer to capture the general information of regulatory elements in the different classes of TF binding site. Moreover, a masked regulatory element mechanism was used to learn the general cis- and trans-interactions between regulatory elements and TFs from different human cell types. Specifically, a random set of positions was uniformly selected to mask out with a mask ratio of 0.5.

Similar to the Vision-Transformer-based Masked Autoencoders⁶², we replaced the regions in the selected positions with a shared but learnable \([{\rm{MASK}}]\) token; the masked input regulatory element is denoted by \({X}^{\text{masked}}=(X,M,[{\rm{MASK}}])\), where \(X={\{{x}_{i}\}}_{i=1}^{n}\) is the input sample with \(n\) regulatory elements. The training goal is to predict the original values of the masked elements \(M\). Specifically, we take masked regulatory element embeddings \({X}^{\text{masked}}\) as input to GET, while a simple linear layer is appended as the prediction head. Therefore, the overall objective of self-supervised training can be formulated as:

where \({x}_{i}\) denotes the masked region to be predicted.

Training scheme

We conducted pretraining in the large-scale single-cell chromatin accessibility data. Then we fine-tuned the pretrained model on the paired chromatin accessibility–gene expression data with the same Poisson negative log-likelihood loss function as Enformer⁴.

The GET implementation is based on the PyTorch framework. For the first training stage, we applied AdamW as our optimizer with a weight decay of 0.05 and a batch size of 256. The model was trained for 800 epochs with 40 warmup epochs for linear learning rate scaling. We set the maximum learning rate to 1.5 × 10⁻⁴. The training usually takes around a week for a cluster with 16 V100 GPUs. For the second fine-tuning stage, we used AdamW⁶³ as our optimizer with a weight decay of 0.05 and a batch size of 256. The model was trained for 100 epochs, which completes in around 8 h using eight A100 GPUs. Inference for all genes in a single cell type takes several minutes, making it possible to perform large-scale screening.

Training details

We include a more detailed description of the optimization hyperparameters, computation infrastructure and convergence criteria used in the development of the model in the section below.

Pretraining phase

1. 1.

   Computation infrastructure: the pretraining of our model was conducted using 16 NVIDIA V100 GPUs or eight A100 GPUs, reflecting the computational demands of our training dataset and the complexity of the model architecture.

2. 2.

   Epochs and duration: the model underwent 800 epochs of training, which spanned approximately 1 week. This extensive training period was essential for the model to learn the regulatory grammar from chromatin accessibility data across a wide array of human cell types.

3. 3.

   Learning rate: a base learning rate of 1 × 10⁻³ together with cosine scheduler and linear annealing warmup in the first epoch.

4. 4.

   Mask ratio: 0.5.

5. 5.

   Optimizer: AdamW with weight decay of 0.05.

Fine-tuning phase

1. 1.

   Computational infrastructure: similar to the pretraining phase, fine-tuning was performed on eight NVIDIA A100 GPUs, ensuring consistency in computational resources.

2. 2.

   Epochs and duration: the fine-tuning process was shorter, consisting of 100 epochs, and completed in around one day. This phase was crucial for adapting the pretrained model to specific gene expression prediction tasks.

3. 3.

   Learning rate: A base learning rate of 1 × 10⁻³ together with a cosine scheduler and linear annealing warmup in the first epoch.

4. 4.

   Optimizer: AdamW with weight decay of 0.05.

5. 5.

   Early stopping: to optimize performance and prevent overfitting, we used early stopping on the basis of validation loss, enabling us to select the best model checkpoints for subsequent evaluation.

Parameter-efficient fine-tuning

GET provides an option to perform parameter-efficient fine-tuning over any specific layer through low-rank adaptation (LoRA)⁶⁴. This is commonly used to adapt to a new assay or platform; we apply LoRA to the region embedding and encoder layers, while doing full fine-tuning on the prediction head. This markedly reduces 99% of the parameters.

Model evaluation

Cross-cell-type prediction

We validated the cross-cell-type prediction performance beyond astrocytes to include a broader range of cell types. The benchmark was performed on fetal cell types with a variable length peak set defined in the original fetal accessibility atlas¹. This comparison includes quantitative ATAC GET (n = 3), binarized ATAC GET, linear probing of the Enformer CAGE output tracks trained on the Basenji¹⁵ training set and inferred genes in the Basenji test set, and a training cell type mean expression baseline. We used Pearson correlation, Spearman correlation and R² to evaluate prediction performance in all settings.

Benchmarking against supervised approaches

We have implemented comparisons with the following methods on the task of expression prediction when leaving out chromosome 11 and leaving out astrocytes, using the same input data as GET. The following parameters were used in our implementation.

1. 1.

   MLP: three linear layers separated by ReLU (layer dimensions: 283 input, 512, 256, two output); SoftPlus was used for output activation.

2. 2.

   CNN: three Conv1d layers (layer dimensions: 283 input, 128, 64, 32, 3 kernel size) followed by FC(32, 512) → ReLU → FC(512, 2); SoftPlus was used for output activation. We used the same optimizer and parameters as used in GET (base learning rate: 1 × 10⁻³, cosine scheduler, linear annealing warmup, AdamW optimizer with weight decay of 0.05).

3. 3.

   CatBoost: we used CatBoostRegressor with loss function MultiRMSE for 1,000 iterations (learning rate: 1 × 10⁻³).

4. 4.

   SVM: we used scikit-learn Support Vector Regression with epsilon 0.2, linear kernel and max iterations 1,000. MultiOutputRegressor was used to handle two-dimensional output.

5. 5.

   Random forest: we used scikit-learn RandomForestRegressor with ten estimators and max depth 10. MultiOutputRegressor was used to handle two-dimensional output.

6. 6.

   Linear regression: we opted to use linear regression instead of logistic regression because our setting aligns better with regression than classification. We used scikit-learn LinearRegression and MultiOutputRegressor with default parameters.

Leave-out-chromosome evaluation

We performed a leave-one-chromosome-out benchmark across all chromosomes and found that the performance remained consistent across chromosomes, conditioned on the same sequencing platform and data sources. We found an average Pearson correlation of 0.78 (minimum: 0.73, maximum: 0.84) on fetal astrocytes. We also extended our evaluation of leave-out chromosomes to tumour cells from patients with IDH1 wild-type GBM from the Human Tumor Atlas Network. We performed fine-tuning of the base GET model on tumour cells from a single patient (case ID: C3L-03405) and evaluated performance on each leave-out chromosome. This evaluation showed an average Pearson correlation of 0.75 (minimum: 0.68, maximum: 0.81) on leave-out chromosomes.

For K562 OmniATAC prediction, we performed leave-one-chromosome-out prediction for all 22 autosomes, finding an average Pearson correlation of 0.81 (minimum: 0.72, maximum: 0.84). For K562 CAGE prediction, we used GET to predict K562 CAGE (FANTOM5 sample ID: CNhs12336). We note that this comparison privileges Enformer, which was trained extensively on CAGE tracks, including K562 (track ID: 4828 and 5111), whereas GET needed to be transferred to the new assay. Here we evaluated fine-tuned GET against Enformer predictions summed across the two CAGE output tracks for a leave-out peak set across chromosome 14. We selected chromosome 14 because it did not appear in the public Enformer checkpoint’s training or validation set. Pretrained GET was fine-tuned in three ways.

1. 1.

   BATAC LoRA from BATAC pretrain: in this setting, the base model was trained on the fetal and adult atlases with binarized ATAC signal. In the fine-tuning, the ATAC data were binarized.

2. 2.

   QATAC LoRA from BATAC pretrain: in this setting, the base model was trained on the fetal and adult atlases with binarized ATAC signal. In the fine-tuning, we used the original aCPM for ATAC signal.

3. 3.

   QATAC LoRA from QATAC fine-tuned: in this setting, the base model was the leave-out astrocyte RNA-seq prediction model trained on the fetal accessibility and expression atlas. In the fine-tuning, we used the original aCPM for ATAC signal.

These experiments leveraged LoRA parameter-efficient fine-tuning to achieve significant gains in time and storage complexity. On a single RTX 3090 GPU, all fine-tuning converged within 30 min, resulting in a 3 MB K562-CAGE-specific adaptor that could be merged into the base model.

Leave-out-motif evaluation

To explore the impact of omitting motifs in the input features, we used K562 scATAC-seq data from ENCODE (accession: ENCFF998SLH) and evaluated the ATAC prediction performance when holding out randomly selected motifs. We first called peaks with MACS2 with a threshold of q = 0.05. Then, we merged this peak set with the union peak set from the fetal pretraining data, keeping the peaks with at least ten counts in K562. For fine-tuning computational efficiency, we used LoRA parameter-efficient fine-tuning of the binary ATAC checkpoint pretrained on fetal and adult ATAC data with a 200-region receptive field (the pretrained checkpoint used for motif analysis in Fig. 4 and onward).

We explored holding out randomly selected 1, 2, 3, 4, 10 and 20 motifs. For each motif, we checked whether a peak’s binding score was larger than the top 20% scores in its score distribution across the genome. During the training stage, if a peak had any of the leave-out motifs passing this threshold, we set all input motif features of that peak as well as the observation aCPM to zero. In this approach, these ‘knockout’ peaks do not contribute to the loss. During the evaluation stage, we calculated Pearson and Spearman correlations of aCPM only on these knockout peaks with the original observed aCPM. For example, when there was only one leave-out motif CTCF, we were in effect be training with about the top 20% of peaks that had low CTCF binding scores on the training chromosomes, assuming evenly distributed binding sites across chromosomes. Similarly, we were evaluating with 20% of peaks with higher CTCF binding scores in the test chromosomes. In these experiments, we evaluated on held-out chromosome 14.

In general, GET showed robust performance when leaving out one to ten motifs. The performance was degraded heavily when using 20 motifs with a top 20% cutoff for each motif independently, owing to removal of most of the training data.

Platform transfer prediction

When transferring to a new sequencing platform, many ___domain shifts need to be addressed. These include but are not limited to the following.

1. 1.

   Sequencing depth: lower depth will lead to fewer captured peaks; it will also affect the signal-to-noise ratio in the accessibility quantification.

2. 2.

   Peak calling threshold and software.

3. 3.

   Technical bias due to different library construction and sequencing methods.

4. 4.

   Biological differences.

Owing to these biases, it is difficult to directly apply a model trained on one dataset to a new platform without fine-tuning. Thus, for a new dataset with multiple cell types available, we took a leave-out cell type approach to fine-tuning. For a dataset of sorted cell types where only one cell type was available, we used leave-out chromosome training.

Transfer to new datasets

The primary challenge in adapting our model to new data lies in ensuring compatibility between the input spaces of the training and new datasets. Variations in cell types, sequencing technologies and preprocessing pipelines can result in substantially different ATAC peak sets, potentially leading to incompatible input and embedding spaces. To address this, we developed a strategy to create a compatible peak set by combining new and training peak sets. When overlaps occur between training and new peaks, we assign priority to the training peak set coordinates. Unique peaks from the new data are incorporated as they are. We used a uniform peak calling pipeline to maintain consistent peak lengths (for instance, 400 bp in the fetal–adult atlas) across training and new datasets. The comprehensive coverage of our fetal-only/fetal–adult peak set (1.3 M peaks) typically results in new, unseen peaks contributing less than 10% of the total peaks. This approach has demonstrated promising transferability to various data types, including SHARE-seq data of perturbed human embryonic stem cells and 10× multiome GBM data.

For example, we tested a ‘one-shot’ fine-tuning procedure using a single patient sample from a new dataset of patients with GBM. We then assessed the performance of this fine-tuned model against the pretrained ‘zero-shot’ model on 16 held-out patient samples. To ensure robust evaluation, we excluded two patients from this analysis to serve as a separate test set for assessing fine-tuning stability. The results were promising: fine-tuning on a single tumour patient sample enabled GET to achieve a Pearson correlation exceeding 0.9 when predicting expression for held-out patients, whereas zero-shot performance reached a 0.67 Pearson correlation. This demonstrates the model’s strong generalization capabilities and its potential for rapid adaptation to new datasets with minimal further training. As the availability of ATAC-seq and multiome data continues to grow, more comprehensive reference peak sets, such as the ENCODE DHS index¹³ and cPeaks⁶⁵, will further facilitate the adaptation of the GET model to an even broader range of cell types and experimental conditions.

Transfer to new assays

Here we show results for transfer of pretrained GET to different functional genomics assays. For K562 bulk ATAC prediction, we collected ENCODE OmniATAC-seq data for K562 (ENCSR483RKN). After calling peaks using MACS2 with default parameters, we computed the log(aCPM) by counting Tn5 insertions located inside the peak and filtered out the peaks with log(aCPM) less than 0.03. The remaining peaks and corresponding aCPM were used for motif scanning and prediction. We performed leave-one-chromosome-out fine-tuning using 200 peaks per input sample. The base checkpoint was trained on the fetal and adult atlas with the binarized ATAC setting and 200 peaks per input sample. LoRA was used for all layers. Each fine-tuning took around 160 s to complete eight epochs, after which the model started to overfit. Pearson correlation was collected at eight epochs for all fine-tuning. For CAGE prediction, we collected the K562 CAGE (CNhs12336) BAM file from FANTOM5 and used bedtools to extract alignment counts in peaks called from ENCODE K562 scATAC-seq data (ENCFF998SLH). Fine-tuning was performed using 200 peaks per input sample in three settings, depending on how ATAC information was used in conjunction with motif features, plus the base model used for fine-tuning.

1. 1.

   BATAC from BATAC pretrain: in this setting, the base model was trained on the fetal–adult atlas with binarized ATAC signal; in the fine-tuning, we used binarized ATAC.

2. 2.

   QATAC from BATAC pretrain: in this setting, the base model was trained on the fetal–adult atlas with binarized ATAC signal; in the fine-tuning, we used the original aCPM ATAC signal.

3. 3.

   QATAC from QATAC fine-tuned: in this setting, the base model was the leave-out-astrocyte RNA-seq prediction model trained on the fetal accessibility and expression atlas. We further fine-tuned this model using quantitative ATAC signal.

Dataset considerations

Overall our results indicate that certain intrinsic cellular characteristics may contribute to the observed variations in model performance. We demonstrate that GET can be applied and extended to non-physiological cell types and states and captures cell-type-specific transcription information. Beyond the intrinsic biological differences between cell types, we believe the following factors could also affect performance when generalizing to new datasets.

1. 1.

   Cell type rarity and library size: rare cell types often have smaller data libraries, which can limit the model’s learning potential and affect the accuracy of predictions.

2. 2.

   Cell type purity and heterogeneity: the dynamic and heterogeneous nature of certain cell types, such as stem cells, and the precision of identification and classification of cell types can introduce variability in gene expression profiles, complicating the prediction task.

Model interpretation

In this study, we conducted thorough model interpretation analyses to ensure that GET learns useful regulatory information and offers valuable biological insights. Below, we outline the method used to interpret GET.

Model used for interpretation

We trained two GET models on data with or without quantitative accessibility:

1. 1.

   Quantitative ATAC model: accessibility scores are set to the log₁₀(CPM) of Tn5 insertions in the given accessible region.

2. 2.

   Binary ATAC model: accessibility scores for all regions are set to \(1\); the model focuses solely on motifs in accessible regions.

In our analysis and regulatory interpretation, we primarily used the binary ATAC model. This approach offers improved attribution to sequence features, ensuring that the model does not overly depend on accessibility signal strength as a surrogate for sequence characteristics.

Feature attribution methods

We used multiple feature attribution methods in different analyses and provided all options to users in our packages. More specifically, the gradient of the model’s output with respect to the input features, represented by the vector \(\nabla f(x)\), measures how much the model output (expression) will change when we change a small amount of the input along a dimension (for instance, a certain motif in a cis-regulatory region). The generalization to multiple outputs in the context of neural network feature attribution extends to the Jacobian matrix \({J}_{i,j}=\frac{\partial {f}_{i}}{\partial {x}_{j}}\), where f_i is the ith output, representing the transcription level on either the positive or negative strand, and x_j is the jth input feature, comprising scanned and summarized binding scores for 282 TF motif clusters and an extra dimension for accessibility scores. This formulation enables computation of the Jacobian matrix, which is vital for understanding the influence of individual features on the transcription levels.

Enhancer–gene pair prediction

We restricted the benchmark dataset to either the fetal erythroblast peak set or K562 DNase peak set for a fair comparison. To obtain an enhancer importance score for each gene from GET, we used the ℓ²s-norm of the region embedding layer Jacobian and weighted it with the aCPM of each region as the GET Jacobian score. This procedure could potentially be improved in the future, for example, by using a random genomic background as the baseline for the Jacobian calculation and other interpretation methods such as Integrated-Gradients⁶⁶ or DeepLIFT⁶⁷. However, we believe the current benchmark dataset size for this task is still limiting compared with the genome scale (10⁴ measured pairs versus 10⁶ to 10⁷ required measurements of genome-wide enhancer–promoter interaction). Thus, we leave the systematic optimization of this task for future work. Other scores used in this study were as follows.

1. 1.

   ABC: we computed ABC Powerlaw by multiplying the powerlaw function in the official ABC repo with γ = 1.024238616787792 and scale = 5.9594510043736655, values that were trained on K562 Hi-C data and provided in the same repo.

2. 2.

   Enformer: we used Enformer’s contribution score (gradient × input) with background normalization, following the normalization procedure described by Gschwind et al.³³.

3. 3.

   HyenaDNA: we used the largest pretrained model available through Hugging Face (context length: 1 Mbp). To score enhancer–gene pairs, we performed in silico mutagenesis by knocking down the enhancer element (that is, setting each base pair in the enhancer region to the unknown nucleotide N in the vocabulary set) and comparing against the wild-type likelihood of observing the promoter sequence.

4. 4.

   DeepSEA: nucleotide-level DeepSEA results were retrieved directly from the original publication and averaged over each peak.

All scores in this benchmark (ABC, Enformer, GET, HyenaDNA, DeepSEA and DNase/ATAC) were further normalized across each gene’s ±100 peaks to make them comparable across genes.

Recent studies have highlighted the dominant importance of one-dimensional genomic distance in governing CRISPRi enhancer knockout effects (for instance, Gschwind et al.³³). In this benchmark, most methods include a component of genomic distance. For example, Enformer incorporates exponential decay in its positional encodings. HyenaDNA incorporates a sinusoidal positional encoding over the DNA sequence, and our benchmarking results follow an exponential decay from the TSS (Fig. 3c; NFIX). We have also extended GET to incorporate distance information. In particular, we designed a simple DistanceContactMap module for GET to convert the pairwise one-dimensional distance map between peaks to a pseudo-Hi-C contact map. DistanceContactMap is a simple three-layer two-dimensional convolutional neural network (kernel size: 3) with \({\log }_{10}(\text{pairwise distance}\,+\,1)\) as input and SCALE-normalized observed contact frequency as output. A Poisson negative log-likelihood loss was used to train the model. We trained DistanceContactMap with the same K562 Hi-C data (ENCFF621AIY) used for training ABC Powerlaw, resulting in a 0.855 Pearson correlation, which mostly captured the exponential decay in contact frequency. We termed the prediction of this model ‘GET Powerlaw’. The other two scores shown in Fig. 3d are defined as follows:

1. 1.

   GET (Jacobian, DNase/ATAC, Powerlaw) = GET Jacobian + aCPM × GET Powerlaw;

2. 2.

   GET (Jacobian, Powerlaw) = GET Jacobian × GET Powerlaw.

This model could be improved in future work by taking GET region embeddings as further input and learning to predict cell-type-specific three-dimensional contacts.

LentiMPRA zero-shot prediction

The experimental procedure involves designing a library of lentivirus vectors that contain both desired sequence elements and a mini promoter. The vector is randomly inserted into the genome through viral infection; the regulatory activity is then measured through sequencing and counting the log copy number of transcribed RNAs and integrated DNA copies.

To simulate this approach using GET, we first collected the sequence element library and constructed the vector sequence for insertion, including both the regulatory sequences and mini promoters. We then followed the same data preprocessing procedure to get the motif scores of the inserted elements. For each element, we performed in silico insertion by summing its motif score with an existing region on the genome. The ±100 regions centred around the insertion region were then used as an input sample for GET to make expression predictions. The mean predicted expression (log₁₀(TPM)) was multiplied by the mean predicted accessibility as the predicted regulatory activity. For each region, we performed 600 insertions across the genome to match the experimental insertion count. We used the GET model fine-tuned on K562 NEAT-seq data to perform the inference. In total, in silico lentiMPRA of all 200,000 elements in K562 took around 5 days.

For Enformer, we performed the same analysis, with the only difference being that we integrated the vector sequence to a random position on the genome and collected a 196,608 bp sequence centred around the insertion site. Enformer is trained on 5,313 human epigenome tracks, with 486 experiments specifically for K562. To compute the regulatory activity, we selected the output from the K562 CAGE track, which is a quantitative and nucleotide-level map of the 5′ regions of transcripts. Following the practice of the original study, we used the average output of the three bins in the centre of the sequence as the predicted expression for a sample. Each element was also inserted into 600 random genome locations to compute the final averaged regulatory activity. We were only able to perform these experiments for 1,000 enhancers and 1,000 non-enhancer elements owing to the time complexity of Enformer inference. The comparison with GET was performed on the same set of elements.

We stratified the K562 lentiMPRA elements (approximately 200,000) by overlapping the annotated 15 ENCODE ChromHMM states computed from histone mark and other ChIP–seq data for K562. We selected the elements overlapping with states ‘12 EnhBiv’, ‘6 EnhG’ and ‘7 Enh’ as enhancers, and those overlapping with ‘13 ReprPC’, ‘14 ReprPCWk’ and ‘15 Quies’ as repressive and quiescent regions.

Identifying important regions and regulators

We first gathered inference samples across the genome by producing 200-region windows centred around each gene’s promoter. Given a specific gene g on strand \(s\in \{0,1\}\), the expression value can be inferred using the GET model f applied to an input matrix \({X}\in {{\mathbb{R}}}^{r\times m}\), where r denotes the number of regions, and m includes motifs and (optionally) accessibility features:

where \([\cdot ]\) is the index-selection operator and s is the strand of the gene.

The Jacobian matrix (tensor) J_X ∈ \({{\mathbb{R}}}^{r\times 2\times r\times m}\) of \(f\) at the point (E, X) evaluates how each output dimension will change when each input dimension changes by a small quantity. We specifically pick the output dimension and strand that correspond to the given gene, represented by \({\rm{\nabla }}g\in {{\mathbb{R}}}^{r\times m}\):

The feature (motif) importance vector \({{\rm{v}}}_{g}\in {{\mathbb{R}}}^{m}\) is obtained by multiplying the gradient element-wise with the original input and summarizing across regions:

where \(\odot \) signifies the element-wise or Hadamard product. As the gene-by-motif matrix is mostly used for feature–feature interaction analysis, we use the \(X\) with quantitative ATAC signal even when we infer \({J}_{X}\) using a binary ATAC model. This facilitates study of the relationship between regulators and observed chromatin accessibility.

The cell-type-specific genome-wide gene-by-motif matrix for cell type c, V_c is acquired by concatenating the \({{\rm{v}}}_{g}\) across the genome. The same process can be applied to different cell types.

Similarly, the region importance vector \({l}_{g}\in {{\mathbb{R}}}^{r}\) is given by:

In practice, we use the l₂-norm of the Jacobian of the region embedding with respect to output for calculating the region importance score as the embedding score distribution is less skewed than the input motif binding score, potentially making the Jacobian more comparable across regions. The per-region Jacobian score is normalized by the maximum score per gene to make scores comparable across genes with different expression levels.

Gene ontology enrichment of top target genes of a regulator

Using the gene-by-motif matrix \({V}_{c}\), we can choose a TF or motif (in our case, GATA) and ask which genes will be mostly affected by this TF by identifying the largest entries in the motif column. We chose the top 1,000 genes and performed gene ontology enrichment analysis using g:Profiler with the default g_SCS multiple hypothesis testing correction. We filtered the results using term size (gene number in a term definition) greater than 500 and less than 1,000. Terms with adjusted P value less than 0.05 were retained as significant terms. We further selected TFs in the ‘Hemopoiesis’ term with expression log₁₀(TPM > 1) for visualization against the GATA motif score.

TF and target gene correlation

In this analysis, we sought to elucidate the relationships between TFs and expression of their target genes across different cell types. Gene-by-motif files were aggregated and organized into a unified structure comprising genes, motifs and corresponding cell features. We identified the target genes for each TF within predefined motif clusters and computed the mean expression levels of both the target genes and the corresponding TFs. To avoid potential artifacts in the expression measurement caused by experimental batch effects, we analysed both adult and fetal cell types, and fetal cell types only, and found similar results. The analysis was performed iteratively for all TFs within the motif clusters specific to fetal cell types.

Regulatory embedding

GET is configured using a cross-cell-type architecture to extract the regulatory context for genes spanning various cell types, embedding them within a shared high-dimensional space. We collected the embedding of each gene after each transformer block of GET. The embedding of a gene g is defined as the embedding vector of the promoter in the output of the ith block. The embedding contains both promoter information and information from surrounding regions owing to the attention mechanism. In general, the deeper the layer, the more its space is dominated by the expression output (Supplementary Fig. 4). tsne-cuda was used to visualize the embedding owing to data size. Louvain clustering was performed on the embedding space to colourize the visualization. Resolution was arbitrarily chosen to keep the cluster number around 10 and close to the UMAP density. For cell-type-based subsampling, UMAP⁶⁸ was used instead for visualization for better visual separation between clusters.

We computed the embeddings in two different settings: the cell-type-specific setting, in which each dot is a gene embedding from a specific cell, and the cell-type-agnostic setting, in which each dot is a gene embedding randomly sampled from all cell types; 50,000 embeddings were sampled in the second case to make the UMAP computation feasible.

Causal discovery of regulator interaction

We performed pairwise Spearman correlation using the gene-by-motif matrix in both cell-type-specific and cell-type-agnostic settings. Input × gradient scores were used to construct the matrix for computational efficiency. For the cell-type-specific settings, all genes with promoter overlap with open chromatin peaks in each cell type were used in the correlation calculation. Causal discovery was performed on the gene-by-motif matrix using LiNGAM⁶⁹. For the cell-type-agnostic settings, 50,000 genes were randomly sampled from all cell types, and the resulting matrix was subjected to the LiNGAM algorithm implemented in the Causal Discovery Toolbox Python package with default parameters.

To benchmark the predicted causal edges in the cell-type-agnostic setting, we downloaded the known physical interaction subnetwork from the STRING v.11 database³⁹ and kept interactions with a combined score greater than 400 as the ground truth label. As the pairs predicted by GET were on the motif cluster level, we mapped the physical interactions between TFs on to the motif clusters on the basis of the motif cluster annotation. The resulting motif–motif physical interaction network was then compared with our prediction to calculate the precision. We also downloaded and compiled all significant interactions determined by mass spectroscopy⁴⁰ and mapped them to motif–motif interactions for comparison. For comparison with ChIP–seq colocalization, we acquired colocalization results between ChIP–seq tracks for 677 TFs in HepG2 from TF Atlas. The method for calculating colocalization is documented in the ChIP-Atlas repo. Each ChIP–seq peak set was stratified into three tiers (high, mid and low). Then, for a pair of TFs P1 and P2, we checked colocalization between every tier pair and assigned scores with a preference for high–high colocalization (score = 9). If the strong binding peaks of P1 overlapped with strong binding peaks of P2, the P1–P2 interaction was considered to be more robust than in the case in which the P1 strong binding sites only overlapped with the P2 weak binding sites. We present the colocalizations stronger than mid–mid interactions (score ≥ 4) in Fig. 4b, as these represent the more reliable interactions. A stronger cutoff (score ≥ 9, keeping only high–high interactions) reduced the performance to a 0.097 macro F1 score at 2% recall.

For comparison with motif colocalization, we collected the GET input matrix (accessible-region-by-motif) for hepatocytes or concatenated the input matrix across all fetal and adult cell types. Pairwise Pearson correlation was computed across all collected regions, resulting in a score for every pair of motifs. For the cell-type-specific motif–motif interactions in the GET catalogue, we performed causal discovery using the gene-by-motif matrix for all cell types. Interactions with the top 5% absolute effect size were retained in the final database. For each interaction, we performed structural analysis between the two TFs with the highest expression in the corresponding cell types.

Structural analysis

AlphaFold benchmark on intrafamily binder prediction

We classified a TF as an intrafamily binder if any two members in its TF family had a known physical interaction annotated in the STRING v.11 database, on the basis of the hypothesis that if a TF can bind as a heterodimer, it should also have the potential to bind as a homodimer owing to sequence and structure similarity (although the dimerization affinity might be different). We thus used AlphaFold to predict the hypothetical homodimer structures of all known TFs and tried to predict whether a TF could be an intrafamily binder using AlphaFold-based metrics. We used several different AlphaFold-based metrics, including mean_plddt (average pLDDT score across all residues), pAE (predicted aligned error across all interchain interactions), pDockQ (predicted DockQ metric using interface pLDDT) and pDockQ × pAE. We found that pDockQ × pAE led to the best area under the receiver operating characteristic curve (0.69) and area under the precision–recall curve (0.41) when classifying intrafamily binder TFs.

Protein sequence segmentation

pLDDT from AlphaFold is a reliable protein ___domain caller owing to its accurate structure prediction performance. We segmented each TF protein sequence into low and high pLDDT regions. Empirically, we found that 80% (recall) of known DNA-binding domains could be easily identified using high pLDDT regions plus a high ratio of positively charged residues. More specifically, we first computed smoothed pLDDT using a ten-amino-acid moving-average kernel and then normalized the score by dividing by the maximum. After that, any region that had a smoothed pLDDT score less than 0.6 was defined as a low pLDDT region. If two low pLDDT regions were close (less than 30 amino acids), they were merged into one. Any region that was not a low pLDDT region was labelled as a high pLDDT region.

Multimer structure prediction

LocalColabFold and ColabFold were used to predict multimer structures with the AlphaFold Multimer v.2.3 model. For homodimer prediction, we used all five models with three recycles. For our large-scale interaction screening, we used model 3 with three recycles for each prediction. The pAE and pLDDT were stored for downstream analysis. pDockQ was calculated using code from FoldDock⁷⁰.

If the multimer structure had a newly appearing peak, we treated it as evidence of potential interaction. pAE, pDockQ and ipTM were further checked to assess the confidence of the interaction. After AlphaFold3 was released, we reperformed structure prediction for full-length PAX5–NR2C2 sequences and identified the same PAX5 G183–NR ___domain interaction.

Molecular dynamics simulation

The initial configuration was prepared from the AlphaFold predicted PDB file. The Amber99SB-dispersion (a99SBdisp) force field was used for system parameterization. A cubic simulation box was defined with a box size of 1 nm. Subsequently, the system was solvated using the TIP4P water model through the solvate module. To neutralize the system and generate physiological ion concentrations, sodium (Na⁺) and chloride (Cl⁻) ions were added using the genion module. The energy minimization terminated upon reaching a maximum force below 1,000 kJ mol⁻¹ nm⁻¹. Each minimization iteration used a step size of 0.01 and was configured to run for a maximum of 50,000 steps. The system was then equilibrated in two steps: first in the NVT (constant number, volume, temperature) ensemble and then in the NPT (constant number, pressure, temperature) ensemble for 100 ps of simulation time. A 100 ns production run was then performed, and trajectories and energy profiles were stored for subsequent analysis. All configs of these are available at the Proscope repo (https://github.com/fuxialexander/proscope). In our analysis, we found that the per-residue pLDDT scores for ZFX, IDR and TFAP2A in the multimer structure were correlated strongly with residue instability, as measured by root mean squared distance, consistent with the results of previous studies indicating that AlphaFold implicitly learns protein folding energy functions.

Structure visualization

ChimeraX was used to visualize the predicted structures.

Biological experiments

Cell lines

HeLa cells (CCL-2) and REH cells (CRL-8286) were purchased from ATCC. Cell lines purchased from a certificated cell line bank were not further authenticated. All cell lines tested negative for mycoplasma. No commonly misidentified cell lines were used in the study.

TFAP2A coimmunoprecipitation

HeLa cells were cultured in DMEM (Gibco, catalogue no. 11965) supplemented with 10% defined fetal bovine serum (HyClone, SH30070), at 37 °C and 5% CO₂. HeLa cell protein lysates were generated with 0.5% NP-40 lysis buffer (50 mM Tris-HCl, 150 mM NaCl, 0.5% NP-40) with a phosphatase and protease inhibitor cocktail (Sigma-Aldrich, PPC1010). Samples were incubated with 5 µg agarose-conjugated TFAP2A primary antibody (Santa Cruz Biotechnology, sc-12726 AC) overnight at 4 °C before being run in Laemmli loading buffer (BioRad, 1610737). Proteins were separated on 10% Tris–glycine gels (ThermoFisher, XP00100), transferred to polyvinylidene fluoride membranes (Immobilon-P, IPVH00010) and probed with primary antibodies against TFAP2A (ABclonal, A2294, 1:750), ZFX (ThermoFisher, PA5-34376, 1:500) and β-actin (Santa Cruz Biotechnology, sc-47778, 1:10000), followed by chemiluminescence detection. A repeat experiment was performed for coimmunoprecipitation negative controls, which were probed with primary antibodies against SRF (Abclonal, A16718, 1:750) and β-actin (Cell Signaling Technology, 4967, 1:10000), followed by chemiluminescence detection.

Proximity labelling assay to detect PAX5–NR2C2 interactions

We initially cloned PAX5-WT and the PAX5 G183S mutant into the pCDNA3.1-MCS-13Xlinker-BioID2-HA (Addgene, catalogue no. 80899)⁷¹. After verification, we subcloned PAX5-WT-13Xlinker-BioID2-HA and PAX5-G183S-13Xlinker-BioID2-HA into the pCDH-GFP-puro vector (System Bioscience, CD513B-1). We transduced the REH B-ALL cell line (ATCC, CRL-8286) with pCDH-PAX5-WT-13Xlinker-BioID2-HA-GFP and with pCDH-PAX5-G183S-13Xlinker-BioID2-HA-GFP and selected transduced cells with puromycin (1 μg ml⁻¹) to generate stable cell lines. The proximity labelling assay was performed following previously published methods^71,72,73. Briefly, REH stable cell lines with control vector pCDH-13Xlinker-BioID2-HA-GFP, pCDH-PAX5-WT-13Xlinker-BioID2-HA-GFP and pCDH-PAX5-G183S-13Xlinker-BioID2-HA-GFP were incubated with 100 μM biotin (Sigma-Aldrich, B4501) for 24 h. We collected the cells, washed them twice in cold phosphate-buffered saline and incubated them for 50 min on ice with occasional vortexing in lysis buffer (150 mM NaCl, 10 mM KCl, 10 mM Tris-HCl pH 8.0, 1.5 mM MgCl, 0.5% IGEPAL) supplemented with protease and phosphatase inhibitors (Life Technologies, catalogue no. 78443) and 63 U of benzonase (Sigma-Aldrich, catalogue no. 70746-3). Proteins were clarified by centrifugation at 21,000g for 15 min at 4 °C. We performed total protein quantification using a Pierce BCA Protein Assay kit (ThermoFisher Scientific, catalogue no. 23225) and incubated 1 mg of total protein extract with 100 μl of magnetic streptavidin beads (Dynabeads MyOne Streptavidin C1, Life Technologies, catalogue no. 65002) on a rotator at 4 °C overnight to isolate biotinylated proteins. We washed the beads twice with lysis buffer, once with 1 M KCl, once with 0.1 M Na₂CO₃, once with 2 M urea 10 mM Tris-HCL pH 8.0, and twice again with lysis buffer. Biotinylated proteins were eluted by boiling in 4× protein loading buffer supplemented with 2 mM biotin and 50 mM dithiothreitol at 95 °C for 10 min. Biotinylated proteins in total protein extracts or immunoprecipitates were detected by western blotting using standard protocols and the following antibodies: streptavidin–HRP antibody (Life Technologies, catalogue no. S911, 1:1000), anti-PAX5 (Cell Signaling, catalogue no. 8970, 1:500), anti-HA (Cell Signaling, catalogue no. 3724, 1:1000), anti-NR2C2 (Cell Signaling, catalogue no. 31646, 1:500), anti-NCOR1 (Cell Signaling, catalogue no. 5948, 1:500), NRIP1–HRP (Santa Cruz Biotechnology, sc-518071, 1:200) and NR3C1 (Cell Signaling, catalogue no. 12041, 1:500). Proteins were detected using a Li-Cor Odyssey OFC instrument and quantified using the GelAnalyzer 23.1 software.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.