Introduction

Artificial Neural Networks (ANNs) are computational models inspired by biological neural structure and function in the human brain1,2. An ANN consists of a series of interconnected networks (neurons). Each neuron receives incoming signals, processes them through activating functions, and gives output signals. ANNs are able to learn from data through a process called training, where they change the weight between neurons to reduce errors and improve performance in specific tasks such as pattern recognition, regression, classification, and more. Artificial neural networks (ANNs) are widely used to solve ordinary differential equations (ODEs) because of their ability to approximate complex functions and models3,4. ANNs have shown promise in solving these ODEs, providing a fast estimation method when the ANN model is optimized and implemented5. It uses feedforward neural networks to generate trial solutions to differential equations, where networks have been trained to solve differential equations to ensure that the boundary conditions are consistent. It extends from a single ODE to systems of ODEs as well as partial differential equations (PDEs).

The history of nanoparticles dates back to the era of ancient civilizations such as the Greeks, Romans, and Egyptians. The Romans used metals of nanometric sizes to make glass, and the Faradays invented colloidal gold in the 19th century6. Nanoparticles and nanoparticle-based devices are of interest in many industrial fields because of their unique and often practical properties7. Nanoparticles have become increasingly essential in nanomedicine throughout time, particularly in drug delivery systems. A relatively new invention, hybrid nanoparticles are chemical mixtures of inorganic and organic elements that combine different features to produce enhanced properties. Applications for hybrid nanoparticles can be found in a number of industries, including electronics, sensors, catalysis, and energy conversion8. Their versatility and adaptability make them valuable in contemporary analytical technologies. Hybrid nanofluids have been developed in temperature control research to overcome the problems of heat transfer and energy stability. Compared to the common fluids, these nanofluids have higher thermal conductivity, specific heat capacity, heat transfer coefficient, and nanosized solid particles in the two heterogeneous materials. After investigating the heat removal performance characteristics of nanofluids, researchers focused on heat management systems and discovered the important contribution of nanoparticles to improving heat transfer9.

The dispersion of a particular type of nanoparticle in a liquid to increase its thermal conductivity is known as nanofluids10. Typically, nanoparticles consist of metal, carbides, silver, oxides, nitride, gold, and carbon nanotubes; however, water, gasoline, and glycol are used as base fluids. Modern, sophisticated fluids, such as nanofluids, are employed in place of older, traditional fluids. Some of the unique properties of nanofluids include increased homogeneity, thermal diffusivity, thermal conductivity, and viscosity; high heat transfer rate efficiency; reduced heat exchanger size and weight; and almost no obstruction during fluid flow passage. Hybrid nanofluids are an improved form of nanofluid that has been created. Two distinct types of nanoparticles are dissolved in a base fluid with a high thermal conductivity in order to create hybrid nanofluids11,12. Therefore, the most crucial factor to consider when selecting a nanoparticle structure is that they should both serve to enhance each other’s favorable aspects. Due to their enhanced thermal and heat transport capacities, hybrid nanofluids are more efficient than nanoparticles. Many scholars are interested in nanofluid because of its many applications in engineering, medicine, and other fields. In loudspeakers, magnetic resonance imaging (MRI) in the medical field, and shaft motors, magnesium ferrite, cobalt ferrite, and other nanoparticle-sized ferrofluid particles are suspended inside a base fluid13.

A combination of cobalt and iron(III) oxide (Co-Fe2O3) nanoparticles is utilized in this study to enhance the thermal conductivity and heat transfer properties of the base fluid, water. These nanoparticles improve the fluid’s ability to transfer heat efficiently, making it suitable for advanced thermal management applications. The size of the (Co-Fe2O3) hybrid nanoparticles used in our study was carefully controlled to be within the nanoscale range, typically ranging from a few to several tens of nanometers14. Thermal properties of water, leading to improved cooling efficiency. In industrial and electronic cooling systems, the use of (Co-Fe2O3) nanoparticles in water can enhance heat transfer and cooling performance, resulting in more effective temperature regulation and reduced overheating risks. The addition of nanoparticles creates a more uniform temperature distribution, reduces thermal resistance, and can alter the fluid’s rheological properties, leading to improved stability and performance in cooling applications. Moreover, the magnetic properties of hybrid nanoparticles like (Co-Fe2O3) enable the manipulation of fluid flow using external magnetic fields, providing precise control over the cooling process. Key applications include computer cooling systems, industrial heat exchangers, HVAC (Heating, Ventilation, and Air Conditioning) systems, power plant cooling towers, and automotive radiator fluids.

Naidu et al.15,16 explored the Magneto-Stefan blow to increase heat and mass transfer flow across the nonlinear elongated surface in a non-Newtonian ternary hybrid nanofluid.Effects of angled Lorentz forces on hybrid carbon nanotubes across a sheet that is exponentially stretching while experiencing slip flow17. The combined effects of radiative heat and Lorentz force influence the flow of a composite nanoliquid over an elastic sheet, as presented by Harish et al.18.The effects of radiation and partial slip on magnetohydrodynamic Jeffrey nanofluid containing gyrotactic microorganisms are studied over a stretching surface by Naidu et al.19. Nasir et al.20,21 conducted a study on the flow of chemically reactive nanofluid over a stretching surface, using numerical soft computing methods to enhance thermal performance. A comparative study of computational models for nanofluids based on magnetite and carbon nanotubes within an enclosure22. Thermal radiation efficiency evaluation using advanced nanocomposites flowing on a riga plate23,24.Nasir et al.25,26 undertook a study employing numerical and intelligent neuro-computational modeling, integrating Fourier’s energy and Fick’s mass flux theory, to analyze 3D fluid flow through a stretchable surface. Also, provide a method for predicting the thermal transport analysis of nanofluid inside a porous enclosure using artificial neural networks. Unsteady, nonlinear convective couple stress Casson hybrid nanofluid flow over a gyrating sphere in a chemically radioactive environment and the flow of water-based hybrid nanofluids via a porous cavity are simulated for heat transfer applications explored by Nasir et al.27,28.Utilizing a medication delivery function, couple stress ternary hybrid nanofluid flow in a contraction channel is done by Alnahdi et al.29.MHD single-wall carbon nanotube rotating flow in three dimensions over a stretched sheet with thermal radiation presented by Nasir et al.30,31,32.

According to a recent study, a lot of mathematical problems are difficult to solve with exact solutions. Various analytical and numerical techniques are applied to these kinds of problems in order to obtain a solution. The first numerical approach for solving non-linear problems was used by Liao33, and it produced an approximation solution that swiftly converged. By incorporating Cattaneo theory, Farooq et al.34 provided an overview of the thermophysical properties of diffusive compressed Newtonian liquid flow. Ijaz and Ayub35 provided an example of the new thermal properties of a Maxwell nanoliquid powered by an inclined cylinder. By controlling the osmosis process, Nadeem et al.36 revealed the thermophysical characteristics of blood moving in a complicated, wavy microchannel. Ahmad et al.37 assessed the Casson hybridized nanoliquid flow over the lubricated configuration in the vicinity of the analytical solution and stagnation point. The analysis of Jan et al.38 looked at the heat and radiation effects as well as the flow between two squeezing plates of hybrid nanofluid connected to both homogeneous and heterogeneous reactions. The heat transmission rate of liquids containing two different types of nanoparticles has been found to be higher than that of liquids containing just one type of nanoparticle. The production of entropy in the Lagrangian-Eulerian method for the issue with the cooling system within an electronic chip is examined by Korei et al.39. By employing Galerkin finite element simulation, Bouslimi et al.40 explore entropy as well as the Sutterby hybrid nanofluid (SBHNF) on a slippery hot surface. Chu et al.41 examine the shape effect of hybrid nanofluid particles of silver-gold in the squeezing channel when MHD is present. Nasir et al.42 examined hybrid nanofluid flow. Using a pair stress fluid model, Ullah et al.43 investigated the radiation effect and the converging and diverging channels for the flow of hybrid nanofluid.

The behavior of the hybrid nanofluids is influenced by the magnetic dipole, which adds another dimension to the investigation. Thermal conductivity and heat dissipation can be impacted by the movement and distribution of nanoparticles inside a fluid, which can be controlled by magnetic fields. Understanding the function of the magnetic dipole in hybrid nanofluids is not only an intriguing study but also has practical implications for uses where the optimization of heat transfer may be achieved through the utilization of magnetic effects44,45. The goal of this creative use of artificial intelligence (AI) and neural networks is to better understand the intricate processes of heat transfer in hybrid nanofluids by emphasizing the function of the magnetic dipole46,47. Advanced theoretical understanding as well as useful recommendations for modifying heat transfer properties in real-world engineering situations are anticipated results. Scholars have employed an array of conventional numerical and analytical techniques to investigate nanoparticles that include nanofluid flows for diverse fluidic systems, mainly ferrofluid flows. However, ferrofluidic flow issues require the application of stochastic numerical approaches due to their importance, effectiveness, and resilience. Stochastic numerical techniques have previously been applied by researchers to a wide range of research issues48,49. The most current artificial intelligence-based methods are the pump flow model for nonlinear unipolar electrohydrodynamics50 and COVID-19 models51. The authors were motivated to conduct a parametric study to investigate the effect of different physical quantities on velocity, concentration, and temperature profiles using a new, more accurate, and reliable algorithm based on flexible computer programming to solve heat generation in the mixed convection Williamson fluid stretch flow problem52. These soft computing infrastructures served as the authors’ inspiration for soft numerical treatment in MATLAB and Mathematica.

There is a research gap in the exploration of advanced methodologies and materials to improve the effectiveness of ordinary differential equations (ODEs) based on FHNFM solution methods. Previous research has primarily focused on using nanoparticles in conjunction with basic numerical techniques to address FHNFM based ODEs. In light of this, our study aims to bridge this gap by employing ferromagnetic hybrid nanoparticles, a novel AI approach, especially artificial neural networks (ANNs), for the solution of ODEs.

The motivation behind this approach stems from the potential of these advanced materials and computational techniques to significantly improve the accuracy, efficiency, and versatility of ODE solving processes. By combining ANNs with ferromagnetic hybrid nanoparticles, it is possible to push the limits of current approaches and eventually improve computational methods for solving differential equations. This has practical uses and implications for several scientific disciplines53.

Mathematical formulation

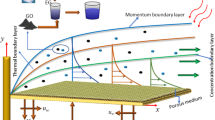
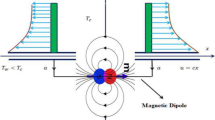
The flow of ferromagnetic hybrid nanoparticles on a stretching sheet is parallel to the x-axis. The magnetic dipole is located at a distance d from the surface. The magnetization of ferromagnetic hybrid nanoparticles is regulated by inducing a temperature difference between the wall temperature \(T_w\) and the curie temperature \(T_c\), while neglecting the pressure gradient, as shown in Fig. 1.

Figure 1
figure 1

The flow configuration through a schematic diagram, with circular lines indicating the presence of the magnetic field.

Full size image

By introducing the applied magnetic field, \(H = -\nabla \delta _{1}\), where \(\delta _{1}\) depicts the magnetic potential and is given as follows54:

$$\begin{aligned} \delta _1=\frac{\xi _1}{2\pi }\cdot \frac{x}{x^{2}+(y+d)^{2}}, \end{aligned}$$

where, \(\xi _1\) the dipole moment per unit length,

$$\begin{aligned} H=\sqrt{\left( \frac{\partial {\delta _1}}{\partial {x}}\right) ^{2}+\left( \frac{\partial {\delta _1}}{\partial {y}}\right) ^{2}}\, \,,\,\, H=\frac{\xi _1}{2\pi }\cdot \frac{(y+d)^{2}-x^{2}}{(y+d)^{4}}. \end{aligned}$$
(1)

The constitutive equations that govern the flow are as follows:55.

Equation of Continuity is as follows:

$$\begin{aligned} \frac{\partial {u}}{\partial {x}}+\frac{\partial {v}}{\partial {y}}=0. \end{aligned}$$
(2)

The following is the momentum equation:

$$\begin{aligned} \rho _{hnf}\bigg (u\frac{\partial {u}}{\partial {x}}+v\frac{\partial {u}}{\partial {y}}\bigg )=-\frac{\partial {p}}{\partial {x}}+\mu _{\circ }M\frac{\partial {H}}{\partial {x}}+ \Omega +\mu _{hnf}\frac{\partial ^{2}{u}}{\partial {y^{2}}}. \end{aligned}$$
(3)

The energy equation is as follows:

$$\begin{aligned} \begin{aligned} k_{hnf}\frac{\partial ^{2}T}{\partial {y^{2}}}= (\rho {Cp})_{hnf}\bigg [\bigg (u\frac{\partial {T}}{\partial {x}}+v\frac{\partial {T}}{\partial {y}}\bigg )+\lambda _1\bigg (u\frac{\partial {u}}{\partial {x}}\frac{\partial {T}}{\partial {x}} +v\frac{\partial {v}}{\partial {y}}\frac{\partial {T}}{\partial {y}} +u\frac{\partial {v}}{\partial {x}}\frac{\partial {T}}{\partial {y}}+v\frac{\partial {u}}{\partial {y}}\frac{\partial {T}}{\partial {x}} +\\2uv\frac{\partial ^{2}T}{\partial {x}\partial {y}}+u^{2}\frac{\partial ^{2}T}{\partial {x^{2}}}+v^{2}\frac{\partial ^{2}T}{\partial {y^{2}}}\bigg )\bigg ]+ \mu _{\circ }{T}\frac{\partial {M}}{\partial {T}}\bigg (u\frac{\partial {H}}{\partial {x}}+v\frac{\partial {H}}{\partial {y}}\bigg ), \end{aligned} \end{aligned}$$
(4)

where \(\mu _o\) represents magnetic permeability, \(\nu _{hnf}\) denotes kinematic viscosity of hybrid nanofluid, \(\mu _{hnf}\) denotes dynamic viscosity of hybrid nanofluid ,\(\rho _{hnf}\) denotes density of hybrid nanofluid, H expresses intensity of magnetic field, P represents pressure, \((\rho {Cp})_{hnf}\) denotes specific heat of hybrid nanofluid, \(\Omega\) mean body force term, \(K_{hnf}\) represents the hybrid nanofluid’s thermal conductivity, M denotes the difference of magnetization with temperature and \(\lambda _1\) is the thermal relaxation parameter of Cattaneo-Christov heat flux.

Associated boundary conditions are as follows55,

$$\begin{aligned} \begin{aligned} u|_{y=0}=U_w=Sx,\;\;\;\;\;\; v|_{y=0}=0,\;\;\;\;\;\; T|_{y=0}=T_w,\;\;u|_{y\rightarrow {\infty }}\rightarrow 0, \;\;\;\;\; T|_{y\rightarrow {\infty }}\rightarrow {T_\infty =T_c}. \end{aligned} \end{aligned}$$
(5)

By introducing the similarity transformation56 into equations (2–5),

$$\begin{aligned} \begin{aligned} \psi (\eta ,\xi )=\frac{\mu _{f}}{\rho _{f}}\eta {f(\xi )},\;\;\theta (\eta ,\xi )=\frac{T_c-T}{T_c-T_w}=\theta _1({\xi })+\eta ^{2}\theta _2({\xi }),\;\;\xi =y\sqrt{\frac{\rho _{f}S}{\mu _{f}}}, \;\; \eta =x\sqrt{\frac{\rho _{f}S}{\mu _{f}}}. \end{aligned} \end{aligned}$$
(6)

Tranformed equations are as follows:

$$\begin{aligned}{}&\frac{{\mu _{hnf}}/{\mu _{f}}}{{\rho _{hnf}}/{\rho _{f}}}{f^{'''}}-f'^2+ff^{''}+\frac{1}{{\rho _{hnf}}/{\rho _{f}}}\frac{2\beta \theta _1}{(\xi +\gamma )^{4}}=0, \end{aligned}$$
(7)
$$\begin{aligned}{}&\bigg [\frac{{k_{hnf}}/{k_{f}}}{{(\rho {C_{p}})_{hnf}}/{(\rho {C_{p}})_f}}-\text {Pr}\alpha {f^{2}}\bigg ]\theta _1^{''}+\text {Pr}(f\theta _1^{'}-\alpha ff^{'}\theta _{1}^{'})+\frac{1}{{(\rho {C_{p}})_{hnf}}/{(\rho {C_{p}})_f}}\frac{2\lambda \beta f(\epsilon -\theta _{1})}{(\xi +\gamma )^{3}}=0, \end{aligned}$$
(8)
$$\begin{aligned}{}&\bigg [\frac{{k_{hnf}}/{k_{f}}}{{(\rho {C_{p}})_{hnf}}/{(\rho {C_{p}})_f}}-\text {Pr}\alpha {f^{2}}\bigg ]\theta _2^{''}-\text {Pr}(2f^{'}{\theta _{2}-f\theta _{2}^{'}}-2\alpha ff^{''}\theta _{2}+4\alpha (f^{'})^{2}\theta _{2}-3\alpha ff^{'}\theta _{2})+\nonumber \\&\quad \frac{1}{{(\rho {C_{p}})_{hnf}}/{(\rho {C_{p}})_f}}{\lambda \beta (\theta _1-\epsilon )}\bigg [\frac{2f^{'}}{(\xi +\gamma )^{4}}+ \frac{4f}{(\xi +\gamma )^{5}}\bigg ]-\frac{1}{{(\rho {C_{p}})_{hnf}}/{(\rho {C_{p}})_f}}\frac{2\lambda \beta f\theta _2}{(\xi +\gamma )^{3}}=0. \end{aligned}$$
(9)

Above equations from (7–9) can be written as,

$$\begin{aligned}{} & {} \frac{C_{1}}{C_{2}}{f^{'''}}-f'^2+ff^{''}+\frac{1}{C_{2}}\frac{2\beta \theta _1}{(\xi +\gamma )^{4}}=0, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \bigg [\frac{C_{3}}{C_{4}}-\text {Pr}\alpha {f^{2}}\bigg ]\theta _1^{''}+\text {Pr}(f\theta _1^{'}-\alpha ff^{'}\theta _{1}^{'})+\frac{1}{C_{4}}\frac{2\lambda \beta , f(\epsilon -\theta _{1})}{(\xi +\gamma )^{3}}=0, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \bigg [\frac{C_{3}}{C_{4}}-\text {Pr}\alpha {f^{2}}\bigg ]\theta _2^{''}-\text {Pr}(2f^{'}{\theta _{2}-f\theta _{2}^{'}}-2\alpha ff^{''}\theta _{2}+4\alpha (f^{'})^{2}\theta _{2}-3\alpha ff^{'}\theta _{2})+ \nonumber \\{} & {} \quad \frac{1}{C_{4}}{\lambda \beta (\theta _1-\epsilon )}\bigg [\frac{2f^{'}}{(\xi +\gamma )^{4}}+ \frac{4f}{(\xi +\gamma )^{5}}\bigg ]-\frac{1}{C_{4}}\cdot \frac{2\lambda \beta f\theta _2}{(\xi +\gamma )^{3}}=0. \end{aligned}$$
(12)

The transformed boundary conditions are given in Equation (13) as follows:

$$\begin{aligned} \begin{aligned} f(0)=0,\;\;\;\;\;f^{'}(0)=1, \;\;\;\;\; \theta _{1}(0)=1,\;\;\;\;\; \theta _{2}(0)=0, \;\;\;\;\;f^{'}(\infty )\rightarrow {0},\;\;\;\;\;\theta _1(\infty )\rightarrow {0},\;\;\;\;\;\theta _2(\infty )\rightarrow {0}. \end{aligned} \end{aligned}$$
(13)

Where, the ferrohydrodynamic interaction parameter \(\beta =\frac{\xi _1}{2\pi }\frac{\mu _\circ K(T_c-T_w)\rho _f}{\mu ^2_{f}}\), Prandtl number \(\text {Pr}=\frac{\nu _f (\rho C_p)_f}{K_f}\), viscous dissipation \(\lambda =\frac{S\mu _f^{2}}{\rho _f k_f(T_c-T_w)}\), thermal relaxation parameter \(\alpha =\lambda _1S\),   Curie temperature \(\epsilon =\frac{T_c}{T_c-T_w}\),   \(\gamma =d\sqrt{\frac{\mu _f}{\rho _f S}}\), \(C_{1}=\frac{\mu _{hnf}}{\mu _{f}}\), \(C_{2}=\frac{\rho _{hnf}}{\rho _{f}}\), \(C_{3}=\frac{k_{hnf}}{k_{f}}\), and \(C_{4}=\frac{(\rho {C_{p}})_{hnf}}{(\rho {C_{p}})_f}\). The wall shear stress is expressed as follows:

$$\begin{aligned} \tau _{w}=\mu _{_{hnf}}\frac{\partial {u}}{\partial {y}}|_{y=0}. \end{aligned}$$

The skin friction coefficient and local Nusselt number are defined as follows55,

$$\begin{aligned} C_f=\frac{-2\tau _w}{\rho _{hnf}U^2w}\;,\;\;\;\;\;\;\; N_u=\frac{xk_{hnf}}{k_f(T_c-T_w)}\cdot \frac{\partial {T}}{\partial {y}}|_{y=0}. \end{aligned}$$

The local Nusselt number and the skin friction coefficient in dimensionless form are as follows respectively,

$$\begin{aligned}{} & {} Re_{x}^{\frac{-1}{2}}Nu_x=\frac{k_{hnf}}{k_{f}}\bigg (\theta ^{'}_1(0)+\eta ^{2}\theta ^{'}_{2}(0)\bigg ),\\{} & {} \frac{1}{2}Re_{x}^{\frac{1}{2}}C_{f}=\frac{1}{(1-\phi _1-\phi _2)^{2.5}}f^{''}(0), \end{aligned}$$

where, \(\text {Re}_x=\frac{Sx^{2}}{\nu _{f}}\) is the local Reynolds number.

Table 1 Hybrid nanofuid’s correlations57.
Full size table

The thermophysical properties of hybrid nanoparticles are shown in Table 1. These properties involve thermal conductivity, specific heat capacity, density, and viscosity, and they are critical to comprehending how hybrid nanoparticles improve fluid thermal performance. The data in the table is derived from the study of Ayub et al. 202457 on the examination of hybrid nanoparticles’ thermophysical properties57. Table (5) contains all of the dimensionless parameters that used in the present study. Table (6) lists the abbreviations used in this study.

Table 2 Thermophysical properties of nanoparticles and base fluid58,59.
Full size table

In Table 2, the thermophysical properties of both nanoparticles and the base fluid are comprehensively outlined for reference and analysis.

Solution methodology

The methodology employed in this research encompasses neural network simulation, training using the Levenberg-Marquardt algorithm, and a comparison of numerical results, as illustrated in Figure (3). This methodical approach includes a block structure detailing procedures for information storage, model development, and problem recognition.

The MATLAB software package is utilized, specifically the numerical solver bvp4c, to solve the system of equations equations (10–12). This solver yields reference numerical solutions with the boundary conditions given in equation (13). The numerical method transforms the model equations into first-order ordinary differential equations (ODEs), providing reference data for the Levenberg-Marquardt backpropagation neural networks by Shoaib et al.60. The bvp4c solver operates with default parameter settings, which include limitations, precision standards, and stopping criteria. The main equations are solved using a step size of \(\xi = 0.0015\), considered appropriate under various conditions, to satisfy the inner convergence criterion with an error tolerance of \(10^{-6}\). Instead of using the interval [0, 2.5], which results in significant differences in fluid temperature, concentration, and velocity distribution, equation (13) imposes a limiting condition as \(\xi \rightarrow 2.5\). The higher-order ODEs for temperature, concentration, and velocity in equations (10–12) have been appropriately adjusted using the ’bvp4c’ method.

The dataset produced by the bvp4c technique is used to build a three-layer neural networks design employing the Levenberg-Marquardt algorithm for supervised learning by Nasir et al.23. This design includes input, hidden, and output layers, with the number of neurons in the hidden layers 10, as shown in Figure (2). Training data is derived from the governing model using the bvp4c technique. The reference data is randomly split into three groups: 70 percent for training, 15 percent for validation, and 15 percent for testing. The current study comprises a total dataset of 1666 samples, with 1166 allocated for training and 250 each for validation and testing. The input data and corresponding targets are fed into the artificial neural network model, where neurons in the hidden layer process them, perform nonlinear operations, and produce outputs in the output layer. The weighted summation of inputs, combined with biases, is handled in the hidden layer using the hyperbolic tangent sigmoid function as the activation function, mathematically defined as:

$$\begin{aligned} \sum _{m=1}^{k}w_{mn}P_{m}+b_{n},\;\; j_{n}=\frac{1}{1+e^{-z}}. \end{aligned}$$

Here, \(w_{mn}\) are the weights of the mth neuron in the previous layer to the nth neurons, where \(j_{n}\)th neuron. To minimize errors and achieve high accuracy, the weights and biases within the networks are adjusted using the Levenberg-Marquardt training algorithm. Figure 3 outlines the Levenberg-Marquardt training procedure.

The training process continues until the target error or fitness level is reached. The efficacy of the model is evaluated by analyzing the neural network’s performance, and the architectural arrangement of the neural network model is shown in Fig. 2. Various error and accuracy metrics are used to assess the model’s performance, as follows:

$$\begin{aligned} \text {MSE} = \frac{\sum _{j=1}^{k}(P_j - T_j)}{k}, \quad R-1 =- \frac{\sum _{j=1}^{k}(P_j - T_j)}{\sum _{j=1}^{k}(P_j - {\bar{T}}_j)} \end{aligned}$$

where \(P_j\) is the predicted value, \(T_j\) is the corresponding target value, and \(\bar{T}_j\) is the average of the target values. Values of \(R\) closer to 1 and lower MSE values indicate more reliable and accurate predictions.

The design technique involves two distinct steps:

  1. 1.

    Using the MATLAB software tool for solving differential systems, the bvp4c technique is applied with automatic stoppage and accuracy objective parameter settings to discover the numerical solution of systems representing nanoparticles in the current flow model.

  2. 2.

    In this step, the neural network toolbox of MATLAB ’nftool’ regimen is used, with 10 hidden layers settings, to implement networks that have been optimized, trained, or learned using Levenberg-Marquardt backpropagation, to obtain approximations for the system model’s solutions.

Figure 2
figure 2

Neural network procedure for FHNFM.

Full size image

To reduce errors and provide highly accurate results, the weights are adjusted using the Levenberg-Marquardt training algorithm. The ANNs process, illustrated in Fig. 2, includes an outline of the Levenberg-Marquardt training procedure. The flow diagram in Fig. 3 of the ferromagnetic hybrid nanofluid flow model provides a comprehensive summary of this study. This visual representation highlights the key components and findings, ensuring clarity and coherence in the presentation of our research.

Figure 3
figure 3

Flow diagram of ferromagnetic hybrid nanofluid flow model.

Full size image
Figure 4
figure 4

Training data analysis with variation of “\(\beta\)” case 1.

Full size image
Figure 5
figure 5

Training data analysis with variation of “\(\lambda\)” case 1.

Full size image
Figure 6
figure 6

Training data analysis with variation of “\(\alpha\)” case 1.

Full size image
Figure 7
figure 7

Training data analysis with variation of “\(\epsilon\)” case 1.

Full size image
Figure 8
figure 8

Graphical comparison between bvp4c and ANN solution.

Full size image
Figure 9
figure 9

Graphical comparison between bvp4c and ANN solution.

Full size image
Table 3 Comparison of skin friction coefficient and Nusselt number for Bvp4c and ANN Solutions.
Full size table
Figure 10
figure 10

Graphical comparison of skin friction coefficient and Nusselt Number between bvp4c and ANN solution.

Full size image

The ANN model’s correctness in replicating Bvp4c findings is verified by the graphical comparison of skin friction coefficient and Nusselt number between Bvp4c and ANN solutions, as shown in Fig. 10. A detailed comparison between Bvp4c and ANN solutions for skin friction coefficient and Nusselt number is given in Table 3, which shows how well they perform for a range of parameters and values. The consistency and dependability of both approaches are demonstrated by the alignment of the solutions.

The parameter \(\gamma\) for the skin friction coefficient in Figure 10(a) exhibits increasing solution values as \(\gamma\) arises: 0.0875 for \(\gamma = 0.5\), 0.1294 for \(\gamma = 1.0\), and 0.1676 for \(\gamma = 1.5\). Likewise, the results vary significantly depending on the parameter \(\beta\): 0.5434 for \(\beta = 1.5\), 0.5372 for \(\beta = 3.5\), and 0.5102 for \(\beta = 7.5\) as illustrated in Fig. 10b. These numbers show how skin friction coefficient is affected by changes in \(\gamma\) and \(\beta\).

When Pr enhances, the parameter Pr for the Nusselt number exhibits a noticeable decline in values: it goes from 0.0621 for Pr = 6.2 (water) to 0.0137 for Pr = 21 (kerosene oil), with a minor increase to 0.0172 for Pr = 500 (engine oil) as depicted in Fig. 10c. When \(\lambda\) increases, the values for the parameter decrease: from 0.0217 at \(\lambda = 1.5\) to 0.0171 at \(\lambda = 2.5\) and 0.0116 at \(\lambda = 3.5\). The impact of Pr and \(\lambda\) on the Nusselt number is demonstrated by these findings.

Figure 10 depicts the effect of the ferrohydrodynamic interaction parameter \(\beta\) and the Prandtl number Pr on wall shear stress. It is shown that skin friction reduces as the Prandtl number increases, whereas the reverse effect is shown when \(\beta\) is increased. The fact that enhancing Pr improves base liquid diffusivity and decreases drag force on molecules at the wall’s surface justifies the decline in skin friction coefficient against Pr. On the other hand, a boost in \(\beta\) causes the surface-induced frictional force to rise because it increases the ferromagnetic interaction factor, which in turn resists the molecules’ ability to move more quickly and increases the magnitude of the drag force. Figure 10 illustrates the variation in the convective heat transfer coefficient with respect to the ferrohydrodynamic interaction parameter \(\beta\) and the Prandtl number Pr. As the temperature in the flow ___domain is measured by the uplift in the kinetic energy of the fluid molecules, it is demonstrated that a rise in Pr causes an increase in heat flux. Heat flows out from the surface when fluid layers are hotter. This creates a temperature gradient. The fluid’s viscosity decreases as its temperature rises in response to an enhancement in the viscous dissipation parameter \(\lambda\). The skin friction coefficient drops as a result of less flow resistance at the boundary layer caused by a lower viscosity.

The Nusselt number shows a noticeable decline for choosing different base fluids like water, kerosene oil, and engine oil. It is evident from Table 3 and Fig. 10 that the heat transfer rate is maximum when choosing water as the base fluid.Overall, the Bvp4c and ANN techniques yielded similar values, demonstrating the accuracy of the ANN model in approximating solutions to complicated problems. This consistency suggests that ANNs, with their potential advantages in computing efficiency and ease of implementation, can be a competitive alternative to established techniques like Bvp4c. The outcomes increase confidence in the application of ANN for high-precision computations in domains like heat transfer and fluid dynamics.

Table 4 Variation of physical parameters for training purpose and estimation of performance, gradient and Mu during training.
Full size table

Analysis and discussion of the findings

The results of ANN-LMBA adopting the artificial neural network-based Levenberg-Marquart method are analyzed for the FHNFM of the proposed model in Eqs. (10–13). Four parameters are defined in the ferromagnetic hybrid nanofluid flow model FHNFM for the temperature and velocity profiles of the FHNFM by three common cases listed in Table 4. These parameters are the ferrohydrodynamic interaction parameter \(\beta\), viscous dissipation parameter \(\lambda\), thermal relaxation parameter \(\alpha\), and curie temperature \(\epsilon\) parameter.

The bvp4c numerical technique from MATLAB determines the dataset used as a reference for possible velocity \(f^{'}(\xi )\) and temperature profiles \(\theta (\xi )\) for ANN-LMBA for \(\xi\) between 0 and 2.5 for each of three scenarios involving four distinct parameters of ANN-LMBA for FHNFM. Employing the nftool feature within the MATLAB software, the ANN-LMBA finds the solution to the ferromagnetic hybrid nanofluid flow model FHNFM. The velocity and temperature profile reference dataset is created, for which 70% are used for training, 15%for each validation, and the remaining 15% for ANN-LMBA testing using the neural networks. Training data analysis with variations of “\(\lambda\)” and “\(\alpha\)” are represented in Figs. 5 and 6, respectively, for case 1. The validation performance of the ANN-LMBA results for each scenario’s first case is shown in Figs. 4a, 5, 6, 7a). Gradient, Mu, and validation checks are represented in Figs. 4b, 5, 6, 7b and the function’s fitness, as further evidenced by error histogram plots for each scenario’s first case shown in Figs. 4c,e, 5, 6, 7c,e, whereas Figs. 4d, 5, 6, 7d display the plots for the regression analysis. Table 4 shows the convergence plots of mean squared error (MSE) for various components, including training performance, testing performance, validation performance, epochs, backpropagated operator as Mu, and time occupied.

The convergence plots of the MSE for the test, training, and validation curves are shown for each first case of all FHNFM situations and are displayed in Figs. 4a, 5, 6, 7a.The optimal level of performance can be achieved at [307, 313, 113, and 96] epochs, with MSE around [9.1703e-10, 7.1313e-10, 3.1462e-10, and 4.8747e-10], respectively are represented in Figs. 4a, 5, 6, 7a. The Levenberg Marquardt backpropagation’s gradient and Mu parameter are [9.848e-08, 9.9066e-08, 9.6715e-08, and 9.8012e-08] and [1e-08, 1e-08, 1e-09, and 1e-09], respectively, as shown in Figs. 4b5, 6, 7b. Results have verified the convergence efficiency and validity of ANN-LMBA for every FHNFM’s case. As seen in Figs. 4e, 5, 6, 7e, the fitness sketch for case 1 each scenario across training, validation, and testing phases. It shows errors of (e-4) per unit time and depicts the relationship between targets and outputs for each phase. Outputs for validation, training, and testing are represented by (+) signs, while targets are indicated by \((\cdot )\) dots. These findings are further supported by investigations of error histograms in Figs. 4c, 5, 6, 7c. The error histograms for case 1 of each scenario demonstrate that the error between the network’s target and output is nearly zero. The error-histogram graph, compared against the reference zero-line error bin, indicates an error of approximately [-4.8 e-07, -7.3 e-06, 1.5 e-05, 2.41 e-06] in Figs. 4c, 5, 6, 7c respectively.

Correlation studies are used to conduct the regression analysis. The regression results of the corresponding variants of FHNFM are displayed in Figs. 4d5, 6, 7d. The regression sketch for case 1 for each scenario indicates a correlation (R) close to 1, thus avoiding a random scenario where R = 0. The regression plot for case 1 confirms a high correlation (R = 1) and demonstrates effectiveness, as evidenced by the minimal empty space, which is due to the absence of missing values in the data represented in Figs. 4d5, 6, 7d. Furthermore, for each parameter, the matching numerical values are stated in Table 4. The performance on MSE was shown for the temperature and velocity profiles of the developed FHNFM about [9.1703e-10, 7.1313e-10, 3.1462e-10, and 4.8747e-10]. All of the numerical values in Table 4 support the reliable and accurate operation of ANN-LMBA.

Impacts on temperature and velocity profiles

The results are analyzed in terms of velocity and temperature profiles of key parameters such as ferrohydrodynamic interaction parameter \(\beta\), viscous dissipation parameter \(\lambda\), thermal relaxation parameter \(\alpha\), and Nanoparticles concentration (\(\phi _{1}, \phi _{2}\)). Figure 8b illustrates that the decline in velocity with the growing ferrohydrodynamic interaction parameter \(\beta\) can be explained by the strong interaction between magnetic field and ferromagnetic hybrid nanofluid medium. This strong interaction gives the fluid greater resistance as it passes through the magnetic field. Consequently, the fluid develops a high drag force, impeding its motion and reducing velocity. This effect is particularly evident when considering the presence of ferromagnetic hybrid nanoparticles in the fluid. These hybrid nanoparticles enhance the interaction between the magnetic field and the fluid, which resists the flow. As a result, Lorentz forces become significant and evolve a resistance that opposes flow motion, which causes the velocity field to decrease. Also, the velocity profile rises as the \(\gamma\) parameter boosts, as depicted in Fig. 8a. The rise in temperature profiles in Figs. 8e and 9b with the growing ferrohydrodynamic interaction parameter \(\beta\) can be explained by considering the energy dissipation in the system due to an increase in magnetic interaction. As \(\beta\) rises, it shows that with stronger interactions between the magnetic field and the fluid, the system experiences a higher resistance to flow. This resistance enhances the frictional force in the fluid, leading to an increase in momentum. Higher energy dissipation manifests as higher temperatures in the system. This is consistent with the principles of thermodynamics, where anti-friction technology converts mechanical energy into thermal energy, consequently raising the temperature of the fluid. These hybrid nanoparticles become more movable and disoriented, which raises the fluid’s temperature by increasing friction force and energy dissipation.

The temperature profiles \(\theta _{1}(\xi )\) and \(\theta _{2}(\xi )\), as illustrated in Figs. 8c and 9d, respectively, grow with the rise in nanoparticle concentrations (\(\phi _{1}\), \(\phi _{2}\)). As the values of (\(\phi _{1}\), \(\phi _{2}\)) increased, the temperature profiles rose. This is because the greater thermal conductivity of nanoparticles allows for the passage of more heat into fluids at higher concentrations. As a result, the fluid temperature increases. The viscous dissipation parameter \(\lambda\) has a significant effect on the temperature profile. Growing the value of \(\lambda\) means more mechanical energy of fluid particles is converted into heat energy, which results in enhancing the internal temperature of the fluid, as depicted in Figs. 8d and 9c. The effect of the thermal relaxation parameter \(\alpha\) on temperature distribution is seen in Figs. 8f and 9a. It is deduced that the temperature distribution declines with an increase in the thermal relaxation parameter \(\alpha\). The system’s temperature decays and the ambient temperature rises as a result of an increase in \(\alpha\). Furthermore, rather than measuring heating, the thermal relaxation parameter \(\alpha\) monitors the system’s rate of cooling.

Conclusion

A machine learning methodology based on artificial neural networks and the Levenberg-Marquardt backpropagation procedure is used to scrutinize the ferromagnetic hybrid nanofluid flow model in the presence of a magnetic dipole within the context of flow over a stretching sheet. The analysis considers key parameters such as the ferrohydrodynamic interaction parameter \(\beta\), viscous dissipation parameter \(\lambda\), thermal relaxation parameter \(\alpha\), and nanoparticles concentration (\(\phi _{1}, \phi _{2}\)). To resolve the model problem, a reference dataset is created using the bvp4c method for discrepancies in the problem illustration. The Levenberg-Marquardt backpropagation algorithm achieves a precision and consistency between the proposed and usual outcomes, with 70% of the data used for training, and 15% each for validation and testing. The effectiveness of the methodology is validated using statistical data, convergence curves, mean square error, regression, and error histograms. The vital results attained by means of the artificial neural networks Levenberg-Marquardt backpropagation solver for the current problem are as follows:

  • The ferromagnetic hybrid nanofluid flow model, influenced by a magnetic dipole and applied to a flow over a stretching sheet, results in a reduction in flow velocity due to the slower movement of the hybrid nanoparticles.

  • The optimal artificial neural network structure achieved a regression coefficient (R) of 1 and an MSE of \(3.1462 \times 10^{-10}\). The reliability and accuracy of the results obtained from the proposed techniques are demonstrated through error histograms and fitness plots.

  • The results generated from the neural networks using the Levenberg-Marquardt backpropagation technique closely match the reference solution, indicating the efficiency of the planned solver. The Levenberg-Marquardt backpropagation solver exhibits a fast convergence rate, as demonstrated by the reducing values of Mu and gradient with each succeeding epoch.

  • A boost in the ferrohydrodynamic interaction parameter \(\beta\) causes the temperature profiles to rise. An increase in viscous dissipation \(\lambda\) results in an enhancement of the temperature. The temperature profile increases with the rise in nanoparticle concentration (\(\phi _{1}, \phi _{2}\)), whereas it declines with the increase in the thermal relaxation parameter \(\alpha\).

  • Novel soft computing methods utilizing artificial neural networks will be developed in the future to improve learning and effectively solve fluid mechanics-related problems. These methods will be expanded for possible engineering applications, improving their usefulness and practical importance in resolving real-world issues.

Table 5 Nomenclature used in FHNFM.
Full size table
Table 6 List of Abbreviations.
Full size table