Introduction

The presence of wall roughness can have a significant impact on the mechanism of load transfer in cohesionless backfill as well as the magnitude of lateral earth pressures. It is important to note that there are two distinct types of wall roughness. Depending on the relative movement between the soil in the backfill and the wall, positive wall friction occurs when the soil moves upward faster than the wall, while negative wall friction occurs when the wall moves upward faster than the soil1,2,3,4.

In active scenarios, friction is predominantly positive, serving as a stabilizing factor for retaining walls and structures4. However, certain conditions, such as excavation for repair work, can lead to situations where negative wall friction occurs, necessitating additional support or bracing against the backfill soil to ensure structural stability. In passive conditions, both positive and negative wall friction can influence the overall stability of the structure3. Understanding the influence of negative wall friction is particularly crucial as it significantly impacts the lateral earth pressure exerted on retaining structures. This phenomenon is especially important in the design of retaining walls and anchors, as it affects the overall load distribution and the potential for failure. For example, in conditions where the wall or anchor moves upward faster than the surrounding soil, the resultant increase in earth pressure may necessitate a more robust design to prevent structural failure. Additionally, the negative wall friction angle is a critical factor in determining the uplift capacity of anchors5, as it influences the relative movement between the anchor or wall and the surrounding soil. Typically analyzed using a curved rupture surface and the limit equilibrium method6, the direction of wall friction (positive or negative) must be determined based on anticipated ground movements under specific field conditions, which is essential for optimizing the design and ensuring the safety of geotechnical structures.

The introduction of wall friction transforms the rupture surface from a simple, planar configuration to a curved one, an observed phenomenon documented by Savage et al.1. Notably, the presence of negative wall–soil friction not only impacts the magnitude of the lateral earth thrust exerted on the wall but also results in substantial deviations in the failure surface, distinct from scenarios involving positive wall–soil friction3. Therefore, gaining a comprehensive understanding of the load transfer mechanisms associated with negative wall–soil friction holds exceptional significance within the realm of geotechnical engineering, as it can carry profound implications for the stability and design of retaining walls and structures.

In contrast to the well-established research with positive wall–soil friction7,8, published work on negative wall–soil friction is scarce. To date, limited attention has been given to the study of passive earth pressure applied on rigid retaining walls under negative wall–soil friction. One of the few works in relation to the effect of negative soil-wall friction is provided by Kérisel and Absi9, who presented a comprehensive table of passive earth pressure with negative soil-wall friction using the slip-line method. Kumar and Rao2 later conducted a study on the passive earth pressure acting on a wall by varying the wall–soil friction from negative to positive, using the limit equilibrium method by adopting Terzaghi’s failure surface10. Choudhury and Rao11 extended this to the seismic context, emphasizing the strong influence of seismic accelerations on passive resistance, especially with negative wall friction. On the other hand, the well-known Coulomb’s solution proposed by Poncelet12 incorporates both negative and positive wall–soil frictions3,13. It’s important to recognize that these methods focus on satisfying the kinematic condition, often at the expense of the equilibrium condition. Consequently, the passive load calculated by these traditional approaches generally exceeds the actual collapse load, as noted by James and Bransby14.

Very recently, Nguyen15 presented precise solutions for passive earth pressures under positive soil-wall friction using a fully plastic solution. The method is also referred to as the Incipient Failure Everywhere (IFE) solution or the rigid-plastic solution16,17. It has a long-established history in geotechnical engineering, and it adopts the assumption of critical limit equilibrium and the Mohr–Coulomb failure criterion18. The fully plastic solution was comprehensively investigated by Booker19 and has its roots in Rankine’s seminal paper20 on the study of slopes with traction-free surfaces and arbitrary inclination. Later, Rankine’s theory was combined with the method of characteristics by Sokolovskii21 for the infinite wedge theory. Nguyen’s solutions15, rooted in a statically admissible stress field, are highly valued for potentially providing an exact solution, as highlighted by Lancellotta22. These solutions incorporate the strengths of Sokolovski’s approach21, including mathematical elegance, a lower bound solution, and effectiveness in handling large soil deformations near walls, as observed by James and Bransby14.

The fully plastic solution, detailed by Nguyen et al.4, effectively addresses negative wall–soil friction in active earth pressure. Leveraging advanced soft computing techniques, this study significantly advances the estimation of active earth pressure in cohesionless backfill. Employing a Bayesian regularization backpropagation neural network, the model demonstrates remarkable alignment with measured values, presenting itself as a versatile tool for retaining wall design, especially in the presence of negative wall–soil friction, thereby pushing the boundaries of geotechnical engineering.

In the realm of passive earth pressure, drawing inspiration from the work of Nguyen and Shiau3, the study investigates the impact of negative wall–soil friction on various rigid wall geometries. Utilizing statically admissible stress fields, conservative solutions for the passive earth pressure coefficient are derived, providing insights into load transfer mechanisms within cohesionless backfill. The study identifies the stress state transition zone and elucidates the influence of wall inclination on passive earth pressure, contributing to the creation of comprehensive design charts for engineering practice. Consequently, a research gap is identified concerning the determination of statically admissible stress fields in cohesionless backfill with a vertical wall’s rear face and negative wall–soil friction under passive earth pressure conditions, posing a challenge in optimizing retaining wall design in engineering practice.

To bridge this research gap, this study explores the statically admissible stress field in the backfill of a rigid retaining wall with a vertical wall’s rear face under negative wall–soil friction, employing the fully plastic solution. Machine learning is integrated to gain deeper insights into the load transfer mechanism, proposing a user-friendly tool for practical retaining wall structure design. The primary objectives of this study are: (1) to determine the accurate passive earth pressure exerted on a rigid wall in the presence of negative soil-wall friction, (2) to investigate the statically admissible stress field using the fully plastic solution, and (3) to utilize machine learning techniques for additional insights into the physical behavior of the backfill material under diverse loading conditions. The outcomes of this research promise to contribute significantly to various fields within granular mechanics, deepening understanding of retaining wall structures, uplift anchor structures, and silo structures.

The theory

Equilibrium and yield criteria

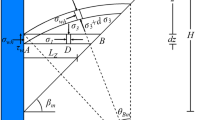
The problem with negative wall–soil friction is presented with a potential curved sliding surface that is concave. Savage et al.1 experimentally demonstrated the existence of this failure surface (ref. Fig. 1a). Note that the stress components in the backfill must satisfy the equilibrium conditions in the polar coordinate system as presented in Eqs. (1) and (2) (ref. Fig. 1b).

$$ \frac{{\partial \sigma_{rr} }}{\partial r} + \frac{1}{r}\frac{{\partial \tau_{r\theta } }}{\partial \theta } + \frac{{\sigma_{rr} - \sigma_{\theta \theta } }}{r} = \gamma \cos \theta $$
(1)
$$ \frac{{\partial \tau_{r\theta } }}{\partial r} + \frac{1}{r}\frac{{\partial \sigma_{\theta \theta } }}{\partial \theta } + 2\frac{{\tau_{r\theta } }}{r} = - \gamma \sin \theta $$
(2)

where r is equal to z/cos(θ) (ref. Fig. 1b).

$$ \left( {\sigma_{r} - \sigma_{\theta } } \right)^{2} + 4\tau_{r\theta }^{2} = \left( {\sigma_{r} + \sigma_{\theta } } \right)^{2} \sin^{2} \phi $$
(3)
Fig. 1
figure 1

(a) Passive earth pressure with negative wall–soil friction; (b) Geometry and stress components along various planes of a rigid retaining wall subjected to negative wall friction.

Full size image

Equation 3 shows a Coulomb-type yield criterion. Using this equation as well as the in-plane mean stress (p) and the relative angle ψ, the polar stress components are shown in Eq. (4).

$$ \left\{ \begin{gathered} \sigma_{rr} = p(1 + \sin \phi \cos 2\psi ) \hfill \\ \sigma_{\theta \theta } = p(1 - \sin \phi \cos 2\psi ) \hfill \\ \tau_{r\theta } = p\sin \phi \sin 2\psi \hfill \\ \end{gathered} \right. $$
(4)

where p = (σrr + σθθ)/2, i.e., p is a mean normal stress. Using the hypothesis of self-similarity proposed by Sokolovskii21, Eqs. (5) and (6) are presented.

$$ p = \gamma r\chi \left( \theta \right) $$
(5)
$$ \psi = \psi \left( \theta \right) $$
(6)

where χ(θ) is a dimensionless mean normal stress function with the key parameter (θ) in the given radial stress field.

Substituting the polar stress components in Eq. (4) and the “self-similarity” equations in Eqs. (5) and (6) into Eqs. (1), (2), a new set of the form of equations for stress equilibrium is generated. Note that the two variables (χ) and (ψ) are involved in the equations as shown in Eqs. (7), (8).

$$ \sin \phi \sin 2\psi \frac{d\chi }{{d\theta }} + 2\chi \sin \phi \cos 2\psi \left( {\frac{d\psi }{{d\theta }} + 1} \right) + \chi \left( {1 + \sin \phi \cos 2\psi } \right) = \cos \theta $$
(7)
$$ \left( {1 - \sin \phi \cos 2\psi } \right)\frac{d\chi }{{d\theta }} + 2\chi \sin \phi \sin 2\psi \left( {\frac{d\psi }{{d\theta }} + 1} \right) + \chi \sin \phi \sin 2\psi = - \sin \theta $$
(8)

Further, a pair of Ordinary Differential Equations (ODEs) is presented in Eqs. (9) and (10) based on Eqs. (7),(8).

$$ \frac{d\chi }{{d\theta }} = \frac{\chi \left( \theta \right)\sin (2\psi ) - \sin (2\psi + \theta )}{{\cos 2\psi - \sin \phi }} $$
(9)
$$ \frac{d\Psi }{{d\theta }} = \frac{d\psi }{{d\theta }} + 1 = \frac{{\sin \phi \cos (2\psi + \theta ) + \chi (\theta )\cos^{2} \phi - \cos \theta }}{{2\chi \left( \theta \right)\sin \phi \left( {\sin \phi - \cos 2\psi } \right)}} $$
(10)

For the processing of numerical solutions, it is necessary to transform the polar coordinate stress system into a Cartesian coordinate system. This is shown in Eqs. (11)–(15).

$$ x = r\sin \theta $$
(11)
$$ z = r\cos \theta $$
(12)
$$ \sigma_{zz} = \frac{{\sigma_{rr} + \sigma_{\theta \theta } }}{2} + \frac{{\sigma_{rr} - \sigma_{\theta \theta } }}{2}\cos 2\theta - \tau_{r\theta } \sin 2\theta = p + q\cos 2\Psi $$
(13)
$$ \sigma_{xx} = \frac{{\sigma_{rr} + \sigma_{\theta \theta } }}{2} - \frac{{\sigma_{rr} - \sigma_{\theta \theta } }}{2}\cos 2\theta + \tau_{r\theta } \sin 2\theta = p - q\cos 2\Psi $$
(14)
$$ \tau_{xz} = \frac{{\sigma_{rr} - \sigma_{\theta \theta } }}{2}\sin 2\theta + \tau_{r\theta } \cos 2\theta = q\sin 2\Psi $$
(15)

where

$$ \Psi = \psi + \theta $$
(16)

Singular line in a radial stress field

A singular line is a characteristic line or a line of stress discontinuity representing wall–soil roughness and the respective geometry conditions3. The passive stress state of positive wall friction causes the major principal stress to rotate in a clockwise direction15. Conversely, in the case of negative wall friction, the direction of the major principal stress rotation is counterclockwise. As a result, the singular line in the backfill of negative wall friction differs from that of positive wall friction, and it exhibits distinct characteristics in comparison to backfill with positive wall friction.

The area between the singular line and the traction-free surface is referred to as Rankine’s region. Depending on the degree of negative wall friction, this region may either vanish or take up the entire backfill region if the traction-free surface coincides with the singular line (see Fig. 2a–c). In the Rankine region, the relative angle (ψ) on the traction-free slope can be determined by solving Eq. (10) with the condition that Ψ remains constant and the slope is traction-free (χ = 0)23. To prevent soil particles from sliding down the traction-free slope, the traction-free surface must maintain an angle that is less than the angle of repose for uncompacted cohesionless sand.

Fig. 2
figure 2

(a) A possible line of stress characteristics for a smooth wall; (b) The Rankine region encompassing the entire backfill for a negatively rough wall; (c) A possible line of stress discontinuity for a perfectly negative rough wall; (d) A Mohr–Coulomb diagram illustrating the stress relationship between two adjacent regions. It is important to note that within the Rankine regions, the direction of the major principal stress remains constant, and the stress components follow a strictly linear pattern. Conversely, outside the Rankine regions, both the direction of the major principal stress and the stress components exhibit nonlinearity.

Full size image

Specifically, when the angle between the slope and the rear face of the wall is an acute angle, the backfill is always bisected by a line of stress discontinuity. On the other hand, if the angle between the slope and the rear face of the wall is obtuse, the backfill will be separated by a stress characteristic line for low levels of negative wall friction. However, for high levels of negative wall roughness, the line of stress characteristic will be replaced by a stress discontinuity line.

The inclusion of a stress discontinuity in the backfill is imperative as it would enable the establishment of a stress field that satisfies all relevant boundary conditions. The study of stress discontinuity in radial stress fields has been explored in numerous works, including Lee24, Shield25, Booker19, Savage18; thus, it will not be repeated here. To ensure stability and balance, the continuity of both normal and tangential stress components must be insisted across the stress discontinuity line. The stress discontinuity line, as a result of self-similarity, is a straight line that separates regions C1 and C2 (see Fig. 2d). The stress jump along the stress discontinuity line, represented by an angular coordinate θD, can be expressed mathematically by Eqs. (17),(18).

$$ \tan \left( {\Psi_{1} - \theta_{D} } \right)\tan \left( {\Psi_{2} - \theta_{D} } \right) = {{\left( {1 - \sin \phi } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \sin \phi } \right)} {\left( {1 + \sin \phi } \right)}}} \right. \kern-0pt} {\left( {1 + \sin \phi } \right)}} $$
(17)
$$ {{\sin 2\left( {\Psi_{1} - \theta_{D} } \right)} \mathord{\left/ {\vphantom {{\sin 2\left( {\Psi_{1} - \theta_{D} } \right)} {\sin 2\left( {\Psi_{2} - \theta_{D} } \right)}}} \right. \kern-0pt} {\sin 2\left( {\Psi_{2} - \theta_{D} } \right)}} = {{p_{2} } \mathord{\left/ {\vphantom {{p_{2} } {p_{1} }}} \right. \kern-0pt} {p_{1} }} $$
(18)

Interestingly, it is to be noted that the stress discontinuity vanishes when the stress discontinuity line coincides with a line of stress characteristics.

Numerical procedures

Equations (9) and (10), which represent the governing equations, involve two primary variables: χ(θ) and ψ(θ). By applying the specified boundary conditions, a numerical solution was obtained for these ordinary differential equations using the initial-boundary value problem approach, where the boundary values for the relative angle (ψ) and the mean stress (χ) are specified at the same angular coordinate (θ). Alternatively, these equations can also be solved using the boundary-value problem method, where (χ) and (ψ) a are defined at different locations.

The boundary conditions for solving boundary-value problems are shown in Table 1. Note that either theoretical postulates or numerical methods can be utilized to convert them into initial-value problems.

Table 1 Initial boundary conditions.
Full size table

Solutions to the governing equations (Eqs. (9) and (10)) were computed using two distinct approaches. For initial-value problems, a 5th order adaptive Runge–Kutta method was chosen to address instability issues in non-smooth domains. In contrast, boundary-value problems were tackled using a combination of the shooting method and the 5th order adaptive Runge–Kutta method, which transformed them into initial-value problems with an interpolation technique. The effectiveness of these numerical approaches in achieving precise solutions is a significant focus of this study.

Runge–Kutta method for an initial-value problem

Mathematically, a typical initial value problem can be stated as,

$$ y^{\prime} = f(x,y),\,\,\,\,\,\,\,y(x = \theta_{o} ) = \alpha $$
(19)

where y is a vector, and it consists of two variables (χ and ψ) that are independent of each other as shown in Eqs. (9) and (10), respectively. The global variable (x) is angular coordinate (θo) and α has two known values (α1 and α2) for the vector y at the same ___location, \(\chi \left| {_{{\theta = \theta_{0} }} } \right. = \alpha_{1} ,\,\psi \left| {_{{\theta = \theta_{0} }} } \right. = \alpha_{2}\). The adaptive step size procedure will be adjusted based on the estimated error (Eq. 20) when the integration process reaches a singular line,

$$ h_{0} = h_{1} \left| {\frac{{\Delta_{0} }}{{\Delta_{1} }}} \right| $$
(20)

where Δ0 is the chosen accuracy, and Δ1 is the error yielded by the step size h1.

A truncation error Δ(h) is estimated as below for the mth order formula,

$$ \Delta (h) = y_{m + 1} (x + h) - y_{m}^{*} (x + h) = \sum\limits_{i = 1}^{6} {\left( {c_{i} - c_{i}^{*} } \right)} k_{i} $$
(21)

Note that the \(y_{m}^{*}\) and \(y_{m + 1}^{{}}\) are the 5th and 4th orders embedded formulas presented in Fehlberg 26. This is defined as follows,

The 5th order formula:

$$ y_{m + 1}^{{}} (x + h) = y_{m} (x) + \sum\limits_{i = 1}^{6} {c_{i}^{{}} k_{i} } + O\left( {h^{6} } \right) $$
(22)

The 4th order formula:

$$ y_{m + 1}^{*} (x + h) = y_{m} (x) + \sum\limits_{i = 1}^{6} {c_{i}^{*} k_{i} } + O\left( {h^{5} } \right) $$
(23)
$$ k_{1} = hf\left( {x,y} \right) $$
(24)
$$ k_{i} = hf\left( {x + a_{i} h,y + \sum\limits_{j = 0}^{i - 1} {b_{ij} k_{j} } } \right),\,\,\,\,\,\,\,i = 2,3,...,6 $$
(25)

Noting that the set of coefficients ai, bi, ci, and c*i proposed by Cash and Karp27 provide better accuracy than Fehlberg’s original values28, hence, they are adopted in this study (ref. Table 2).

Table 2 Cash-Karp coefficients for embedded Runge–Kutta method.
Full size table

The method employed in this study involves adjusting the step size in the integration process based on the truncation error (Δ1) in comparison to a pre-defined error threshold (Δ0). If the truncation error is less than the threshold (Δ1 < Δ0), the step size will be reduced, but if it is greater than or equal to the threshold (Δ1 ≥ Δ0), the step size will be increased. This adaptive step size approach is shown in Fig. 3. The integration process requires setting both an initial step size and a numerical tolerance for each iteration. The numerical tolerance is consistently maintained at eTol = 1E−6 across all runs, The initial step size is initially set to an extremely small value, such as h = 1E−20. However, this value may be dynamically adjusted within a range, potentially as small as h = 1E−50, in response to numerical perturbations that arise when addressing singularities during the computation.

Fig. 3
figure 3

Demonstration of the shooting method for the case (λ = 0, ϕ = δ = 40°, β = − 30°).

Full size image

Shooting method for the two-point boundary value problem

The initial value solution for the ___domain bounded by a characteristics line and the rigid wall may not be an accurate representation of the true one. This is because the initial-value solution fails to extend from Rankine’s region (bounded by the traction-free surface and characteristic line) to the non-Rankine region (bounded by the rear face of the wall and characteristic line). In other words, the solution does not necessarily link the numerical results (χ and ψ) between Rankine’s and non-Rankine’s zones, as reported by Nguyen and Pipatpongsa29. It follows that the problem can be defined as a two-point boundary value problem, as discussed in the works of Kiusalaas30.

$$ \left\{ {\begin{array}{*{20}c} {\chi^{\prime} = \chi^{\prime}\left( {\chi ,\psi ,\theta } \right) = \frac{d\chi }{{d\theta }} \, } \\ {\psi^{\prime} = \psi^{\prime}(\chi ,\psi ,\theta ) = \frac{d\psi }{{d\theta }} = \frac{d\Psi }{{d\theta }} - 1} \\ \end{array} } \right.,\,\,\,\,\left\{ {\begin{array}{*{20}c} {\left. \chi \right|_{{\theta = \theta_{1} }} = u} \\ {\left. {\,\psi } \right|_{{\theta = \theta_{1} }} = \psi_{1} } \\ \end{array} } \right.,\,\,\,\,\left\{ {\begin{array}{*{20}c} {\left. \chi \right|_{{\theta = \theta_{2} }} = \chi_{2} } \\ {\left. {\,\psi } \right|_{{\theta = \theta_{2} }} = v} \\ \end{array} } \right.\,\,\,\,\, $$
(26)

The numerical solution to the set of ordinary differential equations (Eqs. (9) and (10)) involves finding the two values u and v by integrating the equations between the initial point (θ1) and the final point (θ2). This is known as the two-point boundary value problem and is graphically shown in Fig. 3. The shooting method is adopted to obtain accurate numerical results for this problem.

A root-finding method based on Brent’s algorithm21 was adopted to solve for the unknown value of “u”. It is important to note that the solution of “χ” at θ = θ2 is dependent on the unknown value of “u” at θ = θ1, meaning that “u” is the root of Eq. (27):

$$ r(u) = f(u) - \chi \left| {_{{\theta = \theta_{2} }} } \right. = f(u) - \chi_{2} = 0 $$
(27)

herein, r(u) is the boundary residual between the specified boundary-value \(\chi \left| {_{{\theta = \theta_{2} }} } \right. = \chi_{2}\) and, the computed boundary-value for \(\chi \left| {_{{\theta = \theta_{1} }} } \right.\).

The numerical procedure, which involves the use of Brent’s algorithm, is executed in three consecutive steps. In the first step, a range of constraints for the root “u” of Eq. (27) is specified. It is important to note that the results for each problem can vary greatly, so the range of constraints for “u” was carefully determined for each problem. In the second step, Brent’s algorithm is executed iteratively to find “u” from Eq. (27), and the evaluation of f(u) is required for each iteration by solving an initial-value problem using the 5th order adaptive Runge–Kutta method. Finally, the numerical procedure is completed in the third step by solving the differential equations (Eqs. (9) and (10)) once more as an initial-value problem, until the root (u) is found.

Rankine’s and non-Rankine’s regions

A crucial part of the analysis involves identifying the Rankine region within the backfill. This identification requires considering various factors15, including the geometry of the backfill and the level of wall friction. To determine the direction of principal stress at the rear face of the wall, several assumptions related to wall roughness are made, which are outlined below.

For negative soil-wall friction1, it is assumed that the following condition holds at the rear face of the wall (θ = 0).

$$ \tau_{r\theta } = - \sigma_{\theta } \tan \delta $$
(28)

By substituting Eq. (4) into Eq. (28), we obtain the boundary condition (Eq. 29) for the “relative angle” of the major principal stress (ψ) at the wall rear face (θ = 0),

$$ \psi_{w} = \frac{1}{2}\left[ {\pi + \delta + \arcsin \left( {\frac{\sin \delta }{{\sin \phi }}} \right)} \right] $$
(29)

To begin an analysis, the first step is to specify the level of wall roughness for both the wall and backfill geometry (see Fig. 4). Consequently, Rankine regions for the backfill can be determined. When the whole backfill is within the Rankine region, the direction of the major principal stress is constant throughout the backfill (referred to as case 1). However, for higher degrees of wall roughness, a stress discontinuity line divides the backfill into Rankine’s and non-Rankine’s regions (case 2). Conversely, for lower degrees of wall roughness, a stress characteristic line divides the backfills (case 3). For a positive sloping backfill stabilized at the soil’s internal friction angle, the stress characteristic line intersects the traction-free surface, leading to the disappearance of the Rankine region from the backfill (case 4).

Fig. 4
figure 4

The effect of negative wall friction on the mechanism of load transfer.

Full size image

Problems with a stress discontinuity line

The direction of the major principal stress at the traction-free surface is uncertain, as previously indicated in Table 1. Thus, the numerical procedure begins with solving Eq. (30) to obtain the value of ψ at the traction-free surface, as suggested by Booker19.

$$ \cos \theta - \sin \phi \cos \left( {2\psi \left( \theta \right) + \theta } \right) = 0 $$
(30)

Moreover, the direction of the major principal stress at the rear face of the wall is influenced by the wall–soil friction angle, causing it to tilt downward from the horizontal direction. Hence, Eq. (29) is employed to determine the relative angle of the major principal stress (ψw) with respect to the wall–soil friction angle (δ). The flowchart showing the numerical procedure for problems with a stress discontinuity line is presented in Fig. 5.

Fig. 5
figure 5

Problems with a stress discontinuity line ~ a flow chart showing the numerical procedure.

Full size image

To handle the singularities at the rear face of the wall and the traction-free surface, a numerical perturbation technique is used. At the traction-free surface, the initial values for χ and ψ are slightly perturbed by the amount of 10–28 and 10–12, respectively. On the other hand, the integration process for this two-dimensional problem can reach the rear face of the wall without causing numerical stability issues.

Problems with a line of characteristics

The problem with a line of characteristics can be tackled by using the numerical procedures for solving the two-point boundary value problem under various soil backfill geometries and wall roughness.

For cases where the inclination angle of the traction-free surface is less than the internal friction angle, the procedure involves solving the initial value boundary problem in the region bounded by the characteristic line and the traction-free surface, and then shooting the pair of governing equations from the characteristic line to the wall rear face.

For cases where the soil internal friction angle equals the inclination angle of the traction-free surface, the numerical procedure is stepwise, involving an iterative process to find the value of the mean stress (χ) at the traction-free surface, and then extending the solution to the traction-free surface using 6th order polynomial fitting. The details of these procedures are explained in a flowchart shown in Fig. 6.

Fig. 6
figure 6

A flowchart showing the numerical procedure for problems with a characteristic line.

Full size image

Results and discussion

Vertical wall with horizontal backfill

This study compares earth pressure coefficients Kp acting on rigid walls with negative wall friction for a vertical wall (λ = 0) with horizontal backfill (β = 0). The obtained theoretical results are compared with those published ones using the limit equilibrium method and the slip line method. Figure 7 shows that the results obtained in this study are in good agreement with those of Kumar and Rao2, whereas the slip line method proposed by Kérisel and Absi9 overestimated the passive earth pressure coefficient for rough walls with approximately δ/φ > 0.7.

Fig. 7
figure 7

Comparison of passive earth pressure coefficient with various wall friction angles between the present solution and those of Kerisel and Absi9 using slip-line method and Kumar and Rao2 using the limit equilibrium method.

Full size image

The numerical results of mean stress (χ) and relative angle of the major principal stress (ψ) for various degrees of negative wall friction are shown in Fig. 8. Note the presence of negative wall friction is to induce a stress discontinuity in the backfill. The ___location of this line of stress discontinuity is further away from the wall as the negative wall friction increases, accompanied by a pronounced mean stress jump.

Fig. 8
figure 8

Results of the relative angle of the major principal stress (ψ) and mean stress (χ) in case of (ϕ = 30°, λ = 0, and β = 0) with various degrees of negative wall friction.

Full size image

To the best of knowledge, the research conducted by Savage et al.1 provides an in-depth analysis of failure mechanisms in cohesionless soil behind rigid walls subjected to negative soil-wall friction. This seminal study combines both analytical and experimental methods, with the analytical results showing excellent alignment with experimental data, especially concerning the effects of negative wall–soil friction.

A critical aspect of this study is the use of a stress discontinuity surface to meet static equilibrium requirements, which is essential for addressing the boundary conditions associated with negative wall–soil friction. Savage et al.1 validated this approach by demonstrating a close match between theoretical predictions and experimental observations of failure surfaces. The analysis, as compared to the findings of Savage et al.1, is depicted in Fig. 9. This comparison shows a strong correlation, particularly in the ___location of the stress discontinuity surface, where the stress jump occurs. This key feature is crucial for establishing a statically admissible stress field and supports the validity of the proposed model.

Fig. 9
figure 9

Comparison between the present solution and Savage et al.1: (a) Relative angle of the major principal stress (ψ) and (b) Mean stress (χ), (c) the passive earth pressure coefficient (Kp) for the case of ϕ = 38°, λ = 0, and β = 0 with various degrees of negative wall friction.

Full size image

Furthermore, the passive earth pressure coefficient (Kp) is compared with the results from Savage et al.1 (see Fig. 9c). The comparison reveals a significant level of agreement, further reinforcing the robustness of the theoretical model.

The stress distribution in the backfill is significantly affected by negative wall friction. Figure 10 shows that the vertical stress increases as the negative wall roughness increases, whereas the increase in wall friction reduces both the horizontal and shear stresses. Interestingly, the stress state changes from passive to active when the wall roughness reaches a perfectly rough state (δ = − φ). Also note that the wall friction only affects the stress distribution in the non-Rankine’s region bounded by the rear face of the wall and the line of stress discontinuity, whereas stress distribution in the Rankine region is independent of the magnitude of wall roughness.

Fig. 10
figure 10

Cartesian stress components at a height of interest in the backfill in case of (ϕ = 30°, λ = 0, and β = 0) with various degrees of negative wall friction: (a) normalized vertical stress σz/γz; (b) normalized horizontal stress σx/γz; (c) normalized shear stress σx/γz.

Full size image

In the case of a perfectly smooth wall and horizontal backfill, the Rankine region occupies the entire backfill. However, for a rough wall, a line of stress discontinuity appears, dividing the backfill into two separate regions. The major principal stress direction is horizontal in the Rankine region, but in the negative wall backfill, the direction of the major principal stress tilts upward (see Fig. 11). This direction of the major principal stress aligns with the mechanism of negative wall friction, in which the wall moves faster than the soil.

Fig. 11
figure 11

Trajectories of the principal stresses in the backfill in case of (ϕ = 30°, λ = 0, and β = 0) with various degrees of negative wall friction (the stress discontinuity is shown in a red dashed line): (a) perfectly smooth wall (δ = 0); (b) rough wall (δ = − 15°); (c) perfectly rough wall (δ = − 30°).

Full size image

Vertical wall with negative sloping backfills

It is worth noting that the earth pressure coefficient under a smooth wall is equivalent to the earth pressure coefficient at the central line of a symmetrical sand heap under a wedge shape. This has been extensively studied by Booker19 and Michalowski and Park31 using the fully plastic solution for the sand heap problem. Furthermore, the horizontal earth pressure at the center of the symmetrical sand heap is equivalent to the horizontal earth pressure acting on a vertical wall without wall roughness. Thus, their works are used to validate the obtained results in Fig. 12.

Fig. 12
figure 12

Comparison between the present method and those of Booker19 and Michalowski and Park31.

Full size image

Figure 12 shows a comparison of the presented results with those Booker19 and Michalowski and Park31. Numerical results have shown that19’s numerical approximation of the IFE solution was not entirely convincing for small values of tan (θ°) (ref. Fig. 12a and b). By checking the weight balance condition, it is found that the error between the present method and the total weight of the symmetrical sand heap is only 0.00574%, indicating that the results presented by19 can be improved. The slight discrepancies between the results of the current study and those reported by Michalowski and Park31 could be attributed to the limited application of limit analysis for arch action.

The numerical results for the mean stress (χ) and relative angle of principal stress (ψ) are shown in Fig. 13. The degree of wall roughness affects the ___location of the stress discontinuity, with greater degrees of roughness causing it to move further from the wall and result in larger stress jumps.

Fig. 13
figure 13

Results of the mean stress (χ) and relative angle of principal stress (ψ) in case of ϕ = 30°, λ = 0, β = − 30° for various degrees negative wall friction.

Full size image

The stress state in the vicinity of the wall in a negative sloping backfill is significantly influenced by the degree of negative wall friction. As shown in Fig. 14, an increase in negative wall friction results in an increase in the magnitude of the vertical stress at the wall while decreasing the horizontal stress at the wall. Notably, the stress state in the vicinity of the wall undergoes a transition from a passive stress state for smooth walls to an active stress state for perfectly rough walls. Furthermore, it is interesting to observe an abrupt change in the magnitude of the vertical stress as the value of negative wall friction equals the internal friction angle of soils. These findings shed light on the complex stress distribution and behavior of cohesionless materials subjected to negative wall friction, with significant improvement over current considerations in design practices.

Fig. 14
figure 14

Profiles of rectangular stress components at a height of interest in case of (ϕ = 30°, λ = 0, β = − 30°) for various degrees of negative wall friction (δ): (a) normalized vertical stress σz/γz; (b) normalized horizontal stress σx/γz; (c) normalized shear stress σx/γz.

Full size image

The phenomenon of soil arching is evident in the negative sloping backfill, as shown in Fig. 15. The degree of wall roughness has a significant impact on the span of the arch. As the roughness of the wall increases, the arch expands. Moreover, the trajectories of the principal stresses highlight the change in the major principal stress direction from a horizontal orientation to a diagonally upward orientation. This observation suggests that the negative wall friction not only affects the magnitude of stresses in the vicinity of the wall, but also the direction of the stresses in the backfill. Such findings provide valuable insights for the design of retaining structures under negative wall friction.

Fig. 15
figure 15

The trajectories of principal stresses in negative sloping backfill in case of (ϕ = 30°, λ = 0, β = − 30°) with various degrees of negative wall friction (the stress discontinuity is shown in a red dashed line): (a) perfectly smooth wall (δ = 0); (b) rough wall (δ = − 15°); (c) perfectly rough wall (δ = − 30°).

Full size image

Vertical wall with positive sloping backfills

In contrast to the vertical wall with horizontal and negative sloping backfills, the line of stress discontinuity disappears in the positive sloping backfill, but the line of stress characteristic divides the backfill into two regions: namely the Rankine and non-Rankine regions. See Fig. 16 for the numerical results of the mean stress (χ) and relative angle of principal stress (ψ). The magnitude of the negative wall friction causes the direction of the major principal stress to rotate counterclockwise while also reducing the magnitude of the mean stress at the wall’s rear face.

Fig. 16
figure 16

Results of mean stress (χ) and relative angle of the major principal stress (ψ) in case of (ϕ = 30°, λ = 0, β = 30°) for various degrees of negative wall friction (δ).

Full size image

The stress state in the cohesionless backfill of the positively sloping wall undergoes a similar transformation to that of the previous negative sloping wall, i.e., a change from a passive stress state to an active stress state as the degree of negative wall friction increases. This transition to an active stress state was observed for a perfectly rough wall as shown in Fig. 17. Note that the Rankine region vanished from the backfill as the backfill is bounded by the line of stress characteristic on the sloping surface and the wall rear face (ref. Fig. 18). Also note that the major principal stress direction rotates in a counterclockwise direction as the magnitude of negative wall friction increases, resulting in a reduction of the mean stress at the wall rear face (Fig. 17).

Fig. 17
figure 17

Cartesian stress components at a height of interest in case of (ϕ = 30°, λ = 0, β = 30°) for various degrees of negative wall friction (δ): (a) δ = 0; (b) δ = − 15°; (c) δ = − 30°.

Full size image
Fig. 18
figure 18

The trajectories of principal stresses in negative sloping backfill in case of (ϕ = 30°, λ = 0, β = 30°) with various degrees of negative wall friction: (a) δ = 0; (b) δ = − 15°; (c) δ = − 30°.

Full size image

Design charts and tables

Comprehensive design charts are presented in Fig. 19. They can be used to determine passive earth pressure coefficients with negative wall friction for various backfill geometries and internal soil friction angles. These charts also illustrate the effects of the angle of sloping backfills, the degree of negative wall friction, and the internal friction angle on the magnitude of the passive earth pressure coefficient. Notably, the presence of negative wall friction reduces the effect of the sloping angle on the earth pressure coefficient, and the value of the coefficient remains almost constant as the sloping angle increases. These findings have many practical implications for engineering applications and therefore they are presented in tabular form in Tables 3, 4 and 5.

Fig. 19
figure 19

Design charts for determining the passive earth pressure coefficient subjected to negative wall friction.

Full size image
Table 3 Passive earth pressure coefficients for ϕ = 20° with various angles of sloping backfill (negative wall friction).
Full size table
Table 4 Passive earth pressure coefficients for ϕ = 30° with various angles of sloping backfill (negative wall friction).
Full size table
Table 5 Passive earth pressure coefficients for ϕ = 40° with various angles of sloping backfill (negative wall friction).
Full size table

Soft computing approaches

Sensitivity analysis using soft computing approach

Numerical solutions presented in the previous section have demonstrated rigor, accuracy, and efficacy, and a series of design charts and tables been also provided for practical uses. However, further insights into the load transfer mechanism of cohesionless backfill materials required more effort thus the statistical analysis is conducted by employing four well-known and robust machine learning models e.g., XGBoost32,33, decision tree (DT)34, long and short-term memory neural network (LSTM)35,36, and feedforward neural network (FNN)37,38.

The dataset used for conducting soft computing consisted of 529 samples, which were obtained by the analytical solution for both positive (found in Nguyen15) and negative (this paper) wall frictions. The statistical properties of the dataset, such as mean, standard deviation, minimum, and maximum values, are presented in Table 6. The distribution of normalized input and output variables is given in Appendix A1. These properties provide insights into the range of values for the input parameters and the resulting values for the passive earth pressure coefficient.

Table 6 The statistical description of the input and output variables.
Full size table

Among the machine learning models employed, XGBoost consistently demonstrated superior performance, as detailed in Appendix A3. The merits of XGBoost are evident through its exceptional performance metrics. For instance, the R2 values for the training data, testing data, and the entire dataset stand at 1, 0.998, and 1, respectively, as illustrated in Appendix A2.

XGBoost, introduced by Chen39, excels in handling large, complex datasets with high dimensionality. It outperforms other machine learning algorithms by effectively managing missing data and various data types (numeric, categorical, and ordinal variables). Notably, XGBoost is known for its speed and scalability, as confirmed by Chen and Guestrin32. In this study, therefore, XGBoost is employed to develop a soft computing model for determining passive earth pressure coefficients under varying loads and geometries. This model also facilitates sensitivity analyses, providing valuable insights into the problem’s physical behavior.

Figure 20 presents the average relative importance and the gain-based relative importance of each feature via the use of F-score. The results indicate that the internal friction angle (ϕ) has the greatest influence on the passive earth pressure coefficient, with a relative importance of over 40%, followed closely by the ratios of wall–soil friction angle over internal friction angle (δ/ϕ) and sloping angle over internal friction angle (β/ϕ) with a contribution of approximately 30%. Figure 20b shows that the gain of ϕ is approximately 12, while the gains of δ/ϕ and β/ϕ are approximately equal to 8, indicating that ϕ has the highest importance among the input parameters in predicting the target variable. This information is valuable in practice as it can quantify the influence of several design parameters on a specific design outcome such as Kp in this paper.

Fig. 20
figure 20

Feature importance analysis of the XGBoost model: (a) Average relative importance. (b) The gain based relative importance of each feature.

Full size image

The use of partial dependence plots (PDPs) would further show the interaction between the target response and an input feature of interest. The PDPs in Fig. 21 reveal that all input parameters have a proportional impact on the output variable (passive earth pressure coefficient, Kp). That is, an increase in the value of any input parameter results in a nonlinear increase in the value of Kp, despite of the various levels of impact in each parameter. Specifically, for the internal friction angle (ϕ), the magnitude of Kp increases sharply after a value of 30 degrees (ref. Fig. 21a). The positive sloping angle (β/ϕ) also has a significant impact on increasing the value of Kp (ref. Fig. 21b).

Fig. 21
figure 21

PDPs of variables.

Full size image

Finally, the impact of wall–soil friction is elucidated through the statistical analysis, as depicted in Fig. 22c. It becomes evident that while a positive wall friction angle (δ/ϕ) has a pronounced effect in significantly increasing the value of Kp, the presence of negative wall–soil friction diminishes the magnitude of the passive earth pressure exerted on the wall. Specifically, the value of Kp is approximately 4 for a smooth wall, but this value reduces to less than 2 when the wall–soil friction angle becomes negative with a magnitude half that of the friction angle. This observation underscores the critical need for investigating the influence of negative wall–soil friction on passive earth pressure. Such investigations are essential in our pursuit of conservative solutions that accurately account for these nuanced effects.

Fig. 22
figure 22

(a) Graphical User Interface (GUI) of RW: Automatic parameter setting. (b) Graphical User Interface (GUI) of RW: Model training, prediction, convergence history plotting, feature importance calculation, and partial dependence analysis. (c) Graphical User Interface (GUI) of RW: Predicted outcome.

Full size image

In summary, the statistical analysis employing the soft computing model not only provides valuable insights into the behavior of passive earth pressure coefficients but also equips engineers and designers with quantifiable knowledge to optimize their designs and consider the full spectrum of factors influencing these critical structural parameters.

Graphical user interface (GUI)

As the final step of the proposed hybrid soft computing process, a graphical user interface (GUI) is implemented in this study. The developed graphical user interface (GUI), called RW, provides a user-friendly visual interface (e.g., graphical elements such as icons, buttons, menus, and windows) that allows one to interact with, rather than using traditional text-based commands. Several functions, such as automatic parameter setting, model training, prediction, convergence history plotting, feature importance calculation, and partial dependence analysis, are all created, as shown in Fig. 22a,b, and c, which provides a step-by-step guide to using the GUI.

Using the RW GUI, as shown in Fig. 22, numerical output from the user-friendly visual interface is validated with those of Kumar and Rao2 and Krabbenhoft40 as shown in Fig. 23. It is pleased to see that the outputs of the GUI are in excellent agreement with those of Krabbenhoft40 in Fig. 23a and Kumar and Rao2 in Fig. 23b with R2 = 0.997 and 0996 respectively. It can therefore be concluded that the RW GUI makes it easier for one to perform complex analyses and allows friendly interactive analyses in a more intuitive approach. It would also increase productivity in engineering design.

Fig. 23
figure 23

Validation with independent data (a) Krabbenhoft40 with ϕ = 20°, 25°, 30°, 35°, and 40°; δ/ϕ = 0, 1/3, ½, 2/3, and 1, β/ϕ = 0 (b) Kumar and Rao2 with ϕ = 40°, g− 1 ≤ δ/ϕ ≤ 1, β/ϕ = 0.

Full size image

Conclusion

This paper has successfully studied the passive earth pressure exerted on rigid wall with negative wall friction. A subtle numerical procedure was developed to explore the statically admissible stress field in the backfill of the rigid retaining wall with various degrees of negative wall friction and backfill geometries using the fully plastic solution. In addition to the rigorous solution for the passive earth pressure on a rigid wall under negative wall–soil friction, the mechanics of load transfer in the cohesionless backfill material was also presented.

Negative wall friction has substantial effects on the load transfer mechanism, which is very distinct from that of positive wall friction. In particular, the magnitude of the negative wall friction is disproportional to the magnitude of the passive earth pressure. When the wall is fully rough, the value of Kp remains unchanged irrespective of the backfill sloping angle, and the values of Kp are all less than unity. The admissible stress fields have also revealed the mechanism of load transfer in the backfill, in that the negative friction angle would change the stress state in the non-Rankine region from passive to active stress state.

The obtained results of the passive earth pressure under negative wall friction and sloping backfill have been provided with design charts and tables to assist in engineering design practice. In addition, the incorporation of soft computing models in this study has the potential to greatly enhance our understanding of passive earth pressure and improve the design and analysis of retaining structures. The success of the study is a great contribution to the field of granular mechanics in studying the load transfer in a planar wedge, uplift anchor structures, and silo structure. It provides insight into the mechanism of load transfer of the upward relative movement between the wall and the backfill material.

In the future work, the proposed framework coupling statically admissible stress field and soft computing will be applied to investigate the seismic passive resistance in soil for negative wall–soil friction and compared with that of Choudhury and Rao11 using the limit equilibrium method.