Introduction

Presently, with the rapid development of technology and artificial intelligence, autonomous navigation has been successfully used in military and civilian applications1. Global Positioning System (GPS) is capable of providing satisfactory and reliable positioning accuracy for outdoor environment. However, the GPS may perform poorly in indoor venues owing to the satellite signal deterioration induced by signal attenuation, shadowing as well as multipath fading imposed by indoor concrete along with metallic structures2. Many positioning techniques have been developed for indoor mobile device, such as Inertial measurement unit (IMU)3, Bluetooth4, infrared5, ultrasonic6, Zigbee7, camera and simultaneous localization and mapping (SLAM)8. The IMU technique is difficult to achieve longtime positioning due to the drift phenomenon9. Bluetooth and ultrasonic positioning technology are suitable for short-distance positioning, and it is difficult to achieve long-distance spatial positioning10. The Zigbee is susceptible to interference induce by multiple signal types11. The major drawback of the camera and SLAM limits them for extensiveness to be executed and the cost hardware12. Fortunately, the state-of-the-art ultra-wide band (UWB) is more appropriate for indoor localization in virtue of its advantages, such as high precision, resistance to harsh multipath effects and more robustness to interference13, which has been regarded as a potential solution for high precision requirements in GPS-denied environment.

Up to date, many researchers have been working on indoor localization using the UWB system. For example, Cao et al.14 developed a novel positioning method which integrates the multidimensional scaling, particle swarm optimization (PSO) and Taylor series algorithm to minimize the localization error. Deng et al.15 combined a total least squares method and Taylor iterative algorithm to achieve UWB localization based on collaborative networking technology. Fan et al.16 proposed an improved inertial navigation system/pedestrian dead reckoning/UWB integrated localization scheme for indoor environment. Zaric et al.17 proposed a novel trilateration algorithm to calculate positions of the target node (TN). Leitinger et al.18 integrated the maximum likelihood method and the floor plan information in order to improve the estimation accuracy. Kok et al.19 developed an indoor localization technique by integrating inertial sensors and distance measurements from UWB system. Meanwhile, the gradient-based methods20, quasi-Newton method21, Taylor Series algorithm22, Gauss–Newton type Levenberg-Marquardt algorithm23, two stage maximum likelihood (TSML) algorithm24 have been commonly implemented in the UWB system to determine the TN’s position. As stated above, a large number of researches have conventionally focuses on localization approaches in order to return high estimation outcome.

Nevertheless, the UWB positioning technique in indoors scenario may lead to inaccurate localization because of the large ranging errors. To cape with this issue, the Kalman filter (KF) has been utilized to smooth the measurement distance obtained from UWB positioning system to reduce the ranging error in line-of-sight (LOS) condition. Moreover, Li et al.25 demonstrated that optimizing the parameters of KF with the usage of the PSO algorithm was able to enhance the ranging accuracy of UWB system, thereby yielding better estimation result. Fu et al.26 investigated an adaptive unscented Kalman filter (UKF) to determine the TN’s ___location in the UWB system, and the results showed that the positioning performance was obviously improved. Han et al.27 designed a robust UWB indoor localization strategy by taking advantage of extended Kalman filter (EKF) to enhance final estimation accuracy, which has been certified by positioning experiment. However, the methodologies based on the EKF and UKF both suppose that the state noise as well as the measurement noise was certain and known, which is hard to obtain the certain noise in practical situation, making the filtering performance insufficiently effective. To avoid performance deterioration, Cao et al.28 used variational Bayesian adaptive Kalman filter (VBAKF) to accurately re-estimate the measurement distance from the UWB system to enhance the positioning accuracy of the TN. Meanwhile, Cao et al.29 put forward that the variational Bayesian UKF (VBUKF) was used to smooth the ranging of each anchor node (AN) by taking account of time-variant measurement noise, and the experimental results clearly demonstrated the effectiveness of the this approach. However, the UWB wireless signal was sensitive to the extern environment interference, making the measurement noises be contaminated by non-Gaussian noises or producing measurement outliers, which would lead to the smoothing performance degrade considerably. To better handle with these issues in the measurement distance, filtering methods based on maximum correntropy criterion (MCC) have been propounded and theirs effectiveness and usefulness has been certified via a large number of experiments30. Moreover, MCC-based approaches were suitable for online implementation on account of the retained recursive structure and can achieve desirable performance31. The aforementioned localization strategies have been developed to enhance estimation accuracy, nevertheless, their positioning accuracy was not sufficiently high and hard to satisfy the requirement of high-precision positioning.

In this article, enlightened by the idea of MCC method and UKF algorithm, aiming at improving estimation accuracy for indoor mobile localization, a novel positioning approach is developed to handle with the unknown process noise for indoor environment under the LOS condition. The specific contributions of this study are given by:

  1. (1)

    A novel MCCUKF method is developed by integrating the MCC methodology and UKF algorithm to enhance the estimated distance quality, and the adaptive adjustment factor is introduced to adjust the covariance matrix to improve filtering performance of the MCCUKF, taking account of the polluted measurement caused by the outliers or shot noise and unknown process noise.

  2. (2)

    The least square (LS) method is implemented to estimate the ___location of the TN, and the Taylor series algorithm is then performed to achieve more accurate position estimation.

  3. (3)

    The static and dynamic positioning experiments are conducted in indoor environments to demonstrate the superiority of the proposed system, and experimental results show that the TN’s ___location can be more accurately estimated.

Related word

To improve mobile localization performance, numerous methods have been developed to reduce the positioning errors. For instant, Yang et al.32 put forward the UWB localization approach based on support vector machine (SVM), which outperforms the conventional technique in terms of accuracy and time. Nguyen et al.33 proposed the deep learning method that converted the localization issue into a regression problem and combined ranging to obtain the positioning results. Ma et al.34 took advantage of a binary classifier for signal interference discrimination and localization errors compensation model by integrating genetic algorithm along with extreme learning machine to ameliorate estimation accuracy. Poulose et al. 35 presented deep learning model uses a long short-term memory (LSTM) network for predicting, which solved the LOS problems associated UWB system and offered a better localization accuracy than conventional localization approaches. Li et al.36 proposed a novel positioning method by integrating convolutional neural networks, bidirectional long and short-term memory networks, and transfer learning to improve the positioning accuracy. Tian et al.37 presented a long short‑term memory neural network algorithm fused with the KF to improve UWB positioning. However, those UWB positioning methods are only performed theoretically based on simulation experiments, and there is no validation in practical applications.

On the other hand, The KF was an excellent state estimation method that can effectively eliminate the noise and the uncertainty which is beneficial to achieve more accurate positioning results for UWB system38. Guo et al.39 proposed a positioning algorithm by combining KF and dilution of precision, and results shows that the developed method can effectively suppress the positioning error caused by the narrow spatial structure. Meanwhile, García et al.40 employed the skewness of the estimated channel impulse response and the EKF is used for accurate positioning, which handles the nonlinearity by employing simple linearization. Moreover, Xu et al.41 proposed a hybrid colored EKF and colored extended unbiased finite impulse response filter by using measurement differences. Liu et al.42 used the UKF filter for UWB position estimation through traceless transformation of sigma points. Add to that, an adaptive and robust UKF approach based on Gaussian process regression- assisted variational Bayesian (VB) method is presented43. Nonetheless, the measurement noises may be contaminated by non-Gaussian noises and yield measurement outliers in the UWB indoor-positioning process, which would the performance of the EKF and UKF. To overcome this limitation, the MCC method is proposed to introduce to the UKF algorithm to enhance the filtering performance. Liu et al.44 presented a MCCUKF method to enhance the robustness of UKF against impulsive noises, and illustrative examples demonstrate the its superior performance. Zhao et al.45 developed a UWB positioning algorithm based on MCCUKF, in which the MCC was utilized to improve the robustness of the UKF algorithm for heavy-tailed noise. Cao et al.46 proposed a underground environment positioning approach by integrating MCCUKF and VB methodology to enhance the ranging accuracy, and test positioning results demonstrated that the designed method can obtain the better estimation. However, the process noise cannot be measured accurately in practical application.

Although the related literatures propose a number of systems to enhance indoor localization accuracy, the UWB system still requires improvement regarding localization accuracy. Consequently, in order to address this issue, we propose a novel positioning scheme by considering the problem of unknown process noise and the measurement outliers and measurement distance contaminated by non-Gaussian noises. More specifically, we propose to utilize the MCCUKF smoothing method to decrease the ranging error to enhance the estimated distance quality and introduce an adaptive adjustment factor to the MCCUKF to adjust the covariance matrix to further improve the estimation accuracy of the filter. Subsequently, the LS approach is implemented to compute the TN’s initial position coordinate, and then the Taylor series algorithm is performed to the result of MCCUKF-LS in order to achieve more accurate position estimation. Finally, to verify the superiority and applicability of the developed MCCUKF-LS technique, the positioning experiment is undertaken in the evaluation scenario. To highlight the advantages of the designed MCCUKF-LS, we adopt the LS, KF-LS, UKF-LS, as well as MCCUKF-LS method to compute the TN’s ___location coordinates, and compare the positioning performance of the mentioned methods in terms of the estimation accuracy. The flow chart of the proposed positioning approach is illustrated in Fig. 1.

Fig. 1
figure 1

Flow chart of the positioning approach.

Full size image

The rest of this paper is organized as follows. In “Positioning system construction” section introduces the UWB positioning system. In “Measurement distance smoothing” section describes the maximum correntropy criterion and MCCUKF algorithm. In “Position calculation” provide the computation method TN’s position coordinates. In “Experiment and analysis” conducts experiment and analyzes the experimental results. Finally, “Conclusions” concludes the full paper with a summary.

Positioning system construction

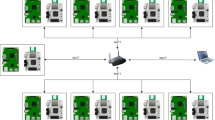
With the aid of GPS, the localization accuracy of the mobile devices can achieve the centimeter-level accuracy in the GPS-free outdoor environments. Nevertheless, the localization accuracy tends to be degraded under the condition where the GPS may be not available in indoor environment, which is due to the fact that the GPS signal is weakened or even no signal. To this end, we proposes to adopt the UWB module to build a local positioning system in GPS-denied environments to realize the indoor positioning for the mobile devices. Usually, the local positioning system in indoor environment can be composed of at least four UWB anchor nodes (ANs) and one TN, and the TN is installed on the body of the mobile device and the ANs are installed in a suitable position in the indoor space. Figure 2 illustrates a schematic diagram of the principle of indoor positioning deployment by using UWB system. The UWB module used in this paper utilizes the principle of the two-way time of flight (TW-TOF) to achieve the ranging between two even more modules24. In the acquisition system, the measurement distance between the TN and each AN can be obtained. Based on the position coordinate of the AN and the real-time measurement distance, the position coordinate of TN is calculated through the positioning model.

Fig. 2
figure 2

Schematic diagram of the indoor positioning principle.

Full size image

Measurement distance smoothing

Maximum correntropy criterion

Correntropy is commonly used to characterize the similarity measure between two random variables47. With respect to random variables X and Y, their correntropy function can be mathematically defined as:

$$V(X,Y) = E[\kappa (X,Y)] = \int {\kappa (x,y)dF_{X,Y} (x,y)}$$
(1)

where E[‧] represents the expectation operator, FX,Y(x,y) is expressed as the joint probability density function concerning X and Y, \(\kappa ( \, , \, )\) denotes the a kernel function. In this article, we choose the Gaussian kernel, expressed as follows:

$$\kappa (x,y) = G_{\sigma } (t) = \exp \left( { - t^{2} /2\sigma^{2} } \right)$$
(2)

where \(t = x - y\), σ indicates the kernel bandwidth.

Generally, in the majority of real-world applications, the correntropy is obtained by taking advantage of the N sampled data points, and the calculation equation is expressed as follows:

$$\hat{V}(X,Y) = \frac{1}{N}\sum\limits_{i = 1}^{N} {G_{\sigma } (t(i))}$$
(3)

where t(i) = x(i)-y(i), x(i) and y(i) are representative as the sequence of sampling points for the variables X and Y. Then the optimal estimate can be obtained when the correlation entropy reaches the maximum value, given by:

$$\hat{\Im } = \arg \max \frac{1}{N}\sum\limits_{i = 1}^{N} {G_{\sigma } (t(i))}$$
(4)

where \(\hat{\Im }\) represents the optimal estimate.

MCCUKF algorithm

In the UWB positioning system, the TN installed on the mobile device can collect the measurement distance between the TN and each AN in real time. Due to the interference from the surrounding environment, the measured distance inevitably produces errors, which will impair the precision and stability. If we directly use the measurement distance to calculate the position coordinates, the positioning error is unreliable and unacceptable. To this end, we propose to use the MCCUKF algorithm to smooth the corresponding AN’s measurement distance so that the accuracy of the ranging of UWB the system is improved. Actually, the MCCUKF algorithm is the combination of MCC methodology and UKF filtering algorithm, and the MCCUKF algorithm update the measurement information by using a non-linear regression model combined the MCC method, where the MCC is utilized to restrain the measurement outlier to reduce the impact of outliers. Moreover, the adaptive adjustment factor is introduced to the MCCUKF algorithm to adjust the covariance matrix to improve the smoothing performance of the MCCUKF algorithm. Without loss of generality, consider discrete-time stochastic system with respect to the measurement distance at the epoch k is modeled as follows:

$$\left\{ \begin{gathered} \Xi_{k} = \Omega \Xi_{k - 1} + Bw_{k - 1} \hfill \\ z_{k} = \Psi_{k} \Xi_{k} + r_{k} \hfill \\ \end{gathered} \right.$$
(5)

where \(\Xi_{k - 1} = [d_{k - 1} ,\dot{d}_{k - 1} ]\) indicates the state vector, \(d_{k - 1}\) is the ranging between the TN and the AN, \(\dot{d}_{k - 1}\) represents the speed of the TN. \(\Omega = \left[ {1, \, \Delta T; \, 0,{ 1}} \right]\),\(B = \left[ {0.5\Delta T^{2} ; \, \Delta T} \right]\), and \(\Psi = [1,{ 0}]\), △T is expressed as sampling interval. The process noise \(w_{k - 1}\) and measurement noise \(r_{k}\) are usually independent with zero-mean and covariance matrices Qk-1and Rk, expressed as:

$$E[w_{k - 1} w_{k - 1}^{T} ] = Q_{k - 1} ,\;E[r_{k} r_{k}^{T} ] = R_{k}$$
(6)

The main procedure of MCCUKF is implemented as follows:

Factorizing the covariance \(\Sigma_{{k - 1\left| {k - 1} \right.}}\) yields:

$$\Sigma_{{k - 1\left| {k - 1} \right.}} = F_{{k - 1\left| {k - 1} \right.}} \cdot \Lambda_{{k - 1\left| {k - 1} \right.}} \cdot F_{{k - 1\left| {k - 1} \right.}}^{T}$$
(7)

Computing the sigma point yields:

$$\left\{ \begin{gathered} X_{0,k - 1|k - 1} = \hat{\Xi }_{k - 1|k - 1} \hfill \\ X_{l,k - 1|k - 1} = \hat{\Xi }_{k - 1|k - 1} + F_{k - 1|k - 1} \cdot \, \left( {\sqrt {\Lambda_{k - 1|k - 1} (n + \beta )} } \right)_{l} , \, l = 1,...,n \hfill \\ X_{l,k - 1|k - 1} = \hat{\Xi }_{{k - 1\left| {k - 1} \right.}} - F_{k - 1|k - 1} \cdot \, \left( {\sqrt {\Lambda_{k - 1|k - 1} (n + \beta )} } \right)_{l} , \, l = n + 1,...,2n \hfill \\ \end{gathered} \right.$$
(8)

where the corresponding weights of the state matrix is defined as follows:

$$\left\{ \begin{gathered} w_{0}^{n} = \beta /(n + \beta ), \, w_{l}^{n} = w_{l}^{c} = \beta /2(n + \beta ) \hfill \\ w_{0}^{c} = (\chi /(n + \beta )) + 1 + \alpha^{2} - \mu \, \hfill \\ \end{gathered} \right.$$
(9)

where \(\beta = \alpha^{2} (n + \delta ) - n\), δ stands for the tuning parameters of the filter and is set as 3-n, the parameter α is commonly set in the interval [0, 0.5]. The transformed points \(\varphi_{{l,k - 1\left| {k - 1} \right.}}\) can be computed as:

$$\varphi_{l,k - 1|k - 1} = \Omega X_{l,k - 1|k - 1}$$
(10)

The predicted state mean \(\hat{\Xi }_{{k\left| {k - 1} \right.}}\) and associated covariance matrix \(\Sigma_{{k\left| {k - 1} \right.}}\) are estimated as follows:

$$\hat{\Xi }_{{k\left| {k - 1} \right.}} = \sum\limits_{l = 1}^{2n} {w_{l}^{n} \varphi_{{l,k - 1\left| {k - 1} \right.}} }$$
(11)
$$\Sigma_{k|k - 1}^{*} = \sum\limits_{l = 1}^{2n} {w_{l}^{c} (\varphi_{l,k - 1|k - 1} - \hat{\Xi }_{k|k - 1} ) \cdot } (\varphi_{l,k - 1|k - 1} - \hat{\Xi }_{k|k - 1} )^{T}$$
(12)
$$\Sigma_{{k\left| {k - 1} \right.}} = \Sigma_{{k\left| {k - 1} \right.}}^{*} + Q_{k}$$
(13)

The predicted measurement mean \(\hat{z}_{{k\left| {k - 1} \right.}}\) can be computed as:

$$\left\{ \begin{gathered} z_{l,k|k - 1} = \Psi_{k} X_{l,k|k - 1} \hfill \\ \hat{z}_{k|k - 1} = \sum\limits_{l = 1}^{2n} {w_{l}^{n} z_{l,k|k - 1} } \hfill \\ \end{gathered} \right.$$
(14)

The covariance matrix \(\Sigma_{{ZZ,k\left| {k - 1} \right.}}\) and state-measurement cross-covariance matrix \(\Sigma_{{XZ,k\left| {k - 1} \right.}}\) are calculated as:

$$\Sigma_{ZZ,k|k - 1} = \sum\limits_{l = 1}^{2n} {w_{l}^{c} (z_{l,k|k - 1} - \hat{z}_{k|k - 1} ) \cdot (z_{l,k|k - 1} - \hat{z}_{k|k - 1} )^{T} } + R_{k}$$
(15)
$$\Sigma_{{XZ,k\left| {k - 1} \right.}} = \sum\limits_{l = 1}^{2n} {w_{l}^{c} (\eta_{{l,k - 1\left| {k - 1} \right.}} - \hat{\Xi }_{{k\left| {k - 1} \right.}} )(z_{{l,k\left| {k - 1} \right.}} - \hat{z}_{{k\left| {k - 1} \right.}} )^{T} }$$
(16)

Actually, the process noise covariance is difficult to be accurately obtained. If we give a defined value to the process covariance, this would substantially reduce the filtering performance. Thus, according to the reported literature48, we utilize an adaptive adjustment factor to adjust the covariance matrix, and the covariance \(\Sigma_{\eta }\) is represented as follows:

$$\Sigma_{\eta } = {\mathbf{R}}_{k} - [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \Sigma_{k\left| k \right.} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1}$$
(17)

The covariance \(\Sigma_{\eta }\) can be rewritten as follows:

$$\Sigma_{\eta } = {\mathbf{R}}_{k} - [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} (\Sigma_{{k\left| {k - 1} \right.}}^{*} + {\hat{\mathbf{Q}}}_{k - 1} )\Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} + [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} {\mathbf{K}}_{k} \Sigma_{{ZZ,k\left| {k - 1} \right.}} {\mathbf{K}}_{k}^{T} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1}$$
(18)

Taking trace operator on both sides of Eq. (18) yields:

$$\begin{gathered} Tr\{ \Sigma_{\eta } \} = Tr\{ {\mathbf{R}}_{k} \} - Tr\{ [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \Sigma_{{k\left| {k - 1} \right.}}^{*} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \} - \lambda_{k - 1} Tr\{ [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} {\mathbf{Q}}_{k - 1} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \} \hfill \\ \, + Tr\{ [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} {\mathbf{K}}_{k} \Sigma_{{ZZ,k\left| {k - 1} \right.}} {\mathbf{K}}_{k}^{T} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \} \hfill \\ \end{gathered}$$
(19)

The residual covariance can be approximated by:

$$Tr\{ \Sigma_{\eta } \} = E\{ \eta_{k} \eta_{k}^{T} \} = \eta_{k} \eta_{k}^{T}$$
(20)

Substituting (20) into (19) leads to

$$\begin{gathered} \eta_{k} \eta_{k}^{T} = Tr\{ {\mathbf{R}}_{k} \} - Tr\{ [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \Sigma_{{k\left| {k - 1} \right.}}^{*} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \} - \lambda_{k - 1} Tr\{ [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} {\mathbf{Q}}_{k - 1} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \} \hfill \\ \, + Tr\{ [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} {\mathbf{K}}_{k} \Sigma_{{ZZ,k\left| {k - 1} \right.}} {\mathbf{K}}_{k}^{T} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \} \hfill \\ \end{gathered}$$
(21)

According to Eq. (21), the adaptive factor can be obtained, expressed as follows:

$$\lambda_{k - 1} = \frac{{\alpha_{k - 1} }}{{\beta_{k - 1} }}$$
(22)

where parameter \(\alpha_{k - 1}\) and \(\beta_{k - 1}\) can be determined by:

$$\alpha_{k - 1} = Tr\{ [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} {\mathbf{K}}_{k} \Sigma_{{ZZ,k\left| {k - 1} \right.}} {\mathbf{K}}_{k}^{T} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \} { + }Tr\{ {\mathbf{R}}_{k} \} - {{\varvec{\upeta}}}_{k} {{\varvec{\upeta}}}_{k}^{T} - Tr\{ [\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \Sigma_{{k\left| {k - 1} \right.}}^{*} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} \}$$
(23)
$$\beta_{k - 1} = Tr\left\{ {[\Sigma_{{XZ,k\left| {k - 1} \right.}} ]^{T} \Sigma_{{k\left| {k - 1} \right.}} {\hat{\mathbf{Q}}}_{k - 1} \Sigma_{{XZ,k\left| {k - 1} \right.}} \Sigma_{{k\left| {k - 1} \right.}}^{ - 1} } \right\}$$
(24)

Then, the adaptive process noise covariance \({\hat{\mathbf{Q}}}_{k - 1}\) can be expressed as follows:

$${\hat{\mathbf{Q}}}_{k - 1} = \lambda_{k - 1} {\mathbf{Q}}_{k - 1}$$
(25)

Furthermore, we define the prior estimation error of the state as:

$$\Upsilon (\Xi_{k} ) = \Xi_{k} - \hat{\Xi }_{{k\left| {k - 1} \right.}}$$
(26)

Based on the prior estimation error, the measurement equation is approximated by:

$$z_{k} = \hat{z}_{{k\left| {k - 1} \right.}} + \Psi_{k} (\Xi_{k} - \hat{\Xi }_{{k\left| {k - 1} \right.}} ) + r_{k}$$
(27)

Using Eq. (26) and (27), we formulate the regression model, expressed as follows:

$$\left[ \begin{gathered} \, \hat{\Xi }_{{k\left| {k - 1} \right.}} \hfill \\ z_{k} - \hat{z}_{{k\left| {k - 1} \right.}} + \Psi_{k} \hat{\Xi }_{{k\left| {k - 1} \right.}} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \, I \hfill \\ \Psi_{k} \hfill \\ \end{gathered} \right]\Xi_{k} + \xi_{k}$$
(28)

where \(\xi_{k} = \left[ { - \Upsilon (D_{k} ), \, r_{k} } \right]^{T}\) matrix Sk can be obtained via using Cholesky decomposition of the covariance of \(\xi_{k}\), given by:

$$E[\xi_{k} \xi_{k}^{T} ] = \left[ \begin{gathered} \Sigma_{{k\left| {k - 1} \right.}} { 0} \hfill \\ { 0 }R_{k} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} S_{{\Sigma ,k\left| {k - 1} \right.}} S_{{\Sigma ,k\left| {k - 1} \right.}}^{T} { 0} \hfill \\ { 0 }S_{r,k} S_{r,k}^{T} \hfill \\ \end{gathered} \right] = S_{k} S_{k}^{T}$$
(29)

Then, left multiplying both sides of equation by \(S_{k}^{ - 1}\) yields:

$$B_{k} = W_{k} \Xi_{k} + e_{k}$$
(30)

where \(B_{k} = S_{k}^{ - 1} \left[ \begin{gathered} \, \hat{\Xi }_{{k\left| {k - 1} \right.}} \hfill \\ z_{k} - \hat{z}_{{k\left| {k - 1} \right.}} + \Psi_{k} \hat{\Xi }_{{k\left| {k - 1} \right.}} \hfill \\ \end{gathered} \right]\), \(W_{k} = S_{k}^{ - 1} \left[ \begin{gathered} \, I \hfill \\ H_{k} \hfill \\ \end{gathered} \right]\), \(e_{k} = S_{k}^{ - 1} \xi_{k}\).

According to MCC principle, we formulate the following objective function \(J_{L} (\Xi_{k} )\), which can be expressed as:

$$J_{L} (\Xi_{k} ) = \sum\limits_{i = 1}^{L} {G_{\sigma } (b_{i,k} - w_{i,k} \Xi_{k} )}$$
(31)

where \(b_{i,k}\) stands for the i-th element of \(B_{k}\), \(w_{i,k}\) stands for the i-th row of \(W_{k}\).

Furthermore, the optimal estimate of \(\hat{\Xi }_{k}\) can be obtained by maximizing the objective function, given by:

$$\hat{\Xi }_{k} = \arg \mathop {\max }\limits_{{D_{k} }} J_{L} (\Xi_{k} ) = \arg \mathop {\max }\limits_{{D_{k} }} \sum\limits_{i = 1}^{L} {G_{\sigma } (t_{i,k} )}$$
(32)

where \(t_{i,k} = b_{i,k} - w_{i,k} D_{k}\), \(t_{i,k}\) represents the i-th element of \(t_{k}\).

To minimize the deviation of the state estimate, the optimal result can be attained by solving Eq. (32):

$$\frac{{\partial J_{L} (\Xi_{k} )}}{{\partial \Xi_{k} }} = \sum\limits_{i = 1}^{L} {\left[ {G_{\sigma } (t_{i,k} )w_{i,k}^{T} (b_{i,k} - w_{i,k} \Xi_{k} )} \right]} = 0$$
(33)

By deformation, we can be easily derived the following37:

$$\Xi_{k} = \left( {\sum\limits_{i = 1}^{L} {\left[ {G_{\sigma } (t_{i,k} )w_{i,k}^{T} w_{i,k} } \right]} } \right)^{ - 1} \times \left( {\sum\limits_{i = 1}^{L} {\left[ {G_{\sigma } (t_{i,k} )w_{i,k}^{T} b_{i,k} } \right]} } \right)$$
(34)

Equation (34) can be regarded as a fixed-point equation solving problem about the variable Dk, which is formulated as:

$$\Xi_{k} = g(\Xi_{k} )$$
(35)

where

$$g(\Xi_{k} ) = \left( {\sum\limits_{i = 1}^{L} {\left[ {G_{\sigma } (b_{i,k} - w_{i,k} \Xi_{k} )w_{i,k}^{T} w_{i,k} } \right]} } \right)^{ - 1} \times \left( {\sum\limits_{i = 1}^{L} {\left[ {G_{\sigma } (b_{i,k} - w_{i,k} \Xi_{k} )w_{i,k}^{T} b_{i,k} } \right]} } \right)$$
(36)

According to the relative literature37, the optimal solution of the fixed-point iterative algorithm is given by:

$$\Xi_{k} = (W_{k}^{T} U_{k} W_{k} )^{ - 1} W_{k}^{T} U_{k} B_{k}$$
(37)

where \(U_{k} = \left[ {U_{x,k} , \, 0; \, 0, \, U_{y,k} } \right]\), \(U_{x,k} = diag(G_{\sigma } (t_{1, \, k} ),...,G_{\sigma } (t_{n, \, k} ))\), \(U_{y,k} = diag(G_{\sigma } (t_{n + 1, \, k} ),...,G_{\sigma } (t_{n + m, \, k} ))\).

Furthermore, Eq. (36) is rewritten as:

$$\hat{\Xi }_{k\left| k \right.} = \hat{\Xi }_{{k\left| {k - 1} \right.}} + K_{k} (z_{k} - \hat{z}_{{k\left| {k - 1} \right.}} )$$
(38)

where \(K_{k}\) represents the Kalman filter gain, which can be computed as:

$$K_{k} = \tilde{\Sigma }_{{k\left| {k - 1} \right.}} \Psi_{k}^{T} (\tilde{R}_{k} + \Psi_{k} \tilde{\Sigma }_{{k\left| {k - 1} \right.}} \Psi_{k}^{T} )$$
(39)

where \(\tilde{\Sigma }_{{k\left| {k - 1} \right.}} = S_{{\Sigma ,k\left| {k - 1} \right.}} U_{x,k}^{ - 1} S_{{\Sigma ,k\left| {k - 1} \right.}}^{T}\), \(\tilde{R}_{k} = S_{r,k} U_{y,k}^{ - 1} S_{r,k}^{T}\).

Simultaneously, computing the covariance matrix yields:

$$\Sigma_{k\left| k \right.} = (I - K_{k} \Psi_{k} )\Sigma_{{k\left| {k - 1} \right.}} (I - K_{k} \Psi_{k} )^{T} + K_{k} R_{k} K_{k}^{T}$$
(40)

The estimated distance obtained by the MCCUKF smoothing can be expressed as:

$$\hat{r}_{k} = \Psi_{k} \hat{\Xi }_{k\left| k \right.}$$
(41)

where \(\hat{r}_{k}\) represents the smoothed distance, and Y = [1, 0]. In the standard UKF algorithm, Kalman filter gain \(G_{k}\), state \(\hat{D}_{k\left| k \right.}\) and covariance matrix \(\Sigma_{k\left| k \right.}\) can be calculated as:

$$\left\{ \begin{gathered} G_{k} = \Sigma_{{XZ,k\left| {k - 1} \right.}} (\Sigma_{{ZZ,k\left| {k - 1} \right.}} )^{ - 1} \hfill \\ \hat{\Xi }_{k\left| k \right.} = \hat{\Xi }_{{k\left| {k - 1} \right.}} + G_{k} (z_{k} - \hat{z}_{{k\left| {k - 1} \right.}} ) \hfill \\ \Sigma_{k\left| k \right.} = \Sigma_{{k\left| {k - 1} \right.}} - G_{k} \Sigma_{{ZZ,k\left| {k - 1} \right.}} G_{k}^{T} \hfill \\ \end{gathered} \right.$$
(42)

Apparently, we can observe that the chief difference between UKF method and MCCUKF method is the error covariance matrix and measurement noise covariance. The proposed MCCUKF method exhibits the better estimation performance, which is due to the fact that the proposed MCCUKF algorithm is able to effectively and efficiently deal with polluted measurement caused by the outliers or shot noise and unknown process noise, thereby automatically adjusting and correcting the measurement noise. Correspondingly, the filtering performance of the proposed MCCUKF method substantially outperform that of the UKF method.

Position calculation

Least squares method

According to the smoothed distance obtained by MCCUKF algorithm and the known position coordinates of the four ANs, the positioning model of the UWB system is formulated and the TN’s ___location coordinates can be determined by utilizing the LS approach, expressed as follows:

$$\left\{ \begin{gathered} \left\| {s_{k} - s_{1} } \right\| = \hat{r}_{1,k} \hfill \\ \left\| {s_{k} - s_{2} } \right\| = \hat{r}_{2,k} \hfill \\ \left\| {s_{k} - s_{3} } \right\| = \hat{r}_{3,k} \hfill \\ \left\| {s_{k} - s_{4} } \right\| = \hat{r}_{4,k} \hfill \\ \end{gathered} \right.$$
(43)

where \(\hat{r}_{1,k}\),\(\hat{r}_{2,k}\),\(\hat{r}_{3,k}\), and \(\hat{r}_{4,k}\) represent the smoothed distance between the TN and corresponding AN by using the MCCUKF method at time k, respectively,\(s_{k} = (x,y,z)\) represents the unknown position of the TN at time k, \(s_{1} = (x_{1} ,y_{1} ,z_{1} )\),\(s_{2} = (x_{2} ,y_{2} ,z_{2} )\),\(s_{3} = (x_{3} ,y_{3} ,z_{3} )\), and \(s_{4} = (x_{4} ,y_{4} ,z_{4} )\) stands for ___location coordinates of four ANs, respectively, which can be measured by the high-precision laser rangefinder.

Squaring Eq. (43) and converting into the form of a matrix yields:

$$\Re \Theta = B$$
(44)

where \(\Re , \, \Theta\), and \(\, B\) can be computed as:

$$\begin{gathered} \Theta = \left[ \begin{gathered} x \hfill \\ y \hfill \\ z \hfill \\ \aleph \hfill \\ \end{gathered} \right], \, B = \frac{1}{2}\left[ \begin{gathered} \hat{r}_{1,k}^{2} - (x_{1}^{2} + y_{1}^{2} + z_{1}^{2} ) \hfill \\ \hat{r}_{2,k}^{2} - (x_{2}^{2} + y_{2}^{2} + z_{2}^{2} ) \hfill \\ \hat{r}_{3,k}^{2} - (x_{3}^{2} + y_{3}^{2} + z_{3}^{2} ) \hfill \\ \hat{r}_{4,k}^{2} - (x_{4}^{2} + y_{4}^{2} + z_{4}^{2} ) \hfill \\ \end{gathered} \right] \hfill \\ \quad \Re = \left[ {\begin{array}{*{20}c} { - x_{1} } & { - y_{1} } & { - z_{1} } & {0.5} \\ { - x_{2} } & { - y_{2} } & { - z_{2} } & {0.5} \\ { - x_{3} } & { - y_{3} } & { - z_{3} } & {0.5} \\ { - x_{4} } & { - y_{4} } & { - z_{4} } & {0.5} \\ \end{array} } \right],\quad \aleph = x^{2} + \, y^{2} + \, z^{2} \hfill \\ \end{gathered}$$
(45)

Then, the LS solution with respect to the TN’s position can be approximated as follows:

$$\Theta = (\Re^{T} \Re )^{ - 1} \Re^{T} B$$
(46)

Position optimization

Although the LS method can calculate the position coordinates of the mobile device, the estimation accuracy of LS approach is still low when the smoothed measurement distance obtained from MCCUKF algorithm is effected by the measurement outliers or unknown process noise. Consequently, the Taylor series algorithm is implemented to optimize the positioning results of LS algorithm to improve the positioning accuracy of mobile devices. Based on the smoothed distance from MCCUKF algorithm and the solution results of the LS method at time k, we formulate the following equation:

$$f_{i} (s_{k} ) = \left\| {s_{k} - s_{i} } \right\| - \hat{r}_{i,k}$$
(47)

where \(s_{k} = (x,y,z)\) stands for the estimated position attained by using LS method at the epoch k, \(s_{i} = (x_{i} ,y_{i} ,z_{i} )\) is expressed as the known ___location of AN, \(\hat{r}_{i,k}\) denotes the estimated distance from the MCCUKF algorithm with i = 1, 2, 3, 4. Implementing Taylor series first order expansion at the estimated position \(s_{0} = (\hat{x},\hat{y},\hat{z})\) yields the following form:

$$e_{i,k} \approx f_{i} (s_{0} ){ + }\nabla f_{i} (s_{0} )(s_{k} - s_{0} ) = f_{i} (s_{0} ){ + }\nabla f_{i} (s_{0} )\delta s_{k}$$
(48)

where \(\delta s_{k} = [\varepsilon_{x,k} ,\varepsilon_{y,k} ,\varepsilon_{z,k} ]^{T}\) represents the error between the estimated coordinates and the true coordinates in the process of the Taylor iteration, \(\varepsilon_{x,k} ,\varepsilon_{y,k} ,and \, \varepsilon_{z,k}\) represent the coordinate error in the orientation of x-, y-, and z-axis, respectively, \(\nabla {\mathbf{f}}_{i} (s_{0} )\) indicates the gradient of \(f_{i} (s_{k} )\) at point \(s_{0}\), given by:

$$\nabla f_{i} (s_{0} ){ = }\left[ {\frac{{\hat{x} - x_{i} }}{{\left\| {s_{0} - s_{i} } \right\|}}, \, \frac{{\hat{y} - y_{i} }}{{\left\| {s_{0} - s_{i} } \right\|}}, \, \frac{{\hat{z} - z_{i} }}{{\left\| {s_{0} - s_{i} } \right\|}}} \right]$$
(49)

Converting Eq. (48) in matrix form yields:

$$U{\mathbb{Q}} = 0$$
(50)

where \(U = \left[ \begin{gathered} \frac{{\hat{x} - x_{1} }}{{\left\| {s_{0} - s_{1} } \right\|}} \, \frac{{\hat{y} - y_{1} }}{{\left\| {s_{0} - s_{1} } \right\|}} \, \frac{{\hat{z} - z_{1} }}{{\left\| {s_{0} - s_{1} } \right\|}} \hfill \\ \frac{{\hat{x} - x_{2} }}{{\left\| {s_{0} - s_{2} } \right\|}} \, \frac{{\hat{y} - y_{2} }}{{\left\| {s_{0} - s_{2} } \right\|}} \, \frac{{\hat{z} - z_{2} }}{{\left\| {s_{0} - s_{2} } \right\|}} \hfill \\ \frac{{\hat{x} - x_{3} }}{{\left\| {s_{0} - s_{3} } \right\|}} \, \frac{{\hat{y} - y_{3} }}{{\left\| {s_{0} - s_{3} } \right\|}} \, \frac{{\hat{z} - z_{3} }}{{\left\| {s_{0} - s_{3} } \right\|}} \hfill \\ \frac{{\hat{x} - x_{4} }}{{\left\| {s_{0} - s_{4} } \right\|}} \, \frac{{\hat{y} - y_{4} }}{{\left\| {s_{0} - s_{4} } \right\|}} \, \frac{{\hat{z} - z_{4} }}{{\left\| {s_{0} - s_{4} } \right\|}} \hfill \\ \end{gathered} \right]\), \({\mathbb{Q}} = \left[ {f_{1} (s_{0} ), \, f_{2} (s_{0} ), \, f_{3} (s_{0} ), \, f_{4} (s_{0} )} \right]^{T}\).

Equation (50) is transformed as follows:

$$U^{T} U\delta s_{k} - U^{T} {\mathbb{Q}} = {\mathbf{0}}$$
(51)

Then, the LS solution of \(\delta s_{k}\) can be obtained by:

$$\delta s_{k} { = (}U^{T} U)^{ - 1} U^{T} {\mathbb{Q}}$$
(52)

Based on the solution of Eq. (51), we can calculate the total error \(\varepsilon { = }\left| {\varepsilon_{x,k} } \right|{ + }\left| {\varepsilon_{y,k} } \right|{ + }\left| {\varepsilon_{z,k} } \right|\). If the total error is larger than the given threshold, the position estimation can be repeatedly refined by using Eq. (53). When the total error is less the given threshold, or the maximum iterations are achieved, the final position estimation of the TN at the epoch k is determined by Eq. (53), expressed as:

$$\hat{s}_{k} = s_{0} + {(}U^{T} U)^{ - 1} U^{T} {\mathbb{Q}}$$
(53)

Based on the calculated position coordinate and real coordinate, we define the root mean square error (RMSE) and absolute error on the three coordinate orientation, which are employed to comprehensively evaluate the developed localization performance, given by:

$$RMSE{ = }\sqrt {(\hat{x} - x_{n} )^{2} + (\hat{y} - y_{n} )^{2} { + (}\hat{z} - z_{n} )^{2} }$$
(54)
$$\left\{ \begin{gathered} \delta_{x} { = }\left| {\hat{x} - x_{n} } \right| \, \hfill \\ \delta_{y} = \left| {\hat{y} - y_{n} } \right| \, \hfill \\ \delta_{z} = \left| {\hat{z} - z_{n} } \right| \hfill \\ \end{gathered} \right.$$
(55)

where \((x_{n} ,y_{n} ,z_{n} )\) is expressed as the real position of the TN, \((\hat{x},\hat{y},\hat{z})\) represents the estimation position obtained from the LS, KF-LS, UKF-LS, and MCCUKF-LS approaches.

Experiment and analysis

Localization experimental setup

To verify the actual effectiveness of the designed algorithm in this paper, five UWB P440 modules are used to build the indoor positioning system, as displayed in Fig. 3, and the specific specifications are available in published literature49. The hardware structure and antenna of the five modules are the same, among which four modules are used as ANs and one module is the TN. The static and dynamic positioning experiments are conducted in the office of Anhui University of Science and Technology, with a site size of 8 m × 8 m. Four ANs are installed and fixed on four tripods, and the position coordinates of each ANs are measured for three times by utilizing the high-precision laser rangefinder, and the average value is taken as the final measurement result of the ANs with AN1 (0.701 m, 0.711 m, 0.794 m), AN2 (2.802, 0.708 m, 1.344 m), AN3 (3.512 m, 5.608 m, 1.027 m), and AN4 (0.703 m, 5.611 m, 2.107 m), respectively. The TN is attached to the mobile device and connects the TN to the computer using a serial port cable, as illustrated in Fig. 4. The TW-TOF principle is utilized to compute the ranging between the TN and the four ANs during motion, and the measured distance is processed in real time by taking advantage of the MCCUKF algorithm, and the LS approach is employed to approximate the real-time position coordinates of the mobile device. Meanwhile, the signal transmission channels of the four ANs and the TN are in the LOS environment, and the experimental scenario and the installation deployment of the ANs are shown in Fig. 4. In the static localization experiment, we choose 14 localization points within the positioning area, and 300 ranging data are collected at each positioning point. In the dynamic localization experiment, the mobile robot is controlled by the telecontroller to make the TN move along the set trajectory. To highlight the goodness of the developed approach, the KF, UKF, and MCCUKF algorithm are employed to smooth the measured distances from the UWB positioning system, and then the position coordinates of the TN are estimated by the LS method and the localization results are optimized using the Taylor series algorithm, which are analyzed by comparative analysis.

Fig. 3
figure 3

Experimental platform.

Full size image
Fig. 4
figure 4

Localization experimental deployment.

Full size image

Results analysis

To verify the effectiveness of the proposed MCCUKF smoothing performance for ranging error elimination, Fig. 5 illustrates the original ranging data between two P440 modules and the MCCUKF smoothing results. It is visible that original ranging data possesses the significant fluctuation. If we directly determine the ___location of the TN by using the initial ranging data, there will lead to unacceptable estimate result with large positioning errors. Fortunately, applying the MCCUKF algorithm to the original measurement distance, the fluctuation range of the ranging data is obviously decreased. This demonstrates the MCCUKF algorithm is capable of improving the ranging quality, and enhance the localization accuracy and stability of the UWB positioning system.

Fig. 5
figure 5

Measurement distance smoothed by using MCCUKF algorithm.

Full size image

The localization performance comparison with regard to the TN’s ___location estimation error and the boxplot of RMSE calculated by employing different positioning algorithm was displayed in Fig. 6. It is straightforward to see that the RMSE of LS method is highest among the compared methods, and the proposed MCCUKF-LS method substantially outperforms the other approaches. Simultaneously, the RMSE of KF-LS is higher than LS method, and the RMSE of UKF-LS method is higher than that of KF-LS method. This is mainly due to the fact that when using the measurement distance to directly approximate the position of the TN, the measurement distance has a large ranging error, so that the position estimation accuracy of the LS method is low. The filtering smoothing performance of the UKF method is better than that of the KF method, which leads to the UKF method produce high-precision distance estimation and thus improves the positioning accuracy of the TN. The MCC criterion is incorporated into the MCCUKF approach, which diminishes the influence of maximum outliers on the smoothing performance and enhances the filtering performance of the UKF algorithm, making the MCCUKF-LS method possess the best localization performance. Moreover, the proposed MCCUKF-LS method has the lowest top edge and the smallest median of localization error contrasted with the mentioned methods, exhibiting the highest accuracy of position estimation.

Fig. 6
figure 6

RMSE for different localization points: (a) RMSE; (b) boxplot of RMSE.

Full size image

To deeply evaluate the performance of the proposed technique in the comparative study, a number of the overall quantitative metrics are computed which chiefly include the minimum, maximum, average, as well as standard deviation (SD) of RMSE, as illustrated in Table 1. Based on these results, it can be observed that the average estimation accuracy of LS, KF-LS, UKF-LS, MCCUKF-LS method are 0.108 m, 0.093 m, 0.083 m, and 0.051 m respectively, and the maximum positioning accuracy with respect to those methods are 0.147 m, 0.131 m, 0.109 m, and 0.086 m respectively. Meanwhile, the minimum RMSE of above mentioned methods are 0.127 m, 0.112 m, 0.097 m, and 0.069 m, respectively. Obviously, the average positioning accuracy of the developed technique is increased by 45.7%, 37.8% and 28.9% as contrasted with LS, KF-LS and UKF-LS methods, respectively. Moreover, one note that the deviation of RMSE for the MCCUKF-LS technique is smallest among the four compared methods, indicating that the localization results of the proposed method fluctuate less than other methods, exhibiting relatively good stability. These results demonstrate that the designed MCCUKF-LS approach is able to yield better localization results and possess the better performance over the LS, KF-LS and UKF-LS methods. The cumulative distribution function (CDF) of RMSE acquired from the result of the above localization algorithms is shown in Fig. 7. Apparently, the MCCUKF-LS approach achieving the lowest RMSE is more excellent than the other involved methods. More specifically, when as the CDF is up to 90%, the RMSE of LS, KF-LS, UKF-LS, and MCCUKF-LS method are approximately 0.145 m, 0.124 m, 0.108 m, and 0.083 m, respectively, which demonstrates that the MCCUKF algorithm is capable of reducing the estimation error efficiently and improve the positioning accuracy of the TN significantly with strong robustness.

Table 1 Statistics of the RMSE for different algorithms.
Full size table
Fig. 7
figure 7

CDF curve of RMSE for different algorithms.

Full size image

To thoroughly investigate the localization performance of the designed MCCUKF-LS approach, the error variation trend of three axes is illustrated in Fig. 8, and the mean error on the x-axis, y-axis and z-axis is computed, as shown in Table 2. Apparently, the error distribution on the three axes orientations are significantly different. From these outcomes, we can intuitively observe that the estimated accuracy of z-axis is obviously higher than that of the x-axis and y-axis, which reveals that the z-axis error is the main source of lower overall positioning accuracy. The TN’s position is approximately estimated by directly using the measured distance, and the error of the three axes is considerably large when compared with other three positioning algorithms. After the implementation of the smoothing measurement distance by utilizing KF technique, the axis orientation error is decreased, but the error on the three coordinate orientations for KF-LS approach is greater than that of the UKF-LS method. This is mainly because the UKF-LS algorithm can provide a more accurate initial coordinates for the Taylor optimization algorithm, thereby producing a small error on the three axes orientations. When compared with KF and UKF method, the MCCUKF algorithm substantially possesses the best smoothing performance, and the MCCUKF-LS technique can provide more accurate initial coordinate values for the Taylor algorithm. As the Taylor algorithm is implemented to optimize the localization results of MCCUKF-LS, the estimation error on the three axes orientations are apparently diminished. The average estimation error on the three axes of the MCCUKF-LS method is respectively 0.036 m, 0.034 m, 0.044 m, and the average estimation accuracy is improved by 51.4%, 49.3% and 55.1%, respectively, when compared with the LS method, demonstrating that the designed fusion approach in this article is able to significantly improve the estimation accuracy of the three axes orientations. The comparisons between the four approaches indicate that the MCCUKF-LS method is capable of achieving better accuracy on the three axes orientations compared to LS, KF-LS and UKF-LS methods, which demonstrates that the positioning performance of the UWB system is substantially improved.

Fig. 8
figure 8

Variation curve of error on the three axes orientations. (a) x-axis error. (b) y-axis error. (c) z-axis error.

Full size image
Table 2 Average error on the three axes orientations.
Full size table

Figure 9 illustrates the dynamic movement trajectory with respect to three coordinate axes, which are calculated from the LS, KF-LS, UKF-LS, and MCCUKF-LS methods, respectively. We can observe that the axes movement trajectories are far away from the real trajectory and possesses the largest fluctuation range, which means that the positioning accuracy of the LS method is relatively lower. The movement trajectory of the proposed MCCUKF-LS method on the axes orientations are close to the real trajectories among four positioning methods, which reveals the positioning accuracy of the proposed method is more superior than that of the other three approaches. This is due to the fact that the proposed MCCUKF algorithm can adaptively adjust the process noise and the measurement noise covariance at each time step, thereby making the MCCUKF-LS method produce the higher estimation accuracy. Accordingly, combined with above analysis results, it can be concluded that the MCCUKF-LS method has better positioning accuracy and stability, which can provide a more accurate positioning result for UWB system.

Fig. 9
figure 9

Movement trajectory obtained from above methods on the three coordinate axes orientations. (a) x-axis direction trajectory. (b) y-axis direction trajectory. (c) z-axis direction trajectory.

Full size image

Conclusion

In order to realize the navigation and positioning of mobile devices in GPS-denied environments in the indoor environment, we propose to construct the indoor local positioning system by utilizing the UWB system. To ameliorate the estimation accuracy of UWB system, we design a novel fusion positioning algorithm that collaborates the MCC and UKF method to reconstruct the measurement distance, using the maximum entropy principle to reduce the influence of outliers and unknown process noise on the smooth effect. Then the LS method is implemented to solve the TN’s initial position, and the Taylor algorithm is performed to further optimize the localization results of the LS method. The experiments are conducted to validate the effectiveness and applicability of the designed strategy via the UWB P440 positioning system. The experimental results show that the developed MCCUKF-LS technique can achieve the lowest RMSE, and remarkably improve the estimation accuracy of the TN compared with the LS, KF-LS, and UKF-LS methods. The overall average RMSE of MCCUKF-LS method is reduced by 45.7% compared with LS method, and the achieved average accuracy in the orientation of the three axes is increased by 51.4%, 49.3% and 55.1% respectively. Moreover, the dynamic trajectory of the proposed MCCUKF-LS algorithm has lowest fluctuation range and is more close to the real trajectory when compared with other three methods, which manifests that the developed approach possesses capability to effectively enhance the positioning accuracy of UWB system, providing a new positioning methodology and reference for indoor positioning. In the future, we will focus on developing the algorithm that is capable of applying in various challenging real-world environments and further explore additional hardware of the UWB system to enhance the positioning accuracy.