Introduction

The permanent magnet synchronous motor (PMSM) is an important type of motor in modern motor applications1. Due to its excellent energy conversion efficiency, high power density, high torque, and wide speed range, it has been widely used in electric power systems, such as in cooperative robots2, electric vehicles3, wind power generation, and ship propulsion4,5, and it has received increasing attention.

The application of high-performance controllers is the key to achieve efficient operation of PMSMs6. To improve the control performance of PMSMs and enable them to undergo fast and accurate dynamic responses to load changes and external disturbances, various advanced control strategies have been proposed, including fuzzy control7, sliding mode control8,9, model predictive control (MPC)10,11, and adaptive control12. Adaptive fuzzy logic speed controllers13 have been developed to improve the DC bus voltage utilization. The combination of a fuzzy method and memory integral sliding mode control reduces the effect of mismatch disturbances on PMSMs14, and the introduction of an adaptive law can further improve the robustness of the drive system15. An adaptive fuzzy control scheme with a command filtering error compensation mechanism proposed16 solved the position tracking problem. Model-free predictive control can enhance the stability of motor operation17,18, and the effects of parameter and external perturbations can be further eliminated by combining it with sliding mode control19.The above model demonstrates good control performance; however, it has the drawback of high model complexity and application costs. Therefore, in industrial environments, proportional integral (PI) control-based direct torque control (DTC)20 and field oriented control (FOC)21 are widely adopted22,23. Despite the PMSM having high nonlinearity, the relationship between the output and input of the control object signals is linearized near the operating point24. The efficiency of the controller can be ensured by selecting suitable PI parameters that match the specific operating conditions.

However, regardless of which control scheme is used, there are hyperparameters in the control model that need to be adjusted. In addition, the PMSM has high nonlinearity, and when operating conditions change, the control parameters must be adjusted to prevent a decline in the control performance. Conventionally, controller parameters were conventionally designed using the trial-and-error method. However, this approach was considered undesirable due to its blind, lengthy, non-optimal, and potentially unsafe nature. Therefore, to meet different operation requirements and working environment, such as the varying control performance demands of reconfigurable production systems25, optimizing the hyperparameters in the drives becomes crucial26. Such optimization problems are widespread in areas such as materials physics27, disease prediction28,29 and power system optimization30. To efficiently address these optimization issues, heuristic optimization algorithms31 and machine learning technologies32 are widely adopted.

Metaheuristic algorithms have garnered significant attention due to their remarkable search capabilities and excellent global optimization performance, among which the genetic algorithm (GA)33, particle swarm optimization algorithm (PSO)34, and differential evolutionary algorithm (DEA)35 have been used for controller parameter tuning during the design stage of the motor control system. In recent studies, a control algorithm combining PSO and PI control was successfully applied to tune controller parameters of PMSM, and its feasibility was verified by simulations36,37. This hybrid method not only improves the performance of a variable-speed drive but also enhances the stability and response speed of the system. By comparing the performances of multiple metaheuristic algorithms in control parameter searches, it was shown that each metaheuristic algorithm is effective in finding the optimal control parameters38. In addition to being combined with PI control algorithms, metaheuristic algorithms were used39 to optimize the output affiliation function of the fuzzy logic controller to achieve the best control performance of the motor. Model downscaling and controller design of the PMSM controller with the help of firefly-based hybrid metaheuristic algorithm was performed40. A combination of the GA and an artificial neural network (ANN) was used41 to adjust the weight factor of the MPC cost function to improve the robustness of motor parameters such as the stator resistance and the permanent magnet flux. Moreover42, used a PSO algorithm combined with fuzzy PID to optimize the control performance. The algorithm was deployed in experiments, eliminating errors caused by differences between the simulation and experimental environments. An artificial bee colony (ABC) algorithm43 was employed for parameter optimization, alleviating issues of instability due to poor solutions in real-world deployment environments.

Despite the performances achieved by existing methods in optimizing control parameters for PMSMs, several unresolved issues remain in practical applications. The primary challenge lies in designing the operational logic of search algorithms embedded in the driver to accurately evaluate the performance with various control parameters under different operating conditions. Furthermore, larger population sizes and iteration counts significantly increase the search times, so improving the convergence speeds of algorithms within limited timeframes is crucial for enhancing the search efficiency. Finally, during the optimization process, it is necessary to assess the control effects of suboptimal solutions, which may lead to declines in the control performance or even system instability. Therefore, constructing effective fault suppression mechanisms is critical.

To address the challenges faced in deploying optimization algorithms in the driver, this paper innovatively proposes a real-time online deployable control parameter optimization scheme (ODPOS). The core advantage of this scheme lies in its adaptability to different operating conditions and its excellent convergence capability. It can be deployed online throughout the entire lifecycle of the equipment, significantly enhancing the system’s control performance under varying operating conditions. Specifically, the ODPOS defines the fitness of individuals by evaluating the step response performance of the system under different operating conditions, ensuring superior performance throughout the optimization process. Additionally, the honey badger algorithm (HBA)44 is employed to effectively enhance the convergence speed and quality of the optimization results. Furthermore, a fault suppression mechanism (FSM) is designed to identify and suppress motor out-of-control behaviors. The proposed ODPOS has been experimentally tested on a rapid prototyping experimental platform and compared with other optimization algorithms. Experimental results demonstrated that the proposed ODPOS exhibits outstanding search capabilities in practical applications, providing new insights and solutions for optimizing PMSM control parameters.

The remainder of the paper is structured as follows. “Modeling of PMSM drive systems” describes the PMSM model and control method based on the field-oriented control approach. “ODPOS for PMSM” proposes a real-time ODPOS based on the HBA. Section “Experiments of real-time online optimization” deploys the parameter tuning scheme using a rapid prototyping control platform and discusses the experimental results. Finally, “Conclusions” summarizes the whole paper and provides conclusions. The symbols used in this article can be found in Supplementary Table S1 online.

Modeling of PMSM drive systems

In this study, a surface permanent magnet synchronous motor (SPMSM) was used. Because a PI controller can clearly show control performance differences when various control parameters are selected to facilitate the evaluation of the optimization algorithm, the traditional three-phase PMSM vector control scheme was adopted in this study, which included the speed loop PI controller and the current loop PI controller.

PMSM system model description

For the SPMSM, the \(i_{d}=0\) control is equivalent to maximum torque per ampere control. To facilitate the design of the controller, a mathematical model of the PMSM in the synchronous coordinate system was chosen. The stator voltage equations of the PMSM are expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {{{u}}_d} = R{i_d} + \dfrac{d}{{dt}}{\psi _\mathrm{{d}}} - {\omega _e}{\psi _q}\\ {{{u}}_q} = R{i_q} + \dfrac{d}{{dt}}{\psi _q} + {\omega _e}{\psi _d} \end{array} \right. , \end{aligned}$$
(1)

where R is the resistance of the three-phase winding, \({\omega _e}\) is the electrical angular velocity of the motor, \({u_d}\) and \({u_q}\) are the voltages of the d and q axes in the synchronous rotating coordinate system, respectively, and \({i_d}\) and \({i_q}\) are the currents of the d and q axes in the synchronous rotating coordinate system, respectively.

The stator flux linkages \({\psi _d}\) and \({\psi _q}\) can be obtained from the \({d-q}\) axis inductance, calculated as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\psi _d} = {L_d}{i_d} + {\psi _f}\\ {\psi _q} = {L_q}{i_q} \end{array} \right. , \end{aligned}$$
(2)

where \({\psi _f}\) represents the permanent magnet flux linkage, and where \(L_d\) and \(L_q\) are the inductances of the d and q axes, respectively.

By combining Eqs. (1) and (2), the stator voltage equations can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} {{{u}}_d} = R{i_d} + {L_d}\dfrac{d}{{dt}}{i_d} - {\omega _e}{L_q}{i_q}\\ \\ {{{u}}_q} = R{i_q} + {L_q}\dfrac{d}{{dt}}{i_q} - {\omega _e}({L_d}{i_d} + {\psi _f}) \end{array} \right. . \end{aligned}$$
(3)

In addition to this, the electromagnetic torque \({T_e}\) of the motor in the natural coordinate system is equal to the derivative of the magnetic field storage energy with respect to the displacement of the mechanical angle \({\theta _m}\). Thus, the electromagnetic torque can be described as

$$\begin{aligned} T_{\textrm{e}}=\dfrac{1}{2} p_{\textrm{n}} \dfrac{\partial }{\partial \theta _{\textrm{m}}}\left( \varvec{i}_{3\textrm{s}}^{\textrm{T}} \cdot \varvec{\psi }_{3\textrm{s}}\right) , \end{aligned}$$
(4)

where \({\varvec{i}_{3s}} = \left[ { \begin{array}{*{20}{c}} {{i_A}}\\ {{i_B}}\\ {{i_\mathrm{{C}}}} \end{array}} \right]\) and \({\varvec{\psi }_{3\textrm{s}}} = \left[ { \begin{array}{*{20}{c}} {{\psi _A}}\\ {{\psi _B}}\\ {{\psi _C}} \end{array}} \right]\) are the phase currents and flux linkages of the three-phase windings, respectively, and \({p_n}\) is the number of pole pairs of the PMSM. Transforming equation into a rotating synchronous coordinate system yields

$$\begin{aligned} T_{\textrm{e}} = \dfrac{3}{2}{p_n}{i_q}\left[ {{i_d}({L_d} - {L_q}) + {\psi _\mathrm{{f}}}} \right] . \end{aligned}$$
(5)

In addition, the mechanical equations of motion of the motor are described as

$$\begin{aligned} J\dfrac{{d{\omega _m}}}{{dt}} = {T_e} - {T_L} - B{\omega _m}, \end{aligned}$$
(6)

where J is the moment of inertia, B is the damping factor, and \(T_L\) is the load torque.

Control parameter calculation of speed loop

The \({i_d}=0\) control scheme was used, and the concept of “active damping” was introduced to set the parameters of the speed loop PI controller, assuming that the motor was started without a load. The following results can be obtained:

$$\begin{aligned} \dfrac{{\mathrm{{d}}{\omega _m}}}{{dt}} = \dfrac{{1.5{p_n}{\psi _f}}}{J}\left( {{{i'}_q} - {B_a}{\omega _m}} \right) - {B}{\omega _m}/{J}. \end{aligned}$$
(7)

Configuring Eq. (7) to the desired closed-loop bandwidth \(\beta\), the q-axis current transfer function corresponding to the rotational speed can be obtained as

$$\begin{aligned} {\omega _m}\left( s \right) = \dfrac{{1.5{p_n}{\psi _f}/J}}{{s + \beta }}{i'_\mathrm{{q}}}(s). \end{aligned}$$
(8)

Comparing Eqs. (7) and (8) yields the active damping factor \(B_a\):

$$\begin{aligned} {B_a} = \dfrac{{\beta J - B}}{{1.5{p_n}{\psi _f}}}. \end{aligned}$$
(9)

Using a conventional PI regulator, the speed loop controller is expressed as

$$\begin{aligned} i_q^ * = \left( {{K_{p\omega }} + \dfrac{{{K_{i\omega }}}}{s}} \right) \left( {\omega _m^ * - {\omega _m}} \right) - {B_a}{\omega _m}, \end{aligned}$$
(10)

where the parameter \(i_q^ *\) denotes the desired q-axis current, and \(\omega _m^ *\) denotes the desired mechanical angular velocity. \(K_{p\omega }\) and \(K_{i\omega }\) of the PI controller can be adjusted by the following equations:

$$\begin{aligned} \left\{ \begin{array}{l} {K_{p\omega }} = \dfrac{{\beta J}}{{1.5{p_n}{\psi _f}}}\\ {K_{i\omega }} = \beta {K_{p\omega }} \end{array} \right. , \end{aligned}$$
(11)

where \(\beta\) is the desired bandwidth of the speed loop.

This method of parameter calculation is simple and the relationship between the control parameters and the dynamic quality of the system is clear.

Control parameter calculation of current loop

Using a conventional PI controller and combining it with a feed-forward decoupling control scheme, the voltage in the d-q axis coordinates is given as

$$\begin{aligned} \left\{ \begin{array}{l} u_{d}^{*}=\left( C K_{p d}+\dfrac{C K_{i d}}{s}\right) \left( i_{d}^{*}-i_{d}\right) -\omega _{e} L_{q} i_{q} \\ u_{q}^{*}=\left( C K_{p q}+\dfrac{C K_{i q}}{s}\right) \left( i_{q}^{*}-i_{q}\right) +\omega _{e}\left( L_{d} i_{d}+\psi _{f}\right) \end{array}\right. , \end{aligned}$$
(12)

where \(CK_{pd}\) and \(CK_{pq}\) are the proportional gains of the PI controller, and \(CK_{id}\) and \(CK_{iq}\) are the integral gains of the PI controller. These parameters can be calculated by the following equation:

$$\begin{aligned} \left\{ \begin{array}{l} C{K_{pd}} = \gamma {L_d}\\ C{K_{id}} = \gamma R\\ C{K_{pq}} = \gamma {L_q}\\ C{K_{iq}} = \gamma R \end{array} \right. . \end{aligned}$$
(13)

The response time \(t_{res}\) is defined as the time required for the system response to go from 10% to 90% of the step signal, and the relationship between \(\gamma\) and \(t_{res}\) can be approximated as \(t_{res}=ln9/ \gamma\). It can be seen that decreasing \(\gamma\) will lengthen the response time and increasing \(\gamma\) will speed up the response of the system. Since the system response time \(t_{res}\) is limited by the electrical time constant, \(\gamma\) cannot be expanded infinitely in practice. The electrical time constant for the d-q axes can be calculated by the following equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} T_d={L_d}/{R}\\ T_q={L_q}/{R} \end{array}\right. }. \end{aligned}$$
(14)

ODPOS for PMSM

The ODPOS built in this paper has capability to search for the optimal control parameters online. The optimal control target is formulated according to the specific demand. The proposed ODPOS contains a reference speed module and an Optimization Algorithm module to realize the deployment of the HBA in the controller. The Optimization Algorithm module utilizes the HBA as the optimization algorithm to reduce the optimization time. Furthermore, the FSM is constructed to suppress the motor control failure caused by the poor solution during the optimization process.

Principle of HBA

The HBA is a metaheuristic algorithm. The design of the algorithm is inspired by the honey badger’s hunting behavior in nature. The algorithm has two parts: an exploration phase and an exploitation phase. The exploration phase mimics the sniffing and digging behavior of the honey badger when locating prey, by extensively searching the solution space to discover new regions that may contain better solutions. The exploitation phase is modeled after the honey badger’s foraging behavior of following a honeyguide bird to locate a hive, and this phase further improves and optimizes the known optimal solution to find a better solution.

The HBA avoids falling into local optimal solutions and tries its best to find global optimal solutions by balancing the exploration phase and the exploitation phase. The algorithm can effectively deal with complex nonlinear problems, and experimental results on several standard benchmark functions and engineering design problems have proven its strong global search capability and fast convergence speed. The operation process of the algorithm is mainly based on the following key steps:

(1) Overall initialization. The initialization parameters include the number of iterations \(iter_{max}\) and the population size n. The candidate solutions to the problem are represented by an \(n \times D\) dimensional matrix \(\mathbf{{P}}\):

$$\begin{aligned} \mathbf{{P}} = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}& {{x_{12}}}& \cdots & {{x_{1D}}}\\ {{x_{21}}}& {{x_{22}}}& \cdots & {{x_{2D}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{x_{n1}}}& {{x_{n2}}}& \cdots & {{x_{nD}}} \end{array}} \right] , \end{aligned}$$
(15)

where each row corresponds to an individual and the columns represent the values of the coordinates in the parameter space; D denotes the dimension of an individual.

The equation to calculate the ___location of each individual is as follows:

$$\begin{aligned} {{x_i}} = l{b_i} + {r_1} \times \left( {u{b_i} - l{b_i}} \right) , \end{aligned}$$
(16)

where \(r_1\) is a random number between 0 and 1, and \(ub_i\) and \(lb_i\) denote the upper and lower bounds of the search ___domain, respectively.

(2) Evaluate fitness of initial individuals. The fitness \(f_i\) of each honey badger is evaluated based on the objective function. The individual with the best fitness in the matrix \(\mathbf{{P}}\) is found. The ___location of this honey badger is defined as \({x_{prey}}\), and the fitness is defined as \(f_{prey}\) for the algorithm to update the population in the next iteration.

(3) Define intensity \(I_i\) and density factor \(\alpha\). \(I_i\) is related to the intensity of the concentration of honey badgers in the search space and the distance between the honey badger and the prey. If \(I_i\) is high, the honey badger will move better and faster. \(I_i\) is defined as follows:

$$\begin{aligned} {I_i} = {r_2} \dfrac{S}{{4\pi d_i^2}}, \end{aligned}$$
(17)

where \(S = {\left( {{{x_i}} - {{x_{i + 1}}}} \right) ^2}\) denotes the density of the distribution of honey badgers, \(d_i = {x_{prey}} - {x_i}\) denotes the distance between the prey and the ith honey badger, and \(r_2\) is a random number between 0 and 1. A smaller value of S indicates that the i-th honey badger is close to other honey badgers, leading the algorithm to reduce \(I_i\) to minimize unnecessary movement and prevent conflicts with other honey badgers. Conversely, a smaller \(d_i\) indicates that the honey badger can more clearly perceive the prey’s ___location, thus requiring an increase in \(I_i\) to accelerate its approach towards the prey.

Equation (18) is used to update the density factor \(\alpha\), which decreases with the number of iterations, thus ensuring a smooth transition from the exploration phase to the exploitation phase.

$$\begin{aligned} \alpha = C_1 \times \exp \left( {-iter}/{iter_{max}} \right) , \end{aligned}$$
(18)

where \(C_1\) is a constant greater than 1, and \(iter_{max}\) is the maximum number of iterations.

(4) Jumping out of local optimum. To prevent the algorithm from falling into a local optimum, a search direction flag F is defined, which is determined by a random number through Eq. (19). The algorithm uses this flag to provide a higher chance of searching the solution space for strict scanning. F is defined as follows:

$$\begin{aligned} F=\left\{ \begin{array}{ll} 1 & \text{ if } r_{3} \le 0.5 \\ -1 & \text{ else } \end{array} \right. , \end{aligned}$$
(19)

where \(r_3\) denotes a random number between 0 and 1.

(5) Honey badger position update. The honey badger algorithm consists of two parts: the “exploration phase” and the “exploitation phase.” In the “exploration phase,” the updated honey badger position is calculated as follows:

$$\begin{aligned} {x_{new}} = {x_{prey}} + F C_2 I {x_{prey}} + F{r_4} \alpha {d_i} \left| {\cos \left( {2\pi {r_5}} \right) \left[ {1 - \cos \left( {2\pi {r_6}} \right) } \right] } \right| , \end{aligned}$$
(20)

In the “exploitation phase”, the updated honey badger position is given by

$$\begin{aligned} {x_{new}} = {x_{prey}} + F {r_7} \alpha {d_i}, \end{aligned}$$
(21)

where \(r_7\) is a random number between 0 and 1.

In the HBA, the determination of whether to use the exploration or exploitation phase of the algorithm to update the ___location of a honey badger individual is determined by a random number. Specifically, when the random number \(r_3\) is less than or equal to 0.5, the algorithm selects the ___location update formula for the exploration phase, while when the random number \(r_3\) is greater than 0.5, the algorithm selects the ___location update formula for the exploitation phase.

(6) Evaluate fitness of updated individuals. The fitness of the new individual is evaluated through the given objective function, and the fitness values of the old and new individuals are compared. If the new individual achieves better fitness, the old honey badger is replaced by the new one; otherwise, the old honey badger position and fitness are retained. After all honey badger positions are updated, the best fitness values of all individuals are found and compared with \({x_{prey}}\). The results of the comparison are used to determine whether to update \({x_{prey}}\) and \(f_{prey}\).

If the algorithm does not reach the end condition after executing step (6), it returns to step (3) and repeats the above steps until the optimum is found. The pseudo-code for HBA is given in Algorithm 1.

figure a

Algorithm 1.

Online operational logic of the HBA deployed in the driver

In the simulation environment, the single-step solution of the control algorithm requires a short time and can be arbitrarily embedded in the metaheuristic algorithm. However, in practical applications, the evaluation of the fitness of a single individual requires the control system to go through the response phase and the stabilization phase completely, and after completing one evaluation, it is necessary to wait for the system to stabilize and then carry out the next fitness calculation, which results in a long solution time and makes it difficult for the simulation scheme to transfer directly to practical applications. For this reason, the HBA was combined with the FSM proposed in the “Design of control FSM” section as an Optimization Algorithm module embedded in the driver. A reference speed module was also designed to assist the operation of the HBA.

Fig. 1
figure 1

Control block diagram after embedding the algorithm into the control program.

Full size image

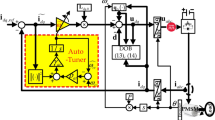
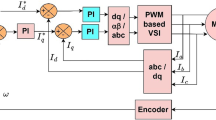
The block diagram of the overall structure of ODPOS is shown in Fig. 1. The reference speed module generates a step speed signal as the reference speed. The control effort of the speed controller is derived from the difference between the reference speed and the actual speed measured by the encoder on the PMSM. The speed controller is constructed using PI control, with its control parameters provided by the Optimization Algorithm module. The q-axis current control effort \(i_q^*\) produced by the speed PI controller is not directly used for the motor but rather serves as the current reference for the internal current PI controller, whose task is to generate the q-axis voltage \(u_q^*\). The current signals required by the current PI controller are obtained from the current sampling circuit and transformed into the synchronous rotating coordinate system using the Clark and Park transformations to obtain \(i_d\) and \(i_q\). Due to the use of the \(i_d=0\) control strategy, the d-axis current reference is set to zero. The d-axis voltage \(u_d^*\) is also generated through the same current PI controller. The reference voltages \(u_q^*\) and \(u_d^*\) are then used to generate the switching sequence controlling the three-phase voltage inverter through inverse Park transformation and space vector pulse width modulation (SVPWM). Ultimately, the DC power source generates three-phase AC power through the inverter to control the motor and thus drive the motor to operate stably.

Fig. 2
figure 2

Signals output from reference speed module and the corresponding HBA steps performed by the Optimization Algorithm module. R indicates that the task of the Optimization Algorithm module is to record the speed error. (2) denotes the execution of step (2) in the HBA to evaluate the fitness of the initial individual. (2–5) means that steps (2) through (5) are executed to update the individual. (6,3–5) indicates that step (6) in the HBA is executed first to evaluate the fitness of the previous individual, and then steps (3) through (5) are executed to update the next individual.

Full size image

The operational logic of the Reference Speed module and the Optimization Algorithm module is illustrated in Fig. 2. The horizontal axis represents the algorithm run time, and the positive part of the vertical axis shows the reference speed output by the Reference Speed module. Below the coordinate axes are the HBA algorithm steps executed by the Optimization Algorithm module and the control parameters it outputs during each corresponding time period. The signal output by the Reference Speed module is a square wave, with a maximum value matching the target operating speed and the minimum value representing the stabilized speed, both lasting for 1 s.

This reference speed signal is also sent to the Optimization Algorithm module at the same time. When the signal indicates a response speed, the module directly outputs the control parameters that require fitness evaluation for the PI controller. Under these parameters, the system completes a step response, and the response results are recorded by the Optimization Algorithm module.When the signal indicates a stabilized speed, the Optimization Algorithm module outputs the best control parameters found so far to stabilize the system. Simultaneously, the module calculates the fitness of the previous parameters based on the response results recorded from the previous phase and executes steps 3 to 5 of the HBA to update individuals. An optimization cycle for an individual consists of a response phase and a stabilization phase, completing one evaluation of the individual fitness and one update of the individuals.

The HBA pseudo-code embedded in the control program is given in Algorithm 2. To adapt to the requirements of deploying the algorithm in the drive, this paper breaks down the algorithm into steps as described in “Principle of HBA” section and different parts are excuted in different stages of the optimization process. The frequency of for loop execution in the algorithm is consistent with the sampling frequency of the control system. t denotes the current execution time of the algorithm. \(t_{max}\) denotes the maximum execution time of the algorithm. The initial value \(x_1\) is calculated according to the mathematical model described in “PMSM system model description” section. This parameter is used to stabilize the system when no better parameter has been found.

figure b

Algorithm 2.

Design of control FSM

In the optimization process, to search the global optimal solution rather than a suboptimal solution within the solution space, the algorithm attempts to traverse all parameters in the solution space. When the control parameters fail to satisfy the stabilization conditions, the system may encounter vibration, overshoot, and even loss of control. In practical deployment environments, this failure has the potential to shorten the service life of the equipment and cause economic losses. Therefore, it is necessary to suppress any potential out-of-control behavior.

To avoid control failures in PMSM systems, an FSM is proposed, which includes overshoot suppression and vibration suppression modules.

(1) Overshoot suppression module: For cases where the speed cannot be controlled near the target speed due to poor control parameters, the upper limit \(H_L\) and lower limit \(L_L\) are introduced to detect whether the speed has exceeded the given threshold.

$$\begin{aligned} \begin{array}{l} {H_L} = response\ speed \times 2\\ {L_L} = stabilized\ speed \times 0.5 \end{array}. \end{aligned}$$
(22)

When the speed feedback is higher than \(H_L\) or lower than \(L_L\), the module switches the output control parameters to the optimal parameters that have been found so far to stabilize the system. The fitness of this individual is also set to infinity.

(2) Vibration suppression module: To address the problem of rotational speed vibrations near the target caused by poor control parameters, the moving average method is first used to calculate the average speed. This method eliminates short-term fluctuations in the sampled speed data and highlights the long-term trend.

First, the sampled speed data points are denoted as \({s_1},{s_2},{s_3}, \cdots ,{s_n}\). Then, the average speed calculated by the moving average method is given by Eq. (23).

$$\begin{aligned} {N_{avg}} = \dfrac{1}{n}\sum \limits _{i = t - n}^t {{s_i}}, \end{aligned}$$
(23)

where \(N_{avg}\) denotes the average rotational speed, t denotes the tth rotational speed sampling point, and n denotes the size of the window for the moving average method, i.e., the number of data points used to calculate the average.

Second, the upper and lower limits of the rotational speed are set based on the average rotational speed, which is given by

$$\begin{aligned} \begin{array}{l} U{N_{avg}} = (1 + \delta ){N_{avg}}\\ L{N_{avg}} = (1 - \delta ){N_{avg}} \end{array}, \end{aligned}$$
(24)

where \(\delta\) indicates that the amplitude of the speed vibration should not exceed a certain percentage of the average speed, \(U{N_{avg}}\) denotes the upper limit of the average speed, and \(L{N_{avg}}\) denotes the lower limit of the average speed.

Finally, a vibration suppression indicator V is introduced as

$$\begin{aligned} V = \left\{ {\begin{array}{*{20}{l}} 1& \mathrm{{if }}\ {f_u} \ge 3\ \mathrm{{ and }}\ {f_l} \ge 3\\ 0& {\mathrm{{otherwise}}} \end{array}} \right. , \end{aligned}$$
(25)

where \(f_u\) denotes the number of times that the motor’s speed exceeds the upper limit of the average speed in a given time range \(T_L\), and \(f_l\) denotes the number of times that the motor’s speed falls below the lower limit of the average speed in \(T_L\).

When the vibration suppression indicator V is equal to 1, it indicates that the algorithm has detected the occurrence of vibration, in which case the output will be switched to \(x_{prey}\) to suppress the vibration problem due to unsuitable control parameters.

Optimization target design

In industrial applications, PMSMs are used in machine tools, pressurized plastic machines, fans, and other equipment. Different industrial applications require different control strategies to satisfy the production requirements. In control parameter optimization problems, different control performances are guided by different optimization objectives. And different ways of calculating fitness values in heuristic algorithms represent different optimization objectives. The selection of evaluation indices directly affects the control performance, and the commonly used evaluation indices are error integration indices. These indices mainly include ISE, ITSE, IAE, and ITAE, which are defined in Table 1. In the integral index calculation formulas defined in the table, e represents the error between the actual speed and the reference speed, and t represents the time.

Table 1 Error integrator index.
Full size table

The system optimization process determines a set of optimal control parameters through the above evaluation indices, and the control parameters obtained under different objectives need to be varied to achieve a trade off between the rise time, overshoot amount, and adjustment time. By analyzing the control effect of the optimal control parameters found by the system for different values of the evaluation indices, the optimization ability of the proposed scheme can be better evaluated.

Experiments of real-time online optimization

Experimental equipment

The proposed ODPOS was validated on an experimental platform built based on Links-RT semi-physical simulation equipment, which could be directly connected with MATLAB/Simulink, and the algorithm deployment was completed by creating fast control models. The whole experimental platform is shown in Fig. 3(a). The LINKS-BOX rapid prototyping control platform was built by Beijing LINKSTM, using the IBOX-704Plus embedded industrial computer with an Intel Core i5 7200U processor.The motor used was a 100 W permanent magnet synchronous servo motor, model SDGA-01C31BD, manufactured by TODE. The detailed parameters of the motor are shown in Table 2. A hysteresis brake was used to simulate the load conditions, capable of providing a stable load ranging from 0 to 1 N·m. Additionally, the experimental platform included a torque sensor, a DRV8302 motor driver board, an EDR-120-24 switching power supply module and a host computer for developing control programs.

Fig. 3
figure 3

Experimental setup.

Full size image
Table 2 Parameters of the 100 W interior PMSM.
Full size table

The ODPOS was coded according to the control architecture shown in Fig.  1 in the Simulink environment, and the compiled program was stored on the rapid prototyping control platform. The connections and communication of the experimental equipment are shown in Fig.  3b. The rapid prototyping platform received control commands from the host computer and generated PWM waveforms based on the stored control program to control the motor operation. The motor’s operational status was also transmitted in real-time to the host computer through the rapid prototyping control platform. The load was controlled by the hysteresis loading controller. In this experiment, the current loop frequency of the control algorithm was 10 kHz, and the speed loop frequency was 1 kHz.

Online optimization process

The embedded parameter optimization technique proposed in this paper was tested and validated using a classical PI control structure, as shown in Fig. 1. Different objective functions for the optimization model could be selected and applied according to specific requirements. This section focuses on the optimization process and the effect of the proposed ODPOS when the objective function was set to ITSE.

Table 3 Parameter values of embedded HBA.
Full size table

As mentioned earlier, the optimization algorithm embedded in the driver requires the system to be stabilized at the stabilized speed signal when evaluating the fitness of an individual. Therefore, we used the calculation method proposed in the “PMSM system model description” section to first calculate a control parameter that could stabilize the system. The value of \(K_P\) was calculated to be 0.059 and \(K_I\) was calculated to be 0.168 in the speed loop of the PMSM control system, while the value of \(CK_p\) was calculated to be 0.38 and \(CK_I\) was calculated to be 38 in the current loop. These parameters were applied as initial parameters in the control system, and the response performance of the motor is shown as curve BPO in Fig. 5. From the figure, it can be seen that under the control using these parameters, the system exhibited a large amount of overshoot, a long stabilization time, and a certain degree of oscillation. All these indicated that the control effect was not ideal and still needed to be further optimized.

Fig. 4
figure 4

Operational status of optimization algorithms at different stages.

Full size image

Although the performance using the control parameters obtained through theoretical calculations was not satisfactory, the parameters ensured the convergence and stability of the system. This was sufficient to ensure the normal operation of the optimization algorithm. On this basis, the parameters of the control system were optimized using the ITSE objective function. The HBA parameter settings are shown in Table 3. Figure 4 shows the optimization process of the system.

The horizontal axis in Fig. 4 represents the time spent in the optimization process, and the vertical axes represent the motor speed and the control parameters of the driver. A complete individual fitness calculation process started when the reference speed module gave the response speed, and the Optimization Algorithm module output the control parameters that needed to be evaluated. When the reference speed changed to the stabilized speed, the control parameters were reset to the currently found optimal parameters until the next time the reference speed module gave the response speed. This process took about 2 s. The population size in the algorithm was 30, the number of iterations was 10, and the whole parameter optimization process took about 600 s.

As shown in Fig. 4b at 302 seconds, the algorithm enters the sixth iteration, corresponding to \(iter=6, i=1\) in the Algorithm 2. According to the description in Algorithm 2, the Optimization Algorithm module synchronously changed the output control parameters and started to record the error between the actual speed and the reference speed when the \(n_{ref}\) changed to response rpm. After the \(n_{ref}\) changed to stabilized rpm at section 303, the control parameters were changed back to the optimal parameters through step(6), (3), (4) and (5) to stabilize the system and prepare for the next control parameter fitness evaluation.

It is worth mentioning that due to the inclusion of the FSM, when the system detected vibrations or runaway failure, the algorithm immediately changed the control parameters back to the optimal values instead of waiting to receive the stabilized speed signal, which is fully demonstrated in Fig. 4a. At the fourth second, for example, the improper control parameters led to severe vibration in the system. The algorithm changed the output control parameters once it detected the vibration, thus preventing the system from getting out of control further.

In the early stage of the optimization process, as shown in Fig. 4a, none of the control effects were satisfactory because all the parameters except the initial control parameters were randomly generated in the first iteration. The control parameters were changed to optimal by the FSM before the end of the response speed signal. With the optimization process, the algorithm started updating the control parameters based on the position of the optimal individual. In the middle stage of the optimization process, as shown in Fig. 4b, most of the control parameters given by the module were able to make the system converge and operate stably. In the final stage of the optimization process, as shown in Fig. 4c, the module performed fine-tuning in the neighborhood of the existing optimal parameters with the aim of finding more ideal control parameters. After 600 s of the optimization process, the Optimization Algorithm module finally provided a set of control parameters that satisfied the control objective, which were the final control parameters.

Fig. 5
figure 5

Comparison of system control effect before and after parameter optimization. BPO represents the control effect generated by the theoretically calculated parameters, and APO signifies the improved control effect achieved through the optimized parameters obtained via the ODPOS.

Full size image

Figure 5 clearly shows the dynamic response of the system when the reference speed increased from 500 to 1000 rpm before and after the parameter optimization. From the figure, it can be seen that after the optimization of the control parameters by the algorithm, the response time of the motor system was significantly shortened, which means that the system responded more quickly to the speed change. At the same time, the amount of overshoot is also significantly reduced, the fluctuations and vibrations of the system in the process of reaching the steady state are reduced, and the stability of the system was improved. In addition, the stabilization time was reduced, and the system was able to reach a steady state more quickly, further enhancing its reliability in practical applications.

Fig. 6
figure 6

Comparison of the response characteristics when the reference speed increased from 0 to 3000 rpm.

Full size image

The proposed OPDOS exhibits strong adaptability to different working conditions and can perform optimization for various control requirements. Figure 6 illustrates the response characteristics of the system under no-load conditions when minimizing the IAE as the optimization objective. The reference speed transitioned from 0 rpm to 3000 rpm at time 0. The “calc” curve represents the control effect based on the initial calculation of the control parameters, while the “optimize” curve shows the control effect achieved after the optimization process with the response speed set to 3,000 rpm and the stabilized speed set to 0 rpm. By comparing the two control effects, it can be seen that the optimized control parameters significantly reduced the overshooting phenomenon of the system, which not only helped to smooth the dynamic process of the system, but also significantly shortened the time required for the system to reach a stable state. Based on the results of Fig. 5, it also showed that the proposed ODPOS optimization algorithm has the ability to find the optimum under operating conditions with different speeds.

Fig. 7
figure 7

Optimized system response characteristics under loaded and no-load conditions.

Full size image

Figure 7 illustrates the optimization results under various loading conditions. Figure 7a shows the response characteristics of the control parameters optimized by the scheme when the response speed was set to 1,000 rpm and the stabilized speed was set to 0 rpm under no load conditions. After the rated load was suddenly applied, the speed dropped by 102.3 rpm, and it took 2.20 s to recover to the rated speed. After the load was removed, there was a speed fluctuation of 110.5 rpm, which took 2.03 s to eliminate. Figure 7b demonstrates the response characteristics of the system with the control parameters optimized under contirions with a 0.32 N·m load condition. Compared to Fig. 7a, the speed fluctuation after loading was only 29.8 rpm, which was better than the optimization result found under no-load conditions. The time for the speed to stabilize also decreased by 1.31 s compared to the no-load conditions. The response characteristics after unloading were also improved. The load experiments showed that applying the proposed ODPOS optimization algorithm under loading conditions can significantly enhance the control performance of the system under load conditions.

Through the above experiments, it was demonstrated that the proposed ODPOS could perform targeted optimizations for different speeds and loading conditions, showing good adaptability to various operating conditions.

Effectiveness of FSM

This section demonstrates the effectiveness of the FSM during the optimization process. The mechanism included an overshoot suppression module and a vibration suppression module, which aimed to ensure that the system would not experience severe instability due to suboptimal solutions found during the optimization process.

The effect of the overshoot suppression module is shown in Fig. 8a. The Upper Speed Limit and Lower Speed Limit in the figure represent the non-fault speed range set in the overshoot suppression module. When the speed exceeded the upper limit or fell below the lower limit, this module could quickly detect the occurrence of overshoot and immediately adjust the control parameters to the optimal ones found during the optimization process. The blue dashed line in the figure indicates the time when the speed fell below the lower speed limit, at which moment the algorithm simultaneously adjusted the control parameters to prevent further loss of control of the system. Although the system could still experience a certain degree of oscillation due to the inertia of the system and the limitations of the control effect with the current optimal parameters, the adjusted parameters were sufficient to stabilize the system in the end.

Fig. 8
figure 8

Effect of FSM.

Full size image

The effect of the vibration suppression module is clearly demonstrated in Fig. 8b. The red dots in the figure mark the moments when the speed exceeded \(UN_{avg}\), while the blue dots mark the moments when the speed fell below \(LN_{avg}\). The green rectangular boxes represent the given time range \(T_L\). The window range n in Eq. (23) was set to 500, the upper and lower limit percentage \(\delta\) in Eq. (24) was set to 5%, and the given time range \(T_L\) was set to 0.2 s. \(T_L\) started timing when the speed first exceeded the threshold. Over the next 0.2 s, the speed exceeded both the upper and lower limits of the average speed more than three times, as indicated by the red and blue dots in the figure, respectively. The last occurrence of overshoot satisfied the vibration suppression trigger condition, and the vibration suppression indicator V changed from 0 to 1, indicating that the module had detected vibration in the system. Subsequently, the output parameters were quickly adjusted to the optimal values found thus far. With this adjustment, the vibration of the system was effectively suppressed, which ensured the stable operation of the system.

The effectiveness of the proposed FSM is fully demonstrated in Fig. 4a. As can be seen in the figure, during the early stages of parameter optimization, inappropriate control parameters often led to overshoot and vibration of the system. However, the FSM ensured the stable operation of the optimization process and played an important role in the whole parameter optimization process.

Comparison of optimization effects under different objectives

The proposed parameter optimization scheme should be capable of finding the optimal control parameters corresponding to different objective functions. For this purpose, four different objective functions,IAE, ISE, ITAE, and ITSE, were used to optimize the control performance at 1000 rpm under no-load operating conditions. Due to the stochastic nature of the optimization algorithm, each objective function was optimized five times.

Fig. 9
figure 9

Comparison of five optimization results.

Full size image
Fig. 10
figure 10

Comparison of optimization search results with different optimization objectives.

Full size image

Figure 9 displays the control performance of the optimal parameters found through five optimizations of the ITSE objective function. The corresponding control performance metrics and fitness values are shown in Table 4. In the table, rise time represents the time when the rotational speed reached 90% of the Setpoint. Overshoot indicates the percentage the percentage by which the maximum speed exceeds the reference speed. Adjustment time was the time when the actual rotational speed enterd within 1%. In Table 4, the third optimization had the smallest fitness value, however, its corresponding rise time, overshoot, and adjustment time were not the smallest. This was primarily because the ITSE is a comprehensive index that takes into account the overall error in a time period, so the optimization goal was not to minimize a certain control performance metric. By comparing the control performance metrics obtained from each optimization, the optimal control performances achieved by each optimization scheme were very similar despite the randomness of the search process.

Figure 10 displays the motor control performance obtained from optimizations using different objective functions. For each objective function, the best result from five optimizations was selected for comparison. To further evaluate the optimal performance of the system under different objective functions, Table 5 lists three indicators for assessing the system’s response performance. Among the indicators for the rise time, ISE performed the best. This was because ISE squared the error, causing the algorithm to prioritize reducing large errors during the optimization process, thereby accelerating the system’s response speed. However, this characteristic also led to an increase in the overshoot. Compared with IAE and ISE, the ITAE and IISE indicators do not square the error, so the penalty for the error is linear. The algorithm did not aggressively attempt to reduce errors during the optimization process, thereby reducing the risk of overshoot. This also led to a longer adjustment time. These results demonstrated that the proposed approach can flexibly address diverse objective requirements and achieve good control performance, thereby validating its optimization capability.

Table 4 Control performances of five optimizations of the ITSE objective function.
Full size table
Table 5 Optimal control performance found with different objective functions.
Full size table
Fig. 11
figure 11

Convergence curves of different algorithms.

Full size image
Table 6 Final fitness value obtained from each optimization.
Full size table

The HBA used in the scheme was compared with the PSO42 and ABC43 algorithms, which have also been used for parameter optimization in motors. All three algorithms were used to optimize the no-load performance of the motor at 1,000 rpm with ITSE as the optimization index. Each algorithm was run five times. Figure 11 shows the convergence curves for each algorithm, and the final results of each optimization are displayed in Table 6. A smaller fitness value indicates a better control performance achieved by the currently found control parameters. The optimization results obtained using the HBA algorithm were all within 730,000. The optimization results had good consistency, which indicated the stable optimization ability of the algorithm. In contrast, two of the optimization results obtained using the ABC algorithm had fitness values exceeding 730,000, suggesting that the stability of the algorithm was poor. The PSO algorithm’s optimization results were scattered between 733,509 and 752,224, and the large difference in each optimization result indicated that the optimization effect of the PSO algorithm was poor. Additionally, in table 6, the coefficient of variation was calculated using multiple operational results from each algorithm. A smaller coefficient of variation indicates a higher consistency in the search results of the algorithm. As shown in the table, the HBA algorithm has a smaller coefficient of variation, indicating that its optimization results are more concentrated and stable. Notably, the HBA algorithm shows a 40% improvement in the consistency of its optimization results compared to the ABC algorithm, which demonstrates the superiority of the HBA algorithm.

The best results of the different algorithms were compared, as shown in Fig. 11d, The HBA had a faster convergence rate, and the final optimization results were improved by 1.2% and 2.2% compared to the ABC and PSO algorithms, respectively. The PSO had poorer optimization capabilities, which was mainly due to the long computation time required for the fitness calculation of a single individual in practical applications. This necessitated a reduction in the number of individuals and the number of iterations to decrease optimization time. The PSO relies heavily on a large number of search individuals, and the reduction of the number of particles has a greater impact on its search effect. The ABC algorithm, which relies on the division of labor among employed bees, onlooker bees, and scout bees to find the best solution, requires more iterations to achieve satisfactory results in the face of complex problems. The reduction in the number of iterations led to a slower convergence rate. The HBA algorithm, benefiting from its “exploration phase” and “exploitation phase,” had strong evolutionary capabilities and fast search speeds. It was also able to achieve good optimization results even when the population size was reduced. Therefore, the HBA is more suitable for solving controller parameters optimization problems.

It is worth noting that the experimental environment differed from the simulation environment, and there was a certain degree of variation in the initial state of the system’s response each time, as well as external disturbances. These factors led to a deviations in the system’s response results under the same parameters. Such deviations could impact the system’s optimization process. However, in terms of overall effectiveness, the proposed ODPOS was still able to find control parameters more suitable for the control objective in the actual deployment environment.

Conclusions

This paper presents a unique online deployable ODPOS for PMSMs, utilising the HSA to tackle the issues of real-time optimisation in drive systems. The ODPOS is intended for integration into the motor control system, facilitating adaptive adjustment of control parameters to accommodate diverse operational requirements. This research introduces a novel evaluation metric that customises the optimisation process to specific control performance indicators, including overshoot, settling time, and stability accuracy, instead of depending simply on conventional integral metrics.

The ODPOS underwent thorough testing on a rapid prototyping control platform, showcasing its efficacy in attaining optimal control performance under various operating situations. The findings demonstrated that the HSA-based optimisation technique converges more rapidly and yields more stable outcomes than alternative algorithms, achieving a 2.2% enhancement in optimisation efficacy over current options.

This discovery is significant due to its potential to revolutionise the optimisation of control parameters in PMSMs, particularly in reconfigurable production settings where adaptability is essential. Integrating the optimisation method within the motor controller has facilitated real-time, self-tuning control systems capable of dynamically adapting to variations in operating conditions, hence improving performance and reliability.

We intend to improve the ODPOS by including ANNs optimised by the Levenberg-Marquardt technique (LMT) to minimise optimisation time. Furthermore, we create new optimisation indices to better align the metrics with the system’s reaction characteristics, facilitating more precise performance optimisation. We also plan to modify the criteria for determining whether the system is stable or not in the stabilized state to further reduce the optimization time. Furthermore, we intend to apply the proposed scheme to the hyperparameter optimization in other more advanced control methods to expand the application scope of this scheme.This research advances the development of intelligent motor control systems, presenting a significant opportunity to enhance the efficiency and adaptability of PMSMs in industrial applications.