Introduction

Alzheimer’s Disease (AD), first identified by Dr. Alois Alzheimer in 1907, is an irreversible neurodegenerative disorder responsible for 60% of dementia cases. With an unknown etiology and no curative treatment, AD ranks among the most complex diseases and is listed as one of the top four causes of death, alongside cardiovascular diseases, cancer, and brain disorders1. The etiology of this disease remains unclear; theoretically, individuals of any age could be affected, yet it predominantly impacts the elderly population over 60 years old. Currently, more than 50 million people worldwide are afflicted with AD. With the aging population, estimates suggest that by 2050, the number of patients could double. This trend undoubtedly presents significant challenges to disability risk, disease burden, and healthcare costs2.

In recent years, advancements in cerebrospinal fluid (CSF) biomarkers, amyloid, and tau positron emission tomography (PET) imaging, along with other sophisticated imaging technologies have facilitated the emergence of a new generation of diagnostic and therapeutic approaches for diseases. Regrettably, many novel diagnostic and treatment methods remain confined to research settings. Consequently, traditional clinical assessments, neuropsychological testing, and magnetic resonance imaging (MRI) remain the primary means of definitive diagnosis.

With the advancement of machine learning technologies, computer-aided diagnosis has become increasingly prevalent in medical imaging classification. Numerous researchers have integrated extensive medical imaging data with machine learning algorithms to develop prediction methods for AD and mild cognitive impairment (MCI)3,4, achieving accuracy rates comparable to those of human expert. Currently, research methods in this field are primarily categorized into traditional machine learning and deep learning. Traditional machine learning algorithms, such as Support Vector Machine5, Decision Tree6, and Random Forest7, rely on manually extracted image features. In contrast, deep learning’s end-to-end training approach eliminates the need for prior knowledge in extracting image features. In practical applications, there is a preference for achieving reliable results with minimal data preprocessing. Consequently, as deep learning evolves, the use of deep learning techniques for Alzheimer’s disease research has become the predominant method. And image data such as MRI, PET and non-image data such as cognitive assessment scores, age and genetic information are widely used in research.

MRI provides high-resolution images of brain structures, effectively capturing anatomical and functional neurological changes associated with AD8. Numerous studies utilizing deep learning techniques have been conducted with MRI as the foundational imaging modality. For instance, Sathish Kumar et al.9 conducted experiments with 2D slice data using classic models such as AlexNet, VGG16, GoogLeNet, and ResNet18 to compare their performance. Salami et al.10, adapted models such as ResNet, Inception-v3, and DenseNet into 3D versions to fully utilize the spatial information in 3D MRI and compared these methods with their proposed 3D convolutional model. In addition to commonly used CNN architectures, other models such as RNN, Transformer, and graph convolution networks have also been applied in current research. For example, Xin et al.11 proposed an efficient model combining CNN and Swin-Transformer, employing lightweight techniques to minimize model parameters and computational costs. Li et al.12 combined 3D CNN with LSTM to extract four-dimensional feature from fMRI, encompassing both spatial and temporal dimensions. Zhang et al.13 utilized a graph convolutional network to develop a novel Multi-Relational Reasoning Network (MRN), which learns multi-relational perceptual representations of brain regions from sMRI data for AD diagnosis, integrating spatial correlations and topological information.

Simultaneously, various deep learning methods, including attention mechanisms, multi-scale convolutions, and multi-tasking, have been utilized in related research. For instance, Zhao et al.14 proposed an Inherited Deformable Attention Network (IDA-Net) aimed at pinpointing discriminative regions in sMRI for AD classification. Zhang et al.15 employed an enhanced residual network framework known as tresnet, integrating slice region and attention mechanisms to amplify gray matter feature detection. Pei et al.16 introduced a hierarchical pseudo-3D convolutional neural network (PKG-Net), based on kernel attention mechanism and a novel global context module, to integrate features across various levels. Turhan et al.17, utilizing sMRI, developed a (2 + 1)-dimensional convolutional neural network structure to distinguish between MCI and AD.

Furthermore, cognitive assessment tools, such as the MMSE and CDR, are widely employed in clinical diagnostics to evaluate subjects’ cognitive abilities and to measure the cognitive state associated with dementia18. Given the variability in MMSE and CDR scores among subjects at different stages, an increasing number of studies have utilized cognitive assessment scores to aid in AD diagnosis or predict the disease’s progression19,20,21,22. For example, after achieving an accuracy rate of 83.4% with sMRI, Qiu et al.23 enhanced the AD diagnostic rate to 96.8% by incorporating MMSE scores. Salami et al.10 increased the image-based diagnostic accuracy from 80.98% to 87.75% by integrating MMSE and AOPE data. These studies demonstrate that MRI and cognitive assessment scores such as MMSE play a crucial role in predicting AD classification and progression stages.

However, despite the significant results achieved in the aforementioned studies, there is a lack of an intuitive explanation for the underlying reasons behind the correlation between cognitive assessment scores and AD. The objective of this study is to gain a more profound understanding of this relationship. Given that cognitive assessment scores can reflect the progression of AD but are not an absolute diagnostic criterion, we propose the following hypothesis: cognitive assessment scores can detect brain changes associated with AD, but the brain regions they target are not entirely consistent.

It is noteworthy that AD predominantly affects the elderly population, indicating a strong correlation between aging and AD. Numerous studies have utilized MRI to predict brain age and have calculated the difference between predicted age and the actual age as a means of quantifying human aging. Many researchers have employed the predicted brain age as a biomarker of brain health24, leading to a series of in-depth discussions on this topic. These studies have yielded promising results, and it also shows that the effects of aging on the brain are effectively represented in MRI25,26,27,28. This sparked our interest in the differences in brain manifestations between aging and AD. Despite the evident pathological discrepancies between AD and normal aging, there may be some similarities in the structural alterations that occur in the brain. Consequently, we put forth the following hypothesis: specific regions of the brain may be influenced by both AD pathology and aging, exhibiting strong correlations with both.

To test the above hypothesis, the study employs MRI data to perform regression analysis on clinical scores and age, enabling high-resolution visualization of brain regions to assess the influence of various brain regions on clinical scores and age. Furthermore, it offers a more intuitive and robust theoretical foundation for evaluating cognitive abilities using the MMSE and CDR scales, while also providing insights into the relationship between aging and AD.

Specifically, this study developed 3D convolutional models based on sMRI for AD classification and for the regression of age, MMSE and CDR. The AD classification model, integrated with a hybrid attention mechanism, can extract AD-related image features from MRI, whereas the regression models focus on features that influence age and cognitive assessment scores. We utilized SHapley Additive exPlanations (SHAP) to quantify the contributions of MRI features to the predictive accuracy of various models, creating high-resolution heatmaps for each voxel within the MRI scans. Subsequently, we projected the contribution matrices onto the 95 brain regions of the Hammersmith brain atlas29, enabling the visualization of various recognition models by brain region and the analysis of brain areas strongly linked to AD classification, age regression, MMSE regression, and CDR regression.

Materials and methods

Data collection

In this study, the sMRI dataset used for training and internal validation was sourced from the Alzheimer’s Disease Neuroimaging Initiative30 (ADNI, https://adni.loni.usc.edu), while external validation was conducted using data from the Australian Imaging Biomarkers and Lifestyle (AIBL, https://aibl.csiro.au). The ADNI and AIBL datasets are publicly accessible and were created by researchers who ensured that informed consent was obtained from each participant during the data collection process. All procedures were performed in accordance with the relevant guidelines and regulations. To ensure the comparability of results, the sample of subjects selected for this study aligns with the dataset used in Qiu’s research23. The inclusion and exclusion criterion was adapted from the baseline recruitment protocol developed by the ADNI study31. Specific criteria are described in the methods section of the supplementary material.

Under the aforementioned selection criteria, our dataset of 417 samples includes 188 Alzheimer’s disease (AD) patients and 229 cognitively normal (CN) individuals. To prevent significant data imbalance during random dataset splitting, we divided the AD and CN samples separately in a 7:2:1 ratio, ensuring that the original class distribution is maintained across the training, validation, and test sets. The overall sample distribution of the dataset is provided in Supplementary Table 1, and a more detailed description of the samples in the training, validation, and test sets can be found in Supplementary Table 7.

MRI preprocessing

All preprocessing procedures in this study were conducted using FSL32. First, the FLIRT command was employed to perform image registration with the MNI152 template at a resolution of 1 mm, producing images with dimensions of 182 mm × 218 mm × 182 mm. Skull stripping was then performed using the BET command on the registered images. Rather than applying normalization, the skull-stripped images were directly segmented using the FAST command, yielding probability maps and segmentation results for gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF). The GM probability maps were ultimately chosen as the training data. During this process, we meticulously reviewed the registered images, and the automatic registration performed as expected.

For brain parcellation and visualization, we followed the approach of Qiu et al.29, using the FNIRT command to perform nonlinear registration with the Hammersmith Adult Brain Atlas. Upon manual review, the registration for all ADNI samples was satisfactory. However, three samples from the AIBL dataset exhibited poor quality and were excluded from the visualization analysis.

Convolutional neural network model development

Pipeline of the designed method

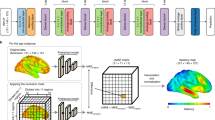
In this study, an experimental workflow was designed (Fig. 1a). Initially, a series of preprocessing steps was applied to the acquired sMRI data to extract gray matter MRI. Subsequently, the gray matter MRI was input into distinct models for AD classification, MMSE regression, CDR regression, and age regression for training. It is important to note that, due to differences between classification and regression tasks, attention modules were employed solely in the AD classification model. During the model training phase, optimal models were selected based on their performance on the validation set, which was then further evaluated on the test set. We did not use cross-validation in our model; all performance metrics are based on a single run. Moreover, to elucidate the model’s decision-making process, the SHAP value matrix was calculated for each task’s corresponding model. The SHAP matrix can elucidate the contribution of each voxel within the MRI to the model’s predictive outcomes. Based on these SHAP values, high-resolution heatmaps were constructed, thus achieving an intuitive visualization of model feature contributions. Subsequently, by registering the Hammersmith atlas with the gray matter MRI data, a personalized MRI template comprising 95 brain regions was generated. This step facilitated the mapping of corresponding SHAP values to respective brain regions, enabling detailed visualization analysis at the level of brain regions.

Fig. 1
figure 1

Proposed method. (a) Pipeline of the designed method. (b) Model Structure. (c) and (d) Channel Attention Module and Spatial Attention Module. (e) and (f) Improved 3D-Channel Attention Module and 3D-Spatial Attention Module. (g) CBAM-3D module.

Full size image

3D convolutional model

In current research, convolutional neural networks are commonly employed to construct deep learning models. Numerous researchers utilize 2D convolution; however, as 2D convolution necessitates slicing MRIs into 2D images for training, it results in the loss of spatial information. Consequently, we opted for experiments utilizing 3D convolution. Moreover, although many researchers have adopted complex structures such as transformers and graph convolutions, these models are more susceptible to overfitting when the sample size is small. Given the relatively small dataset currently employed, overly complex models fail to leverage their potential advantages. To enhance the feature extraction capabilities of the standard 3D convolution, an improved 3D-convolutional based attention module (CBAM-3D) attention mechanism was employed (Fig. 1g).

Specifically, we proposed a 3D convolution-based model for AD classification tasks, comprising six convolutional layers and fully connected (FC) layers (Fig. 1b). To enhance the model’s capability to extract image features and localize pathological brain regions, the CBAM-3D was incorporated within the convolutional layers. Additionally, Batch Normalization (BN) layers were utilized to accelerate model convergence, and the ReLU activation function was applied for nonlinear mapping (Supplementary Table S8).

The traditional CBAM focuses not only on the channel ___domain, analyzing the interactions between feature map channels, but also on the spatial ___location information within the image. CBAM introduces two analytical dimensions: spatial attention and channel attention, starting from the channel and spatial domains and establishing a sequential attention structure from channel to space. Spatial attention enables neural networks to focus more on pixel areas in the image that are decisive in classification, while ignoring irrelevant regions. Channel attention manages the distribution relationship among feature map channels. The simultaneous attention allocation to both dimensions enhance the effect of the attention mechanism in improving model performance.

The channel attention mechanism module of CBAM is depicted (Fig. 1c). This process begins by separately globally max-pooling and globally average-pooling the input feature maps, compressing these maps along two dimensions to yield feature descriptions of varying dimensions. The pooled feature maps are processed through a shared multilayer perceptron (MLP) network, which first reduces the number of channels via a fully connected layer, then restoring the original channel count with another fully connected layer. Subsequently, the two feature maps (Vector1 and Vector2) are stacked along the channel dimension, and a sigmoid activation function is applied to normalize each channel’s weight within the range between 0 and 1, thus deriving the weight information for different channels of the feature map. Finally, the normalized weights are multiplied by the input feature map to produce the channel-weighted feature map.

The spatial attention mechanism module (Fig. 1d) processing the output feature map from the channel attention mechanism within the spatial ___domain. Initially, max pooling and average pooling are conducted on the input feature map along the channel dimension, and the pooled feature maps are then stacked together in the channel dimension. Subsequently, a convolution kernel of size 5 × 5 (or 3 × 3) is employed to integrate channel information, altering the shape of the feature map from [b,c,h,w] to [b,1,h,w]. Finally, the convolved result is subjected to a sigmoid function to normalize the spatial weights of the feature map, which are then multiplied by the input feature map to adjust the spatial emphasis.

To more effectively focus on key areas within an MRI’s 3D space that significantly impact classification, CBAM was modified to be suitable for 3D convolution (Fig. 1e–g).

Initially, for the channel attention component, slices from identical locations across different channels of the three-dimensional feature map are extracted along the x, y, and z axes, forming groups of two-dimensional slices. Subsequently, channel attention weights are calculated for the slice groups at various positions along each axis, enabling the determination channel weights for each pixel point across the three spatial axes. Next, the channel weights of the slice groups at varying positions on each axis are concatenated according to the corresponding directional axis dimension and then multiplied with the original MRI to produce the channel-weighted results of the feature maps in three directions. Finally, by summing the feature maps from the three directions, we obtain the result of the feature map after channel attention computation in three-dimensional space.

Similarly, for the spatial attention component, slices from identical locations across different channels of the MRI are extracted along the x, y, and z axes to form groups of two-dimensional slices. Spatial attention weights are then computed for the slice groups at various positions along each axis, thereby determining the spatial position weights for each pixel point across the three axes. Subsequently, the spatial position weights of the slice groups at different positions on each axis are concatenated according to the respective directional axis dimension and multiplied with the original MRI to produce the spatially weighted outcomes of the feature maps in three directions. The feature maps from the three directions are then aggregated to yield the final result of the feature map after spatial attention computation in three-dimensional space.

The overall process flow of CBAM-3D is depicted in Fig. 1g. Initially, the input feature map passes through the channel attention mechanism; following the multiplication of the channel weights with the input feature map, it is subsequently fed into the spatial attention mechanism. In this stage, the normalized spatial weights are multiplied with the input feature map of the spatial attention mechanism to obtain the final weighted feature map.

Explainability method

In numerous research fields, understanding the reasons behind a model’s predictions is as crucial as the accuracy of those predictions. In this study, we opted to employ SHapley Additive exPlanations (SHAP)33 for the interpretability analysis of our model.

SHAP constitutes a unified framework for interpreting machine learning models. It evaluates the contribution of each feature by calculating the marginal contribution of each feature across all possible prediction tasks and averaging these values. This process enables the assignment of a value to each feature, indicating its importance in a specific prediction. We can treat each voxel in an MRI as a unique feature and construct high-resolution heatmaps for the input MRI by assigning SHAP values to individual voxels on a voxel-by-voxel basis.

The visualization method in this study is divided into three distinct phases. Initially, we calculate the average images of AD and CN samples across the dataset and, through differential analysis of these images, identify regions that distinctly differ between the two sample types. As illustrated in Fig. 2g, the hippocampus and amygdala are closely associated with AD pathology. Subsequently, we conduct a visualization analysis of the results from the model proposed in this paper. We utilize SHAP values to ascertain the contribution of each voxel in the MRI to the prediction outcome, constructing high-resolution MRI heatmaps that focus on key areas associated with AD pathology. Finally, we establish a mapping relationship between the constructed high-resolution heatmaps and the Hammersmith brain atlas, calculating SHAP values for various brain regions. Based on these regions, we conduct an interpretive analysis of the results from AD classification and regression involving MMSE, CDR and age metrics. For the method of selecting highly correlated brain regions, please refer to the Methods section in the Supplementary Materials.

Fig. 2
figure 2

Analysis of misclassified samples and visualization of heat maps for AD, CDR, and MMSE models. (a) t-SNE visualization of the AD classification model on the test set, where orange represents samples labeled as AD and green represents samples labeled as CN. We also annotated the samples with incorrect judgments. (b) and (c) Average and Difference images of AD, CN, and misclassified samples in the test set. (d) MRI mean and difference of AD, CN, and misclassified samples in the test set. (e) The performance of AD, CN and misclassified difference templates in 95 brain regions in the test set. (f) Heat maps of brain regions highly correlated with AD, CDR, and MMSE and the difference between the average images of AD and CN samples. (g) Average images and difference graph of AD and CN samples in dataset.

Full size image

Ablation studies

To test whether the brain regions identified by the cross-analysis of AD, MMSE, and CDR are closely associated with AD, this study performed ablation experiments on the selected cross-brain regions. Specifically, we used brain region masks to exclude areas outside the identified cross-regions and retrained the AD classification model on this basis to observe changes in performance. We then masked each of the identified cross-regions individually and repeated the experimental process, recording the model’s performance for each instance. By analyzing the model’s performance across these experiments, we aim to validate the association between each cross-brain region and AD.

Analyses regarding aging, AD, and cognitive assessment Scores

To investigate the connection between aging and AD, the other two regression methods were also employed: Partial Least Squares Regression (PLSR) and Elastic Net (EN). The prediction results of the proposed 3D CNN model, as well as the PLSR and EN regression models, were analyzed and compared with the actual age of the samples.

To reveal the differences between AD and CN during aging, we calculated the cAgeDiff34 between the two types of samples, as defined below:

$$\text{AgeDiff}=\text{PredictedAge}-\text{Age}$$
$$\text{cAgeDiff}=\text{AgeDiff}-\text{loess}(\text{AgeDiff }\sim \text{ Age})$$

By examining the performances of cAgeDiff across different models for two types of samples, and its performances at various time points, we explored the associations between aging and AD, MMSE, and CDR in both the horizontal and vertical dimensions. Specifically, we specify that the initial data used to establish the prediction model is the initial stage data (m0). Subsequently, sMRI data are collected from the ADNI database for samples at two time points, one year later (m12) and two years later (m24), and different models are used to predict these data. The distribution of specific samples is detailed in Supplementary Table S6. Then, we calculate the cAgeDiff of these samples using different models at various times and conduct an analysis.

Statistical analysis

We calculated the sum of gray matter probability values for each brain region in all samples from the ADNI dataset and the number of voxels in each corresponding brain region. By computing the ratio between these two values, we derived the gray matter probability density for each sample across different brain regions.

Subsequently, we performed group comparison tests on the GM probability density values in various brain regions using two-tailed t-tests or Mann–Whitney U tests. Additionally, we performed a comprehensive analysis of the performance differences between the two sample groups in the age regression model. This step was intended to further investigate the potential relationship between age and AD.

Results

The prediction results

The performance of the attention-based 3D CNN model proposed in this study for AD/CN classification on the ADNI dataset is illustrated in Table 1. As evidenced by Table 1, the model presented in this study has a higher accuracy and specificity. Particularly when compared to the 3D CNN method employed by Qiu et al.23, our model has a better classification performance.

Table 1 Comparison with existing methods using ADNI database for AD vs CN classification.
Full size table

Additionally, we conducted a t-SNE dimensionality reduction visualization analysis on the model’s performance in the test set. As depicted in Fig. 2a, this indicates that the classification model developed in this study is capable of effectively distinguishing between AD and CN. However, all misclassified samples involved instances where AD samples were incorrectly identified as CN. To investigate the reasons behind these misclassifications, we analyzed the clinical information of the erroneously classified samples, as detailed in Supplementary Table S2. The analysis revealed that these samples generally featured lower ages, and their CDR and MMSE scores indicated mild cognitive impairment or were similar to those of normal individuals. This could potentially contribute to the model’s misjudgments. Furthermore, we calculated the average images for the AD, CN, and misclassified samples within the test set. Subsequently, we compared the differences among these images (Fig. 2b, c). The results suggest that the MRIs of the misclassified samples more closely resemble those of normal individuals. For the quantitative analysis, we calculated the mean MRI signal intensity of the three types of samples. It was discovered that the misclassified samples exhibited MRI signal intensities that were closer to those of the normal samples (Fig. 2d). To reveal the brain regions that exhibit significant differences among the three types of samples, we conducted a detailed analysis of the differences in 95 brain regions (Fig. 2e). Based on the analyses above, it can be concluded that the misclassified samples possess clinical information and MRI characteristics similar to those of normal individuals. Furthermore, their AD pathological features are less pronounced, which likely resulted in the model misclassifying them.

Table 2 presents the results of the external validation of the classification model on the AIBL dataset. A comparison of the results reveals that the proposed model outperforms other methods, demonstrating its superior generalization capability.

Table 2 Comparison with existing methods using AIBL database for AD vs CN classification.
Full size table

Table 3 compares the results of the MMSE, CDR, and age regression models, demonstrating that the model proposed in this paper consistently shows better performance.

Table 3 Comparison of RMSE and MAE for MMSE, CDR and Age prediction tasks.
Full size table

The experimental results above confirm that our AD classification model has successfully identified image features significantly impacting AD classification. Similarly, the regression models have also identified features that substantially influence their respective age and cognitive assessment scores. Based on these conclusions, high-resolution voxel-based heatmaps were constructed for the AD classification model, as well as the MMSE, CDR and age regression models, to visually highlight the key areas in each task and validate our initial hypotheses.

Explainability analysis

Visual heat map for brain regions highly correlated with AD, CDR, MMSE and age recognition

As demonstrated in Fig. 2f, we have visualized the MRI regions of interest for AD, CDR, and MMSE. Given that our visualization relies on SHAP values, it provides distinct interpretations for classification and regression tasks. Typically, when SHAP values are used to explain the impact of features on a classification model, a value less than 0 indicates a negative contribution to the model’s current prediction, while a value greater than 0 indicates a positive contribution. For instance, in our AD classification model, certain brain regions exhibit different SHAP values when the sample is classified as AD or CN, suggesting these areas may influence the model’s prediction and are indicative of lesion regions affecting AD classification. Therefore, in the AD classification model’s visual heatmap, we can identify lesion regions that significantly impact the model’s predictions by comparing the colors of the same area across different predicted categories. As the figure indicated, key areas impacting AD classification primarily include regions such as the hippocampus and amygdala. This corresponds with the results from the average differential brain templates of the two types above mentioned, as well as with established medical diagnostic knowledge.

For the MMSE and CDR regression models, our objective is to pinpoint the brain regions that have a significant impact on the prediction results of the respective models. Furthermore, there is no need for a comparison to show the differences between the different prediction categories. Thus, we can identify the regions of focus that influence the assessment scores solely by the shade of the color. The key areas for the MMSE and CDR regression tasks also include regions such as the hippocampus and amygdala (Fig. 2f), mirroring the key areas of attention in the AD classification model.

The analysis of age regression tasks indicates that although the model considers brain regions such as the hippocampus and amygdala, the influence of these areas is relatively minor (Fig. 4c). Conversely, the model mainly focuses on regions such as the frontal and occipital lobes.

Analysis of brain regions with high contributions to AD, CDR, and MMSE recognition

Initially, SHAP was employed to generate global feature maps, displaying the top 15 brain regions with the most significant impact on the AD classification, CDR, and MMSE regression prediction models (Fig. 3a, b, d). To visually highlight the regions of interest for various tasks, the key areas of focus for each of the three recognition models were listed in Supplementary Table S3. In addition, we visualized the prediction results of the classification model in the AIBL database (Fig. 3c). By comparing the visualization results of the two datasets, we found that the brain regions strongly associated with AD classification were largely consistent across both databases. This indicates that the brain regions identified by our model are indeed closely linked to AD, which also indirectly confirms the robustness of the model.

Fig. 3
figure 3

Visualization of brain regions with high contributions to AD, CDR, and MMSE recognition. (a), (b) and (d) Global feature map of AD classification model, CDR regression model and MMSE regression model. (c) Global feature map of the AD classification model on the AIBL dataset. (e) and (f) Local feature map of CN and AD classes. (g) Venn diagram of cross brain regions that contribute significantly to the recognition of AD, CDR, and MMSE. (h) and (i) Visualization of cross brain regions that contribute significantly to the recognition of AD, MMSE, and CDR.

Full size image

In Fig. 3a, the top 15 brain regions with the greatest impact on AD classification are illustrated, such as the hippocampus, parahippocampal gyrus, amygdala, and sections of the temporal lobe.

Subsequently, we explored the specific relationship between the sMRI of samples and the model’s prediction results. We developed a local feature map to examine how different brain regions affect the model’s predictions on the test set. By comparing Fig. 3e and f, we noted that the smaller the feature value of a brain region, the more likely the SHAP value for that region is to be negative in the CN category and positive in the AD category. This indicates that the smaller the feature value of a brain region, the greater the likelihood the model will classify the sample as AD; conversely, the larger the feature value, the higher the probability the sample will be categorized as CN. Given that we conducted experiments using gray matter probability maps from sMRI, the feature values of brain regions can reflect the volume of gray matter tissue in those areas. In other words, samples with reduced gray matter volumes in specific brain regions are more prone to being classified as AD by the model, as these areas are likely to have undergone atrophic changes. This confirms that the model’s results are influenced by the size of the gray matter volume in specific brain regions, offering a reasonable explanation that aligns with existing medical knowledge for our models.

The data from Supplementary Table S3 indicate that, for the prediction models of MMSE and CDR, the most influential brain regions include the hippocampus, amygdala, parahippocampal gyrus, and parts of the temporal lobe, which significantly overlap with the key areas identified in the AD classification task. A Venn diagram was employed to illustrate the connections between the highly correlated brain regions of AD, CDR, and MMSE (Fig. 3g). Specifically, the brain regions closely associated with all three recognition models comprise seven areas: the left hippocampus, the left amygdala, the left and right parahippocampal gyrus, the anterior medial part of the left temporal lobe, the posterior part of the left temporal lobe and the right cerebellum.

Furthermore, we observed an intriguing phenomenon: the influence weights of identical brain tissue in different hemispheres varied across different tasks. In the AD classification task, the impact of identical brain tissue in the left hemisphere on model predictions was exceeded that in the right hemisphere. This phenomenon is clearly evident in the visualization results of both the ADNI and AIBL datasets (Fig. 3a, c). This suggests that pathological changes related to AD in sMRI may develop asymmetrically, with the left brain exhibiting more significant lesions in the stage of AD compared to the right brain. Similarly, in the MMSE regression task, the influence of the left brain on prediction outcomes was greater than that of the right, showing the same asymmetric features as in the AD categorization task. Conversely, in the CDR regression task, the right brain had a greater influence on prediction outcomes than the left.

Finally, we visualized the seven key brain regions common to AD, CDR, and MMSE (Fig. 3h, i).

Analysis of brain regions with high contributions to AD and age recognition

Figure 4d displays the results of the age regression model. The 95 brain regions were ranked based on SHAP values, and the top 15 regions were selected. The experimental results suggest that the brain regions most closely associated with aging are the cerebellum, temporal lobe, and other regions. Simultaneously, observations revealed that the top 15 key brain regions did not include the hippocampus and the parahippocampal gyrus.

Fig. 4
figure 4

Visualization of brain regions with high contributions to AD and age recognition. (a) Raincloud plots were used to display the group differences between AD and CN in cross brain regions. Significance levels are denoted as ns (not significant) for p ≥ 0.05; *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001. (b) Raincloud plots were used to illustrate the temporal changes in group differences between AD and CN in cross brain regions. The results of the two-tailed t-tests test showed that differences between groups increased over time. m0 (T = 10.83, p = 3.79e−21). m12 (T = 12.76, p = 3.55e−26), m24 (T = 13.68, p = 1.69e−29). (c) Heat maps of brain regions highly correlated with age and AD recognition. (d) Global feature maps of age regression models. (e) Venn diagram of cross brain regions for AD and age. (f) and (g) Visualization of cross brain regions of AD and age. (h) Scatter plot of cAgeDiff for AD and CN in the 3D CNN model. (i) Scatter plot of cAgeDiff for AD and CN in the PLSR model. (j) Scatter plot of cAgeDiff for AD and CN in the EN model.

Full size image

Through a cross-analysis of brain regions associated with aging and AD (Fig. 4e and Supplementary Table S5), it was found that the shared brain regions include the left and right cerebellum, the left and right posterior temporal lobes, the left medial anterior temporal lobe, and the anterior central gyrus. This indicates that brain regions undergo changes not only due to aging but also as a result of AD. The brain regions affected by both normal aging and AD may be easily mistaken for normal aging in the early stages of the disease.

It is noteworthy that an asymmetry exists between the sensitivity of the brain’s left and right hemispheres to aging. This asymmetry is confirmed by both Fig. 4c and d, as well as the cross-analysis of aging and AD brain regions.

Finally, we visualized six key brain regions commonly affected by both AD and aging (Fig. 4f, g).

Ablation study results

To further substantiate the close association between the aforementioned brain regions and AD pathological changes, ablation experiments were conducted on the key brain areas common to the AD, CDR, and MMSE, with the results presented in Supplementary Table S4. When classifying using only the intersecting brain regions of AD, CDR, and MMSE, accuracy reached 86.36%, comparable to that achieved using the entire brain MRI; conversely, when different brain regions were occluded during AD classification, a decline in classification accuracy occurred, confirming that the selected brain regions are indeed strongly correlated with AD-related pathology. Additionally, this finding indicates that MMSE and CDR scores can effectively reflect the AD pathological state of brain regions, thus validating the rationale for using these two cognitive assessment tools in the diagnosis of AD.

An exploration of the relationship between aging and AD, MMSE, and CDR

The MAE for age prediction using PLSR and EN were 4.32 and 7.87, respectively. The prediction results of the proposed 3D CNN model, as well as the PLSR and EN regression models, were analyzed and compared with the actual age of the samples (Supplementary Fig. S1). The results indicated that across all three models, the predicted age for AD samples exceeded their actual age, while for CN samples, it was lower than their actual age. This finding suggests that AD may have a significant impact on the normal aging process in humans.

Then, we calculate the cAgeDiff of these samples using different models at various times and conduct an analysis. The one-tailed Mann–Whitney U test showed that the cAgeDiff in AD samples was significantly higher than in CN samples for the 3D CNN (U = 331, p = 0.018) and EN (U = 359, p = 0.003) regression models, but not significant in the PLSR model (U = 331, p = 0.053). However, the two-tailed Kolmogorov–Smirnov test indicated a significant group difference in cAgeDiff for the PLSR model (KS = 0.41, p = 0.035). Overall, there were significant group differences in cAgeDiff across the three models, with a general trend showing higher cAgeDiff values in AD samples compared to CN samples (Fig. 4 h–j). This suggests that the predicted ages of the AD samples were generally overestimated, while those of the CN samples were generally underestimated. In the longitudinal study, we observed that the distribution of cAgeDiff for AD sample was consistently higher than for CN samples at the m12 and m24 time points (Supplementary Fig. S2). Additionally, we found that cAgeDiff demonstrated a positive correlation with CDR and a negative correlation with MMSE scores (Supplementary Fig. S3). In other words, cAgeDiff increases as the CDR score increases and the MMSE score decreases. The aforementioned results indicate that AD and CN exhibit distinct characteristics during the aging process, with AD significantly accelerating aging. Simultaneously, this also suggests that the discrepancy between chronological age and the actual degree of aging serves as a crucial biomarker for distinguishing AD from CN.

Statistical analysis results

We conducted statistical analyses of the gray matter probability density distribution in the aforementioned brain regions for the two sample groups. The results showed significant differences between AD and CN samples in the left hippocampus (U = 6493, p = 1.23e−34), the left amygdala (T = 12.34, p = 1.01e−28), the left and right parahippocampal gyrus (T = 7.8, p = 1.09e−13; T = 8.86, p = 6.997e−17), the anterior medial part of the left temporal lobe (U = 11,560, p = 4.03e−16), the posterior part of the left temporal lobe (T = 8.61, p = 2.42e−16), and the right cerebellum (U = 17492, p = 9.89e−4). As shown in Fig. 4a. Meanwhile, we grouped the samples by CDR and MMSE, respectively, and analyzed the group differences across the overlapping brain regions. The results showed significant differences between groups in these brain regions (Supplementary Fig. S4, S5 and S6).

Additionally, we conducted an in-depth study on the longitudinal changes in the aforementioned brain regions. From the 417 samples in the ADNI dataset, we identified 285 samples with MRI data available at three time points: m0, m12, and m24. The distribution of specific samples is detailed in Supplementary Table S9. We then calculated the GM probability density for each sample in the key brain regions and tested for differences between AD and CN individuals. As shown in Fig. 4b, we compared the mean values of the cross brain regions between the two groups at different time points. The results indicate that, over time, the differences between AD patients and CN individuals in these intersecting brain regions gradually increase. This finding clearly demonstrates that these regions are indeed affected by the pathological progression of AD. We also compared the group differences over time in different brain regions, and the results were consistent with the findings above. The group differences in these brain regions increased over time (Supplementary Fig. S7 and S8).

Discussion

In this study, we innovatively proposed a hybrid attention module and developed different 3D convolutional neural network models for AD classification, as well as MMSE, CDR, and age regression tasks. These models are capable of accurately extracting features highly relevant to each specific task from sMRI data. By applying the SHAP method for visual analysis of the models, we successfully identified brain regions in the sMRI that are closely related to AD pathology, cognitive assessment scores, and age. Furthermore, through cross-analysis of these key brain regions, we discovered some overlapping regions between AD and cognitive assessment scores, as well as commonly affected regions between AD and aging. This significant finding indicates that, while cognitive assessment scores effectively reflect AD-related brain pathology, the regions of focus are not entirely consistent. Moreover, AD and the aging process jointly influence certain specific brain regions. This not only validates our research hypotheses but also uncovers some intriguing insights.

Specifically, through an in-depth analysis of the overlapping brain regions identified in the cross-analysis of AD, MMSE, and CDR, we pinpointed brain areas that are strongly associated with AD pathology and relatively easy to monitor. The existence of these regions provides solid theoretical support for using traditional assessment tools such as MMSE and CDR in AD diagnosis and aids in more accurately capturing disease-related brain structural changes, thereby improving diagnostic accuracy and reliability. Notably, the importance of the left hippocampus, left amygdala, and parahippocampal gyrus among these key brain regions has been confirmed by numerous previous studies53,54,55,56,57, which aligns with our findings and further reinforces the scientific validity and credibility of our research outcomes.

The temporal lobe is strongly associated with language and auditory abilities, particularly the Wernicke area, which encompasses both the auditory and visual language centers. This region is located in the posterior part of the brain’s dominant hemisphere, typically the left hemisphere for the majority of individuals. Damage to the Wernicke area typically results in sensory aphasia, thus affecting language comprehension abilities, which corresponds with the clinical symptoms exhibited by AD patients. This suggests that the posterior part of the left temporal lobe is a crucial region affected by AD pathology. The medial anterior temporal lobe is proximate to brain regions such as the hippocampus, which is strongly associated with memory function and is highly susceptible to AD58.

Regarding the right cerebellar region, the role of the cerebellum in AD diagnosis has been frequently overlooked in previous research. However, recent research has increasingly focused on the function of the cerebellum in neurodegenerative diseases59. Although there are still differing opinions regarding whether the cerebellum is involved in AD or at what stage it is affected by AD60,61,62,63,64, we consider this to be an interesting point of discussion. Our findings suggest that the right cerebellar region is closely associated with AD, which aligns with the findings of previous studies65,66. However, we are still unable to explain the underlying reasons for this association.

Additionally, regarding the analysis results of the overlapping brain regions between AD and aging, we noted that the hippocampus, amygdala, and parahippocampal gyrus are not included. These findings align with previous studies67,68,69,70. This implies that during the aging process, the impact on the hippocampus and amygdala is minimal. Therefore, in disease diagnosis, it is crucial to focus on areas such as the hippocampus to accurately distinguish between normal aging and AD. Moreover, for regions of mutual concern in aging and AD, this indicates that the function of these areas is both influenced by aging and closely related to the pathological changes of AD. This further substantiates the close association between aging and AD, emphasizing aging as a significant factor in the onset of AD. Consequently, conducting comprehensive research on these areas can yield crucial insights into the pathogenesis of AD and its distinction from the normal aging process.

Further analysis indicated that asymmetric lesions in the left and right brain are evident in both AD and aging. Similar conclusions have been supported by several studies28,71,72,73,74. A possible explanation for this asymmetry is that, for most individuals, the left hemisphere is dominant and typically more active. Considering that both aging and AD exhibit the same left–right asymmetry, this feature likely constitutes another significant factor in their close association. Similarly, in the MMSE regression task, the influence of the left brain on prediction outcomes was greater than that of the right, likely because the MMSE test includes numerous language assessment items, thereby being more sensitive to cognitive dysfunction caused by left hemisphere lesions. This trend aligns with AD pathology; therefore, we contend that the MMSE score can more accurately reflect the various stages of AD progression and will play an increasingly crucial role in future research.

In addition, we found that AD can accelerate aging to some extent, and a significant correlation exists between the rate of aging and cognitive assessment scores. This offers new insights into the relationship between AD and aging.

Although our study has made some progress in identifying AD-related brain regions, it is important to acknowledge that there are still several limitations to our current work. First, our interpretability analysis of the model is not yet comprehensive. We employed a 3D convolutional model to extract features from sMRI data for our analysis. In theory, this model is capable of capturing the spatial structure of brain regions as well as the distribution characteristics of the data. However, while we analyzed the gray matter probability distribution characteristics of the brain regions, we did not delve deeply into the spatial structural changes of these regions. Second, in terms of data selection, we primarily relied on sMRI for our study, which has led to some limitations in the functional interpretation of our findings. It is worth noting that structural changes in brain regions are often accompanied by functional changes. Therefore, to gain a more comprehensive understanding of these changes and their relationship with AD, we need to utilize functional magnetic resonance imaging (fMRI) in future studies to explore these brain regions in greater depth. By integrating data from both sMRI and fMRI, we aim to achieve a more complete and accurate understanding, which in turn will provide stronger support for the early diagnosis and treatment of AD.

Conclusions

In this study, we introduced a 3D CNN model with a hybrid attention mechanism for classifying AD and employed sMRI data to perform regression analyses to predict age, MMSE, and CDR scores. This approach aimed to explore the potential connections among MRI data, these two cognitive assessment scales, and aging. Precise localization and visualization of AD lesion areas and brain regions affecting age, MMSE and CDR scores in the MRI were achieved through voxel-based heatmap representations. To further explore the relationship between AD and cognitive assessment scores. Our research has analyzed the relationships between AD, MMSE, and CDR scores based on specific brain regions. It identified key areas closely associated with these conditions, confirming the tight linkage between MMSE and CDR scores and AD pathological status in both an intuitive and a reliable manner. This provides supports for the theoretical basis and technical foundation for using these scores as cognitive assessment and clinical diagnostic tools for AD. Traditional methods have focused primarily on distinguishing AD, with few studies investigating the differences and connections between these assessment scales and the actual degree of AD. Our work has undertaken a systematic and in-depth study of AD, CDR, and MMSE, analyzing the correlations between these medical assessment scales and brain imaging. The classification effect can be achieved with a small amount of selected brain regions’ data, which achieves similar results to using whole-brain data for classification. However, data from other brain regions did not achieve such an effect. This further demonstrates that the selected brain regions are indeed related to both the disease and cognitive assessment scores. Through this work, we have gained a deeper understanding of the relationship between medical assessment scales and the actual degree of AD pathology.

Similarly, we conducted a detailed, brain region-based exploration of the link between AD and aging. By localizing key brain regions associated with aging, we confirmed that aging is closely related to AD and determined that memory impairment is primarily associated with AD. Through the aforementioned work, we have gained a deeper understanding of both aging and AD.

Furthermore, our research has revealed the differential influences of the left and right cerebral hemispheres on their respective tasks. And we discovered asymmetric lesions in the left and right brain regions associated with AD and aging.